Computational Modeling and Empirical Analysis of a Biomass-Powered Drinking Water Pasteurization Technology
Abstract
:1. Introduction
1.1. Thermal Drinking Water Treatment
1.2. Other Water Treatment Processes
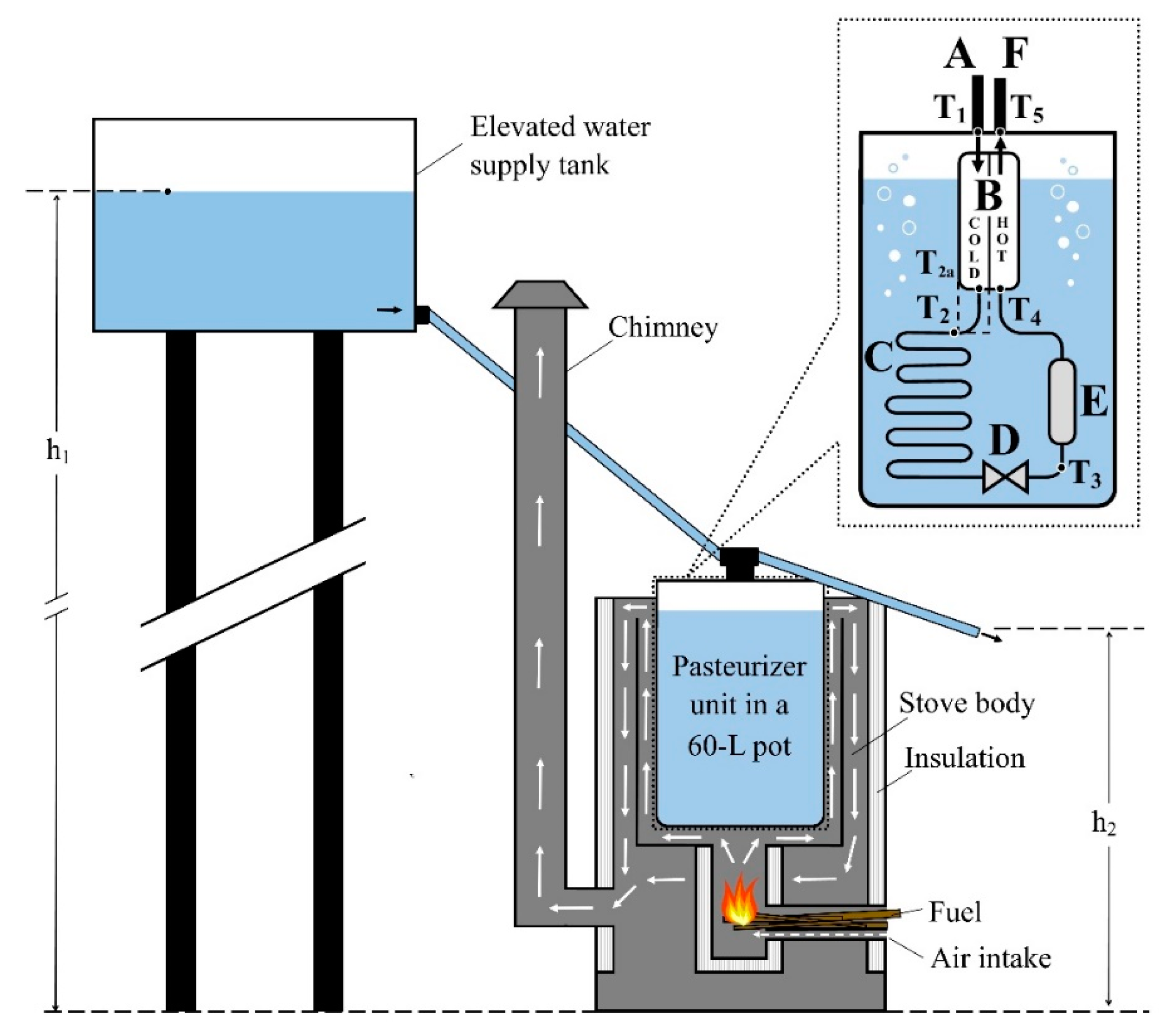
1.3. Water Pasteurizer Design
2. Materials and Methods
2.1. Computational Model
2.2. Empirical Data Collection
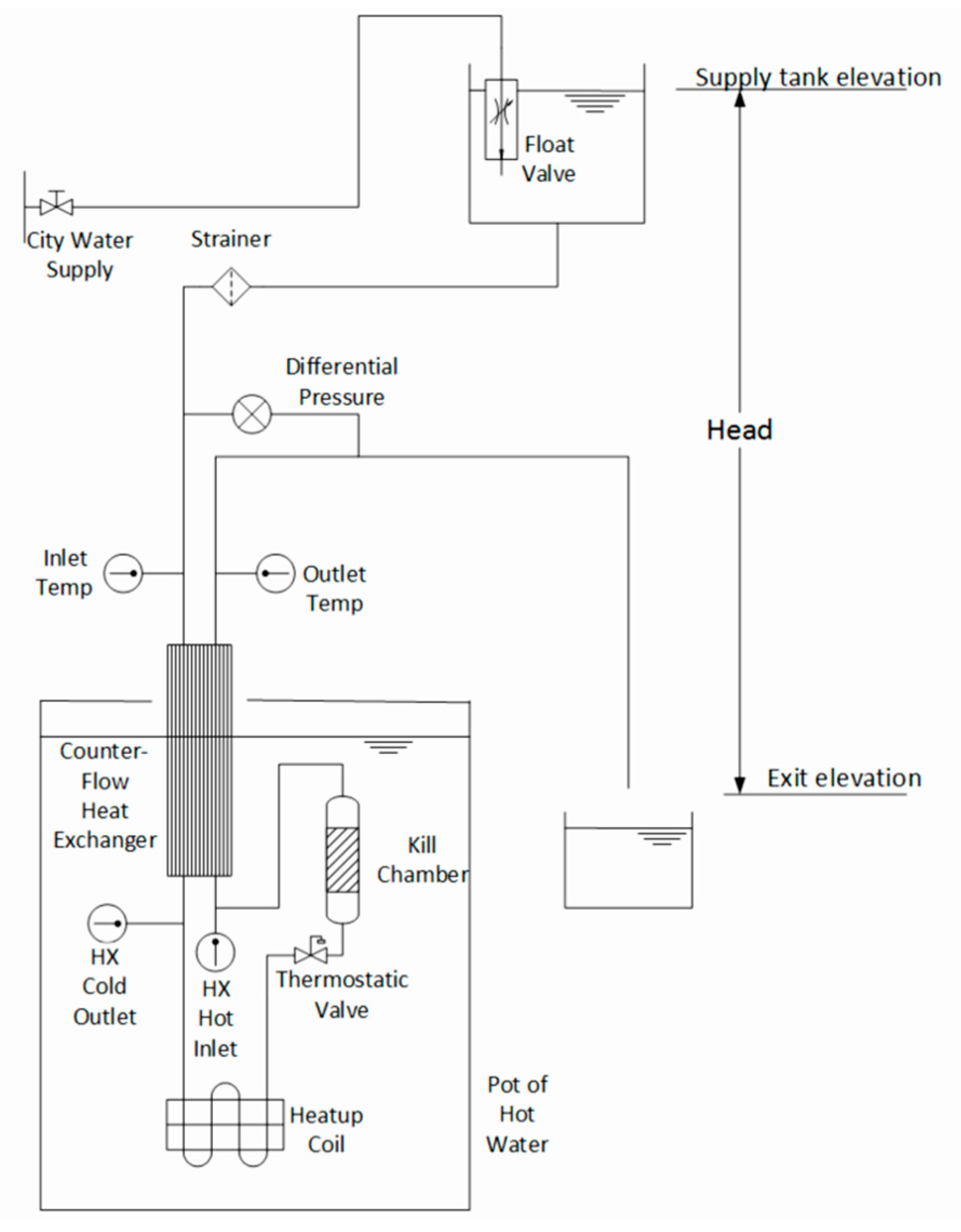
2.2.1. Temperature, Pressure Drop, and Flow Rate
2.2.2. Fuel Usage
2.2.3. Inactivation of Fecal Indicators
3. Results
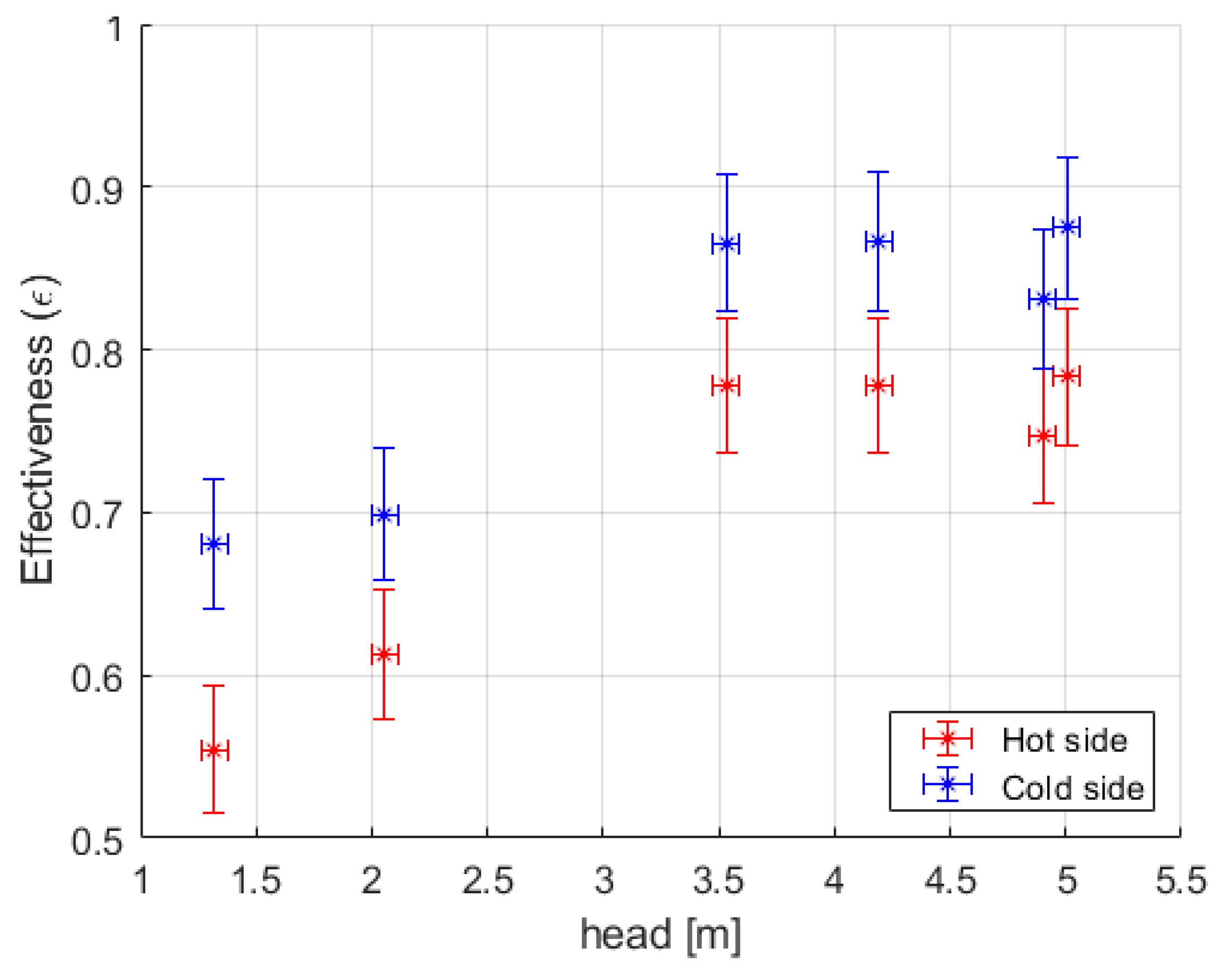
3.1. Heat Exchanger Effectiveness
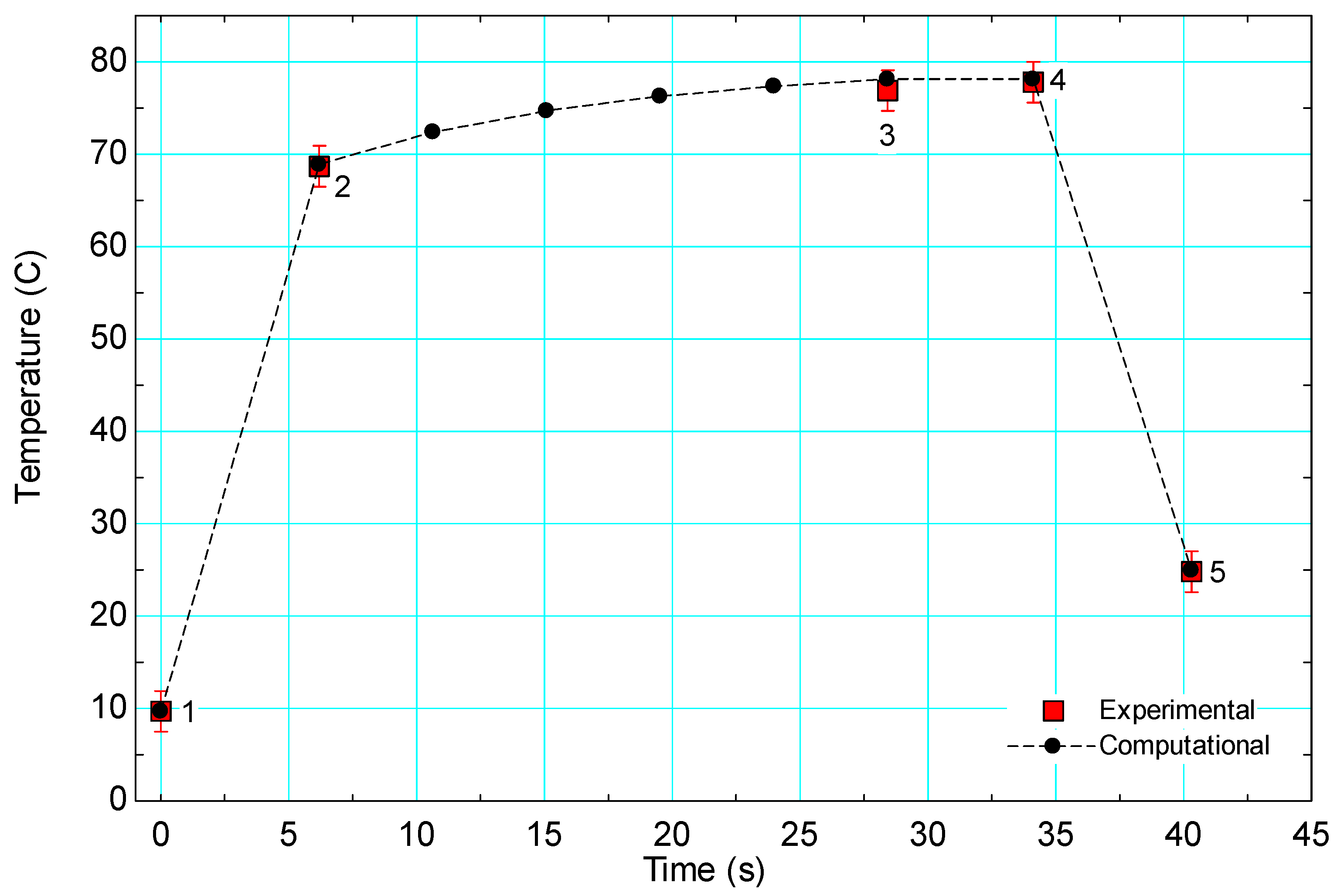
3.2. Model Validation
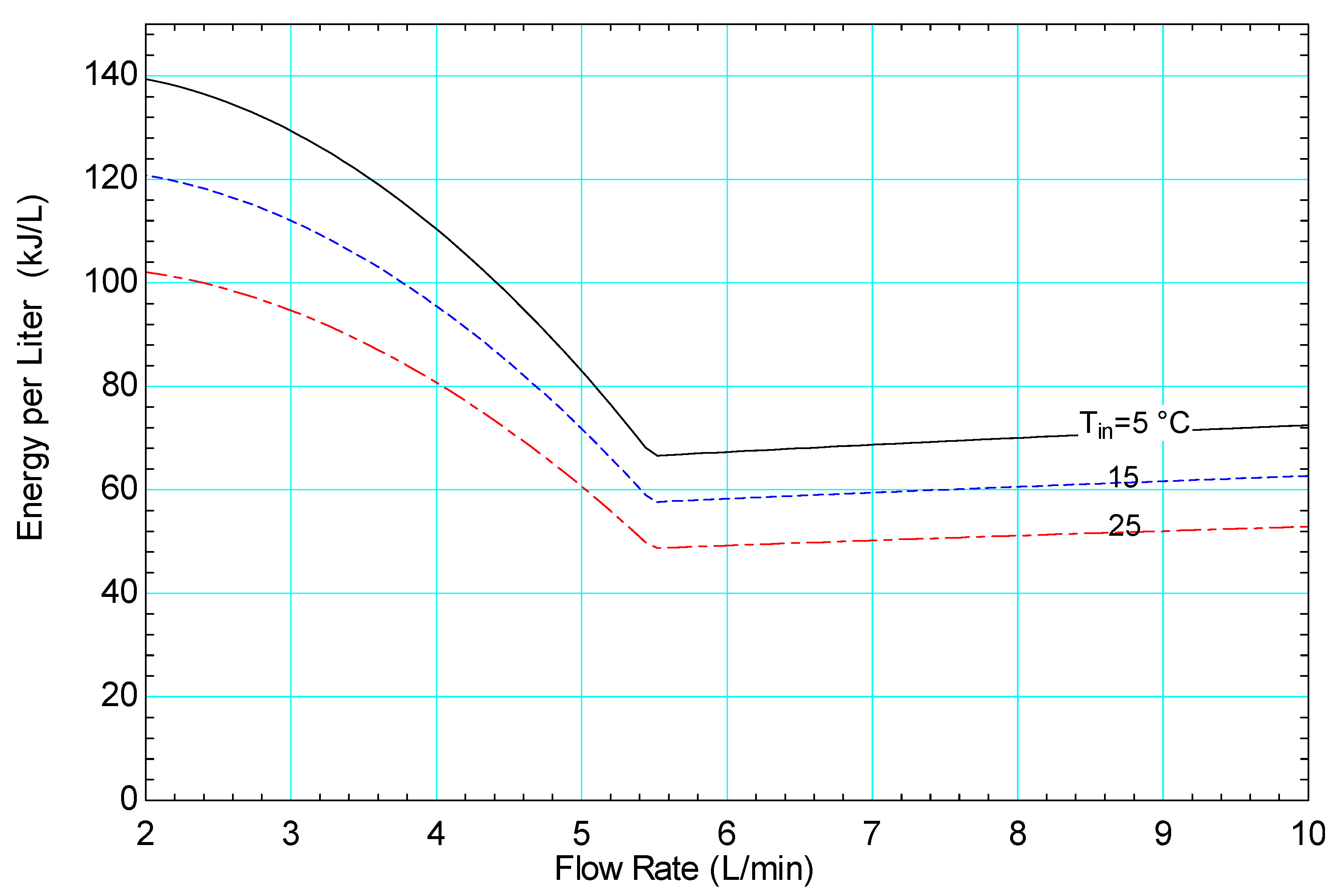
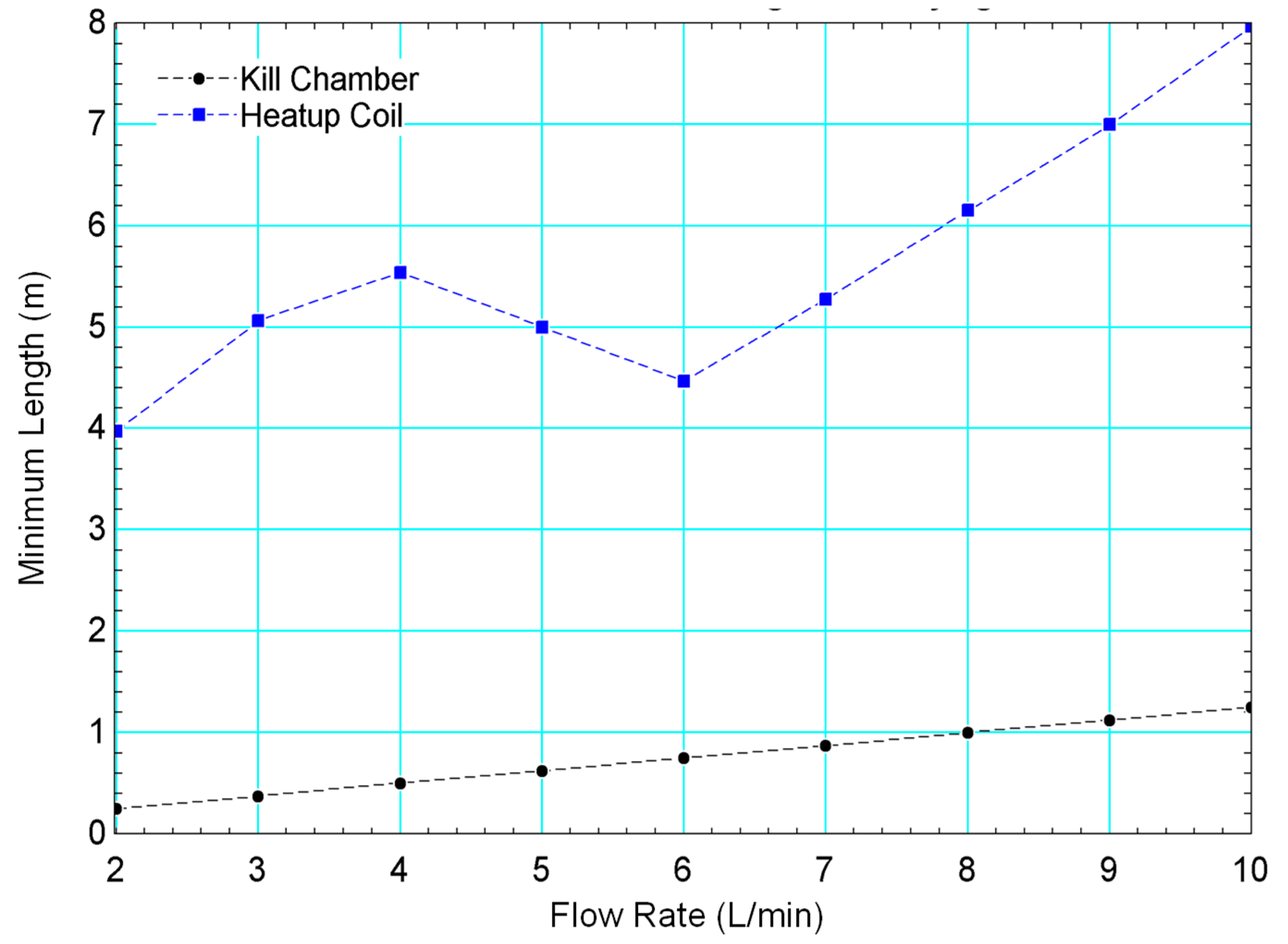
3.3. Computational System Performance
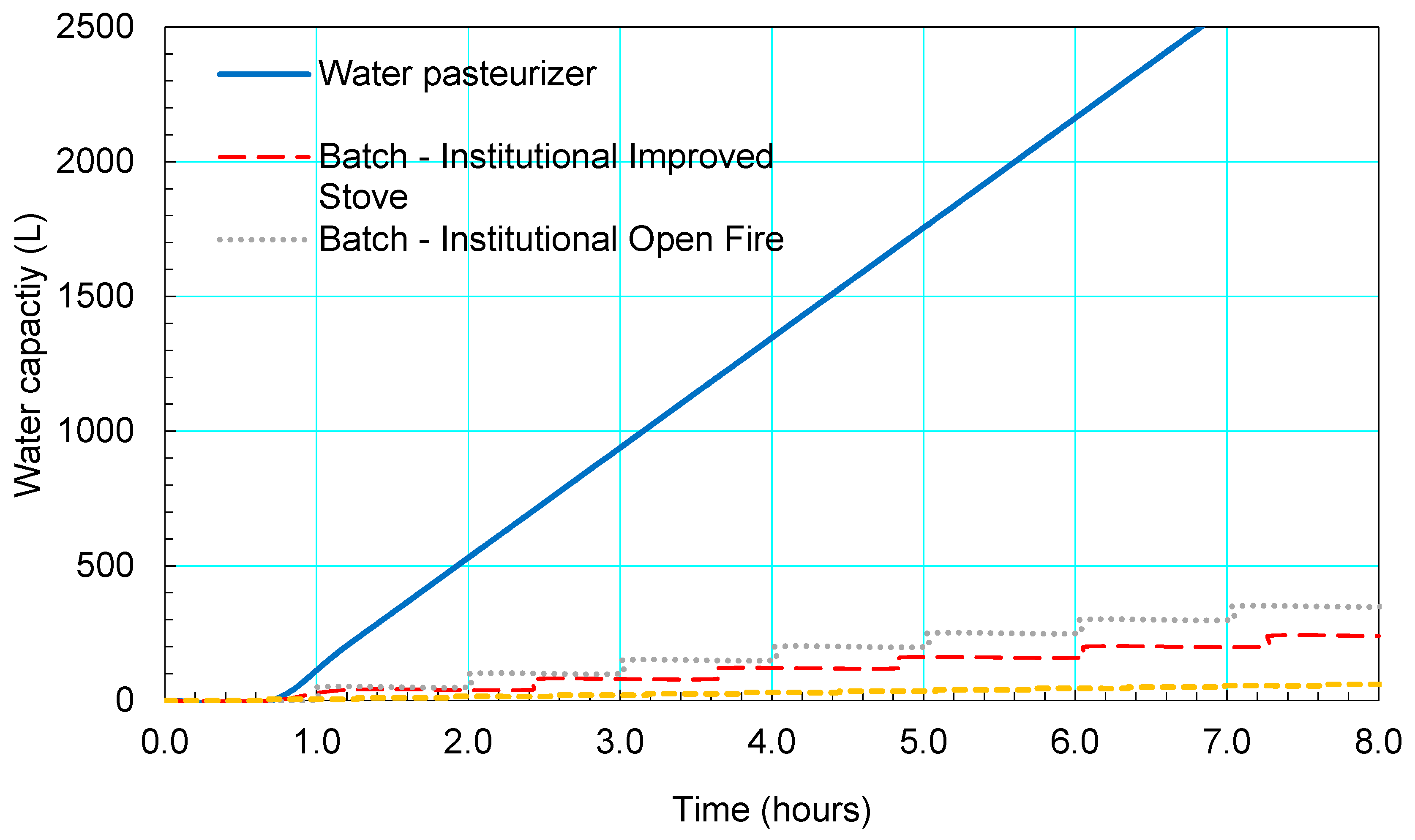
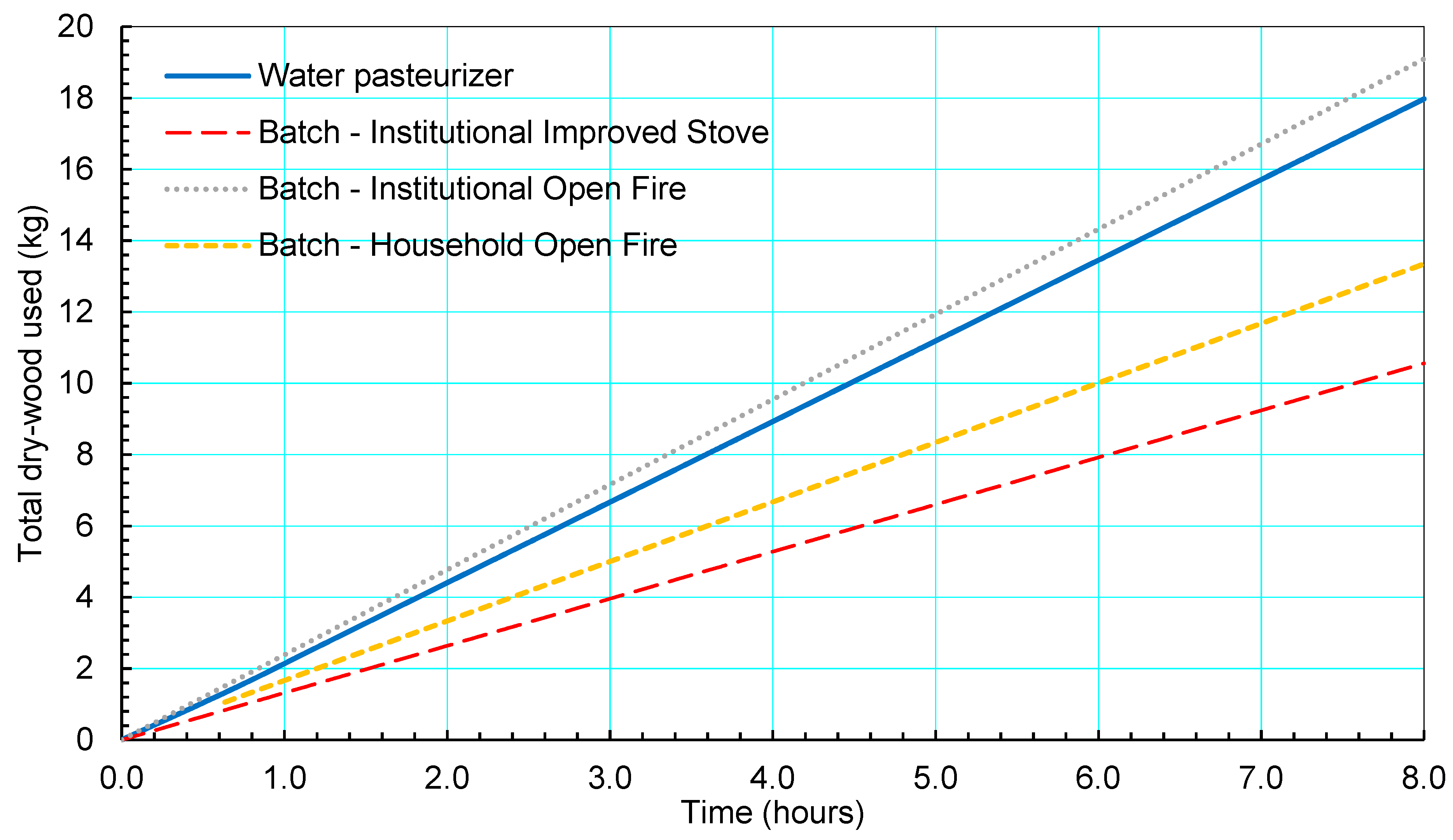
3.4. Fuel Usage
3.5. Inactivation of Fecal Indicators
4. Discussion
4.1. Comparison to Traditional Purification Methods
4.2. Use of the Model to Inform Design and Operation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| A | area |
| DT | D value |
| D | diameter |
| cp | specific heat at constant pressure |
| f | friction factor |
| heat transfer coefficient | |
| h | height |
| k | thermal conductivity |
| mass flow rate | |
| m | mass |
| L | length |
| P | pressure |
| P | perimeter |
| q | heat |
| R | resistance |
| t | time |
| t | thickness |
| T | temperature |
| U | overall heat transfer coefficient |
| V | mean velocity |
| x | distance |
| β | thermal expansion coefficient |
| ε | heat exchanger effectiveness |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Ra | Rayleigh number |
| Subscripts | |
| atm | atmospheric |
| c | cold |
| cond | conduction |
| h | hot |
| i | inner |
| kill | kill by maintaining at required temperature for required time |
| o | outer |
| s | surface |
| LM | log-mean |
| pot | stockpot |
Appendix A. Heat Transfer Model
| Geometrical Parameters | Operational Parameters | ||
|---|---|---|---|
| Do,coil | 12.7 mm | Elevation | 0 m |
| tcoil | 0.63 mm | Tpot | 80 °C |
| Lcoil | 15.24 m | Tin | 10 °C |
| Do,kill | 53.85 mm | Tpasteurize | 71 °C |
| tkill | 1.7 mm | ||
| Lkill | 0.305 m | ||
Appendix A.1. Overall System
Appendix A.2. Heat Exchanger
Appendix A.3. Heating Coil and Kill Chamber

References
- Burch, J.D.; Thomas, K.E. Water disinfection for developing countries and potential for solar thermal pasteurization. Sol. Energy 1998, 64, 87–97. [Google Scholar] [CrossRef]
- WHO. Progress on Household Drinking Water, Sanitation and Hygiene 2000–2017: Special Focus on Inequalities. 2019. Available online: https://washdata.org/reports (accessed on 9 June 2018).
- Ojomo, E.; Elliott, M.; Goodyear, L.; Forson, M.; Bartram, J. Sustainability and scale-up of household water treatment and safe storage practices: Enablers and barriers to effective implementation. Int. J. Hyg. Environ. Health 2015, 218, 704–713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- WHO. Household Water Treatment and Safe Storage Technologies. 2007. Available online: http://www.wpro.who.int/environmental_health/documents/docs/Household_Water_Treatment_Safe_Storage_PARTICIPANT.pdf (accessed on 9 June 2018).
- WHO. Guidelines for Drinking-Water Quality: Fourth Edition Incorporating the First Addendum; World Health Organ: Geneva, Switzerland, 2017. [Google Scholar]
- Macdougall, P.; Milburn, M.P. Using solar energy to treat microbiologically contaminated water: A multidisciplinary approach to public health and aboriginal science education. Environ. Health Rev. 2004, 38–43. [Google Scholar]
- Okpara, C.G.; Oparaku, N.F.; Ibeto, C.N. An overview of water disinfection in developing countries and potentials of renewable energy. J. Environ. Sci. Technol. 2011, 4, 18–30. [Google Scholar] [CrossRef] [Green Version]
- MacCarty, N.; Still, D.; Ogle, D. Fuel use and emissions performance of fifty cooking stoves in the laboratory and related benchmarks of performance. Energy Sustain. Dev. 2010, 14, 161–171. [Google Scholar] [CrossRef]
- Olago, D.; Marshall, M.; Wandiga, S.O. Climatic, socio-economic, and health factors affecting human vulnerability to cholera in the Lake Victoria basin. East Africa Ambio 2007, 36, 350–358. [Google Scholar] [CrossRef]
- Psutka, R.; Peletz, R.; Michelo, S.; Kelly, P.; Clasen, T. Assessing the microbiological performance and potential cost of boiling drinking water in urban Zambia. Environ. Sci. Technol. 2011, 45, 6095–6101. [Google Scholar] [CrossRef] [Green Version]
- Hornsey, I.S. The History of Beer and Brewing; Royal Society of Chemistry: London, UK, 2004. [Google Scholar]
- Madigan, M.T.; Martinko, J.M.; Stahl, D.A.; Clark, D.P. Brock Biology of Microorganisms; Benjamin Cummings: San Fransisco, CA, USA, 2012. [Google Scholar] [CrossRef]
- Ray, C. Drinking Water Treatment Focusing on Appropriate Technology and Sustainability; Springer Publishing Company: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Spinks, A.T.; Dunstan, R.H.; Harrison, T.; Coombes, P.; Kuczera, G. Thermal inactivation of water-borne pathogenic and indicator bacteria at sub-boiling temperatures. Water Res. 2006, 40, 1326–1332. [Google Scholar] [CrossRef]
- Osaili, T.; Griffis, C.L.; Martin, E.M.; Beard, B.L.; Keener, A.; Marcy, J.A. Thermal inactivation studies of Escherichia coli O157:H7, Salmonella, and Listeria monocytogenes in ready-to-eat chicken-fried beef patties. J. Food Prot. 2006, 69, 1080–1086. [Google Scholar] [CrossRef]
- Thermal Inactivation of Viruses. 1977. Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a048068.pdf (accessed on 9 June 2018).
- WHO. Technical Brief: Boil Water. 2011. Available online: http://www.who.int/water_sanitation_health/dwq/Boiling_water_01_15.pdf (accessed on 9 June 2018).
- Harp, J.A.; Fayer, R.; Pesch, B.A.; Jackson, G. Effect of pasteurization on infectivity of Cryptosporidium parvum oocysts in water and milk. Appl. Environ. Microbiol. 1996, 62, 2866–2868. [Google Scholar] [CrossRef] [Green Version]
- Laurent, P. Household Drinking Water Systems and Their Impact on People with Weakened Immunity, World Health Organ. 2005. Available online: http://www.who.int/household_water/research/HWTS_impacts_on_weakened_immunity.pdf (accessed on 9 June 2018).
- Kim, B.R.; Anderson, J.E.; Mueller, S.A.; Gaines, W.A.; Kendall, A.M. Literature review—Efficacy of various disinfectants against Legionella in water systems. Water Res. 2002, 36, 4433–4444. [Google Scholar] [CrossRef]
- Lin, Y.E.; Stout, J.E.; Yu, V.L.; Vidic, R.D. Disinfection of water distribution systems for Legionella. Semin. Respir. Infect. 1998, 13, 147–159. [Google Scholar] [PubMed]
- Thirugnanasambandam, M.; Iniyan, S.; Goic, R. A review of solar thermal technologies. Renew. Sustain. Energy Rev. 2010, 14, 312–322. [Google Scholar] [CrossRef]
- Islam, M.F.; Johnston, R.B. Household pasteurization of drinking water: The Chulli Water-Treatment System. J. Health Popul. Nutr. 2006, 24, 356–362. [Google Scholar]
- Gupta, S.K.; Islam, M.S.; Johnston, R.; Ram, P.K.; Luby, S.P. The Chulli Water Purifier: Acceptability and effectiveness of an innovative strategy for household water treatment in Bangladesh. Am. J. Trop. Med. Hyg. 2008, 78, 979–984. [Google Scholar] [CrossRef] [Green Version]
- Stauber, C.E.; Elliott, M.A.; Koksal, F.; Ortiz, G.M.; DiGiano, F.A.; Sobsey, M.D. Characterisation of the biosand filter for E. coli reductions from household drinking water under controlled laboratory and field use conditions. Water Sci. Technol. 2006, 54, 1. [Google Scholar] [CrossRef] [Green Version]
- Stauber, C.E.; Ortiz, G.M.; Loomis, D.P.; Sobsey, M.D. A randomized controlled trial of the concrete biosand filter and its impact on diarrheal disease in Bonao, Dominican Republic. Am. J. Trop. Med. Hyg. 2009, 80, 286–293. [Google Scholar] [CrossRef]
- Kikkawa, I. Modification of a Biosand Filter in the Northern Region of Ghana. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2008. [Google Scholar]
- Duke, W.F.; Nordin, R.N.; Baker, D.; Mazumder, A. The use and performance of BioSand filters in the Artibonite Valley of Haiti: A field study of 107 households. Rural Remote Health 2006, 6, 570. [Google Scholar]
- Ngai, T.K.K.; Coff, B.; Baker, D.; Lentz, R. Global Review of the Adoption, Use, and Performance of the Biosand Filter. In Progess in Slow Sand and Alternative Biofiltration Processes; Nakamoto, N., Graham, N., Collins, M.R., Gimbel, R., Eds.; IWA Publishing: London, UK, 2014; pp. 309–317. [Google Scholar]
- Loo, S.-L.; Fane, A.G.; Krantz, W.B.; Lim, T.-T. Emergency water supply: A review of potential technologies and selection criteria. Water Res. 2012, 46, 3125–3151. [Google Scholar] [CrossRef]
- Thompson, M. A critical review of water purification technology appropriate for developing countries: Northern Ghana as a case study. Desalin. Water Treat. 2015, 54, 3487–3493. [Google Scholar] [CrossRef]
- Sobsey, M.D.; Stauber, C.E.; Casanova, L.M.; Brown, J.M.; Elliott, M.A. Point of use household drinking water filtration: A practical, effective solution for providing sustained access to safe drinking water in the developing world. Environ. Sci. Technol. 2008, 42, 4261–4267. [Google Scholar] [CrossRef] [PubMed]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- MacCarty, N.; Burleson, G.; Moses, N.; Johnson, J.; Andreyka, E.; Ogle, D.; Colgan, F.; Creighton, A.; Carter, T.; Andreatta, D. Design and testing of a high-efficiency rapid throughput community-scale water pasteurization system. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Cheremisinoff, N. Properties of Wood: Wood for Energy Production; Ann Arbor Science Publishers: Ann Arbor, MI, USA, 1980. [Google Scholar]
- US-EPA. National Primary Drinking Water Regulations. 2018. Available online: https://www.epa.gov/ground-water-and-drinking-water/national-primary-drinking-water-regulations (accessed on 9 Jun 2018).
- WHO. Guidelines for Drinking-Water Quality, 4th ed.; WHO: Geneva, Switzerland, 2017; pp. 117–153. ISBN 978 92 4 154815 1. [Google Scholar]
- Jetter, J.; Ebersviller, S.; Williams, C.; Faircloth, J. Test Report: InStove 60-Liter Institutional Stove with Wood Fuel, U.S Environ. prot. Agency. 2016. Available online: http://www.instove.org/sites/default/files/InStove%25test%25report.pdf (accessed on 9 June 2018).
- Burleson, G.; Tilt, B.; Sharp, K.; MacCarty, N. Reinventing boiling: A rapid ethnographic and engineering evaluation of a high-efficiency thermal water treatment technology in Uganda. Energy Res. Soc. Sci. 2019, 52, 68–77. [Google Scholar] [CrossRef]
- Global Alliance for Clean Cookstoves. The Water Boiling Test Version 4.2.3. 2014. Available online: http://cleancookstoves.org/technology-and-fuels/testing/protocols.html (accessed on 9 June 2018).
- International Organization for Standardization. International Workshop Agreement 11: 2012 Guidelines for Evaluating Cookstove Performance, IWA 11 2012. Available online: http://www.iso.org/iso/catalogue_detail?csnumber=61975 (accessed on 9 June 2018).





| Method. | Advantages | Disadvantages | Cost |
|---|---|---|---|
| Filtration | Various types and sizes (sand, charcoal, ceramic, etc.); effective in many geographic or weather conditions | Prone to failure due to lack of maintenance; some types lack indicator; some require chlorination; risk of recontamination | >$0.001/L |
| Chlorination | Easy to use; lowers risk of recontamination; effective in any geographic or weather condition | Requires precise does; requires ongoing supply of chlorine; distasteful; can be effected by turbidity; lacks indicator | >$0.001/L |
| Solar UV Treatment | Reusable; typically portable; minimal maintenance required | Requires indicator; requires sufficient sunlight; relatively slow; water must be cooled to usable temperatures; risk of recontamination | >$0.001/L |
| Boiling | Accessible; visual indicator; effective in many geographic or weather conditions | High energy use; high emissions; water must be cooled to usable temperatures; timely; risk of recontamination | >$0.10/L |
| Solar Pasteurization | Reusable; sustainable | Requires indicator; requires sufficient sunlight; relatively slow; low capacity; risk of recontamination | <$0.001/L |
| Biomass Pasteurization | Efficient use of local resources; large capacity; effective in many geographic or weather conditions; high flowrate | Requires indicator; risk of recontamination | <$0.01/L |
| Parameters | Equations | Values Measured | Sensors Used |
|---|---|---|---|
| Heat exchanger effectiveness () | HX cold inlet temp HX cold outlet temp HX hot inlet temp HX hot outlet temp | Type-K thermocouples | |
| Flow rate () | Mass of water, time | Hanging scale, stopwatch | |
| Pressure drop | Directly measured | Differential pressure | Differential pressure transducer |
| Supplied head | Supply water level height, Outlet hose exit height | Measuring tape |
| Flow Rate (L/min) | Texperimental−Tpredicted at Each Location (°C) | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 2.20 | 0.00 | −0.20 | 0.50 | −0.30 | −0.13 |
| 3.61 | 0.50 | 0.63 | 1.64 | 0.64 | 0.63 |
| 6.06 | 0.30 | −0.34 | 0.17 | −0.63 | 0.06 |
| 6.43 | 0.30 | −0.26 | 0.67 | −0.23 | 0.27 |
| 6.20 | 0.40 | 2.80 | 1.19 | 0.29 | −1.70 |
| 5.48 | 0.20 | 1.03 | 1.90 | 1.10 | 0.52 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burleson, G.; Caplan, D.; Mays, C.; Moses, N.; Navab-Daneshmand, T.; Sharp, K.; MacCarty, N. Computational Modeling and Empirical Analysis of a Biomass-Powered Drinking Water Pasteurization Technology. Energies 2020, 13, 936. https://doi.org/10.3390/en13040936
Burleson G, Caplan D, Mays C, Moses N, Navab-Daneshmand T, Sharp K, MacCarty N. Computational Modeling and Empirical Analysis of a Biomass-Powered Drinking Water Pasteurization Technology. Energies. 2020; 13(4):936. https://doi.org/10.3390/en13040936
Chicago/Turabian StyleBurleson, Grace, Daniel Caplan, Catherine Mays, Nicholas Moses, Tala Navab-Daneshmand, Kendra Sharp, and Nordica MacCarty. 2020. "Computational Modeling and Empirical Analysis of a Biomass-Powered Drinking Water Pasteurization Technology" Energies 13, no. 4: 936. https://doi.org/10.3390/en13040936





