Improvement in Voltage Gain of Interleaved High Step-Down Converter
Abstract
1. Introduction
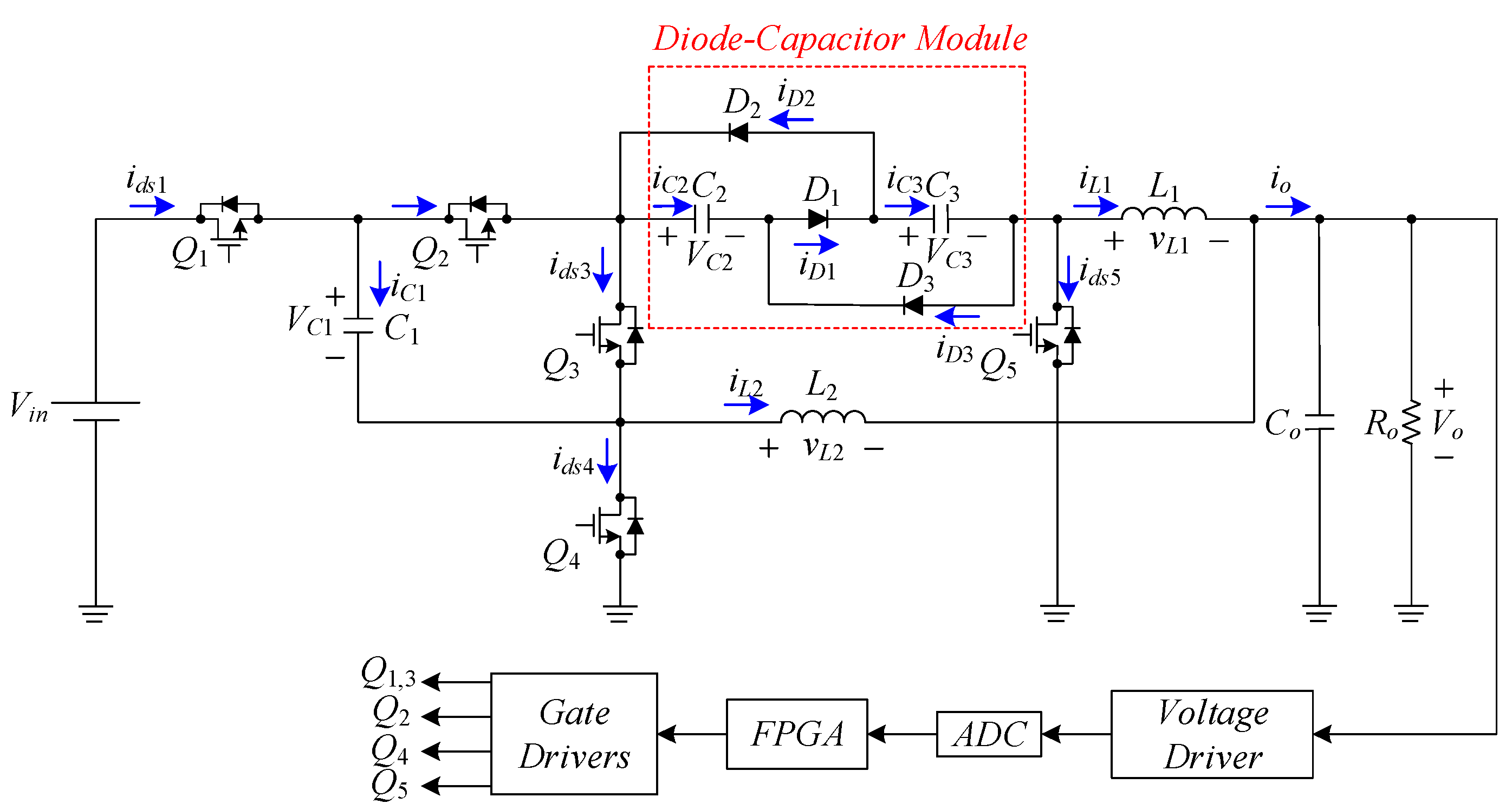
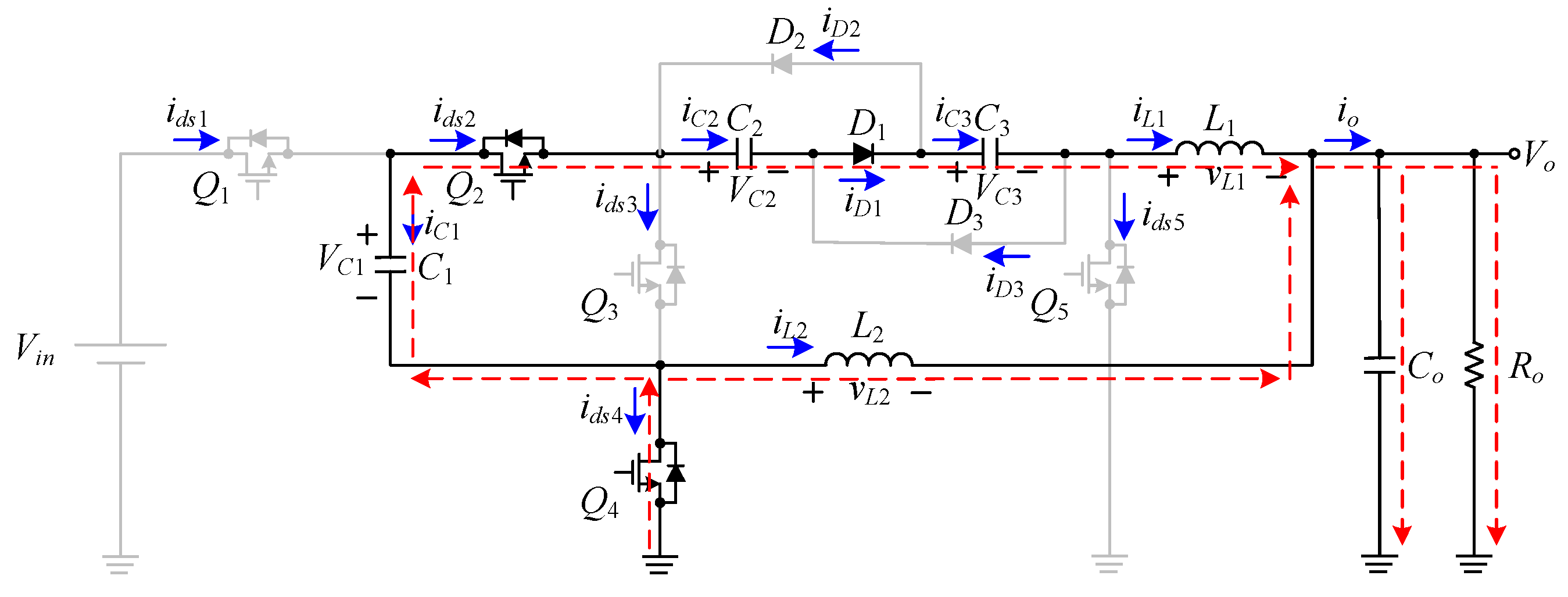
2. Basic Operating Principles
- (1)
- The input voltage is signified by Vin and the output is denoted by Vo.
- (2)
- The values of the capacitors C1, C2, and C3 are large enough such that the voltages across them can be regarded as some constant values.
- (3)
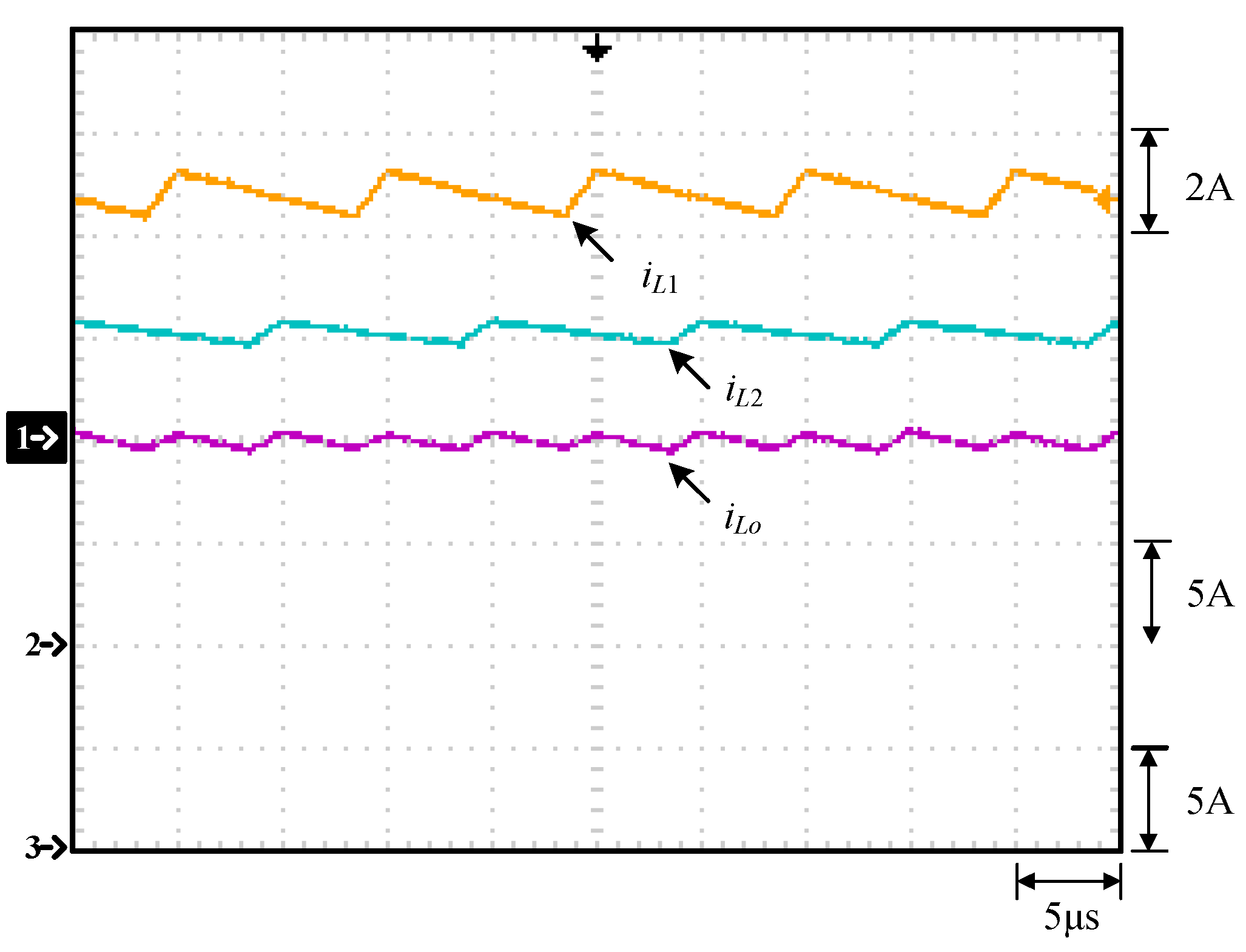
- The currents in Q1, Q2, Q3, Q4, and Q5 are expressed by ids1, ids2, ids3, ids4, and ids5, respectively; the currents in C1, C2, and C3 are represented by iC1, iC2, and iC3, respectively; the currents in L1 and L2 are indicated by iL1 and iL2, respectively; the current iLo is the sum of iL1 and iL2; the currents in D1, D2, and D3 are signified by iD1, iD2, and iD3, respectively; the current Ro is expressed by Io.
- (4)
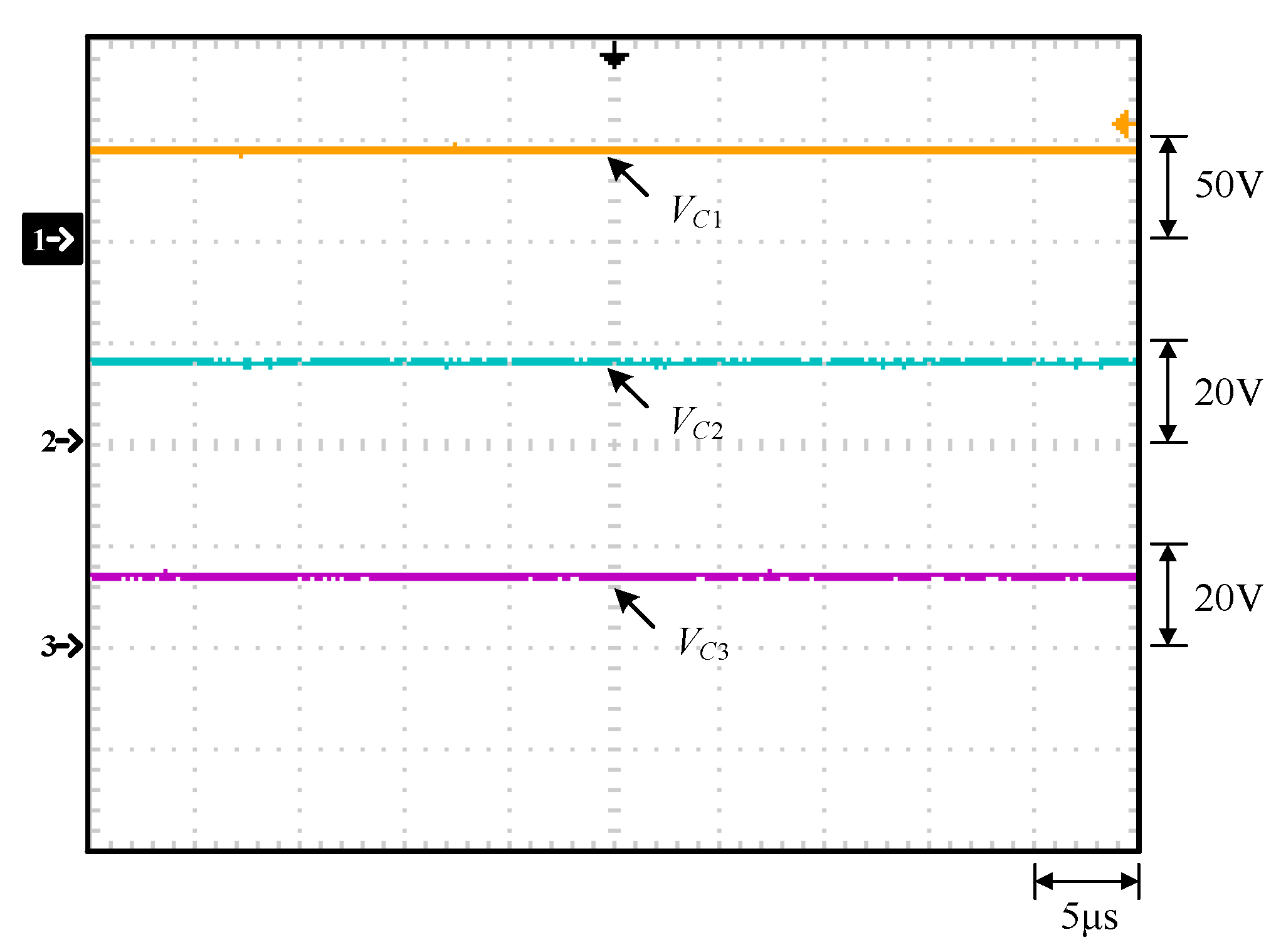
- The voltages on L1 and L2 are denoted by vL1 and vL2, respectively; the voltages on C1, C2, and C3 are expressed by VC1, VC2, and VC3, respectively; the voltage across Co is represented by Vo.
- (5)
- The switching period and frequency are indicated by Ts and fs, respectively.
- (6)
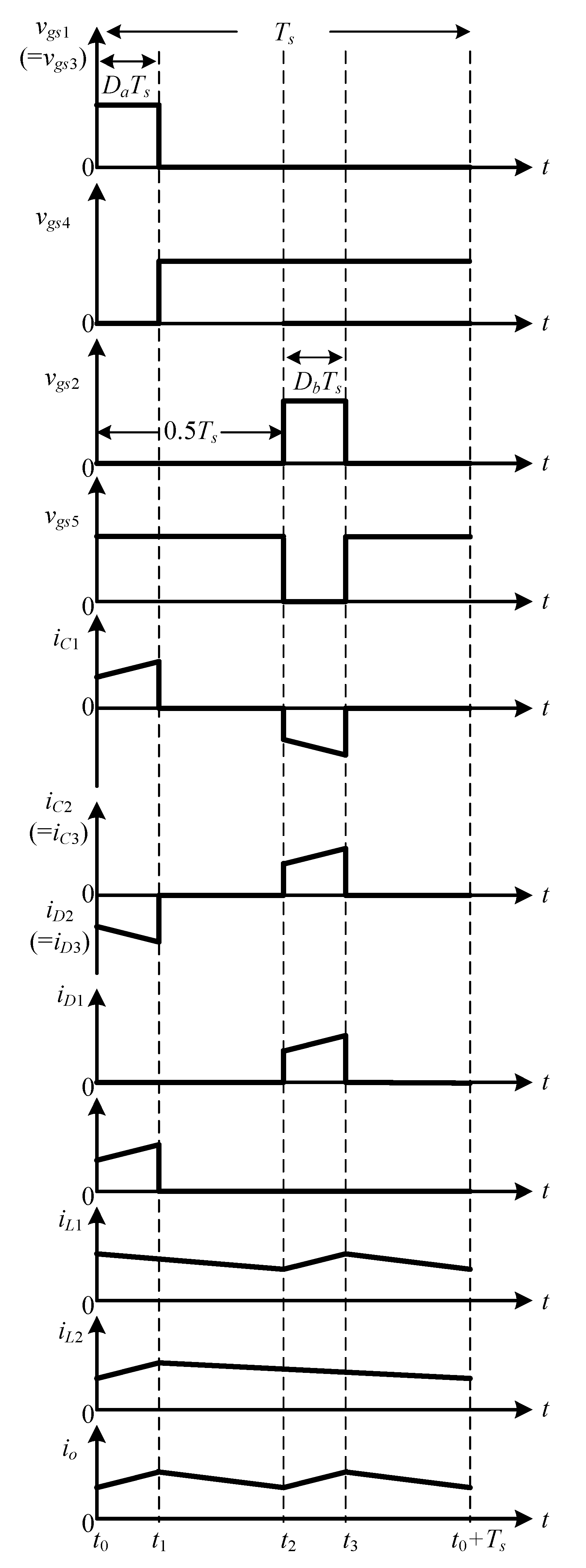
- The gate driving signals for Q1, Q2, Q3, Q4, and Q5 are denoted by vgs1, vgs2, vgs3, vgs4, and vgs5, respectively. Furthermore, vgs1 is in phase with vgs3 but is complimentary to vgs4, whereas vgs2 is complimentary to vgs5 and is shifted by 180o from vgs1. In addition, the duty cycle of vgs1 is Da, the duty cycle of vgs2 is Db and Da = Db = D.
- (7)
- Because the proposed circuit operates in the continuous conduction mode (CCM), there are four operating states over one switching period as shown in Figure 2.
2.1. Basic Operating Principles
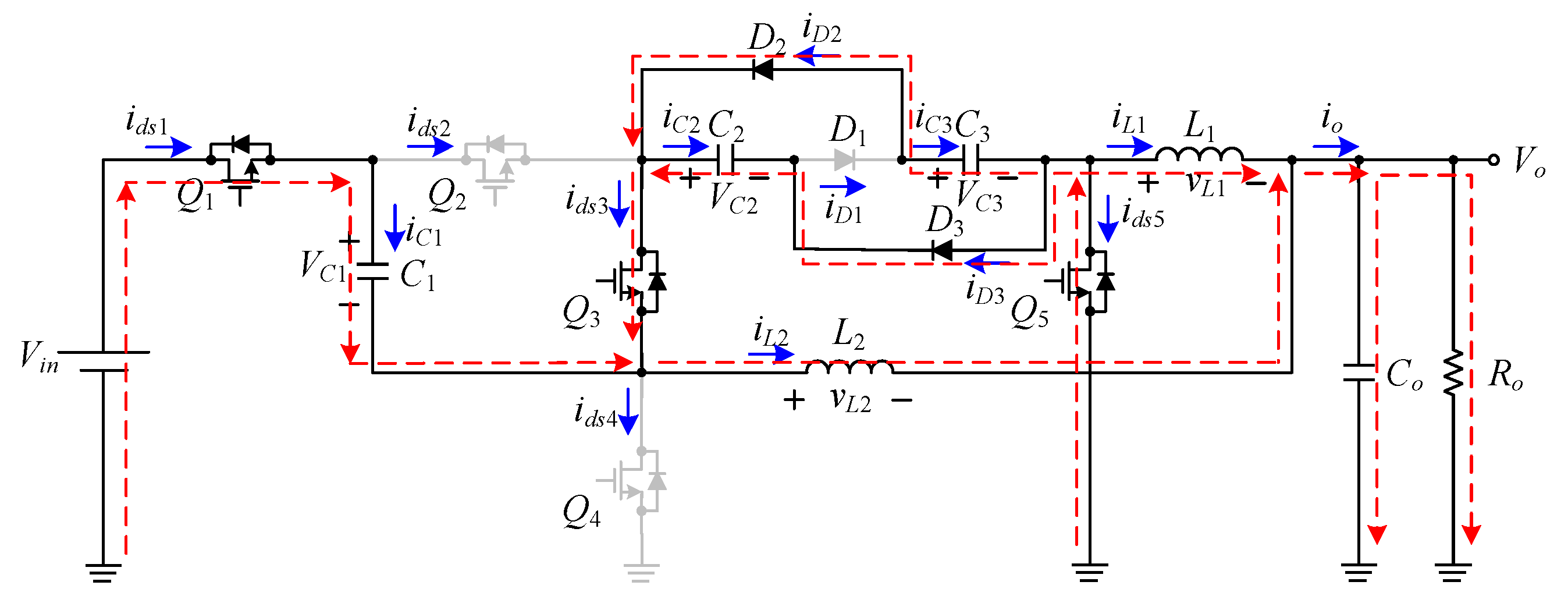
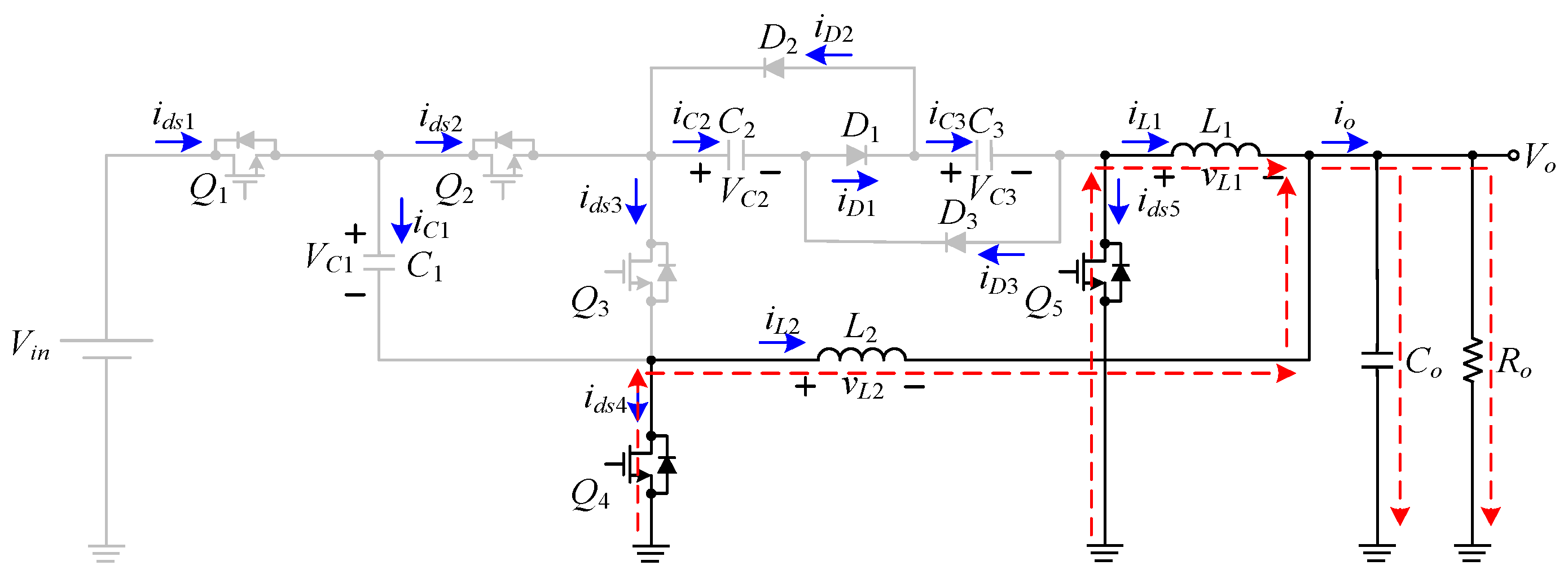
2.1.1. State 1:
2.1.2. States 2 and 4:
2.1.3. State 3:
2.2. Voltage Gain
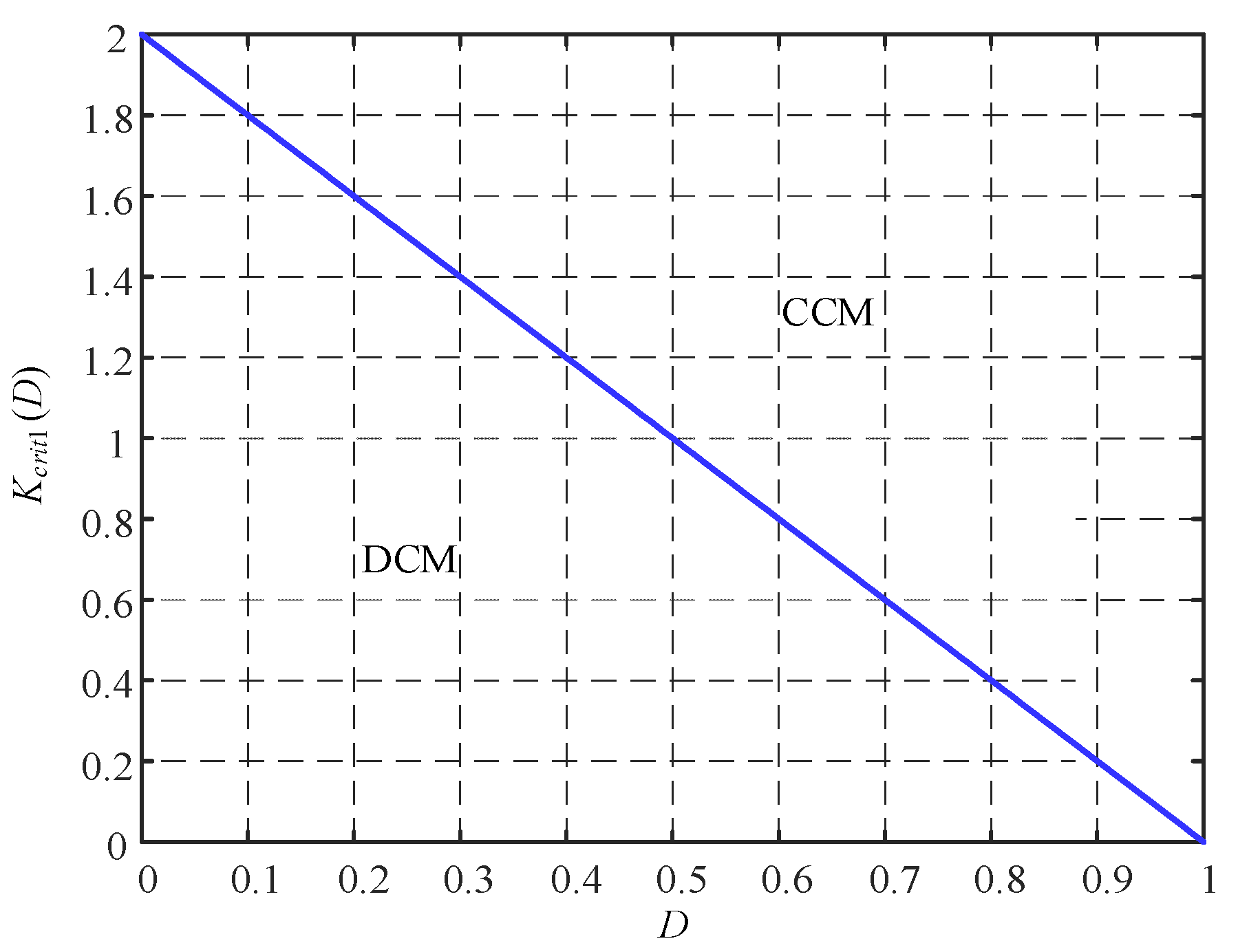
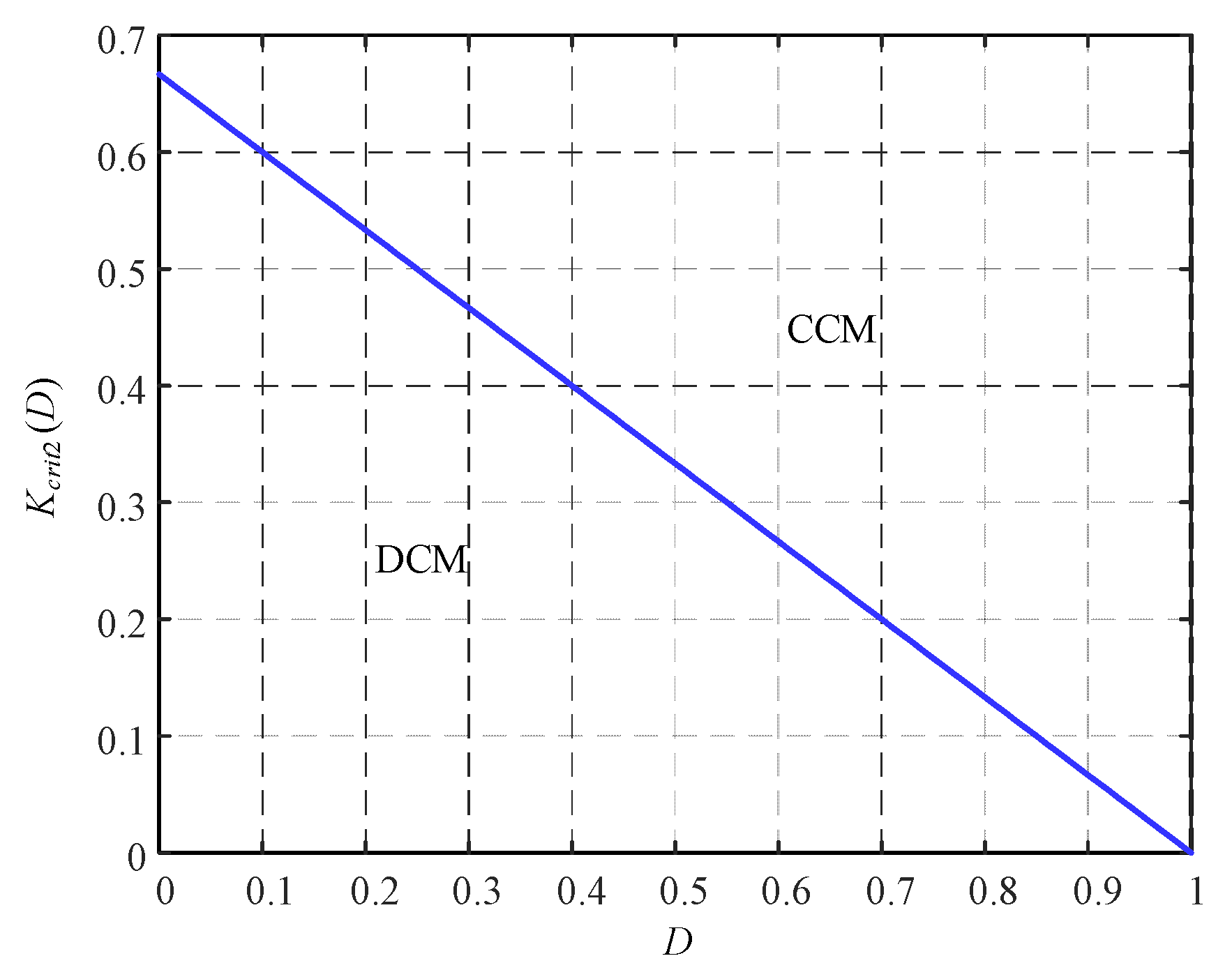
2.3. Boundary Conditions of L1 and L2
2.3.1. BCM Curve of L1
2.3.2. BCM Curve of L2
2.4. Circuit Comparison
3. Design Considerations
3.1. Design of Inductors L1 and L2
3.2. Design of Energy-Transferring Capacitors C1 to C3
3.3. Design of Output Capacitor Co
4. System Control Strategy
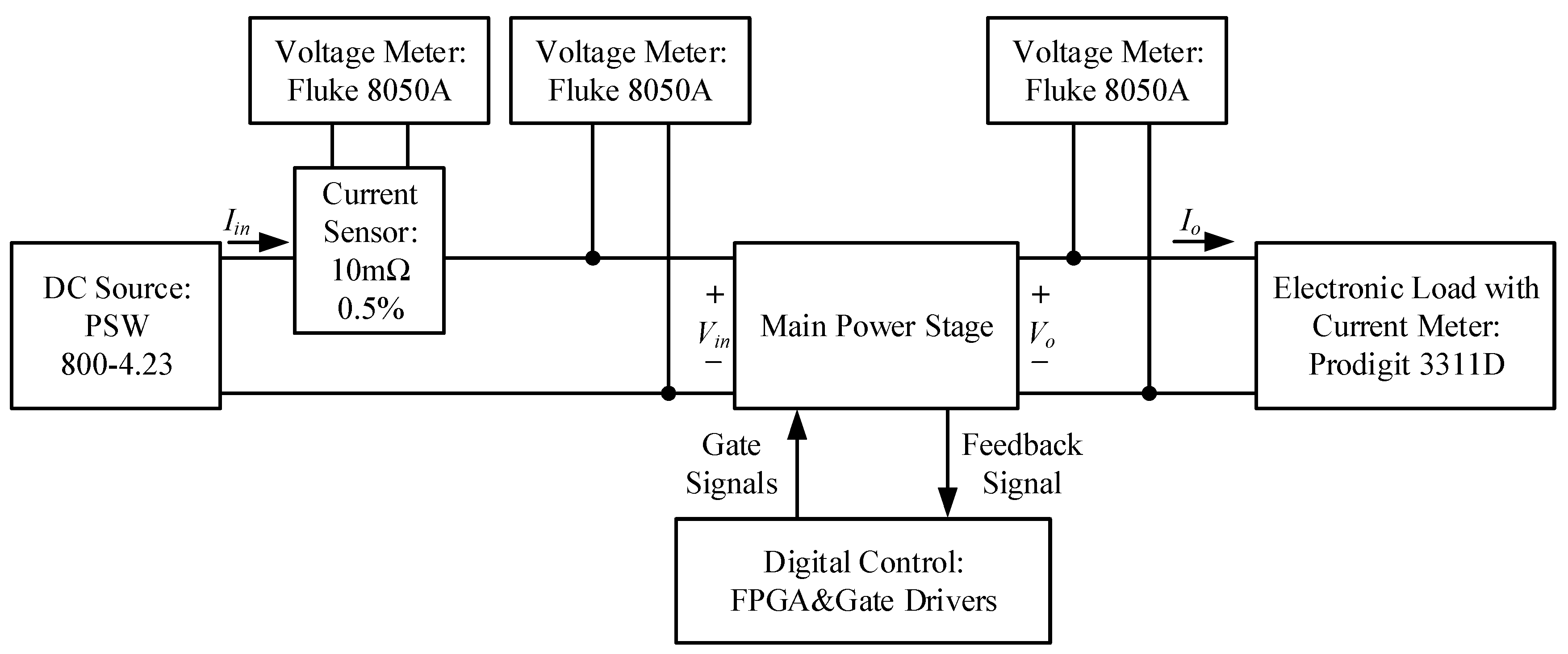
5. Experimental Results
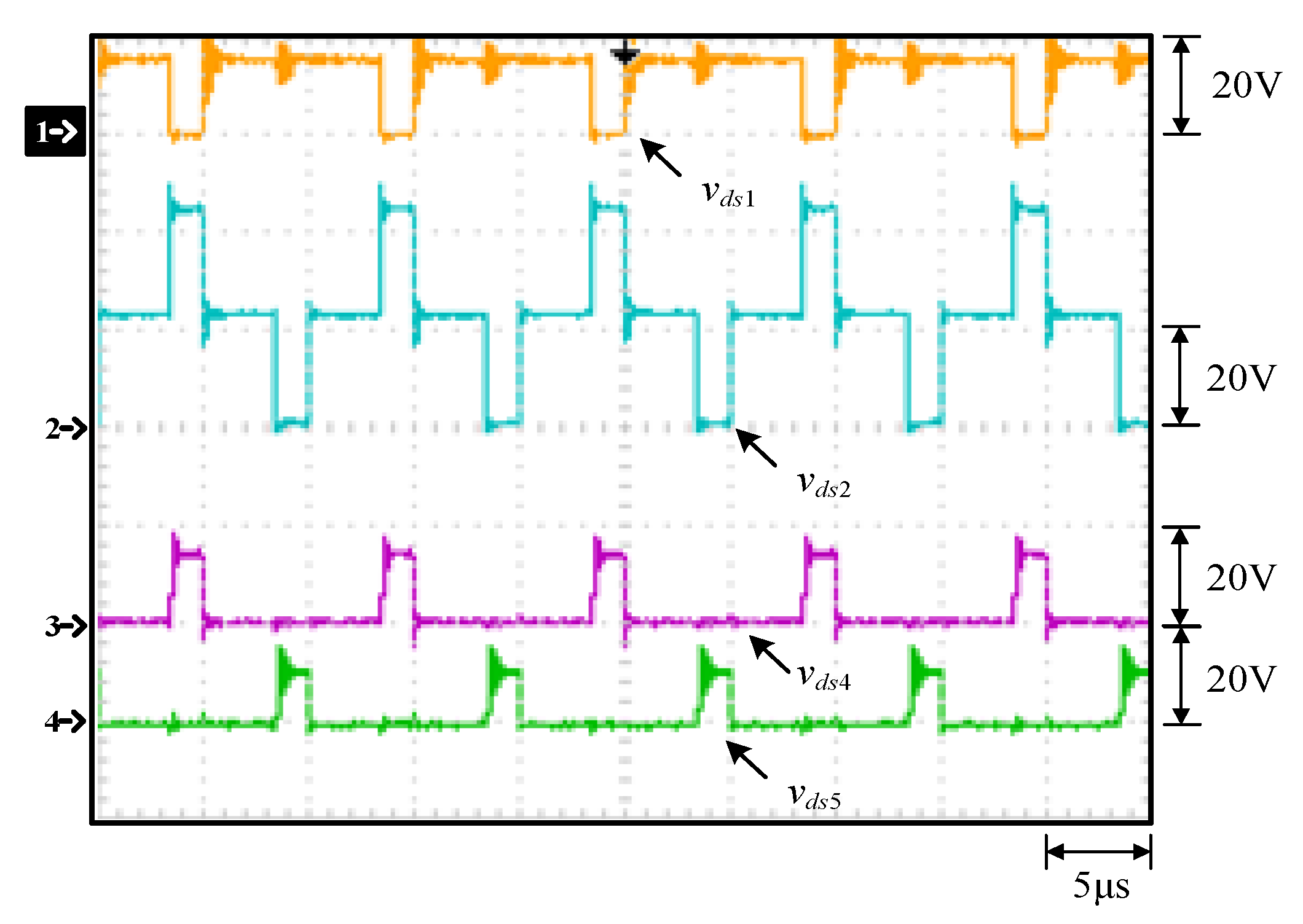
5.1. Measured Waveforms
5.2. Efficiency Measurement
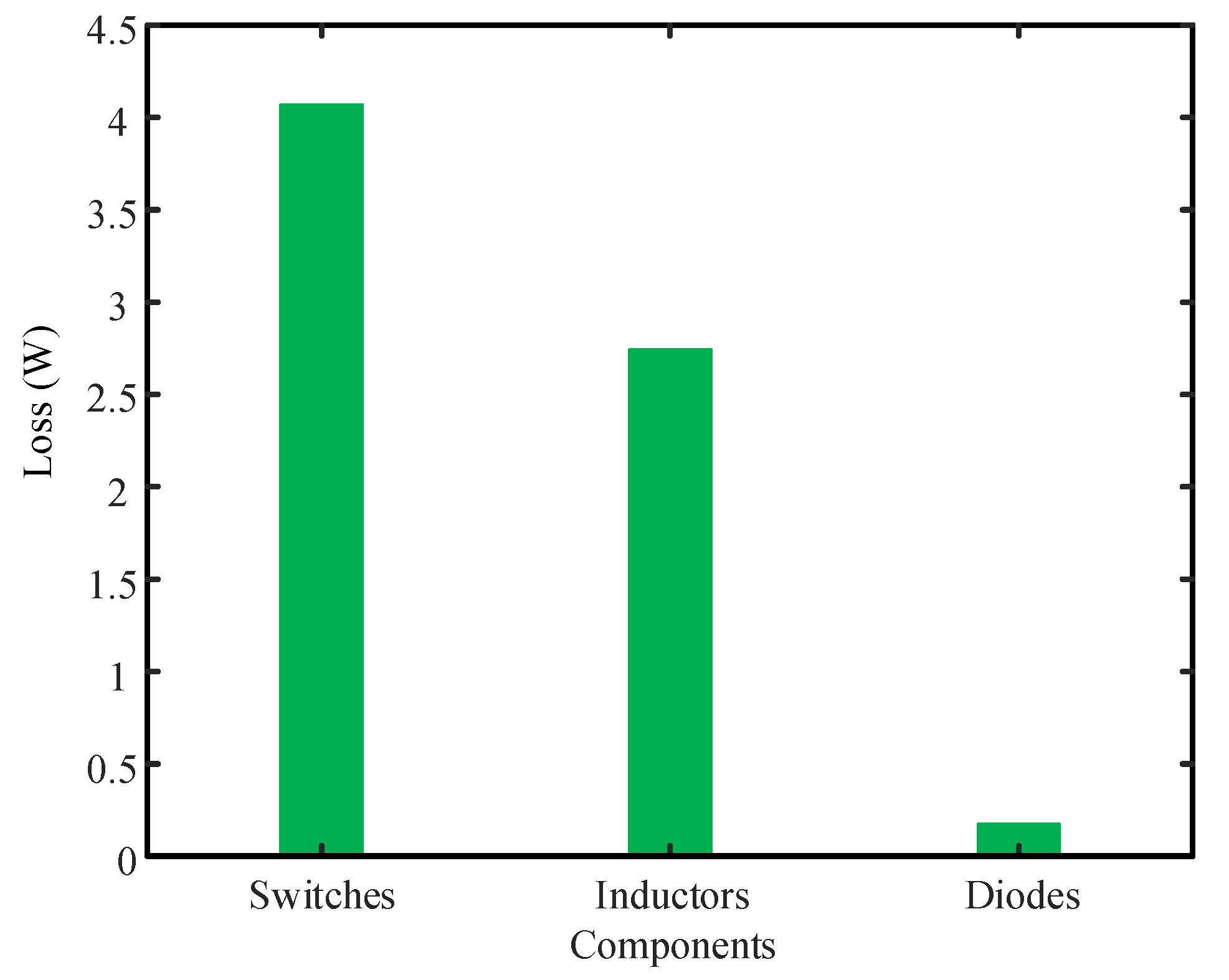
5.3. Power Loss Breakdown Analysis
5.3.1. Power Losses in Switches
5.3.2. Power Losses in Diodes
5.3.3. Power Losses in Inductors
5.3.4. Estimated Efficiency
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ren, Y.; Xu, M.; Yao, K.; Lee, F.C. Two-stage 48V power pod exploration for 64-bit microprocessor. In Proceedings of the Eighteenth Annual IEEE Applied Power Electronics Conference and Exposition, Miami Beach, FL, USA, 9–13 February 2003; Volume 1, pp. 426–431. [Google Scholar]
- Ren, Y.; Xu, M.; Yao, K.; Meng, Y.; Lee, F.C. Two-stage approach for 12-V VR. IEEE Trans. Power Electron. 2004, 19, 1498–1506. [Google Scholar] [CrossRef]
- Mao, H.; Abu-Qahouq, J.A.; Luo, S.; Batarseh, I. Zero-voltage-switching (ZVS) two-stage approaches with output current sharing for 48V input dc-dc converter. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 22–26 February 2004; Volume 2, pp. 1078–1082. [Google Scholar]
- Ren, Y.; Xu, M.; Meng, Y.; Lee, F.C. 12V VR efficiency improvement based on two-stage approach and a novel gate driver. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 16 June 2005; pp. 2635–2641. [Google Scholar]
- Fei, C.; Ahmed, M.H.; Lee, F.C.; Li, Q. Two-stage 48V-12V/6V-1.8V voltage regulator module with dynamic bus voltage control for light load efficiency improvement. IEEE Trans. Power Electron. 2017, 32, 5628–5636. [Google Scholar] [CrossRef]
- Xu, P.; Lee, F.C. Multiphase coupled-buck converter-novel high efficient 12 V voltage regulator module. IEEE Trans. Power Electron. 2003, 18, 74–84. [Google Scholar]
- Marvi, F.; Adib, E.; Farzanehfard, H. Interleaved zero voltage switching coupled inductor buck converter for low voltage-high current applications. In Proceedings of the 4th Annual International Power Electronics, Drive Systems and Technologies Conference, Tehran, Iran, 13–14 February 2013; pp. 236–241. [Google Scholar]
- Hwu, K.I.; Jiang, W.Z.; Wu, P.Y. An expandable two-phase interleaved ultrahigh step-down converter with automatic current balance. IEEE Trans. Power Electron. 2017, 32, 9223–9237. [Google Scholar] [CrossRef]
- Matsumoto, K.; Nishijima, K.; Sato, T.; Nabeshima, T. A two-phase high step down coupled-inductor converter for next generation low voltage CPU. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 2813–2818. [Google Scholar]
- Oraw, B.; Ayyanar, R. Small signal modeling and control design for new extended duty ratio, interleaved multiphase synchronous buck converter. In Proceedings of the INTELEC 06-Twenty-Eighth International Telecommunications Energy Conference, Providence, RI, USA, 10–14 September 2006; pp. 1–8. [Google Scholar]
- Esteki, M.; Poorali, B.; Adib, E.; Farzanehfard, H. Interleaved buck converter with continuous input current, extremely low output current ripple, low switching losses, and improved step-down conversion ratio. IEEE Trans. Ind. Electron. 2015, 62, 4769–4776. [Google Scholar] [CrossRef]
- Esteki, M.; Poorali, B.; Adib, E.; Farzanehfard, H. High step-down interleaved buck converter with low voltage stress. IET Power Electron. 2015, 8, 2352–2360. [Google Scholar] [CrossRef]
- Kirshenboim, O.; Peretz, M.M. High efficiency non-isolated converter with very-high step-down conversion ratio. IEEE Trans. Power Electron. 2017, 32, 3683–3690. [Google Scholar] [CrossRef]
- Nagaraja, H.N.; Patra, A.; Kastha, D. Design and analysis of four-phase synchronous buck converter for VRM applications. In Proceedings of the IEEE INDICON 2004. First India Annual Conference, Kharagpur, India, 20–22 December 2004; pp. 575–580. [Google Scholar]
- Lee, I.-O.; Cho, S.-Y.; Moon, G.-W. Interleaved buck converter having low switching losses and improved step-down conversion ratio. IEEE Trans. Power Electron. 2012, 27, 3664–3675. [Google Scholar] [CrossRef]
- Suja, A.; Sivakumar, S.; Ramkumar, P.S. Modified interleaved buck converter implementation for higher step-down conversion ratio. In Proceedings of the 2015 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 19–20 March 2015; pp. 1–4. [Google Scholar]
- Hwu, K.I.; Jiang, W.Z.; Wu, P.Y. An expandable four-phase interleaved high step-down converter with low switch voltage stress and automatic uniform current sharing. IEEE Trans. Ind. Electron. 2016, 63, 6064–6072. [Google Scholar] [CrossRef]
- Pan, C.-T.; Chuang, C.-F.; Chu, C.-C. A novel transformerless interleaved high step-down conversion ratio dc-dc converter with low switch voltage stress. IEEE Trans. Ind. Electron. 2014, 61, 5290–5299. [Google Scholar] [CrossRef]
- Chuang, C.-F.; Pan, C.-T.; Cheng, H.-C. A novel transformer-less interleaved four-phase step-down dc converter with low switch voltage stress and automatic uniform current-sharing characteristics. IEEE Trans. Power Electron. 2016, 31, 406–417. [Google Scholar] [CrossRef]
- Liao, S.-H.; Teng, J.-H.; Chen, S.-W. Bidirectional dc-dc converter with high step-down and step-up voltage gain. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–6. [Google Scholar]
- Ayachit, A.; Reatti, A.; Kazimierczuk, M.K. Magnetising inductance of multiple-output flyback dc-dc convertor for discontinuous-conduction mode. IET Power Electron. 2017, 10, 451–461. [Google Scholar] [CrossRef]
- Davoudi, A.; Jatskevich, J.; Chapman, P.L. Averaged modelling of switched-inductor cells considering conduction losses in discontinuous mode. IEEE Electron. Power Appl. 2007, 1, 402–406. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. Pulse-width Modulated dc-dc Power Converters, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Iftikhar, M.U.; Lefranc, P.; Sadarnac, D.; Karimi, C. Theoretical and experimental investigation of averaged modeling of non-ideal PWM DCDC converters operating in DCM. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 2257–2263. [Google Scholar]
- Nashed, M.; Fayed, A.A. A current-mode hysteretic buck converter with spur-free control for variable switching noise mitigation. IEEE Trans. Power Electron. 2018, 33, 650–664. [Google Scholar] [CrossRef]
- Davoudi, A.; Jatskevich, J.; Rybel, T.D. Numerical state-space average-value modeling of PWM DC-DC converters operating in DCM and CCM. IEEE Trans. Power Electron. 2006, 21, 1003–1012. [Google Scholar] [CrossRef]
- Amir, S.; Zee, R.V.D.; Nauta, B. An improved modeling and analysis technique for peak current-mode control-based boost converters. IEEE Trans. Power Electron. 2015, 30, 5309–5317. [Google Scholar] [CrossRef]
- Davoudi, A.; Jatskevich, J.; Chapman, P.L. Numerical dynamic characterization of peak current-mode-controlled DC-DC converters. IEEE Trans. Circuits Syst. II 2009, 56, 906–910. [Google Scholar] [CrossRef]
- Suntio, T. Average and small-signal modeling of self-oscillating flyback converter with applied switching delay. IEEE Trans. Power Electron. 2006, 21, 479–486. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, C.J.; Wang, S.S. Small-signal model of flyback converter in continuous-conduction mode with peak-current control at variable switching frequency. IEEE Trans. Power Electron. 2018, 33, 4145–4156. [Google Scholar] [CrossRef]





| Circuit | Voltage Gain | Component Number | Switch Voltage Stress | Diode Voltage Stress | Floating Output |
|---|---|---|---|---|---|
| Proposed | 14 | No | |||
| [20] | 9 | ; | No | Yes | |
| [13] | 10 | No | Yes | ||
| [17] | 16 | No | |||
| [19] | 17 | Yes |
| System Parameters | Specifications |
|---|---|
| Operating mode | CCM |
| Rated input voltage (Vin) | 60 V |
| Rated output voltage (Vo) | 1.8 V |
| Rated output current (Io,rated)/power (Po,rated) | 20 A/36 W |
| Minimum output current (Io,min)/power (Po,min) | 2 A/3.6 W |
| Switching frequency (fs)/period (Ts) | 100 kHz/10 μs |
| Components | Specifications | |
|---|---|---|
| MOSFET | Q1, Q4, Q5 | FDP047AN |
| Q2, Q3 | FDP047AN | |
| Diode | D1, D2, D3 | STPS30L45CT |
| Energy-transferring Capacitor | C1 | 47 470 μF/100 V Rubycon Electrolytic Capacitor |
| C2, C3 | 470 μF/35 V Rubycon Electrolytic Capacitor | |
| Capacitor | Co | 68 μF/6.3 V Rubycon Electrolytic Capacitor |
| Inductor | Core CH330125, L1 = L2 = 20 μH | |
| Gate driver | TLP250 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwu, K.-I.; Shieh, J.-J.; Tu, H.-H. Improvement in Voltage Gain of Interleaved High Step-Down Converter. Energies 2020, 13, 1019. https://doi.org/10.3390/en13051019
Hwu K-I, Shieh J-J, Tu H-H. Improvement in Voltage Gain of Interleaved High Step-Down Converter. Energies. 2020; 13(5):1019. https://doi.org/10.3390/en13051019
Chicago/Turabian StyleHwu, Kuo-Ing, Jenn-Jong Shieh, and Hsiang-Hao Tu. 2020. "Improvement in Voltage Gain of Interleaved High Step-Down Converter" Energies 13, no. 5: 1019. https://doi.org/10.3390/en13051019
APA StyleHwu, K.-I., Shieh, J.-J., & Tu, H.-H. (2020). Improvement in Voltage Gain of Interleaved High Step-Down Converter. Energies, 13(5), 1019. https://doi.org/10.3390/en13051019








