Comparative Study on Optimization Solvers for Implementation of a Two-Stage Economic Dispatch Strategy in a Microgrid Energy Management System
Abstract
:1. Introduction
- The computational capabilities of the four widely employed optimization solvers, including CPLEX and Gurobi as commercial solvers and GNU linear programing kit (GLPK) and CBC as open-source solvers, are compared in terms of optimal cost, scheduling results, and computational time. The results will be helpful for MG operators, who seek to find a cost-effective optimization solver that best fits their technical requirements and budgetary constraints.
- To examine the applicability to both day-ahead and real-time scheduling, the two-stage scheduling algorithm was adopted as an ED strategy, whereby operation set points of ESSs and the power injected from the main-grid are coordinated to minimize the operating costs of grid-connected MGs.
- To compare the optimization solvers considering actual operating conditions, a 6-bus campus MG with actual renewable generation and load data [15] was used as a simulation test-bed. For a more comprehensive investigation, additional simulation case studies were conducted on IEEE 33-bus and 123-bus test systems [21], which were modified slightly to emulate mid- and large-scale MGs, respectively.
- A modularized programming strategy is presented for a fair comparison between the optimization solvers. The modularized programming strategy provides an effective way to avoid redundant usage of functions and variable definitions. It also allows the overall architecture of the code to be developed easily with enhanced readability, which is critical for managing and debugging the programming code.
2. Overview of the ED Implementation Environment
2.1. Configuration of the ED Implementation Enviroment
2.2. Modularized Programming Architecture
3. Description of the Two-Stage ED Strategy
3.1. MG Configuration
3.2. Two-Stage ED Strategy
- First-stage scheduling: In this first-stage (i.e., day-ahead scheduling), hourly schedules for a day are performed one day in advance. The objective function is to minimize the operating cost. The total time window is 24 h, and the single scheduling time interval is 1 h. The scheduled profiles do not change during an hour.
- Second-stage scheduling: In the second stage (i.e., hour-ahead scheduling), the optimal schedule obtained from the first stage is updated every 5 min during the day of operation to compensate for the uncertainties in load demands and PV output power. It should be noted that hour-ahead scheduling is not performed at the beginning of every 5-min interval, but rather follows the day-ahead scheduled profile. In other words, the second stage runs 11 times per an hour. Only the first interval of each run set serves as a final decision and the rest of the intervals are for reference only.
3.2.1. Objective Function
3.2.2. Equality Constraints
3.2.3. Inequality Constraints
3.3. Implementation of the Two-Stage Strategy with the Modular Architecture
- Module (1)
- Loading the input data for each scheduling stage as follows:
—First-stage scheduling: MG topology; PV generation and load demand forecasts; electricity price; initial SOC level of ESSs; ESS parameters. —Second-stage scheduling: First-stage scheduled utility power; MG topology;
5-min sampled measurements of PV generation, load demand, SOC levels, and utility power; electricity price; initial SOC level of ESSs;
ESS parameters. - Module (2)
- Creating the A and b matrices that represent the equality constraints of an optimization problem using the following Equations:
—First-stage scheduling: Equations (6)–(9). —Second-stage scheduling: Equations (6), (7), and (10). - Module (3)
- Creating the A and b matrices that represent the inequality constraints of an optimization problem using the following Equations:
—First-stage scheduling: Equations (11)–(13), (15), and (16). —Second-stage scheduling: Equations (11)–(14), (17), and (19). - Module (4)
- Formulating the optimization problem from the A and b matrices obtained from M2 and M3 using the modeling package or modeling library of the optimization solver in a GPL-based platform or using the inherent interface provided in the AML-based environment; solving the optimization problem by executing the optimizer library of the optimization solver.
4. Simulation Case Studies for Comparison
4.1. Simulation Conditions
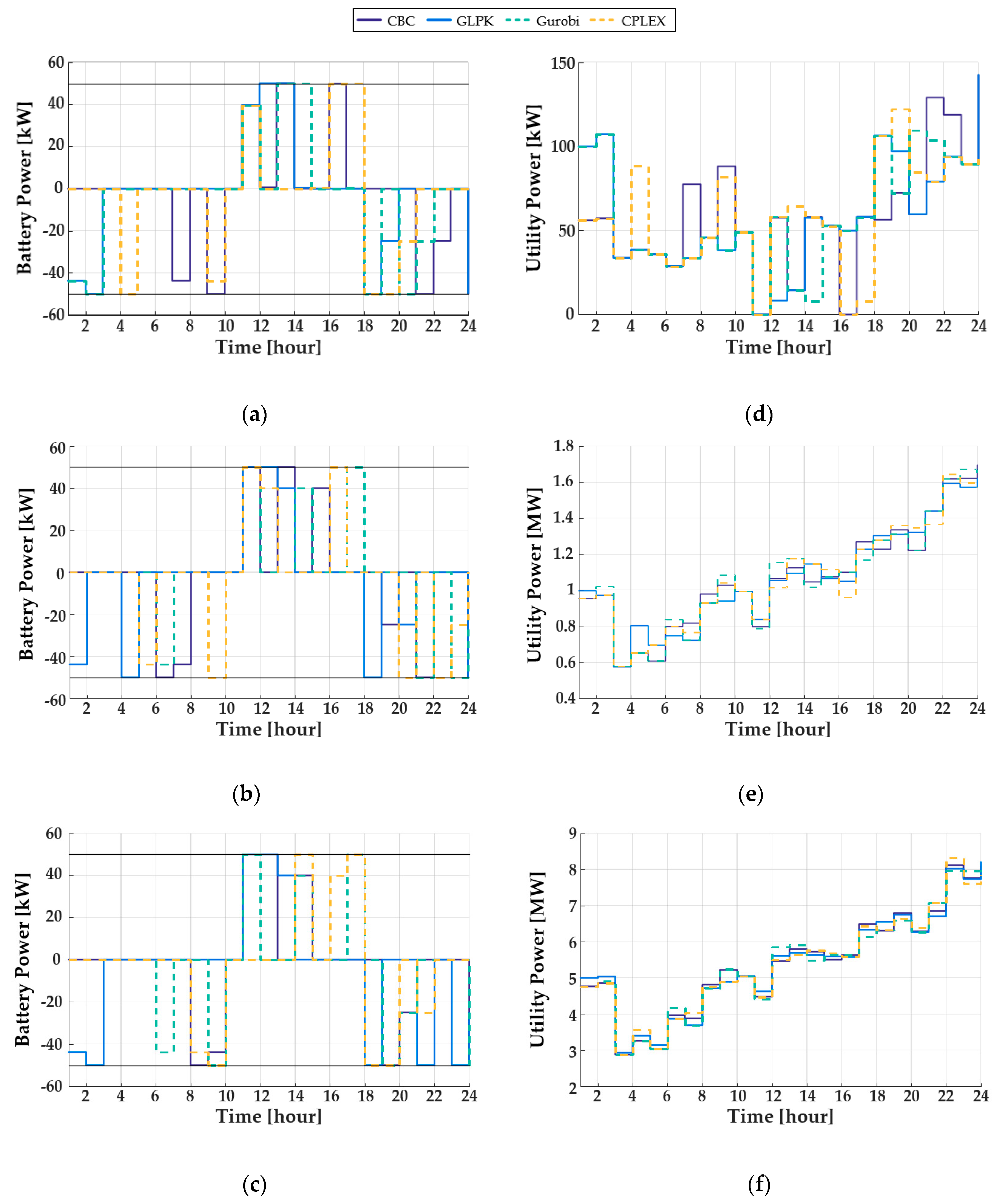
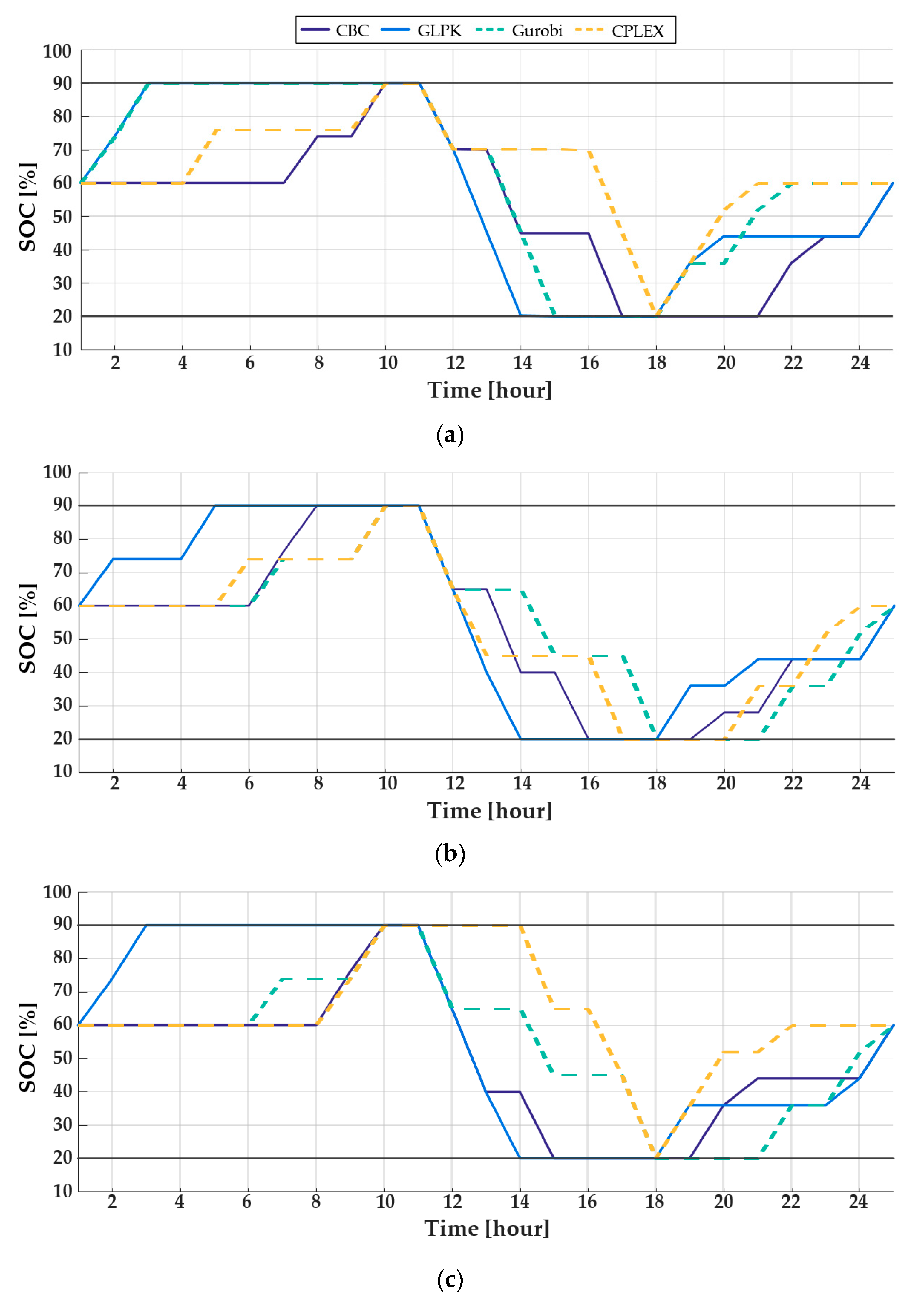
4.2. Comparison of Optimal Costs and Scheduled Profiles
4.3. Comparison of Computation Time
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Acronyms | |
| AML | Algebraic modeling language |
| AOA | AIMMS outer approximation algorithm |
| API | Application programming interface |
| CBC | Coin-or branch and cut |
| CCHP | Combined cooling, heating and power |
| DER | Distributed energy resource |
| ED | Economic dispatch |
| ESS | Energy storage system |
| EV | Electric vehicle |
| GAMS | General algebraic modeling system |
| GLPK | GNU linear programing kit |
| GPL | General-purpose programming language |
| KEPCO | Korea electric power corporation |
| LP | Linear programming |
| MEMS | Microgrid energy management system |
| MG | Microgrid |
| MIP | Mixed-integer programming |
| OPF | Optimal power flow |
| PV | Photovoltaic |
| SCADA | Supervisory control and data acquisition |
| SOC | State-of-charge |
| SVM | Support vector machine |
| TOU | Time-of-use |
| Sets and Indices | |
| d | Day-ahead stage values |
| h | Hour-ahead stage values |
| Td | Set of hourly periods in the first stage (i.e., t ∈ Td and Td = [0, 1, ···, 23]) |
| Th | Set of 5 minute periods in the second stage (i.e., Th = [5, 10, ···, 55]) |
| t | Index for a scheduling time step (i.e., t ∈ Td and t ∈ Th) |
| i, j, k | Indices for buses in an MG |
| L | Set of lines of the topology in the MG (i.e., (i, j), (k, i) ∈ L) |
| B | Set of buses in the MG (i.e., i, j, k ∈ B) |
| n, N | Index and total number of ESSs, (i.e., n ∈ N) |
| f | Forecasted values |
| max, min | Maximum/minimum values |
| Parameters and Constants | |
| Pcont | Contracted power (kW) |
| α | Weighting coefficients for penalty functions |
| r | Parameter for objective function linearization |
| SOCnmin, SOCnmax | Minimum/maximum SOC limit of the nth ESS (%) |
| ƞch,n, ƞdch,n | Charging/discharging efficiency of the nth ESS (%) |
| CAPnmax | Maximum capacity of the nth ESS (kWh) |
| Pch,nmax, Pdch,nmax | Maximum charging/discharging power of nth ESS (kW) |
| SOCn,init,SOCn,final | SOC levels of nth battery at the initial/final times steps of a day (%) |
| Variables | |
| ct | Hourly electricity price at time t ($/kWh) |
| Pu,td | Imported power from the utility at time t (kW) |
| Pu,th | Hour-ahead scheduled utility power at time t (kW) |
| Ut | Continuous decision variable determining the penalty function at time t |
| St | Binary variable for objective function linearization at time t |
| Pj,i,t, Pi,k,t | Power flow from bus j to bus i and from bus i to bus k at time t |
| PLi,tf, PPV,tf | Forecasted load demand/PV generation at bus i at time t (kW) |
| Pch,n,t, Pdch,n,t | Scheduled charging/discharging power of nth ESS at time t (kW) |
| SOCn,t | SOC level of the nth ESS at time t (%) |
| un,t | Binary decision variable to determine the operation status of the nth ESS at time t |
References
- Valencia, F.; Collado, J.; Sáez, D.; Marín, L.G. Robust Energy Management System for a Microgrid Based on a Fuzzy Prediction Interval Model. IEEE Trans. Smart Grid 2016, 7, 1486–1494. [Google Scholar] [CrossRef]
- Kim, Y.; Wang, J.; Lu, X. A Framework for Load Service Restoration Using Dynamic Change in Boundaries of Advanced Microgrids With Synchronous-Machine DGs. IEEE Trans. Smart Grid 2018, 9, 3676–3690. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Fanti, M.P.; Mangini, A.M.; Roccotelli, M.; Ukovich, W. District Microgrid Management Integrated with Renewable Energy Sources, Energy Storage Systems and Electric Vehicles. IFAC-PapersOnLine 2017, 50, 10015–10020. [Google Scholar] [CrossRef]
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust Energy Management for Microgrids With High-Penetration Renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953. [Google Scholar] [CrossRef] [Green Version]
- Malysz, P.; Sirouspour, S.; Emadi, A. An Optimal Energy Storage Control Strategy for Grid-connected Microgrids. IEEE Trans. Smart Grid 2014, 5, 1785–1796. [Google Scholar] [CrossRef]
- Luo, Z.; Wu, Z.; Li, Z.; Cai, H.; Li, B.; Gu, W. A two-stage optimization and control for CCHP microgrid energy management. Appl. Therm. Eng. 2017, 125, 513–522. [Google Scholar] [CrossRef]
- Wang, D.; Qiu, J.; Reedman, L.; Meng, K.; Lai, L.L. Two-stage energy management for networked microgrids with high renewable penetration. Appl. Energy 2018, 226, 39–48. [Google Scholar] [CrossRef]
- Tuffaha, M.; Gravdahl, J.T. Discrete state-space model to solve the unit commitment and economic dispatch problems. Energy Syst. 2017, 8, 525–547. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Dong, Z.Y.; Ma, J. Robust Operation of Microgrids via Two-Stage Coordinated Energy Storage and Direct Load Control. IEEE Trans. Power Syst. 2017, 32, 2858–2868. [Google Scholar] [CrossRef]
- Morais, H.; Kádár, P.; Faria, P.; Vale, Z.A.; Khodr, H.M. Optimal scheduling of a renewable micro-grid in an isolated load area using mixed-integer linear programming. Renew. Energy 2010, 35, 151–156. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-H.; Lu, S.-Y.; Chang, Y.-R.; Lee, T.-T.; Hu, M.-C. Economic analysis and optimal energy management models for microgrid systems: A case study in Taiwan. Appl. Energy 2013, 103, 145–154. [Google Scholar] [CrossRef]
- Luna, A.C.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Mixed-Integer-Linear-Programming-Based Energy Management System for Hybrid PV-Wind-Battery Microgrids: Modeling, Design, and Experimental Verification. IEEE Trans. Power Electron. 2017, 32, 2769–2783. [Google Scholar] [CrossRef] [Green Version]
- De la Hoz, J.; Martín, H.; Alonso, A.; Carolina Luna, A.; Matas, J.; Vasquez, J.C.; Guerrero, J.M. Regulatory-framework-embedded energy management system for microgrids: The case study of the Spanish self-consumption scheme. Appl. Energy 2019, 251, 113374. [Google Scholar] [CrossRef]
- Jeong, B.-C.; Shin, D.-H.; Im, J.-B.; Park, J.-Y.; Kim, Y.-J. Implementation of Optimal Two-Stage Scheduling of Energy Storage System Based on Big-Data-Driven Forecasting—An Actual Case Study in a Campus Microgrid. Energies 2019, 12, 1124. [Google Scholar] [CrossRef] [Green Version]
- Gearhart, J.L.; Adair, K.L.; Detry, R.J.; Durfee, J.D.; Jones, K.A.; Martin, N. Comparison of Open-Source Linear Programming Solvers; Technical Report SAND2013-8847; Sandia National Laboratories: Albuquerque, NM, USA, 2013.
- Pfenninger, S.; DeCarolis, J.; Hirth, L.; Quoilin, S.; Staffell, I. The importance of open data and software: Is energy research lagging behind? Energy Policy 2017, 101, 211–215. [Google Scholar] [CrossRef]
- Groissböck, M. Are open source energy system optimization tools mature enough for serious use? Renew. Sustain. Energy Rev. 2019, 102, 234–248. [Google Scholar] [CrossRef]
- Weibezahn, J.; Kendziorski, M. Illustrating the Benefits of Openness: A Large-Scale Spatial Economic Dispatch Model Using the Julia Language. Energies 2019, 12, 1153. [Google Scholar] [CrossRef] [Green Version]
- Meindl, B.; Templ, M. Analysis of Commercial and Free and Open Source Solvers for Linear Optimization Problems; Technical Report; Vienna University of Technology: Vienna, Austria, 2012. [Google Scholar]
- Kersting, W.H. Radial distribution test feeders. IEEE Trans. Power Syst. 1991, 6, 975–985. [Google Scholar] [CrossRef]
- Vergara, P.P.; López, J.C.; Rey, J.M.; da Silva, L.C.P.; Rider, M.J. Energy Management in Microgrids. In Microgrids Design and Implementation; Zambroni de Souza, A.C., Castilla, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 195–216. [Google Scholar] [CrossRef]
- Kim, Y.; Del-Rosario-Calaf, G.; Norford, L.K. Analysis and Experimental Implementation of Grid Frequency Regulation Using Behind-the-Meter Batteries Compensating for Fast Load Demand Variations. IEEE Trans. Power Syst. 2017, 32, 484–498. [Google Scholar] [CrossRef]
- Feng, C.; Cui, M.; Hodge, B.-M.; Lu, S.; Hamann, H.F.; Zhang, J. Unsupervised Clustering-Based Short-Term Solar Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 2174–2185. [Google Scholar] [CrossRef]
- Bae, K.Y.; Jang, H.S.; Sung, D.K. Hourly Solar Irradiance Prediction Based on Support Vector Machine and Its Error Analysis. IEEE Trans. Power Syst. 2016, 32, 935–945. [Google Scholar] [CrossRef]
- Tuohy, A.; Meibom, P.; Denny, E.; O’Malley, M. Unit Commitment for Systems With Significant Wind Penetration. IEEE Trans. Power Syst. 2009, 24, 592–601. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, P.A.; Philbrick, C.R.; Zak, E.; Cheung, K.W.; Sauer, P.W. Uncertainty Management in the Unit Commitment Problem. IEEE Trans. Power Syst. 2009, 24, 642–651. [Google Scholar] [CrossRef]
- Ruiz, P.A.; Philbrick, C.R.; Sauer, P.W. Modeling Approaches for Computational Cost Reduction in Stochastic Unit Commitment Formulations. IEEE Trans. Power Syst. 2010, 25, 588–589. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Oren, S.S.; Rountree, B. Applying High Performance Computing to Transmission-Constrained Stochastic Unit Commitment for Renewable Energy Integration. IEEE Trans. Power Syst. 2015, 30, 1109–1120. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.; Qu, C. A Hierarchical Framework for Generation Scheduling of Microgrids. IEEE Trans. Power Deliv. 2014, 29, 2448–2457. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Begovic, M.M.; Chen, C. Coordinated Energy Management of Networked Microgrids in Distribution Systems. IEEE Trans. Smart Grid 2015, 6, 45–53. [Google Scholar] [CrossRef]
- Nemati, M.; Braun, M.; Tenbohlen, S. Optimization of unit commitment and economic dispatch in microgrids based on genetic algorithm and mixed integer linear programming. Appl. Energy 2018, 210, 944–963. [Google Scholar] [CrossRef]
- Kwon, S.; Park, J.; Kim, Y. Optimal V2G and Route Scheduling of Mobile Energy Storage Devices Using a Linear Transit Model to Reduce Electricity and Transportation Energy Losses. IEEE Trans. Power Electron. 2020, 56, 34–47. [Google Scholar] [CrossRef]
- Amoasi Acquah, M.; Kodaira, D.; Han, S. Real-Time Demand Side Management Algorithm Using Stochastic Optimization. Energies 2018, 11, 1166. [Google Scholar] [CrossRef] [Green Version]
- Electric Rates Table. Available online: http://cyber.kepco.co.kr/ckepco (accessed on 20 February 2020).
- Open Innovation Bigdata Center. Available online: http://oibc.postech.ac.kr (accessed on 20 February 2020).
- Python. Available online: https://www.python.org (accessed on 20 February 2020).
- PuLP. Available online: https://www.coin-or.org/PuLP/ (accessed on 20 February 2020).
- CBC. Available online: https://projects.coin-or.org/Cbc (accessed on 20 February 2020).
- GLPK. Available online: https://www.gnu.org/software/glpk (accessed on 20 February 2020).
- Gurobi. Available online: https://www.gurobi.com/ (accessed on 20 February 2020).
- CPLEX. Available online: https://www.ibm.com/analytics/cplex-optimizer (accessed on 20 February 2020).
- Comparison of Programming Languages. Available online: https://modelingguru.nasa.gov/docs/DOC-2625/diff?secondVersionNumber=19 (accessed on 20 February 2020).









| Ref | Optimization Algorithms (1) | Solver Types (2) | Language Types (3) | Demonstration Methods (4) | |||||
|---|---|---|---|---|---|---|---|---|---|
| OS | CS | Solver | AML | GPL | S | I | Test-Beds | ||
| [4] | LP | ✓ | GLPK | ✓ | ✓ | Grid-connected MG | |||
| [5] | CONVEX | ✓ | MOSEK | ✓ | ✓ | Grid-connected MG | |||
| [6] | MIP | ✓ | CPLEX | ✓ | ✓ | Grid-connected MG | |||
| [7] | MIP (T-S) | ✓ | CPLEX | ✓ | ✓ | Grid-connected MG | |||
| [8] | MIP (T-S) | ✓ | CPLEX | ✓ | ✓ | Grid-connected MGs | |||
| [9] | MIP (T-S) | ✓ | Gurobi | ✓ | ✓ | Islanded MG | |||
| [10] | MIP (T-S) | ✓ | SCIP | ✓ | ✓ | IEEE 33-bus radial system | |||
| [11] | MIP | ✓ | CPLEX | ✓ | ✓ | Budapest Tech Renewable System, Hungary | |||
| [12] | MIP | ✓ | CPLELX | ✓ | ✓ | Institute of Nuclear Energy Research MG, Taiwan | |||
| [13] | MIP (T-S) | ✓ | CPLEX | ✓ | ✓ | MG Research Lab. in Aalborg Univ., Denmark | |||
| [14] | MIP | ✓ | AOA | ✓ | ✓ | MG Research Lab. in Aalborg Univ., Denmark | |||
| [15] | MIP (T-S) | ✓ | CBC | ✓ | ✓ | Grid-connected Campus MG, South Korea | |||
| Solver | Solver Types (1) | Python Modeling Packages | Julia Modeling Packages | ||
|---|---|---|---|---|---|
| OS | CS | PuLP | Pyomo | JuMP | |
| CBC | ✓ | ✓ | ✓ | ✓ | |
| GLPK | ✓ | ✓ | ✓ | ✓ | |
| CPLEX | ✓ | ✓ | ✓ | ✓ | |
| Gurobi | ✓ | ✓ | ✓ | ✓ | |
| SCIP | ✓ | ✓ | ✓ | ||
| XPRESS | ✓ | ✓ | ✓ | ✓ | |
| MOSEK | ✓ | ✓ | ✓ | ||
| Parameters | Values | Units |
|---|---|---|
| Pchmax | 50 | [kW] |
| Pdchmax | 50 | [kW] |
| ECmax | 250 | [kWh] |
| SOCmax | 90 | [%] |
| SOCmin | 20 | [%] |
| ƞch | 80 | [%] |
| ƞdch | 80 | [%] |
| Classifications | Time Periods | Prices ($/kWh) |
|---|---|---|
| Off-peak load | 23:00–09:00 | 0.038 |
| Mid-load | 09:00–10:00 | 0.076 |
| 12:00–13:00 | ||
| 17:00–23:00 | ||
| Peak-load | 10:00–12:00 | 0.130 |
| 13:00–17:00 |
| Functionality | Software | Types | Versions | |
|---|---|---|---|---|
| GPL | Python | Open-source | 3.6.9 | [37] |
| Modeling Package | PuLP | Open-source | 1.6.8 | [38] |
| Optimization Solver | CBC | Open-source | 2.10 | [39] |
| GLPK | 4.65 | [40] | ||
| Gurobi | Commercial | 8.1.1 | [41] | |
| CPLEX | 12.9 | [42] | ||
| Cases | Modeling Packages | Solvers (1) | First Stage (s) | Second Stage (s) | |
|---|---|---|---|---|---|
| Avg. Initial Scheduling | Max. Initial Scheduling | ||||
| Case 1 6 Bus system | PuLP | CBC | 1.32 | 0.44 | 0.47 |
| GLPK | 1.25 | 0.42 | 0.47 | ||
| Gurobi | 1.02 | 0.38 | 0.43 | ||
| CPLEX | 1.03 | 0.41 | 0.49 | ||
| Gurobi (API) | 0.26 | 0.03 | 0.03 | ||
| CPLEX (API) | 0.13 | 0.02 | 0.02 | ||
| Case 2 33 Bus system | PuLP | CBC | 12.42 | 3.80 | 3.93 |
| GLPK | 11.55 | 3.81 | 3.96 | ||
| Gurobi | 10.94 | 3.59 | 3.68 | ||
| CPELX | 10.98 | 3.76 | 3.98 | ||
| Gurobi (API) | 2.67 | 0.25 | 0.28 | ||
| CPLEX (API) | 0.61 | 0.07 | 0.08 | ||
| Case 3 123 Bus system | PuLP | CBC | 113.64 | 37.61 | 42.42 |
| GLPK | 110.87 | 38.74 | 42.70 | ||
| Gurobi | 105.13 | 36.52 | 39.11 | ||
| CPELX | 105.36 | 35.57 | 39.10 | ||
| Gurobi (API) | 27.82 | 2.42 | 2.52 | ||
| CPLEX (API) | 3.55 | 0.76 | 0.80 | ||
| Case | MIP Solver | First Stage | Second Stage | ||||
|---|---|---|---|---|---|---|---|
| Inequality Const. (s) | Equality Const. (s) | Time Ratio (%) | Inequality Const. (s) | Equality Const. (s) | Time Ratio (%) | ||
| Case 1 6 Bus system | CBC | 0.39 | 0.50 | 67.42 | 0.14 | 0.13 | 61.93 |
| GLPK | 71.20 | 64.88 | |||||
| Gurobi | 87.25 | 71.71 | |||||
| CPLEX | 86.40 | 66.46 | |||||
| Case 2 33 Bus system | CBC | 2.61 | 7.67 | 82.77 | 1.06 | 1.78 | 74.90 |
| GLPK | 89.00 | 74.71 | |||||
| Gurobi | 93.96 | 79.29 | |||||
| CPLEX | 93.62 | 75.70 | |||||
| Case 3 123 Bus system | CBC | 17.19 | 86.43 | 91.18 | 8.87 | 20.82 | 78.97 |
| GLPK | 93.46 | 76.66 | |||||
| Gurobi | 98.56 | 81.33 | |||||
| CPLEX | 98.35 | 83.50 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G.-H.; Park, J.-Y.; Ham, S.-J.; Kim, Y.-J. Comparative Study on Optimization Solvers for Implementation of a Two-Stage Economic Dispatch Strategy in a Microgrid Energy Management System. Energies 2020, 13, 1096. https://doi.org/10.3390/en13051096
Lee G-H, Park J-Y, Ham S-J, Kim Y-J. Comparative Study on Optimization Solvers for Implementation of a Two-Stage Economic Dispatch Strategy in a Microgrid Energy Management System. Energies. 2020; 13(5):1096. https://doi.org/10.3390/en13051096
Chicago/Turabian StyleLee, Gi-Ho, Jae-Young Park, Seung-Jun Ham, and Young-Jin Kim. 2020. "Comparative Study on Optimization Solvers for Implementation of a Two-Stage Economic Dispatch Strategy in a Microgrid Energy Management System" Energies 13, no. 5: 1096. https://doi.org/10.3390/en13051096
APA StyleLee, G.-H., Park, J.-Y., Ham, S.-J., & Kim, Y.-J. (2020). Comparative Study on Optimization Solvers for Implementation of a Two-Stage Economic Dispatch Strategy in a Microgrid Energy Management System. Energies, 13(5), 1096. https://doi.org/10.3390/en13051096





