Numerical and Experimental Studies on the Effect of Surface Roughness and Ultrasonic Frequency on Bubble Dynamics in Acoustic Cavitation
Abstract
:1. Introduction
2. Materials and Methods
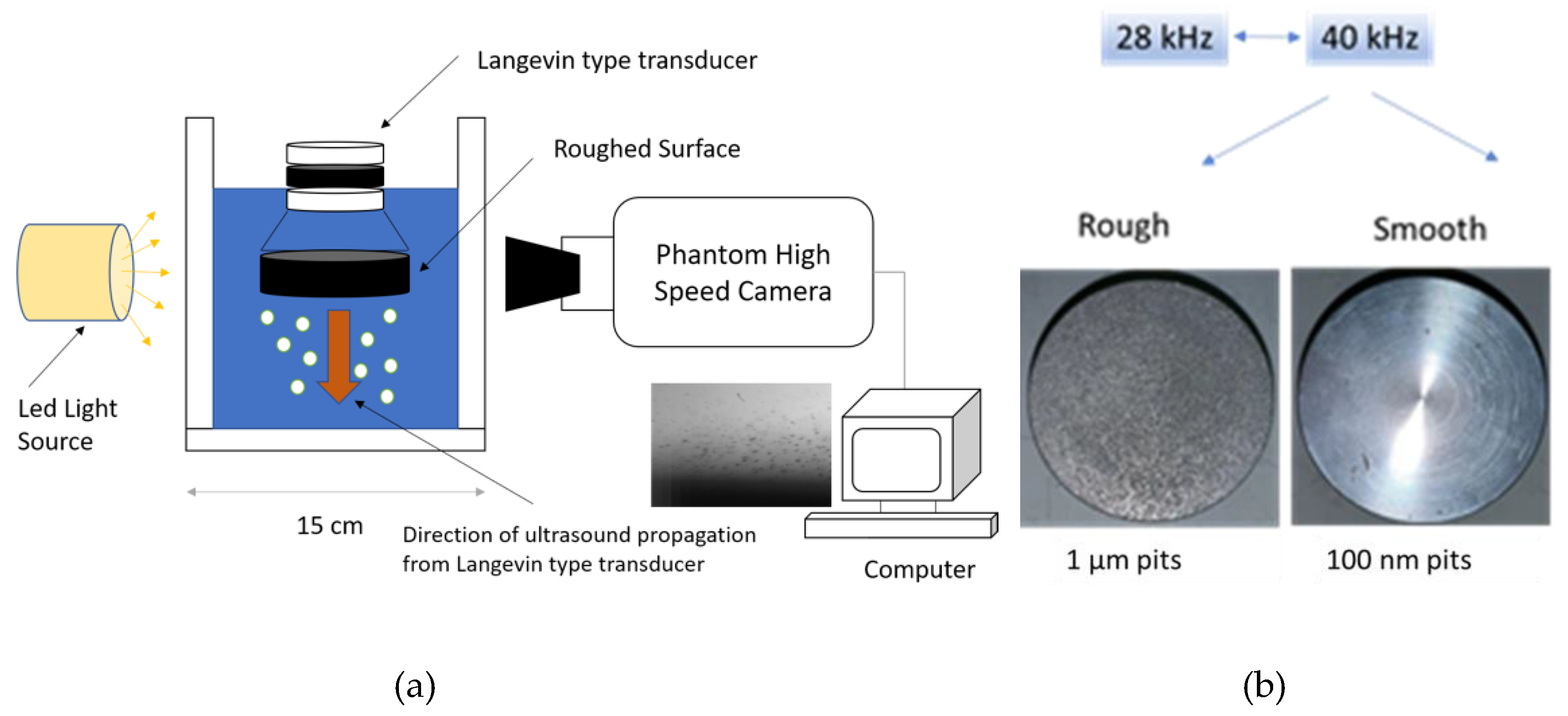
2.1. Experimental Setup
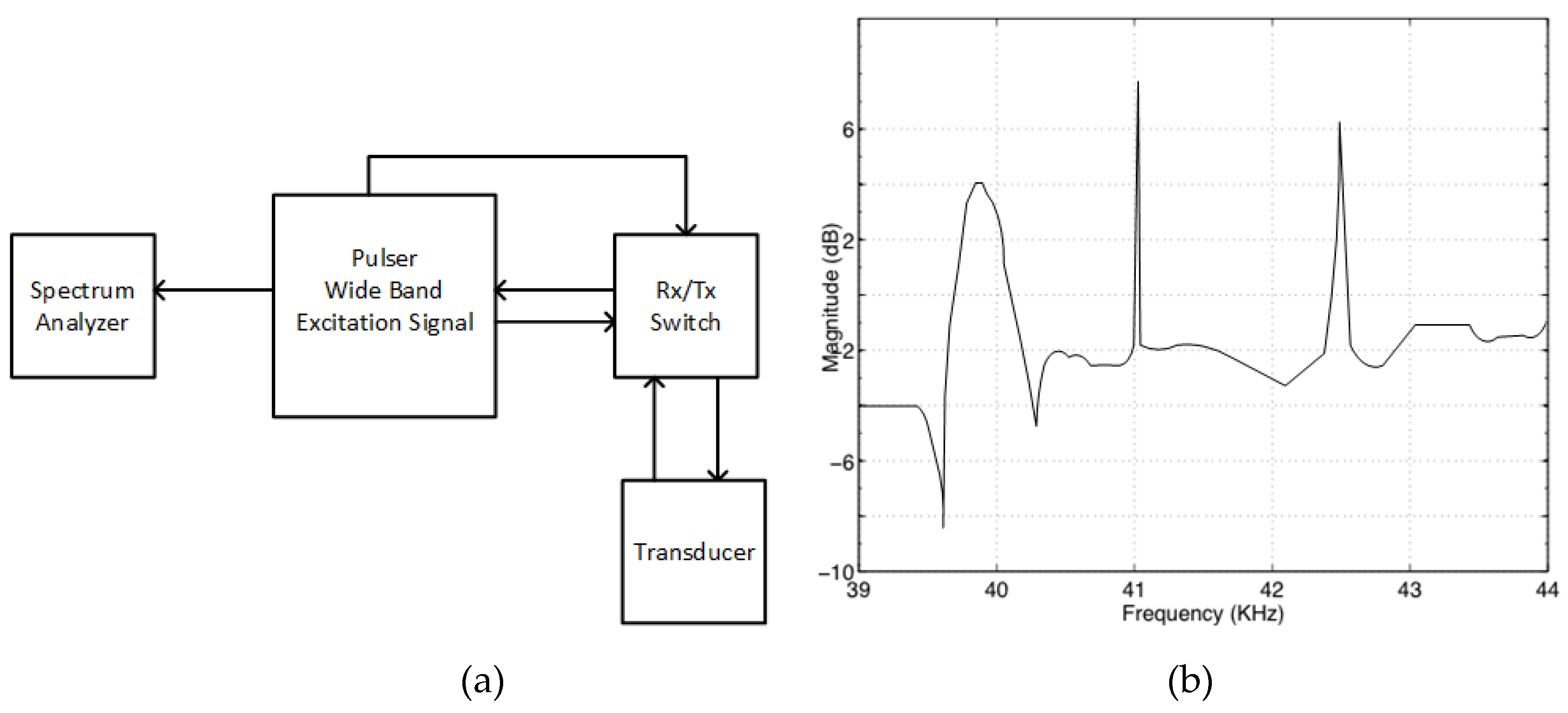
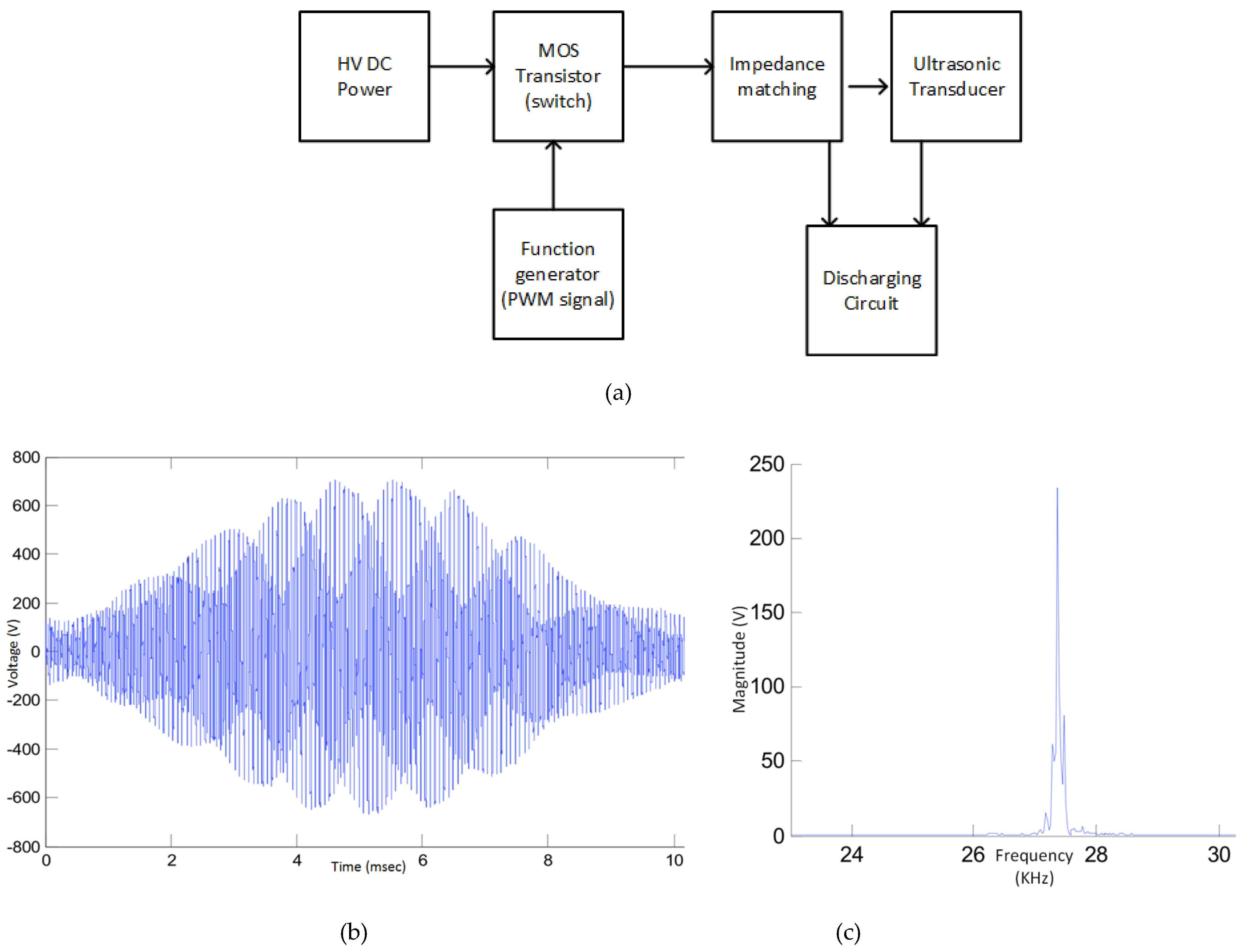
2.2. Acoustic Characterization and Control Circuit
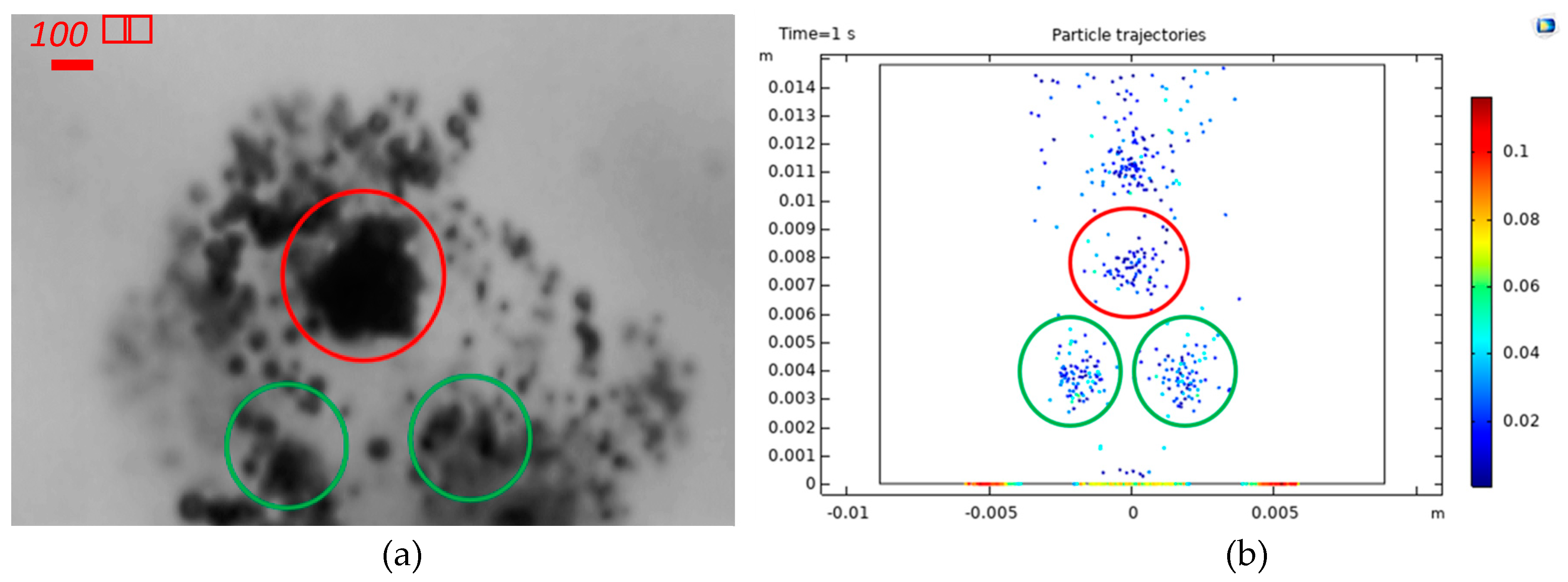
2.3. Numerical Analysis
3. Results and Discussion
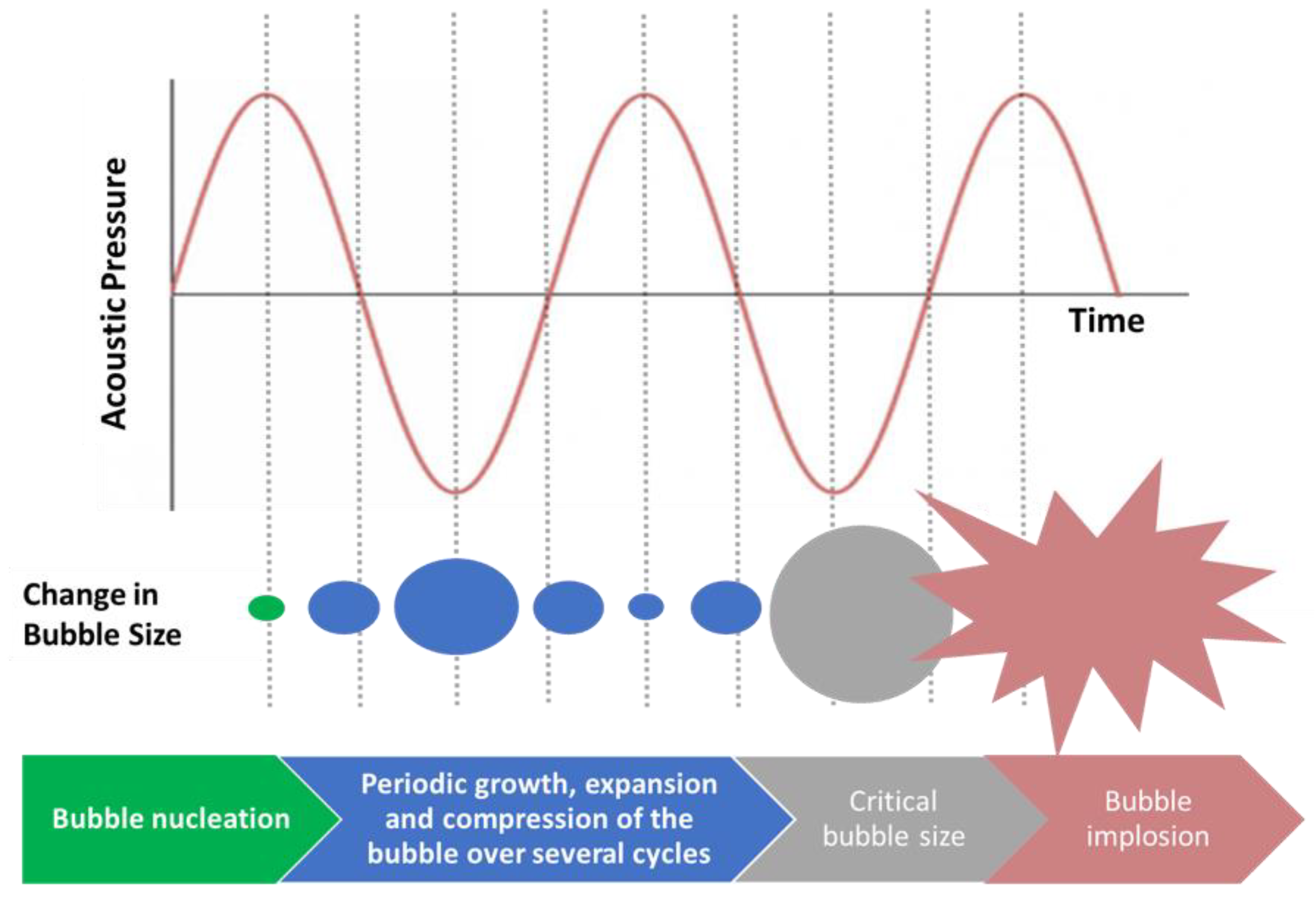
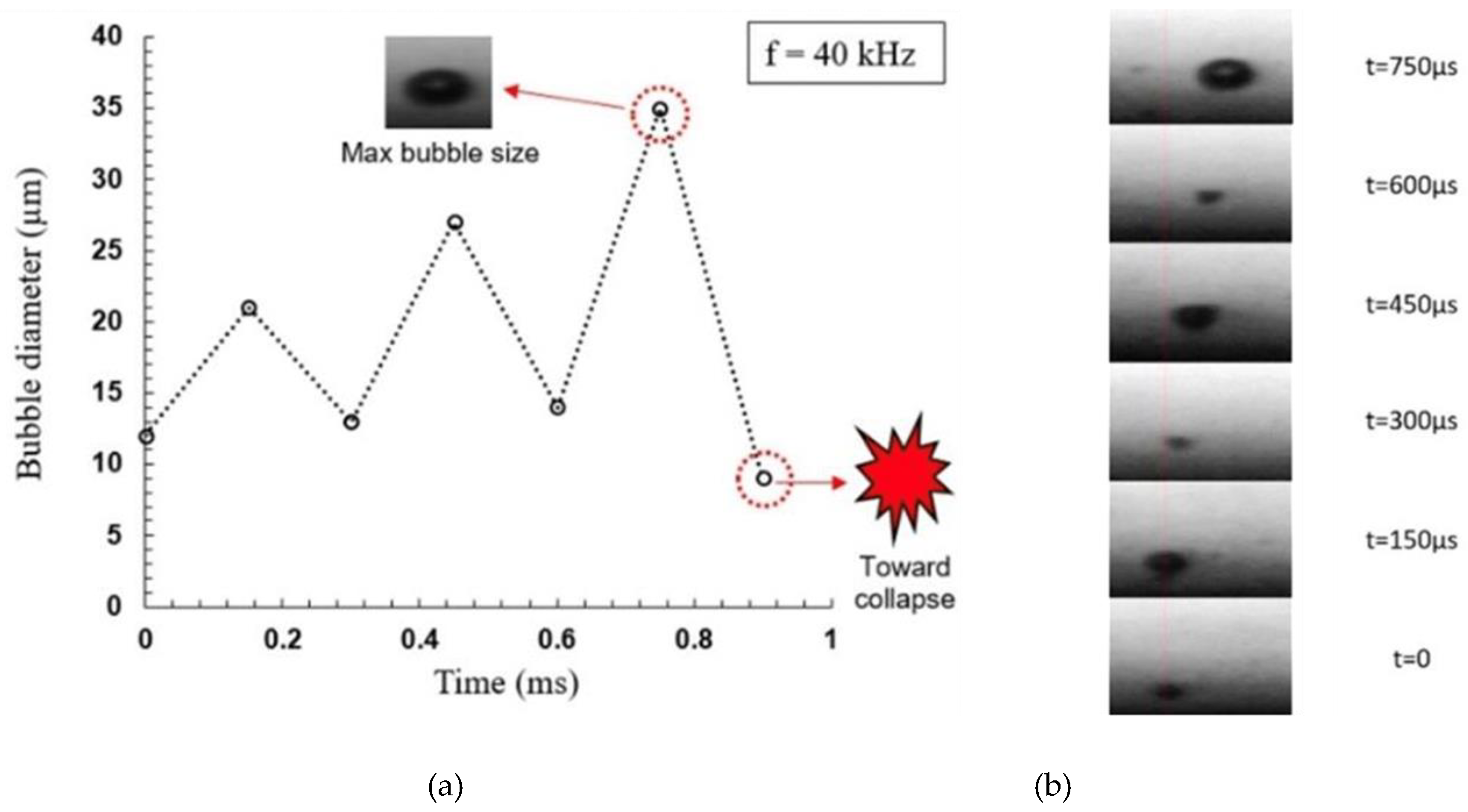
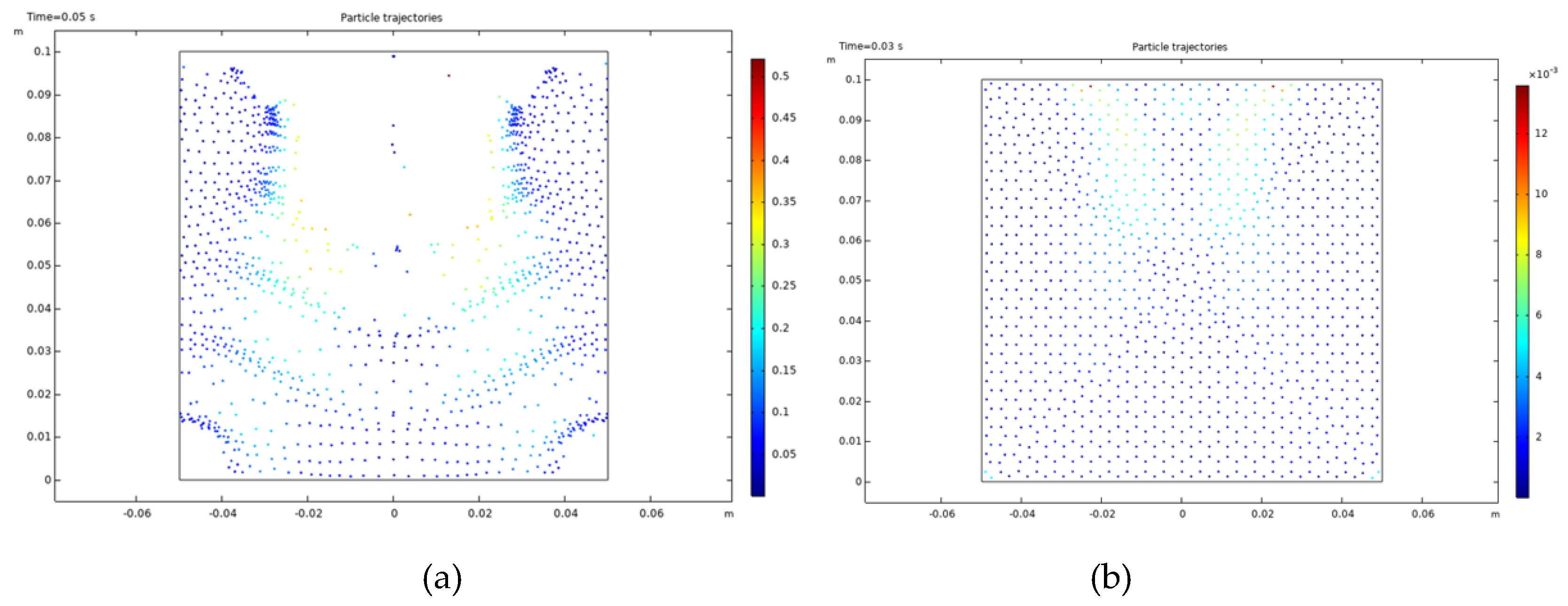
3.1. Single Bubble Dynamics in an Acoustic Field
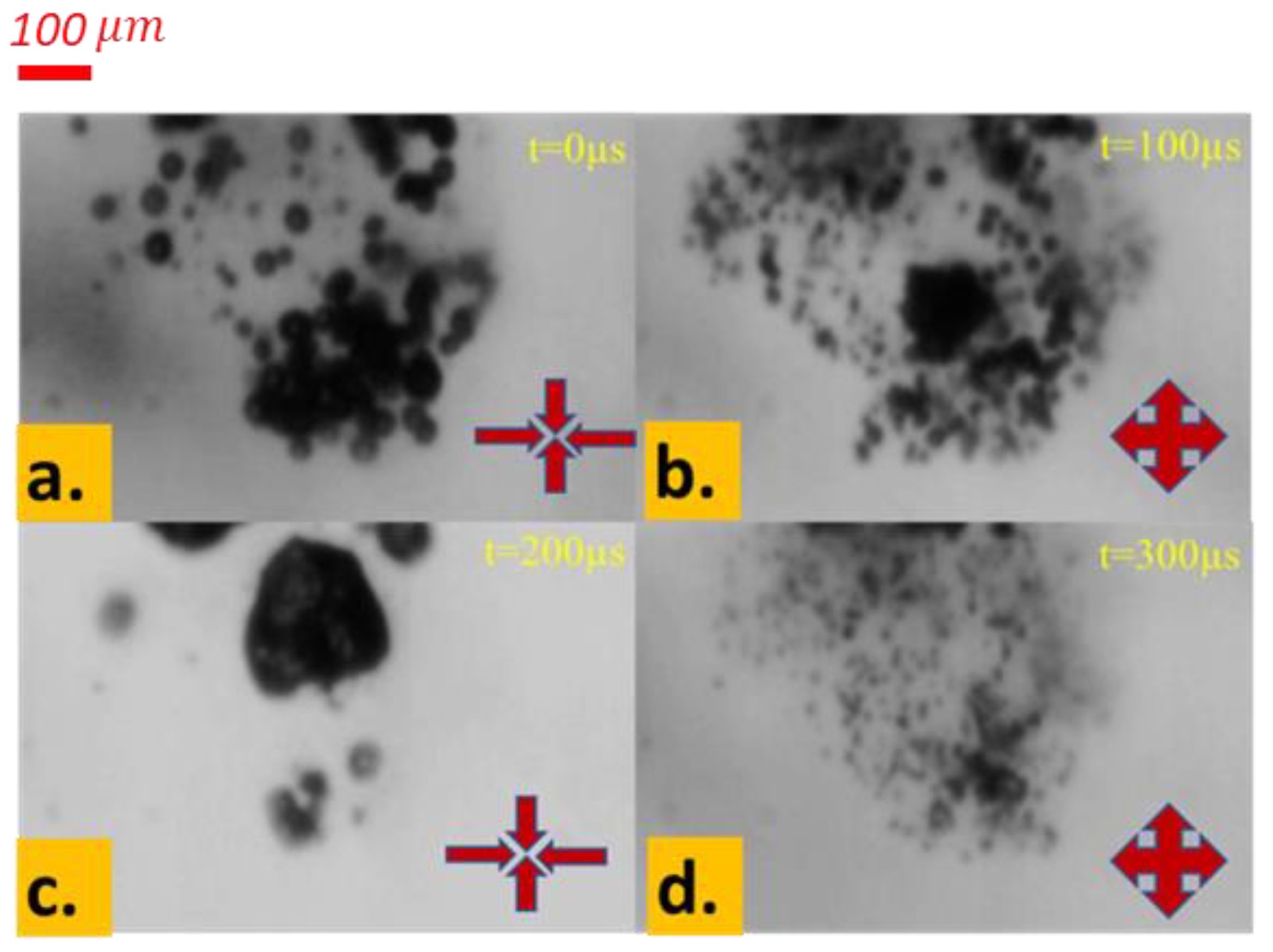
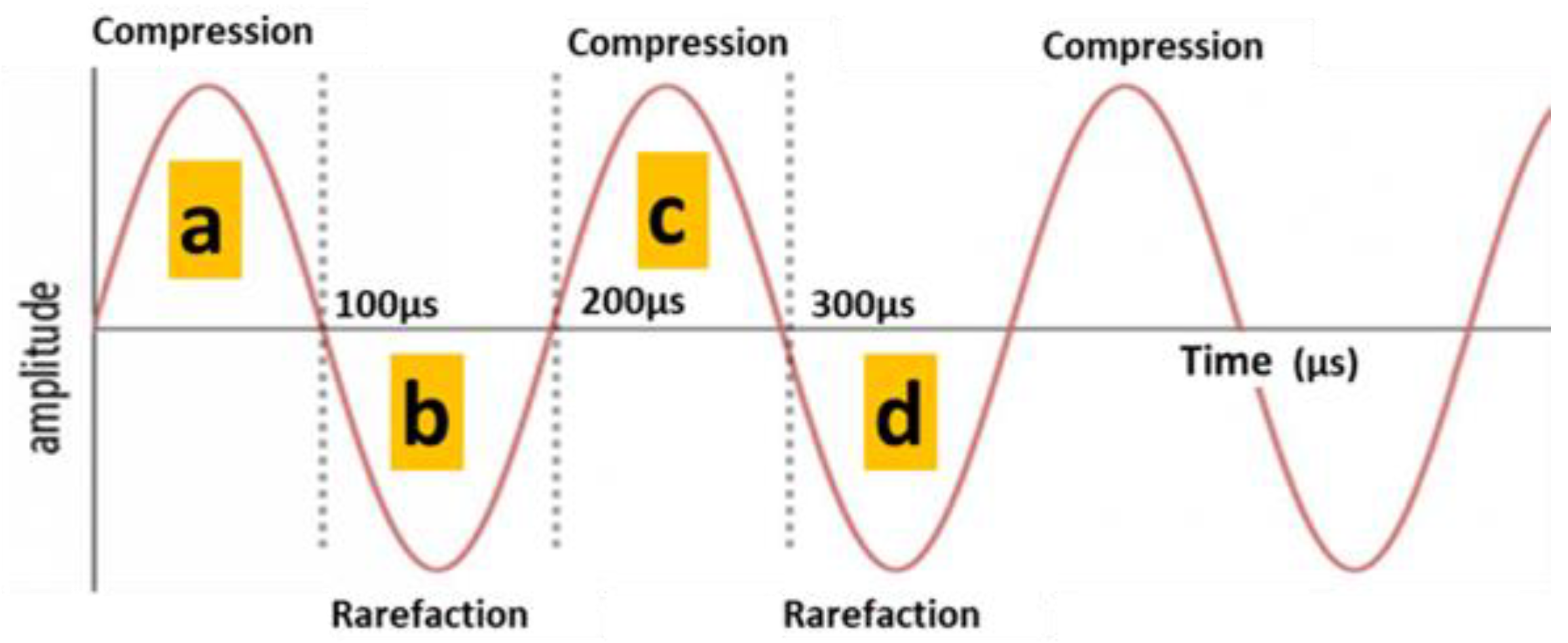
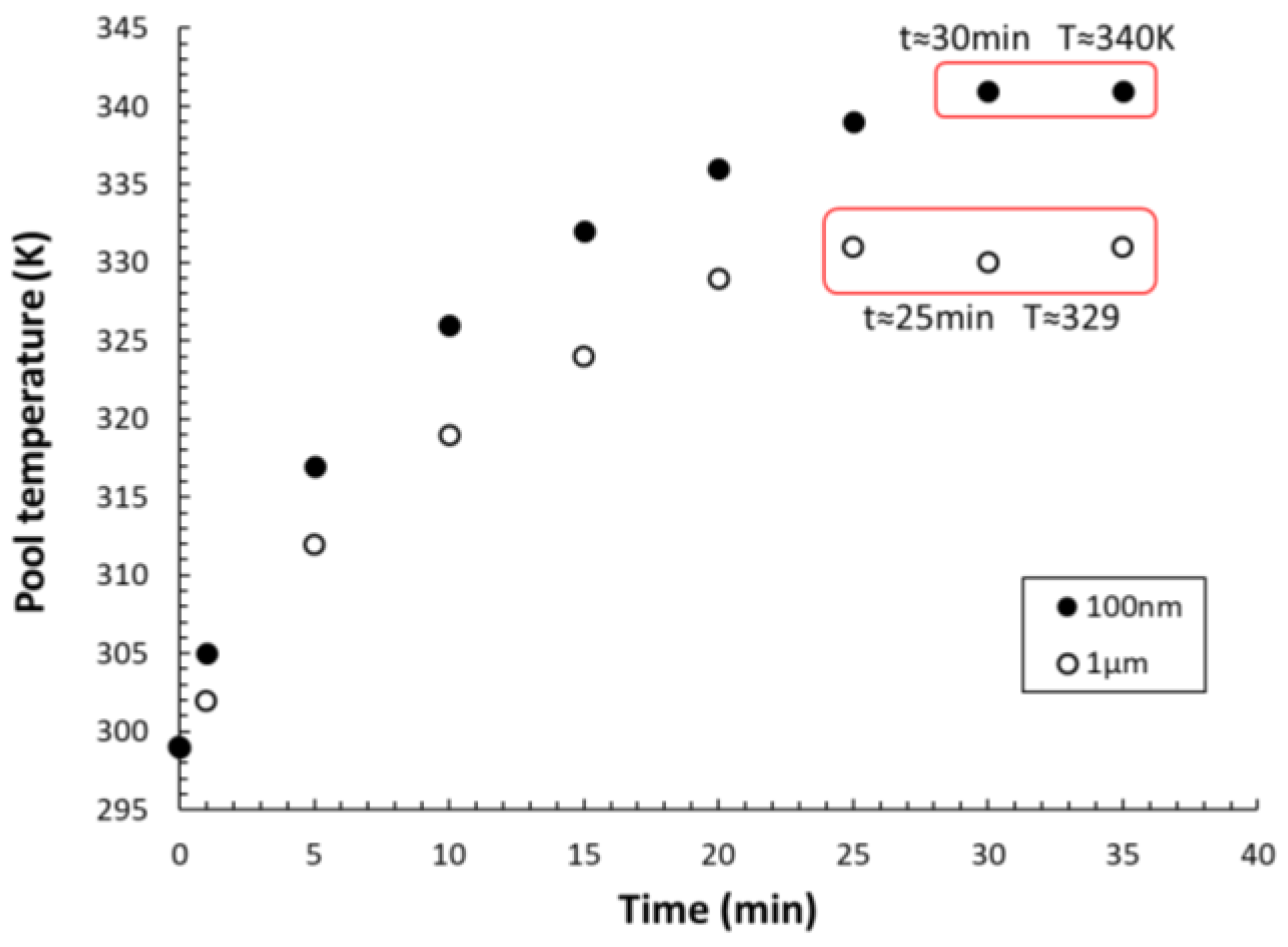
3.2. Bubble Behavior in Acoustic Field
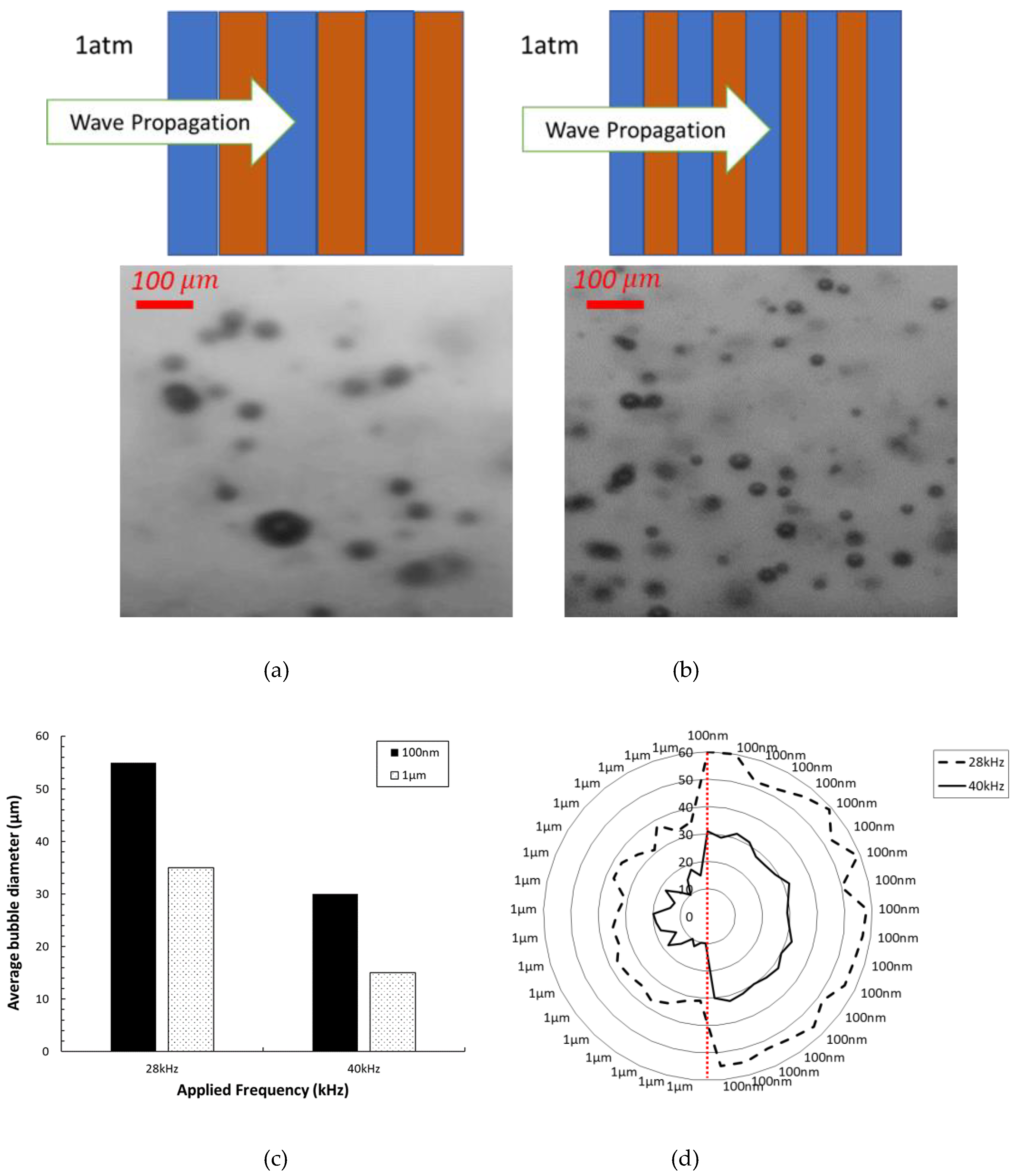
3.3. Effect of Surface Roughness and Ultrasonic Frequency
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameter | Description |
| c | Sound velocity (m/s) |
| f | Frequency (1/s) |
| FR | Radiation force (N) |
| FQS | Quasi-static drag force (N) |
| k | Wave number (1/m) |
| P | Pressure (kPa) |
| P0 | Ambient pressure (kPa) |
| R | Bubble radius (m) |
| St | Stokes number (-) |
| t | Time (s) |
| u(t) | Velocity (m/s) |
| ur | Relative velocity (m/s) |
| V | Velocity (m/s) |
| Greek letters | |
| ρ | Density (kg/m3) |
| ω | Angular frequency (1/s) |
| σ | Surface tension (N/m) |
| γ | Density ration (-) |
| ν | Kinematic viscosity (m2/s) |
| Abbreviations | |
| CCD | Charge-coupled device |
| MOS transistor | Metal–oxide–semiconductor transistor |
| HV-DC | High-voltage direct current |
| AC | Alternating current |
| PWM signal | Pulse-width modulation signal |
References
- Leong, T.; Ashokkumar, M.; Kentish, S. The growth of bubbles in an acoustic field by rectified diffusion. Handb. Ultrason. Sonochemistry 2016, 10, 978–981. [Google Scholar]
- Holzfuss, J.; Rüggeberg, M.; Billo, A. Shock wave emissions of a sonoluminescing bubble. Phys. Rev. Lett. 1998, 81, 5434. [Google Scholar] [CrossRef] [Green Version]
- Peshkovsky, S.L.; Peshkovsky, A.S. Shock-wave model of acoustic cavitation. Ultrason. Sonochemistry 2008, 15, 618–628. [Google Scholar] [CrossRef]
- Suslick, K.S.; Didenko, Y.; Fang, M.M.; Hyeon, T.; Kolbeck, K.J.; McNamara III, W.B.; Mdleleni, M.M.; Wong, M. Acoustic cavitation and its chemical consequences. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 357, 335–353. [Google Scholar] [CrossRef]
- Sazgarnia, A.; Shanei, A.; Taheri, A.R.; Meibodi, N.T.; Eshghi, H.; Attaran, N.; Shanei, M.M. Therapeutic effects of acoustic cavitation in the presence of gold nanoparticles on a colon tumor model. J. Ultrasound Med. 2013, 32, 475–483. [Google Scholar] [CrossRef] [Green Version]
- Coussios, C.; Farny, C.; Ter Haar, G.; Roy, R. Role of acoustic cavitation in the delivery and monitoring of cancer treatment by high-intensity focused ultrasound (HIFU). Int. J. Hyperth. 2007, 23, 105–120. [Google Scholar] [CrossRef]
- Aw, M.S.; Paniwnyk, L.; Losic, D. The progressive role of acoustic cavitation for non-invasive therapies, contrast imaging and blood-tumor permeability enhancement. Expert Opin. Drug Deliv. 2016, 13, 1383–1396. [Google Scholar] [CrossRef]
- Yusof, N.S.M.; Babgi, B.; Alghamdi, Y.; Aksu, M.; Madhavan, J.; Ashokkumar, M. Physical and chemical effects of acoustic cavitation in selected ultrasonic cleaning applications. Ultrason. Sonochemistry 2016, 29, 568–576. [Google Scholar] [CrossRef]
- Muthukumaran, S.; Yang, K.; Seuren, A.; Kentish, S.; Ashokkumar, M.; Stevens, G.W.; Grieser, F. The use of ultrasonic cleaning for ultrafiltration membranes in the dairy industry. Sep. Purif. Technol. 2004, 39, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Bryson, L.; Fernandez Rivas, D.; Boutsioukis, C. Cleaning of used rotary nickel-titanium files in an ultrasonic bath by locally intensified acoustic cavitation. Int. Endod. J. 2018, 51, 457–468. [Google Scholar] [CrossRef]
- Pradhan, A.A.; Gogate, P.R. Degradation of p-nitrophenol using acoustic cavitation and Fenton chemistry. J. Hazard. Mater. 2010, 173, 517–522. [Google Scholar] [CrossRef]
- Pétrier, C.; Francony, A. Ultrasonic waste-water treatment: Incidence of ultrasonic frequency on the rate of phenol and carbon tetrachloride degradation. Ultrason. Sonochemistry 1997, 4, 295–300. [Google Scholar] [CrossRef]
- Fang, Y.; Hariu, D.; Yamamoto, T.; Komarov, S. Acoustic cavitation assisted plasma for wastewater treatment: Degradation of Rhodamine B in aqueous solution. Ultrason. Sonochemistry 2019, 52, 318–325. [Google Scholar] [CrossRef]
- Xu, H.; Zeiger, B.W.; Suslick, K.S. Sonochemical synthesis of nanomaterials. Chem. Soc. Rev. 2013, 42, 2555–2567. [Google Scholar] [CrossRef] [Green Version]
- Han, J.T.; Jang, J.I.; Kim, H.; Hwang, J.Y.; Yoo, H.K.; Woo, J.S.; Choi, S.; Kim, H.Y.; Jeong, H.J.; Jeong, S.Y. Extremely efficient liquid exfoliation and dispersion of layered materials by unusual acoustic cavitation. Sci. Rep. 2014, 4, 5133. [Google Scholar] [CrossRef]
- Hockham, N.; Coussios, C.C.; Arora, M. A real-time controller for sustaining thermally relevant acoustic cavitation during ultrasound therapy. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 2685–2694. [Google Scholar] [CrossRef]
- Leong, T.; Wooster, T.; Kentish, S.; Ashokkumar, M. Minimising oil droplet size using ultrasonic emulsification. Ultrason. Sonochemistry 2009, 16, 721–727. [Google Scholar] [CrossRef] [Green Version]
- Lad, V.N.; Murthy, Z.V.P. Enhancing the stability of oil-in-water emulsions emulsified by coconut milk protein with the application of acoustic cavitation. Ind. Eng. Chem. Res. 2012, 51, 4222–4229. [Google Scholar] [CrossRef]
- Canselier, J.; Delmas, H.; Wilhelm, A.; Abismail, B. Ultrasound emulsification-an overview. J. Dispers. Sci. Technol. 2002, 23, 333–349. [Google Scholar] [CrossRef]
- Ganz, S.; Gutierrez, E. Cavitation: Causes, Effects, Mitigation and Application; Rensselaer Polytech. Inst.: Hartford, CT, USA, 2012. [Google Scholar]
- Abedini, M.; Reuter, F.; Hanke, S. Corrosion and material alterations of a CuZn38Pb3 brass under acoustic cavitation. Ultrason. Sonochemistry 2019, 58, 104628. [Google Scholar] [CrossRef]
- Blake, F., Jr. The Properties of Gaseous Solutions as Revealed by Acoustic Cavitation Measurements. J. Acoust. Soc. Am. 1949, 21, 464. [Google Scholar] [CrossRef]
- Noltingk, B.E.; Neppiras, E.A. Cavitation produced by ultrasonics. Proc. Phys. Soc. Sect. B 1950, 63, 674. [Google Scholar] [CrossRef]
- Neppiras, E.; Noltingk, B. Cavitation produced by ultrasonics: Theoretical conditions for the onset of cavitation. Proc. Phys. Soc. Sect. B 1951, 64, 1032. [Google Scholar] [CrossRef]
- Leith, W.C. Cavitation Damage of Metals. Ph.D. Thesis, McGill University, Montréal, QC, Canada, 1960. [Google Scholar]
- Tian, Y.; Ketterling, J.A.; Apfel, R.E. Direct observation of microbubble oscillations. J. Acoust. Soc. Am. 1996, 100, 3976–3978. [Google Scholar] [CrossRef]
- Mettin, R. Bubble structures in acoustic cavitation. In Bubble and Particle Dynamics in Acoustic Fields: Modern Trends and Applications; Research Signpost: Kerala, İndia, 2005. [Google Scholar]
- Reuter, F.; Lesnik, S.; Ayaz-Bustami, K.; Brenner, G.; Mettin, R. Bubble size measurements in different acoustic cavitation structures: Filaments, clusters, and the acoustically cavitated jet. Ultrasonics Sonochemistry 2019, 55, 383–394. [Google Scholar] [CrossRef]
- Tuziuti, T.; Yasui, K.; Iida, Y.; Sivakumar, M.; Koda, S. Laser-light scattering from a multibubble system for sonochemistry. J. Phys. Chem. A 2004, 108, 9011–9013. [Google Scholar] [CrossRef]
- Harba, N.; Hayashi, S. Dust particles counteract the boosting of single-bubble sonoluminescence by glycerol droplets. Jpn. J. Appl. Phys. 2003, 42, 2971. [Google Scholar] [CrossRef]
- Brotchie, A.; Grieser, F.; Ashokkumar, M. Effect of power and frequency on bubble-size distributions in acoustic cavitation. Phys. Rev. Lett. 2009, 102, 084302. [Google Scholar] [CrossRef]
- Frohly, J.; Labouret, S.; Bruneel, C.; Looten-Baquet, I.; Torguet, R. Ultrasonic cavitation monitoring by acoustic noise power measurement. J. Acoust. Soc. Am. 2000, 108, 2012–2020. [Google Scholar] [CrossRef]
- Vichare, N.P.; Senthilkumar, P.; Moholkar, V.S.; Gogate, P.R.; Pandit, A.B. Energy analysis in acoustic cavitation. Ind. Eng. Chem. Res. 2000, 39, 1480–1486. [Google Scholar] [CrossRef]
- Laborde, J.L.; Bouyer, C.; Caltagirone, J.-P.; Gérard, A. Acoustic bubble cavitation at low frequencies. Ultrasonics 1998, 36, 589–594. [Google Scholar] [CrossRef]
- Apfel, R. Acoustic cavitation: A possible consequence of biomedical uses of ultrasound. Br. J. Cancer. Suppl. 1982, 5, 140. [Google Scholar]
- Son, Y.; Lim, M.; Khim, J. Investigation of acoustic cavitation energy in a large-scale sonoreactor. Ultrason. Sonochemistry 2009, 16, 552–556. [Google Scholar] [CrossRef]
- Sunartio, D.; Ashokkumar, M.; Grieser, F. Study of the coalescence of acoustic bubbles as a function of frequency, power, and water-soluble additives. J. Am. Chem. Soc. 2007, 129, 6031–6036. [Google Scholar] [CrossRef]
- Ashokkumar, M. The characterization of acoustic cavitation bubbles-an overview. Ultrason. Sonochemistry 2011, 18, 864–872. [Google Scholar] [CrossRef]
- Zhou, D. A novel concept for boiling heat transfer enhancement. J. Mech. Eng. 2005, 51, 366–373. [Google Scholar]
- Cui, J.; Zhang, Z.; Liu, X.; Liu, L.; Peng, J. Studies on viscosity reduction and structural change of crude oil treated with acoustic cavitation. Fuel 2020, 263, 116638. [Google Scholar] [CrossRef]
- Yakut, M.; Tangel, A.; Tangel, C. A microcontroller based generator design for ultrasonic cleaning machines. Istanb. Univ. J. Electr. Electron. Eng. 2009, 9, 853–860. [Google Scholar]
- Mason, T.J. Ultrasonic cleaning: An historical perspective. Ultrason. Sonochemistry 2016, 29, 519–523. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, H.; Su, X.; Lu, M. A new design of the high-power ultrasonic generator. In Proceedings of the 2008 Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008; pp. 3800–3803. [Google Scholar]
- Lin, S. Study on the multifrequency Langevin ultrasonic transducer. Ultrasonics 1995, 33, 445–448. [Google Scholar] [CrossRef]
- Fabijański, P.; Łagoda, R. Intelligent Control Unit for Ultrasonic Cleaning System. Przegląd Elektrotechniczny 2012, 88, 115–119. [Google Scholar]
- Shuyu, L. Load characteristics of high power sandwich piezoelectric ultrasonic transducers. Ultrasonics 2005, 43, 365–373. [Google Scholar] [CrossRef]
- Fabijanski, P.; Lagoda, R. Modeling and Identification of Parameters the Piezoelectric Transducers in Ultrasonic Systems. In Advances in Ceramics-Electric and Magnetic Ceramics, Bioceramics, Ceramics and Environment; IntechOpen: London, UK, 2011; pp. 154–176. [Google Scholar]
- Leighton, T. The Acoustic Bubble; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- COMSOL Multiphysics. Introduction to COMSOL multiphysics®. COMSOL Multiphysics 1998, 9, 2018. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altay, R.; Sadaghiani, A.K.; Sevgen, M.I.; Şişman, A.; Koşar, A. Numerical and Experimental Studies on the Effect of Surface Roughness and Ultrasonic Frequency on Bubble Dynamics in Acoustic Cavitation. Energies 2020, 13, 1126. https://doi.org/10.3390/en13051126
Altay R, Sadaghiani AK, Sevgen MI, Şişman A, Koşar A. Numerical and Experimental Studies on the Effect of Surface Roughness and Ultrasonic Frequency on Bubble Dynamics in Acoustic Cavitation. Energies. 2020; 13(5):1126. https://doi.org/10.3390/en13051126
Chicago/Turabian StyleAltay, Rana, Abdolali K. Sadaghiani, M. Ilker Sevgen, Alper Şişman, and Ali Koşar. 2020. "Numerical and Experimental Studies on the Effect of Surface Roughness and Ultrasonic Frequency on Bubble Dynamics in Acoustic Cavitation" Energies 13, no. 5: 1126. https://doi.org/10.3390/en13051126
APA StyleAltay, R., Sadaghiani, A. K., Sevgen, M. I., Şişman, A., & Koşar, A. (2020). Numerical and Experimental Studies on the Effect of Surface Roughness and Ultrasonic Frequency on Bubble Dynamics in Acoustic Cavitation. Energies, 13(5), 1126. https://doi.org/10.3390/en13051126






