Multi-Objective Optimization and Matching of Power Source for PHEV Based on Genetic Algorithm
Abstract
1. Introduction
2. Powertrain Model of PHEV
2.1. Engine Model
2.2. Driving Motor Model
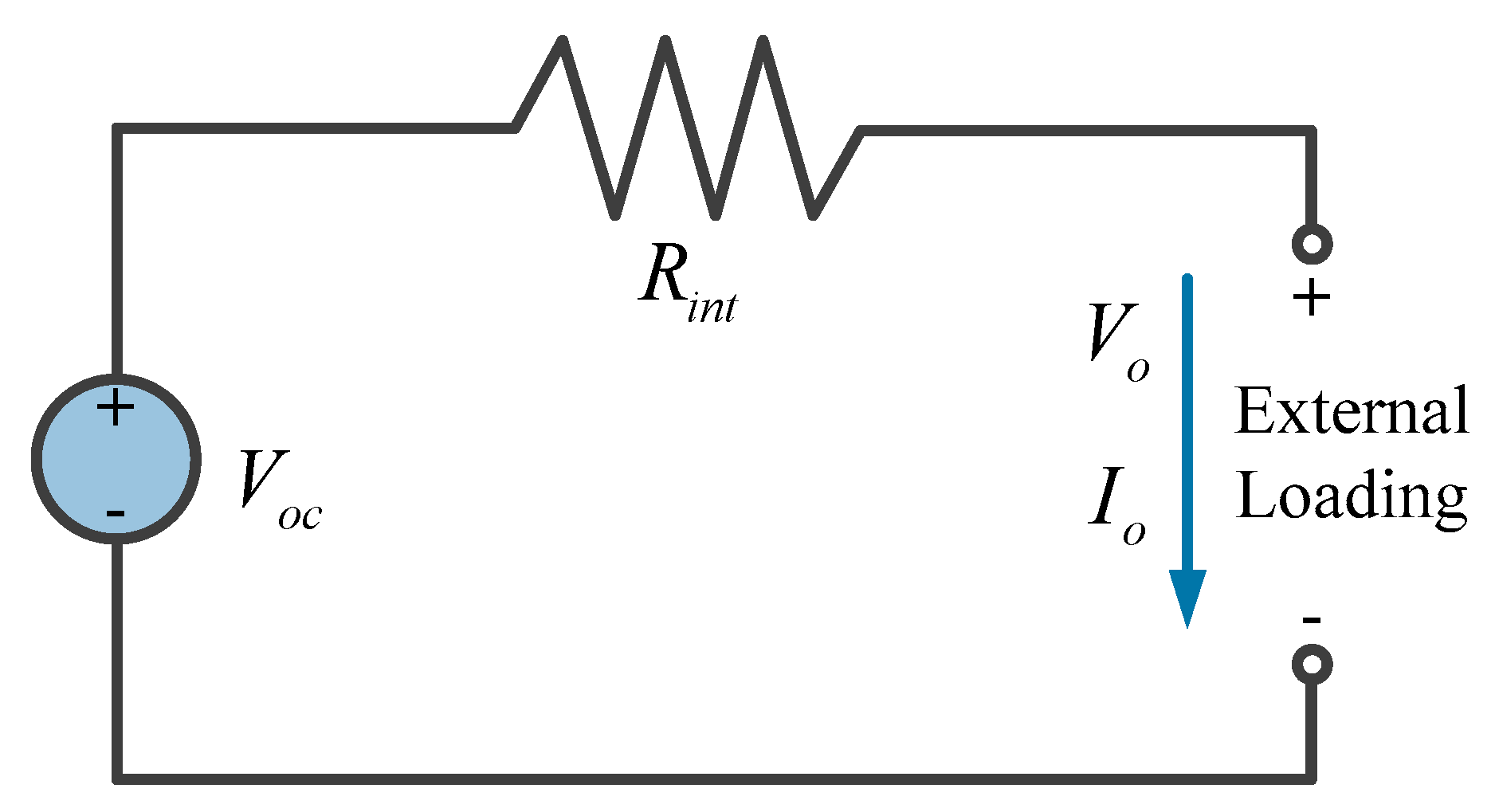
2.3. Power Battery Model
2.4. Longitudinal Dynamic Model
3. Optimization and Matching Design Method of PHEV
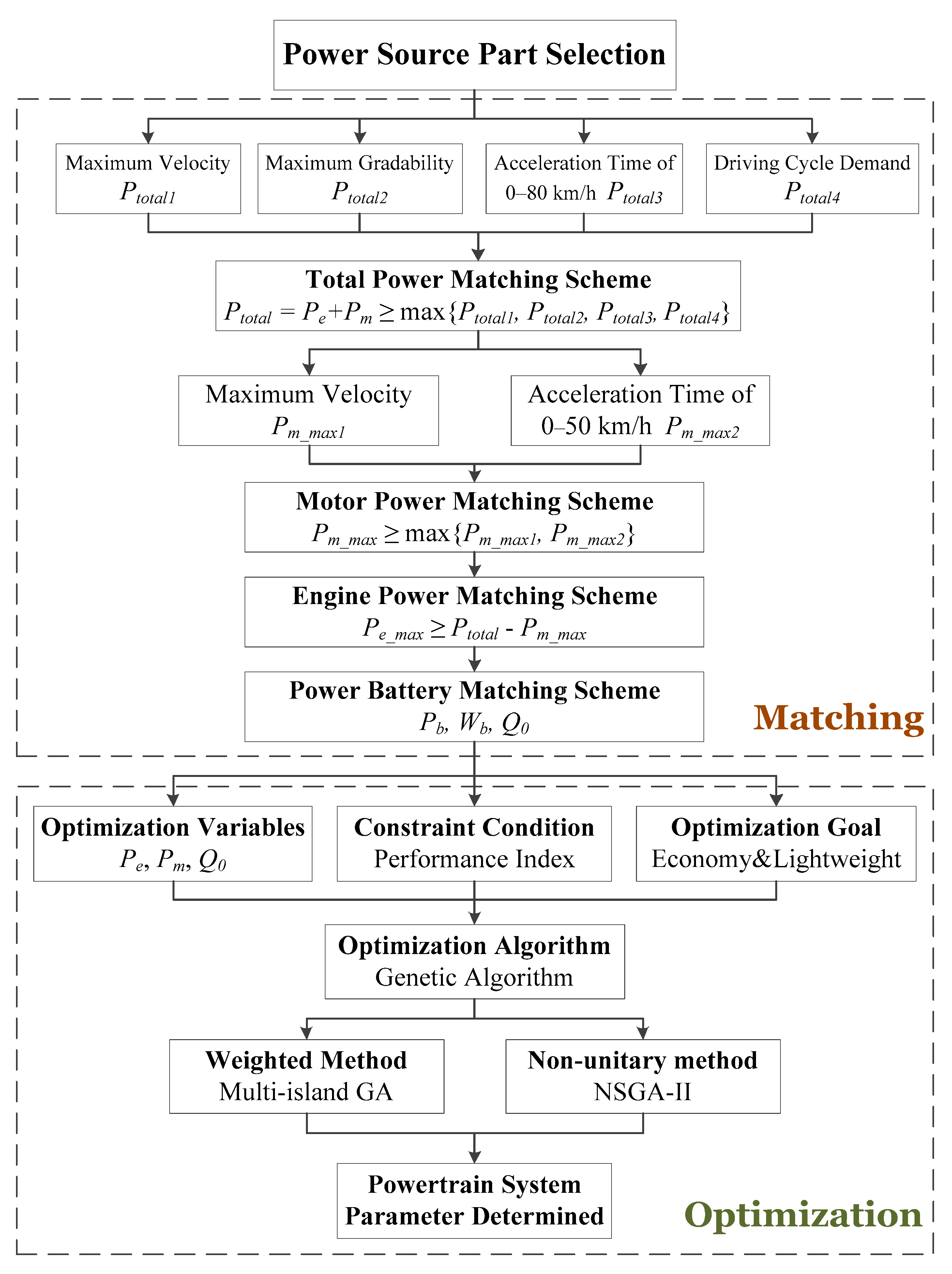
3.1. Analysis of Power Unit Parameters
3.1.1. Determination of Power Source Total Power
3.1.2. Determination of Motor and Engine Power
3.1.3. Determination of Power Battery Parameters
3.2. Construction of Optimization Model
3.2.1. Optimization Variables
3.2.2. Constraint Conditions
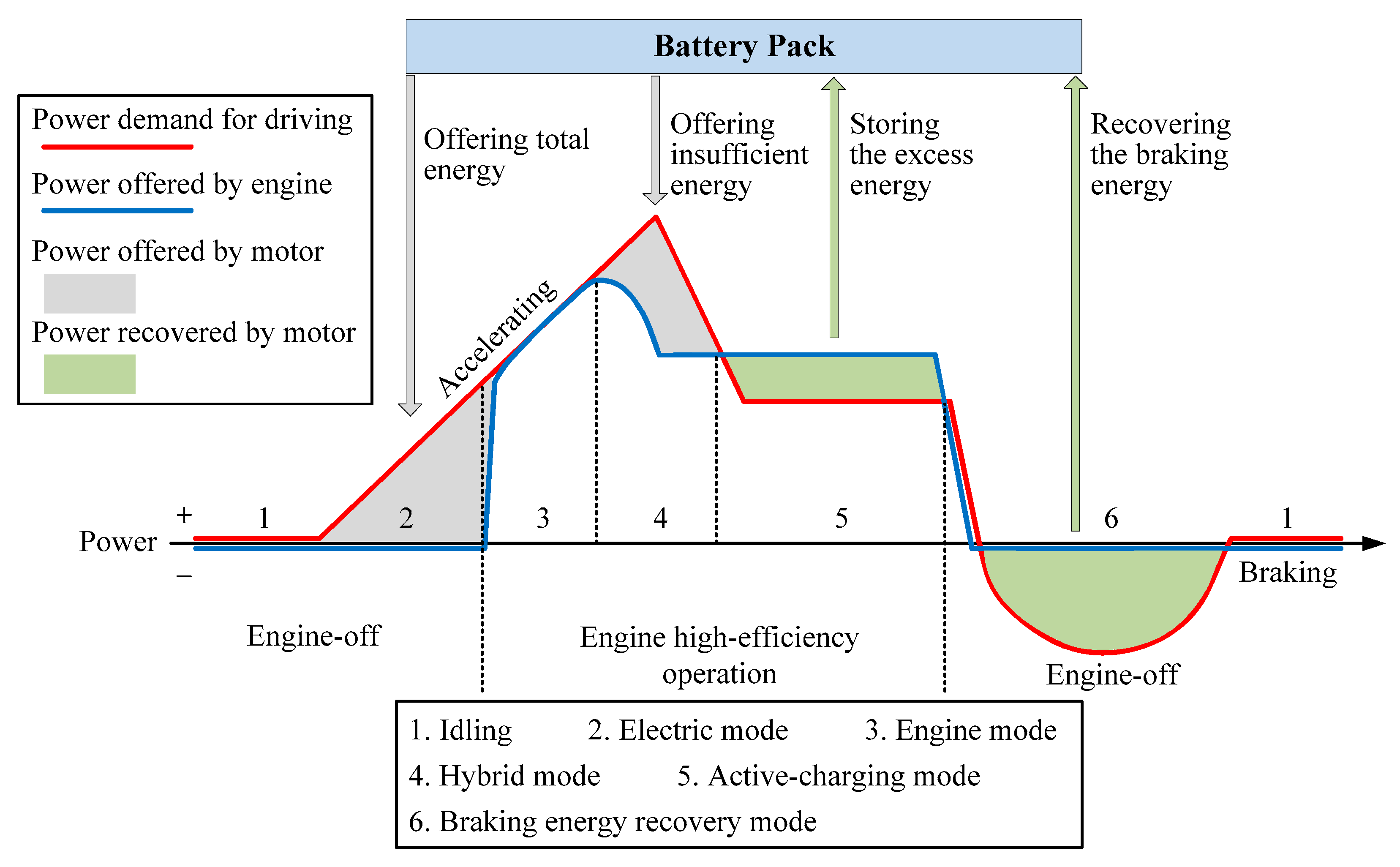
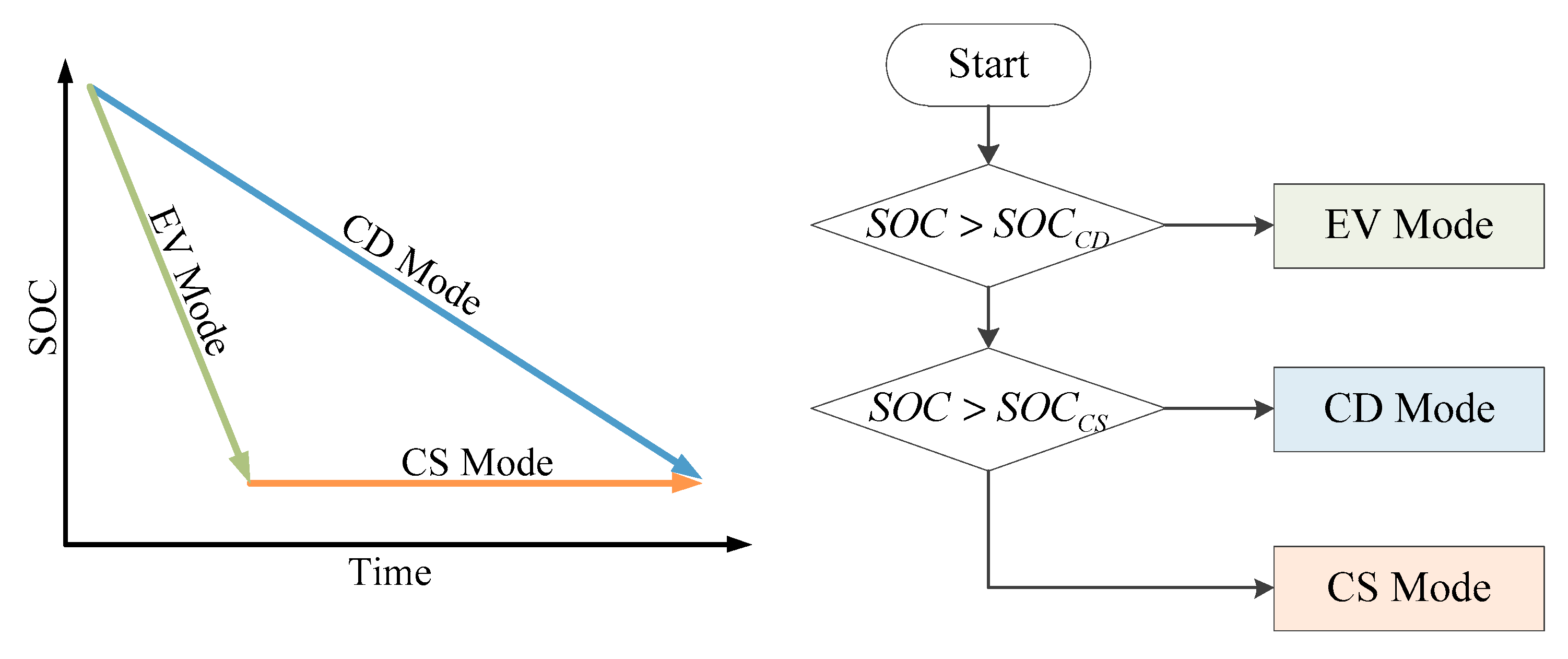
3.2.3. Selection of Energy Management Strategy
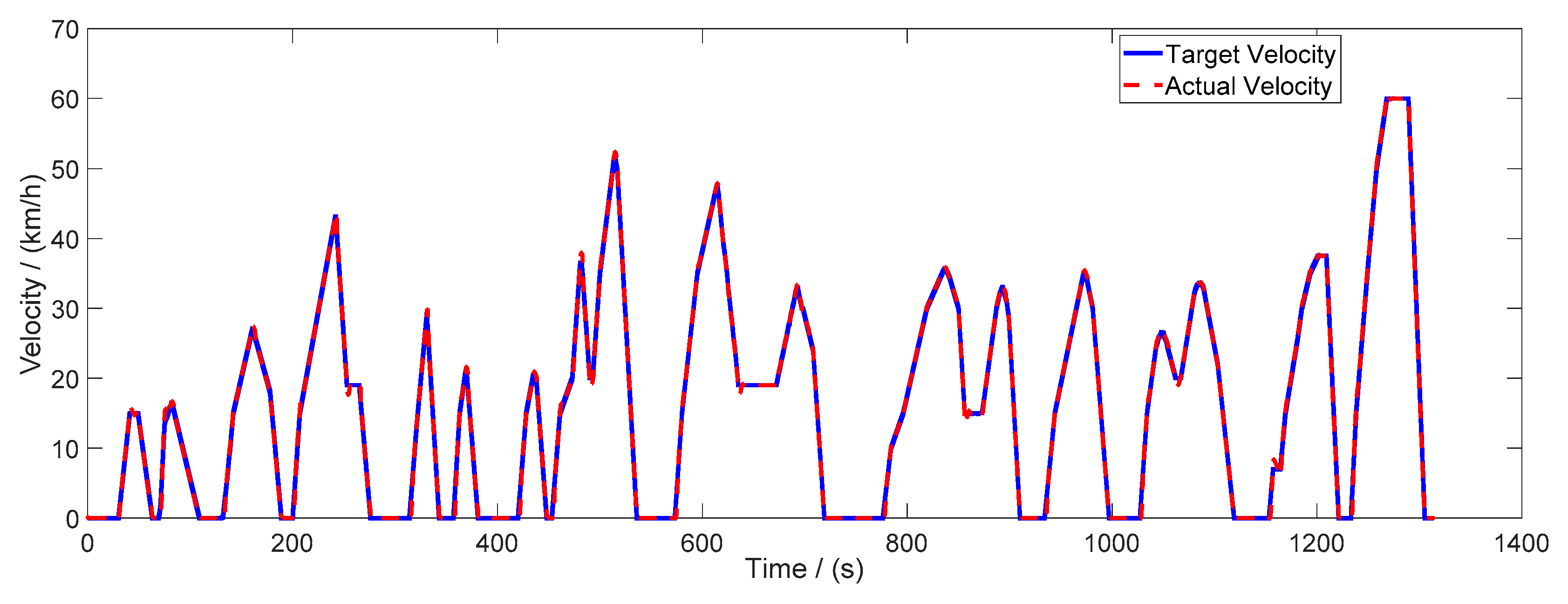
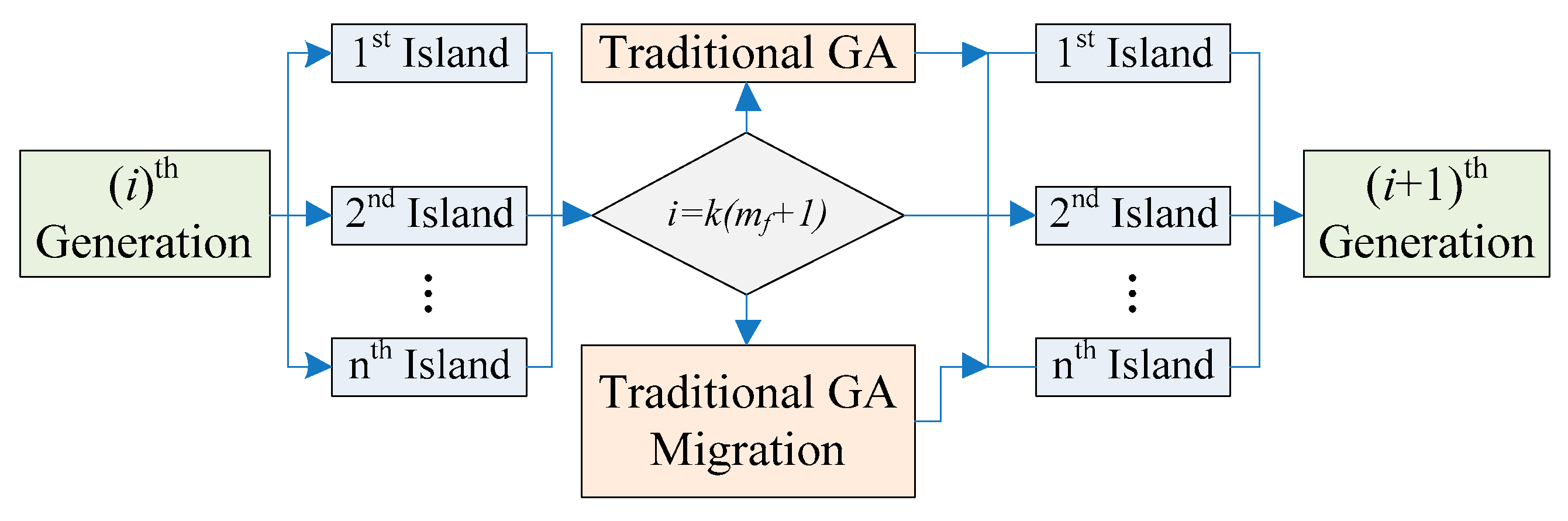
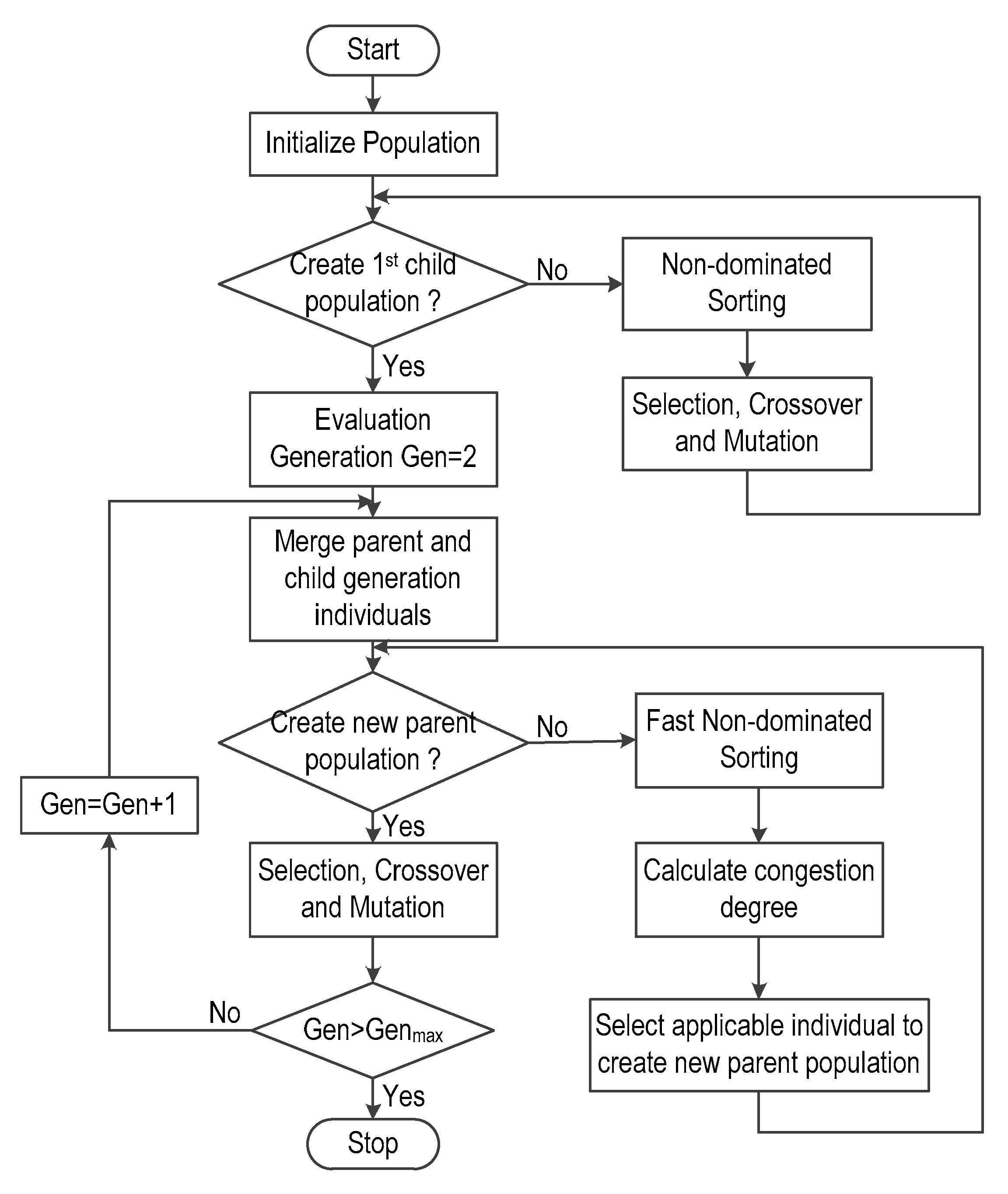
3.2.4. Optimization Platform
4. Multi-Objective Optimization Considering Fuel Economy and Lightweight
4.1. Weighted Method
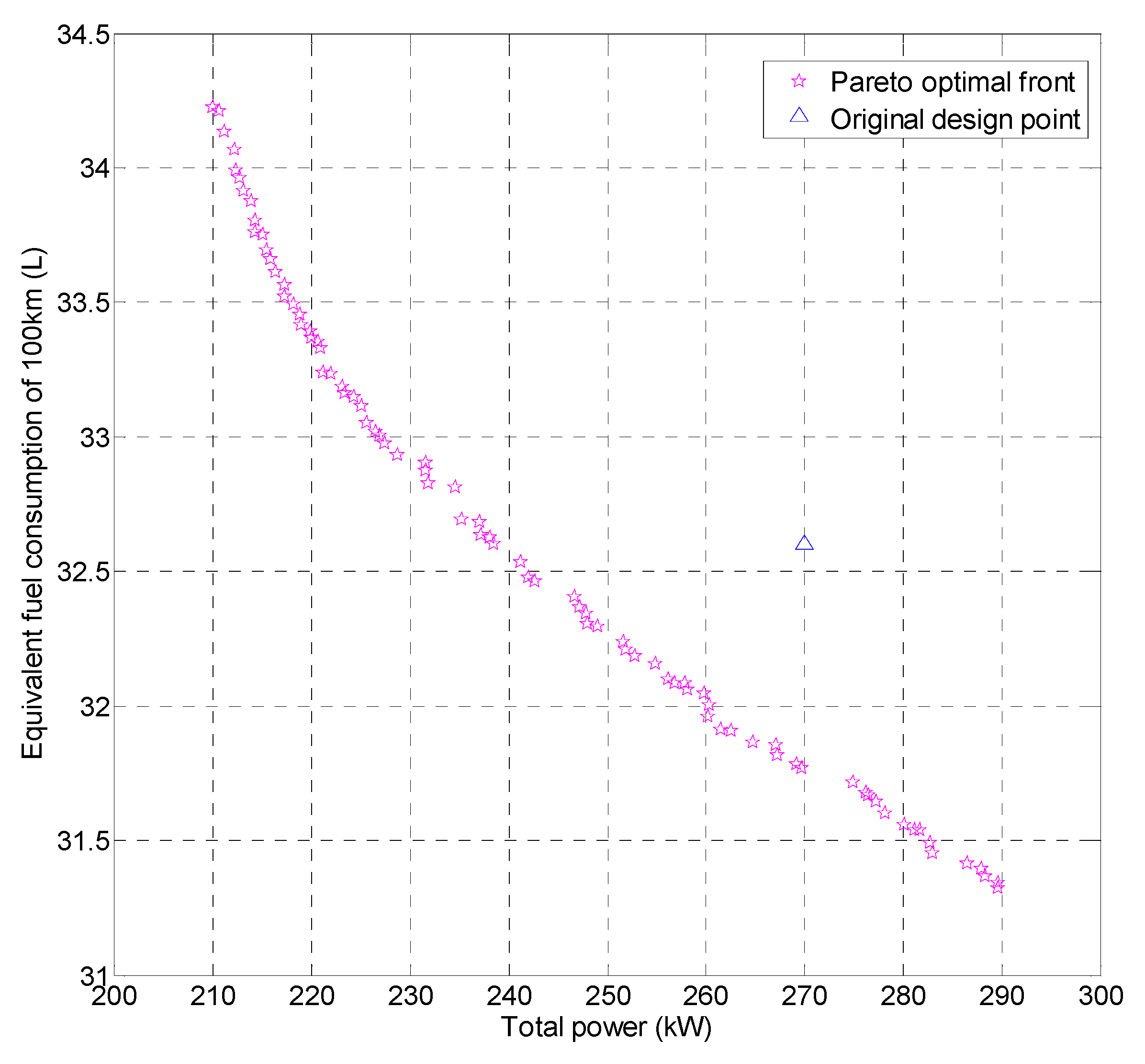
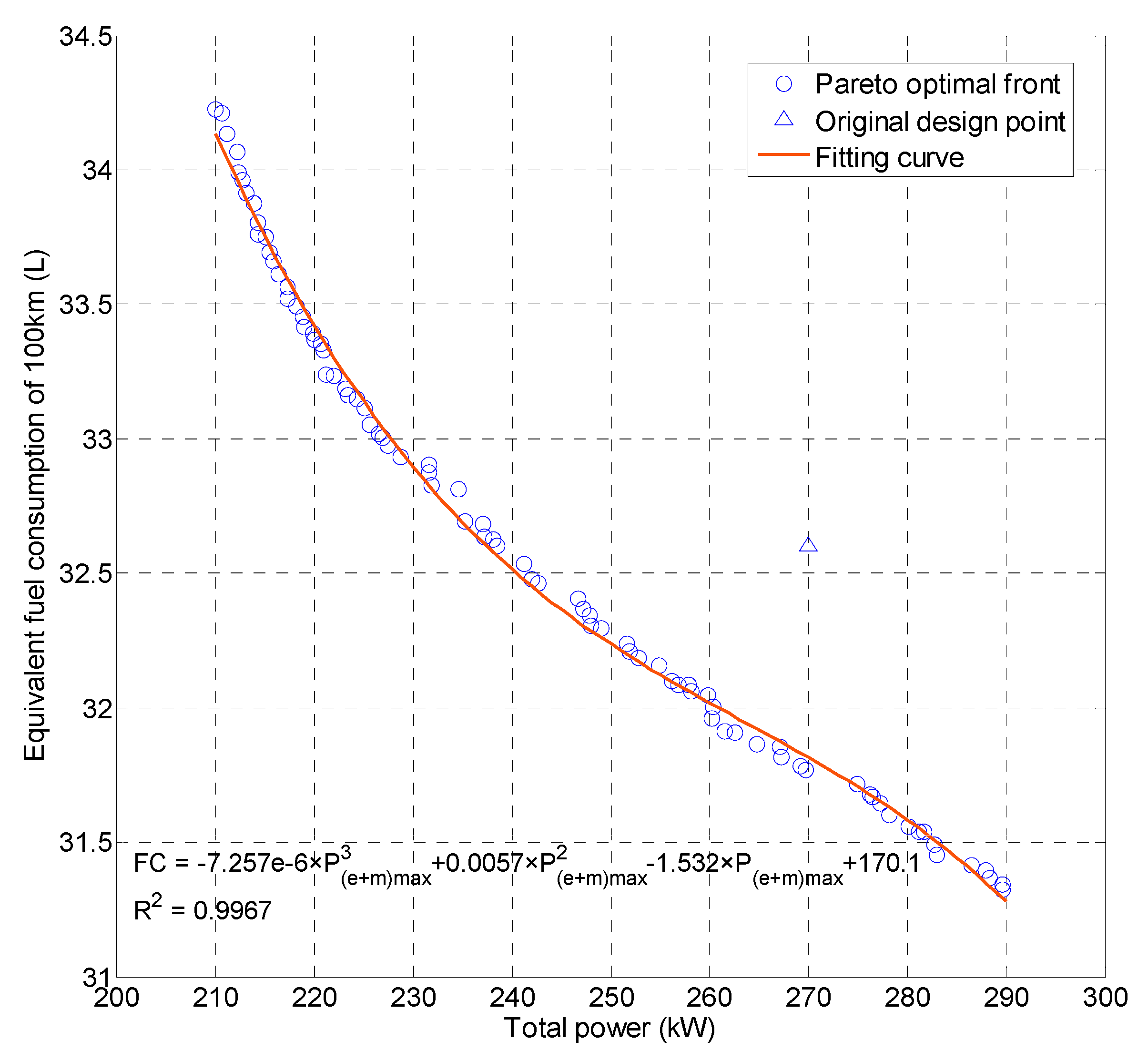
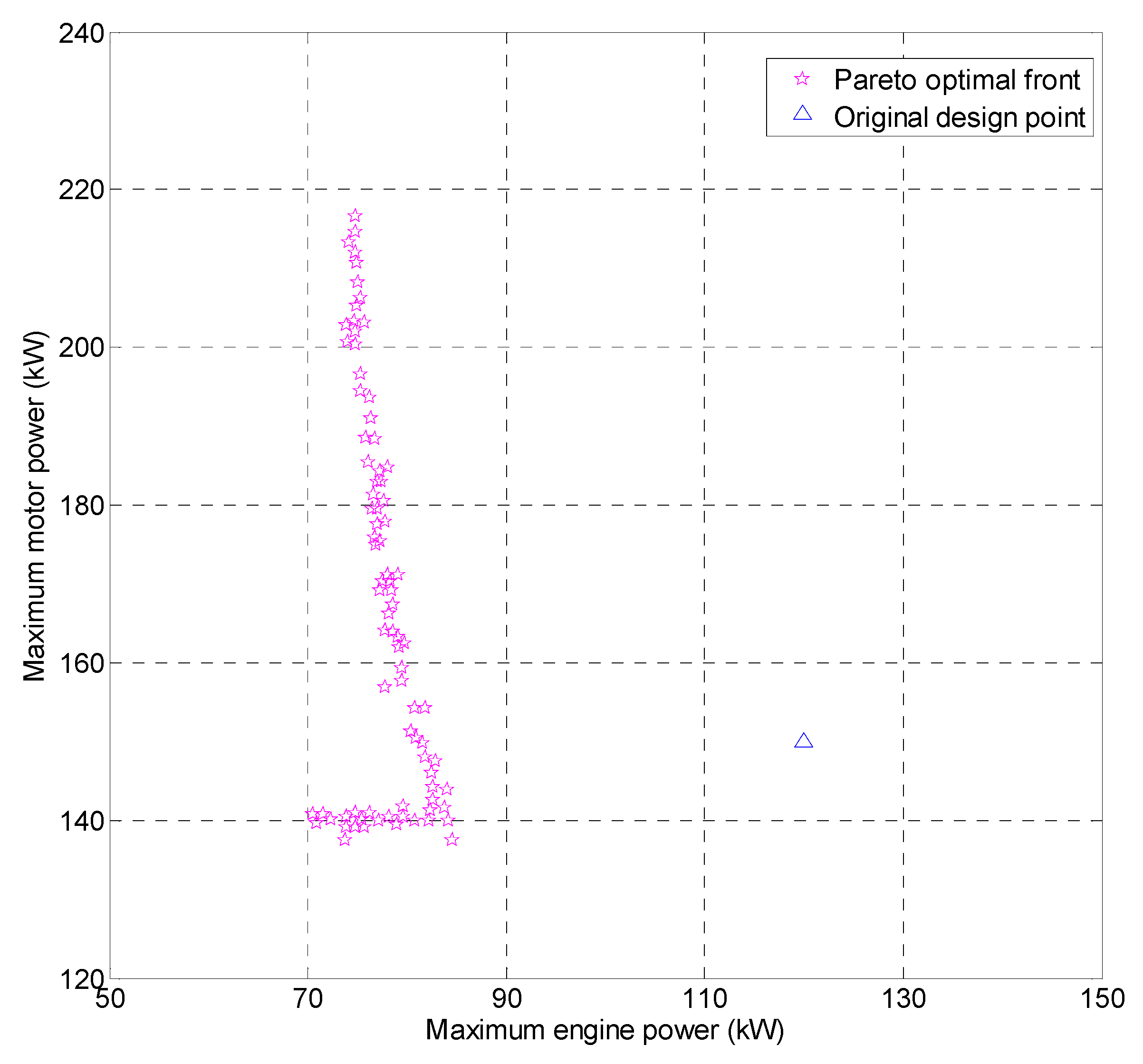
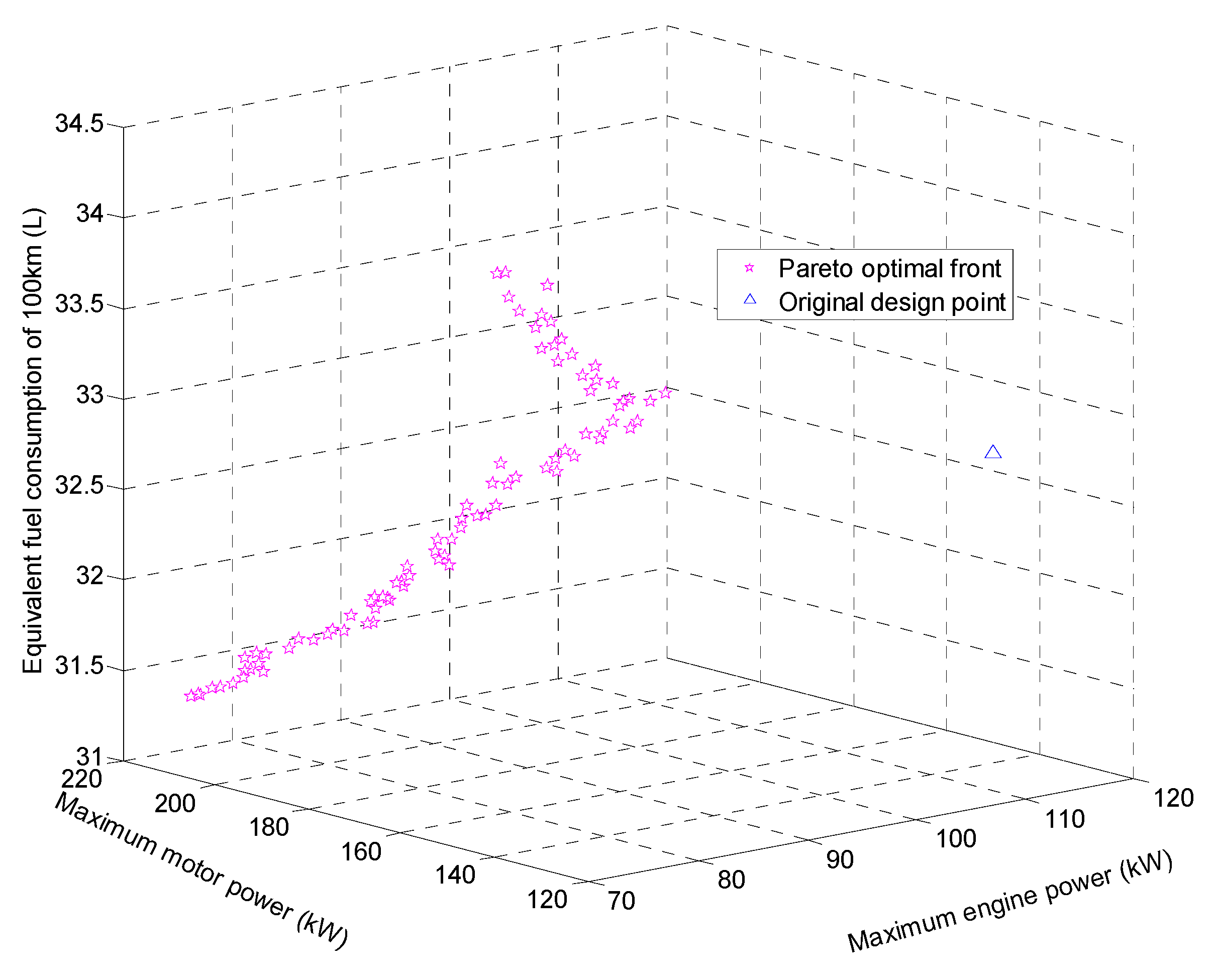
4.2. Non-Normalized Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Al-Alawi, B.M.; Bradley, T.H. Total cost of ownership, payback, and consumer preference modeling of plug-in hybrid electric vehicles. Appl. Energy 2013, 203, 488–506. [Google Scholar] [CrossRef]
- Khayyam, H.; Bab-Hadiashar, A. Adaptive intelligent energy management system of plug-in hybrid electric vehicle. Energy 2014, 69, 319–335. [Google Scholar] [CrossRef]
- Bashash, S.; Moura, S.J.; Forman, J.C.; Fathy, H.K. Plug-in hybrid electric vehicle charge pattern optimization for energy cost and battery longevity. J. Power Sources 2011, 196, 541–549. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.P. Modeling of plug-in hybrid electric vehicle charging demand in probabilistic power flow calculations. IEEE Trans. Smart Grid 2012, 3, 492–499. [Google Scholar] [CrossRef]
- Peng, J.K.; Fan, H.; He, H.W.; Pan, D. A rule-based energy management strategy for a plug-in hybrid school bus based on a controller area network bus. Energies 2015, 8, 5122–5142. [Google Scholar] [CrossRef]
- Amjad, S.; Rudramoorthy, R.; Neelakrishnan, S.; Sri Raja Varman, K.; Arjunan, T.V. Evaluation of energy requirements for all-electric range of plug-in hybrid electric two-wheeler. Energy 2011, 36, 1623–1629. [Google Scholar] [CrossRef]
- Wang, X.M. Optimization Study on Powertrain Matching and System Control for Plug-in Hybrid Electric Urban Bus. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
- Zeng, X.H.; Wang, Q.N.; Wang, W.H. Study on design method for DOH of HEV. Trans. Chin. Soc. Agric. Mach. 2006, 12, 8–12. [Google Scholar]
- Yun, H.T.; Wan, G.; Sun, Z.C. A study on configuration and parameters optimization of drive-train for fuel cell vehicle. Automot. Eng. 2006, 8, 729–733. [Google Scholar]
- Wang, B.H.; Jin, Y.; Luo, Y.G. Parametric optimization of EQ6110HEV hybrid electric bus based on orthogonal experiment design. Int. J. Automot. Technol. 2010, 11, 119–125. [Google Scholar] [CrossRef]
- Wei, Y.Y.; Zhan, W.Z.; Lin, Y. A study on the matching and optimization of FCHEV powertrain. Automot. Eng. 2008, 10, 918–922. [Google Scholar]
- Zhao, Y.E.; Zhang, J.W. Parameter matching and optimization for the powertrain of a FWD fuel cell electric vehicle. Automot. Eng. 2007, 05, 409–414. [Google Scholar]
- Hu, X.S.; Johannesson, L.; Murgovski, N.; Egardt, B. Longevity-conscious dimensioning and power management of the hybrid energy storage system in a fuel cell hybrid electric bus. Appl. Energy 2015, 137, 913–924. [Google Scholar] [CrossRef]
- Gao, W.Z.; Mi, C. Hybrid vehicle design using global optimisation algorithms. Int. J. Electr. Hybrid Veh. 2007, 1, 57–69. [Google Scholar] [CrossRef]
- Wu, X.L.; Cao, B.G.; Wen, J.P.; Wang, Z.B. Application of particle swarm optimization for component sizes in parallel hybrid electric vehicles. In Proceedings of the IEEE World Computational Intelligence, Hong Kong, China, 1–6 June 2008. [Google Scholar]
- Wu, J.; Zhang, C.H.; Cui, N.X. PSO algorithm based parameter optimization for HEV powertrain and its control strategy. Int. J. Automot. Technol. 2008, 9, 53–69. [Google Scholar] [CrossRef]
- Hegazy, O.; Van Mierlo, J. Particle swarm optimization for optimal powertrain component sizing and design of fuel cell hybrid electric vehicle. In Proceedings of the 12th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 20–22 May 2010. [Google Scholar]
- Hegazy, O.; Van Mierlo, J.; Barrero, R.; Omar, N.; Lataire, P. PSO algorithm-based optimal power flow control of fuel cell/supercapacitor and fuel cell/battery hybrid electric vehicles. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2012, 31, 86–106. [Google Scholar] [CrossRef]
- Wu, G.Q.; Chen, H.Y. Multi-objective optimization of HEV parameters based on genetic algorithm. Automot. Eng. 2009, 31, 60–64. [Google Scholar]
- Geng, B.; Mills, J.K.; Sun, D. Energy management control of microturbine-powered plug-in hybrid electric vehicles using the telemetry equivalent consumption minimization strategy. IEEE Trans. Veh. Technol. 2011, 60, 4238–4248. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R. A novel dual-scale cell state-of-charge estimation approach for series-connected battery pack used in electric vehicles. J. Power Sources 2015, 274, 582–594. [Google Scholar] [CrossRef]
- Yu, Z.S. Automobile Theory, 5th ed.; China Machine Press: Beijing, China, 2009; pp. 2–18. [Google Scholar]
- Liu, Y.G.; Li, J.; Ye, M.; Qin, D.T.; Zhang, Y.; Lei, Z.Z. Optimal energy management strategy for a plug-in hybrid electric vehicle based on road grade information. Energies 2017, 10, 412. [Google Scholar] [CrossRef]
- Ba, T. Energy Conservation Analysis and Evaluation for Typical Series-Parallel Hybrid Electric Bus. Ph.D. Thesis, Jilin University, Changchun, China, 2016. [Google Scholar]
- Wu, L.H.; Wang, Y.N.; Yuan, X.F.; Chen, Z.L. Multiobjective optimization of HEV fuel economy and emissions using the self-adaptive differential evolution algorithm. IEEE Trans. Veh. Technol. 2011, 60, 2458–2470. [Google Scholar] [CrossRef]
- Peng, J.K.; He, H.W.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Zhan, S. Energy Management Strategy of Hybrid Electric Vehicle Based on the Recognition of Driving Cycle and Driving Style. Ph.D. Thesis, Chongqing University, Chongqing, China, 2016. [Google Scholar]
- Markel, T.; Simpson, A. Cost-benefit analysis of plug-in hybrid electric vehicle technology. World Electr. Veh. J. 2007, 1, 294–301. [Google Scholar] [CrossRef]
- Hu, X.Z.; Chen, X.Q.; Zhao, Y.; Yao, W. Optimization design of satellite separation systems based on multi-island genetic algorithm. Adv. Space Res. 2014, 53, 870–876. [Google Scholar] [CrossRef]
- Deng, T.; Liu, C.S.; Li, Y.N.; Lu, R.Z. A multi-objective optimization method for energy management control of hybrid electric vehicles using NSGA-II algorithm. J. Xian Jiaotong Univ. 2015, 10, 23. [Google Scholar] [CrossRef]


| Vehicle Parameter | |
| Full mass | 18,000 kg |
| Curb mass | 12,000 kg |
| Aerodynamic resistance coefficient | 0.55 |
| Windward area | 6.6 m2 |
| Wheel radius | 0.473 m |
| Performance Index | |
| Maximum speed | 80 km/h |
| Maximum gradeability | 20% |
| 0–50 km/h Accelerating time (HEV) | 20 s |
| 0–50 km/h Accelerating time (EV) | 25 s |
| Engine | |
| Maximum power | 120 kW (2500 rpm) |
| Maximum torque | 704 Nm (1200–1800rpm) |
| Driving Motor | |
| Rated power/Maximum power | 76 kW/150 kW |
| Rated power/Maximum power | 535 Nm/1584 Nm |
| Power Battery | |
| Voltage class | 576 V |
| Battery capacity | 60 Ah |
| Constraint Conditions | Lower Boundary | Upper Boundary |
|---|---|---|
| Maximum velocity (EV) | 50 km/h | - |
| Maximum velocity (Hybrid) | 80 km/h | - |
| 0-50km/h Accelerating time (EV) | - | 25 s |
| 0-50km/h Accelerating time (Hybrid) | - | 20 s |
| Maximum gradeability | 20% | - |
| Fuel consumption of 100 km | - | 32.6 L |
| Engine power | 68 kW | 150 kW |
| Driving motor power | 120 kW | 225 kW |
| Power battery capacity | 50 Ah | 100 Ah |
| 1st Set | 2nd Set | 3rd Set | 4th Set | |
|---|---|---|---|---|
| w1 | 0.7 | 0.1 | 0.1 | 0.25 |
| w2 | 0.1 | 0.7 | 0.1 | 0.25 |
| w2 | 0.1 | 0.1 | 0.7 | 0.25 |
| w4 | 0.1 | 0.1 | 0.1 | 0.25 |
| Title Design Variables | 1st Set | 2nd Set | 3rd Set | 4th Set | Original |
|---|---|---|---|---|---|
| Pe (kW) | 72.4 | 102.3 | 97.8 | 80.5 | 120 |
| Variation (%) | −39.67 | −14.75 | −18.5 | −32.92 | 0 |
| Pm (kW) | 165.5 | 136.4 | 143.9 | 141.2 | 150 |
| Variation (%) | 10.33 | −9.06 | −4.07 | −5.87 | 0 |
| Q0 (Ah) | 67.3 | 54.3 | 56.1 | 57.7 | 60 |
| Variation (%) | 12.17 | −9.5 | −6.5 | −3.83 | 0 |
| FC (L/100 km) | 32.92 | 32.8 | 32.73 | 32.15 | 32.6 |
| Variation (%) | 0.98 | 0.61 | 0.4 | −0.99 | 0 |
| Parameters | Design Variables | Design Target | |||
|---|---|---|---|---|---|
| Pe_max(kW) | Pm_max(kW) | Q0(Ah) | P(e+m)_max(kW) | FC (L/100 km) | |
| Original | 120 | 150 | 60 | 270 | 32.6 |
| 1st Set | 78.48 | 169.23 | 67.69 | 247.71 (−8.26%) | 32.46 (−0.41%) |
| 2nd Set | 77.50 | 170.30 | 68.12 | 247.80 (−8.22%) | 32.40 (−0.60%) |
| 3rd Set | 78.36 | 170.30 | 68.12 | 248.66 (−7.90%) | 32.37 (−0.71%) |
| 4th Set | 78.11 | 171.11 | 68.44 | 249.22 (−7.69%) | 32.34 (−0.78%) |
| 5th Set | 79.10 | 171.11 | 68.44 | 250.21 (−7.33%) | 32.30 (−0.93%) |
| 6th Set | 76.89 | 174.87 | 69.95 | 251.76 (−6.75%) | 32.28 (−0.98%) |
| 7th Set | 77.26 | 175.41 | 70.16 | 252.67 (−6.42%) | 32.24 (−1.11%) |
| 8th Set | 76.77 | 175.95 | 70.38 | 252.72 (−6.40%) | 32.21 (−1.21%) |
| 9th Set | 77.02 | 177.56 | 71.02 | 254.58 (−5.71%) | 32.18 (−1.28%) |
| 10th Set | 77.75 | 177.83 | 71.13 | 255.58 (−5.34%) | 32.16 (−1.35%) |
| 11th Set | 76.53 | 179.45 | 71.78 | 255.97 (−5.20%) | 32.10 (−1.54%) |
| 12th Set | 77.02 | 179.45 | 71.78 | 256.46 (−5.01%) | 32.09 (−1.57%) |
| 13th Set | 76.65 | 181.33 | 72.53 | 257.98 (−4.45%) | 32.07 (−1.63%) |
| 14th Set | 77.63 | 180.52 | 72.21 | 258.15 (−4.39%) | 32.06 (−1.65%) |
| 15th Set | 77.02 | 182.94 | 73.18 | 259.96 (−3.72%) | 32.04 (−1.70%) |
| 16th Set | 77.39 | 182.94 | 73.18 | 260.33 (−3.58%) | 32.00 (−1.83%) |
| 17th Set | 76.16 | 185.36 | 74.14 | 261.52 (−3.14%) | 31.96 (−1.96%) |
| 18th Set | 77.27 | 184.29 | 73.72 | 261.55 (−3.13%) | 31.91 (−2.11%) |
| 19th Set | 78.00 | 184.82 | 73.93 | 262.83 (−2.66%) | 31.90 (−2.15%) |
| 20th Set | 75.80 | 188.59 | 75.44 | 264.38 (−2.08%) | 31.86 (−2.26%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, P.; Lei, Y.; Fu, Y. Multi-Objective Optimization and Matching of Power Source for PHEV Based on Genetic Algorithm. Energies 2020, 13, 1127. https://doi.org/10.3390/en13051127
Song P, Lei Y, Fu Y. Multi-Objective Optimization and Matching of Power Source for PHEV Based on Genetic Algorithm. Energies. 2020; 13(5):1127. https://doi.org/10.3390/en13051127
Chicago/Turabian StyleSong, Pengxiang, Yulong Lei, and Yao Fu. 2020. "Multi-Objective Optimization and Matching of Power Source for PHEV Based on Genetic Algorithm" Energies 13, no. 5: 1127. https://doi.org/10.3390/en13051127
APA StyleSong, P., Lei, Y., & Fu, Y. (2020). Multi-Objective Optimization and Matching of Power Source for PHEV Based on Genetic Algorithm. Energies, 13(5), 1127. https://doi.org/10.3390/en13051127




