The Influence of the Injected Water on the Underground Coalbed Methane Extraction

Abstract

The increasing demand on coal production has led to the gradually increase of mining depth and more high methane mines, which bring difficulties in terms of coalbed methane (CBM) extraction. Hydraulic fracturing is widely applied to improve the production of CBM, control mine gas, and prevent gas outbursts. It improves coal bed permeability and accelerate desorption and migration of CBM. Even though the impacts of hydraulic fracturing treatment on the coal reservoirs are rare, negative effects could not be totally ignored. To defend this defect, the presented work aims to study the influence of water filtration on coal body deformation and permeability evolution. For this purpose, a simulation based finite element method was developed to build a solid-fluid coupled two-phase flow model using commercial software (COMSOL Multiphysics 5.4). The model was verified using production data from a long strike borehole from Wangpo coal mine in Shanxi Province, China. Several simulation scenarios were designed to investigate the adverse impacts of hydraulic fracturing on gas flow behaviors. The mechanisms of both relative and intrinsic permeability evolutions were analyzed, and simulation results were presented. Results show that the intrinsic permeability of the fracture system increases in the water injection process. The impacts of water imitation were addressed that a critical time was observed beyond which water cannot go further and also a critical pressure exists above which the hydraulic pressure would impair the gas flow. Sensitivity analysis also showed that a suitable time and pressure combination could be observed to maximize gas extraction. This work provides an efficient approach to guide the coal bed methane exploitation and other unconventional gas reservoirs.

1. Introduction

Coal is one of the major energy resources worldwide, and the increasing demand on coal products led to the gradually increasing of mining depth [1]. As a result, higher methane gas mines will be replacing the low methane mines, and new challenges will arise not only in the coal seam mining but also in the coalbed methane (CBM) drainage. Currently, hydraulic fracturing technology plays a basic role in the exploitation of CBM. It is widely used to improve the production of CBM by transforming a reservoir with low permeability and porosity [2]. Additionally, hydraulic fracturing is conducted to control mine gas and prevent gas outbursts [3].

In summary, hydraulic fracturing of coal and rock mass uses high pressure pump to inject water or other fracturing fluids into the coal seam through the borehole. As the injection rate of liquid is higher than the absorption rate of coal rock, tensile or compressive stress is generated on the borehole surface [4]. When the stress exceeds the tensile or compressive strength, fractures in the coal body will be generated, and as the injection process continues, hydraulic fractures extended from the borehole surface to the deep reservoir extension, increasing the number of fractures in the coal and rock and forming the fracture network [5]. This is to improve the coal flow channel, and to achieve the goal of improving the permeability of the coal seam. According to the technical characteristics, the hydraulic fracturing can be divided into four sub-stages as described in Figure 1: (1) Initial and rising pressure stage; (2) fracturing stage; (3) Water drainage stage; and (4) Gas production stage.

Previous studies have mainly focused on fracture expansion direction, formation stress, influencing factors and numerical method modeling [6]. In addition, researches were also focused on the gas flow behavior in the gas extraction process [1,7,8,9,10], from the early single-phase gas flow model to the later two-phase water-gas flow model [11]. Furthermore, the effects of initial permeability, Young’s modulus, water saturation, and other factors on the fluid flow were studied [12]. However, studies on the impact of hydraulic fracturing treatment on the coal reservoirs are limited and only considered the positive impact of hydraulic fracturing on the reservoir, while most of the studies ignoring the negative influences.

The presented work aims to study the influence of water filtration on coal body deformation and permeability, and reveals the mechanism of the effect of water loss on coal body deformation and permeability during hydraulic fracturing, which helps to deepen the process of fracturing and drainage understanding. For this purpose, a simulation based finite element method was developed to build a solid-fluid coupled two-phase flow model using commercial software (COMSOL Multiphysics 5.4). The model was verified using production data from a long strike borehole from Wangpo coal mine in Shanxi Province, China. Several simulation scenarios were designed to investigate the adverse impacts of hydraulic fracturing on gas flow behaviors. The mechanisms of both relative and intrinsic permeability evolutions were analyzed, and simulation results are presented.

2. Method

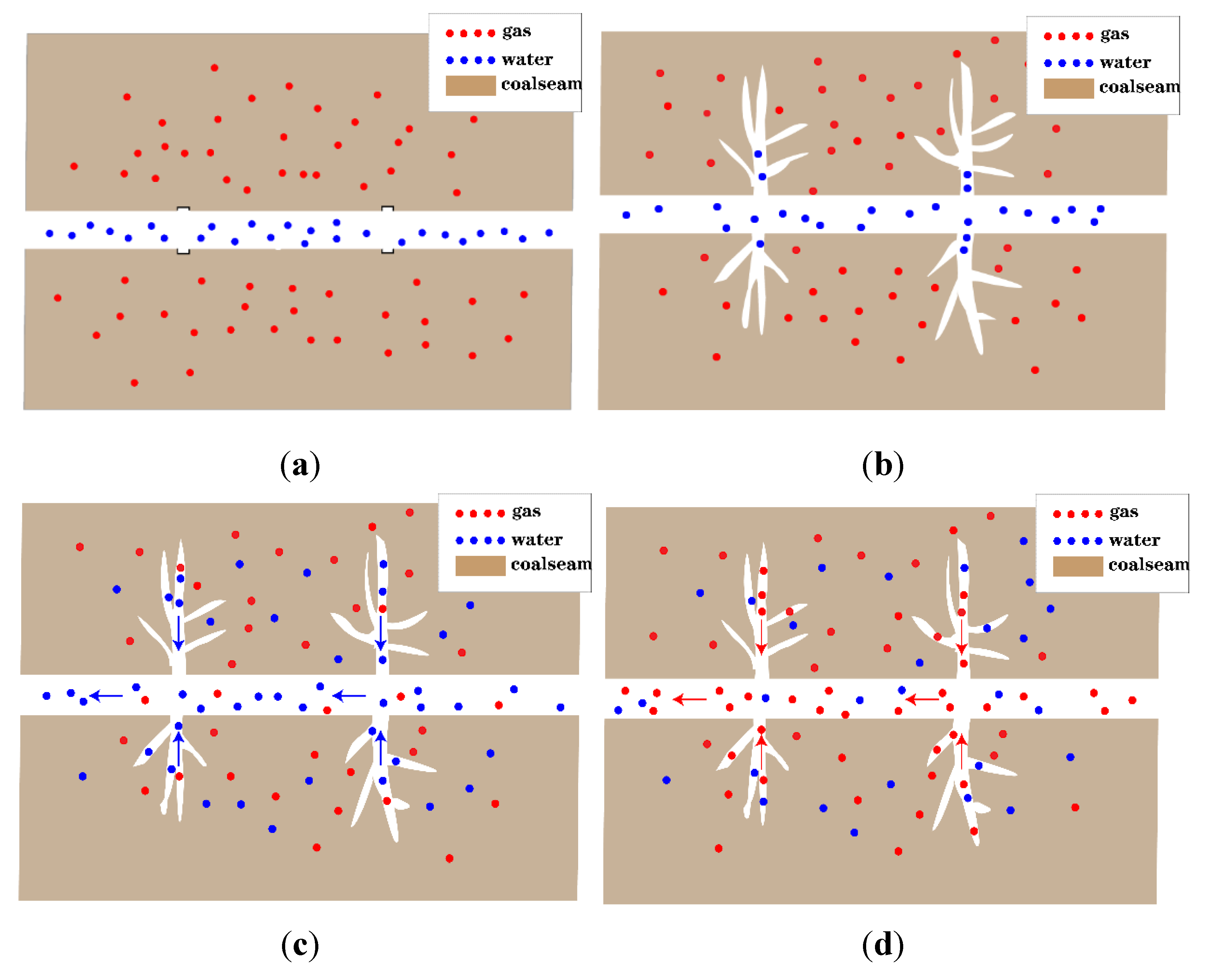
2.1. Model Concept

Hydraulic fracturing of coal and rock mass is a complex Multiphysics process. During the hydraulic pressure rising stage and the hydraulic fracturing stage, there is a fluid loss effect of the fracturing fluid (water). The fluid loss effect of the fracturing fluid causes the liquid water to enter the coal body through the fracture or pore [13], which affects coal volume and permeability.

As shown in Figure 1, under the action of water pressure, the water environment is formed after the fractures penetrate, and the water entering the coal fractures continuously diffuses. Water molecules enter the main fracture network under injection pressure as shown in Figure 2a, and this process could be described by non-Darcy’s law. Water molecules Then enter the secondary fractures partly or mostly into micro-fractures as shown in Figure 2b. This process could be described by Darcy’s law. As water is continuously injected into the coal, the effect of water filtration will become increasingly apparent. When the filtered water enters the pores in the coal matrix of the body from the main or graded fractures or primary fractures in a diffused manner as shown in Figure 2c, the volume and permeability of the coal body will be changed. Water filtration will cause the coal to swell, affecting both the absolute permeability and relative permeability.

2.2. Numerical Analysis

As mentioned before, the hydraulic fracturing is a complex multi-physics, multistage process, and the solid-fluid coupled two-phase flow process could be described by Darcy’s and non-Darcy’s laws, depending on the stage physical requirements. Briefly, the two-phase flow in the main fracture system mass conservation law can be described as:

$$\frac{\partial m_{mf\alpha }}{\partial t}+\nabla \cdot J_{mf\alpha }=Q_{mf\alpha }$$

(1)

where m_mfα is the mass flow, kg/m³, Q_mfα is the flow source or sink, kg/(m³·s), the subscript α represents water (w) and gas (g), the subscript mf is the main fracture system. The mass flux J_mfα of fluid was obtained from [1]. Forchheimer equation was applied to describe non-Darcy effect, as in [10]. The water and gas mass can be calculated as [14]:

$$m_{mfa}=s_{mfa}{\rho }_{mfa}{\varphi }_{mf}$$

(2)

where ρ_mfa is the density of the water or gas (w or g), kg/m³, s_mfa is the saturation of water or gas (w or g), φ_mf is the porosity of the main fracture system where only the free gas is assumed in the main fracture system. For CBM, the gas in the fracture system consists of free gas and adsorbed gas, and the mass sources supplied by the matrix system could be described as [15]:

$$m_{fg}=s_{fg}{\rho }_{fg}{\varphi }_f+{\rho }_{ga}{\rho }_{\mathrm{c}}\frac{V_{fL}{p}_{fg}}{p_{fL}+p_{fg}}+{\rho }_{ga}{\rho }_{\mathrm{c}}{m}_b$$

(3)

where ρ_fg is the density of the gas, kg/m³; s_fg is the saturation of gas; V_fL is the Langmuir volume constant, m³/kg; and p_fL is the Langmuir pressure, Pa. The assumption of pseudo-steady state is made, and the interface pressure pwall is equal to the fracture pressure p_f. The absorbed gas content in equilibrium m_e(p_wall) is calculated by the Langmuir isotherm:

$$m_e(p_{wall})=\frac{V_L{p}_f}{P_L+p_f}$$

(4)

The constitutive deformation relation for the porous medium is defined as [16,17,18]:

$$G{u}_{i,kk}+\frac{G}{1-2v}{u}_{k,ki}-f_f(p_m,p_f,p_{mf})-f_a(p_m,p_f)=f_i$$

(5)

where u is the displacement; K is the bulk modulus, Pa; G is the shear modulus, Pa; f_f is the body force caused by the fluid flow, Pa; f_a is the body force caused by adsorption, Pa, and f_i is the other body force, Pa; p is gas pressure, Pa; α is the Biot coefficient; Subscripts m and f represent the matrix system and fracture system, respectively. As the main fracture and fracture systems contain both gas and water, the fluid pressure can be described as:

$$p=s_w{p}_w+s_g{p}_g$$

(6)

where s_w is water saturation, s_g is gas saturation, p_w (Pa) is water pressure, and p_g (Pa) is gas pressure. The gas adsorption strain can be given as:

$${\epsilon }_s=\frac{{\epsilon }_{L}p}{P_L+p_{}}$$

(7)

where ε_L is the Langmuir strain constant and P_L is Langmuir pressure constant for swelling strain, Pa. The relative permeability can be described by the following equations [19]:

$$k_{rg}=(1-s_{ew}{)}^2(1-s_{ew}{}^2)$$

(8)

$$k_{rw}=\sqrt{s_{ew}}{(1-{(1-s_{ew}{}^{1/m})}^m)}^2$$

(9)

where k_rg and k_rw are the relative permeabilities of gas and water, respectively.

The specific capacity of the water phase $c_{p,w}$ depends on changes in the effective saturation with respect to the capillary pressure as [20]:

$$c_{p,w}=\left(s_r-s_s\right)\frac{\partial s_{ew}}{\partial p_c};s_r=s_{wr}+s_{gr};s_s=1-s_r$$

(10)

In the same way, the specific capacity of the gas phase $c_{p,nw}$ is defined as:

$$c_{p,nw}=\left(s_s-s_r\right)\frac{\partial s_{e,nw}}{\partial p_c}=\left(s_r-s_s\right)\frac{\partial \left(1-s_{ew}\right)}{\partial p_c}=-c_{p,w}$$

(11)

The permeability model of the fracture can be given as:

$$\frac{k_f}{k_{f0}}={(1+\frac{{\alpha }_{mf}}{{\varphi }_{mf0}}(\Delta {\epsilon }_{mfv}+\frac{p_{mf}-p_f}{K_{mf}}))}^3$$

(12)

where φ_f0 is the initial fracture porosity, φ_f is the current fracture porosity. The effective strain of the fracture can be given as [21]:

$$\Delta {\epsilon }_{fe}=\Delta {\epsilon }_{fv}+\delta \Delta {\epsilon }_{fs}-\frac{p_m-p_f}{K_f}-{\mathrm{c}}_{lf}\delta \Delta {\epsilon }_{ms}$$

(13)

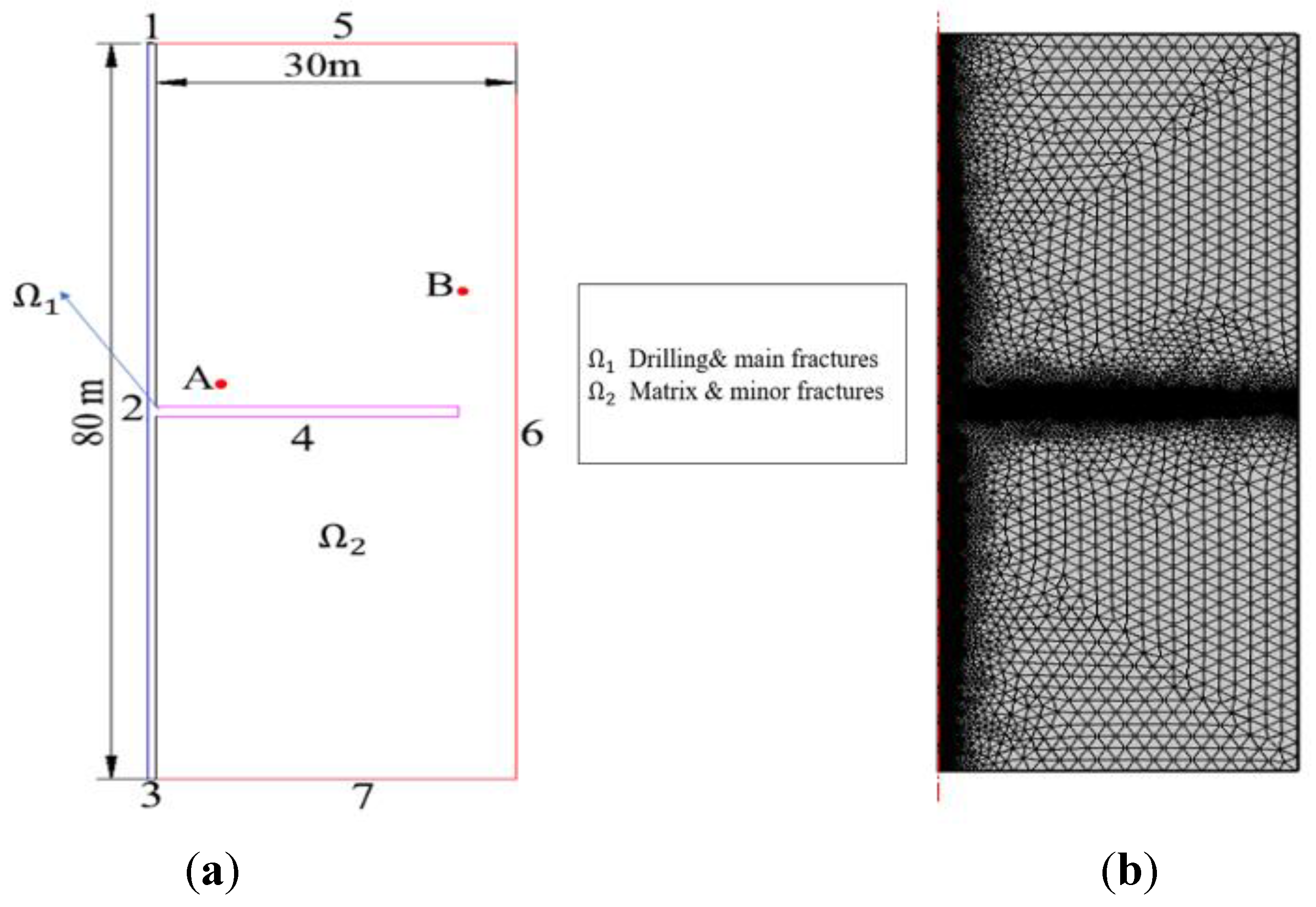
2.3. Model Establishment

Considering that the borehole is symmetrical about the borehole axis in the coal seam and in order to reduce the number of grids, the simulation uses an axisymmetric planar two-dimensional model for calculation shown in Figure 3a. The geometric model had a length of 80 m and a width of 30 m; the radius of the borehole was 0.025 m. The main fracture width was 0.005 m and length was 19.95 m. The model was subjected to overburden gravity of 40 MPa, and the initial pore pressure was 1.2 MPa. The geometric model was meshed with a free-triangle mesh. The complete mesh, shown in Figure 3b, contains 66,025 domain elements and 5302 boundary elements. The average mesh quality is 0.9584 indicating a good mesh. Among them, boundaries 1, 2, 3, 4, 5, 6, and 7 are the corresponding boundaries of the calculation area, the rectangular area surrounded by boundaries 1 and 2 represents the borehole, and boundary 4 is marked with the main fracture.

Physics Field and boundary conditions were set up to mainly model the following two physical processes: (1) water injection stage, (2) gas extraction stage. For the above two processes, in the solution domain (Ω1), two high-speed Darcy flow physics were used to describe the water and gas two-phase flow in the borehole and the main fracture. For the solution domain (Ω2), four Darcy flow physics were used to describe water and gas flow in the matrix and the fracture. The water-gas two-phase flow model of the dual-medium system can be obtained by solving the physical quantity distribution changes of the water phase and gas phase pressure and saturation. For the water injection process, the boundary conditions are defined as following:

• P₁ = P_in (boundary 1)
• P₃ = P_in (boundary 3)

where P_in is the water injection pressure.

During the gas production process, the gas-water two-phase flow in the coal matrix is treated as a Darcy two-phase flow in a dual-porosity medium. The water pressure and gas pressure in the matrix pores are continuous at the boundary. The corresponding mathematical form of this physical part was set to be:

• P_w = P_wf (boundary 4)
• P_g = P_gf (boundary 4)

where P_w and P_g are the water pressure and gas pressure in the matrix, respectively, and P_wf and P_gf are the water pressure and gas pressure in the fracture, respectively.

In both processes of water injection or drainage, the coal seam is confined by compression stress. The mathematical form of the solid mechanical boundary is set to be:

• P = P_s (boundaries 5, 6 and 7)
• n * u = 0 (boundary 7)

where P_s is the formation pressure, n is the boundary normal direction, and u is the displacement vector.

The relevant parameters used in the numerical simulation are shown in

Table 1. Experimental parameters used in the simulation.

Parameter Name	Unit and Value	Parameter Name	Unit and Value
Gas viscosity	1.3 × 10−5 Pa.s	Matrix initial porosity	0.08
Initial reservoir pressure	1.2 MPa	Secondary fracture initial porosity	0.2
Langmuir constant PL	4 MPa	Secondary fracture residual volume fraction	0.05
Langmuir constant VL	0.005 m3/kg	Poisson’s ratio of coal body	0.3
Initial gas density	0.717 kg/m3	Water injection time	10 h
water permeability in matrix	1 × 10−18 m2	Hydraulic fracturing inlet pressure	20 MPa
Initial storage coefficient	3.84 × 10−10 [1/Pa]	Initial gas permeability in fractures	15 × 10−16 m2
Coal density	1300 kg/m3	Biot constant of coal	0.67
Initial gas permeability in matrix	5 × 10−18 m2	Fracture bulk modulus	4 GPa
Initial water pressure in coal	1500 Pa	Initial density of water	1000 kg/m3

[22,23].

2.4. Field Verification

In order to verify the simulation model validity, a field test was conducted in Shanxi Tiandi Wangpo Coal Industry Co., Ltd., Which is located near Jincheng City, Shanxi Province. It is a part of the Fanzhuang exploration area in Qinshui Coalfield. The nearest coal mine is about 20 km northeast whose impact on the studied area can be ignored.

The test site is located at the 3308-working surface of Wangpo Mine. The average thickness of the working surface is 5.5 m, the coal seam inclination is 3°, the coal seam hardness is 0.7, the bedding is stable, the endogenous joint fractures are relatively developed, and the local coal is soft and broken. The gas content is 12 to 14 m³ /t, and the gas pressure is 1.2 MPa. The roof consists of a basic roof of 8.89 m-thick medium sandstone, a direct roof of 4 m thick sandy mudstone, and a pseudo roof of 0.3-m thick carbonaceous mudstone. The floor consists of a direct bottom of 2.1 m thick mudstone or fine sandstone with a thickness of 3.2 m shown in Figure 4.

In order to improve the gas drainage efficiency, the 3308 working surface was transported along the trough to the 3308 working surface coal seam for drilling and hydraulic fracturing. The designed hole depth was 250 m and the hole diameter was 96 mm. Five fracturing boreholes at intervals of 80 m were evenly arranged as shown in Figure 5. From 21 December 2018 to 30 January 2019, hydraulic fracturing was performed on the coal seam of 3308 working surface in Wangpo Coal Mine. Packers with a pressure capacity of 40 MPa were used to perform three-stage fracturing of the borehole. Five holes with the final depth of each borehole were between 246 and 257 m, and the packers are located at 160, 85, and 25 m from the tunnel. The starting pressure of the fracturing sections is 19.1 to 26.3 MPa. During the fracturing process, the holding pressure was 20 MPa, the holding time was 10 h, and the water injection volume in the fracturing section was between 103.74 and 119.3 m³.

3. Results and Discussion

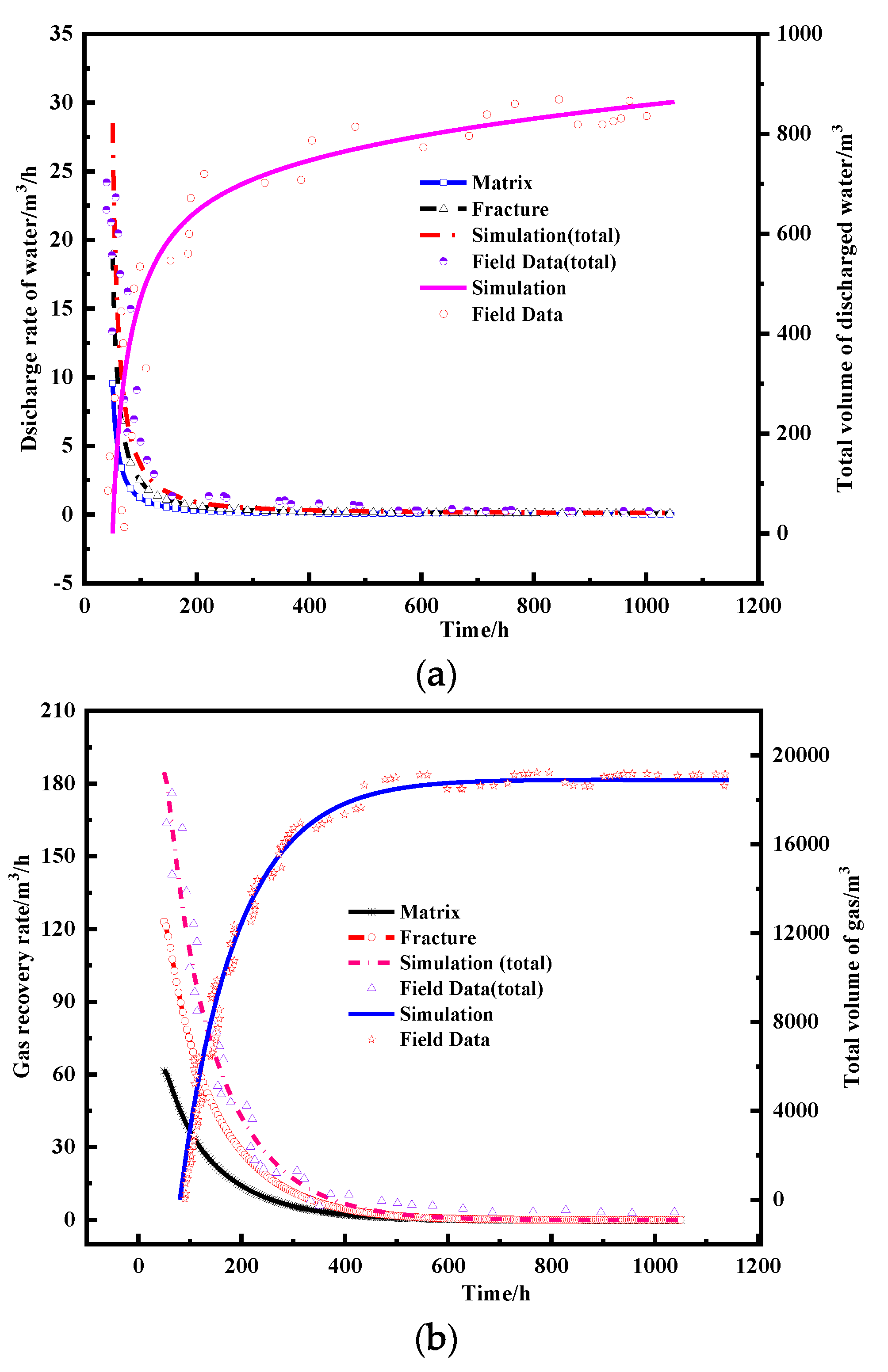
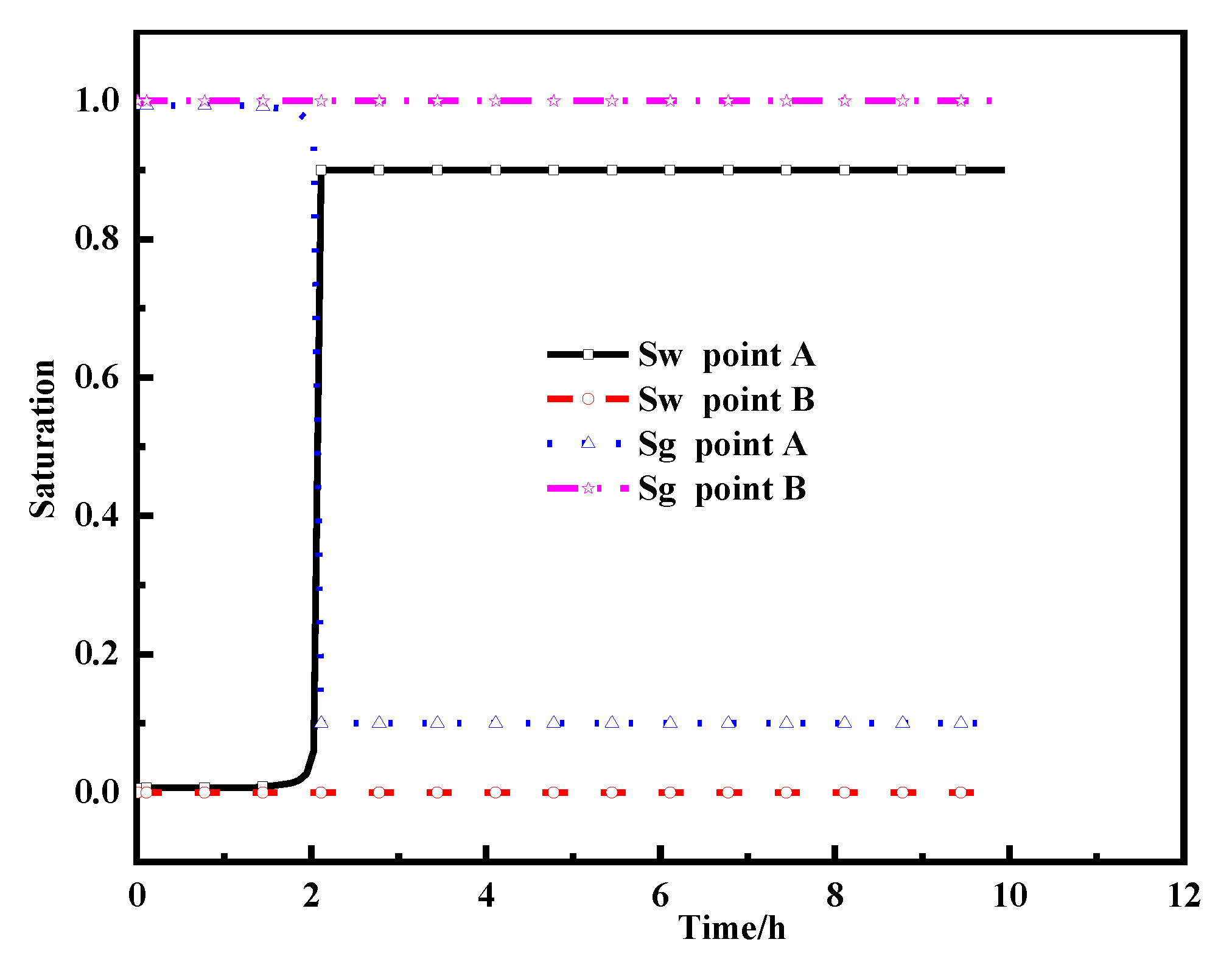
3.1. Field Verification Results

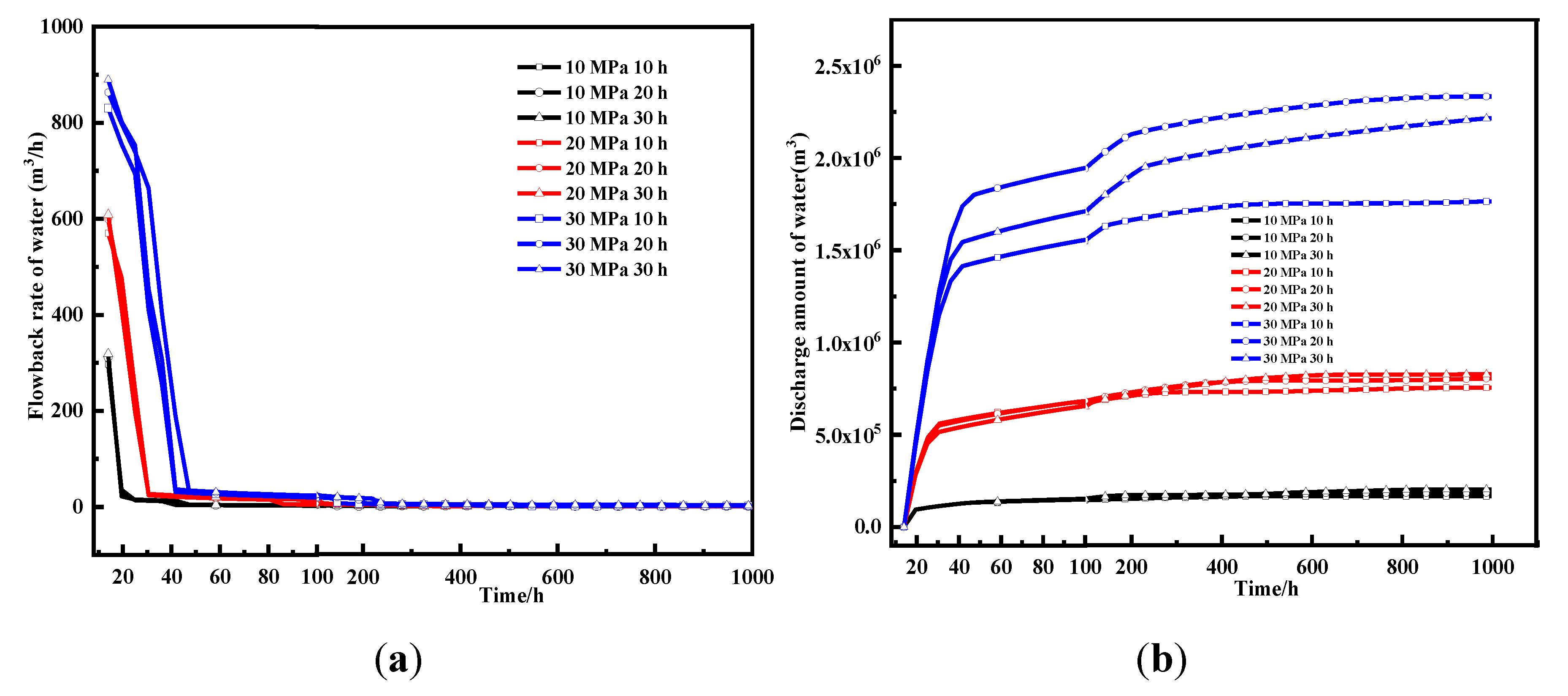
3.1.1. Water Flowback Data

In the hydraulic fracturing process, the water injection flow rate was not recorded. Therefore, the water flowback rate and amount were used for verification. As shown in Figure 6a, it could be observed that the simulation results are in good agreement with the field data both for flow rate and total amount. The total amount increases rapidly within 400 h, then gradually flattens, and then stabilizes after 1000 h, which is close to 890 m³.

3.1.2. Gas Flow Rate

Similarly, it could be noticed that the change trend of the total gas production is in line with the volume, and it also grows rapidly in 400 h, and finally stabilizes at 1.8 × 10⁴ m³. Furthermore, Figure 6b also shown that the gas production rate of the fracture was high before reaching steady state and the gas extraction rate of the fracture system and matrix tends to be the same after 400 h.

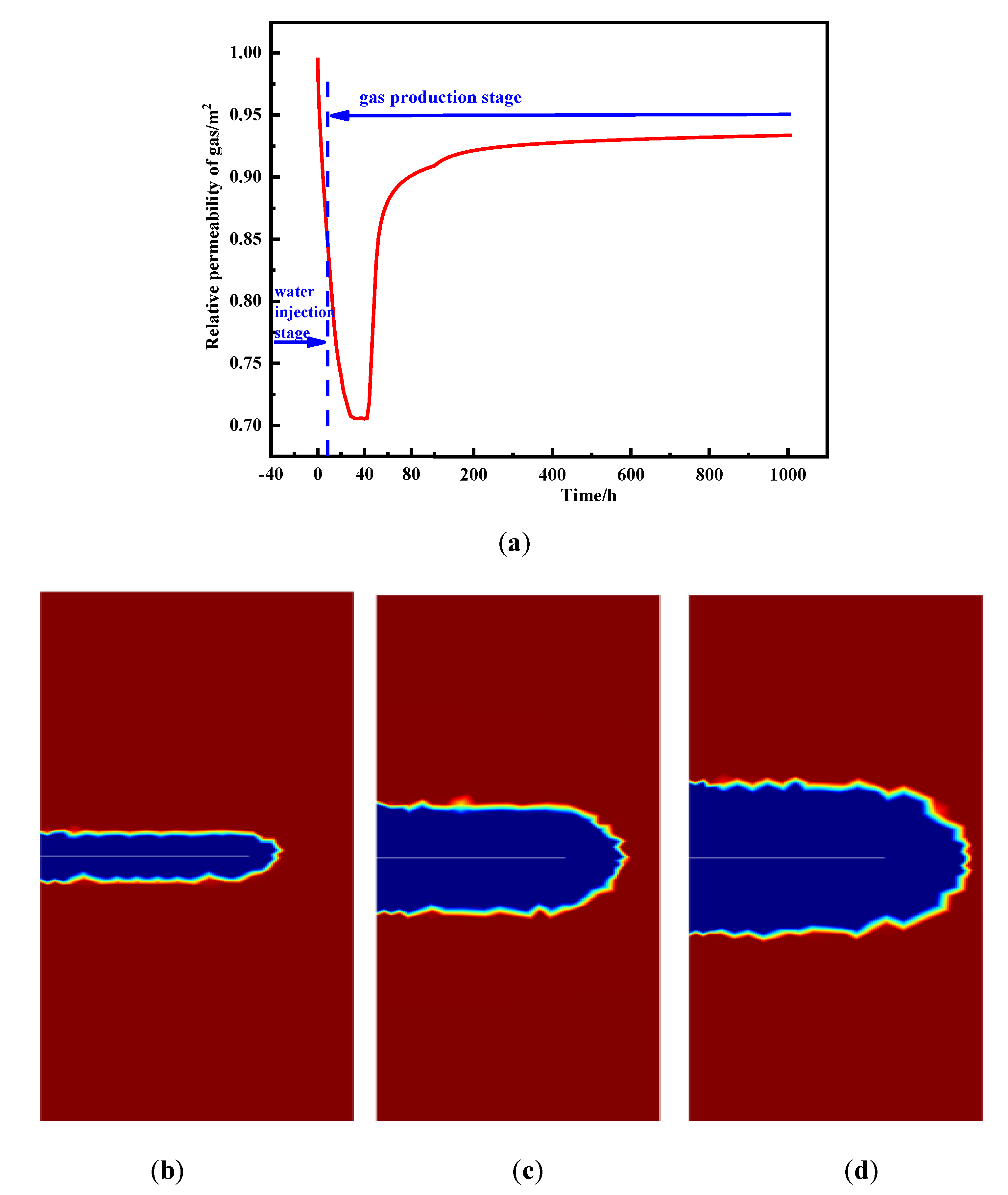
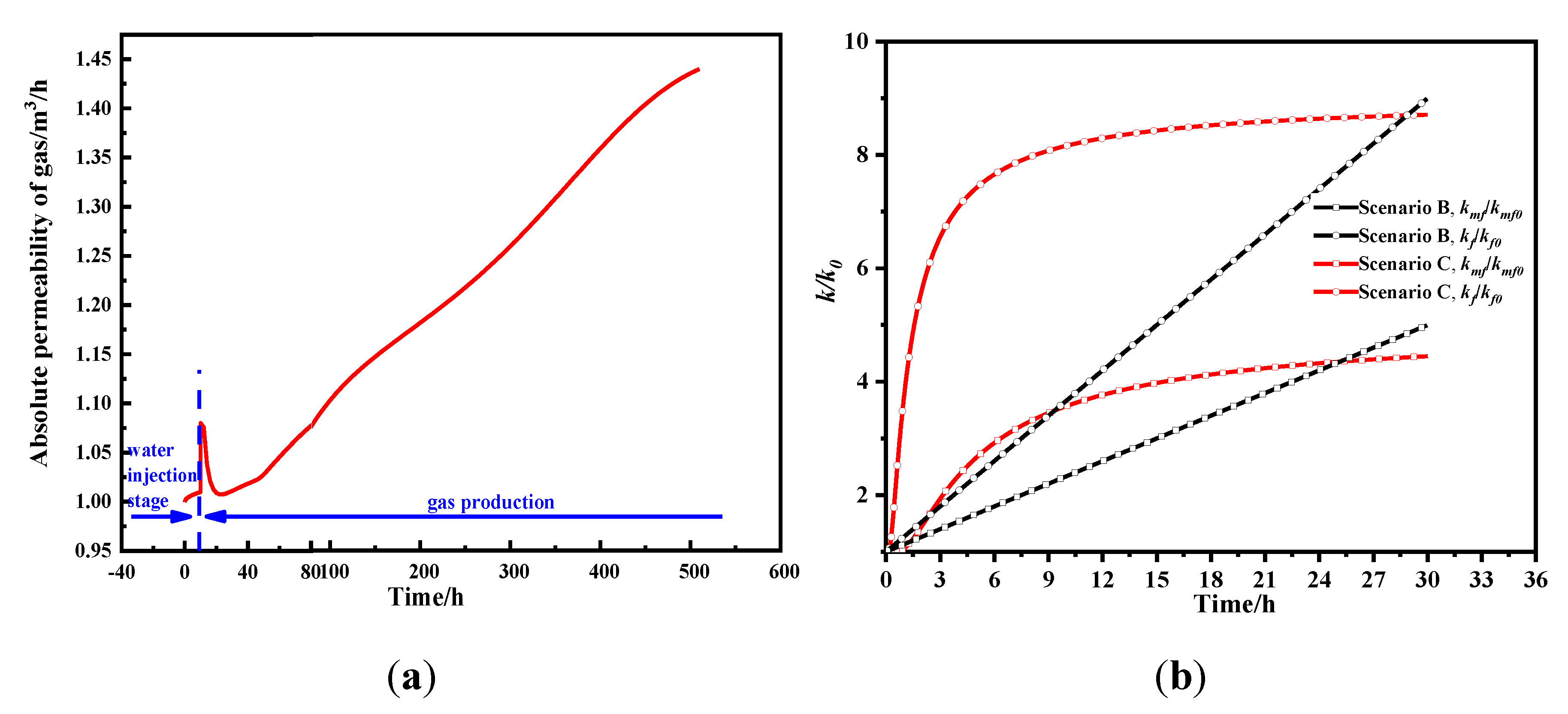
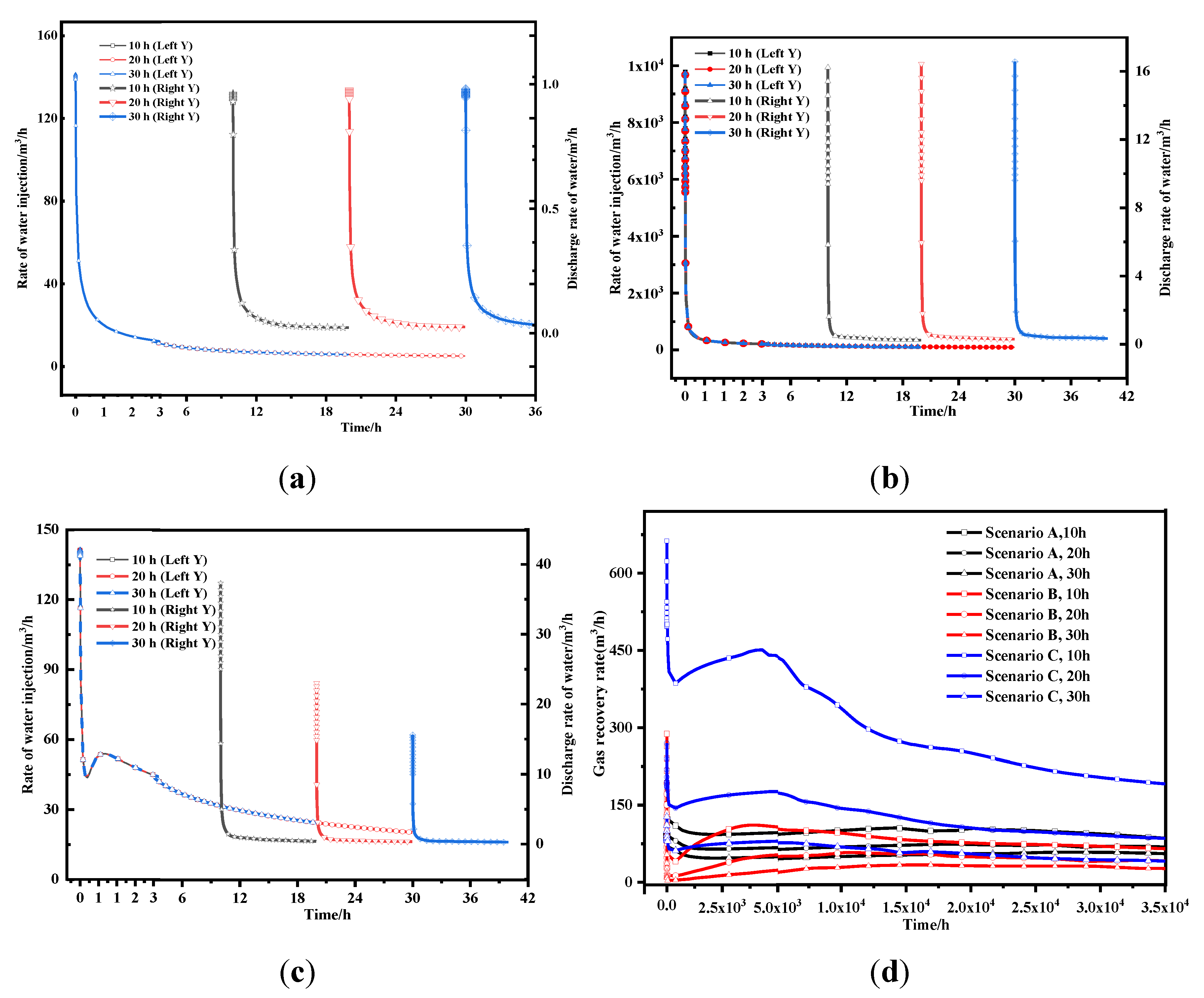
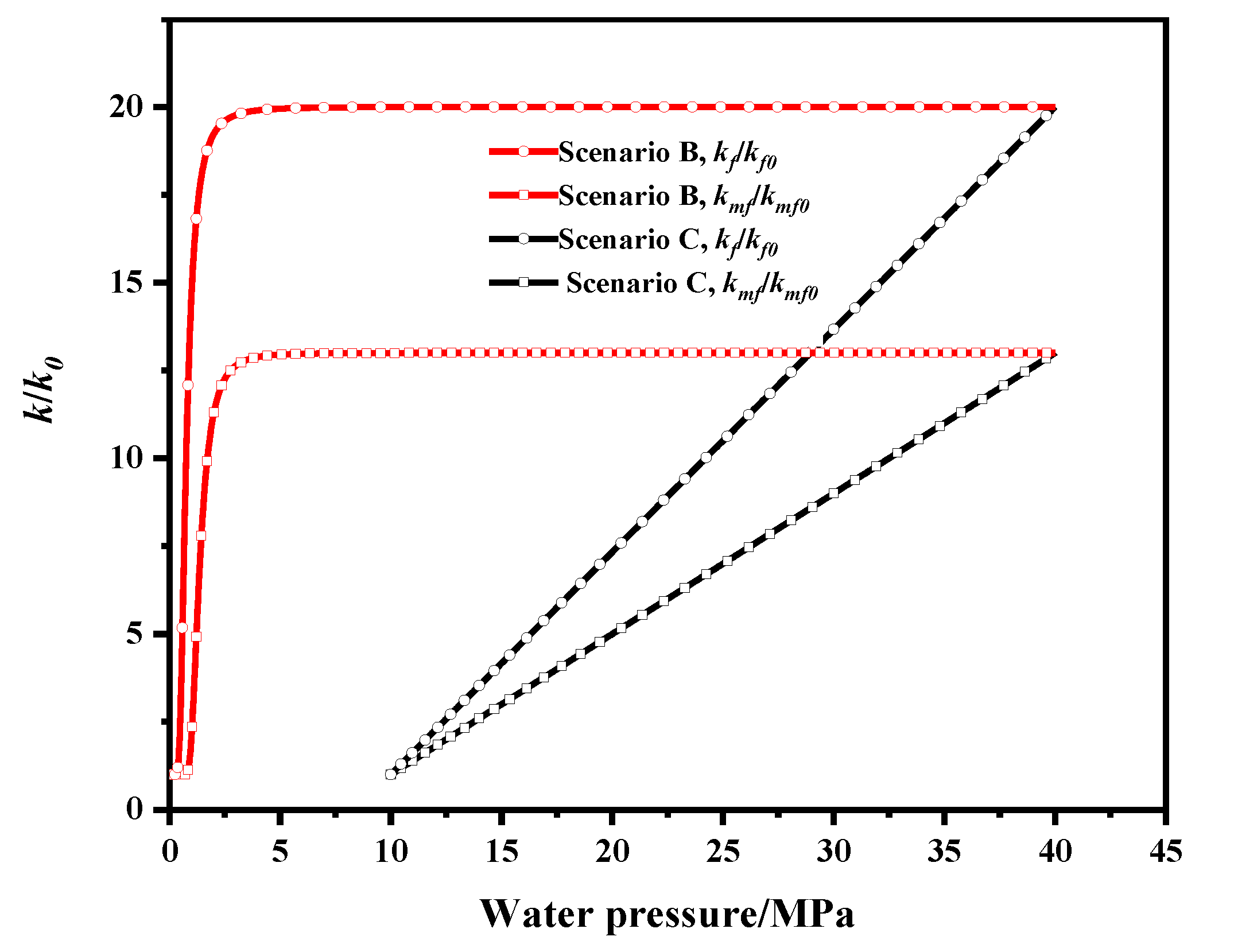
3.2. Simulation Results

As discussed above, the proposed model is in good agreement with the field data. Consequently, the aforementioned model is selected as the benchmark model to investigate the parameter sensitivity. The relative permeability of gas is firstly investigated, and the average value is used here. As it could be noticed from Figure 7, the relative permeability of the gas phase gradually decreases with time in the water injection stage (0–10 h). While in the gas production stage, as time increases, the relative permeability of gas changes with time, showing a trend of first decrease and then increase, and finally tends to a certain fixed value. The first decrease is caused by the high-water saturation in main fracture. The later increase is because of the water flowback process. On the other hand, Figure 7 shows that, as the water injection time advances, the area of the water saturation zone is increasing but remains at a constant volume at the later stage.

Two points were selected to illustrate the variations of gas relative permeability evolution with the point A is in the water saturation area and Point B is out of the water saturation area shown in Figure 3. As Shown in Figure 8, the saturation sum of the water phase and the gas phase is equal to 1. The initial state assumes that the water saturation of the system is 0, and the saturation of point A starts to increase at 2 h and quickly reaches fully saturation state. At the same time, the gas phase saturation of point A decreases rapidly from the initial value of 1. Since point B is far away from the main fracture, its water saturation remains at 0 at the end of water injection, which is exactly consistent with Figure 7d. This characteristic also demonstrates that at the end of water injection process, a large amount of area without water infiltration exists.

The variations of intrinsic permeability were shown in Figure 9a below. Results indicate that: (1) In the water injection stage, the intrinsic permeability gradually increases with time since the internal pressure of the reservoir gradually increases, which further causes the effective volumetric strain of the coal body to increase, and eventually the intrinsic permeability of the coal body continues to increase. (2) In the gas extraction stage, the intrinsic permeability of the gas phase gradually decreases with time, and then rebound. The first decrease is caused by the decrease of fluid pressure and the later increase is caused by the decrease of the adsorption strain because of the gas desorption.

To fully investigate the impact of the injection time on the gas flow characteristic, three scenarios were designed as follows. (1) The intrinsic permeability is independent with the water injection time. (2) The intrinsic permeability is linearly proportion with the water injection time. Where it is assumed that as the water injection time increases, the absolute permeability of the matrix and fractures shows a linear growth trend, the absolute permeability of the matrix is lower than that of the fractures as shown in Figure 9. (3) The intrinsic permeability is proportion with the water injection time but with a threshold. The relationship between hydraulic fracture permeability and water injection time was assumed to follow a non-monotonic rising relationship. As shown in Figure 9b, the fracture permeability begins to saturate at about 3.3 h, and the final value is about nine times the initial value. The permeability tends to stabilize after about five hours, and the final value is about four times the initial value. The water and gas production rate for the three scenarios were shown in Figure 10 below.

Generally, the water injection rate gradually decreases and stabilizes with the increase of the water injection time. This directly illustrates that the water injection rate is not directly related to the total length of the water injection time, and also indirectly reflects that the fracture permeability is not related to the length of the total water injection time. In addition, the reverse discharge rate of water increases with the extension of the total water injection time as shown in Figure 9a.

The increased gas relative permeability and the adsorbed gas in matrix may contribute the multi-peak in gas flow rate. The different among the varied scenarios are also apparent, (1) the gas production rate of Scenario B has approximately doubled compared with results from Scenario A, although the overall change trend is approximately the same. However, the increase in gas production rate is relatively limited. (2) At the same injection time, the gas production rate in Scenario C increased significantly compared to Scenario B, because under the assumption of non-monotonic rise, the absolute permeability growth rate is faster than the monotonic rise, and the gas phase matrix and fracture permeability are larger.

The impact of water injection pressure on gas production was also investigated. Three scenarios were designed to investigate the impacts on the gas flow extractions as shown in Figure 10. (1) The intrinsic permeability is independent with the water injection pressure. (2) The intrinsic permeability is linearly proportional with the water injection pressure. (3) The intrinsic permeability is proportion with the water injection pressure but with a threshold.

The intrinsic permeability variations with injection pressure, the water injection and gas production rate of the three Scenarios were shown in Figure 11 and Figure 12, respectively. Comparing with the previous results, it can be clearly observed that the increase in pressure has significantly improved the water injection rate and the flowback rate.

To investigate the threshold value for the effect of water injection time and water injection pressure on hydraulic fracture permeability, nine working conditions were introduced and solved cumulatively. The water injection times were 10 h, 20 h and 30 h and the water injection pressure were 10 MPa, 20 MPa and 30 MPa. The two influencing factors were cross-combined. Results are shown in Figure 13 and Figure 14.

As it could be noticed in Figure 13, (1) as the water injection pressure is constant, the reverse flow rate of water corresponding to the total time of different water injections shows a decreasing law as a whole, and the change trend is basically identical. It also shows that when the water injection pressure is constant, the longer the total water injection time, the later the time corresponding to the significant difference in the water flowback rate. (2) When the total time of water injection is constant, the impact of the injection pressure on the water flowback rate is obviously not affected.

As shown in Figure 14, the water injection pressure and water injection time have a complicated effect on the gas production rate after comprehensive consideration of the actual situation. Generally speaking, the increase in pressure helps to increase the absolute permeability, but too long a water injection time will lead to a lower relative permeability of the gas phase.

Through comprehensive comparison, it is determined that the working condition of 30 MPa-10 h is the optimal working condition when the extraction time is 10 h. With the extension of the water injection time, the water saturation of the reservoir will gradually increase, which will adversely affect the drainage during the extraction phase; while the water injection pressure will increase the absolute permeability and promote the gas recovery rate during the gas recovery phase, it will also cause the water injection volume in the water injection stage to increase and the water saturation of the reservoir to be higher. This further proves that the initial conjecture in the presented study, that is the effect of hydraulic fracturing on the extraction stage, cannot be ignored.

In the presented study, the ultra-long borehole is taken as an example under the assumption that coal seams are treated as primitive coal seams, and the mining influence of adjacent coal seams is ignored. The proposed research concept and theoretical model can be applied to the CBM extraction through surface vertical well. Only the geometric model and boundary conditions need to be changed for the horizontal wells, vertical wells, and different hydraulic fracturing treatments.

The research ideas in this article can also be applied to other unconventional gas, such as shale gas. The widely application of horizontal well and hydraulic fracturing make the economic exploration of low porosity and permeability shale gas possible [24]. Different from hydraulic fracturing in coal reservoir, a large amount of proppant is usually injected keep the fractures open in shale reservoir [25]. In addition, the pore structure of shale is more complicated, and the heterogeneity is more evident [26], while the research concept in this work is applicable with the modified flow and permeability models.

In order to find a suitable water injection pressure and time for CBM production, a series of assumptions have been made in this work and discussed as the following: (1) the relationship of reservoir intrinsic permeability with water injection pressure and time are assumed artificially. It is well known that a relationship exists between intrinsic reservoir permeability and water injection pressure and time [27,28], while the details about the relationship remain controversial and more experimental work is required. (2) The main fracture network formed by hydraulic fracturing is treated as a rectangular area for equivalence. In fact, the field monitoring equipment such as micro-seismic and acoustic emission shows that the stimulated zone formed by hydraulic fracturing is ellipsoidal, However, the rectangular approach is still widely applied with good results [24,29]. (3) The gas pre-extraction in coal seam by ultra-long boreholes is studied in this work under the assumption that the coal seams in the extraction area are not mined and the mining in the adjacent seam has little impact. Therefore, it is assumed that the change in permeability is only caused by fluid flow. This assumption is feasible.

Nevertheless, further research remains needed, addressing: (1) Determination of the relationship of water injection pressure and time with intrinsic permeability. The relationship is artificially assumed in this work, but in fact this relationship is related to the coal intrinsic properties and needs to be determined experimentally. (2) The representation of the stimulation area induced by hydraulic fracturing. In this article, a fracturing network formed by hydraulic fracturing was equivalently replaced by a rectangle. Although this equivalent efficiency is not bad, it cannot truly reflect the formed fracture network morphology. The fracture network morphology better to be drawn based on acoustic emission or micro-seismic signals and then imported to the numerical model. (3) The anisotropies of the coal seam, including the gas transport abilities and the mechanic properties, were ignored during this research [30]. This might be better to include in any future work.

4. Conclusions

In the presented study, a solid-fluid coupled two-phase flow model is proposed to investigate the impact of injected water imitation on the gas flow behavior. The model is first verified using gas and water production data from a long strike borehole from the Wangpo coal mine in Shanxi Province, China with good fitting results. Several simulation scenarios were designed to address the mechanism of relative and intrinsic permeability evolutions and the impact of the injection time and pressure. Based on the results, the following conclusions could be obtained;

• The evolutions of relative and intrinsic permeability during both water injection and gas production stages are analyzed. The relative gas permeability declines in the water injection process because of water imitation and then rebounds during the gas production stage. The intrinsic permeability of the fracture system increases in the water injection process and is determined by the competing mechanism between effective stress and gas desorption in the gas production stage.
• Regarding water injection time and pressure impacts, the longer water injection time and larger injection pressure brings larger intrinsic permeability increase and also significant decrease in gas relative permeability. Furthermore, there is a critical injection time beyond which water cannot go further while a critical injection pressure exists above which the hydraulic pressure would impair the gas flow.
• To maximize gas extraction efficiency; a suitable injection time and injection pressure combination can be designed in the presented simulation, where the injection time should be short to prevent water imitation while the injection pressure should be in the middle scale once beyond the strength of the coal.