Direct Consideration of Eddy Current Losses in Laminated Magnetic Cores in Finite Element Method (FEM) Calculations Using the Laplace Transform
Abstract
:1. Introduction
2. Proposed Computational Method
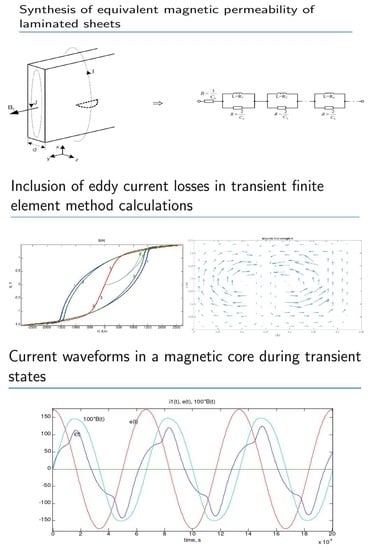
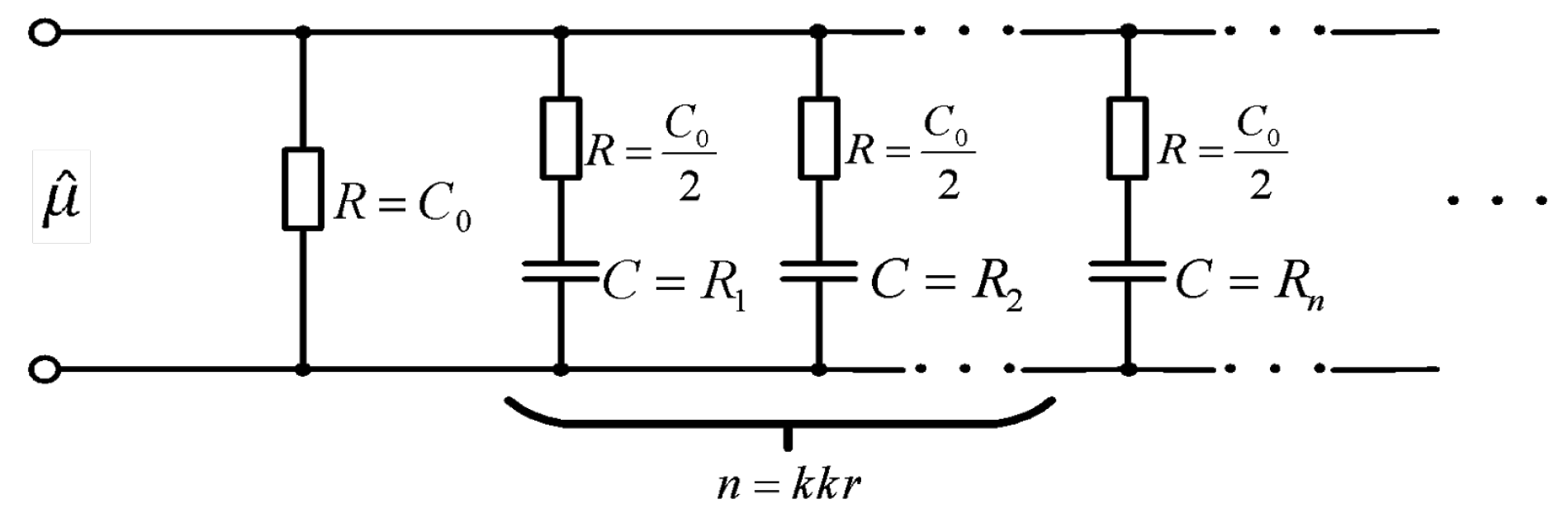
2.1. Direct Synthesis of Equivalent Magnetic Permeability of Laminated Sheets in the Form of a Transfer Function of an IIR Filter
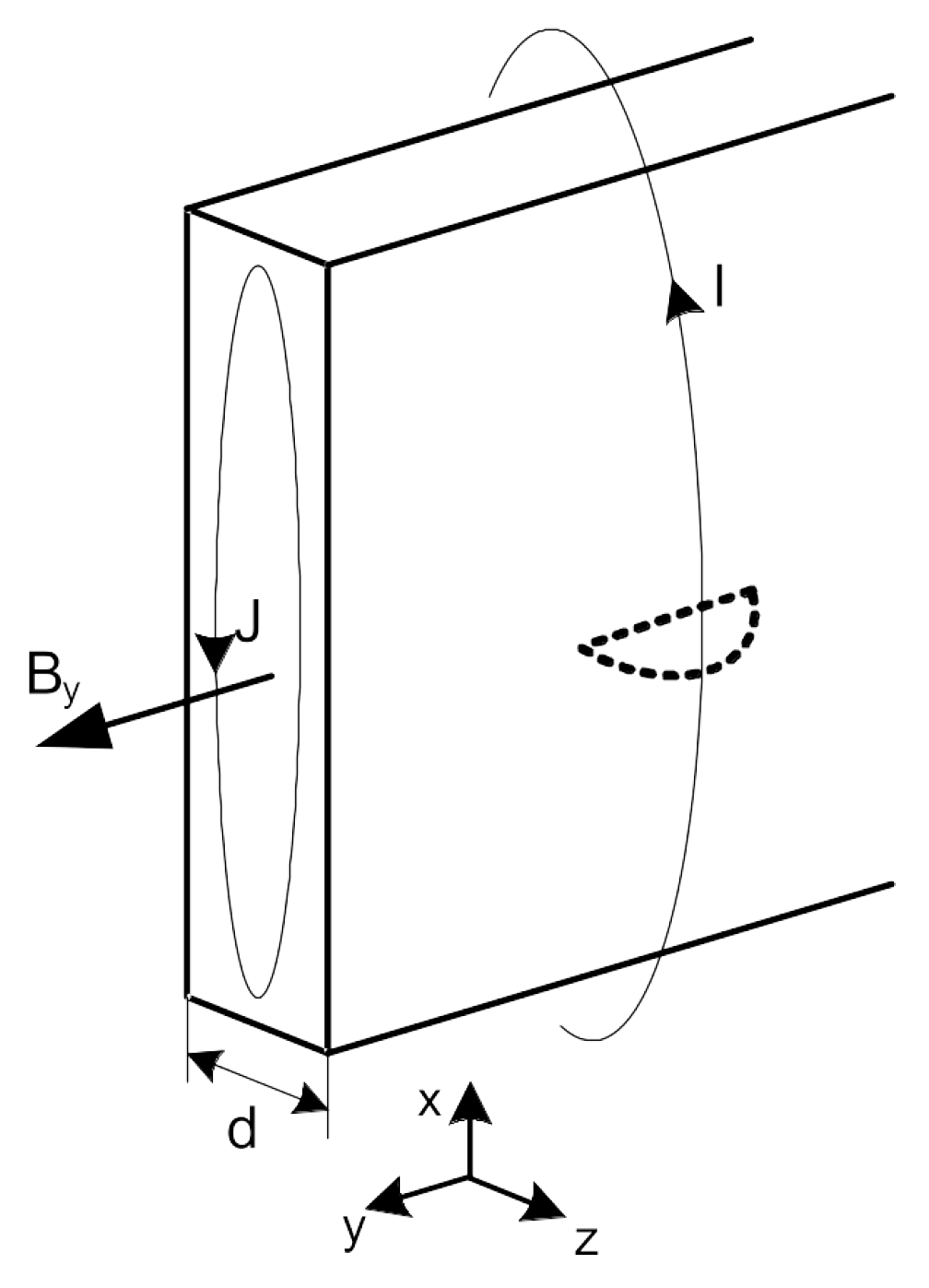
2.2. Inclusion of Eddy Current Losses in the Laminated Magnetic Circuit in Transient Finite Element Method Calculations
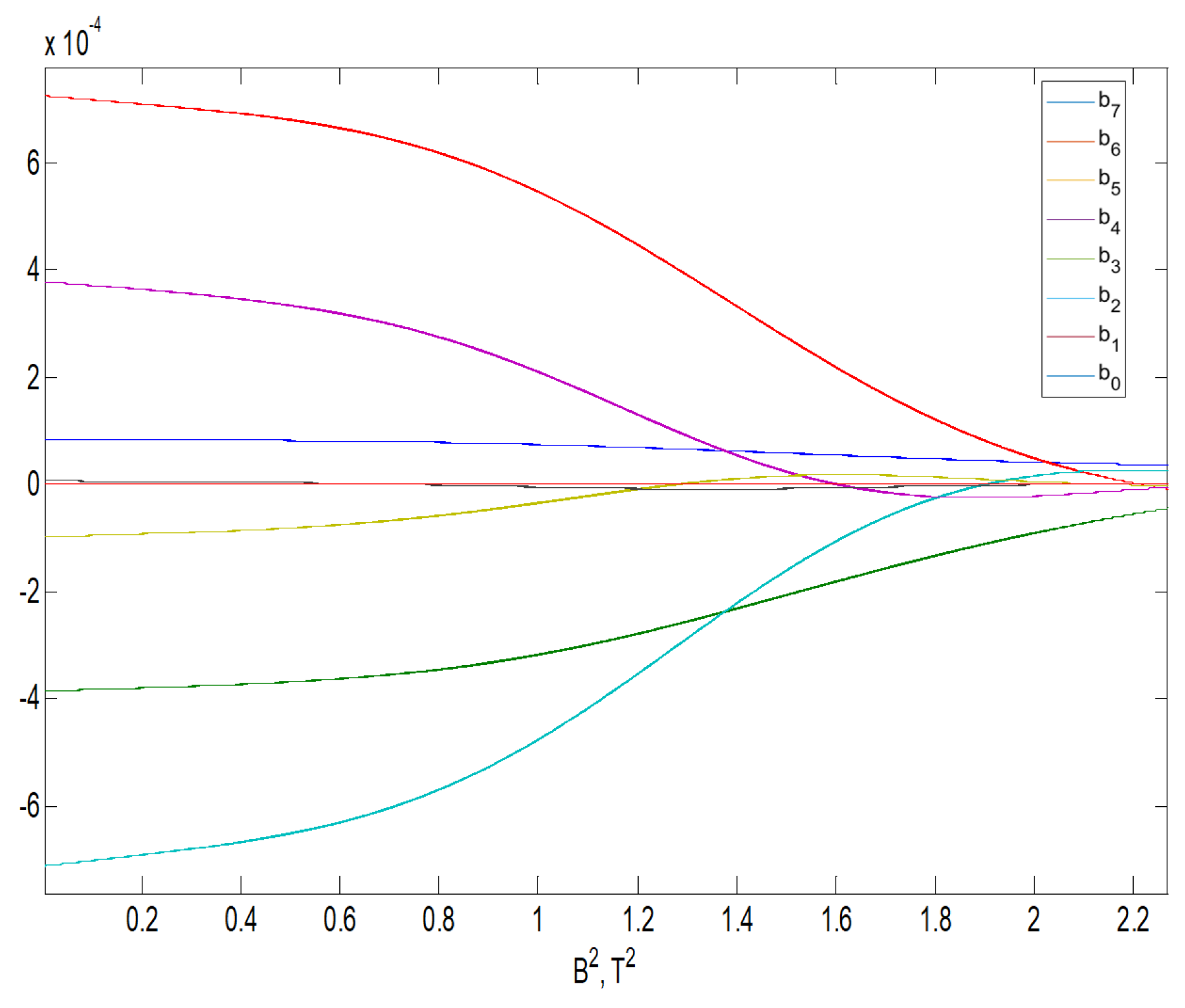
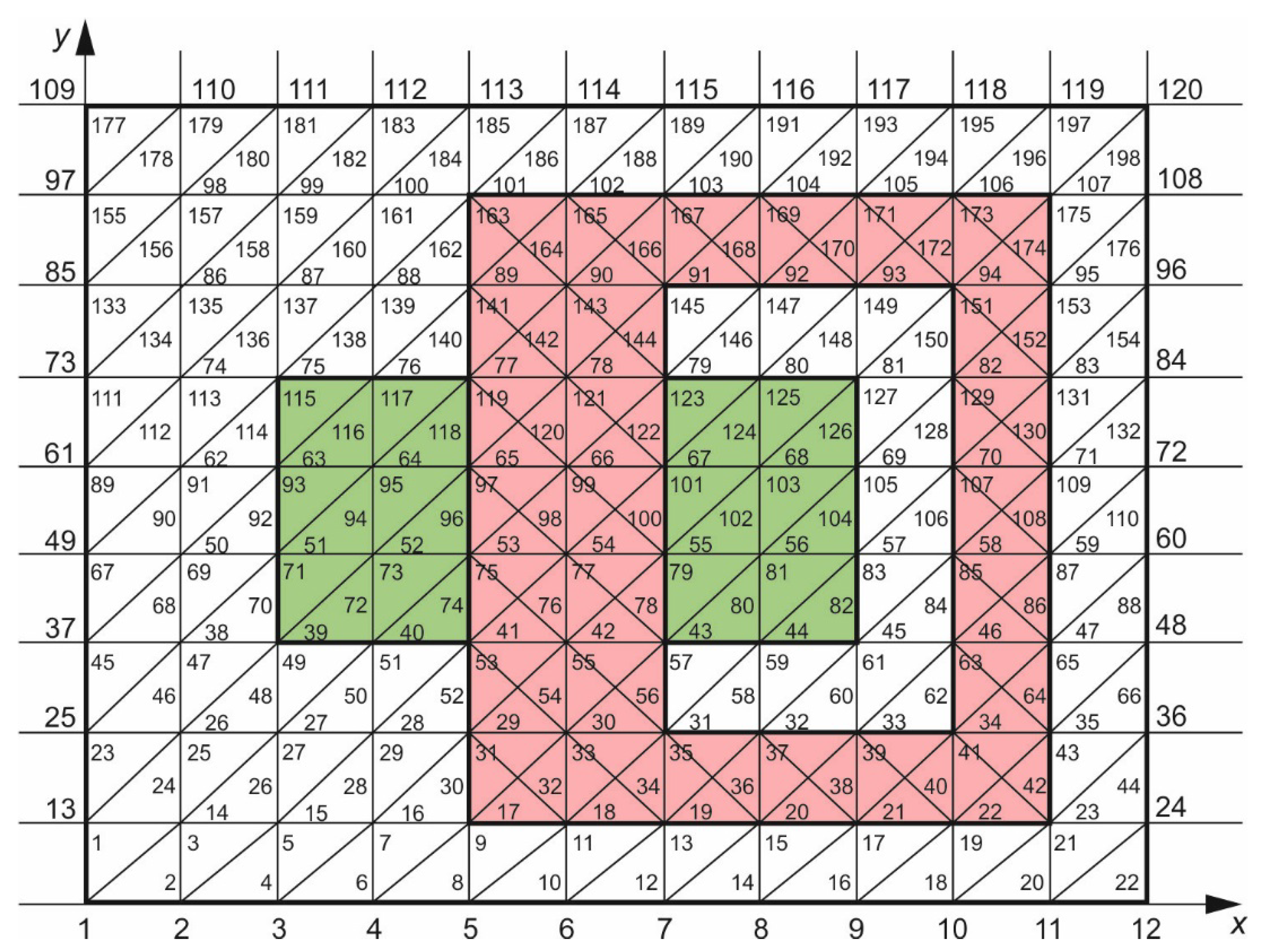
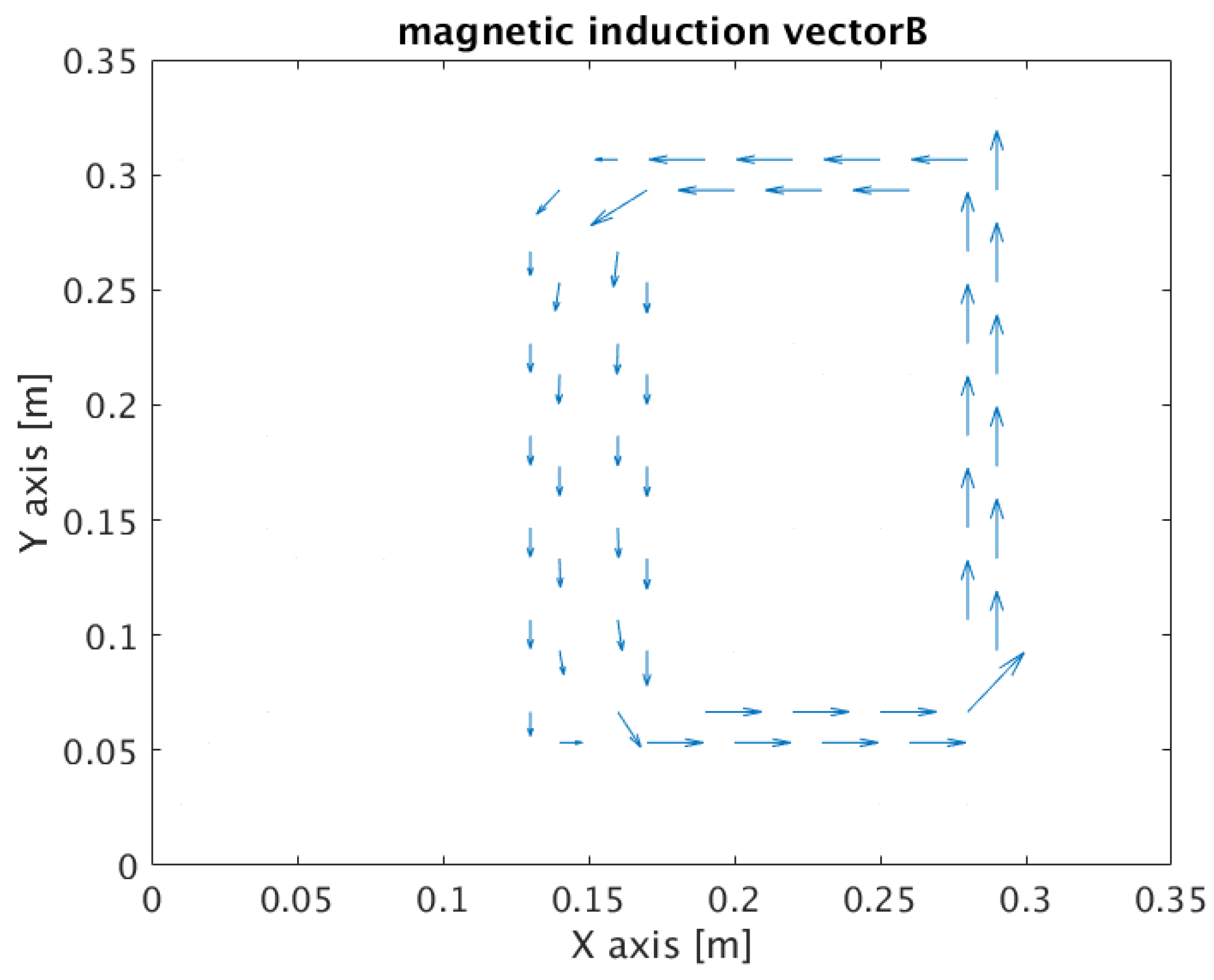
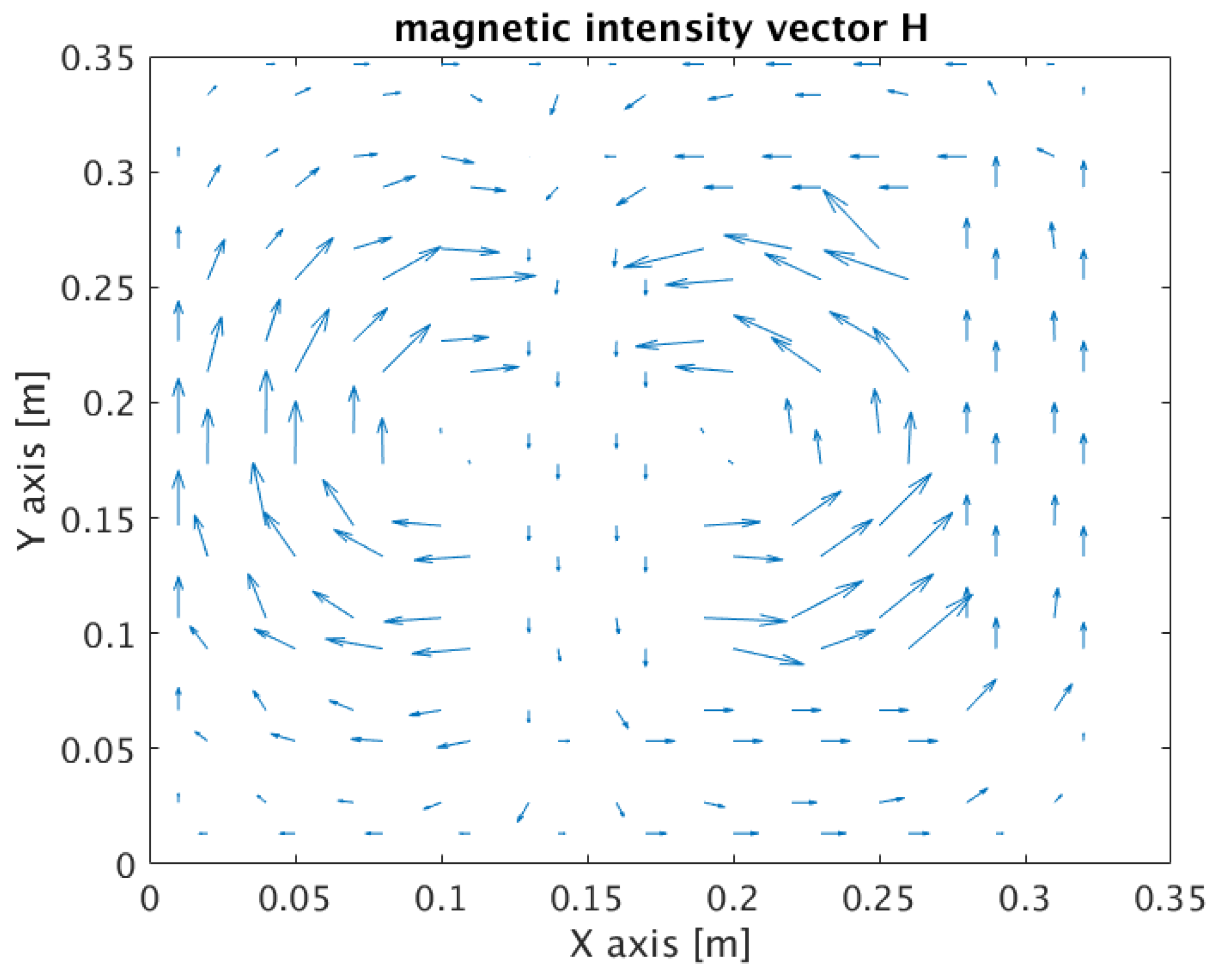
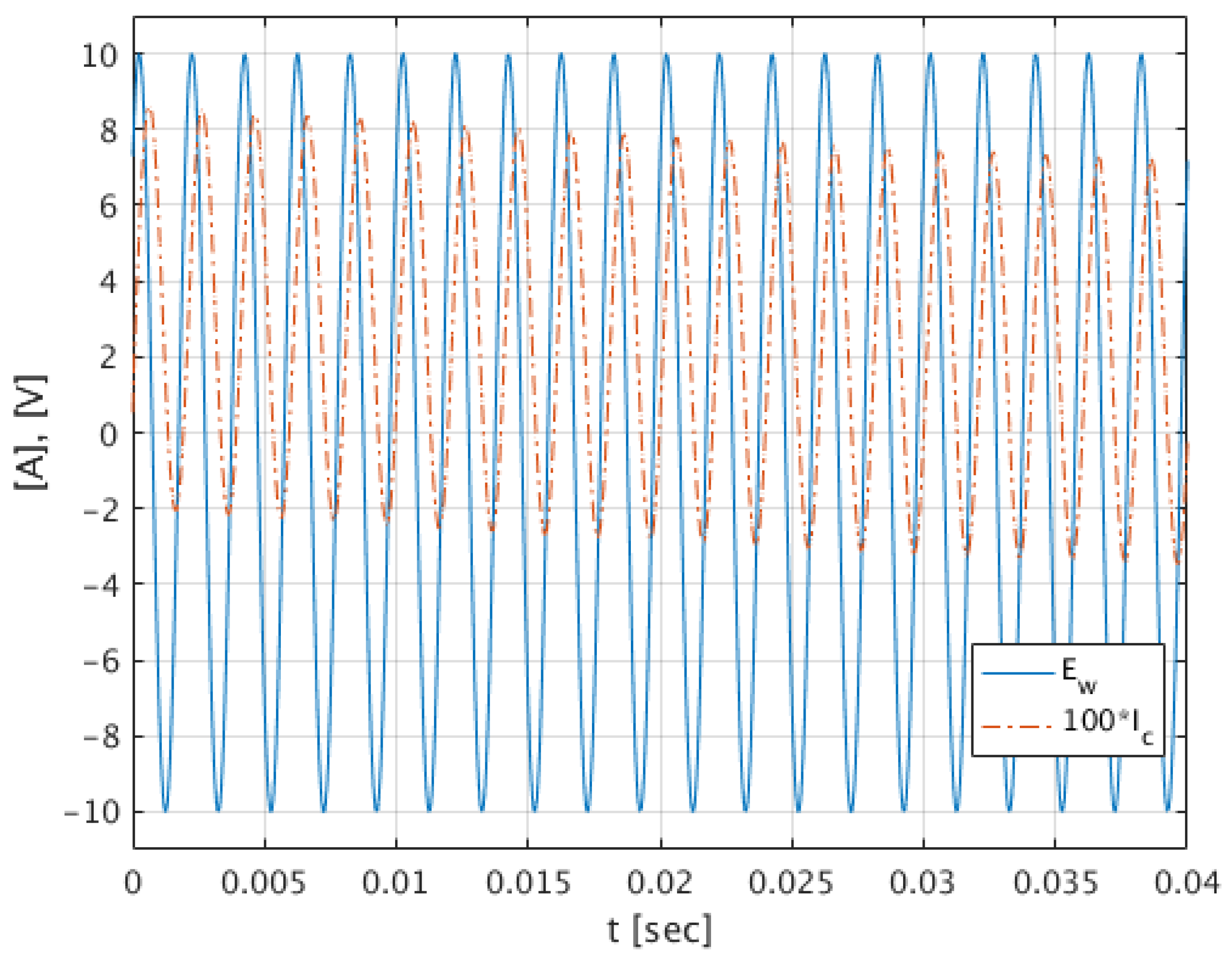
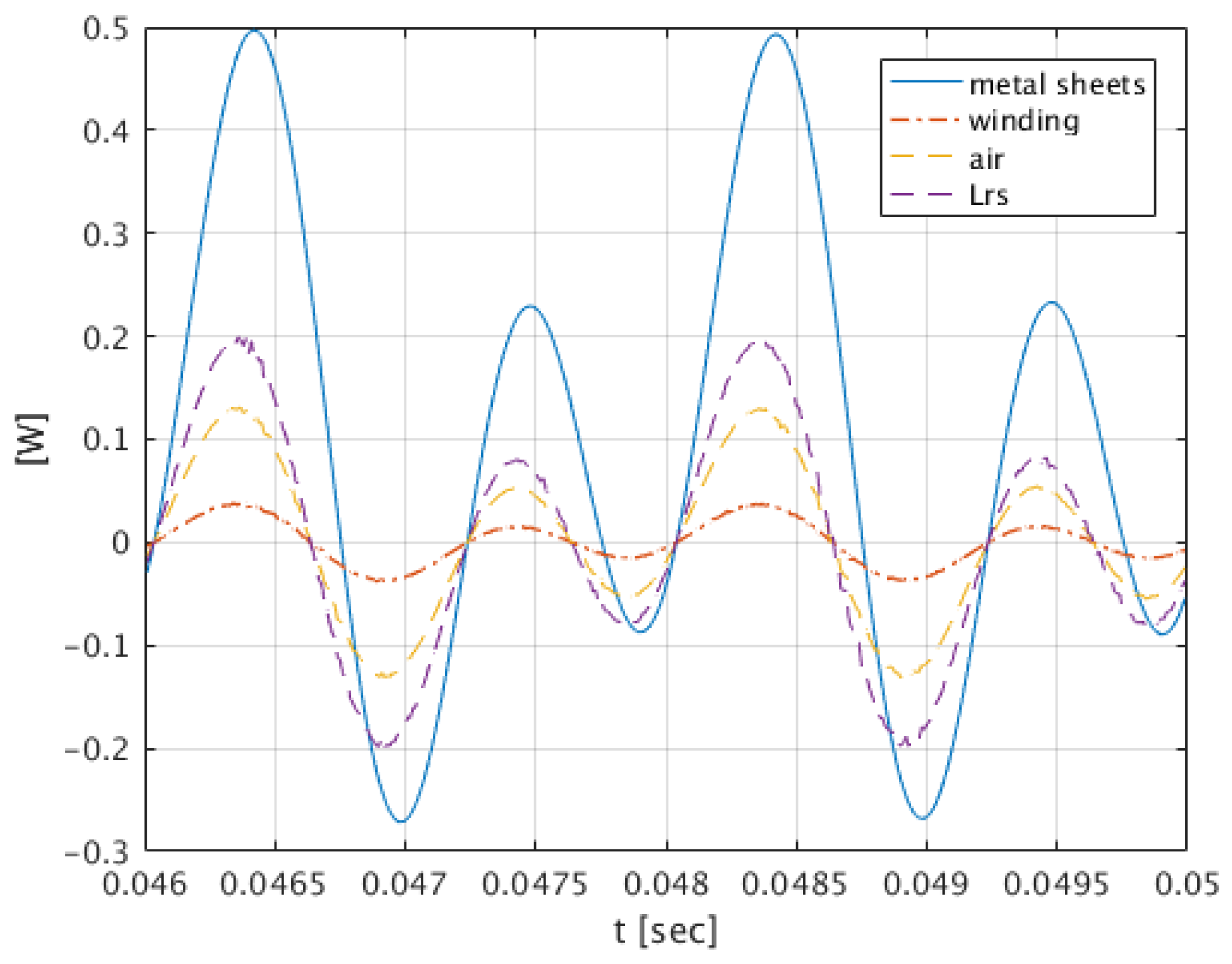
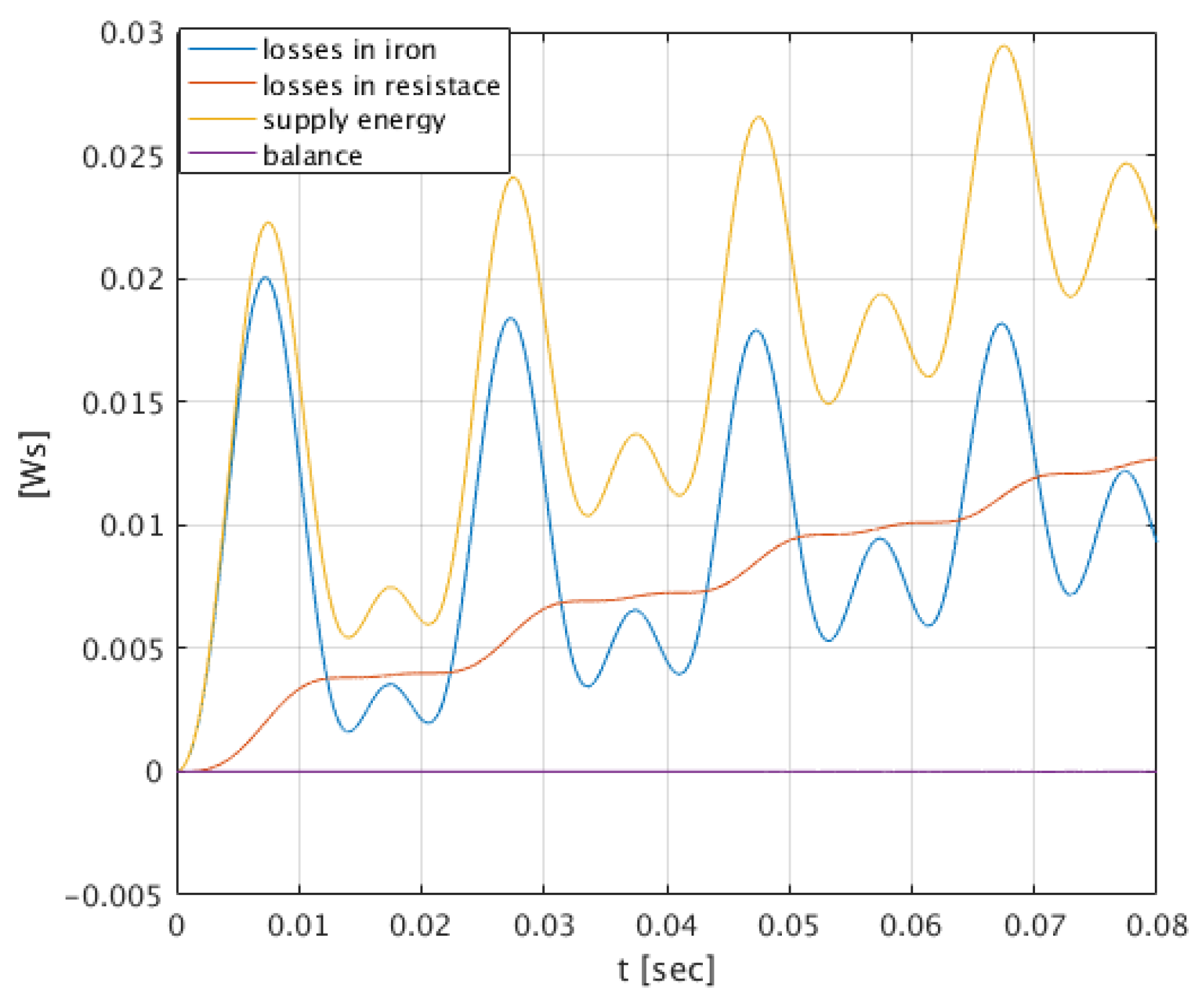
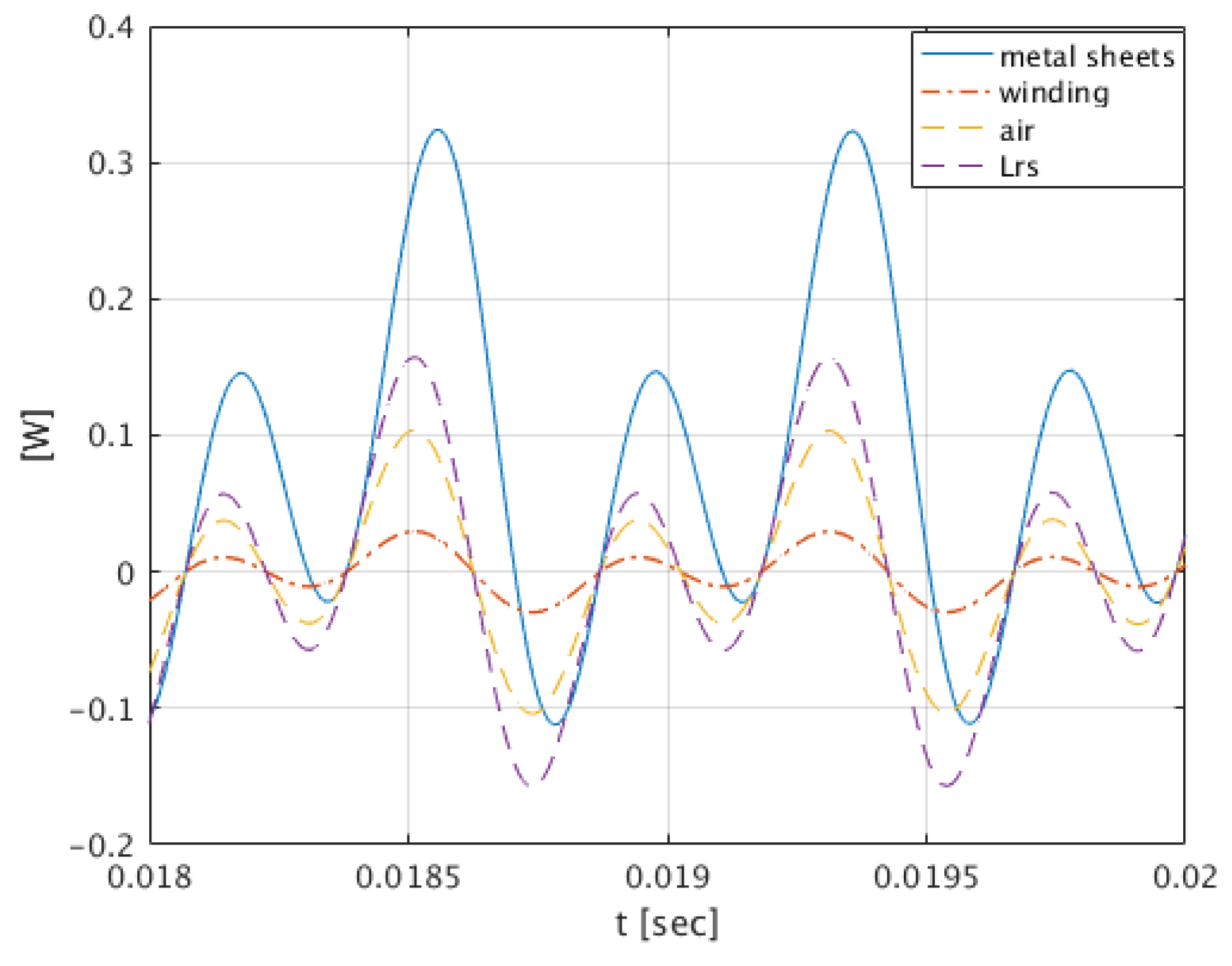
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Senda, K.; Uesaka, M.; Yoshizaki, S.; Oda, Y. Electric Steel and Their Evaluation for Automobile Motors. World Electr. Veh. J. 2019, 10, 31. [Google Scholar] [CrossRef] [Green Version]
- Gołębiowski, L.; Lewicki, J. Electromagnetic Systems in Power Electronics; Printing House of Rzeszow University of Technology: Rzeszów, Poland, 2012. (In Polish) [Google Scholar]
- Chen, W.; Ma, J.; Huang, X.; Fang, Y. Predicting Iron Losses in Laaminated Steel with Given Non-Sinusoidal Waveforms of Flux Density. Energies 2015, 8, 13726–13740. [Google Scholar] [CrossRef] [Green Version]
- Demenko, A. Discrete methods of magnetic field description. Electrotech. Rev. 2009, 85, 107–110. (In Polish) [Google Scholar]
- Jin, J. The Finite Element Method in Electromagnetics, 3rd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- Belahcen, A.; Arkkio, A. Comprehensive Dynamic Loss Model of Electrical Steel Applied to FE Simulation of Electrical Machines. IEEE Trans. Magn. 2008, 44, 886–889. [Google Scholar] [CrossRef]
- Bermúdez, A.; Gómez, D.; Salgado, P. Eddy-Current Losses in Laminated Cores and the Computation of an Equivalent Conductivity. IEEE Trans. Magn. 2008, 44, 4730–4738. [Google Scholar] [CrossRef]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Bertotti, G. Hysteresis in Magnetism; IEEE Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Boglietti, A.; Cavagnino, A. Iron Loss Prediction with PWM Supply: An Overview of Proposed Methods from an Engineering Application Point of View. In Proceedings of the 2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 81–88. [Google Scholar]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: An engineering approach. IEEE Trans. Magn. 2003, 39, 981–989. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. Two simplified methods for the iron losses prediction in soft magnetic materials supplied by PWM inwerter. In Proceedings of the IEEE International Electric Machines and Drives Conference (Cat. No. 01EX485), Boston, MA, USA, 17–20 June 2001; pp. 391–395. [Google Scholar]
- Ionel, D.; Popescu, M.; Dellinger, S.J.; Miller, T.J.E.; Heideman, R.J.; McGilp, M.I. Computation of core losses in electrical machines using improved model for laminated steel. IEEE Trans. Ind. Appl. 2007, 43, 1554–1564. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Lin, H.; Huang, Y.; Sun, X. A New Formulation of Anisotropic Equivalent Conductivity in Laminations. IEEE Trans. Magn. 2010, 47, 1378–1381. [Google Scholar] [CrossRef]
- Zhu, S.; Cheng, M.; Dong, J.; Du, J. Core loss analysis and calculation of stator permanent-magnet machine considering dc-biased magnetic induction. IEEE Trans. Ind. Electron. 2014, 61, 5203–5212. [Google Scholar] [CrossRef]
- Novak, G.; Kokošar, J.; Nagode, A.; Petrovi, D.S. Core-Loss Prediction for Non-Oriented Electrical Steels Based on the Steinmetz Equation Using Fixed Coefficients with a Wide Frequency Range of Validity. IEEE Trans. Magn. 2014. [Google Scholar] [CrossRef]
- Tietz, M.; Biele, P.; Jansen, A.; Herget, F.; Telger, K.; Hameyer, K. Application-specific development of non oriented electrical steel for EV traction drives. In Proceedings of the 2nd International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 15–18 October 2012; pp. 1–5. [Google Scholar]
- Barbisio, E.; Fiorillo, F.; Ragusa, C. Predicting loss in magnetic steels under arbitrary induction waveform and with minor hysteresis loops. IEEE Trans. Magn. 2004, 40, 1810–1819. [Google Scholar] [CrossRef] [Green Version]
- Mthombeni, L.T.; Pillay, P. Core losses in motor laminations exposed to high frequency or nonsinusoidal excitation, Industry Applications. IEEE Trans. Magn. 2004, 40, 1325–1332. [Google Scholar]
- Exnowski, S. Transientes Verhalten des Wickelkopfes groser Turbogeneratoren bei unterschiedlichen Betriebszuständen. Ph.D. Thesis, Der Fakultät für Elektrotechnik und Informationstechnik der Technischen Universität Dortmund vorgelegte, Dortmund, Germany, 2009. [Google Scholar]
- Łukaniszyn, M.; Jagieła, M.; Wróbel, R. Electromechanical Properties of a Disc-type Salient-pole Brushless DC Motor with Different Pole Numbers. COMPEL 2003, 22, 285–303. [Google Scholar] [CrossRef]
- Łukaniszyn, M.; Jagieła, M.; Wróbel, R. Field-circuit analysis of construction modifications of a torus-type PMDC motor. COMPEL 2003, 22, 337–355. [Google Scholar] [CrossRef]
- Shintemirov, A.; Tang, W.H.; Wu, Q.H. Transformer Core Parameter Identification Using Frequency Response Analysis. IEEE Trans. Magn. 2010, 46, 141–149. [Google Scholar] [CrossRef]
- Lin, D.; Zhou, P.; Fu, W.N.; Badics, Z.; Cendes, Z.J. A dynamic core loss model for soft ferromagnetic and power ferrite materials in transient finite element analysis. IEEE Trans. Magn. 2004, 40, 1318–1321. [Google Scholar] [CrossRef]
- Gyselinck, J.; Sabariego, R.V.; Dular, P. A Nonlinear Time-Domain Homogenization Technique for Laminated Iron Cores in Three-Dimensional Finite-Element Models. IEEE Trans. Magn. 2006, 42, 763. [Google Scholar] [CrossRef]
- Rasilo, P.; Arkkio, A. Modeling the Effect of Inverter Supply on Eddy-Current Losses in Synchronous Machines. In Proceedings of the SPEEDAM 2010, Pisa, Italy, 14–16 June 2010. [Google Scholar]
- Gyselinck, J.; Robert, F. Frequency- and Time-Domain Homogenization of Windings in Two-Dimensional Finite-Element Models. Gdzieś Nie Wiadomo Gdzie 2014, 61, 5203–5212. [Google Scholar]
- Shindo, Y.; Miyazaki, T.; Matsuo, T. Cauer Circuit Representation of the Homogenized Eddy-Current Field Based on the Legendre Expansion for a Magnetic Sheet. IEEE Trans. Magn. 2016, 52, 6300504. [Google Scholar] [CrossRef]
- Gołębiowski, M. Calculation of eddy current and hysteresis losses during transient states in laminated magnetic circuits. Compel 2017, 36, 665–682. [Google Scholar] [CrossRef]
- Gołębiowski, L.; Mazur, D. Comparison of calculations methods of dissipation inductance in DC- supplied multiple-winding autotransformers. In Proceedings of the 21st Symposium of Electromagnetic Phenomena in Nonlinear Circuits (EPNC), Dortmund and Essen, Germany, 29 June–2 July 2010; pp. 55–56. [Google Scholar]
- Gołębiowski, L.; Kulig, S.T. Numerical Methods in Technology; Printing House of Rzeszow University of Technology: Rzeszów, Poland, 2012. (In Polish) [Google Scholar]
- Bolkowski, S.; Stabrowski, M.; Skoczylas, J.; Sikora, J.; Wincenciak, S. Computer Aided Methods of Magnetic Field Analysis; WNT: Warszawa, Poland, 1993. (In Polish) [Google Scholar]
- De Tommasi, L.; De Magistris, M.; Deschrijver, D.; Dhaene, T. An algorithm for direct identification of passive transfer matrices with positive real fractions via convex programming. Int. J. Numer. Model. Electron. Netw. Devices Fields 2011, 24, 375–386. [Google Scholar] [CrossRef] [Green Version]
- De Tommasi, L.; de Magistris, M.; Deschrijver, D.; Dhaene, T. Validation of Positive Fraction Vector Fitting Algorithm in the identification of Passive Immittances. In Proceedings of the X-th International Workshop on Optimization and Inverse Problems in Electromagnetism, Ilmenau, Germany, 14–17 September 2008. [Google Scholar]
- Tellinen, J. A Simple Scalar Model for Magnetic Hysteresis. IEEE Trans. Magn. 1998, 34, 2200–2206. [Google Scholar] [CrossRef]
- Smoleń, A.; Gołębiowski, M. Computationally efficient method for determining the most important electrical parameters of Axial Field Permanent Magnet machine. Biuletin Yhe Pol. Acad. Sci. Tech. Sect. 2018, 66, 947–959. [Google Scholar]
- Mayergoyz, I.D.; Abdel-Kader, F.M.; Emad, F.P. On penetration of electromagnetic fields into nonlinear conducting ferromagnetic media. J. Appl. Phys. 1984, 618. [Google Scholar] [CrossRef]
- Coulomb, J.L. A methodology for the determination of global electromechanical quantities from a finite element analysis and its application to the evaluation of magnetic forces, torques and stiffness. IEEE Trans. Magn. 1983, 19, 2514–2519. [Google Scholar] [CrossRef]
- Saad, Y. Numerical Methods for Large Eigenvalues Problems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2011. [Google Scholar]
- Nowak, L. Field Models Transients in Electromechanical Converters; Poznań University of Technology Publishing House: Wrocław, Poland, 1999. (In Polish) [Google Scholar]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gołębiowski, M.; Gołębiowski, L.; Smoleń, A.; Mazur, D. Direct Consideration of Eddy Current Losses in Laminated Magnetic Cores in Finite Element Method (FEM) Calculations Using the Laplace Transform. Energies 2020, 13, 1174. https://doi.org/10.3390/en13051174
Gołębiowski M, Gołębiowski L, Smoleń A, Mazur D. Direct Consideration of Eddy Current Losses in Laminated Magnetic Cores in Finite Element Method (FEM) Calculations Using the Laplace Transform. Energies. 2020; 13(5):1174. https://doi.org/10.3390/en13051174
Chicago/Turabian StyleGołębiowski, Marek, Lesław Gołębiowski, Andrzej Smoleń, and Damian Mazur. 2020. "Direct Consideration of Eddy Current Losses in Laminated Magnetic Cores in Finite Element Method (FEM) Calculations Using the Laplace Transform" Energies 13, no. 5: 1174. https://doi.org/10.3390/en13051174