Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV
Abstract
:1. Introduction
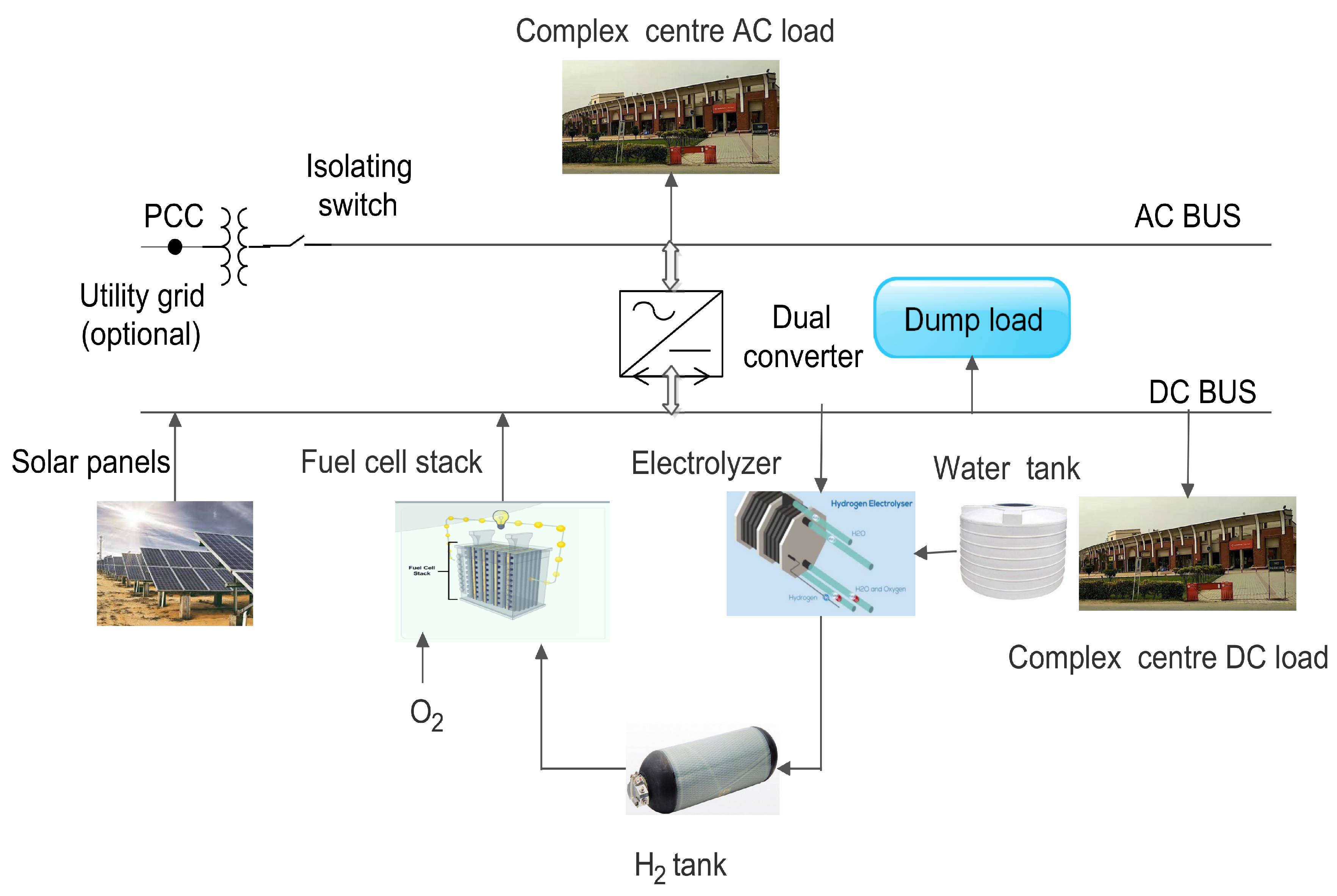
2. Modeling System Components
2.1. Solar Photo Voltaic Panel
2.2. Fuel Cell
2.3. Electrolyzer
2.4. Hydrogen Tank
2.5. Converter
3. Energy Management System and Objective Function
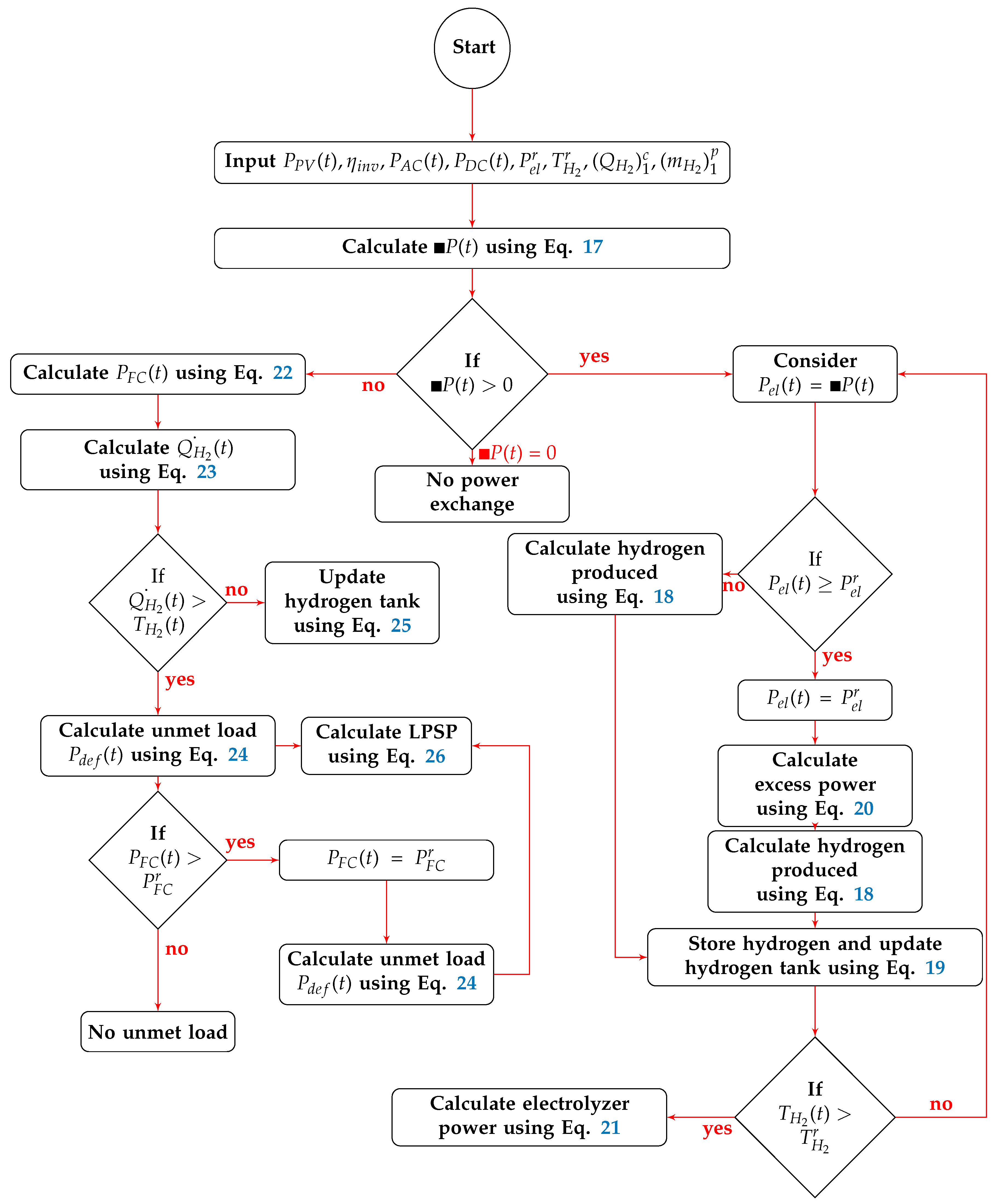
3.1. Energy Management System
- Case I:
- If , then the remaining power is fed to electrolyzer (). If power fed to electrolyzer is greater than the rating of electrolyzer () then, and remaining power is treated as excess electricity. This excess electricity can be given to some dump load or non priority load. The mass flow rate of hydrogen produced by the electrolyzer is calculated as:where and are the mass flow rate of hydrogen at any time t and hydrogen produced by 1kW electrolyzer, respectively. The hydrogen tank is updated as:where is the status of hydrogen tank at previous hour. The excess electricity can be calculated asIf , then repeat the process using Equations (18) and (19). In case the hydrogen accumulated as per Equation (19) in tank becomes greater than the size of the tank, i.e., , then electrolyzer is not run on rated capacity, the desired electrolyzer power can be calculated as:
- Case II:
- If , then there is no power exchange, and the total demand is met by the solar generation.
- Case III:
- If , then required power is provided by fuel cells. Power produced by fuel cell can be calculated as:The mass flow rate of hydrogen taken by fuel cell from hydrogen tank at a particular time to produce is calculated as:In case hydrogen tank does not have sufficient hydrogen i.e., , then unmet load is calculated as:If , then there is no unmet load and hydrogen storage tank is updated as:If the power required by fuel cells is greater than the rating of fuel cell (i.e., ), then assign , and further the power deficiency can be calculated by using Equation (24).The unmet load must be zero to ensure that the total load is served reliably, while minimizing the objective function. The loss of power supply probability (LPSP) during a considered period of time must be lower than a certain predetermined value. Mathematically, LPSP can be calculated as:
3.2. Objective Function and Constraints
4. Algorithm Description
- Food source is searched by employed bees and its location is stored in memory.
- That food source or location goes to onlooker bees.
- The onlooker bee do the quality search on food source given by employed bees by exploring it and the best one is selected.
- Input, , Control parameters of the ABC algorithm, i.e., maximum cycle number, colony size, population of food sources , dimension of the problem D, and limit.
- Consider the number of food sources equals the half of the colony size.
- Generate a randomly distributed population within the range of boundaries of the parameters by using the following equationwhere …, and …D.
- Set trial counters (to store the number of solution trials) to zero.
- According to initial guess solutions (number of PV panels, fuel cells, electrolyzer, and size of hydrogen storage tank) perform the following steps.
- Power management using as per flow chart shown in Figure 3
- The objective function as described in Equation (27) is evaluated for initial food source.
- Cycle = 1.
- Repeat.
- Produced a new modified food location for the employed bees by using the following equationwhere …, is a randomly chosen index. Whereas, is the random integer between the range of [−1,1].
- If a parameter generated exceeds its predetermined limits, it can be set to an acceptable boundary.
- Evaluate the objective function described in Equation (27) using new solutions by following the procedure mentioned in step 5.
- Apply the greedy selection process for the employed bees.
- Calculate the probability value, , for the solutions using fitness value by following equationwhere is the fitness value corresponding to solution.
- Produce the new solutions by using Equation (35) for the onlookers bees from the solutions selected depending upon the value of .
- Evaluate the objective function described in Equation (27) using new solutions by following the procedure mentioned in step 5.
- Apply the greedy selection process for the onlookers bees.
- Determine the abandoned solution for the scout, if exists and replace it with a new randomly produced solution.
- Memorize the best solution obtained as of now.
- Cycle = Cycle + 1.
- Until (Cycle = Maximum cycle number).
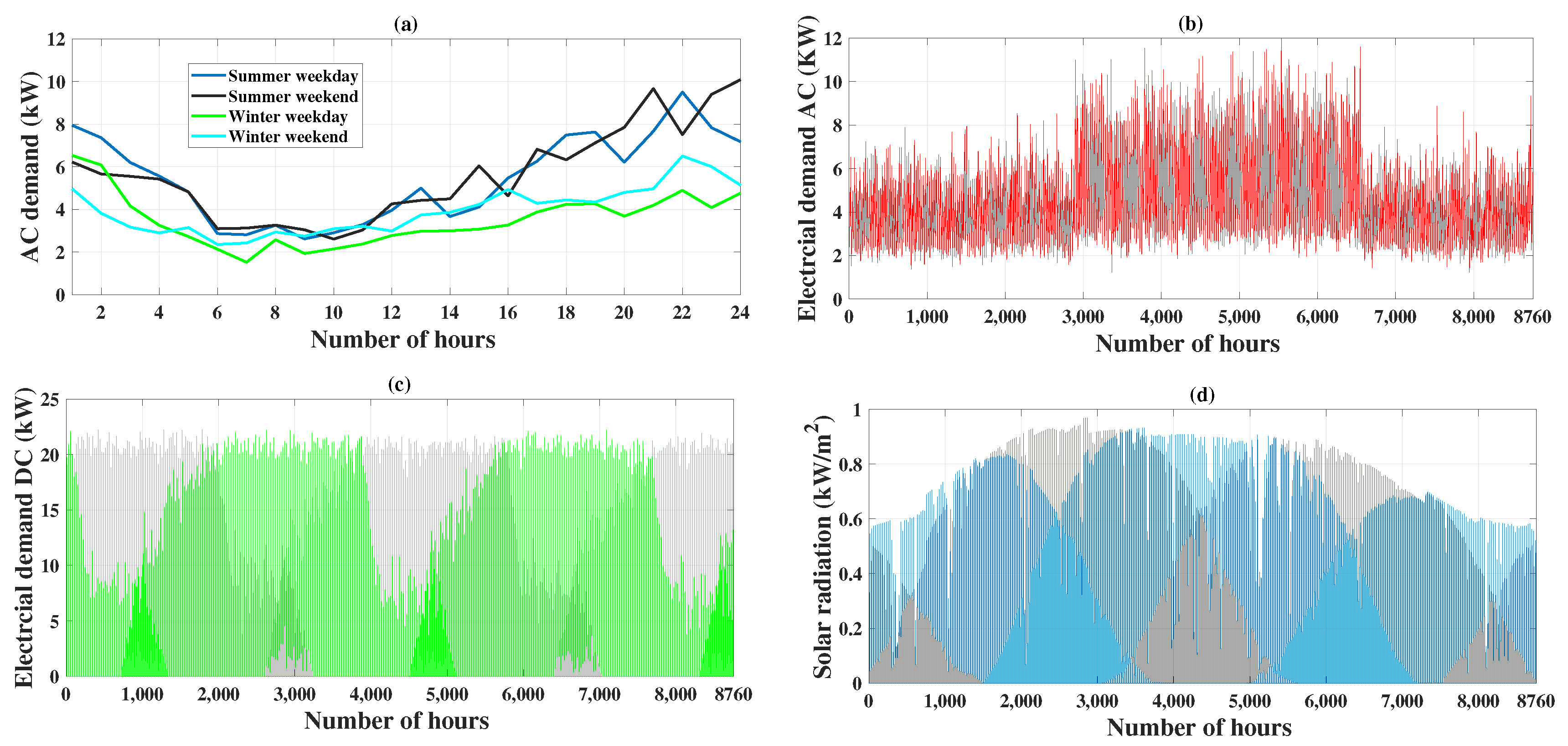
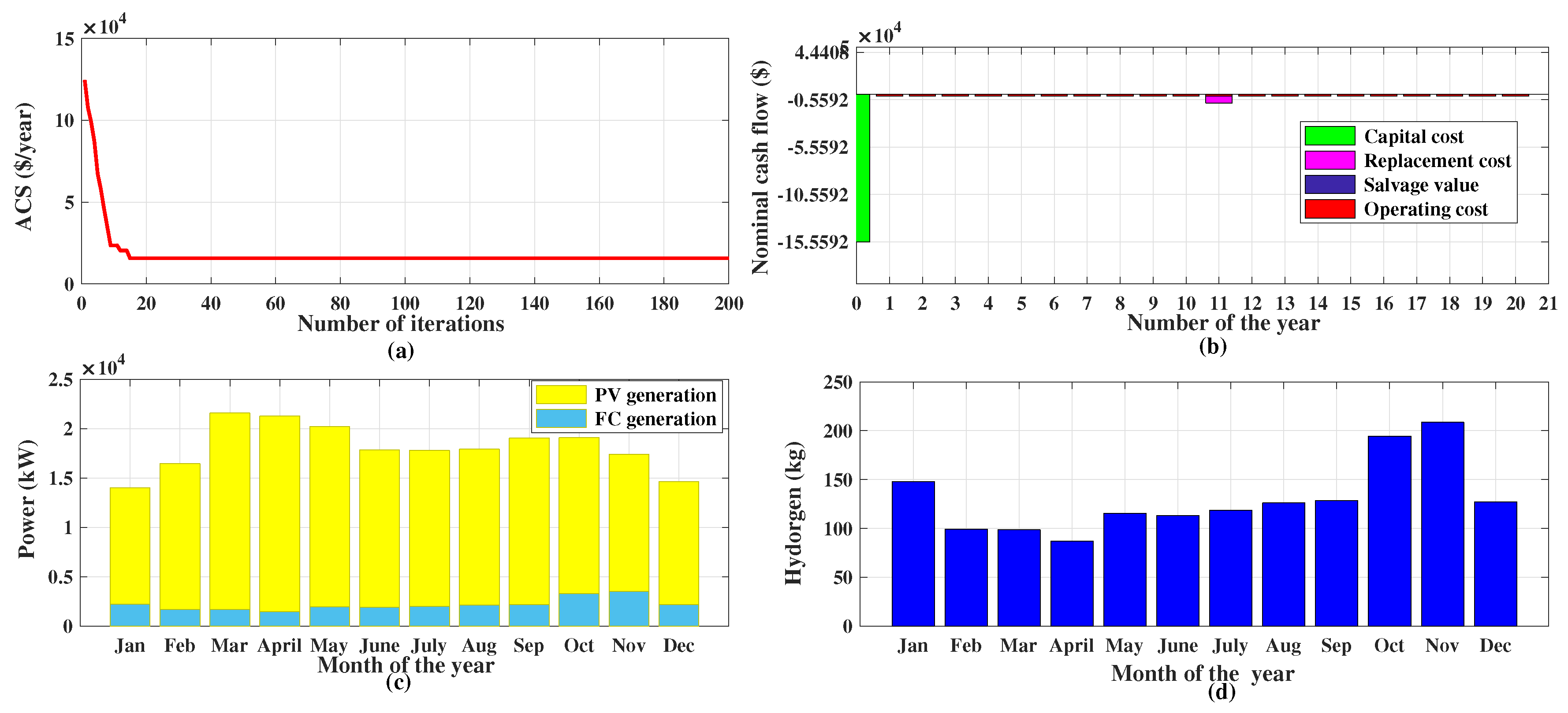
5. Result and Discussions
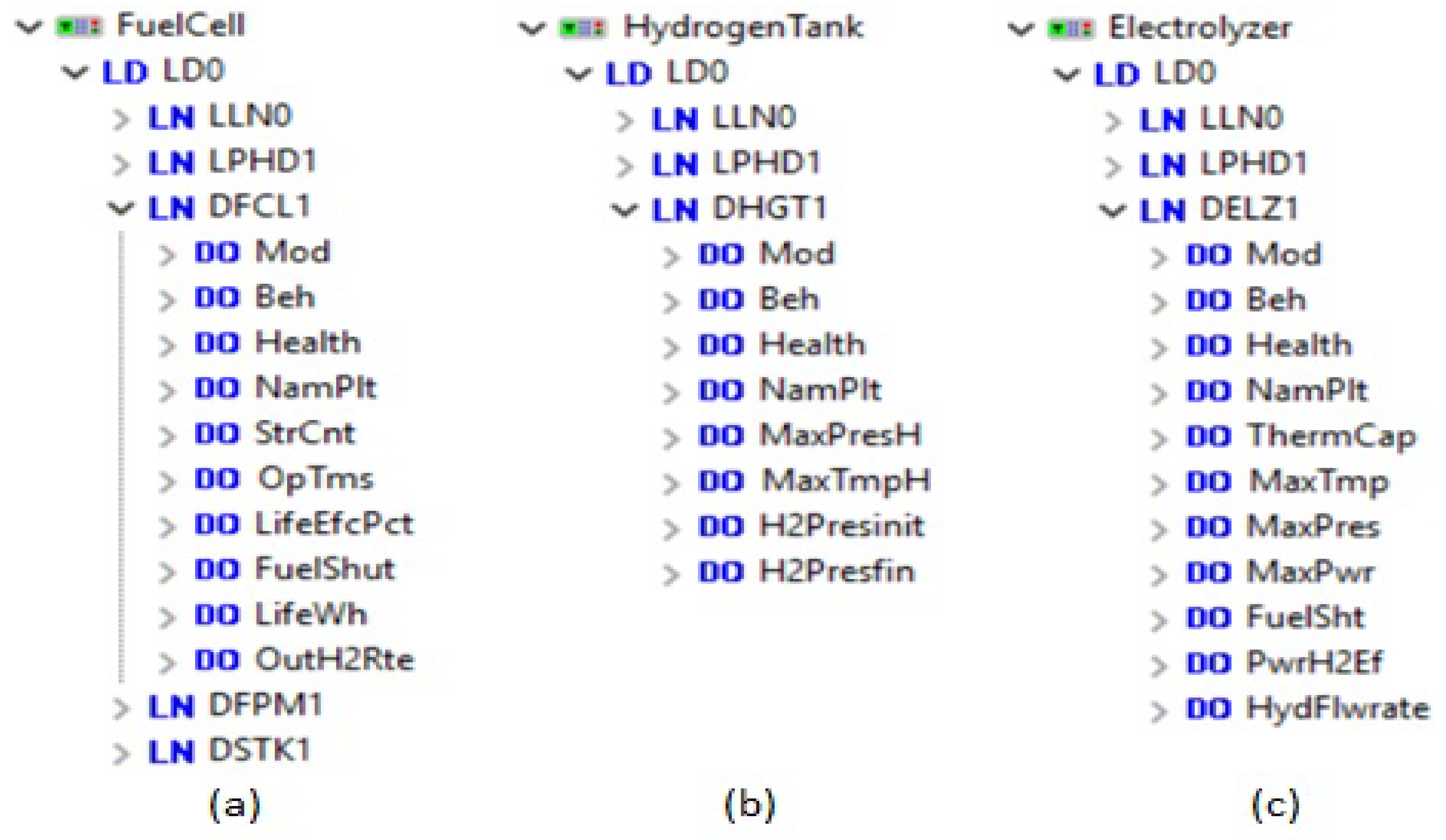
6. IEC 61850 Implementation
6.1. IEC 61850 Based Information Modeling Of FC-PV Hybrid System
6.2. Communication Message Exchanges for Realizing Energy Management
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Masters, G.M. Renewable and Efficient Electric Power Systems; Willy Inter Science: Hoboken, NJ, USA, 2004; ISBN 0-471-28060-7. [Google Scholar]
- John, A.T.; Amawarisenua, K.T. Generation power through hydrogen-oxygen fuel cells. Int. J. Eng. Sci. 2014, 4, 56–62. [Google Scholar]
- Rahman, S.; Tam, K. A feasibility study of photovoltaic-fuel cell hybrid energy system. IEEE Trans. Energy Convers. 1988, 3, 50–55. [Google Scholar] [CrossRef]
- Rekioua, D.; Bensmail, S.; Bettar, N. Development of hybrid photovoltaic-fuel cell system for stand-alone application. Int. J. Hydrog. Energy 2014, 39, 1604–1611. [Google Scholar] [CrossRef]
- Bayrak, G.; Mehmet, C. Grid connected fuel cell and PV hybrid power generating system design with Matlab Simulink. Int. J. Hydrog. Energy 2014, 39, 8803–8812. [Google Scholar] [CrossRef]
- Jiang, Z. Power management of hybrid Photovoltaic—Fuel Cell power systems. In Proceedings of the IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Saeed, W.; Warkozek, G. Modeling and analysis of renewable PEM Fuel Cell System. Energy Proc. 2015, 74, 87–101. [Google Scholar] [CrossRef] [Green Version]
- Ganguly, A.; Misra, D.; Ghosh, S. Modeling and analysis of solar photovoltaic-electrolyzer-fuel cell hybrid power system integrated with a floriculture greenhouse. Energy Build. 2010, 42, 2036–2043. [Google Scholar] [CrossRef]
- Mostofi, F.; Safavi, M. Application of ABC Algorithm for grid-independent hybrid Hydro/Photovoltaic/Wind/Fuel Cell power generation system considering cost and reliability. Int. J. Renew. Energy Res. 2013, 3, 928–940. [Google Scholar]
- Khemariya, M.; Mittal, A.; Baredar, P.; Singh, A. Cost and size optimization of solar photovoltaic and fuel cell based integrated energy system for un-electrified village. J. Energy Storage 2017, 14, 62–70. [Google Scholar] [CrossRef]
- Singh, A.; Baredar, P.; Gupta, B. Techno-economic feasibility analysis of hydrogen fuel cell and solar photovoltaic hybrid renewable energy system for academic research building. Energy Convers. Manag. 2017, 145, 398–414. [Google Scholar] [CrossRef]
- Ghenai, C.; Salameh, T.; Merabet, A. Technico-economic analysis of off grid solar PV/ Fuel cell energy system for residential community in desert region. Int. J. Hydrog. Energy 2018. [Google Scholar] [CrossRef]
- Hybrid Power System Optimization Software. Available online: https://www.homerenergy.com (accessed on 4 January 2020).
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–671. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A comparative study of Artificial Bee Colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Ali, I.; Hussain, S.M.S. Control and management of distribution system with integrated DERs via IEC 61850 based communication. Eng. Sci. Tech. Int. J. 2017, 20, 956–964. [Google Scholar] [CrossRef]
- Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. IEC 61850 and XMPP Communication Based Energy Management in Microgrids Considering Electric Vehicles. IEEE Access 2018, 6, 35657–35668. [Google Scholar] [CrossRef]
- EG&G Technical Services, Inc. Fuel Cell Handbook, 7th ed.; Solid State Energy Conversion Alliance: Torrance, CA, USA, 2002.
- Mao, L.; Jackson, L.; Davies, B. Effectiveness of a Novel Sensor Selection Algorithm in PEM Fuel Cell On-Line Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 7301–7310. [Google Scholar] [CrossRef] [Green Version]
- Ghenai, C.; Bettayeb, M. Optimized design and control of an off grid solar PV/hydrogen fuel cell power system for green buildings. IOP Conf. Ser. Earth Environ. Sci. 2017, 93, 1–11. [Google Scholar] [CrossRef]
- Singh, S.; Singh, M.; Kaushik, S.C. Feasibility study of an islanded microgrid in rural area consisting of PV, wind, biomass and battery energy storage system. Energy Convers. Manag. 2016, 128, 178–190. [Google Scholar] [CrossRef]
- Singh, S.; Kaushik, S.C. Optimal sizing of grid integrated hybrid PV-biomass energy system using artificial bee colony algorithm. IET Renew. Power Gen. 2016, 10, 642–650. [Google Scholar] [CrossRef]
- Singh, S.; Chauhan, P.; Singh, N.J. Capacity optimization of grid connected solar/fuel cell energy system using hybrid ABC-PSO algorithm. Int. J. Hydrog. Energy 2020. [Google Scholar] [CrossRef]
- Zhanga, W.; Malekic, A.; Rosend, M.A.; Liu, L. Sizing a stand-alone solar-wind-hydrogen energy system using weather forecasting and a hybrid search optimization algorithm. Energy Convers. Manag. 2019, 180, 609–621. [Google Scholar] [CrossRef]
- Heydari, A.; Askarzadeh, A. Optimization of a biomass-based photovoltaic power plant for an off-grid application subject to loss of power supply probability concept. Appl. Energy. 2016, 165, 601–611. [Google Scholar] [CrossRef]
- Samy, M.M.; Barakata, S.; Ramadan, H.S. Techno-economic analysis for rustic electrification in Egypt using multi-source renewable energy based on PV/ wind/ FC. Int. J. Hydrog. Energy 2019. [Google Scholar] [CrossRef]
- Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Ustun, T.S. Novel SCL Configuration Method for Modeling Microgrids With IEC 61850. IEEE Syst. J. 2019. [Google Scholar] [CrossRef]
- Hussain, S.M.S.; Aftab, M.A.; Ali, I. IEC 61850 Modeling of DSTATCOM and XMPP Communication for Reactive Power Management in Microgrids. IEEE. Syst. J. 2018, 12, 3215–3225. [Google Scholar] [CrossRef]
- Ali, I.; Hussain, S.M.S. Communication Design for Energy Management Automation in Microgrd. IEEE Trans. Smart Grid 2018, 9, 2055–2064. [Google Scholar]
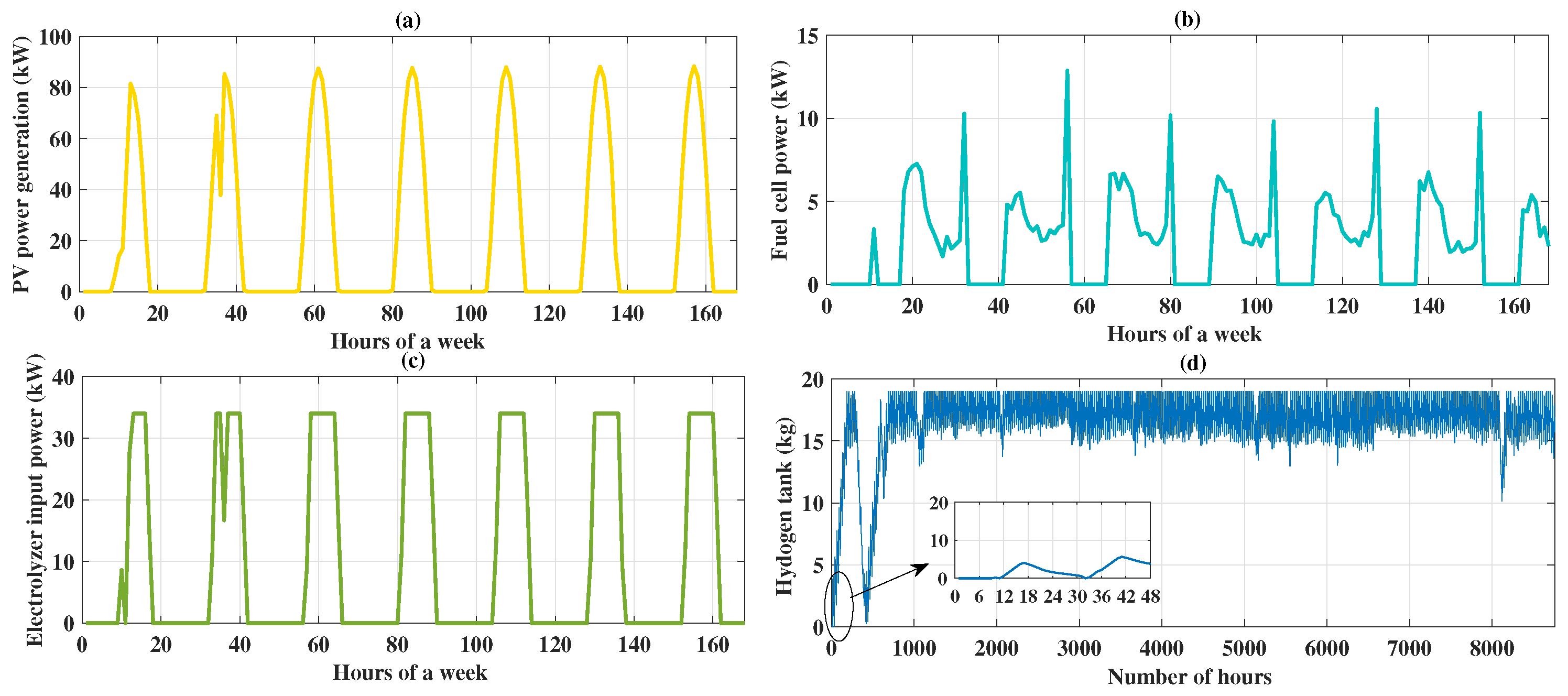
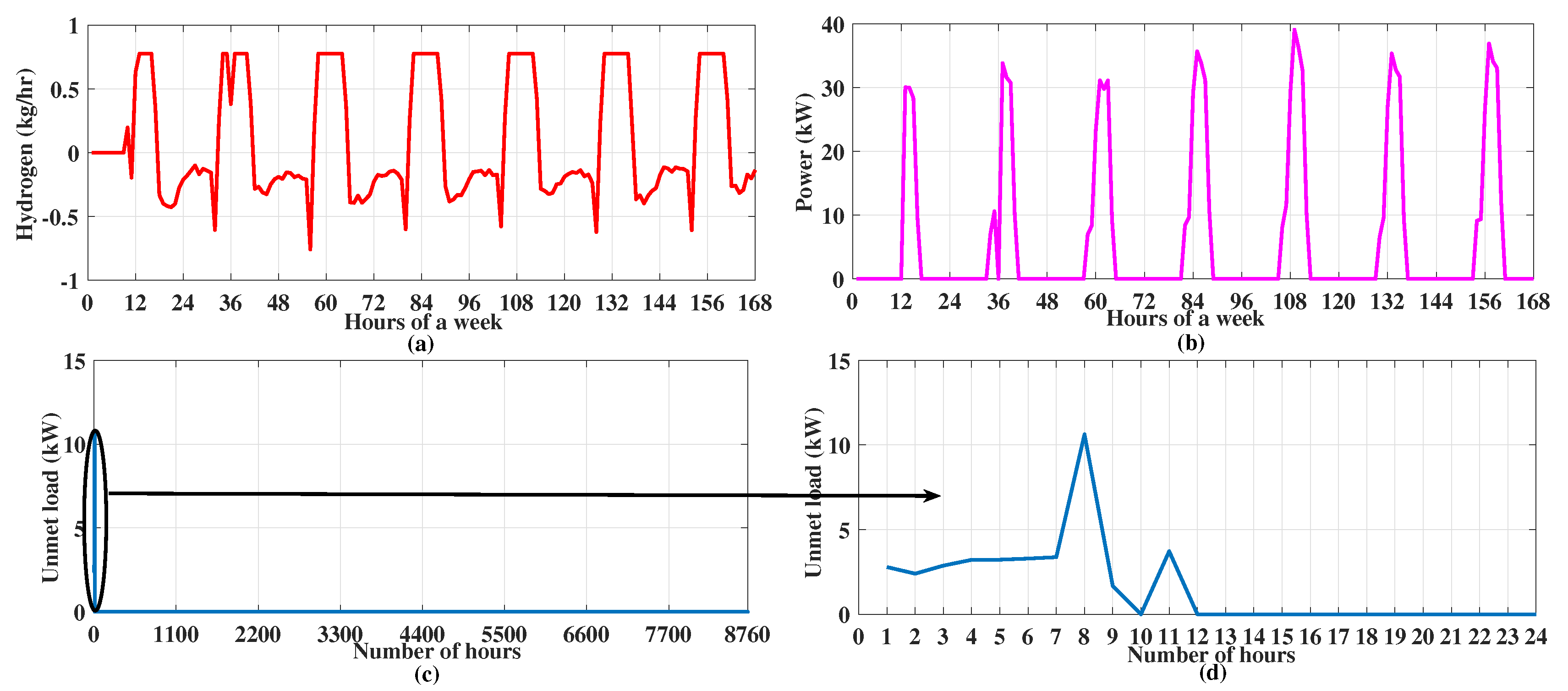
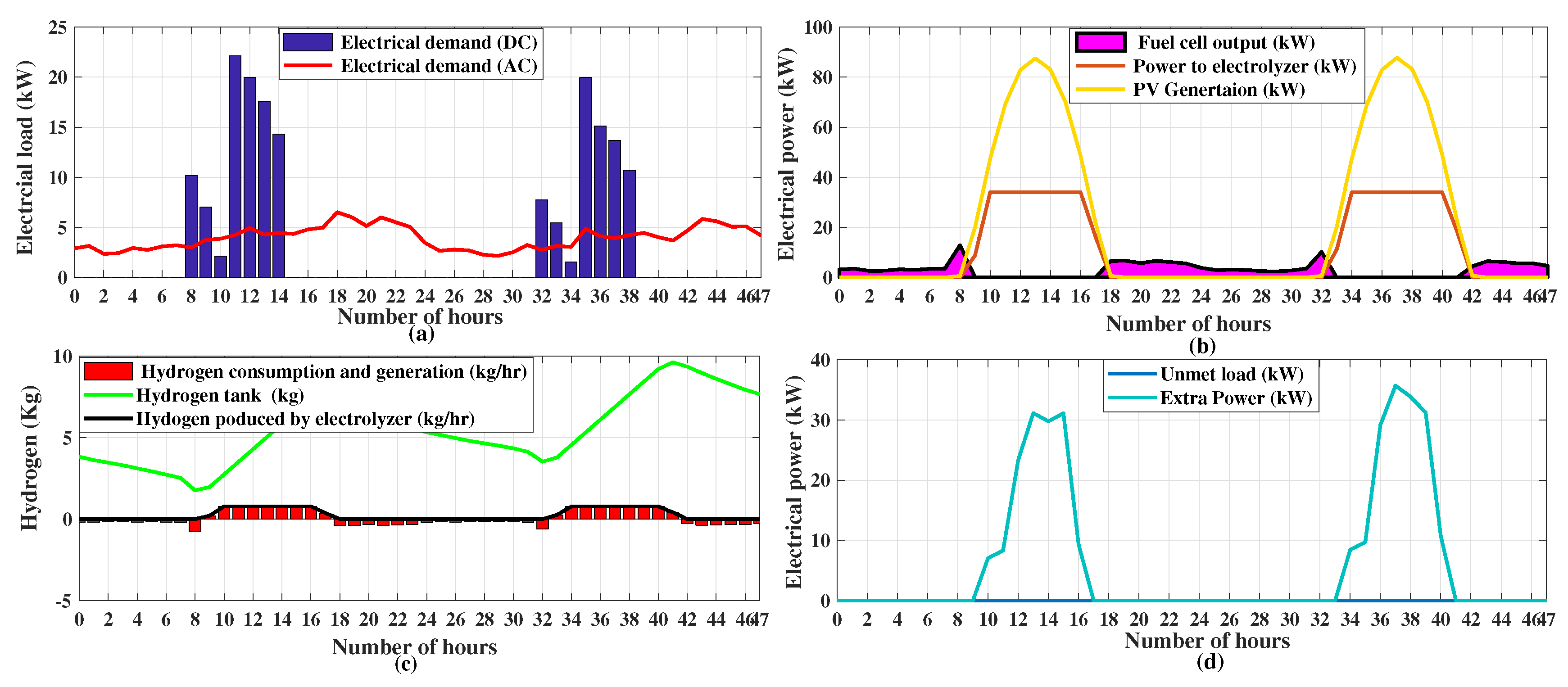
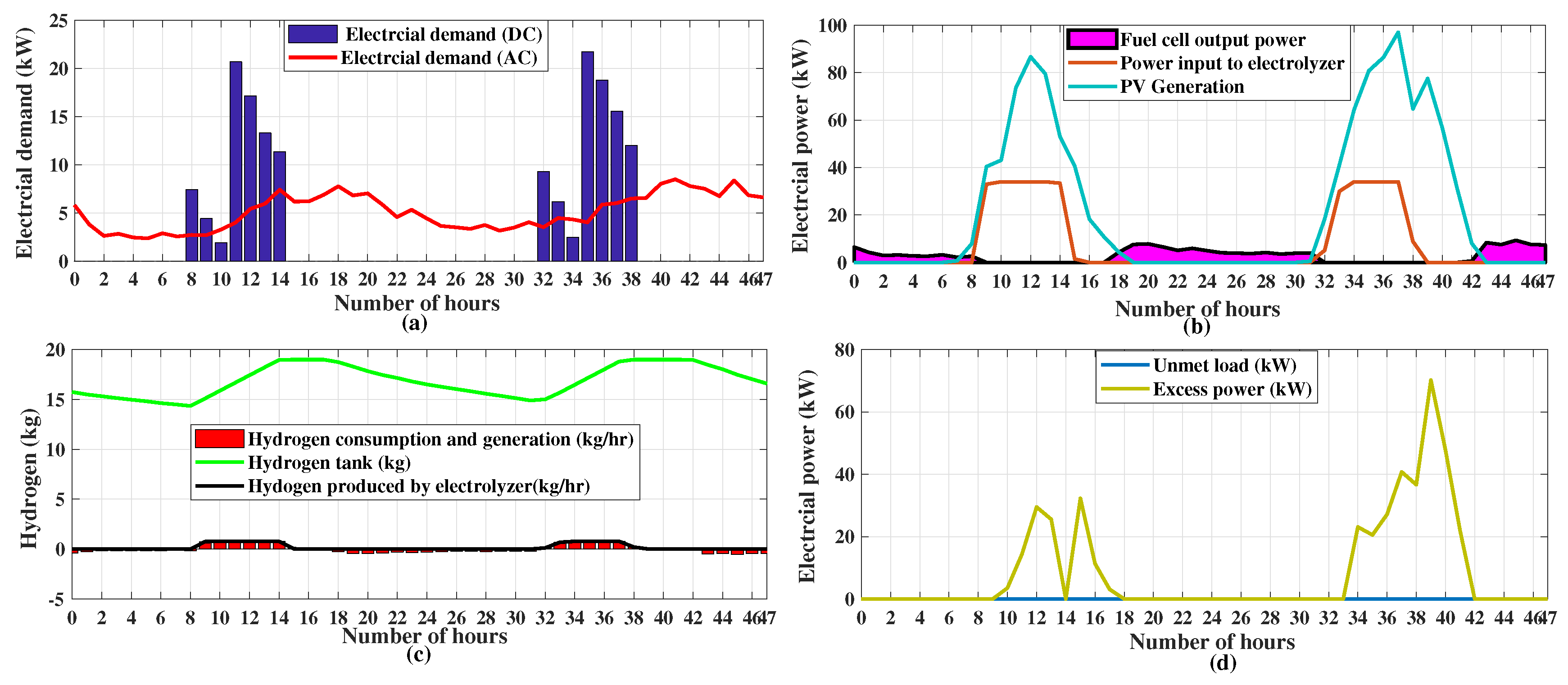

| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| PV panel | Inverter | ||||
| Maximum power ( ) | 100 | W | Rated power | 1 | kW |
| Maximum power voltage () | 18 | V | Inverter () efficiency | 90 | % |
| Maximum power current () | 5.56 | A | Capital and replacement cost | 127 | $/kW |
| Open circuit voltage () | 22.3 | V | O&M cost | 1 | $/yr |
| Short circuit voltage () | 6.1 | A | Life time | 20 | yr |
| Number of cells | 36 | - | |||
| Nominal operating cell temperature | 45 | ||||
| Capital cost and replacement cost | 1084 (per kW) | $ (per kW) | |||
| O&M cost | 5 (per kW) | $/yr | |||
| Life time | 20 | yr | |||
| Fuel cell | Electrolyzer | ||||
| Rated power | 1 | kW | Capital and replacement cost | 150 | $/kW |
| Capital and replacement cost | 600 | $/kW | O&M cost | 8 | $/yr/kW |
| O&M cost | 0.01 | $/hr/kW | Efficiency | 90 | % |
| Fuel cell coefficient | 0.0003 | $/hr/kW | Life time | 20 | yr |
| Hydrogen to electricity conversion by fuel cell ( | 0.059 | $/hr/kW | |||
| Life time of FC | 50,000 | h | |||
| Hydrogen tank | Others | ||||
| Capital cost | 1.3 | $/kg | DC bus voltage | 120 | V |
| Replacement cost | 0.5 | $/kg | Project life (N) | 20 | yr |
| O&M cost | 0.6 | $/yr/kg | Interest rate (i) | 6 | % |
| Life time | 20 | yr |
| Algorithm | PV | FC | Electrolyzer | Tank | Inverter | NPC | ACS | LCOE | FC Hours |
|---|---|---|---|---|---|---|---|---|---|
| (kW) | (kW) | (kW) | (kg) | (kW) | ($) | ($) | ($/kWh) | (hrs) | |
| ABC | 129 | 15 | 34 | 19 | 12 | 179,747.7 | 15,674 | 0.228 | 4974 |
| HOMER | 130 | 15 | 34 | 20 | 12 | 180,917.4 | 15,776 | 0.232 | 4972 |
| HOMER | ABC Algorithm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Component | Capital | Repl | O&M Cost | Salvage | Total | Capital | Repl | O&M Cost | Salvage | Total |
| ($/yr) | ($/yr) | ($/yr) | ($/yr) | ($/yr) | ($/yr) | ($/yr) | ($/yr) | ($/yr) | ($/yr) | |
| PV | 12,286 | 0 | 650 | 0 | 12,936 | 12,191 | 0 | 645 | 0 | 12,836 |
| Fuel Cell | 785 | 437 | 746 | −3 | 1965 | 785 | 437 | 745 | −4 | 1963 |
| Electrolyzer | 445 | 0 | 272 | 0 | 717 | 445 | 0 | 272 | 0 | 717 |
| tank | 2 | 0 | 12 | 0 | 14 | 1.9 | 0 | 11.4 | 0 | 13 |
| Inverter | 133 | 0 | 12 | 0 | 145 | 133 | 0 | 12 | 0 | 145 |
| Total system | 13,615 | 437 | 1692 | −3 | 15,777 | 13,556 | 437 | 1685 | −4 | 15,674 |
| Energy Production | Energy Consumption | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ABC Algorithm | HOMER | ABC Algorithm | HOMER | ||||||
| kWh/yr | % | kWh/yr | % | kWh/yr | % | kWh/yr | % | ||
| PV panels (DC) | 217,284 | 90.4 | 218,968 | 91 | DC Primary load | 28,422 | 22 | 28,426 | 22 |
| Fuel cells (DC) | 22,945 | 9.5 | 22,927 | 9.4 | AC Primary load | 40,114 | 31 | 40,120 | 31 |
| Total | 240,229 | 100 | 241,895 | 100 | Electrolyzer load | 60,065 | 46.7 | 59,997 | 46.7 |
| Total | 128,601 | 100 | 128,543 | 100 | |||||
| Excess electricity | 108,162 | 180,894 | Unmet load / LPSP (%) | 36.92 | 0.053 | 37.3 | 0.054 | ||
| DFCL Class | |||
|---|---|---|---|
| Data Name | CDC | Explanation | M/O/C |
| LN Name | - | Shall be inherited from the logical-node class (see IEC 61850-7-2) | |
| Data | |||
| System logical node data | |||
| LN shall inherit all mandatory data from common logical node class | M | ||
| Settings | |||
| VRtg | ASG | Voltage rating of fuel cell stack | M |
| IRtg | ASG | Current rating of fuel cell stack | M |
| Plim | ASG | Power limit | M |
| Controls | |||
| FuelSht | DPC | True for fuel cell operation, False for Fuel cell shutdown | M |
| Measured Values | |||
| OutH2Rte | MV | Measures the rate of hydrogen. | M |
| DELZ Class | |||
|---|---|---|---|
| Data Name | CDC | Explanation | M/O/C |
| LN Name | Shall be inherited from the logical-node class (see IEC 61850-7-2) | ||
| Data | |||
| System logical node data | |||
| LN shall inherit all mandatory data from common logical node class | M | ||
| Settings | |||
| ThermCap | ASG | Defines the thermal capacity of conversion of electrolyzer | M |
| MaxTmp | ASG | The maximum permissible temperature of electrolyzer | M |
| MaxPres | ASG | The maximum permissible pressure of electrolyzer | M |
| MaxPwr | ASG | The maximum power of electrolyzer | M |
| Controls | |||
| FuelSht | SPS | For operating the electrolyzer when excess energy is available. True = ON, False = OFF | M |
| Measured Values | |||
| PwrH2Ef | MV | Defines the efficiency of conversion from power to hydrogen | M |
| HydFlwrate | MV | Defines the flow rate of hydrogen produced. | M |
| DHGT Class | |||
|---|---|---|---|
| Data Name | CDC | Explanation | M/O/C |
| LN Name | Shall be inherited from the logical-node class (see IEC 61850-7-2) | ||
| Data | |||
| System logical node data | |||
| LN shall inherit all mandatory data from common logical node class | M | ||
| Settings | |||
| MaxTmpH | ASG | The maximum permissible temperature of tank | M |
| MaxPresH | ASG | The maximum permissible pressure of tank | M |
| Measured Values | |||
| H2Presinit | MV | Defines the hydrogen pressure available in the tank | M |
| H2Presfin | MV | Defines the hydrogen pressure after hydrogen addition in the tank | M |
| Message Exchanges for Energy Management in FC-PV Hybrid System | ACSI Service | Type of PDU/Message | |
|---|---|---|---|
| Source IED | Destination IED | ||
| PV IED → DPVM → MdulWRtg | MGCC | GetDataValues | Read-MMS Request, Read-MMS Response |
| Fuel Cell IED→ DFCL→ OutHydRate | MGCC | GetDataValues | Read-MMS Request, Read-MMS Response |
| Electrolyzer IED→ DELZ→MaxPwr | MGCC | GetDataValues | Read-MMS Request, Read-MMS Response |
| Hydrogen Tank IED →DHGT→MaxPresH | MGCC | GetDataValues | Read-MMS Request, Read-MMS Response |
| AC, DC loads→CNLO →WRtg | MGCC | GetDataValues | Read-MMS Request Read-MMS Response |
| Case I | |||
| MGCC | XCBR4→DELZ→FuelSht | SendGOOSEMessage | GoosePDU |
| Hydrogen Tank IED→DHGT→H2Presinit | MGCC | GetDataValues | Read-MMS Request, Read-MMS Response |
| MGCC | Hydrogen Tank IED→DHGT→H2Presfin | SetDataValue | Write-MMS Request, Write-MMS Response |
| Case III | |||
| MGCC | XCBR3→DFCL→FuelSht | SendGOOSEMessage | GoosePDU |
| Fuel Cell IED→DFCL→ PwrH2Ef | MGCC | GetDataValues | Read-MMS Request Read-MMS Response |
| MGCC | Fuel Cell IED→DFCL→Plim, OutHydRate | SetDataValue | Write-MMS Request, Write-MMS Response |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Chauhan, P.; Aftab, M.A.; Ali, I.; Hussain, S.M.S.; Ustun, T.S. Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV. Energies 2020, 13, 1295. https://doi.org/10.3390/en13051295
Singh S, Chauhan P, Aftab MA, Ali I, Hussain SMS, Ustun TS. Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV. Energies. 2020; 13(5):1295. https://doi.org/10.3390/en13051295
Chicago/Turabian StyleSingh, Shakti, Prachi Chauhan, Mohd Asim Aftab, Ikbal Ali, S. M. Suhail Hussain, and Taha Selim Ustun. 2020. "Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV" Energies 13, no. 5: 1295. https://doi.org/10.3390/en13051295
APA StyleSingh, S., Chauhan, P., Aftab, M. A., Ali, I., Hussain, S. M. S., & Ustun, T. S. (2020). Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV. Energies, 13(5), 1295. https://doi.org/10.3390/en13051295







