Adaptive Multi-Model Switching Predictive Active Power Control Scheme for Wind Generator System

Abstract

To deal with the randomness and uncertainty of the wind power generation process, this paper proposes the use of the clustering method to complement the multi-model predictive control algorithm for active power control. Firstly, the fuzzy clustering algorithm is adopted to classify actual measured data; then, the forgetting factor recursive least square method is used to establish the multi-model of the system as the prediction model. Secondly, the model predictive controller is designed to use the measured wind speed as disturbance, the pitch angle as the control variable, and the active power as the output. Finally, the parameters and measured data of wind generators in operation in Western China are adopted for simulation and verification. Compared to the single model prediction control method, the adaptive multi-model predictive control method can yield a much higher prediction accuracy, which can significantly eliminate the instability in the process of wind power generation.

1. Introduction

The uncertainty of wind speed makes the output power of the wind power generation system fluctuate greatly [1,2,3]. Frequent switching control will result in a transient overload of the transmission chain and an overshoot of output power. As a result, the system shows very strong nonlinearity. Since the multi-model predictive control (MMPC) method can effectively cope with complex nonlinear systems—i.e., wind generation systems—it has been widely used recently.

In [4], a model predictive control (MPC)-based optimal active power control scheme for a doubly-fed induction generator (DFIG) was proposed, which was applied to wind farms with a distributed energy storage system (ESS). For such a multi-input and multi-output (MIMO) wind generation system, the dynamic characteristics of the converter and wind turbines (WTs) were considered in MPC. By using MPC, the reference for active power between WTs and ESS was optimized according to the local wind conditions. The results showed that such a control scheme can greatly reduce the control error of active power for WTs. Similarly, an online model-based predictive control method was proposed in [5], which was used for the real-time optimal operation of a wind power integrated system including demand response (DR) and ESS. This method took into account all the interaction effects of the control facilities according to the estimated output of the future wind farms and realized the maximum utilization of wind power. The model has good universality and adaptability, and is suitable to resolve the high uncertainty of wind power generation and customer behavior. Compared with the online no-prediction method and offline prediction method, the daily wind energy utilization of this method is increased by 13.9% and 4.9%, respectively. In [6], an active power control architecture based on the combination of MPC and wind turbine state classification was proposed, where an equivalent model of an MPC controller was established. Compared with traditional methods, this method is more suitable for the active power control t the wind farm level since it ensures that the wind farm operates as a single controllable entity on the grid and acts like a traditional power plant.

Considering that wind farms always cooperate and interact with traditional thermal power plants, a comprehensive model of the hybrid system including both a wind farm and thermal power plant was established in [7] by combining the wind farm model with the well-known thermal power model. In [8], an improved load frequency control (LFC) method based on MPC was proposed, and the simulation results showed that this method could effectively improve the frequency response level of both the wind farm and thermal power plant, thus improving the frequency performance of the connected system.

To effectively coordinate the control of active power and reactive power, an MPC-based distributed information synchronization scheme and distributed coordination control scheme for wind farms was proposed and verified on a wind farm containing 10 WTs in [9]. For the distributed coordination control scheme, the pitch angle and generator torque of the WTs were optimized to reduce the fatigue load of the WTs and track the power reference of the wind farm. In [10], the MPC was utilized to replace the proportional integral (PI) controller for the speed control of a permanent magnet synchronous generator (PMSG). Similarly, the MPC was also applied to replace the traditional PI controller in [11,12]. The MPC avoids the disadvantages of the traditional PI controller; e.g., a slow dynamic response, coupling, complex structure, difficulty in determining the PI’s parameters, etc. Compared with the PI control, the MPC has better performance in speed tracking, irrespective of whether the step speed is increased or step speed is decreased.

In [13], a variable-weight MPC strategy was introduced to optimize the coordination of mechanical load and the power of the wind power generation system. In the variable-weight MPC strategy, the pitch and torque are coordinated by Pareto analysis to optimize the output and load of the generator. Through the evaluation of the wind condition, the weight matrix of MPC can be updated adaptively. Finally, compared with the traditional gain scheduling PI control, the results showed that the strategy is effective. According to the operation areas of the wind turbine, three kinds of controllers—classic MPC and two kinds of economic model predictive control (EMPC)—were designed in [14]. The simulation results showed that the performance of the three predictive control strategies was better than that of the traditional LQR controller. EMPC can not only effectively reduce the fatigue load of all operation areas, but also increase the utilization of wind energy when the wind speed fluctuates near the rated wind speed. When the power grid operates under an unbalanced condition, the low-voltage ride-through capability becomes a difficulty for managers. Therefore, a finite set model predictive control strategy was proposed in [15], which could ensure the converter provides a balanced current and both active and reactive power support during grid connection. Compared with the traditional MPC, this method increases the control delay, and the waveform quality is much better.

Besides, the MPC method was also applied to a new type of converter control a the wind turbine with PMSG in [16], and the separation control of the machine and the grid side was realized by minimizing the value function. Further study on MMPC for PMSG control was also reported in [17]. The MMPC can ensure the smooth control of the active power output of WTs while ensuring high wind energy utilization efficiency. In the low wind speed condition, the fluctuation of active power can be reduced. The overshoot of active power can be reduced when WT operates near the rated wind speed. A smooth control can be realized, and the fluctuation of active power can also be significantly reduced when the WT operates above the rated wind speed.

From the above studies, it is apparent that the MPC method can solve the uncertainties and random changes of wind speed in the wind power generation system. However, there is little discussion about the short-term rapid change of wind speed in the above studies, especially for the case in which the wind speed varies through three different wind speed sections in a few seconds.

In view of this situation, this paper proposes an MMPC method for wind turbines under all wind conditions. The main contents of this paper include the following: (1) the classification of the collected 1000 groups of field-collected data using the fuzzy clustering method (FCM) and establishment of a multivariable prediction model using the forgetting factor recursive least square method (FFR-LSM), (2) the design of the multi-model predictive controller (MMPCR) with measurable wind speed as disturbance signal and pitch angle as the control variable, (3) the application of the designed MMPCR to the actual power control of wind turbine, and a comparison of the results with those of the single model predictive control method. The rest of this paper is organized as follows: Section 2 introduces the modeling of the wind turbine data from actual field using fuzzy clustering, Section 3 presents the design of the generalized predictive controller and Section 4 details the realization of multi-model switching control. Case study and simulation analysis are carried out in Section 5, while the conclusions are finally drawn in Section 6.

2. Fuzzy Clustering Modeling of the Field-Collected Wind Turbine Data

2.1. Mathematical Model of Variable Speed Variable Pitch Wind Turbine

Generally, a variable speed variable pitch wind turbine is mainly composed of a wind wheel, transmission part, and generator. The output power can be described as [18]

$$P=\{\begin{array}{l}\eta P_r,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{v}_{\mathrm{cutin}}\le v<v_N\\ P_N,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{v}_N\le v\le v_{\mathrm{cutout}}\end{array}$$

(1)

with

$$P_r=0.5\rho v^{3}S{C}_p(\lambda ,\beta )$$

(2)

and

$$C_P=(0.44-0.0167\beta )\sin \left[\frac{\pi (\lambda -3)}{15-0.3\beta }\right]-0.00184(\lambda -3)\beta$$

(3)

$$\lambda =\frac{2\pi nR}{v}=\frac{\omega R}{v}$$

(4)

where η is the conversion efficiency of wind energy, P is the mechanical power of WT, ρ represents air density, S stands for the swept area of the blade, λ is the tip speed ratio, β is the pitch angle, v is the wind speed, ω is the speed of the main shaft, and R is the diameter of the wind turbine.

2.2. Fuzzy Clustering of Data Sets

The measured data of WTs including the wind speed, pitch angle and active power of the generator are classified by the subtraction clustering algorithm–fuzzy c-means clustering, and then multiple models are generated by FFR-LSM. The fuzzy c-means clustering algorithm determines the category of each data point according to the membership degree. When the fuzzy objective function is the smallest, the data group is divided into C fuzzy categories. Details of the algorithm can be found in [19] and [20]. The Davies Bouldin index (DBI) is used to evaluate the cluster performance. The process of subtractive clustering is as follows [21,22]:

• Step 1: Determine the number of categories C and fuzzy weight index m, and initialize the clustering center V.
• Step 2: Calculate the fuzzy membership matrix U according to Equation (5).

  $$u_{ij}=\{\begin{array}{cc}{\left[{\displaystyle \sum _{k=1}^c\frac{{\Vert x_i-V_j\Vert }^{\frac{2}{m-1}}}{{\Vert x_i-V_k\Vert }^{\frac{2}{m-1}}}}\right]}^{-1}& \Vert x_i-V_k\Vert \ne 0\\ 1& \Vert x_i-V_k\Vert =0\mathrm{and}k=j\\ 0& \Vert x_i-V_k\Vert =0\mathrm{and}k\ne j\end{array}$$

  (5)

  where u_ij is the membership of x_i belonging to category j, and V_j or V_k is the clustering center of category j or k.
• Step 3: Calculate the category center V_j using Equation (6).

  $$V_j=\frac{{\displaystyle \sum _{i=1}^n{u}_{ij}^m{x}_i}}{{\displaystyle \sum _{i=1}^n{u}_{ij}^m}}$$

  (6)
• Step 4: Calculate the objective value J of cluster V_j using Equation (7) and judge whether target value is met or not. If it is met, the clustering will end; otherwise, return to step 2.

  $$J={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^c{(u_{ij})}^m\Vert x_i-V_j\Vert }}$$

  (7)

In this paper, a total of 1000 groups of field measured data set M (m1, m2, m3) are classified, where m1 stands for the pitch angle, m2 represents wind speed, and m3 is the active power of the generator. The clustering result shows that a minimum DBI can be obtained when the number of clusters is equal to five. The clustering result is shown in

Table 1. The clustering result of field-collected wind turbine data. DBI: Davies Bouldin index.

Number of Clustering	3	4	5	6	7
DBI	1.4473	0.6923	0.1978	1.1791	0.9733

.

When the number of clusters is five, all clustering center of the data can be summarized as

$$\mathrm{Center}=\left[\begin{array}{ccc}0.00& 2.07& 661.09\\ 0.04& 4.43& 709.23\\ 5.94& 7.02& 870.10\\ 10.07& 9.78& 1300.79\\ 13.08& 11.06& 1508.43\end{array}\right]$$

Considering that some of the data may overlap with each other—e.g., the wind speed can increase or decrease in a short time—the output power is consequently affected by the wind speed. Therefore, the wind generation system can be regarded as a system with a strong disturbance.

2.3. Least Square Modeling

Based on the results of the above clustering data, the wind speed and pitch angle are used as inputs, and the output power is taken as the output for the least squares modeling and to perform the index function determination. To overcome the shortcoming of the poor correction ability of the least square method (LSM), the forgetting factor recursive LSM (FFR-LSM) is adopted in this paper [22]. The performed index function is

$$J={\displaystyle \sum _{k=1}^L{\lambda }^{L-k}}[y(k)-{\phi }^{\mathrm{T}}(k)\stackrel{\wedge }{\theta }(k)]$$

(8)

where $\widehat{\theta }(k)$ is the parameter under-identification, $\phi (k)$ is the observation matrix, λ is the forgetting factor, L is the times of observation, and y(k) is the output of the system.

For the objective function given in Equation (8), Equation (9) can be used to express the recursive least square parameter estimation formula of the forgetting factor.

$$\{\begin{array}{l}\stackrel{\wedge }{\theta }(k)=\stackrel{\wedge }{\theta }(k-1)+K(k)\left[y(k)-{\phi }^T(k)\stackrel{\wedge }{\theta }(k-1)\right]\\ K(k)=\frac{P(k-1)\phi (k)}{\lambda +{\phi }^T(k)P(k-1)\phi (k)}\\ P(k)=\frac{1}{\lambda }\left[1-K(k){\phi }^T(k)\right]P(k-1)\end{array}$$

(9)

with K(k) representing the gain matrix and P(k) standing for the covariance matrix.

According to the measured data and the operating characteristics of the wind generator system, the cumulative abnormal return (CAR) model expressed in Equation (11) is used to identify the parameters. Combined with the classification results of the field-collected wind turbine data, five mathematical models are established.

$$Y(k+1)={\phi }^T(k)\theta$$

(10)

with

$$\begin{gathered} Y(k+1)={[y_1(k+1),y_2(k+1),y_3(k+1),y_4(k+1),y_5(k+1)]}^{\mathrm{T}} \\ \theta =\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\\ a_{41}& a_{42}& a_{43}\\ a_{51}& a_{52}& a_{53}\end{array}\right] \\ {\phi }^T(k)=\left[\begin{array}{ccc}-y_1(k)& u_1(k)& {\xi }_1(k)\\ -y_1(k)& u_2(k)& {\xi }_2(k)\\ -y_1(k)& u_3(k)& {\xi }_3(k)\\ -y_1(k)& u_4(k)& {\xi }_4(k)\\ -y_1(k)& u_5(k)& {\xi }_5(k)\end{array}\right] \end{gathered}$$

Taking the initial value θ(0) = 0, P(0) = 10⁵ I, λ = 0.95, I is the unit matrix, and five mathematical models of wind generation system can be obtained, as shown in Equation (11).

$$\{\begin{array}{c}{y}_1(k+1)=0.9374y_1(k)+0.3711u_1(k)+v_1(k)\\ y_2(k+1)=0.9695y_1(k)+0.3371u_1(k)+v_2(k)\\ y_3(k+1)=0.9217y_1(k)+0.2091u_1(k)+v_3(k)\\ y_4(k+1)=0.9241y_1(k)+0.3821u_1(k)+v_4(k)\\ y_5(k+1)=0.9801y_1(k)+0.2891u_1(k)+v_5(k)\end{array}$$

(11)

where y_i(k) is the output power of the wind generator, u_i(k) is the pitch angle, and v_i(k) is the wind speed. Therefore, Equation (11) is taken as the prediction model for the system.

3. Design of the Generalized Predictive Controller

In this paper, the controlled auto-regressive integrated moving-average (CARIMA) model is used as the prediction model [21,22]. The discrete difference equation is shown in Equation (12).

$$A\left(z^{-1}\right)y\left(k\right)=B\left(z^{-1}\right)u\left(k-1\right)+C\left(z^{-1}\right)\xi \left(k\right)/\Delta$$

(12)

where y(k) and u(k) are the output and input of the controlled object, Δ = 1 − k⁻¹ is the difference operator, A(z⁻¹), B(z⁻¹), and C(z⁻¹) are polynomials of backward operators, and ξ(k) is the white noise sequence with zero mean value. If the time delay of the system d > 1, then let the coefficients of the first d − 1 terms of B(z⁻¹) be zero. The polynomials also satisfy the following:

$$\{\begin{array}{l}A(z^{-1})=1+a_{1,1}{z}^{-1}+a_{1,2}{z}^{-2}+\cdots +a_{1,n_{\mathrm{a}}}{z}^{-n_{\mathrm{a}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ B(z^{-1})=b_{1,0}+b_{1,1}{z}^{-1}+b_{1,2}{z}^{-2}+\cdots +b_{1,n_{\mathrm{b}}}{z}^{-n_{\mathrm{b}}}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{l}_{1,0}\ne 0\\ C(z^{-1})=1+c_{1,1}{z}^{-1}+c_{1,2}{z}^{-2}+\cdots +c_{1,n_{\mathrm{c}}}{z}^{-n_{\mathrm{c}}}\end{array}$$

3.1. Objective Function

In general, for the sake of the following smoothness, tracking control is carried out by following the reference track after softening. The reference trajectory is shown as follows:

$$w\left(k+j\right)=a^{j}y\left(k\right)+\left(1-a^j\right)y_r\left(k\right)$$

(13)

where y_r(k) stands for a set value for output, w(k) represents the reference trajectory, and α is the softening coefficient with 0 < α < 1.

The performance function can be represented by using the following equation:

$$\min J\left(k\right)={\displaystyle \sum _{j=1}^n{\left[y\left(k+j\right)-w\left(k+j\right)\right]}^2}+{\displaystyle \sum _{j=1}^m\lambda }\left(j\right){\left[\Delta u\left(k+j-1\right)\right]}^2$$

(14)

where n is the maximum prediction length, m is the control time-domain (m ≤ n), and λ(j) is the control weighting coefficient. To prevent the variation caused by a drastic change of control increment, a certain value is set for λ(j), while Δu(k) is the control increment of the system. Therefore, the generalized predictive control method can be understood to find a reasonable control increment sequence Δu(k), Δu(k + 1), …, Δu(k + m − 1) to make the objective function J have the minimum value.

3.2. Output Prediction

In order to predict the output ahead of step j, the Diophantine equation is introduced in the generalized predictive control method:

$$E_j\left(z^{-1}\right)A\left(z^{-1}\right)\Delta +z^{-j}{F}_j\left(z^{-1}\right)=1$$

(15)

where E_j and F_j are determined by prediction length and system parameter.

The optimal output prediction value can be obtained by combining Equations (13) and (15):

$$Y=G\Delta U+f$$

(16)

with

$$\begin{gathered} Y={\left[y\left(k+1\right),y\left(k+2\right),\cdot \cdot \cdot ,y\left(k+n\right)\right]}^{\mathrm{T}} \\ \Delta U=\left[\Delta u\left(k\right),\Delta u\left(k+1\right),\cdot \cdot \cdot ,\Delta u\left(k+m-1\right)\right] \\ f=H\Delta u\left(k\right)+Fy\left(k\right)={\left[f\left(k+1\right),f\left(k+2\right),\cdot \cdot \cdot ,f\left(k+n\right)\right]}^{\mathrm{T}} \\ G=\left[\begin{array}{cccc}{g}_0& & & 0\\ g_1& g_0& & \\ ⋮& ⋮& \ddots & \\ g_{n-1}& g_{n-2}& \cdots & g_0\end{array}\right]=\left[\begin{array}{c}{g}_{11}{z}^{-1}+g_{12}{z}^{-2}+\cdots \\ g_{22}{z}^{-1}+g_{23}{z}^{-2}+\cdots \\ ⋮\\ g_{nn}{z}^{-1}+g_{n\left(n+1\right)}{z}^{-2}+\cdots \end{array}\right] \\ H=\left[\begin{array}{c}{G}_1-G_0\\ z\left(G_2-z^{-1}{g}_1-g_0\right)\\ ⋮\\ z^{n-1}\left(G_n-z^{-n+1}{g}_{n-1}-\cdots -z^{-1}{g}_1+g_0\right)\end{array}\right] \\ F={\left[F_1,F_2,\cdot \cdot \cdot ,F_n\right]}^{\mathrm{T}} \end{gathered}$$

where G is the control matrix. The parameters of E_j, F_j, G_j, and H_j are determined by the prediction length and system parameter, and satisfy the following:

$$\{\begin{array}{l}{E}_j\left(z^{-1}\right)=e_{j,0}+e_{j,1}{z}^{-1}+\dots +e_{j,j-1}{z}^{-(j-1)}\\ F_j\left(z^{-1}\right){=\mathrm{f}}_{j,0}+f_{j,1}{z}^{-1}+\dots +f_{j,j-1}{z}^{-(j-1)}\\ G_j\left(z^{-1}\right)=g_{j,0}+g_{j,1}{z}^{-1}+\dots +g_{j,j-1}{z}^{-(j-1)}\\ H_j\left(z^{-1}\right)=h_{j,0}+h_{j,1}{z}^{-1}+\dots +h_{j,j-1}{z}^{-(j-1)}\end{array}$$

3.3. Determination of the Optimal Control Law

The hypothesis is that $W={\left[w\left(k+1\right),w\left(k+2\right),\cdots ,w\left(k+n\right)\right]}^{\mathrm{T}}$; when $\frac{\partial J}{\partial \Delta u}=0$, the optimal performance index function of Equation (17) can be obtained, as shown in Equation (18).

$$\Delta U={\left(G^{T}G+\lambda I\right)}^{-1}{G}^T\left(W-f\right)$$

(17)

$$u\left(k\right)=u\left(k-1\right)+\Delta u$$

(18)

To make full use of remaining control information and prevent the predictive control increament of Δu(k) from being reduced due to interference, a smooth filter is used as the input to carry out weighted control, as shown in Equation (19).

$$u\left(k\right)=\frac{{\displaystyle \sum _{i=j}^{s}q\left(i\right)}u\left(k|k-i+1\right)}{{\displaystyle \sum _{i=1}^{s}q\left(i\right)}}$$

(19)

where s stands for the control steps in the time domain and q(i) represents the control weighting coefficient.

The generalized predictive control method can make the control output close to the reference trajectory or target curve as much as possible through rolling optimization and feedback correction. In this paper, the control input u(k + 1) optimizes and corrects the control input u(k) at step k through the optimal prediction at step k + 1, which can slow down the excessive increase or decrease of the control input increment in a certain trend and effectively reduce the occurrence probability of overshoot. The actual control variable is

$$u_s\left(k\right)=\frac{u\left(k\right)+u\left(k+1/k\right)}{2}=u\left(k\right)+\Delta u\frac{\left(k+1/k\right)}{2}$$

(20)

with

$$\Delta u\left(\frac{k+1}{k}\right)=\frac{{\displaystyle \sum _{i=1}^m\beta \left(k\right)\Delta u\left(k+i/k\right)}}{{\displaystyle \sum _{i=1}^m\beta \left(k\right)}}$$

(21)

where Δu(k + i/k) is the predictive control increment at time k + 1 and β(k) is the weighting factor (0 < β < 1).

4. Multi-Model Switching Control

The structure diagram of the MMPC system of the wind generation system is given in Figure 1, where the stability of the multi-model switching control system has been demonstrated in Equation [18]. In the figure, ${\widehat{y}}_i(i=1,2,\dots ,5)$ is the output of M₁, M₂, …, M₅, and y_r is the reference input. At each sampling time, the optimal sub-model will be selected for predictive control [19,21].

Suppose at time k, $e_i(k)=y(k)-{\widehat{y}}_i(k)$ represents the error between actual output and the output of sub-model i, define the switching performance index function:

$$J_i(k)=a{e}_i^2(k)+b{\displaystyle \sum _{j=1}^l{\rho }^j}{e}_i^2(k-j)$$

(22)

where l is the time length, a and b (a > 0, b > 0) are the error weighting coefficients representing the matching degree of current and past time length l, respectively, while ρ is the forgetting factor. The smaller the J_i(k), the higher the matching degree of model M_i.

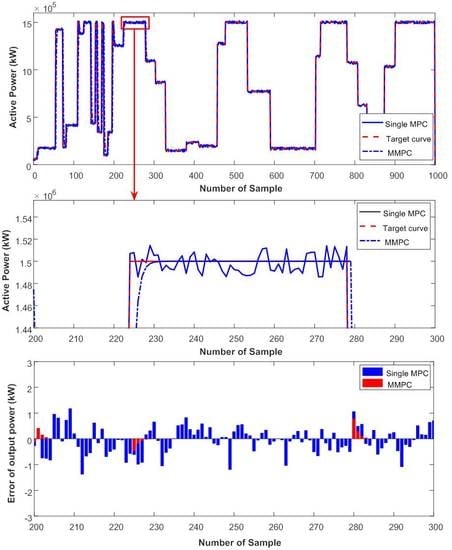
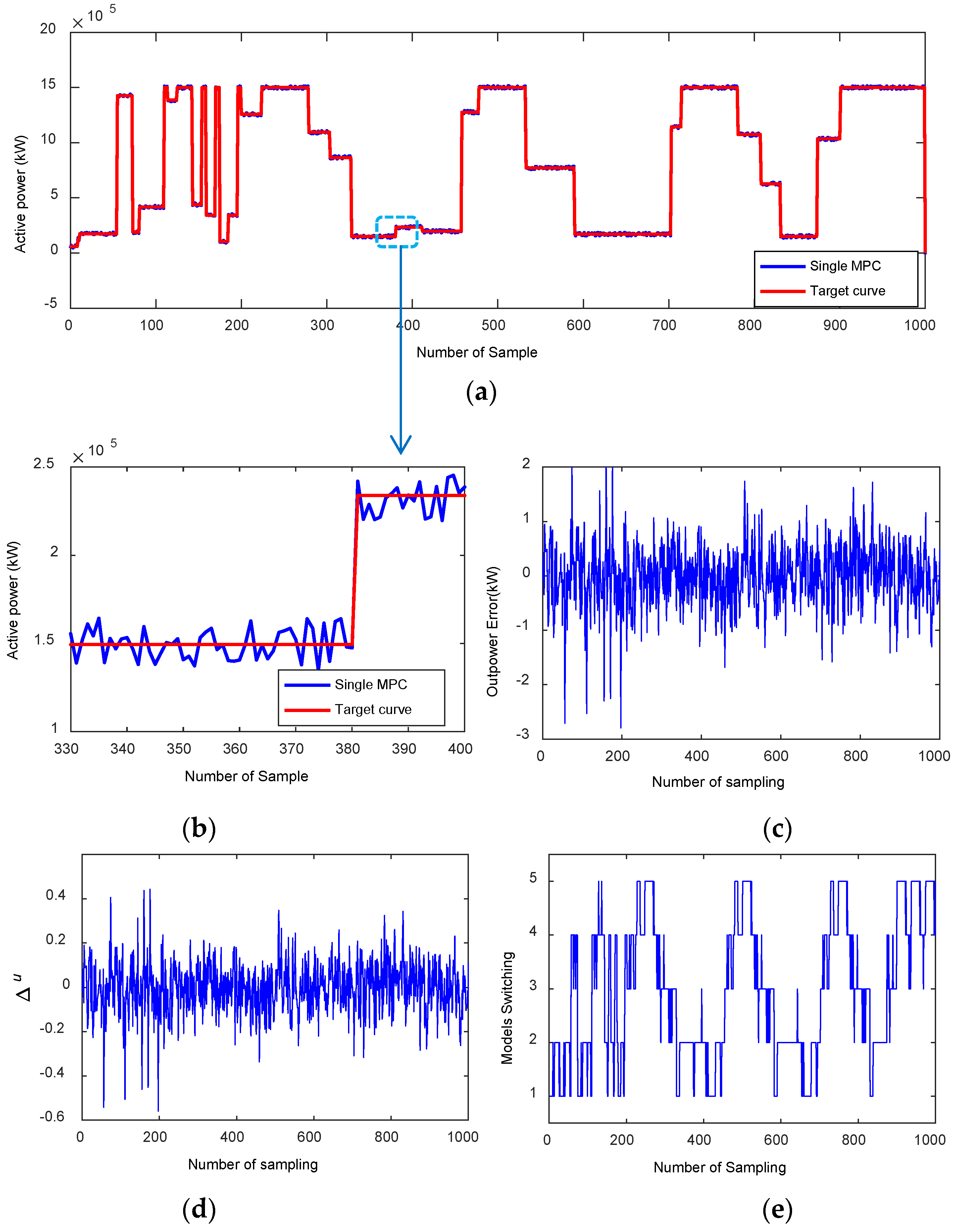
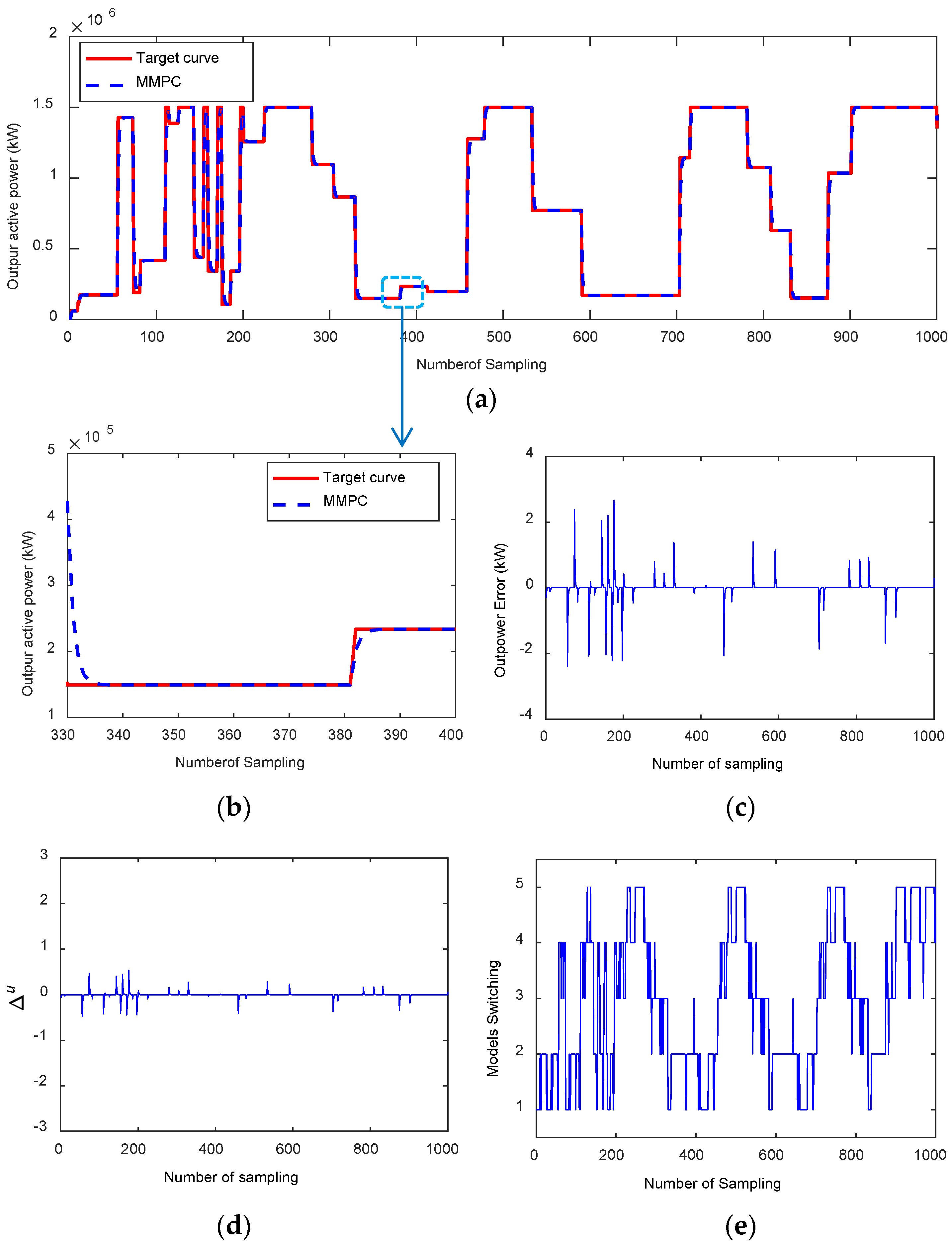
5. Case Study and Simulation Analysis

In order to verify the effectiveness of the proposed method, the wind turbines with a doubly-fed induction generator (DFIG) in Guazhou Wind Farm of Western China are utilized for the case study. The parameters of wind turbine can refer to the Appendix A.

The wind generation system is given in Equation (11) and is adopted for simulation analysis (see in Figure 2), where the pitch angle is taken as the control variable and the wind speed is considered as a disturbance. The pitch angle is controlled according to the disturbance signal to ensure that the output of the wind turbine can follow the predetermined target. In this paper, the forgetting factor ρ = 0.7, the softening coefficient α = 0.35, the unit value is adopted as the control length, and the value of control weighting coefficient λ(j) is 0.9. The simulation results of the single MPC and the MMPC are given in the following figures.

From Figure 3, it is apparent that the tracking effect of the MPC algorithm is satisfactory, and the maximum error of output power is 2.8 kW for the wind farm. As presented in Figure 3c and Figure 4c (the local zoom of Figure 3a and Figure 4a), it is apparent that the output active power from the results derived by the MMPC method is more smooth than that yield from the single MPC method. In comparison, the MMPC can derive a much smaller output error under the same model switch strategy shown in Figure 3e or Figure 4e. The maximum active output error using the single MPC is almost 3 kW (in Figure 3c), while that yield from MMPC is about 2kW (in Figure 4c). It is mainly because that the proposed adaptive multi-model switching predictive control method can switch to different models according to the wind speed variation, which can ensure the wind generation system operates in an optimal condition by selecting the most suitable model given in Figure 1. For the single MPC method, however, there is no additional choice but to adapt to the variation of the wind speed and tune the control parameters according to the predicted control error. Since the wind speed sometimes varies rapidly in a very short time, the performance of the MPC method becomes inferior when compared with the MMPC method.

Additionally, as is reflected in Figure 3d and Figure 4d, the switching control accuracy of MMPC is much higher than that of the single MPC. The results show that the MMPC strategy can reduce the tracking error in the dynamic process of the system and improve the convergence speed and tracking accuracy of the system. The simulation results proves that, with the fuzzy clustering method used, the wind speed data is pre-processed and classified to certain groups, and corresponding predictive control scheme with suitable model given in Figure 1 is assigned, which enables the MMPC outperformances the single MPC to a great extent.

6. Conclusions

In this paper, up to 1000 groups of field-collected datasets are adopted for the case study. These data are firstly classified into five groups using the classical clustering algorithm–fuzzy c-means clustering. After this, the predictive controller is designed for multi-model switching control, and both the single MPC and MMPC are applied to the wind generation system for the active power control of a local wind farm in Gansu Province. For the case study and result analysis, it is proved that the proposed adaptive MMPC for the active power of a wind generator is effective and efficient, and the combination of the fuzzy c-means clustering and the MMPC solves the problem of randomness and uncertainty in the active power prediction of the wind generation system. By pre-clustering and multi-model switching, the impact of wind speed randomness and uncertainty on the output power is minimized, and the prediction accuracy is effectively improved. The proposed method is of guiding significance for the active power prediction in the system and the near future.