Modeling the Charging Behaviors for Electric Vehicles Based on Ternary Symmetric Kernel Density Estimation
Abstract
:1. Introduction
2. Ternary Symmetric KDE Model of EVs Charging Behaviors
2.1. Data Transformation Model
2.2. Ternary Symmetric KDE Model
2.3. Optimum Bandwidth Model
2.4. Estimation Evaluation Model
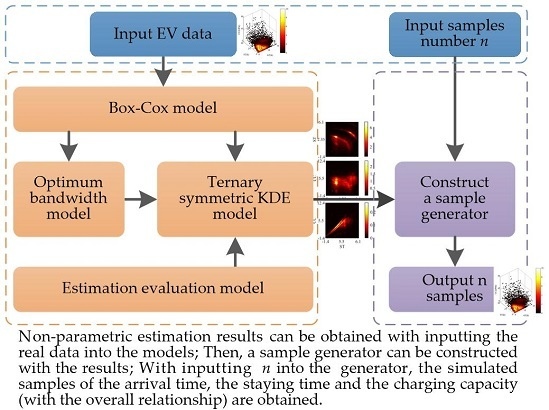
3. Algorithm Flowchart
- Step 1:
- Extract effective data records of the EVs arrival time, stay time, and charging capacity in the work area to conduct normal transformations on it with Equation (1) sequentially and estimate the transformed parameters with the Equations (3) and (4) sequentially before solving the parameter estimation model with the genetic algorithm (GA). Moreover, the data transformation model is solved by using the GA function in Toolbox in MATLAB to obtain the estimated value of the transformation parameter;
- Step 2:
- Substitute the original data and the transformed data into Equations (16) and (17), respectively, and solve the optimal bandwidth model through using the Fmincon function in Toolbox in MATLAB to obtain corresponding optimal bandwidths;
- Step 3:
- After reading the original and transformed data and the corresponding optimal bandwidth, model the ternary symmetric KDE on the original data and the transformed data distributions through calling the KDE software package in MATLAB. At the same time, estimation modeling is conducted on the original data and transformed data, respectively, by means of using the Ksdensity function and the Copulafit function in Toolbox in MATLAB;
- Step 4:
- Implement the Monte Carlo random sampling through calling the Sample function in the KDE software package in MATLAB by setting the number of simulations and the sampling size, and reading the results of the ternary symmetric KDE. Meanwhile, the Monte Carlo random sampling can be implemented through calling the Copularnd function in Toolbox in MATLAB. It should be noted that the random sampling of the transformed data estimation should be inversely transformed in Equation (2);
- Step 5
- Read the frequency matrix of the binary frequency histogram of the original data and the simulated data, and solve the frequency matrix similarity between the original data and the simulated data through calling the Corr2 function in Toolbox in MATLAB. Besides, results of the ternary symmetric KDE are compared with that of the joint estimation based on the edge KDE and the Copula function to verify the effectiveness of the ternary symmetric KDE model.
4. Numerical Simulation
4.1. EVs Data
4.2. Results and Analysis
- (1)
- Data Transformation Analysis
- (2)
- Estimation Model Analysis
- (3)
- Evaluation Analysis for Estimation Model
5. Conclusions
- Effective data records are aggregated from space and time. On the one hand, every CS is classified into the work area, the residential area, the commercial area, and other areas through searching the name of the CS from the map at the spatial dimension. On the other hand, EVs arrival times of multiple days are aggregated into one day at the time dimension.
- A ternary symmetric KDE model of EVs charging behaviors is established. A higher fitting level can be achieved by the proposed ternary symmetric KDE method, in comparison to the joint estimation method based on the edge KDE and the TTCF.
Author Contributions
Funding
Conflicts of Interest
References
- Abagnale, C.; Cardone, M.; Iodice, P.; Strano, S.; Terzo, M.; Vorraro, G. Power requirements and environmental impact of a pedelec. A case study based on real-life applications. Environ. Impact Assess. Rev. 2015, 53, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Iodice, P.; Senatore, A. Industrial and Urban Sources in Campania, Italy: The Air Pollution Emission Inventory. Energy Environ. 2015, 26, 1305–1317. [Google Scholar] [CrossRef]
- Yang, T.Y.; Xu, X.X.; Guo, Q.L.; Zhang, L.; Sun, H.B. EV charging behavior analysis and modelling based on mobile crowdsensing data. IET Gener. Transm. Distrib. 2017, 11, 1683–1691. [Google Scholar] [CrossRef]
- Rao, R.; Cai, H.; Xu, M. Modeling electric taxis’ charging behavior using real-world data. Int. J. Sustain. Transp. 2018, 12, 452–460. [Google Scholar] [CrossRef]
- Shao, Y.C.; Mu, Y.F.; Yu, X.D.; Dong, X.H.; Jia, H.J.; Wu, J.Z.; Zeng, Y. A spatial-temporal charging load forecast and impact analysis method for distribution network using EVs-traffic-distribution model. Proc. CSEE 2017, 37, 5207–5219. [Google Scholar]
- Su, J.; Lie, T.; Zamora, R. Modelling of large-scale electric vehicles charging demand: A New Zealand case study. Electr. Power Syst. Res. 2019, 167, 171–182. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Z.; Huang, X.; Jin, L. A Study on Price-Based Charging Strategy for Electric Vehicles on Expressways. Energies 2016, 9, 385. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Zhu, T.; Wan, S.; Zhang, S.; Li, K. Optimal charging scheduling for large-scale EV (electric vehicle) deployment based on the interaction of the smart-grid and intelligent-transport systems. Energy 2016, 97, 359–368. [Google Scholar] [CrossRef]
- Wei, W.; Wu, L.; Wang, J.; Mei, S. Network Equilibrium of Coupled Transportation and Power Distribution Systems. IEEE Trans. Smart Grid 2018, 9, 6764–6779. [Google Scholar] [CrossRef]
- Chen, L.; Huang, X.; Chen, Z.; Jin, L. Study of a New Quick-Charging Strategy for Electric Vehicles in Highway Charging Stations. Energies 2016, 9, 744. [Google Scholar] [CrossRef] [Green Version]
- U.S. Department of Transportation. Federal Highway Administration. National Household Travel Survey. Available online: https://nhts.ornl.gov/ (accessed on 19 December 2019).
- Arias, M.B.; Bae, S. Electric vehicle charging demand forecasting model based on big data technologies. Appl. Energy 2016, 183, 327–339. [Google Scholar] [CrossRef]
- Lojowska, A.; Kurowicka, D.; Papaefthymiou, G.; Van Der Sluis, L. Stochastic Modeling of Power Demand Due to EVs Using Copula. IEEE Trans. Power Syst. 2012, 27, 1960–1968. [Google Scholar] [CrossRef]
- Wang, H.L.; Zhang, Y.J.; Mao, H.P. Charging load forecasting method based on instantaneous charging probability for electric vehicles. Electr. Power Autom. Equip. 2019, 39, 207–213. [Google Scholar]
- Wang, D.; Gao, J.; Li, P.; Wang, B.; Zhang, C.; Saxena, S. Modeling of plug-in electric vehicle travel patterns and charging load based on trip chain generation. J. Power Sources 2017, 359, 468–479. [Google Scholar] [CrossRef]
- Yi, T.; Zhang, C.; Lin, T.; Liu, J. Research on the spatial-temporal distribution of electric vehicle charging load demand: A case study in China. J. Clean. Prod. 2020, 242, 118457. [Google Scholar] [CrossRef]
- Sun, X.-H.; Yamamoto, T.; Morikawa, T. Fast-charging station choice behavior among battery electric vehicle users. Transp. Res. Part D Transp. Environ. 2016, 46, 26–39. [Google Scholar] [CrossRef]
- Sadeghianpourhamami, N.; Refa, N.; Strobbe, M.; Develder, C. Quantitive analysis of electric vehicle flexibility: A data-driven approach. Int. J. Electr. Power Energy Syst. 2018, 95, 451–462. [Google Scholar] [CrossRef] [Green Version]
- Flammini, M.G.; Prettico, G.; Julea, A.; Fulli, G.; Mazza, A.; Chicco, G. Statistical characterisation of the real transaction data gathered from electric vehicle charging stations. Electr. Power Syst. Res. 2019, 166, 136–150. [Google Scholar] [CrossRef]
- Xydas, E.; Marmaras, C.; Cipcigan, L.M.; Jenkins, N.; Carroll, S.; Barker, M. A data-driven approach for characterising the charging demand of electric vehicles: A UK case study. Appl. Energy 2016, 162, 763–771. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhang, Z.; Zhao, J.; Wu, B.; Huang, X. An Analysis of the Charging Characteristics of Electric Vehicles Based on Measured Data and Its Application. IEEE Access 2018, 6, 24475–24487. [Google Scholar] [CrossRef]
- Zhao, H.; Yan, X.; Ren, H. Quantifying flexibility of residential electric vehicle charging loads using non-intrusive load extracting algorithm in demand response. Sustain. Cities Soc. 2019, 50, 101664. [Google Scholar] [CrossRef]
- Xue, L. Introduction to Modern Nonparametric Statistics; Science Press: Beijing, China, 2015. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Springer Science and Business Media LLC: Berlin, Germany, 1986. [Google Scholar]
- Xie, Z. MATLAB Statistic Analysis and Application: 40 Cases Analysis; Beihang University Press: Beijing, China, 2015. [Google Scholar]
- Miao, P.B.; Yu, J.; Liu, G.P.; Liang, M.; Li, W.Y.; Ren, Z.Y. Electric public bus load model based on improved kernel density estimation and latin hypercube sampling. Trans. China Electrotech. Soc. 2016, 31, 187–193. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations Revisited, Rebutted. J. Am. Stat. Assoc. 1982, 77, 209–210. [Google Scholar] [CrossRef]
- Wang, R.; Thakur, C.S.; Hamilton, T.J.; Tapson, J.; Van Schaik, A. A neuromorphic hardware architecture using the Neural Engineering Framework for pattern recognition. IEEE Trans. Biomed. Circuits Syst. 2015, 11, 574–584. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, N.; Huang, Y.; Ye, X.W.; Li, H.S.; Li, S.Y.; Dong, B.T. Modeling of output correlation of multiple wind farms based on adaptive multivariable nonparametric kernel density estimation. Proc. CSEE 2018, 38, 3805–3812. [Google Scholar]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kernel Density Estimation Toolbox. Available online: https://www.ics.uci.edu/~ihler/code/kde.html (accessed on 19 December 2019).











| Items | Min(M) | |
|---|---|---|
| Original data | (0.5865, 0.0733, 0.2027) | −0.0012 |
| Transformed data | (0.0069, 0.0456, 0.0908) | −0.5371 |
| Items | Original Data | Transformed Data |
|---|---|---|
| TNCF | ||
| TTCF |
| Items | Case 1 | Case 2 |
|---|---|---|
| AT-ST | 0.6805 | 0.8001 |
| AT-CC | 0.7102 | 0.8751 |
| ST-CC | 0.9530 | 0.9630 |
| Mean | Standard Deviation | |||
|---|---|---|---|---|
| Case 1 | Case 2 | Case 1 | Case 2 | |
| AT-ST | 0.7499 | 0.8256 | 0.0650 | 0.0461 |
| AT-CC | 0.7592 | 0.8612 | 0.0597 | 0.0321 |
| ST-CC | 0.9075 | 0.9130 | 0.0864 | 0.0815 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Huang, X.; Zhang, H. Modeling the Charging Behaviors for Electric Vehicles Based on Ternary Symmetric Kernel Density Estimation. Energies 2020, 13, 1551. https://doi.org/10.3390/en13071551
Chen L, Huang X, Zhang H. Modeling the Charging Behaviors for Electric Vehicles Based on Ternary Symmetric Kernel Density Estimation. Energies. 2020; 13(7):1551. https://doi.org/10.3390/en13071551
Chicago/Turabian StyleChen, Lixing, Xueliang Huang, and Hong Zhang. 2020. "Modeling the Charging Behaviors for Electric Vehicles Based on Ternary Symmetric Kernel Density Estimation" Energies 13, no. 7: 1551. https://doi.org/10.3390/en13071551
APA StyleChen, L., Huang, X., & Zhang, H. (2020). Modeling the Charging Behaviors for Electric Vehicles Based on Ternary Symmetric Kernel Density Estimation. Energies, 13(7), 1551. https://doi.org/10.3390/en13071551