A Virtual Negative Resistor Based Common Mode Current Resonance Suppression Method for Three-Level Grid-Tied Inverter with Discontinuous PWM
Abstract
1. Introduction
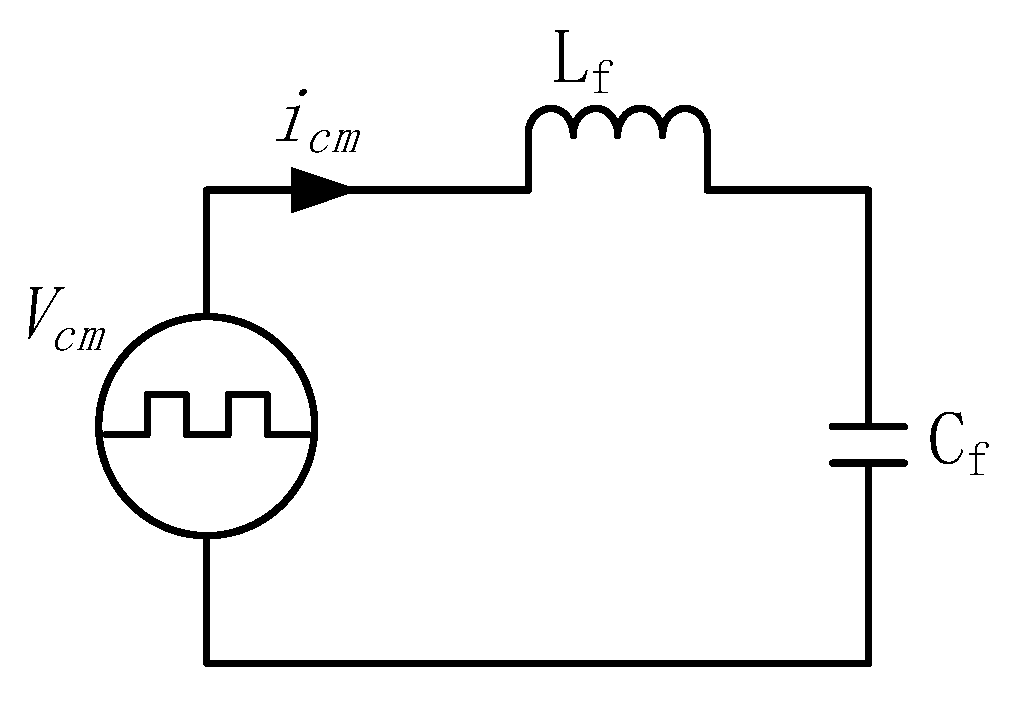
2. Model of CM Current Resonance in Grid-Tied Inverter with ILC Filter
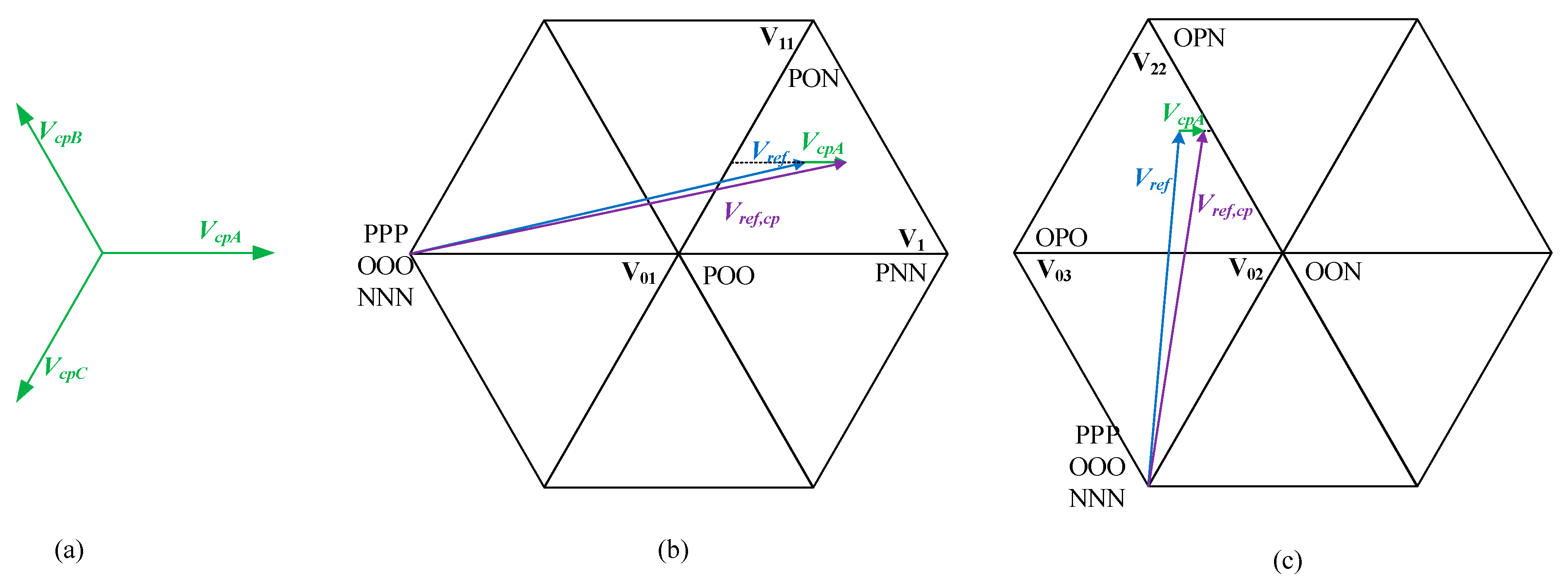
3. Harmonics Comparison of Zero Sequence Quantity of DPWM and CPWM
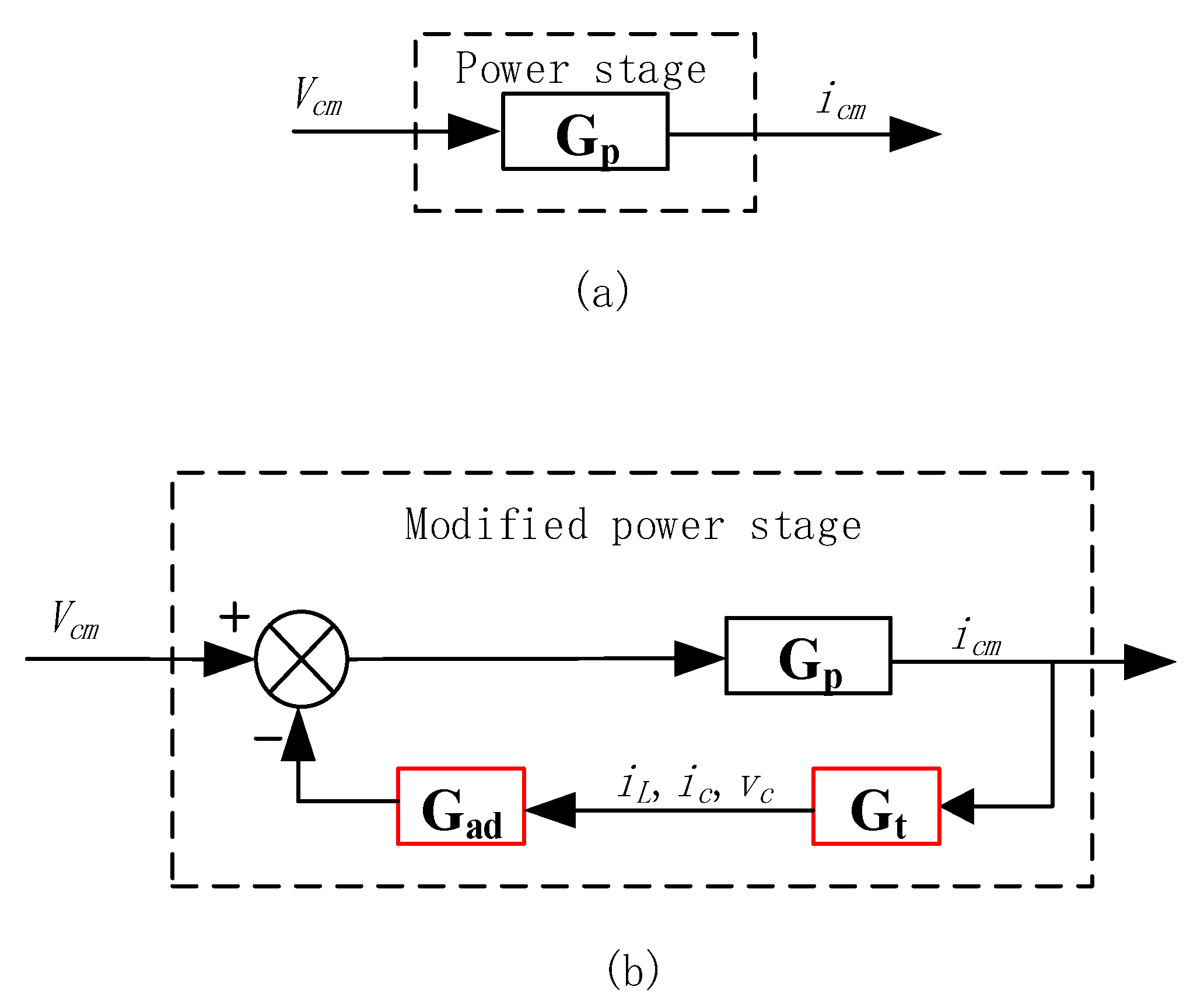
4. The Proposed VNRBAD Method for CM Current Resonance
4.1. VNRBAD for CM Current Resonance
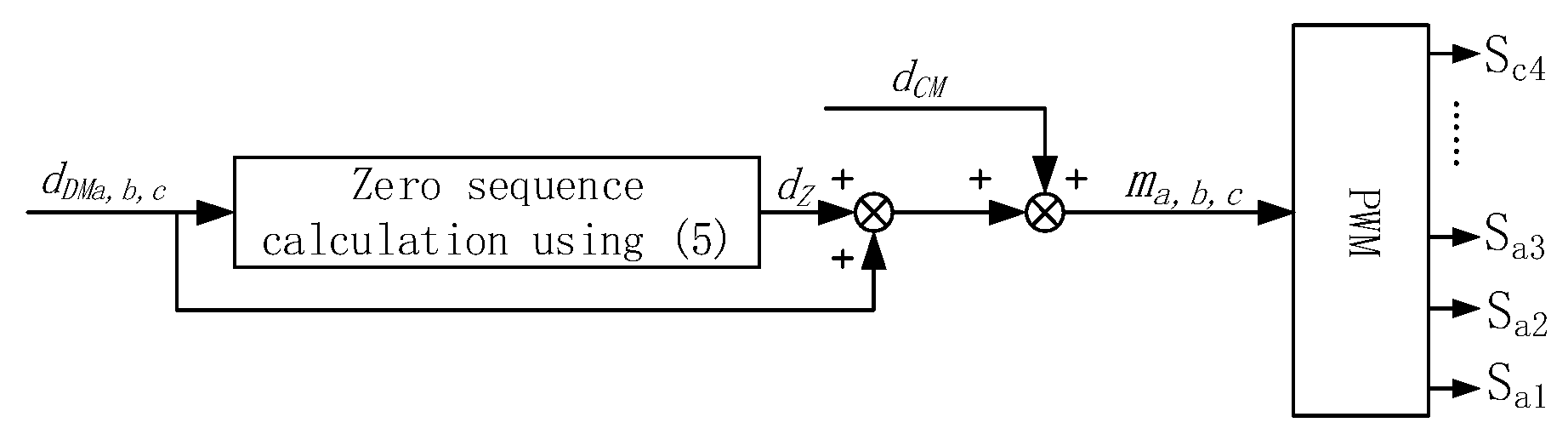
4.2. The Implementation of VNRBAD for DPWM Application
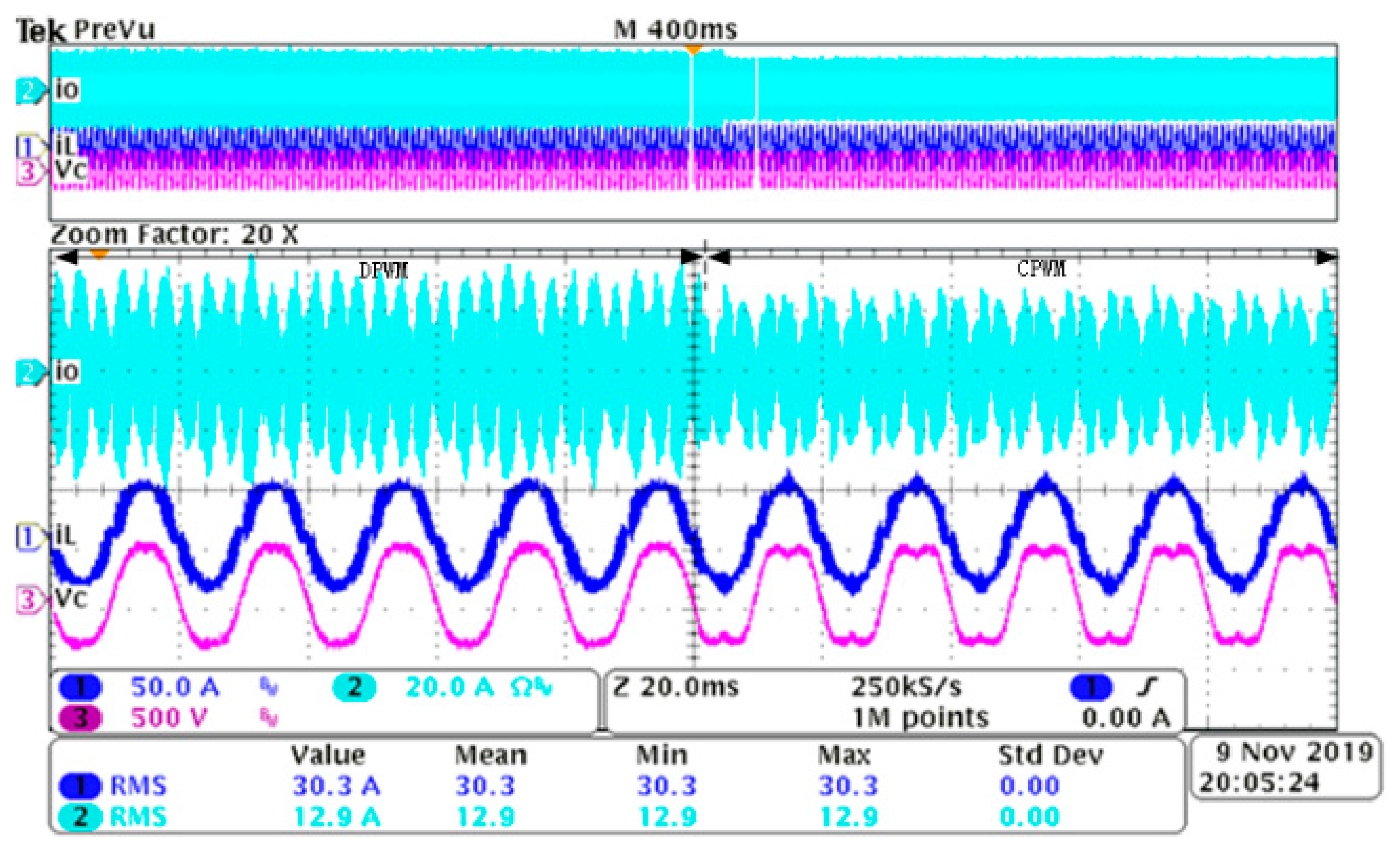
5. Experiments and Discussion
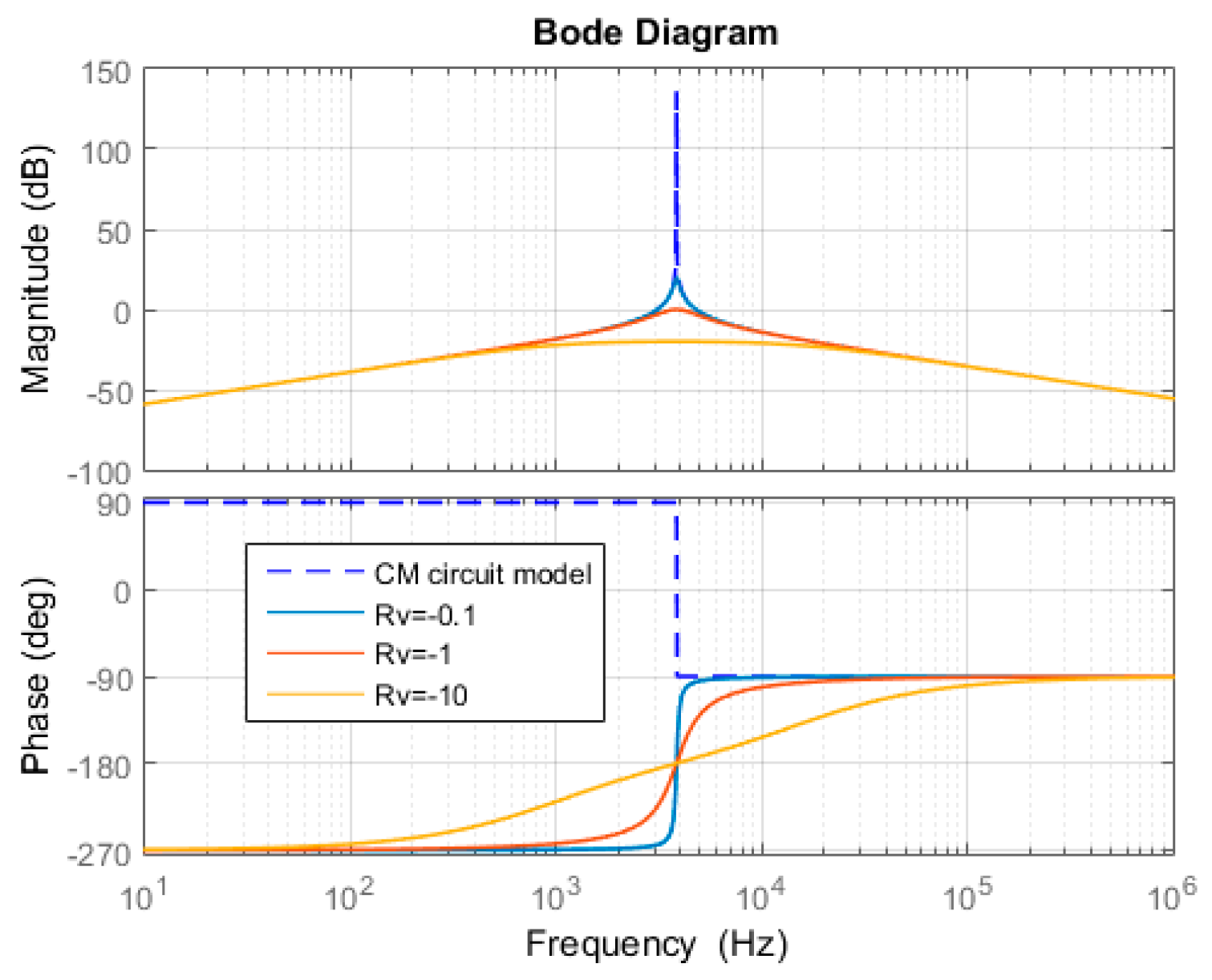
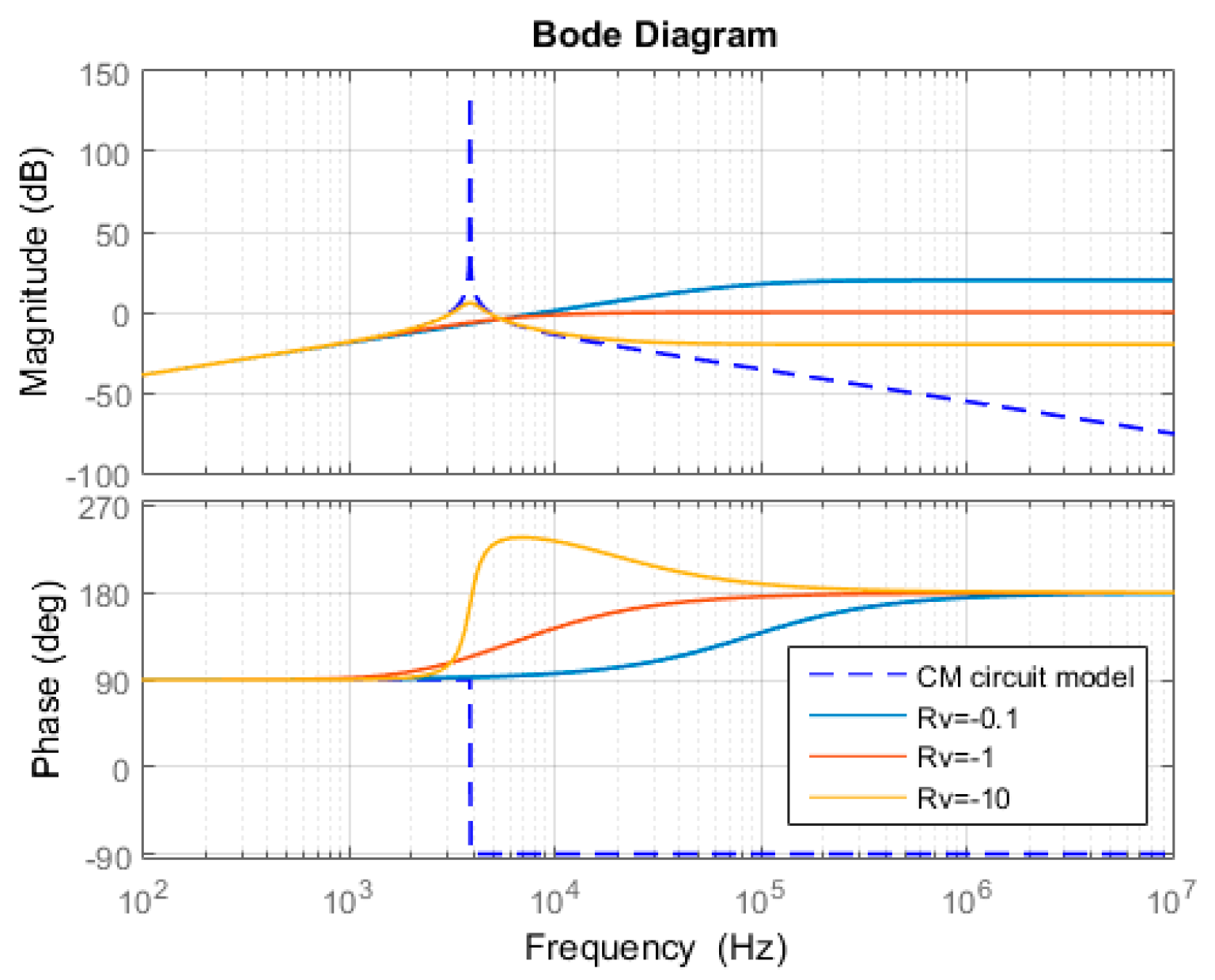
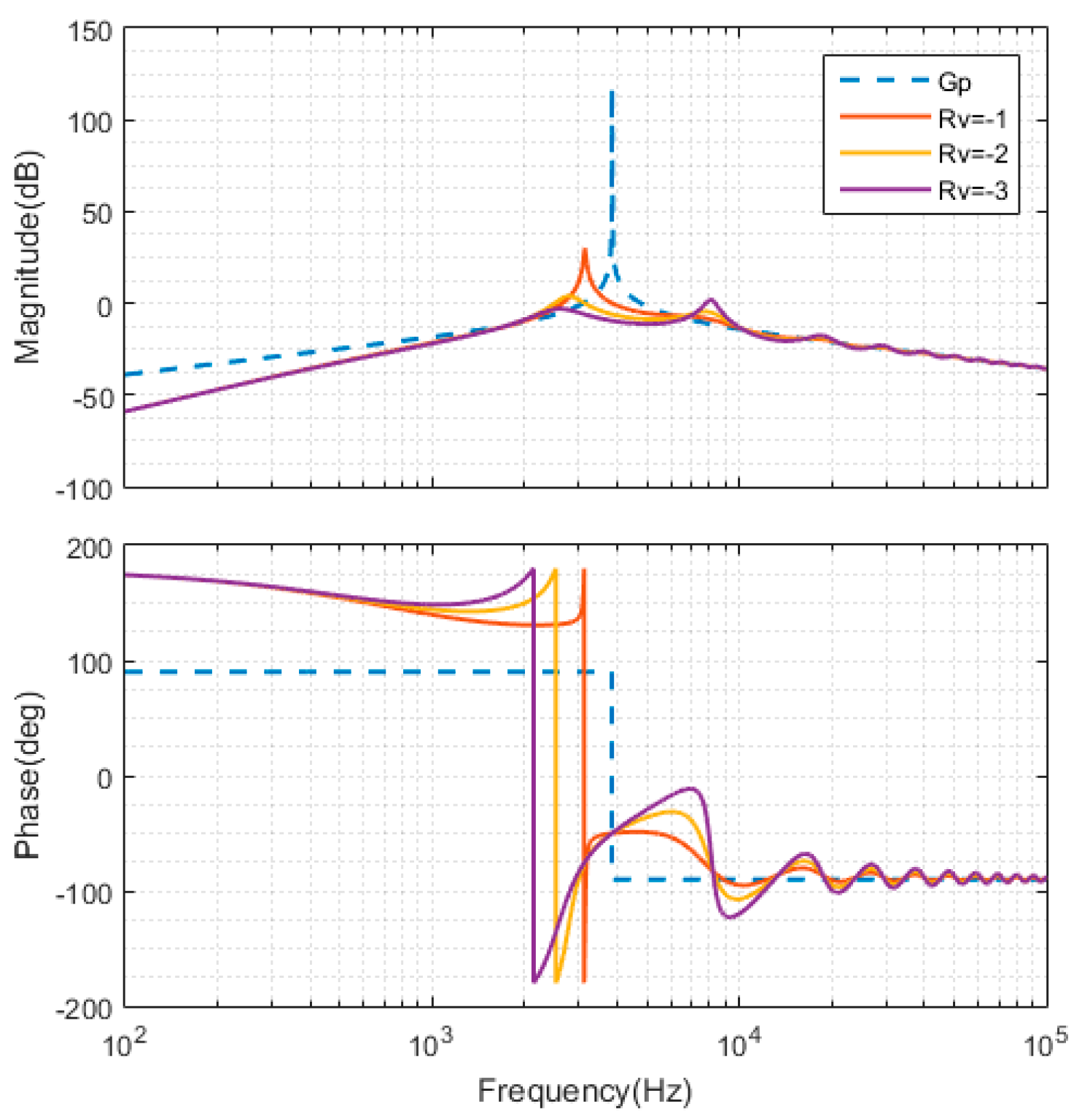
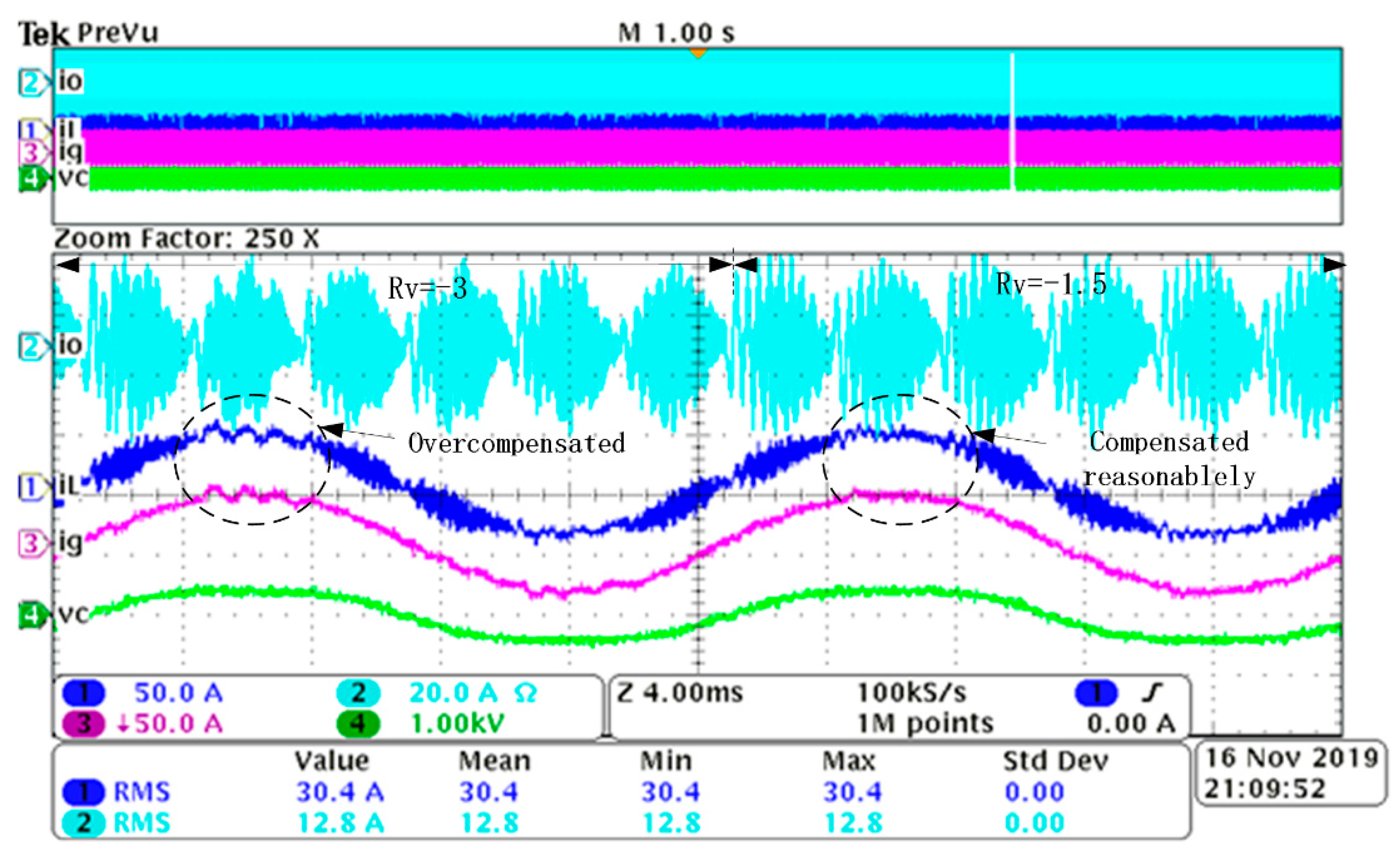
5.1. The Value of Rv
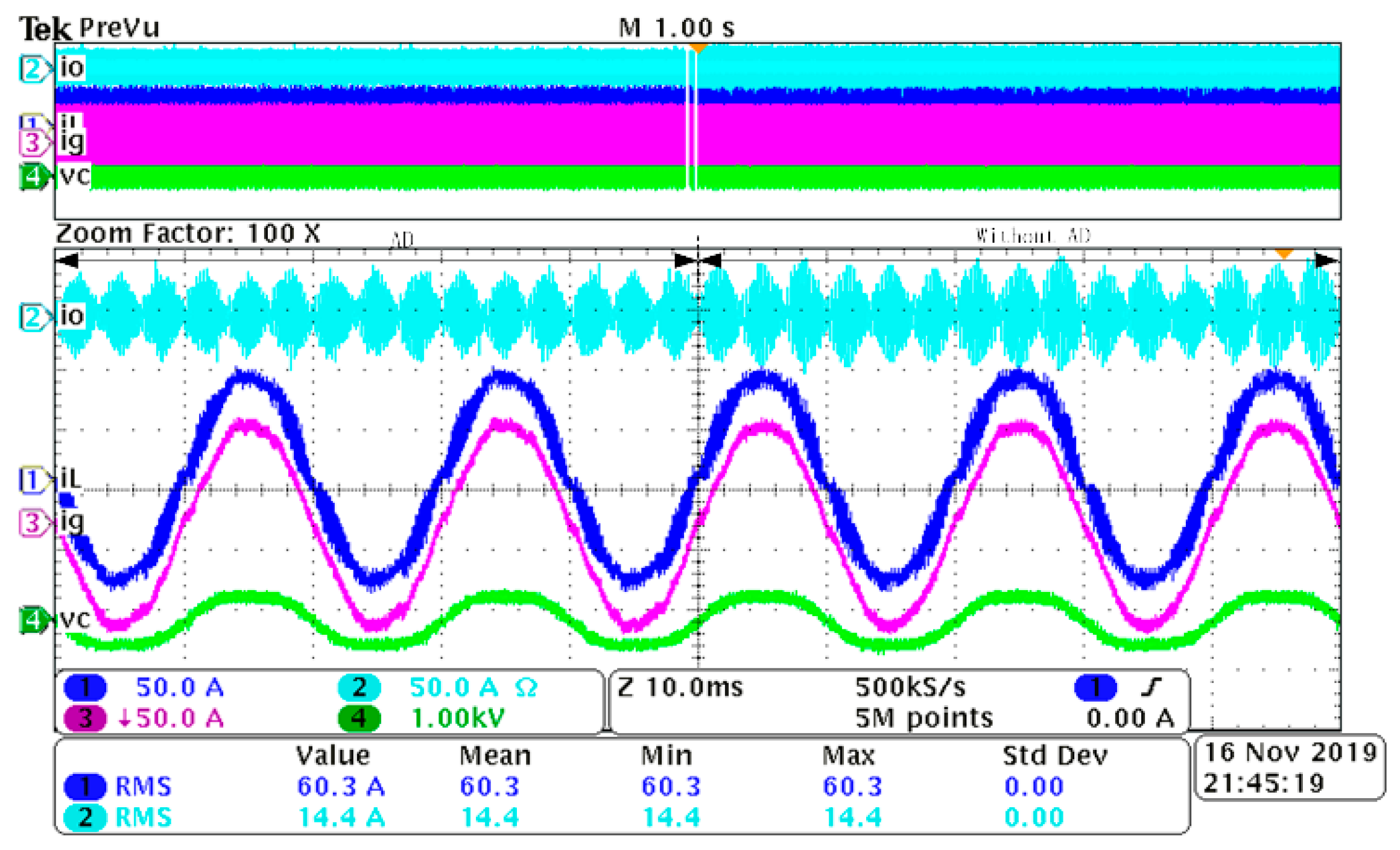
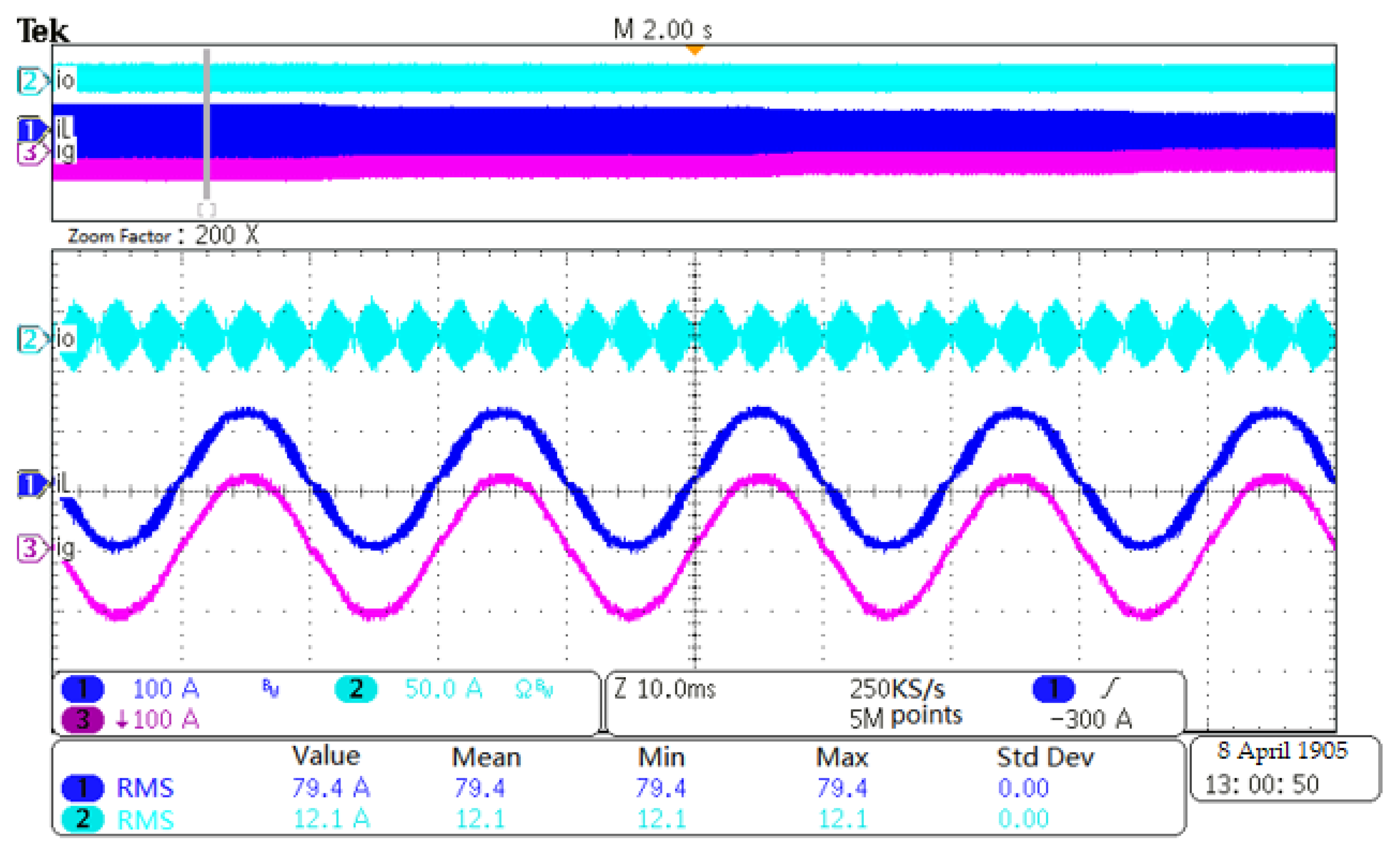
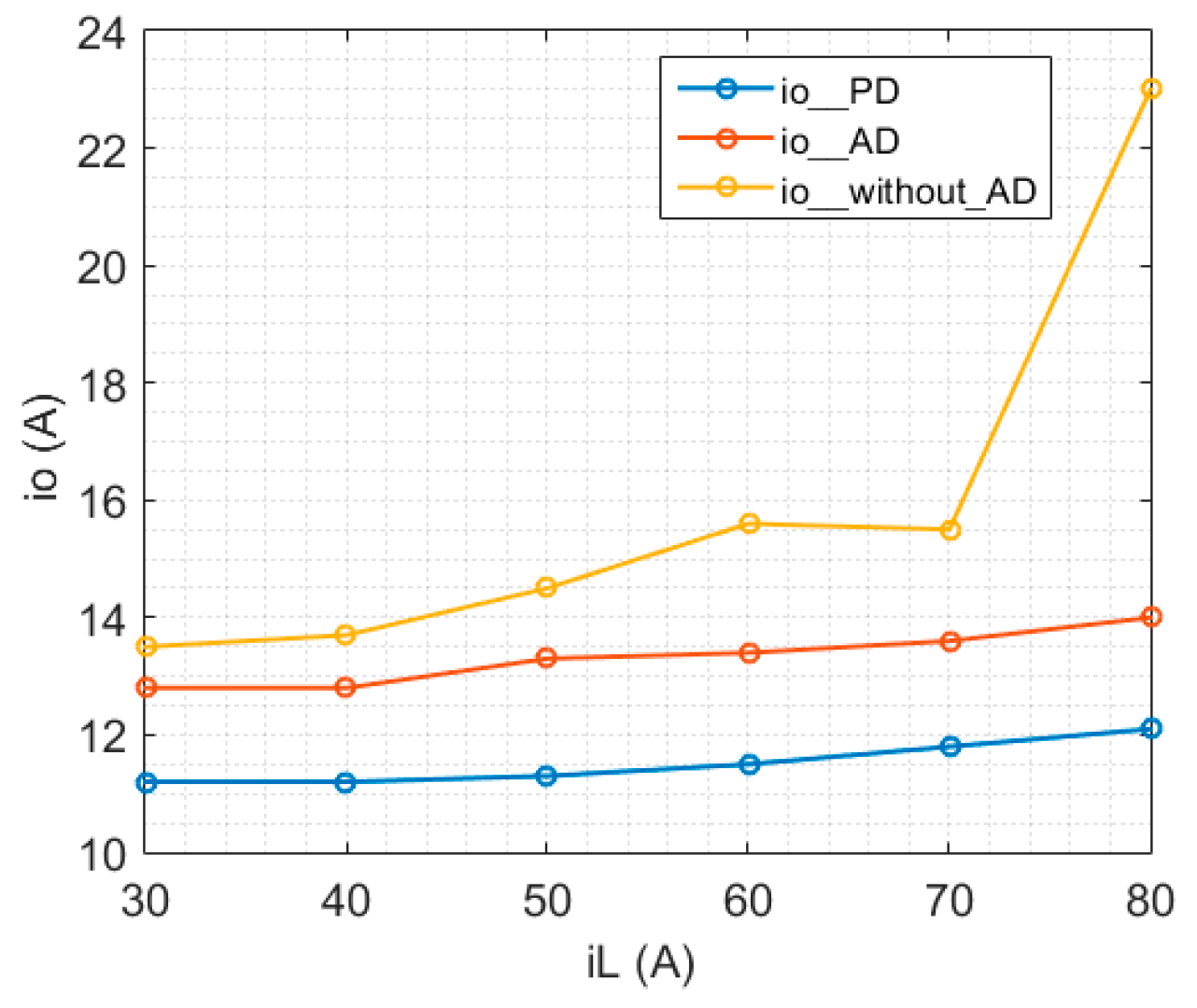
5.2. Comparison between VNRBAD and Without VNRBAD under Different iL
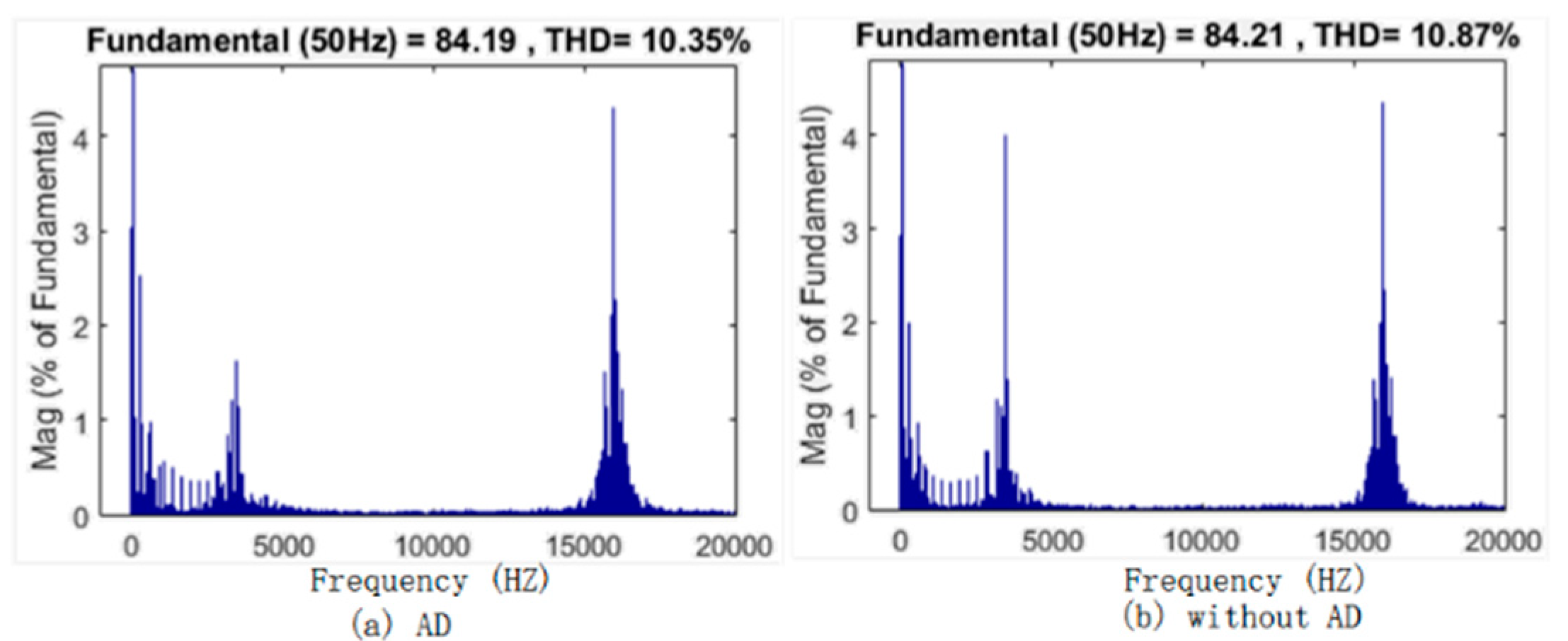
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IEEE. Recommended Practice and Requirements for Harmonic Control. In Electric Power Systems; IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [Google Scholar]
- Büyük, M.; Tan, A.; Tümay, M.; Bayındır, K.Ç. Topologies, generalized designs, passive and active damping methods of switching ripple filters for voltage source inverter: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 62, 46–69. [Google Scholar] [CrossRef]
- Liang, X.; Karim, C.A.B. Harmonics and Mitigation Techniques Through Advanced Control in Grid-Connected Renewable Energy Sources: A Review. IEEE Trans. Ind. Appl. 2018, 54, 3100–3111. [Google Scholar] [CrossRef]
- Gomes, C.C.; Cupertino, A.F.; Pereira, H.A. Damping techniques for grid-connected voltage source converters based on LCL filter: An overview. Renew. Sustain. Energy Rev. 2018, 81, 116–135. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; He, Y.; Chung, H.S.; Liserre, M.; Blaabjerg, F. Damping Methods for Resonances Caused by LCL-Filter-Based Current-Controlled Grid-Tied Power Inverters: An Overview. IEEE Trans. Ind. Electron. 2017, 64, 7402–7413. [Google Scholar] [CrossRef]
- Erika, T.; Holmes, D.G. Grid current regulation of a three-phase voltage source inverter with an LCL input filter. IEEE Trans. Power Electron. 2003, 18, 888–895. [Google Scholar] [CrossRef]
- Liserre, M.; Dell’Aquila, A.; Blaabjerg, F. Stability improvements of an LCL-filter based three-phase active rectifier. In Proceedings of the 2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference Proceedings (Cat No02CH37289), Cairns, QLD, Australia, 23–27 June 2002; Volume 3, pp. 1195–1201. [Google Scholar]
- Dannehl, J.; Liserre, M.; Fuchs, F.W. Filter-Based Active Damping of Voltage Source Converters With $LCL$ Filter. IEEE Trans. Ind. Electron. 2011, 58, 3623–3633. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.W.; Blaabjerg, F.; Loh, P.C. Virtual-Impedance-Based Control for Voltage-Source and Current-Source Converters. IEEE Trans. Power Electron. 2015, 30, 7019–7037. [Google Scholar] [CrossRef]
- Liu, T.; Liu, J.; Liu, Z.; Liu, Z. A Study of Virtual Resistor-Based Active Damping Alternatives for LCL Resonance in Grid-Connected Voltage Source Inverters. IEEE Trans. Power Electron. 2020, 35, 247–262. [Google Scholar] [CrossRef]
- Dong, D.; Luo, F.; Zhang, X.; Boroyevich, D.; Mattavelli, P. Grid-Interface Bidirectional Converter for Residential DC Distribution Systems—Part 2: AC and DC Interface Design With Passive Components Minimization. IEEE Trans. Power Electron. 2013, 28, 1667–1679. [Google Scholar] [CrossRef]
- Rendusara, D.A.; Enjeti, P.N. An improved inverter output filter configuration reduces common and differential modes dv/dt at the motor terminals in PWM drive systems. IEEE Trans. Power Electron. 1998, 13, 1135–1143. [Google Scholar] [CrossRef]
- Giacomini, J.C.; Michels, L.; Pinheiro, H.; Rech, C. Active Damping Scheme for Leakage Current Reduction in Transformerless Three-Phase Grid-Connected PV Inverters. IEEE Trans. Power Electron. 2018, 33, 3988–3999. [Google Scholar] [CrossRef]
- Li, X.; Xing, X.; Zhang, C.; Chen, A.; Qin, C.; Zhang, G. Simultaneous Common-Mode Resonance Circulating Current and Leakage Current Suppression for Transformerless Three-Level T-Type PV Inverter System. IEEE Trans. Ind. Electron. 2019, 66, 4457–4467. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. A high-performance generalized discontinuous PWM algorithm. IEEE Trans. Ind. Appl. 1998, 34, 1059–1071. [Google Scholar] [CrossRef]
- Dalessandro, L.; Round, S.D.; Drofenik, U.; Kolar, J.W. Discontinuous Space-Vector Modulation for Three-Level PWM Rectifiers. IEEE Trans. Power Electron. 2008, 23, 530–542. [Google Scholar] [CrossRef]
- Hassaine, L.; Olias, E.; Quintero, J.; Salas, V. Overview of power inverter topologies and control structures for grid connected photovoltaic systems. Renew. Sustain. Energy Rev. 2014, 30, 796–807. [Google Scholar] [CrossRef]
- Keliang, Z.; Danwei, W. Relationship between space-vector modulation and three-phase carrier-based PWM: A comprehensive analysis [three-phase inverters]. IEEE Trans. Ind. Electron. 2002, 49, 186–196. [Google Scholar] [CrossRef]
- Blasko, V. Analysis of a hybrid PWM based on modified space-vector and triangle-comparison methods. IEEE Trans. Ind. Appl. 1997, 33, 756–764. [Google Scholar] [CrossRef]
- Bruckner, T.; Holmes, D.G. Optimal pulse-width modulation for three-level inverters. IEEE Trans. Power Electron. 2005, 20, 82–89. [Google Scholar] [CrossRef]
- Xue, V. Center-Aligned SVPWM Realization for 3- Phase 3- Level Inverter. Available online: www.ti.com/cn/lit/pdf/sprabs6 (accessed on 1 October 2019).









| Connection Type of the Virtual Negative Resistor Rv | Modified Power Stage | Variable Feedback for the Active Damping | |
|---|---|---|---|
| iL or ic | vc | ||
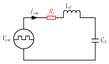 | |||
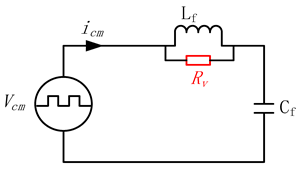 | |||
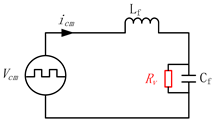 | |||
| Item | Symbol | Value |
|---|---|---|
| Filter capacitor | Cf | 18 μF |
| Inverter-side filter inductor | Lf | 95 μH at 80A |
| rate power | P | 80 kW |
| grid line voltage | Vg | 540 V |
| DC voltage | Vdc | 800 V |
| switch frequency | fs | 16 kHz |
| Device | Model Number |
|---|---|
| PV simulator | Chroma 62150H-1000S |
| Regenerative grid simulator | Chroma 61860 |
| PV String inverter | TBEA TS80KTL_PLUS |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Zhou, H.; Zhang, J.; Zhao, S.; Lu, J. A Virtual Negative Resistor Based Common Mode Current Resonance Suppression Method for Three-Level Grid-Tied Inverter with Discontinuous PWM. Energies 2020, 13, 1595. https://doi.org/10.3390/en13071595
Li Q, Zhou H, Zhang J, Zhao S, Lu J. A Virtual Negative Resistor Based Common Mode Current Resonance Suppression Method for Three-Level Grid-Tied Inverter with Discontinuous PWM. Energies. 2020; 13(7):1595. https://doi.org/10.3390/en13071595
Chicago/Turabian StyleLi, Qiyu, Hongwei Zhou, Jiansong Zhang, Shengdun Zhao, and Jingfeng Lu. 2020. "A Virtual Negative Resistor Based Common Mode Current Resonance Suppression Method for Three-Level Grid-Tied Inverter with Discontinuous PWM" Energies 13, no. 7: 1595. https://doi.org/10.3390/en13071595
APA StyleLi, Q., Zhou, H., Zhang, J., Zhao, S., & Lu, J. (2020). A Virtual Negative Resistor Based Common Mode Current Resonance Suppression Method for Three-Level Grid-Tied Inverter with Discontinuous PWM. Energies, 13(7), 1595. https://doi.org/10.3390/en13071595






