1. Introduction
According to the 2030 Agenda for Sustainable Development, seventeen Sustainable Development Goals (SDGs) are set for action by both developed and developing countries. Among the seventeen SDGs, one of the most crucial goals is “Affordable and Clean Energy.” The objective of the goal “Affordable and Clean Energy” is to ensure not only affordable, resilient, and modern forms of energy, but also sustainable and carbon-free electricity for the planet [
1].
Electricity is a fundamental requirement for global advancement and economic growth. The demand for electricity is growing proportionally to the population and economic development. Currently, the world is undergoing two challenges for managing the high demand for electricity; one problem is how to support the high demand for electricity without exploiting finite energy resources (mainly fossil fuels), and another challenge is how to produce electricity without affecting the environment [
2].
Currently, most of the electric energy is produced from conventional sources like coal, gas, and oil. The production of electricity by using these resources tends to raise the emission of greenhouse gases (GHGs) in the atmosphere. Research is ongoing to reduce the impact of using traditional sources for electricity generation in the environment. For instance, one such initiative is the implementation of carbon capture and storage (CCS) policies. In this process, the waste carbon dioxide from the power plant can be captured and transported to a storage site for disposal so that it cannot disperse in the environment [
3].
In recent times, the world is looking for sustainable energy sources that will be used to meet today’s demand without putting them into danger for future usages. Consequently, renewable energy sources (RESs), such as solar, wind, geothermal, hydropower, and ocean energy, are being recognized as sustainable sources for electric energy production [
4]. RESs are intermittent, and electricity cannot be stored economically for an extended period, so some other sources of energy that can provide a back-up for the RESs during their unavailability period and act as a base load or critical load supplier are needed.
The research and development plan for dynamic modeling and simulation of large scale nuclear-renewable hybrid energy system (N-R HES) is addressed in [
5]. The N-R HES is interpreted as a combination of a nuclear reactor, a turbine for electricity generation from thermal energy, at least a RES, and a product produced from the N-R HES by an industrial process. In the report, the authors categorized the N-R HES into three types: tightly coupled HES, thermally coupled HES, and loosely coupled electricity-only HES. The potential vital benefits of N-R HES include GHG-free electricity, a resilient electric grid, and low COE. The authors have also regarded the integration of SMR and RES for future work.
A combination of renewable energy generation, nuclear reactors, and industrial processes, including the versatility of grid and making the best possible use of investment, have been explored in [
6]. Six features of interconnection have been identified here—electrical, thermal, chemical, hydrogen, mechanical, and information. This study concluded that the integration of nuclear and renewable energy could be a potential solution for a long-term and ample amount of power and heat supply that is free from sudden price changes like fossil-fuels. This document also pointed out that the nuclear-renewable hybrid system can supply load-following power, and excess energy can be used for the production of secondary energy-intensive products. Nevertheless, system analysis, technical advancement, and optimization are required to implement this hybrid system in practice.
Currently, the International Atomic Energy Agency (IAEA) has published a technical document of nuclear-renewable integration. The report addresses the national strategies on nuclear and RESs, opportunities and challenges of nuclear-renewable integration, and the role of the small-scale reactors in nuclear-renewable hybridization [
7].
A comparison of three scenarios, namely a nuclear power plant, a combination of a nuclear plant and a wind facility, and a mixture of nuclear and wind energy sources with a hydrogen generation facility, have been done in [
8]. This study reported that with optimization, the nuclear-wind system with a hydrogen production facility could be an economically viable option in the future. Sensitivity analysis has also been carried out to realize the impact of the energy market, depreciation rate, discount rate, and time horizon in terms of internal rate of return (IRR), levelized cost of energy (LCOE), net present value (NPV), and payback period.
In [
9], the author highlighted the critical challenges of nuclear-renewable integration, such as integration values, regulatory, financial, technological, plant testing, and plant operation. The author suggested that the information linkage-based nuclear-renewable coupling would be able to overcome the complexities of the integration process.
Three scenarios of N-R HES to supply thermal energy from the system have been examined in [
10]. The first arrangement includes a nuclear reactor, thermal power cycle, wind power plant, and electric boiler; the second scenario comprises a nuclear reactor, thermal power cycle, wind power plant, and electric thermal storage; the third configuration is a combination of a nuclear reactor, thermal power cycle, wind power plant, electric boiler, and thermal storage. The electric thermal storage stores thermal energy that is generated by electricity. The financial performance analysis tells us that the third arrangement has the lowest NPV, lowest IRR, and highest TCI. The analysis results are evident because the thermal power supply is elevated significantly by introducing the electric boiler and the thermal storage simultaneously in the third scenario. The result is also evident since the authors assumed that the cost of heat generated from the nuclear reactor is less than the price of heat generated from gas (electric boiler) [
10].
The Hybrid Optimization Model for Electric Renewable (HOMER) software has been used for predicting the viability of a HES in [
11]. The HES consists of photovoltaic (PV) cells, diesel generator, and battery bank. Paper [
11] summarized that the PV-diesel-battery system has one-third fuel-savings compared to the diesel-only system. It is also concluded that hydrogen technologies can technically replace the diesel-battery system. The PV-diesel-battery configuration will also reduce emissions and increase the penetration of renewable energy. Besides, the authors found that the implementation of 20% renewable energy would reduce a massive amount of CO
2 compared to the present value of emission [
11].
However, small scale nuclear reactors like the micro modular reactor (MMR) are gaining attention currently for their small size, affordability, security, reliability, and innovativeness. Several companies are now working on these types of reactors. For example, U-Battery, an MMR manufacturer, is expecting to demonstrate this type of reactor by 2026 [
12]. Some other very small reactors are being developed, such as the eVinci
TM micro reactor with combined heat and power (CHP) rated from 200 kWe to 5 MWe [
13]. Consequently, these types of micro reactors can replace the FFTGs (diesel generators), which are now being employed with RESs either as the backup power supply or as the main electric power- generating source.
In this paper, the planning and optimization of different HES models have been developed and evaluated based on multiple techno-economic key performance indicators (KPIs). The grid-connected as well as off-grid mode have been analyzed in this paper. Five different scenarios with CHP have been developed and assessed using the HOMER software. Comparison among all situations has been made based on three KPIs - NPC, COE, and GHG emission. This document is divided as follows: the detailed nuclear-renewable hybrid energy system is discussed in
Section 2. System configurations are addressed in
Section 3.
Section 4 covers the design considerations that are made for system evaluation. Part 5 illustrates the system simulations. The simulation results, based on selected KPIs, are compiled in
Section 6. The discussion is presented in
Section 7.
3. System Configuration
A case study has been conducted to assess some specific KPIs—net present cost (NPC), cost of energy (COE), and greenhouse gas (GHG) emissions—of an N-R MHES. The grid-level coupling method is reflected in the study. The case study includes the system equipment with some conservative assumptions that are listed with each component in the subsections. The load data are obtained from the National Aeronautics and Space Administration (NASA) Surface Meteorology and Solar Energy database [
18]. The data are synthesized in a MATLAB simulator, and the Hybrid Optimization of Multiple Energy Resources (HOMER) Pro software is used for system modeling, simulations, and KPI analysis. In the study, the project lifetime is assumed as a whole 30 years – starting in 2007 and ending in 2036. The prices of the system component are pragmatic compared to the present market value. The RESs data, such as solar radiation, wind speed, and water flow of the hydro dam, are assumed to be the same during the complete project lifetime. However, some important system parameters, such as load demand and equipment cost, change in each year of project life. To address the effect of these variations on the whole system, an additional study is conducted by “Multiyear Analysis” module in the HOMER Pro software. The details of individual system equipment are demonstrated in the next few subsections. The project life, inflation rate, and discount rate are considered as 30 years, 2%, and 8%, respectively. The costs of all system equipment, mentioned in the specification table in this study, are the first-year cost of the whole project life.
The HOMER software uses the inflation rate and discount rate to calculate the actual discount rate. The actual discount rate is used to determine the discount factors and annualized costs. The inflation rate, discount rate, and actual discount rate are mathematically related as follows [
19]:
where r, d, and i represent actual discount rate, discount rate, and inflation rate, respectively.
3.1. Electric Load
The electric load data has been collected for the year of 2018 from several facilities of Ontario Tech University (UOIT, Oshawa, ON, Canada). These data are deemed as input electric load data for the first year of the project life. The data are collected from UOIT since it has a significant variation in the load profile of the UOIT facilities. As a micro HES is considered for this analysis, the actual load profile is scaled-down to a comparable size to emulate the load profile of a small-scale energy system. The scaled-down data also reduces the simulation time. Nevertheless, the scaled-down process does not change the load characteristics.
The load profile that is collected from UOIT is designed and named “Electric Load #1” in the HOMER Pro software interface. Another electric load is modeled in HOMER Pro, entitled “Electric Load #2,” to create “diversity” in the system load profile. The peak occurs for “Electric Load #1” at noon, whereas the peak occurs for “Electric Load #2” at evening. Thus, the diversity is created. A deferrable electrical load is also designed in the HOMER Pro software. The value of average energy demand, storage capacity, peak power demand, and minimum load ration of the deferrable load are 12 kWh/day, 48 kWh, 8 kW, and 80%, respectively. The “Electric Load #1” and “Electric Load #2” are given the highest priority for demand fulfillment in the system and considered as the primary load in simulation; whereas, the deferrable electric load gets less priority. In the simulation, the resources always supply electricity to the primary load first, then go for the deferrable load.
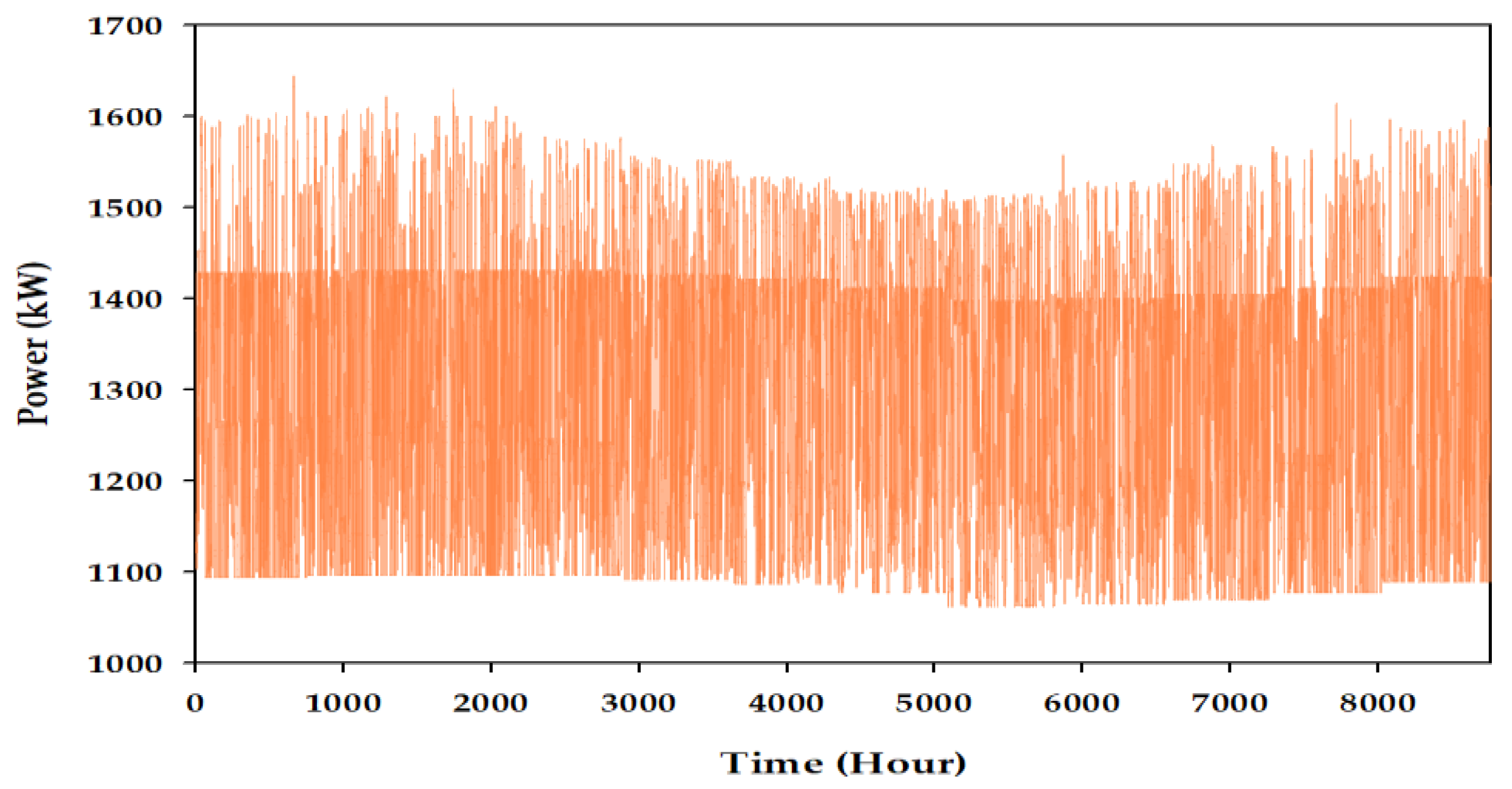
Figure 1 illustrates the total electric load profile - summation of Electric Load #1, Electric Load #2, and deferrable load - of the system.
Table 1 represents the details of system electric load.
The yearly total electrical load profiles are depicted in
Figure 1. The characteristics of the electrical loads are summarized in
Table 1.
3.2. Thermal Load
Since the actual thermal load data is not available for the project, a standard thermal load profile is modeled in this study from HOMER Pro software library. Two types (commercial load and community load) of thermal loads are designed to introduce variety into the N-R MHES. The thermal loads are compatible and comparable to the typical hybrid energy system.
The yearly total thermal load profiles are depicted in
Figure 2. The peak demand occurs at noon and evening for Thermal Load #1 and Thermal Load #2, respectively. The characteristics of thermal loads are summarized in
Table 2.
3.3. Diesel Generator
Though the FFTG is not a compulsory part of N-R MHES, a Diesel genset is studied here to investigate and compare the KPIs between conventional fossil fuel-based thermal hybrid energy systems and N-R MHES. The traditional hybrid energy system combines FFTGs, RESs, energy storage, and power electronic components. In this project, a 1 MW diesel generator is compared with a 1 MW MMR, side by side, to obtain the most feasible system in terms of economic and environmental viewpoints. The heat recovery ratio and diesel price are assumed 40% and 0.79 UDS/Liter [
20], respectively in this study. The economic parameters of a typical diesel generator, used in the simulation, is listed in
Table 3. The HOMER Pro software automatically calculates the total emission by diesel generator while the Diesel genest produces electricity.
3.4. Solar Power
Solar photovoltaic (PV) technology is used in this project to convert solar radiation into useful electricity. The solar radiation data of UOIT have been collected from NASA Surface Meteorology and Solar Energy database. The solar radiation data are assumed to be the same throughout the 30 years of the project lifetime.
The output of the PV array is calculated as follows [
21]:
where
,
,
,
,
,
, and
denote the rated capacity of the PV array under standard test conditions (kW), PV derating factor (%), solar radiation incident on PV in the current time step (kW/m
2), solar incident radiation at standard test condition (1 kW/m
2), temperature coefficient (%/°C), PV cell temperature in the current time step (°C), and PV cell temperature under standard test conditions (25 °C), respectively.
The manufacturers set the PV power rating at a specific condition called “Standard Test Conditions (STC).” In STC, the solar radiation is assumed to be 1 kW/m2, the cell temperature is taken as 25 °C, and no wind flow is considered around the PV cell. However, in practical cases, the full-sun cell temperature is always greater than 25 °C, and there is a significant wind flow encompassing the PV system. The derating factor is also regarded to model the PV cell explicitly since it is related to the panel losses, wiring losses, and aging. The derating factor is a scaling factor to match the PV rating of the manufacturers with the real-world conditions.
If the temperature effect is ignored to design the PV panel, Equation (3) can be simplified as follows:
The yearly solar irradiance data are represented in
Figure 3. A flat panel 400 kW PV array, having an operating temperature 25 °C, is used here. The PV array consists of 400 solar cell units; each unit is rated at 1 kW. The details specifications of the solar PV cell are summarized in
Table 3.
3.5. Wind Power
Two (2) wind turbine units, each rated as 330 kW, are used in this N-R MHES. The hub height and rotor diameter of the turbine are 55 m and 33 m, respectively. It has been assumed that the wind speed is the same for the entire project life. The details of the wind turbine are presented in
Table 3.
Three steps are maintained to calculate the output of the wind turbine in HOMER [
22]. The first step is to estimate wind speed at the hub height of the wind turbine. The wind speed at the hub height is calculated by Equation (4):
where
,
,
,
, and
denote wind speed at the hub height of the wind turbine (
), Wind speed at the anemometer height (
), Hub height of the wind turbine (
, Surface roughness length (
, and Anemometer height (
, respectively.
The second step is to calculate the turbine power at standard air density; this is done with the help of the turbine power curve given by the manufacturer. The wind power output at standard air density is estimated from the corresponding wind speed value, calculated in the previous step.
The third step deals with the application of density correction. The following equation is used for density correction to calculate the exact wind power extracted by the wind turbine:
where
,
,
, and
represent actual power output of the wind turbine (
), actual air density (
), air density at standard temperature and pressure (
), and power output of the wind turbine at standard temperature and pressure (
), respectively.
Figure 4 represents the wind speed profile at UOIT for one year.
3.6. Hydro Power
A run-of-river hydroelectric plant is considered in this study. The average yearly (2018) mass flow rates of Lake Ontario, Canada are collected and shown in
Figure 5. The economic specifications of the hydro plant and hydro turbine are summarized in
Table 3.
The nominal power of a hydropower plant can be calculated from the following equation [
23]:
where
,
,
,
, and
denote available water head (
), water density (
), gravitational constant (
), mass flow rate (
), and hydro turbine efficiency (%), respectively.
The mass flow rate or hydro turbine flow rate is the amount of water that flows through the hydro turbine. In this study, the mass flow rate is calculated using Equation (7) [
23]:
where
,
, and
represent available mass flow rate to hydro turbine (
), available minimum mass flow rate to hydro turbine (
), and available maximum mass flow rate to hydro turbine (
), respectively.
The available water head, design flow rate, minimum flow rate, and maximum flow rate of the hydroelectric plant are considered as 25 m, 500 L/s, 50%, and 150%, respectively, in this case study.
3.7. Nuclear Power Plant
Due to the high initial cost and necessity of a large installation site of the conventional NPP, a micro modular reactor (MMR) is a promising solution for reducing the capital cost and eliminating the need for a massive installation area. MMRs have some benefits over conventional NPPs; MMR takes a shorter time to construct, design of MMR is simple and flexible, and MMR is appropriate for small-scale electricity generation systems [
24].
According to the IAEA, the NPP rated under 300 MWe can be interpreted as ’small’ NPP. IAEA defines the NPP as ’medium’ if the reactors have the power rating up to 700 MWe. The ’small’ and ’medium’ NPP collectively have been called ’small and medium reactor (SMR),’ but commonly, they are termed as ’small modular reactor (SMR).’ One subclass of SMR is ’very small reactors (vSMRs)’ that are rated under 15 MWe, and are very competent for remote communities [
25].
The MMR, a generation-IV reactor, is a small-scale reactor, characterized by a power rating in between 1 MWe to 20 MWe. The MMR provides a safe, emission-free, and cost-efficient energy source for both on-grid and off-grid applications. Due to its modular nature, small footprint, in-factory construction, cogeneration capability, high-level safety measures, insignificant installation area, design simplicity, scalability, and transportability, the MMR has a high impact on energy system modeling consideration. The MMR could be an outstanding solution for large-scale generating station back-up power, remote industries, and transportation electrification [
26]. A feasibility assessment of the MMR for military ground application has been conducted in [
27]. Based on inherent risk, strategical complication, and cost associated with using diesel generators in a forward operating base (FOB), the authors found that the MMR is better than diesel generator for longer-term operation.
The TRISO fuel, a proven technology, is used in the MMR. TRISO is a uranium fuel coated with three layers; the uranium center is covered with a carbon layer, followed by silicon carbide, followed by an outer carbon layer. This extraordinary design ensures the utmost safety of the fuel under extreme conditions. The TRISO fuel can sustain up to 1800 °C, which is 200 °C hotter than the accident condition. The MMR is a gas-cooled reactor where helium is circulated in a primary circuit, and nitrogen is used in the secondary circuit. Since helium is an inert gas, clean, free of fission product, and does not react chemically with reactor or fuel, helium provides numerous benefits to the MMR. The fuel enrichment is around 9–12% for MMR. The molten salt is used in MMR as thermal storage to supply electricity and process heat. The power density, outlet temperature, and the process heat temperature of MMR are 1.24 W/cm
3, 630 °C, and 750 °C, respectively. The active system is not required to extract heat in the MMR-based plant. Moreover, off-site service, such as electric power, is also not needed for the safe operation of this type of reactor [
28].
A 1 MWe MMR is considered in this research. It always supplies a constant 1 MWe to the load. Since the MMR has the CHP capability, 40% of the waste heat of the MMR can be utilized to support the thermal load of the system. There are no GHG emissions to produce electricity from MMR and there is no GHG emissions during operation. However, if fossil fuel is burnt in the construction of NPP, or if the fossil fuel is used in mining or refining uranium ore, GHG will be produced; but, this types of GHG emissions are not considered in this study. A detail specification of MMR is listed in
Table 4. The MMR can operate without refueling up to 5 years [
29]. However, the spent fuel transportation cost is not considered in this study.
The capital cost of an exact 1 MW*
e MMR is also not available. Therefore, the capital cost of a 1 MW
e MMR is calculated as 11.25 million USD by linear estimation from the capital cost of a 2 × 10 MW**
t (2 units, each having a power rating of 10 MW
t) [
30]. The refurbishment cost of the plant is approximated as 2.3 million USD [
31]. (*MW
e = megawatt electric, **MW
t = megawatt thermal).
3.8. Electric Grid
The studied N-R MHES is analyzed for the grid-connected mode of operation. An electric grid, with the “net metering” provision, is considered here. The purchase and the sale capacity of the grid are determined and optimized by the HOMER software. The grid capacities (purchase and sale) are optimized in such a way that the availability of electric power is always guaranteed for all cases, discussed in
Section 5.1,
Section 5.2,
Section 5.3,
Section 5.4 and
Section 5.5. The optimized grid capacities confirm that if the energy resources fail to supply the electricity demand, the grid is competent in providing the required electric power to the load. The measured purchase and sale capacity of the electric grid are 0.9 MW and 1000 MW, respectively. The purchase capacity is the maximum amount of power that can be consumed from the grid at a time. The sale capacity is the maximum power that can be sold to the grid by “net metering “at any time.
The electric energy that is being supplied to the grid is typically generated by burning fossil fuel. In this study, natural gas is considered as the fuel to generate the grid electricity. As the research also focuses on the environmental consequences of the N-R MHES, the grid emission is also considered. Though natural gas is a clean form of fuel, it still releases different types of gases to the atmosphere. The amount of emission from natural gas is listed in
Table 5.
Furthermore, the energy rate is not the same for all day long; it varies with time and types of load, such as industrial load, community load, residential load, and commercial load. For example, the electricity price is not equal in the morning, and at the mid of the day. Even the cost of electricity in summer and winter also differs. Similarly, the electricity charge is different for household loads and industries. By studying all these perspectives, different electricity prices are discussed in this study for different times of the day and the year. The energy rates of the electric grid are summarized in
Table 6.
3.9. Energy Storage
A lithium-ion battery bank, comprising 500 battery cells (each has nominal capacity of 1 kWh), is regarded as the energy storage component in this project. Both the capital and replacement cost of a single cell are considered as 180 USD. The battery lifetime, SOCmin, SOCmin are 15 years, 100%, and 30%, respectively, for this case.
3.10. Boiler
The boiler produces thermal power by heating fluids inside the boiler vessel to serve the thermal load. Though the generators, considered in this project, have CHP capability, the boiler is kept inside the scenarios to support the thermal load for severe cases. If the extracted heat from the generators is not adequate to serve the thermal load demand, the boiler supplies the rest of the thermal power. For this study, diesel is used as fuel for the boiler, and the boiler has an efficiency of 85%. The HOMER software assumes that the boiler is an existing infrastructure, and its capital cost is not included in the total project expenses. However, the fuel price is added to the project cash-flow.
6. Results
The study has investigated three important KPIs of N-R MHES. To evaluate the KPIs, the N-R MHES is compared with four other different energy systems (from case-01 to case-04). The computed NPC, for both grid-connected and off-grid mode, of the five cases are recorded in
Table 17. The HOMER Pro software optimizes the system based on the NPC of the system.
For the grid-connected mode, case-01 has the highest NPC and COE, whereas case-04 and case-05 has the lowest NPC and COE, respectively. In case-01 (grid-connected mode), 99.99% electricity of the total electric demand is purchased from the grid. Furthermore, a massive amount of Diesel fuel (161,438 L/year) is utilized in the boiler to serve the thermal load that raises the total system cost. Consequently, the NPC and COE are quite high for this case. Case-04 (grid-connected mode) has the lowest NPC due to lower capital cost and operating cost. In case-05 (grid-connected mode), a large number of surplus electric energy is being generated by the combination of MMR and RES, and the system makes a significant amount of revenue by selling the excess energy to the grid. Besides, the cogenerated heat from MMR is adequate to serve the thermal demand fully; thus, no additional fuel is required to serve the thermal load. Therefore, COE is the lowest for this case. The NPC of case-05 (grid-connected mode) is slightly higher than case-04 (grid-connected mode) due higher initial cost of different RES equipment, such as wind turbine, hydro turbine, and PV panel.
In the off-grid mode of operation, case-01 exhibits the highest NPC and COE. On the other hand, case-04 (off-grid mode) has the lowest NPC and COE. It should be remarked that case-02 does not provide any feasible solution, implying that the system cannot support the electric demand studied in this paper. In case-01 (off-grid mode), the genset supplies the total electric load by burning fuel, which increases the system cost significantly. However, boiler fuel cost is less in this case since the boiler provides only 2.57% of thermal demand. In case-04, the NPC is lowest because the system consists of only MMR; no RESs are involved here. The absence of RESs reduces the system cost significantly as there is no high initial cost.
Furthermore, the substantial excess electric energy is utilized by the thermal load controller to serve the thermal load. Since the boiler is not operated, and there is no additional fuel cost to fulfill the thermal demand, the NPC and COE of the overall system are reduced in case-04 (off-grid mode). Nevertheless, it should be mentioned that a vast amount of excess electric energy (6,210,660 kWh/year) and thermal energy (9,765,760 kWh/year) is generated in case-05 (off-grid mode) compared to the case-04 (off-grid mode). The excess electric and thermal energy produced in case-04 (off-grid mode) are estimated as 4,193,123 kWh/year and 7,748,223 kWh/year, respectively. Due to the absence of electric grid in case-05 (off-grid mode), the excess electric energy is not being sold to the grid; hence, both NPC and COE are higher in case-05 (off-grid mode) than case-04 (off-grid mode).
Table 18 presents the amount of GHG emissions in various cases. In this project, five types of GHGs are studied: carbon dioxide, carbon monoxide, sulfur dioxide, nitrogen oxide, and particulate matter. The particulate matter includes smoke, soot, and liquid droplets. For grid-connected mode, in case-01, all types of GHG emissions are highest because 99.99% of the electric demand is supplied by the electric grid in case-01 and the burning of natural gas produces the grid electricity. As there is no burning of fossil fuel in case-04 (both grid-connected and off-grid mode) and case-05 (both grid-connected and off-grid mode), and the MMR fulfills the demand (both electric and thermal) implicitly, GHG emissions are zero for these cases. It should be mentioned that the amount of GHG emissions is only accounted for the electricity production process in this study; the carbon footprint for construction of the site and equipment manufacturing (i.e., PV panel) are not reflected here. Surprisingly, the GHG emissions are significant in case-02 (grid-connected mode) and case-03 (grid-connected mode). Generally, the GHG emission should be minimal in both cases because these are RES-based grid-connected hybrid energy system, and only the fossil fuel is burnt to support the thermal demand. However, since the amount of purchased electricity from the grid is extensive in these cases and the grid electricity is being generated by burning natural gas, case-02 (grid-connected mode) and case-03 (grid-connected mode) cause a significant amount of GHG emissions.
For off-grid mode, case-01 also produces the maximum emissions due to the burning of diesel in the Genset and the boiler. Case-04 and case-05 show zero-emission since the full demand (both electrical and thermal) is satisfied by the combination of MMR, RESs, and cogenerated heat from MMR.
However, the discussion mentioned above cannot draw a single conclusion explicitly since this techno-economic study depends on several variables. Therefore, a sensitivity analysis is also carried out to identify the impact of three critical parameters- discount rate, inflation rate, and project lifetime – on the system performance. Three different values are taken for each parameter, and the system is evaluated based on these values, presented in
Table 19. From
Table 19, the stand-alone off-grid RES-based system (case-02) is not feasible despite the higher or lower discount rate, inflation rate, and project lifetime in this study. Case-01 (off-grid mode) and case-04 (off-grid mode) cannot also manage the selected electric and thermal load demand, studied here, for longer project lifetime (60 and 100 years), depicted in
Table 19. Moreover, case-03 (off-grid mode) is not capable of fulfilling the studied electric and thermal load for a long project lifetime (100 years). All the system infeasibility happens due to capacity shortage. Since the electric and thermal demand is increasing at a certain percentage each year without increasing the capacities of the resources, the current resources cannot serve the demand fully. The higher inflation rate has a notable impact also in the infeasible system. However, the N-R MHES (case-05, both grid-connected and off-grid mode) shows that it can support the demand always with considerably lower NPC, regardless of the higher or lower discount rate, inflation rate, and project lifetime. Higher inflation rate increases the NPC of case-01, case-02, and case-03 significantly.
For the lower discount rate (3% and 8%) and short project lifetime (30 years), case-04 (off-grid mode) could have better performance than case-05 (off-grid mode) in terms of NPC, for instance, scenario No. 1,4,7,10,13, and 16 in
Table 19. Sometimes, the NPC could also be lesser in case-04 (off-grid mode) in the high discount rate (10%) and small project lifetime (30 years), such as scenario No. 19,22, and 25.
For the lower value of project lifetime (30 and 60 years) or smaller value of inflation rate (2% and 4%), case-04 (grid-connected) may also show a slightly lower amount, compared to case-05 (grid-connected), of NPC for a few cases (e.g., scenario No. 10 and 19). However, for the higher value of project lifetime (60 and 100 years), case-05 always provides the most economical NPC.
7. Discussion
Large-scale N-R HES is not a new concept. Research and innovation for the expansion of N-R HES are taking place in several countries. Nevertheless, due to significant risk and high capital cost of large-scale NPP, small-scale NPP integration with RESs has been proposed and evaluated in this paper. Although the N-R MHES depends on the availability of the local RESs, the N-R MHES always provides a baseload supply to strengthen the resiliency and stability of the hybrid energy system. This paper is intended to provide a clear idea of the technical and economic aspects of small-scale N-R HES. The key findings of this study can be summarized as follows.
From the sensitivity analysis, it can be concluded that the N-R MHES could be a resilient energy supply source for sustainable energy solutions in the future. The N-R MHES shows a significant benefit for the long-term planning of a reliable energy system. Furthermore, the MMR can be a suitable replacement for a Diesel genset in terms of NPC, COE, and emissions. From case-02 (off-grid mode), it is observed that the off-grid RES-based energy system is rarely capable or not capable of handling large/medium-scale electricity demand adequately. However, the off-grid RES-based energy system can be an impactful solution for small-scale electric/thermal demand. The case-02 (grid-connected mode) shows that the grid-energy is not always a clear form of an electric power source if the grid-energy comes from the burning of fossil fuel, although the grid-energy is deemed to be clean. Grid-connected N-R MHES could be the most cost-effective solution in terms of COE to provide medium/large-scale electric power supply, depicted in case-05 (grid-connected mode). Moreover, as an extensive amount of excess electric and thermal energy is available in case-05 (off-grid mode), off-grid N-R MHES could be a suitable option for medium/large-scale remote industrial applications, such as desalination plants, mining stations, and EV charging platforms. Also, N-R MHES can provide the best solution for decarbonization pathways project since there are no emissions in case-05.
Few other parameters, e.g., availability of RES, extreme conditions of RES, and abrupt change in electric and thermal load demand, also may influence the whole system performance and system stability. But these kinds of severe conditions are not regarded in this study. Furthermore, the carbon tax incorporation with the NPC and COE is beyond this study. If the carbon tax is included in the study, the NPC and COE of the case-01, case-02, and case-03 would be increased further. In addition, grid stability consideration is beyond of the scope of this study.