Dynamics of Large Scale Turbulence in Finite-Sized Wind Farm Canopy Using Proper Orthogonal Decomposition and a Novel Fourier-POD Framework
Abstract
:1. Introduction
2. Numerical Setup
3. Analysis Methods—Proper Orthogonal Decomposition
3.1. 3D POD—Method of Snapshots
3.2. Fourier-POD Methodology
4. Results
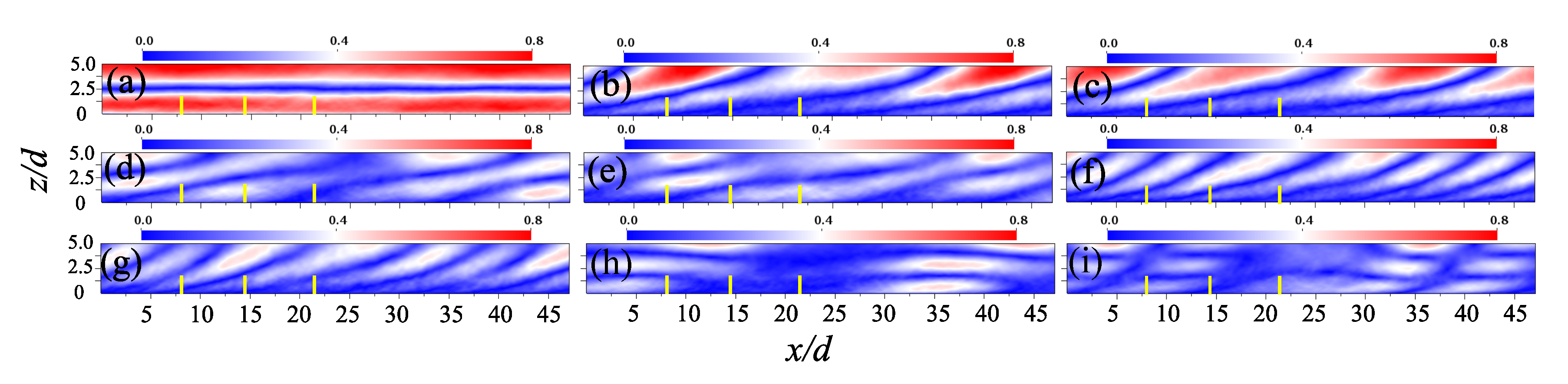
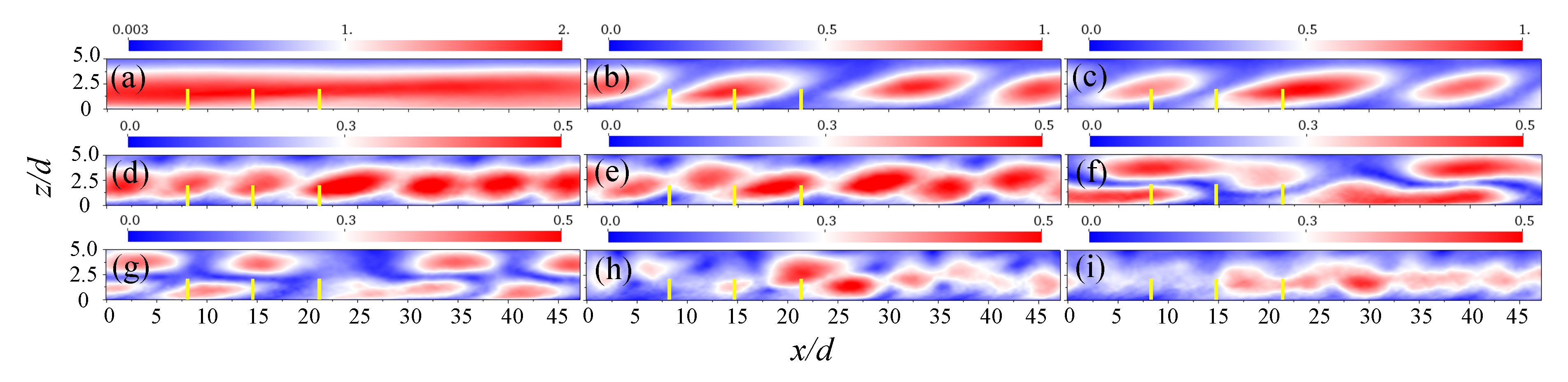
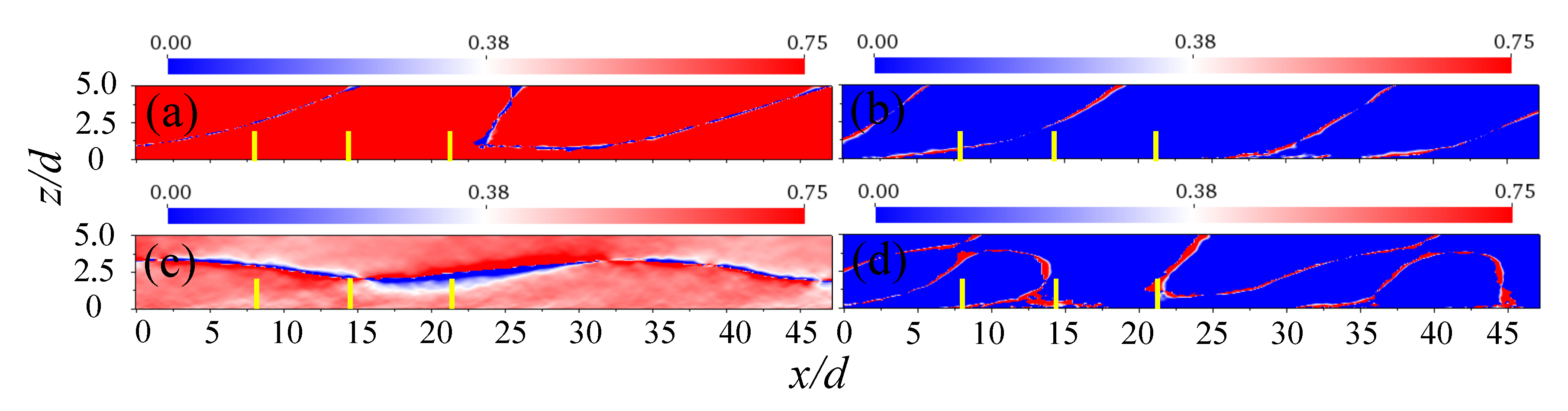
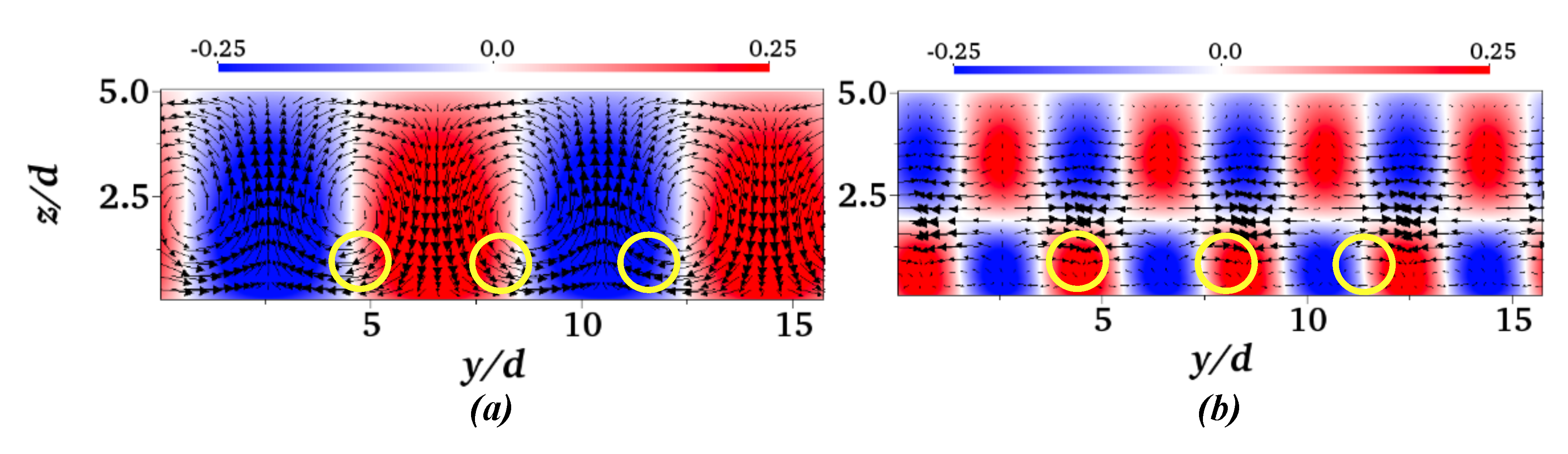
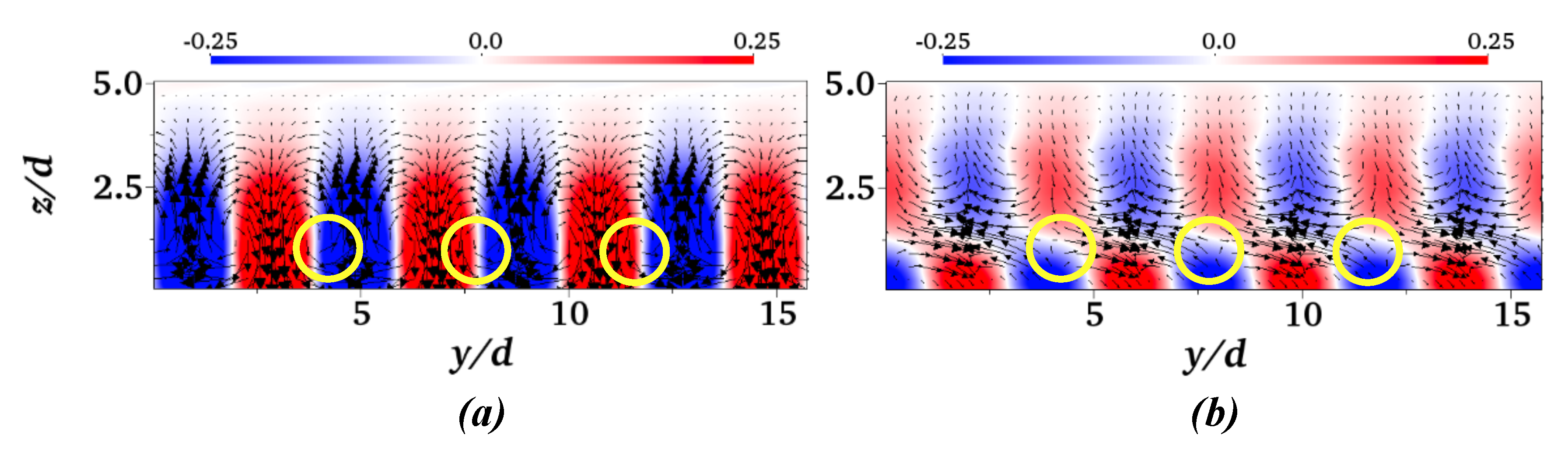
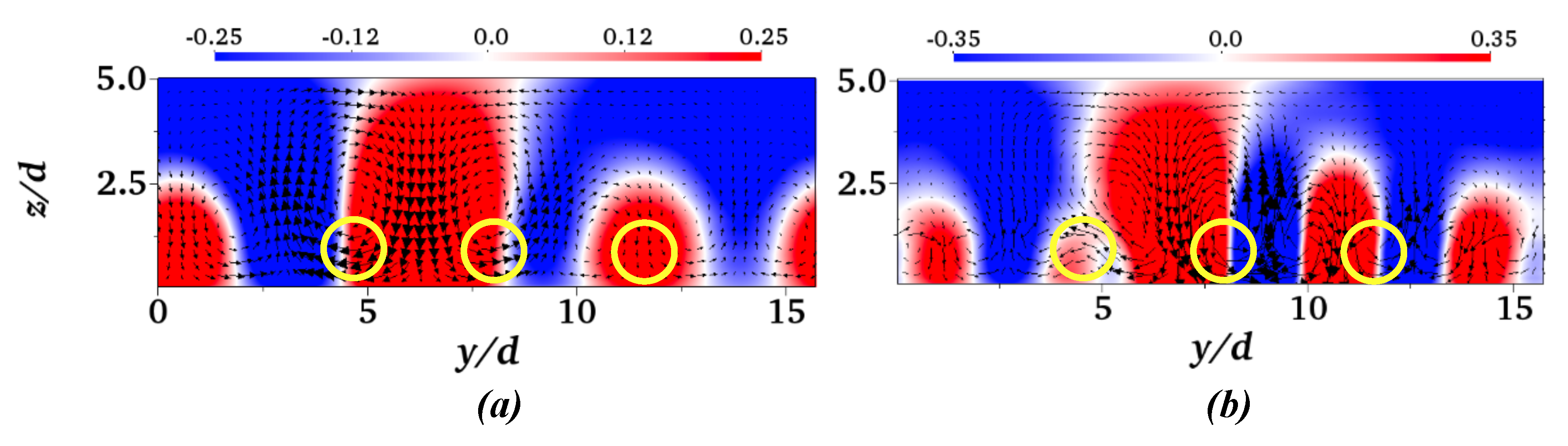
4.1. 3D POD
4.2. Fourier-POD
4.3. Reconstruction of 3D Modes from Fourier-POD
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| d | Turbine rotor diameter |
| Kronecker delta | |
| Turbine hub-height | |
| H | Atmospheric boundary layer thickness |
| 3D - POD mode | |
| Number of snapshots used for POD | |
| 3D - POD diagonal eigenvalue matrix | |
| 3D - POD eigenvalue corresponding to mode | |
| Resolved length scale in the wind farm LES in direction | |
| Velocity in the direction | |
| Velocity fluctuations in the direction | |
| Fourier-transform of velocity fluctuations in the direction | |
| Projection operation on a variable in a reduced order space | |
| Projection operation on a spanwise Fourier-transformed variable in a reduced order space | |
| index of correlation matrix in 3D - POD | |
| index of correlation matrix in Fourier - POD | |
| Summation | |
| norm | |
| lower, upper limit of the streamwise size of the domain | |
| lower, upper limit of the spanwise size of the domain | |
| lower, upper limit of the vertical size of the domain | |
| Spanwise wavenumber | |
| flow through time | |
| Domain size in x direction | |
| Domain size in z direction | |
| Domain size in y direction | |
| Freestream velocity at the top of the ABL | |
| Velocity at the hub-height | |
| f | Temporal frequency |
| Energy spectra of the fluctuating velocity | |
| Extent of averaging time span, | |
| 3D real space | |
| Space of square-integrable functions defined in 3D real space | |
| Topological manifold in which the N-S equations are solved | |
| time averaging operator | |
| Maximum wavenumber used in the Fourier-reconstruction | |
| Inner product | |
| Wavenumber dependent weight functions acting as filters to fourier transforms | |
| 3D POD mode vector from velocity snapshot | |
| 2D Fourier-POD mode vector from Fourier-transformed velocity snapshot | |
| Reconstructed 3D POD mode vector from 2D Fourier-POD mode | |
| Superscripts used in POD modes denoting streamwise, spanwise and wall-normal direction | |
| Phase of the complex 2D Fourier-POD mode for streamwise component | |
| Real component of the Fourier transform of velocity fluctuations, | |
| Imaginary component of the Fourier transform of velocity fluctuations, | |
| streamwise root mean square of velocity fluctuations | |
| integral length scale | |
| integral length scale at hub-height | |
| Reynolds number based on free-stream velocity and chord length | |
| Thrust coefficient in wind turbine rotor | |
| Reynolds number based on friction velocity |
References
- Fang, J.; Porté-Agel, F. Large-eddy simulation of very-large-scale motions in the neutrally stratified atmospheric boundary layer. Bound. Layer Meteorol. 2015, 155, 397–416. [Google Scholar] [CrossRef] [Green Version]
- Calaf, M.; Meneveau, C.; Meyers, J. Large Eddy Simulation Study of Fully Developed Wind-Turbine Array Boundary Layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef] [Green Version]
- Chamorro, L.P.; Lee, S.J.; Olsen, D.; Miliren, C.; Marr, J.; Arndt, R.; Sotiropoulos, F. Turbulence effects on a full-scale 2.5MW horizontal-axis wind turbine under neutrally stratified conditions. Wind Energy 2015, 18, 339–349. [Google Scholar] [CrossRef]
- Önder, A.; Meyers, J. On the interaction of very-large-scale motions in a neutral atmospheric boundary layer with a row of wind turbines. J. Fluid. Mech. 2018, 841, 1040–1072. [Google Scholar] [CrossRef]
- Chatterjee, T.; Peet, Y.T. Contribution of Large Scale Coherence to wind turbine power: A large eddy simulation study in periodic wind farms. Phys. Rev. Fluids 2018, 3, 034601. [Google Scholar] [CrossRef]
- Balakumar, B.J.; Adrian, R.J. Large and very-large-scale motions in channel and boundary-layer flows. Philos. Trans. R. Soc. 2007, 365, 665–681. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Porté-Agel, F. Turbulent Flow Inside and Above a Wind Farm: A Wind-Tunnel Study. Energies 2011, 4, 1916–1936. [Google Scholar] [CrossRef]
- Etling, D.; Brown, R. Roll vortices in planetary boundary layer: A review. Bound. Layer Meteorol. 1993, 65, 215–248. [Google Scholar] [CrossRef]
- Young, G.S.; Kristovich, D.A.R.; Hjelmfelt, M.R.; Foster, R.C. Rolls, Streets, waves and more: A review of quasi-two-dimensional structures in the atmospheric boundary layer. Bull. Am. Meteorol. Soc. 2002, 83, 997–1001. [Google Scholar]
- Chauhan, K.; Hutchins, N.; Monty, J.; Marusic, I. Structure inclination angles in convective atmospheric surface layer. Bound. Layer Meteorol. 2013, 147, 41–50. [Google Scholar] [CrossRef]
- Hutchins, N.; Chauhan, K.; Monty, J.; Klewicki, J. Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and the laboratory. Bound. Layer Meteorol. 2012, 145, 273–306. [Google Scholar] [CrossRef]
- Kelley, N.D.; Jonkman, B.J.; Scott, G.N.; Bialasiewicz, J.T.; Redmond, L.S. The Impact of Coherent Turbulence on Wind Turbine AeroElastic Response and Its Simulation; NREL/CP-500-38074; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2005. [Google Scholar]
- Chamorro, L.; Hong, J.; Gangodagamage, C. On the scale-to-scale coupling between a full- scale wind turbine and turbulence. J. Turbul. 2015, 16, 617–632. [Google Scholar] [CrossRef]
- Cortina, G.; Sharma, V.; Calaf, M. Wind farm density and harvested power in very large wind farms: A low order model. Phys. Rev. Fluids 2017, 2, 074601. [Google Scholar] [CrossRef]
- VerHulst, C.; Meneveau, C. Large eddy simulation study of the kinetic energy entrainment by energetic turbulent flow structures in large wind farms. Phys. Fluids 2014, 8, 025113. [Google Scholar] [CrossRef]
- Peet, Y.T.; Chatterjee, T. The contribution of large scale structures in the power generation of finite scale wind farms using large eddy simulation. In Proceedings of the 10th International Symposium on Turbulence and Shear Flow Phenomena (TSFP10), Chicago, IL, USA, 6–9 July 2017. [Google Scholar]
- Zhang, M.; Stevens, R.J.A.M. Characterizing the Coherent Structures Within and Above Large Wind Farms. Bound. Layer Meteorol. 2019. [Google Scholar] [CrossRef] [Green Version]
- Stevens, R.J.; Gayme, D.F.; Meneveau, C. Effects of turbine spacing on the power output of extended wind-farms. Wind Energy 2016, 19, 359–370. [Google Scholar] [CrossRef] [Green Version]
- Orell, A.; Preziuso, D.; Foster, N.; Morris, S.; Homer, J. 2018 Distributed Wind Market Report; Pacific Northwest National Laboratory operated by Battele; Office of Energy Efficiency and Renewable Energy (EERE), U.S. Department of Energy: Washington, DC, USA, 2018.
- Sirovich, L. Turbulence and dynamics of coherent structures. Part I: Coherent structures. Q. J. Appl. Math. 1987, XLV, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Park, H.; Sirovich, L. Turbulent thermal convection in a finite domain: Part II. Numerical results. Phys. Fluids A Fluid Dyn. 1990, 2, 1659–1668. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. Wind tunnel study of the wind turbine interaction with a boundary-layer flow: Upwind region, turbine performance, and wake region. Phys. Fluids 2017, 29, 065105. [Google Scholar] [CrossRef]
- Towne, A.; Schmidt, O.T.; Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 2018, 847, 821–867. [Google Scholar] [CrossRef] [Green Version]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, N.; Tutkun, M.; Cal, R.B. Low-order representations of the canonical wind turbine array boundary layer via double proper orthogonal decomposition. Phys. Fluids 2016, 28, 025103. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, N.; Tutkun, M.; Cal, R.B. Wind turbine boundary layer arrays for Cartesian and staggered configurations: Part II, low-dimensional representations via the proper orthogonal decomposition. Wind Energy 2015, 18, 297–315. [Google Scholar] [CrossRef]
- Glegg, S.; Devenport, W. Proper Orthogonal Decomposition Of Turbulent Flows For Aeroacoustic And Hydroacoustic Applications. J. Sound Vib. 2001, 239, 767–784. [Google Scholar] [CrossRef]
- Sakievich, P. Identification, Decomposition and Analysis of Dynamic Large-Scale Structures in Turbulent Rayleigh-Bénard Convection. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2017. [Google Scholar]
- Pandey, S.; Schumacher, J. Reservoir computing model of two-dimensional turbulent convection. arXiv 2020, arXiv:2001.10280. [Google Scholar]
- Chatterjee, T.; Peet, Y. Large Eddy Simulation of a 3 × 3 wind turbine array using Actuator Line model with spectral elements. In Proceedings of the 34th Wind Energy Symposium, San Diego, CA, USA, 4–8 January 2016. AIAA paper 2016–1988. [Google Scholar]
- Chatterjee, T.; Cherukuru, N.W.; Peet, Y.; Calhoun, R.J. Incorporating realistic geophysical effects of mean wind from LIDAR measurements in Large Eddy Simulation of Wind Turbine Arrays. J. Phys. Conf. Ser. 2018, 1037, 072056. [Google Scholar] [CrossRef]
- Fischer, P.F.; Lottes, J.W.; Kerkemeier, S.G. Nek5000: An Open Source CFD Solver. 2008. Available online: http://nek5000.mcs.anl.gov (accessed on 29 March 2020).
- Deville, M.O.; Fischer, P.F.; Mund, E.H. High-Order Methods for Incompressible Fluid Flow; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Chatterjee, T.; Peet, Y. Incorporating realistic geophysical effects of mean wind from LIDAR measurements in Large Eddy Simulation of Wind Turbine Arrays. In Proceedings of the 35th Wind Energy Symposium, Grapevine, TX, USA, 9–13 January 2017. AIAA paper 2017-1165. [Google Scholar]
- McTavish, S.; Rodrigue, S.; Feszty, D.; Nitzsche, F. An investigation of in-field blockage effects in closely spaced lateral wind farm configurations. Wind Energy 2015, 18, 1989–2011. [Google Scholar] [CrossRef]
- Mason, P.J.; Thompson, D.J. Stochastic backscatter in large-eddy simulations of boundary layers. J. Fluid. Mech. 1992, 242, 51–78. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A scale-dependent dynamics model for large eddy simulation: Application to a neutral atmospheric boundary layer. J. Fluid. Mech. 2000, 415, 261–284. [Google Scholar] [CrossRef] [Green Version]
- Bou-Zeid, E.; Meneveau, C.; Parlange, M. A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 2005, 415, 025125. [Google Scholar] [CrossRef] [Green Version]
- Hayat, I.; Chatterjee, T.; Liu, H.; Peet, Y.T.; Chamorro, L.P. Exploring wind farms with alternating two- and three-bladed wind turbines. Renew. Energy 2019, 138, 764–774. [Google Scholar] [CrossRef]
- Hutchins, N.; Nickels, T.B.; Marusic, I.; Chong, M.S. Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid. Mech. 2009, 635, 103–136. [Google Scholar] [CrossRef] [Green Version]
- Lettau, H. A re-examination of the Leipzig wind profile considering some relations between wind and turbulence in the frictional layer. Tellus 1950, 2, 125–129. [Google Scholar] [CrossRef] [Green Version]
- Sillero, J.A.; Jiménez, J.; Moser, R. Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to δ+ 2000. Phys. Fluids 2014, 26, 105109. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, T.; Peet, Y.T. Effect of artificial length scales in large eddy simulation of a neutral atmospheric boundary layer flow: A simple solution to log-layer mismatch. Phys. Fluids 2017, 29, 075175. [Google Scholar] [CrossRef]
- Troldborg, N. Actuator Line Modeling of Wind Turbine Wakes. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2008. [Google Scholar]
- Chatterjee, T.; Peet, Y. Actuator Line Wind Turbine Simulations in Atmospheric Turbulent Flows using Spectral Element Method. In Proceedings of the 33rd Wind Energy Symposium, Kissimmmee, FL, USA, 5–9 January 2015. AIAA paper 2015-0727. [Google Scholar]
- Chatterjee, T.; Peet, Y.T. Exploring the benefits of vertically staggered wind farms: Understanding the power generation mechanisms of turbines operating at different scales. Wind Energy 2019, 22, 283–301. [Google Scholar] [CrossRef]
- Meyers, J.; Meneveau, C. Flow visualization using momentum and energy transport tubes and applications to turbulent flow in wind farms. J. Fluid. Mech. 2013, 715, 335–358. [Google Scholar] [CrossRef] [Green Version]
- Allaerts, D.; Meyers, J. Effect of inversion-layer height and Coriolis forces on developing wind-farm boundary layers. In Proceedings of the 34th Wind Energy Symposium, San Diego, CA, USA, 4–8 January 2016. AIAA Paper 2016-1989. [Google Scholar]
- Allaerts, D.; Meyers, J. Boundary-layer development and gravity waves in conventionally neutral wind farms. J. Fluid Mech. 2017, 814. [Google Scholar] [CrossRef] [Green Version]
- Cava, D.; Katul, G.G.; Scrimieri, A.; Poggi, D.; Cescatti, A.; Giostra, U. Buoyancy and The Sensible Heat Flux Budget Within Dense Canopies. Bound. Layer Meteorol. 2011, 118, 217–240. [Google Scholar] [CrossRef]
- Banerjee, T.; De Roo, F.; Mauder, M. Connecting the Failure of K Theory inside and above Vegetation Canopies and Ejection–Sweep Cycles by a Large-Eddy Simulation. J. Appl. Meteorol. Climatol. 2017, 56, 3119–3131. [Google Scholar] [CrossRef]
- Wu, S.; Christensen, K.T.; Pantano, C. Modelling smooth- and transitionally rough-wall turbulent channel flow by leveraging inner–outer interactions and principal component analysis. J. Fluid Mech. 2019, 863, 407–453. [Google Scholar] [CrossRef]
- Peet, Y.; Fischer, P.; Conzelmann, G.; Kotamarthi, V. Actuator line aerodynamics model with spectral elements. In Proceedings of the 51st Aerospace Sciences Meeting, Grapevine, TX, USA, 7–10 January 2013. AIAA Paper 2013-1210. [Google Scholar]
- Holmes, P.; Lumley, J.H.; Berkooz, C.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Brandt Belson, J.T.; Rowley, C. 2019. Available online: https://modred.readthedocs.io/en/stable/intro.html (accessed on 29 March 2020).
- Mathis, R.; Monty, J.P.; Hutchins, N.; Marusic, I. Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 2009, 21, 111703. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Laima, S.; Li, H. Numerical study of amplitude modulation in the atmospheric boundary layer at very high Reynolds number. AIP Adv. 2019, 9, 105112. [Google Scholar] [CrossRef]
- Perry, A.E.; Henbest, S.; Chong, M.S. Theoretical and Experimental studies of wall turbulence. J. Fluid. Mech. 1986, 165, 163–199. [Google Scholar] [CrossRef] [Green Version]
- Adrian, R.J. Hairpin vortex organization in wall turbulence. Phys. Fluids 2007, 19, 041301. [Google Scholar] [CrossRef] [Green Version]
- Tung, K.K.; Orlando, W.W. The k−3 and the k−5/3 Energy Spectrum of Atmospheric Turbulence: Quasigeostrophic Two-Level model simulation. J. Atmos. Sci. 2003, 60, 824–835. [Google Scholar] [CrossRef] [Green Version]
- Kraichnan, R.H. Inertial ranges of two-dimensional turbulence. Phys. Fluids 1967, 10, 1417–1423. [Google Scholar] [CrossRef] [Green Version]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Ann. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef] [Green Version]
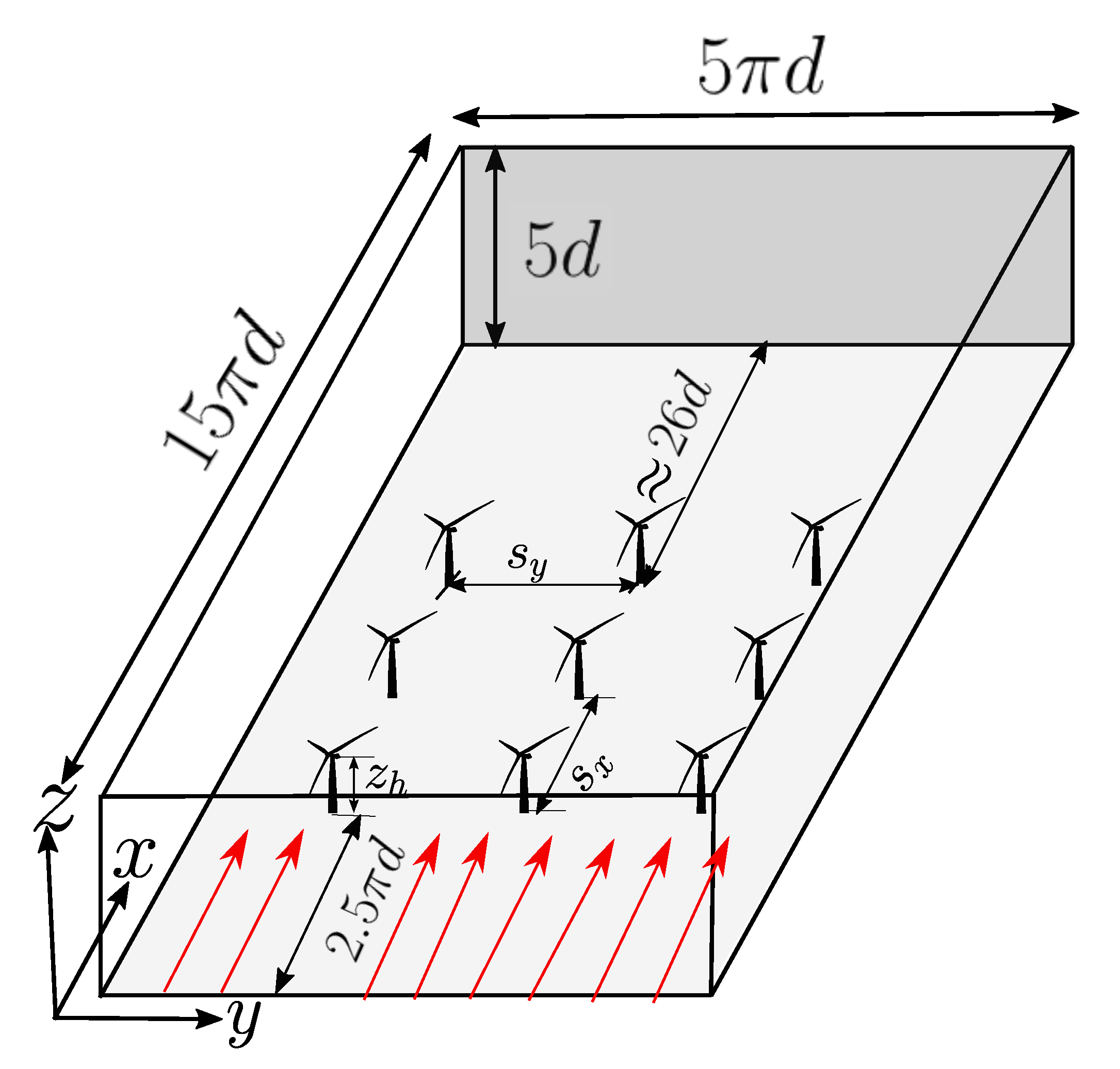
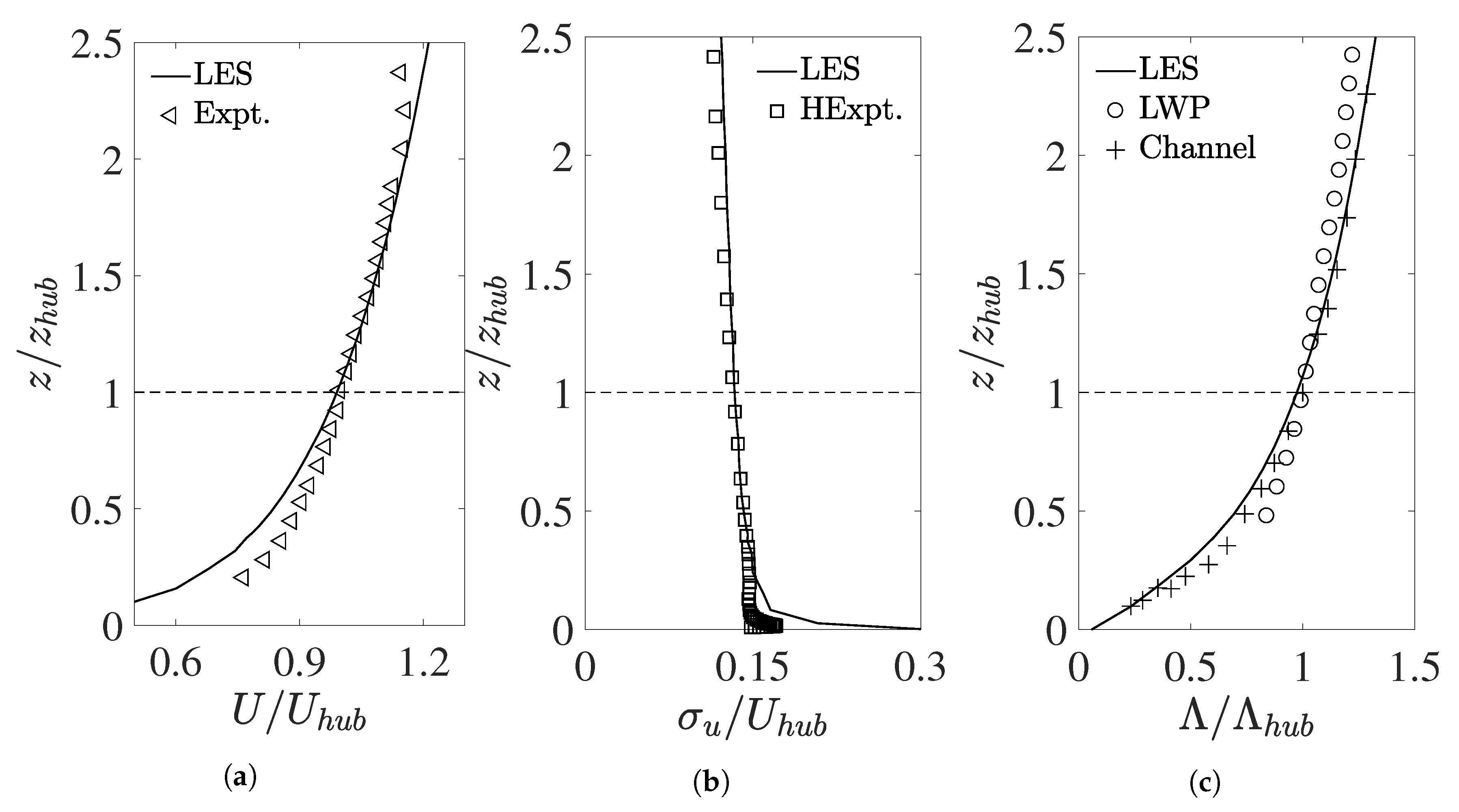
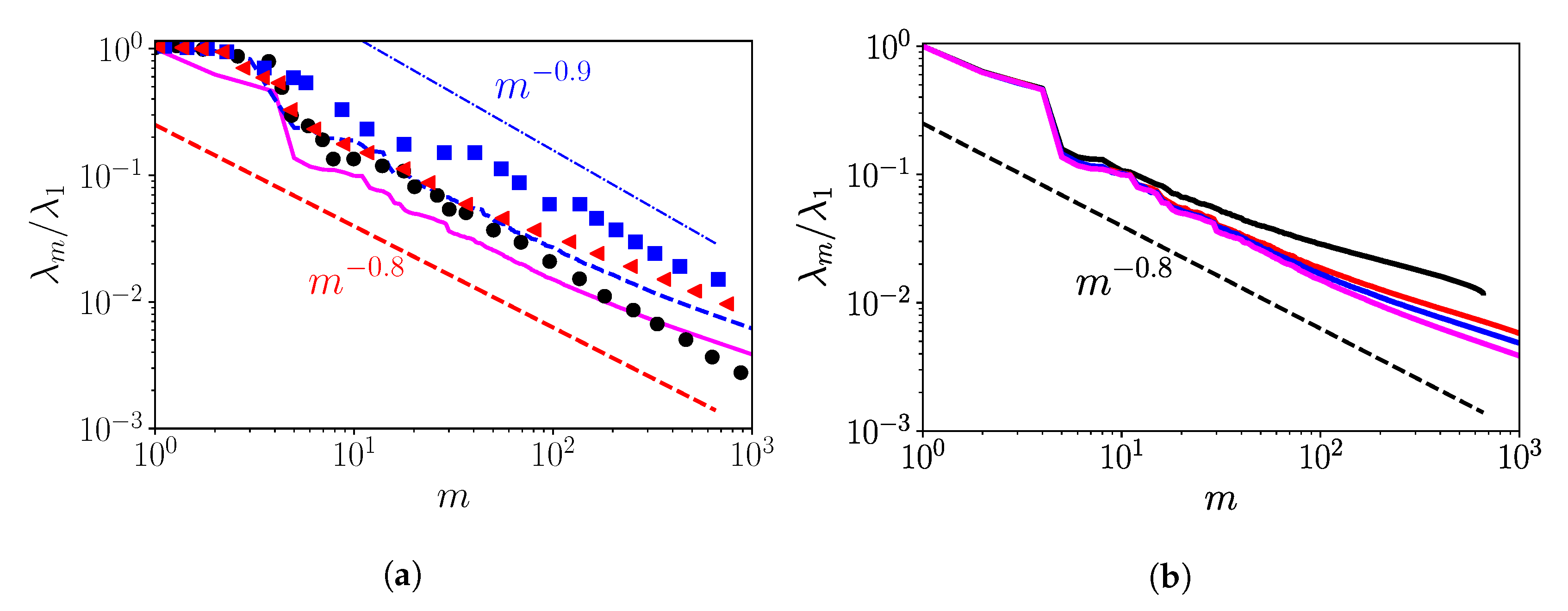
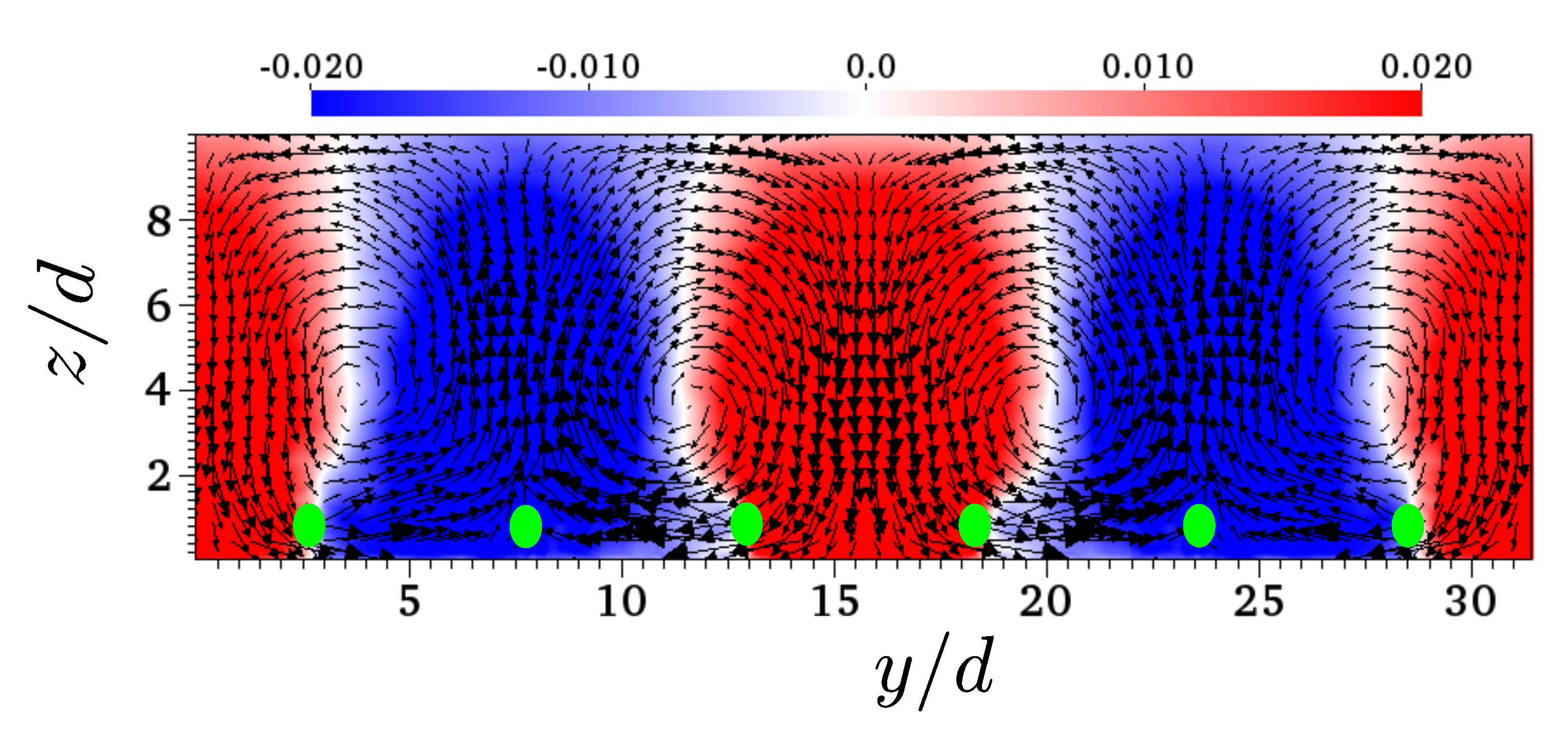



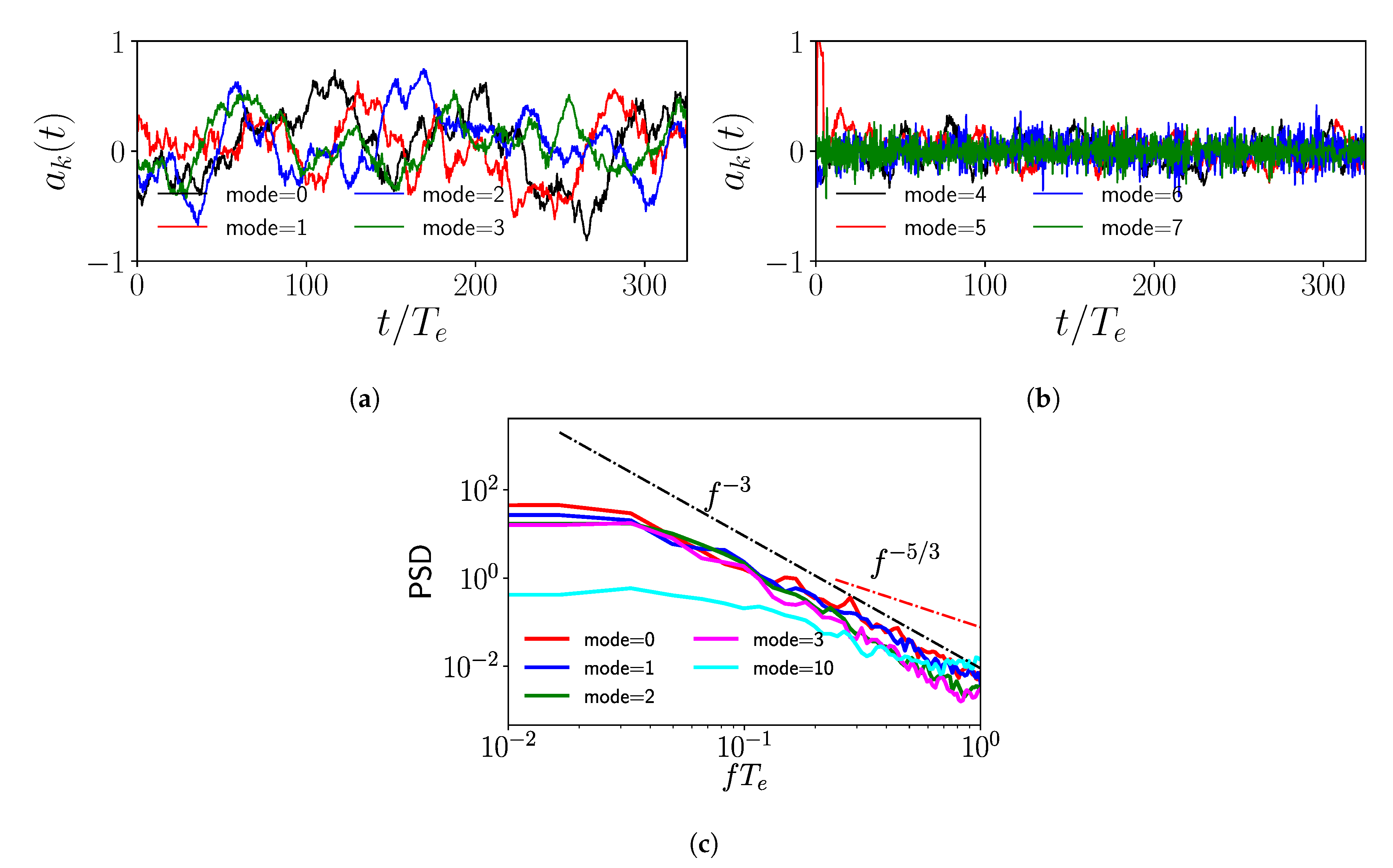
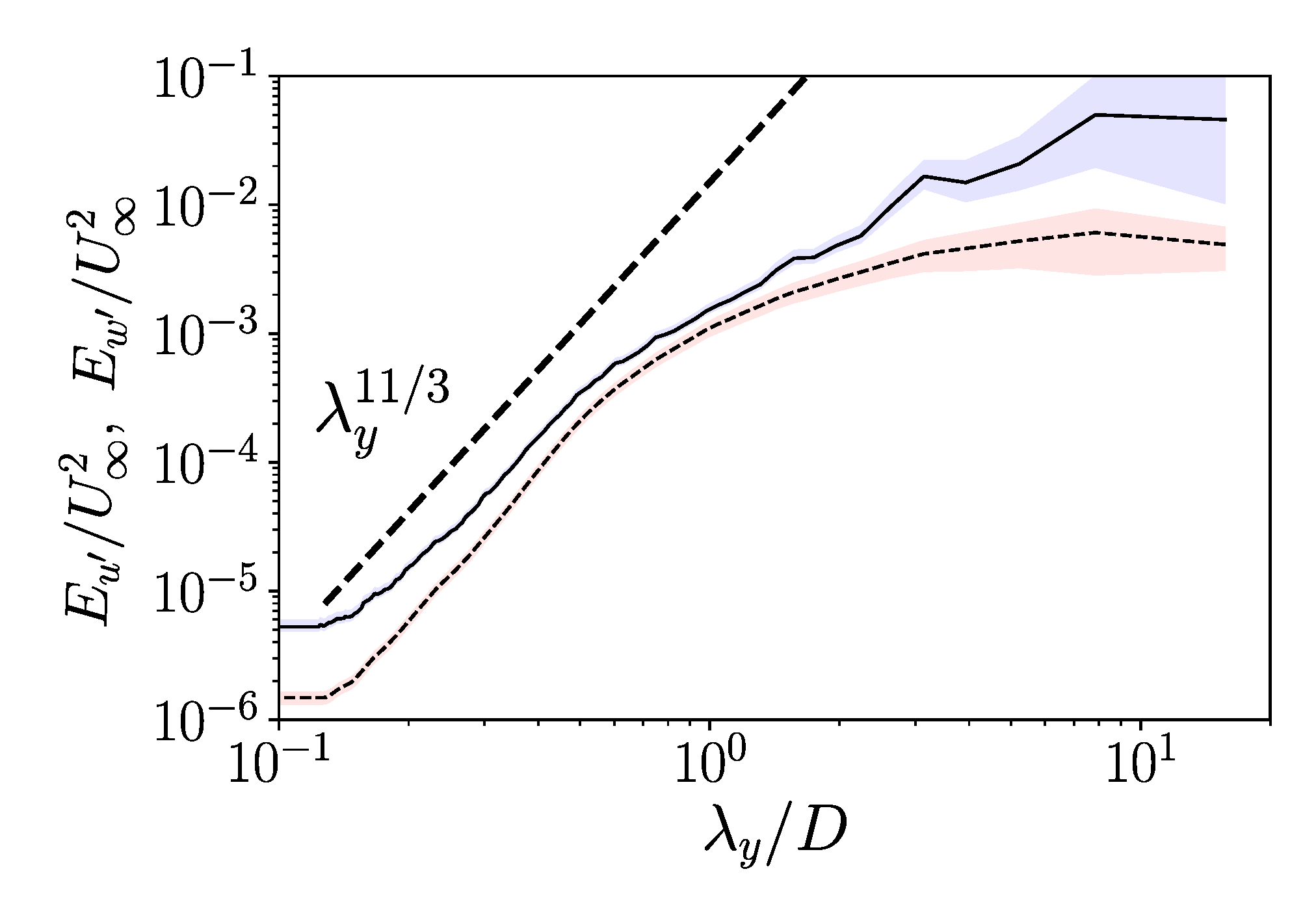

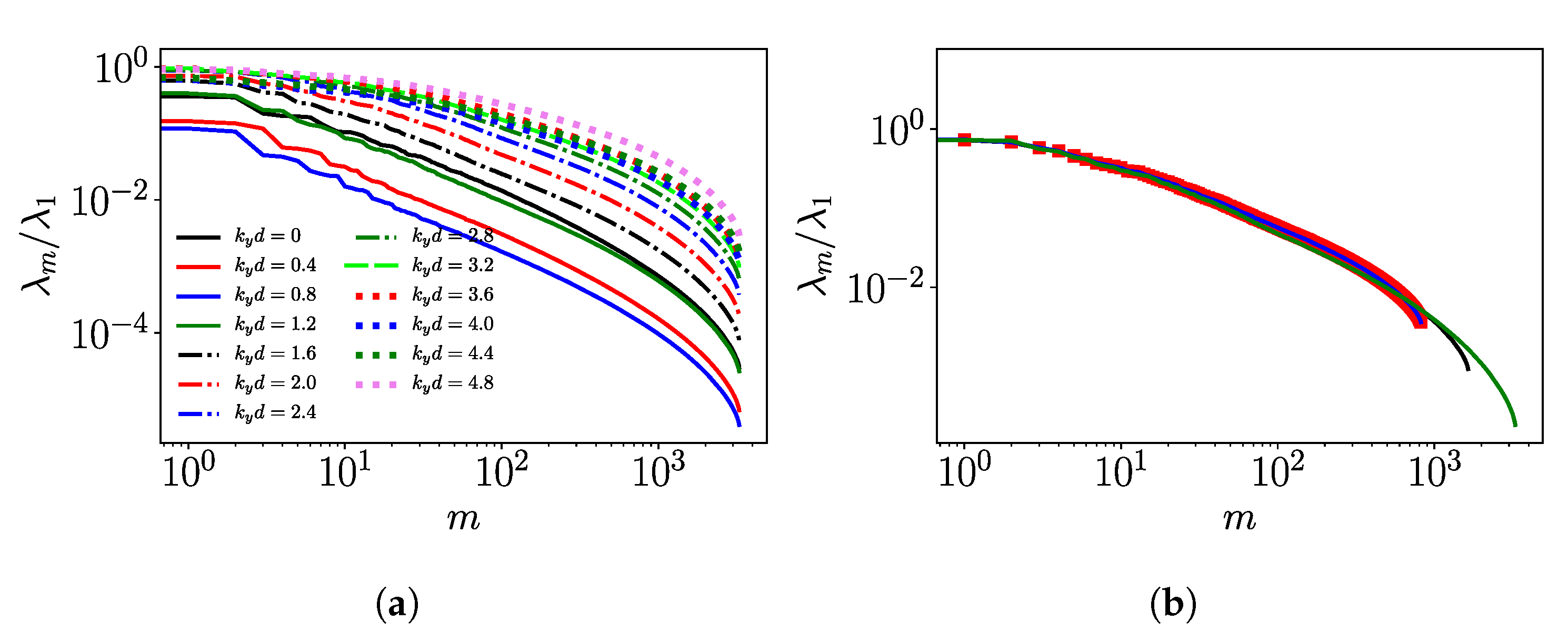
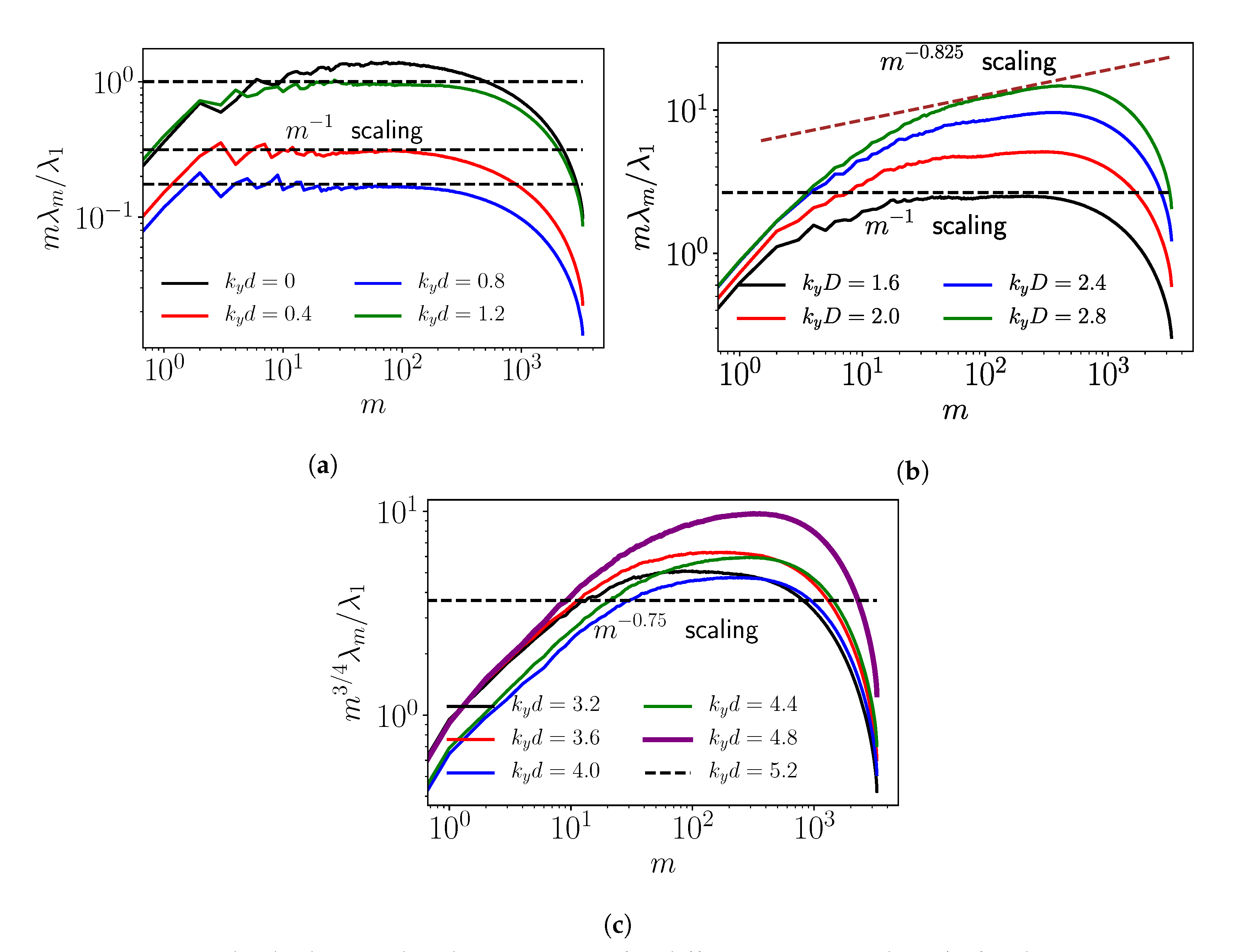


| Case | Geometry | Inter-Turbine Distance | Grid Points | |
|---|---|---|---|---|
| Neutral ABL | ||||
| WT Array |
| Neutral ABL | WT Array | |||||
|---|---|---|---|---|---|---|
| Direction | ||||||
| x | 0.2992d | 0.2992d | 0.2992d | 0.3366d | 0.0944d | 0.2804d |
| y | 0.3316d | 0.0358d | 0.1402d | |||
| z | 0.0942d | 0.0476d | 0.0596d |
| Geometry () | Inter-Turbine Distance, | Roll Size | Roll Density | Roll Height |
|---|---|---|---|---|
| [5] | ||||
| [15] | ∼15.7d | |||
| [17] | – |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, T.; Peet, Y.T. Dynamics of Large Scale Turbulence in Finite-Sized Wind Farm Canopy Using Proper Orthogonal Decomposition and a Novel Fourier-POD Framework. Energies 2020, 13, 1660. https://doi.org/10.3390/en13071660
Chatterjee T, Peet YT. Dynamics of Large Scale Turbulence in Finite-Sized Wind Farm Canopy Using Proper Orthogonal Decomposition and a Novel Fourier-POD Framework. Energies. 2020; 13(7):1660. https://doi.org/10.3390/en13071660
Chicago/Turabian StyleChatterjee, Tanmoy, and Yulia T. Peet. 2020. "Dynamics of Large Scale Turbulence in Finite-Sized Wind Farm Canopy Using Proper Orthogonal Decomposition and a Novel Fourier-POD Framework" Energies 13, no. 7: 1660. https://doi.org/10.3390/en13071660
APA StyleChatterjee, T., & Peet, Y. T. (2020). Dynamics of Large Scale Turbulence in Finite-Sized Wind Farm Canopy Using Proper Orthogonal Decomposition and a Novel Fourier-POD Framework. Energies, 13(7), 1660. https://doi.org/10.3390/en13071660




