Beating the Naïve—Combining LASSO with Naïve Intraday Electricity Price Forecasts
Abstract
:1. Introduction
2. The Dataset
2.1. The ID3-Price Index and DA Prices
2.2. Exogenous Variables
- the system-wide load and its day-ahead forecast ,
- the total wind power generation (WPG; off- and on-shore) and its day-ahead forecast ,
- and the total photovoltaic generation (PVG) and its day-ahead forecast ,
2.3. Variance Stabilizing Transformation
3. The Models
3.1. The Naïve Benchmark
3.2. LASSO-Estimated Models
3.2.1. The Baseline Model
3.2.2. The Model with Exogenous Variables
3.2.3. The Model with Partial ID Prices
3.2.4. The Full Model
3.3. LASSO Estimation
3.4. Forecast Averaging
4. Results
4.1. Forecast Evaluation
4.2. MAE and RMSE Errors
- In terms of the MAE, three models outperform the naïve benchmark even without averaging forecasts. However, only the full-diff approach manages to beat the benchmark in terms of the RMSE, see the values emphasized in bold in Table 1 in columns labeled ‘model’.
- All baseline model extensions yield lower errors than the baseline model itself, both in terms of the MAE and RMSE.
- The full model outperforms the model with partial ID prices, which suggests that using the exogenous variables discussed in Section 2.2 improves forecast accuracy.
- Interestingly, for the full-diff model we observe that back-transformation (3) performs better than the mathematically correct VST defined in Equation (4). The difference vanishes when the forecasts are averaged, which is probably caused by the fact that the correction improves performance mainly in the tails, and in the full-diff model the less heavy-tailed price differences are predicted.
- The improvements from averaging forecasts are much higher (ca. 12–14%) for models that do not use the naïve benchmark as a regressor. However, what is surprising, the gains are noticeable (ca. 2–4%) even for models which include this explanatory variable. Apparently, the LASSO scheme does not put enough weight to this variable. Setting in the full-diff model helps, but does not solve the problem completely. We return to this issue in Section 4.4.
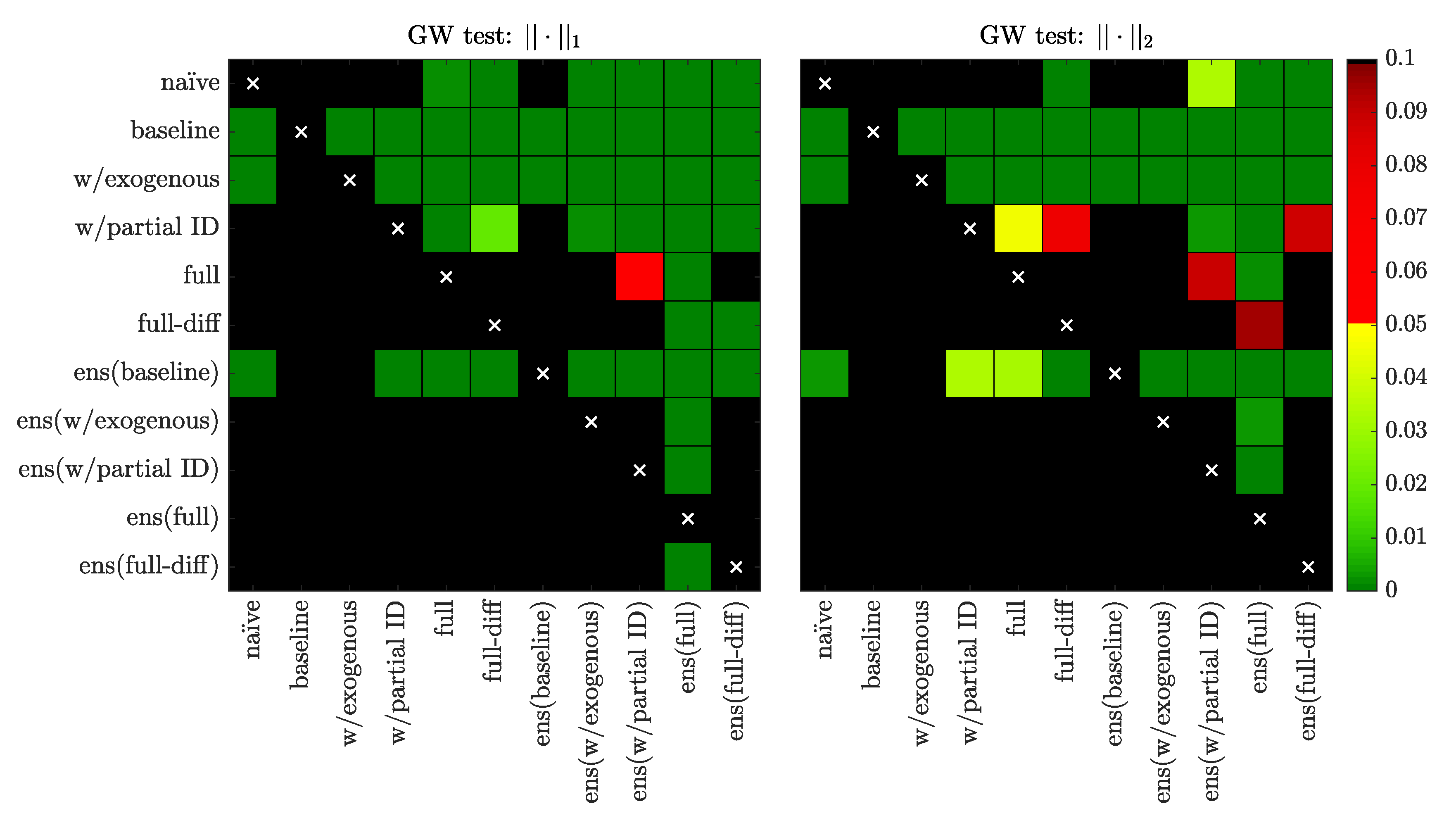
4.3. Conditional Predictive Ability
- The naïve forecasts can be significantly outperformed by predictions of models that include partial ID information and exogenous variables (full and full-diff models) without averaging, and by most of models after ensembling.
- Forecasts of the baseline model are significantly outperformed by those of any other LASSO-estimated model.
- For all considered models, ensembling significantly improves the accuracy in terms of the linear errors.
- Forecasts of the ens(full) model significantly outperform those of any other model, both in terms of the linear and quadratic errors.
4.4. Why Does Ensembling Improve the Results?
5. Discussion and Conclusions
5.1. The Moment of Forecasting the ID3-Price Index
5.2. Selecting the LASSO Regularization Parameter
5.3. The Impact of Intraday Updates of the Fundamentals
5.4. Model Size
5.5. Directions for Future Research
Author Contributions
Funding
Conflicts of Interest
References
- Narajewski, M.; Ziel, F. Econometric modelling and forecasting of intraday electricity prices. J. Commod. Mark. 2019. [Google Scholar] [CrossRef] [Green Version]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef] [Green Version]
- Goodarzi, S.; Perera, H.; Bunn, D. The impact of renewable energy forecast errors on imbalance volumes and electricity spot prices. Energy Policy 2019, 134, 110827. [Google Scholar] [CrossRef]
- Kath, C. Modeling intraday markets under the new advances of the cross-border intraday project (XBID): Evidence from the German intraday market. Energies 2019, 12, 4339. [Google Scholar] [CrossRef] [Green Version]
- Maciejowska, K. Assessing the impact of renewable energy sources on the electricity price level and variability—A quantile regression approach. Energy Econ. 2020, 85, 104532. [Google Scholar] [CrossRef]
- Ciarreta, A.; Muniain, P.; Zarraga, A. Modeling and forecasting realized volatility in German–Austrian continuous intraday electricity prices. J. Forecast. 2017, 36, 680–690. [Google Scholar] [CrossRef]
- Kiesel, R.; Paraschiv, F. Econometric analysis of 15-minute intraday electricity prices. Energy Econ. 2017, 64, 77–90. [Google Scholar] [CrossRef] [Green Version]
- Bunn, D.; Gianfreda, A.; Kermer, S. A trading-based evaluation of density forecasts in a real-time electricity market. Energies 2018, 11, 2658. [Google Scholar] [CrossRef] [Green Version]
- Kath, C.; Ziel, F. The value of forecasts: Quantifying the economic gains of accurate quarter-hourly electricity price forecasts. Energy Econ. 2018, 76, 411–423. [Google Scholar] [CrossRef] [Green Version]
- Maciejowska, K.; Nitka, W.; Weron, T. Day-ahead vs. Intraday—Forecasting the price spread to maximize economic benefits. Energies 2019, 12, 631. [Google Scholar] [CrossRef] [Green Version]
- Uniejewski, B.; Marcjasz, G.; Weron, R. Understanding intraday electricity markets: Variable selection and very short-term price forecasting using LASSO. Int. J. Forecast. 2019, 35, 1533–1547. [Google Scholar] [CrossRef] [Green Version]
- Janke, T.; Steinke, F. Forecasting the price distribution of continuous intraday electricity trading. Energies 2019, 12, 4262. [Google Scholar] [CrossRef] [Green Version]
- Narajewski, M.; Ziel, F. Estimation and simulation of the transaction arrival process in intraday electricity markets. Energies 2019, 12, 4518. [Google Scholar] [CrossRef] [Green Version]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Applications in R; Springer: New York, NY, USA, 2013. [Google Scholar]
- Nowotarski, J.; Raviv, E.; Trück, S.; Weron, R. An empirical comparison of alternate schemes for combining electricity spot price forecasts. Energy Econ. 2014, 46, 395–412. [Google Scholar] [CrossRef]
- Giacomini, R.; White, H. Tests of conditional predictive ability. Econometrica 2006, 74, 1545–1578. [Google Scholar] [CrossRef] [Green Version]
- Uniejewski, B.; Weron, R.; Ziel, F. Variance stabilizing transformations for electricity spot price forecasting. IEEE Trans. Power Syst. 2018, 33, 2219–2229. [Google Scholar] [CrossRef] [Green Version]
- de Marcos, R.; Bello, A.; Reneses, J. Electricity price forecasting in the short term hybridising fundamental and econometric modelling. Electr. Power Syst. Res. 2019, 167, 240–251. [Google Scholar] [CrossRef]
- Uniejewski, B.; Weron, R. Efficient forecasting of electricity spot prices with expert and LASSO models. Energies 2018, 11, 2039. [Google Scholar] [CrossRef] [Green Version]
- Ziel, F.; Weron, R. Day-ahead electricity price forecasting with high-dimensional structures: Univariate vs. multivariate modeling frameworks. Energy Econ. 2018, 70, 396–420. [Google Scholar] [CrossRef] [Green Version]
- Uniejewski, B.; Nowotarski, J.; Weron, R. Automated variable selection and shrinkage for day-ahead electricity price forecasting. Energies 2016, 9, 621. [Google Scholar] [CrossRef] [Green Version]
- Monteiro, C.; Ramirez-Rosado, I.; Fernandez-Jimenez, L.; Conde, P. Short-term price forecasting models based on artificial neural networks for intraday sessions in the Iberian electricity market. Energies 2016, 9, 721. [Google Scholar] [CrossRef]
- Andrade, J.; Filipe, J.; Reis, M.; Bessa, R. Probabilistic price forecasting for day-ahead and intraday markets: Beyond the statistical model. Sustainability 2017, 9, 1990. [Google Scholar] [CrossRef] [Green Version]
- Ziel, F. Forecasting electricity spot prices using LASSO: On capturing the autoregressive intraday structure. IEEE Trans. Power Syst. 2016, 31, 4977–4987. [Google Scholar] [CrossRef] [Green Version]
- Elliott, G.; Timmermann, A. Economic Forecasting; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Diebold, F.X.; Shin, M. Machine learning for regularized survey forecast combination: Partially-egalitarian LASSO and its derivatives. Int. J. Forecast. 2018, 35, 1679–1691. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. On the importance of the long-term seasonal component in day-ahead electricity price forecasting. Energy Econ. 2016, 57, 228–235. [Google Scholar] [CrossRef] [Green Version]
- Marcjasz, G.; Uniejewski, B.; Weron, R. On the importance of the long-term seasonal component in day-ahead electricity price forecasting with NARX neural networks. Int. J. Forecast. 2019, 35, 1520–1532. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Muniain, P.; Ziel, F. Probabilistic forecasting in day-ahead electricity markets: Simulating peak and off-peak prices. Int. J. Forecast. 2020. [Google Scholar] [CrossRef] [Green Version]
- Oksuz, I.; Ugurlu, U. Neural network based model comparison for intraday electricity price forecasting. Energies 2019, 12, 4557. [Google Scholar] [CrossRef] [Green Version]
- Hubicka, K.; Marcjasz, G.; Weron, R. A note on averaging day-ahead electricity price forecasts across calibration windows. IEEE Trans. Sustain. Energy 2019, 10, 321–323. [Google Scholar] [CrossRef]



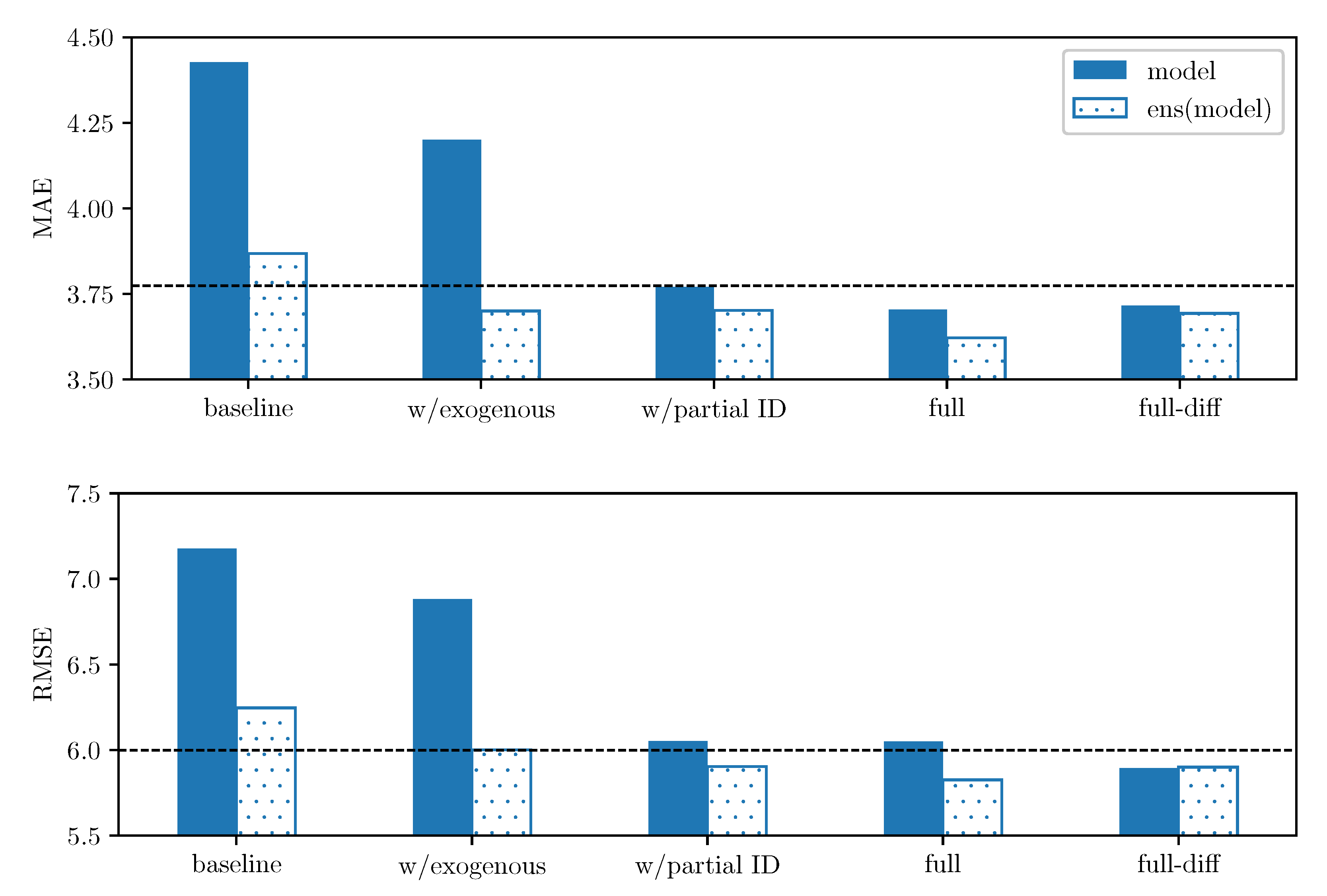


| Back- | Model | MAE | RMSE | ||
|---|---|---|---|---|---|
| Transformation | Class | Model | ens(Model) | Model | ens(Model) |
| naïve | 3.774 | — | 5.999 | — | |
| With correction proposed in [1], see Equation (4) | baseline | 4.427 | 3.868 | 7.178 | 6.246 |
| w/exogenous | 4.200 | 3.700 | 6.882 | 6.001 | |
| w/partial ID | 3.771 | 3.702 | 6.052 | 5.903 | |
| full | 3.704 | 3.622 | 6.050 | 5.826 | |
| full-diff | 3.716 | 3.693 | 5.894 | 5.900 | |
| As originally introduced in [17], see Equation (3) | baseline | 4.433 | 3.866 | 7.294 | 6.285 |
| w/exogenous | 4.208 | 3.703 | 6.990 | 6.046 | |
| w/partial ID | 3.807 | 3.708 | 6.182 | 5.942 | |
| full | 3.725 | 3.627 | 6.154 | 5.862 | |
| full-diff | 3.691 | 3.703 | 5.887 | 5.918 | |
| Model | Percentiles | ||||
|---|---|---|---|---|---|
| 0 to 2.5 | 2.5 to 25 | 25 to 75 | 75 to 97.5 | 97.5 to 100 | |
| MAE | |||||
| naïve | 12.35 | 3.882 | 2.795 | 3.982 | 11.94 |
| full | 14.04 | 3.757 | 2.668 | 3.836 | 12.42 |
| ens(full) | 12.43 | 3.672 | 2.663 | 3.815 | 11.81 |
| RMSE | |||||
| naïve | 17.03 | 5.452 | 3.781 | 5.296 | 18.54 |
| full | 19.46 | 5.206 | 3.555 | 5.111 | 18.82 |
| ens(full) | 17.26 | 5.118 | 3.576 | 5.086 | 18.33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marcjasz, G.; Uniejewski, B.; Weron, R. Beating the Naïve—Combining LASSO with Naïve Intraday Electricity Price Forecasts. Energies 2020, 13, 1667. https://doi.org/10.3390/en13071667
Marcjasz G, Uniejewski B, Weron R. Beating the Naïve—Combining LASSO with Naïve Intraday Electricity Price Forecasts. Energies. 2020; 13(7):1667. https://doi.org/10.3390/en13071667
Chicago/Turabian StyleMarcjasz, Grzegorz, Bartosz Uniejewski, and Rafał Weron. 2020. "Beating the Naïve—Combining LASSO with Naïve Intraday Electricity Price Forecasts" Energies 13, no. 7: 1667. https://doi.org/10.3390/en13071667
APA StyleMarcjasz, G., Uniejewski, B., & Weron, R. (2020). Beating the Naïve—Combining LASSO with Naïve Intraday Electricity Price Forecasts. Energies, 13(7), 1667. https://doi.org/10.3390/en13071667






