Development of Operational Strategies of Energy Storage System Using Classification of Customer Load Profiles under Time-of-Use Tariffs in South Korea
Abstract
:1. Introduction
2. Clustering
2.1. TOU Indices
2.2. Evaluation Parameter
2.3. Clustering Methodology
3. Customer-Installed ESS
3.1. Supporting Policies
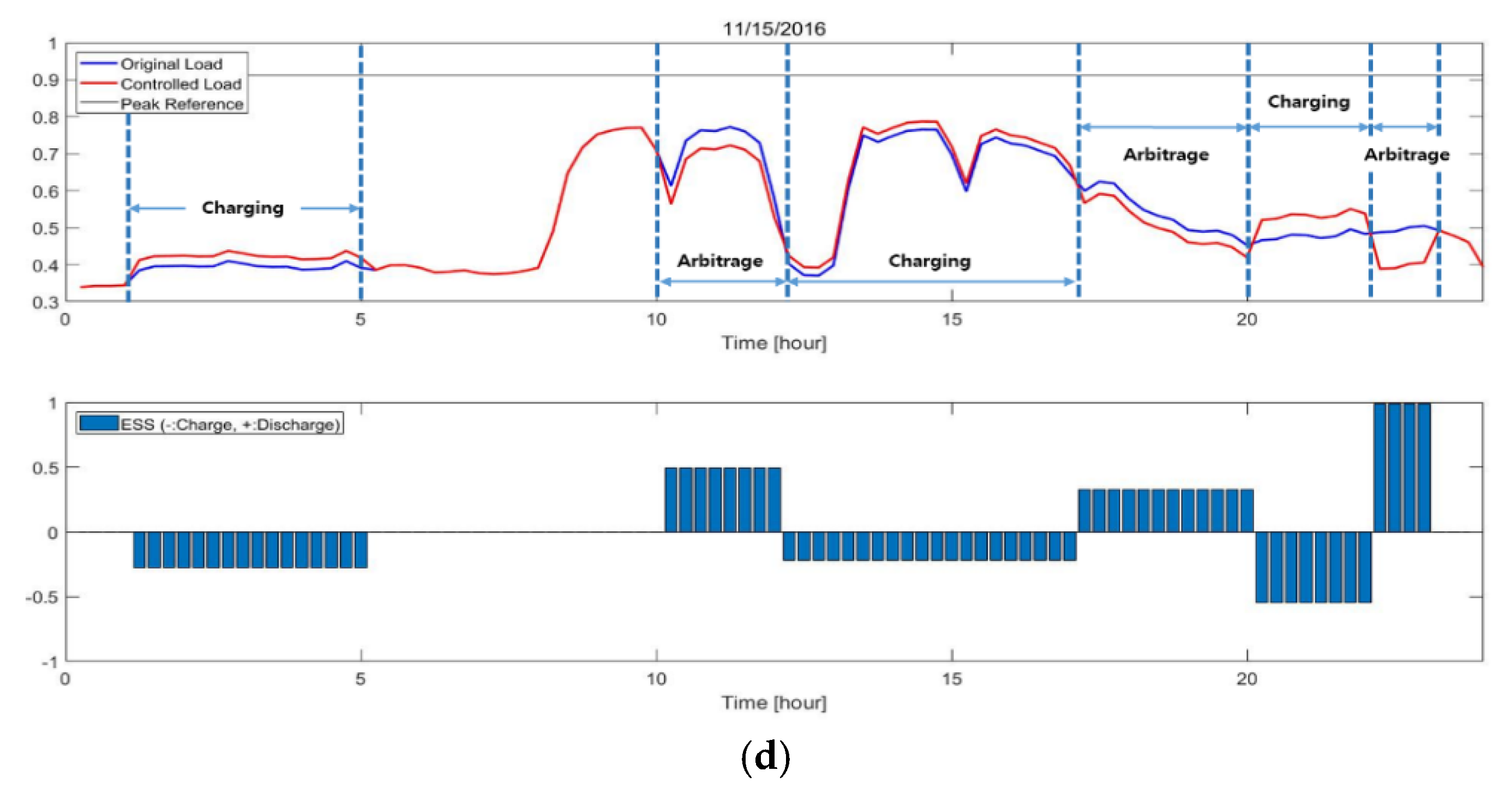
3.2. Operational Algorithm
4. Simulation
4.1. Load Profile
4.2. Clustering Result
4.2.1. K-means
4.2.2. SOM
4.3. Feasibility Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lloret, J.; Tomas, J.; Canovas, A.; Parra, L. An Integrated IoT Architecture for Smart Metering. IEEE Commun. Mag. 2016, 54, 50–57. [Google Scholar] [CrossRef]
- Hernandez, L.; Baladrón, C.; Aguiar, J.M.; Carro, B.; Sánchez-Esguevillas, A.; Lloret, J.; Chinarro, D.; Gomez-Sanz, J.J.; Cook, D. A multi-agent system architecture for smart grid management and forecasting of energy demand in virtual power plants. IEEE Commun. Mag. 2013, 51, 106–113. [Google Scholar] [CrossRef]
- Lee, Y.; Hwang, E.; Choi, J. A Unified Approach for Compression and Authentication of Smart Meter Reading in AMI. IEEE Access 2019, 7, 34383–34394. [Google Scholar] [CrossRef]
- Yang, H. [KEPCO] Implementation of next-generation power portal service ‘i-SMART’. Electr. Power 2011, 52, 39. [Google Scholar]
- Motlagh, O.; Berry, A.; O’Neil, L. Clustering of residential electricity customers using load time series. Appl. Energy 2019, 237, 11–24. [Google Scholar] [CrossRef]
- Chicco, G.; Napoli, R.; Piglione, F. Application of clustering algorithms and self organising maps to classify electricity customers. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; IEEE: Piscataway, NJ, USA, 1963; pp. 23–26. [Google Scholar]
- Lee, S.E.; Chung, C.T.; Lee, S.B. Electric consumption analysis using Korea Standard Industrial Classification Code. In Proceedings of the Korean Institute of Electrical Engineers Summer Conference, Yongpyong, Korea, 16–18 July 2014; pp. 471–472. [Google Scholar]
- Bidoki, S.M.; Kohan, N.M.; Gerami, S. Comparison of several clustering methods in the case of electrical load curves classification. In Proceedings of the 16th Electrical Power Distribution Conference, Bandar Abbas, Iran, 19–20 April 2011; pp. 1–7. [Google Scholar]
- Zhou, K.L.; Yang, S.L.; Shen, C. A review of electric load classification in smart grid environment. Renew. Sustain. Energy Rev. 2013, 24, 103–110. [Google Scholar] [CrossRef]
- AbuBaker, M. Data Mining Applications in Understanding Electricity Consumers’ Behavior: A Case Study of Tulkarm District, Palestine. Energies 2019, 12, 4287. [Google Scholar] [CrossRef] [Green Version]
- Manz, D.; Piwko, R.; Miller, N. Look before you leap: The role of energy storage in the grid. IEEE Power Energy Mag. 2012, 10, 75–84. [Google Scholar]
- United States Department of Energy. DOE Global Energy Storage Database. Available online: https://www.energystorageexchange.org/projects/data_visualization (accessed on 23 September 2017).
- Sobieski, D.W.; Bhavaraju, M.P. An economic assessment of battery storage in electric utility systems. IEEE Trans. Power Appar. Syst. 1985, 104, 3453–3459. [Google Scholar]
- Reihani, E.; Motalleb, M.; Ghorbani, R.; Saoud, L.S. Load peak shaving and power smoothing of a distribution grid with high renewable energy penetration. Renew. Energy 2016, 86, 1372–1379. [Google Scholar] [CrossRef] [Green Version]
- Pimm, A.J.; Cockerill, T.T.; Taylor, P.G. The potential for peak shaving on low voltage distribution networks using electricity storage. J. Energy Storage 2018, 16, 231–242. [Google Scholar] [CrossRef]
- Karmiris, G.; Tomas, T. Peak Shaving Control Method for Energy Storage; Corporate Research Center: Vasterås, Sweden, 2013. [Google Scholar]
- Dejvises, J. Energy storage system sizing for peak shaving in Thailand. ECTI Trans. Electr. Eng. Electron. Commun. 2016, 14, 49–55. [Google Scholar]
- Arghandeh, R.; Woyak, J.; Onen, A.; Jung, J.; Broadwater, R.P. Economic optimal operation of Community Energy Storage systems in competitive energy markets. Appl. Energy 2014, 135, 71–80. [Google Scholar] [CrossRef] [Green Version]
- Kang, B.O.; Lee, M.; Kim, Y.; Jung, J. Economic analysis of a customer-installed energy storage system for both self-saving operation and demand response program participation in South Korea. Renew. Sustain. Energy Rev. 2018, 94, 69–83. [Google Scholar] [CrossRef]
- Cha, H.J.; Lee, S.E.; Won, D. Implementation of Optimal Scheduling Algorithm for Multi-Functional Battery Energy Storage System. Energies 2019, 12, 1339. [Google Scholar] [CrossRef] [Green Version]
- Korea Electric Power Corp. Electrical Supply Terms and Conditions. Available online: http://cyber.kepco.co.kr (accessed on 19 October 2019).
- Lee, K.M.; Lee, K.M.; Lee, C.H. Statistical cluster validity indexes to consider cohesion and separation. In Proceedings of the 2012 International Conference on Fuzzy Theory and Its Applications (iFUZZY2012), Taichung, Taiwan, 16–18 November 2012; pp. 228–232. [Google Scholar]
- Lu, S.; Lin, G.; Liu, H.; Ye, C.; Que, H.; Ding, Y. A Weekly Load Data Mining Approach Based on Hidden Markov Model. IEEE Access 2019, 7, 34609–34619. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Xiong, H.; Gao, X.; Wu, J. Understanding of Internal Clustering Validation Measures. In Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, NSW, Australia, 13–17 December 2010; pp. 911–916. [Google Scholar]
- Yeung, K.Y.; Ruzzo, W.L. Details of the Adjusted Rand index and Clustering Algorithms Supplement to the paper “An empirical study on Principal Component Analysis for clustering gene expression data” (to appear in Bioinformatics). Bioinformatics 2001, 17, 763–774. [Google Scholar] [CrossRef]
- Doreian, P.; Batagelj, V.; Ferligoj, A. Advances in Network Clustering and Blockmodeling, 1st ed.; Wiley: Hoboken, NJ, USA, 1807; p. 199. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef]
- Chaudhary, V.; Bhatia, R.S.; Ahlawat, A.K. A novel Self-Organizing Map (SOM) learning algorithm with nearest and farthest neurons. Alex. Eng. J. 2014, 53, 827–831. [Google Scholar] [CrossRef] [Green Version]
- Lee, S. Analysis of Energy Storage System (ESS) Demand Management Effect and Research on Market Formation Plan; Korea Energy Economics Institute: Ulsan, Korea, 2014. [Google Scholar]
- Kang, B.O.; Hwang, B.G.; Kwon, K.; Jung, J. Operational Strategy of Energy Storage System (ESS) to Participate in Demand Response (DR) Market for Industrial Customer. New Renew. Energy 2017, 13, 4–12. [Google Scholar] [CrossRef]
- Majima, M.; Ujiie, S.; Yagasaki, E.; Koyama, K.; Inazawa, S. Development of long-life lithium ion battery for power storage. J. Power Sources 2001, 101, 53–59. [Google Scholar] [CrossRef]
- Jeon, S.; Kim, Y.K.; Jung, J.; Kim, S. Feasibility Analysis of Tariff System for the Promotion of Energy Storage Systems (ESSs). New Renew. Energy 2019, 15, 69–76. [Google Scholar] [CrossRef]
- Park, J.; Heo, J.; Shin, S.; Kim, H. Economic Evaluation of ESS in Urban Railway Substation for Peak Load Shaving Based on Net Present Value. J. Electr. Eng. Technol. 2017, 12, 981–987. [Google Scholar] [CrossRef] [Green Version]





| Classification | Spring, Summer and Fall (Mar.1~Oct.31) | Winter (Nov.1~Feb.28) |
|---|---|---|
| Off-peak load | 23:00~09:00 | 23:00~09:00 |
| Mid-peak load | 09:00~10:00 12:00~13:00 17:00~23:00 | 09:00~10:00 12:00~17:00 20:00~22:00 |
| On-peak load | 10:00~12:00 13:00~17:00 | 10:00~12:00 17:00~20:00 22:00~23:00 |
| Classification | ||||||
|---|---|---|---|---|---|---|
| Time Period | Summer | Spring/Fall | Winter | |||
| Industrial Service B, High-Voltage B | Option Ⅰ | 6630 | Off-peak load | 60.0 | 60.0 | 67.0 |
| Mid-peak load | 112.3 | 82.3 | 112.3 | |||
| On-peak load | 193.5 | 112.6 | 168.5 | |||
| Option Ⅱ | 7380 | Off-peak load | 56.2 | 56.2 | 63.2 | |
| Mid-peak load | 108.5 | 78.5 | 108.5 | |||
| On-peak load | 189.7 | 108.8 | 164.7 | |||
| Option Ⅲ | 8190 | Off-peak load | 54.5 | 54.5 | 61.6 | |
| Mid-peak load | 106.8 | 76.9 | 106.8 | |||
| On-peak load | 188.1 | 107.2 | 163.0 | |||
| General Service B, High-Voltage A | Option Ⅰ | 7220 | Off-peak load | 61.6 | 61.6 | 68.6 |
| Mid-peak load | 114.5 | 84.1 | 114.7 | |||
| On-peak load | 196.6 | 114.8 | 172.2 | |||
| Option Ⅱ | 8320 | Off-peak load | 56.1 | 56.1 | 63.1 | |
| Mid-peak load | 109.0 | 78.6 | 109.2 | |||
| On-peak load | 191.1 | 109.3 | 166.7 | |||
| Option Ⅲ | 9810 | Off-peak load | 55.2 | 55.2 | 62.5 | |
| Mid-peak load | 108.4 | 77.3 | 108.6 | |||
| On-peak load | 178.7 | 101.0 | 155.5 | |||
| Sums | |||||||
|---|---|---|---|---|---|---|---|
| Sums | |||||||
| Classification | Index | Cluster Number | |||
|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | ||
| Weekdays (Non-winter) | DBI | 0.739 | 0.704 | 0.814 | 0.861 |
| SI | 0.725 | 0.676 | 0.642 | 0.604 | |
| SI-DBI | −0.014 | −0.027 | −0.172 | −0.257 | |
| Weekdays (Winter) | DBI | 0.530 | 0.672 | 0.795 | 0.850 |
| SI | 0.792 | 0.761 | 0.658 | 0.595 | |
| SI-DBI | 0.262 | 0.089 | −0.137 | −0.255 | |
| Saturdays | DBI | 0.561 | 0.659 | 0.654 | 0.700 |
| SI | 0.800 | 0.741 | 0.717 | 0.675 | |
| SI-DBI | 0.238 | 0.082 | 0.063 | −0.026 | |
| Method | Weekdays (Non-winter) | Weekdays (Winter) | Saturdays | Total |
|---|---|---|---|---|
| K-means | 0.890 | 0.797 | 0.942 | 0.919 |
| Classification | Index | Cluster Number | ||||
|---|---|---|---|---|---|---|
| 2 × 1 | 3 × 1 | 4 × 1 | 2 × 2 | 5 × 1 | ||
| Weekdays (Non-winter) | DBI | 0.739 | 0.809 | 0.777 | 0.777 | 0.821 |
| SI | 0.725 | 0.620 | 0.657 | 0.657 | 0.622 | |
| SI-DBI | −0.014 | −0.189 | −0.119 | −0.119 | −0.199 | |
| Weekdays (Winter) | DBI | 0.530 | 0.671 | 0.724 | 0.724 | 0.847 |
| SI | 0.792 | 0.761 | 0.716 | 0.716 | 0.585 | |
| SI-DBI | 0.262 | 0.089 | −0.008 | −0.008 | −0.262 | |
| Saturdays | DBI | 0.561 | 0.626 | 0.629 | 0.629 | 0.673 |
| SI | 0.800 | 0.777 | 0.760 | 0.760 | 0.681 | |
| SI-DBI | 0.238 | 0.151 | 0.131 | 0.131 | 0.008 | |
| Method | Weekdays (Non-winter) | Weekdays (Winter) | Saturdays | Total |
|---|---|---|---|---|
| K-means | 0.891 | 0.798 | 0.944 | 0.922 |
| Customer | PPeak [KRW/kWh] | BATcp [KRW/kWh] | CPBps [KRW/kWh] | CPBar [KRW/kWh] | NPV [KRW] | |||
|---|---|---|---|---|---|---|---|---|
| Cluster 1 | Customer A | 11,328 | 1133 | 1-cycle | 56,595 | 1-cycle | 126,759 | 292.77M |
| multi-cycle | 90,081 | 2-cycle | 210,597 | 840.26M | ||||
| 3-cycle | 241,111 | 826.68M | ||||||
| Customer B | 20,803 | 2080 | 1-cycle | 57,596 | 1-cycle | 125,998 | 295.36M | |
| multi-cycle | 86,761 | 2-cycle | 209,024 | 1086.78M | ||||
| 3-cycle | 231,770 | 1022.84M | ||||||
| Cluster 2 | Customer C | 2120 | 212 | 1-cycle | 79,611 | 1-cycle | 139,975 | 88.22M |
| multi-cycle | 86,894 | 2-cycle | 263,263 | 202.97M | ||||
| 3-cycle | 309,743 | 206.63M | ||||||
| Customer D | 4314 | 431 | 1-cycle | 63,491 | 1-cycle | 139,375 | 92.86M | |
| multi-cycle | 63,703 | 2-cycle | 251,561 | 282.88M | ||||
| 3-cycle | 298,041 | 302.58M | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, H.C.; Jung, J.; Kang, B.O. Development of Operational Strategies of Energy Storage System Using Classification of Customer Load Profiles under Time-of-Use Tariffs in South Korea. Energies 2020, 13, 1723. https://doi.org/10.3390/en13071723
Jeong HC, Jung J, Kang BO. Development of Operational Strategies of Energy Storage System Using Classification of Customer Load Profiles under Time-of-Use Tariffs in South Korea. Energies. 2020; 13(7):1723. https://doi.org/10.3390/en13071723
Chicago/Turabian StyleJeong, Hyun Cheol, Jaesung Jung, and Byung O Kang. 2020. "Development of Operational Strategies of Energy Storage System Using Classification of Customer Load Profiles under Time-of-Use Tariffs in South Korea" Energies 13, no. 7: 1723. https://doi.org/10.3390/en13071723
APA StyleJeong, H. C., Jung, J., & Kang, B. O. (2020). Development of Operational Strategies of Energy Storage System Using Classification of Customer Load Profiles under Time-of-Use Tariffs in South Korea. Energies, 13(7), 1723. https://doi.org/10.3390/en13071723





