Towards Smart Energy Grids: A Box-Constrained Nonlinear Underdetermined Model for Power System Observability Using Recursive Quadratic Programming

Abstract

This paper introduces an underdetermined nonlinear programming model where the equality constraints are fewer than the design variables defined on a compact set for the solution of the optimal Phasor Measurement Unit (PMU) placement. The minimization model is efficiently solved by a recursive quadratic programming (RQP) method. The focus of this work is on applying an RQP to attempt to find guaranteed global minima. The proposed minimization model is conducted on IEEE systems. For all simulation runs, the RQP converges superlinearly towards optimality in a finite number of iterations without to be rejected the full step-length. The simulation results indicate that the RQP finds out the minimal number and the optimal locations of PMUs to make the power system wholly observable.

1. Introduction

Phasor measurement unit (PMU) is a metering device that can provide real-time voltage and current synchrophasor measurements with high accuracy. PMUs play an imperative role in state estimation, monitoring, protection and wide area control in power systems [1]. Due to cost reasons, a full deployment of PMUs in the network is not realistic. One of the most important addressed issues is the strategic choice of the minimum number and locations of PMUs, ensuring complete network observability. Therefore, the optimal PMU placement (OPP) problem should be solved in order to make the power system completely observable by optimally placed PMUs at network buses [2,3].

Deterministic and stochastic algorithms are implemented for the solution of the OPP problem [2,3]. Several deterministic algorithms have been published in the literature for the solution of the OPP problem. The dominant optimization method regarding the OPP problem is the Binary Integer Linear Programming (BILP) technique. The BILP model requires the minimization of the objective function with inequality constraints and binary-valued decision variables [4,5,6,7,8,9,10].

A Weighed Least Square (WLS) algorithm is developed in [11] for the OPP problem. Authors of [12] proposed a nonlinear programming model for the solution of the OPP problem. In [13,14,15] the OPP problem is unraveled using the mixed-integer semi-definite programming approach subjected to linear matrix inequality. This technique is based on numerical observability, whereas most of the other techniques are based on topological observability, which may or may not ensure numerical observability to be executed successfully for state estimation. In [16,17], mixed-integer linear programming and nonlinear programming techniques are compared to check their suitability for networks of different sizes.

Stochastic algorithms have also been used for the OPP problem. A recursive tabu search is suggested in [18], which has been claimed superior to multiple Tabu search and higher observability. Binary particle swarm optimization (BPSO) algorithm is developed for the solution of the OPP problem in [19]. In [20], the authors proposed a BPSO algorithm to minimize the number of substations in which installations must be performed for making all voltage levels observable while being subject to various practical constraints. Authors of [21] proposed the binary gravitational search algorithm to solve the OPP problem. Authors in [22], presented a modified binary Cuckoo optimization algorithm for the solution of the OPP problem with maximum redundancy. Genetic algorithms (GA) have been applied to determine the optimal allocation of PMUs in [23,24].

Accurate knowledge of transmission system parameters, such as series impedance, optimizes distance relay settings and impedance-based fault location. A new method is developed to measure transmission line impedances and admittances from synchronized phasor measurements in [25].

A new on-line method for estimating transmission line constants of a power system is proposed in [26]. In [27], a new State Estimation (SE) framework is proposed for processing Remote Terminal Unit (RTU) and PMU measurements separately in order to leave the traditional weighted least square (WLS)-based SE software unchanged. Phasor measurement unit based fault location techniques are proposed in [28,29,30]. Other methods, such as an optimized extreme learning machine-based approach, use synchrophasors to ensure real-time power transient stability prediction [31].

Up to now, a BILP model is written to its standard form in which the number of the constraints is equal to the number of optimization variables for the OPP problem [4,5,6,7,8,9,10]. This work introduces an underdetermined system of nonlinear equations, where the equations are fewer than the design variables for the solution of the OPP problem. When a significant fraction of the optimization problem constraints are eliminated, the feasibility diagnosis is accelerated and speeds up the solution algorithm in finding the optimality [32,33,34,35,36]. Thus, a reduction in problem size typically translates to a reduction in total running time in comparison with past studies such as [11,12,17].

The solution to such underdetermined systems is based on the Recursive Quadratic Programming (RQP) method [35]. The contribution of this work is fourfold as follows:

• The proposed nonlinear model is solved using a Recursive Quadratic Programming (RQP) method with super-linear convergence properties avoiding the Maratos effect.
• The innovation of the local search procedure is that the RQP converges super-linearly towards optimality, satisfying the binary restriction.
• The RQP presents a fast convergence rate towards optimality.
• The RQP method delivers multiple optimal solutions in a reasonable time with those consumed by a BILP model being solved by the branch-and-bound method (BBM).

The remainder of this paper is organized as follows. Section 2 presents the basics of the Recursive Quadratic Programming (RQP) method. Section 3 formulates the OPP problem as an RQP optimization model. Section 4 gives an overview of computational results, whereas a performance evaluation of the proposed RQP algorithm for the solution of the OPP problem is carried out in Section 5. Finally, Section 6 concludes the paper.

2. A Recursive Quadratic Programming Βackground

The Recursive Quadratic Programming Algorithm solves nonlinear optimization problem of the form [35]:

$$\begin{array}{l}\underset{x\in {\mathsf{\Re }}^n}{\min }J(x)\\ s.t\{\begin{array}{l}{G}_i(x)=0,i=1,\dots ,M_e\\ G_j(x)\le 0,j=M_e+1,\dots ,M\end{array}\end{array}$$

(1)

The RQP methods belong to the most frequently used algorithms for the solution of practical optimization problems due to their robustness and their good convergence properties. RQP methods can be proven to achieve global convergence and locally superlinear convergence rate; even locally quadratic convergence can be attained if the Hessian of the Lagrangian ${\nabla }_{xx}^{2}L(x,\lambda )$ is available. Note that, the Lagrangian is given by:

$$L(x,\lambda )=J(x)+{\lambda }^{{\rm T}}G(x)$$

(2)

where $\lambda \in {\mathsf{\Re }}^m$ is the vector of Lagrange multipliers.

The fundamental principle of RQP methods is to find Karush–Kuhn–Tucker (KKT) points, i.e., points that satisfy the necessary optimality conditions [35]. RQP methods mainly apply Newton’s method to find zeros of

$${\nabla }_{x}L(x,\lambda )={\nabla }_{x}J(x)+{(\lambda )}^{{\rm T}}{\nabla }_{x}G(x)$$

(3)

that satisfy the constraints $G$, using a local linearization.

In this basic form, quadratic subproblems of the form

$$\begin{array}{l}\underset{d\in {\mathsf{\Re }}^n}{\min }\frac{1}{2}{\nabla }_{xx}^{2}L(x,\lambda )d+{\nabla }_{x}J(x)d\\ subject\mathrm{to}\{\begin{array}{l}{G}_i(x)+{\nabla }_x{G}_i(x)d=0,i=1\dots M_e\\ G_j(x)+{\nabla }_x{G}_j(x)d\le 0,i=M_e+1\dots M\end{array}\end{array}$$

(4)

are solved to obtain a search direction $d$.

Often, the Hessian of the Lagrangian ${\nabla }_{xx}^{2}L(x,\lambda )$ is replaced by an update of Broydon–Fletcher–Goldfarbo–Shanno (BFGS) type, which has the additional benefit that only strictly convex quadratic programs have to be solved [35]. The computation of derivatives is a crucial element in nonlinear optimization. Mainly the first derivatives, i.e., the gradient of the objective function and the Jacobian of the constraints, is necessary to find a descent direction. The RQP is an iterative process that defines a series of points $x^{\left[k\right]}$ (called iterates) that (ideally) converge to an optimal point. It consists very roughly of the following steps [35]:

• Check termination criteria: For testing an iterate $x^{\left[k\right]}$, the first-order optimality conditions KKT have to be evaluated.
• Solve approximate the QP sub-problem.
• Use the solution from 2, to define a new iterate employing a merit function to find a suitable step-length.

Merit functions are needed to obtain a scalar measure of goodness of the trial point

$$x^{\left[k+1\right]}=x^{\left[k\right]}+a^{\left[k\right]}{d}^{\left[k\right]}$$

(5)

which is an update of the current iterate $x^{\left[k\right]}$ by the result $d^{\left[k\right]}$ of Esq. QP and a scalar step-length $a^{\left[k\right]}$ that is introduced to achieve global convergence (since RQP is derived from Newton’s method that also depends on line search for globalization). The merit function is given by [35]:

$$L\left(x;n\right)\triangleq J(\overrightarrow{x})+{\displaystyle \sum _{i=1}^{Me}{n}_i\times \left|G_i(\overrightarrow{x})\right|}+{\displaystyle \sum _{i=Me+1}^M{n}_i\max \left\{0,G_i(x)\right\}}$$

(6)

After determining the search direction $d^{\left[k\right]}$ from the QP, we have to find a suitable step-length $a^{\left[k\right]}$. The line search procedure can be used to determine a step-length parameter $a^{\left[k\right]}$ based on the Armijo rule. The step-length is chosen to yield a sufficient decrease of a suitable merit function, which measures progress towards optimality [35]. Figure 1 shows RQP’s flowchart.

A difficulty in the context of RQP methods is that the line search procedure may prevent the full step from being taken [37]. The step-length $a\in \left(0,1\right]$ is chosen to yield a sufficient decrease of a suitable penalty function, which measures progress towards optimality [37]. The convergence rate depends upon the reduction on the penalty function at each iteration, which relies on the choices of the descent directions and the step-length $a$ [37]. The penalty function may not allow a unity step-length near the solution and thus may prevent q-superlinear convergence [37].

This phenomenon is called as the Maratos effect [37]. By using the RQP method through the fmincon of MATLAB optimization toolbox [38], the unity step-length is being taken decreasing the nonsmooth exact penalty function whenever the current iterate is sufficiently close to a local minimum point. Thus, the Maratos effect can be obviated, ensuring superlinear convergence to the optimum point. The RQP is converged when the difference between the current objective value and the previous objective value is less than the optimality tolerance [35].

Additionally, the constraints are satisfied within the feasibility tolerance, whereas step-tolerance specifies the termination tolerance for the design variable [36]. Therefore, the termination is succeeded based on the tolerance criteria in terms of objective evaluation, maximum constraint violation and first-order optimality [36].

3. Optimum Design Model Formulation

Let the continuous decision variables $x_i$ denote the presence ($x_i=1$) or absence ($x_i=0$) of PMU at bus $i$. The OPP problem is formulated as a nonlinear minimization model [12]:

$$\underset{\overrightarrow{x}\in R^n}{\min }J\left(\overrightarrow{x}\right)={\overrightarrow{x}}^T.W.\overrightarrow{x}={\displaystyle \sum _{i=1}^n{w}_i.x_i^2},W\in R^{n\times n}=I_n$$

(7)

$$\mathrm{s}.\mathrm{t}.\{\begin{array}{l}f(x)=\widehat{0}\\ \widehat{0}\le x\le \widehat{1}\end{array}$$

(8)

where, $x={(x_1,\cdots ,x_n)}^T$ is a decision variable vector, whose entry $x_i$ is set to either 1 or 0 to denote the presence or absence of a PMU at bus $i$, $W=diag\left(w_1,\cdots ,w_n\right)$ is the PMU cost or weight matrix, $n$ is the number of buses, $\widehat{0}$, $\widehat{1}$ is a vector whose entries are all zeros and ones, respectively, and $f(x)$ is a vector function whose $ith$ entry defines an observability constraint for the $ith$ bus [11,12]:

$$f_i(x)=(1-x_i){\displaystyle \prod _{j\in {\mathcal{N}}_i}(1-x_j)}=0,\forall i\in \mathcal{N}$$

(9)

where $\mathcal{N}$ is the set of all buses and ${\mathcal{N}}_i$ is the set of buses adjacent to bus $i$. Each Equality Constraint (3) implies that at least one PMU should be installed at any one of the buses $i$ and $j\in {\mathcal{N}}_i$ in order to make bus $i$ observable. The optimal values of decision variables $x_i$ will be 1 or 0 as it has been proved in [12]. The above minimization model is reformulated and extended to employ with the underdetermined case.

Since we want to solve problems with a large number of constraints, many of them maybe are redundant [33,34]. The constraint redundancy gives rise to Jacobian rank deficiency, i.e., a singularity in iterative estimates of the constraint-set [34]. The preprocessing phase aims to simplify a given optimization problem by detecting and removing redundant constraints [33,34]. The preprocessing phase is applied to the primary constraint function to remove redundancies from the given constraints [33,34]. A redundant constraint is not required to define the boundaries of the feasible set, so the solution space is not affected. When the redundant constraints are dropped, the feasible region is expanded and more feasible solutions are located, whereas more constraints shrink the feasible region [35]. Since the enlarged feasible region involves more feasible points than the feasible region of the original model, more local minima are detected.

If a pre-solve procedure is applied after the model has been built, but before solving it, then a reduction in size can be achieved [33]. During the pre-solve process, an entirely new optimization problem is constructed. After the algorithm model has been optimized, the optimal solution is valid for the original problem [34].

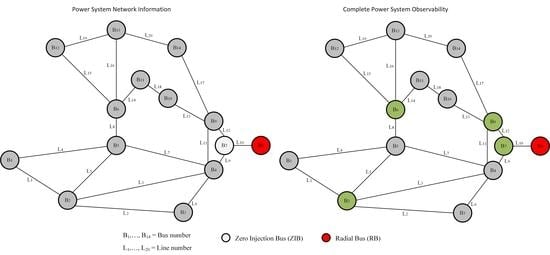
Illustrative Example of Deletion Presolve Using the IEEE-14 Bus System

The size-reducing transformation, which leads to an underdetermined nonlinear model, is shown using the IEEE-14 bus system (Figure 2). The observability constraint function $\mathrm{f}:{\mathrm{R}}^{\mathrm{n}}\to {\mathrm{R}}^{\mathrm{n}}$ in case of the IEEE 14-bus system is as follows [12]:

$$\overrightarrow{f(\overrightarrow{x})}=\{\begin{array}{l}{f}_1=(1-x_1)(1-x_2)(1-x_5)=0\hfill \\ f_2=(1-x_2)(1-x_1)(1-x_3)(1-x_4)(1-x_5)=0\hfill \\ f_3=(1-x_3)(1-x_2)(1-x_4)=0\hfill \\ f_4=(1-x_4)(1-x_2)(1-x_3)(1-x_5)(1-x_7)(1-x_9)=0\hfill \\ f_5=(1-x_5)(1-x_1)(1-x_2)(1-x_4)(1-x_6)=0\hfill \\ f_6=(1-x_6)(1-x_5)(1-x_{11})(1-x_{12})(1-x_{13})=0\hfill \\ f_7=(1-x_7)(1-x_4)(1-x_8)(1-x_9)=0\hfill \\ f_8=(1-x_8)(1-x_7)=0\hfill \\ f_9=(1-x_9)(1-x_4)(1-x_7)(1-x_{10})(1-x_{14})=0\hfill \\ f_{10}=(1-x_{10})(1-x_9)(1-x_{11})=0\hfill \\ f_{11}=(1-x_{11})(1-x_6)(1-x_{10})=0\hfill \\ f_{12}=(1-x_{12})(1-x_6)(1-x_{13})=0\hfill \\ f_{13}=(1-x_{13})(1-x_6)(1-x_{12})(1-x_{14})=0\hfill \\ f_{14}=(1-x_{14})(1-x_9)(1-x_{13})=0\hfill \end{array}$$

(10)

As can be observed, some equality constraints are dependent on others and they are redundant constraints for the system of concern. A redundant constraint can be chosen as the one to be eliminated, for it can be reconstructed from those remaining [33]. Such a non-binding constraint could just as well be left out of the model, as this would not affect the optimum point [33].

For example, $f_2$ is obtained by multiplying $f_1=0$ by additional terms yielding the Esq. $\left(1-x_3\right)\left(1-x_4\right)f_1=0$. The $f_2$ is unnecessary since the constraint is always satisfied i.e., $\left\{f_i=0\right\}$ and it is removed. When a constraint is satisfied $\left\{f_i=0\right\}$, it can be removed from the system of interest. Let us consider the equality constraints $\left\{f_{12},f_{13}\right\}$ so that:

$$\{\begin{array}{l}{f}_{12}=(1-x_{12})(1-x_6)(1-x_{13})=0\\ f_{13}=(1-x_{13})(1-x_6)(1-x_{12})(1-x_{14})=0\end{array}\to f_{12}(1-x_{14})=0\to f_{13}\mathrm{is}\mathrm{always}\mathrm{satisfied}$$

The product $f_{13}$ is resulting by multiplying the equation $f_{12}$ with an additional term and thus, it is always satisfied. Then, the constraint function involves only mutually independent constraints expanding the feasible region without changing the solution structure. The constraint function is as:

$$\overrightarrow{h(\overrightarrow{x})}={\left[h_1(\overrightarrow{x}),h_2(\overrightarrow{x}),\dots ,h_m(\overrightarrow{x})\right]}^T=0$$

(11)

where the constraint function $h:R^n\to R^m$$\left(\mathrm{n}>\mathrm{m}\right)$ is considered to be an underdetermined system of equations defined on a Box Constraint set, that is, $\overrightarrow{x}\in \left[0,1\right]$ [35].

$$\overrightarrow{h(\overrightarrow{x})}=\{\begin{array}{l}{h}_1=(1-x_1)(1-x_2)(1-x_5)=0\\ h_2=(1-x_2)(1-x_3)(1-x_4)=0\\ h_3=(1-x_7)(1-x_8)=0\\ h_4=(1-x_4)(1-x_7)(1-x_9)(1-x_{10})(1-x_{14})=0\\ h_5=(1-x_9)(1-x_{10})(1-x_{11})=0\\ h_6=(1-x_6)(1-x_{10})(1-x_{11})=0\\ h_7=(1-x_6)(1-x_{12})(1-x_{13})=0\\ h_8=(1-x_9)(1-x_{13})(1-x_{14})=0\end{array}$$

(12)

A solution that verifies the nonlinear system of equations and optimizes the quadratic objective function has been determined.

$$J\left(\overrightarrow{x}\right)={\displaystyle \sum _{i=1}^n{w}_i.x_i^2}(w_i=1)$$

(13)

The optimal solutions derived by the RQP are {2, 6, 8, 9}, {2, 6, 7, 9}, {2, 7, 11, 13}, {2, 7, 10, 13}, {2, 8, 10, 13} satisfying the equality constraints. Each optimum point is a feasible solution satisfying the equality constraints. The constraint function for different size power systems is as follows: $\mathsf{\Omega }=\{0\le x_i\le 1;i=1\dots n|h_l\left(\overrightarrow{x}\right)=0;l=1\dots m\},\left\{n=14,30,57,118,300\right\},\left\{m=8,21,52,91,238\right\}$.

4. Simulation Results and Discussion

In this section, we solve the proposed nonlinear model by using the RQP method. To prove the effectiveness of the RQP to achieve optimality, the obtained objective value is compared to the one found by solving the Integer Linear Programming (ILP) model with binary-valued variables for each benchmark test system. The pure ILP model is solved by using the BBM. In this method, a relaxed continuous linear programming (LP) problem is formulated by ignoring the integer constraints. The relaxed problem is comprised of continuous variables. If the solution to the above relaxed continuous problem contains only involves integers, it is the optimal solution. If the solution has non-integer variables, one non-integer variable is selected and two sub-problems (two branches) are generated [39,40]. For one of them, a ceil constraint is added to the selected non-integer variable and, for the other branch, a floor constraint is added to it. If a branch has no feasible solutions, this branch is terminated [39,40]. If the solution only has integers, it becomes a candidate for the final optimal solution. If the solution has non-integer values, the process of the branching is again solved with these additional constraints. Once the branching process is completed for all the variables, all the integer solutions obtained by the difference branches are compared. The best solution is considered the final optimal solution as shown in the flowchart of Figure 3.

Several MILP routines implement the static-BBM, namely a BBM, including Cut Generation and Heuristics approaches via MATLAB intlinprog optimizer [38], a spatial BBM implemented by solving constraint integer programs (SCIP) [41], an LP-BBM using a primal-and-dual simplex implemented by MOSEK [42] and Gurobi optimizer [43]. Starting from the initial default point, MILP solvers can get only one optimal solution. This is because MILP employs the BB algorithm, and the solution is only updated when a better one is found. This means that solutions with the same results (same objective function value) are overlooked. Without considering other possible optimal solutions, the existing MILP solver stops searching and delivers the result when one optimal solution is found [39,40].

The optimal solutions derived by static-BBM are listed in

Table A1. Optimal Phasor Measurement Unit (PMU) locations for IEEE 14-, 30-, 57-, 118- bus systems.

IEEE System	ILP Routines for Solving the Pure Constraint Integer Linear Problem
	Gurobi	MOSEK	Intlinprog	SCIP
	Optimal PMU Locations
14 bus	2, 7, 10, 13	2, 6, 7, 9	2, 8, 10, 13	2, 7, 11, 13
30 bus	1, 5, 6, 9, 10, 12, 15, 19, 25, 27	1, 5, 8, 9, 10, 12, 18, 23, 25, 30	1, 5, 8, 10, 11, 12, 19, 23, 26, 29	2, 4, 6, 9, 10, 12, 15, 19, 25, 30
57 bus	1, 6, 9, 15, 19, 20, 24, 25, 28, 32, 36, 38, 39, 41, 47, 50, 53	1, 2, 6, 13, 19, 22, 25, 27, 32, 36, 41, 43, 47, 51, 52, 55, 57	1, 4, 9, 20, 23, 27, 29, 30, 32, 36, 38, 41, 45, 46, 50, 54, 57	2, 6, 12, 14, 19, 22, 25, 27, 32, 36, 39, 41, 44, 47, 50, 52, 55
118 bus	1, 5, 9, 12, 15, 17, 21, 23, 28, 30, 36, 40, 44, 46, 50, 51, 54, 62, 63, 68, 71, 75, 77, 80, 85, 86, 91, 94, 102, 105, 110, 114	1, 6, 9, 11, 12, 17, 21, 25, 29, 34, 37, 41, 45, 49, 53, 56, 62, 63, 68, 71, 72, 75, 77, 80, 85, 86, 90, 94, 102, 105, 110, 114	2, 5, 10, 12, 15, 17, 21, 25, 29, 34, 37, 41, 45, 49, 53, 56, 62, 64, 72, 73, 75, 77, 80, 85, 87, 91, 94, 101, 105, 110, 114, 116	3, 5, 9, 11, 12, 17, 21, 25, 28, 34, 37, 40, 45, 49, 52, 56, 62, 63, 68, 70, 71, 75, 77, 80, 85, 86, 90, 94, 101, 105, 110, 114

and

Table A2. Optimal PMU locations for IEEE 300- bus systems.

Optimal PMU Locations of PMUs using SCIP
1, 2, 3, 11, 12, 15, 17, 22, 23, 25, 26, 27, 33, 37, 38, 43, 48, 49, 53, 54, 55, 58, 59, 60, 62, 64, 65, 68, 71, 73, 79, 83, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 124, 132, 133, 138, 139, 143, 145, 152, 157, 160, 163, 173, 177, 183, 187, 189, 190, 193, 196, 200, 204, 208, 210, 211, 213, 216, 217, 219, 222, 225, 228, 267, 268, 269, 270, 272, 273, 274, 276, 294
Optimal Locations of PMUs Through Intlinprog of MATLAB Optimization Toolbox
1, 2, 3, 11, 15, 21, 23, 25, 27, 30, 33, 37, 38, 41, 43, 48, 49, 53, 54, 64, 68, 69, 71, 79, 83, 86, 88, 93, 96, 98, 99, 101, 109, 111, 112, 113, 116, 119, 128, 132, 135, 139, 141, 152, 157, 160, 164, 170, 183, 187, 188, 189, 190, 193, 196, 202, 209, 210, 212, 215, 216, 217, 222, 224, 228, 230, 233, 236, 237, 238, 240, 242, 251, 252, 253, 262, 264, 265, 268, 269, 270, 272, 275, 276, 277, 299, 300
Optimal Locations of PMUs using Gurobi
1, 2, 3, 11, 12, 15, 17, 20, 22, 23, 25, 27, 29, 33, 37, 38, 43, 48, 49, 53, 54, 55, 58, 59, 60, 62, 64, 65, 68, 71, 79, 83, 85, 86, 88, 89, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 124, 132, 133, 138, 139, 143, 145, 152, 157, 163, 167, 168, 173, 183, 184, 189, 190, 193, 196, 200, 204, 208, 210, 211, 213, 216, 217, 219, 224, 225, 228, 267, 268, 269, 270, 272, 273, 274, 276, 294
Optimal Locations of PMUs using MOSEK
1, 2, 3, 11, 12, 13, 15, 17, 22, 23, 25, 27, 30, 33, 37, 38, 43, 48, 49, 53, 54, 55, 58, 59, 60, 62, 64, 65, 68, 71, 76, 80, 85, 86, 88, 92, 93, 96, 98, 99, 101, 109, 111, 112, 113, 116, 118, 122, 125, 132, 135, 139, 141, 145, 152, 157, 160, 163, 171, 173, 183, 187, 188, 189, 190, 193, 196, 202, 208, 210, 211, 213, 216, 217, 219, 222, 226, 229, 267, 268, 269, 270, 272, 273, 274, 276, 294

of Appendix A for each IEEE bus system [44]. As observed, each static-BBM results in a different optimal solution with the same number of PMUs for each IEEE bus system [44]. On the other hand, the RQP solves the proposed nonlinear program. The RQP is a gradient-based algorithm implemented through a fmincon optimizer routine [38]. To accelerate the convergence towards optimality, the gradient’s vectors are given analytically to the optimizer routine [38]. The RQP algorithm model is applied to standard IEEE test systems [44]. The simulation results indicate that the RQP detects the minimum number and the optimal locations of PMUs to make the power system completely observable.

Now let us apply the RQP algorithm to the IEEE-300 system [44]. The nonlinear program is as follows:

$$\underset{\overrightarrow{x}\in R^n}{\min }J\left(\overrightarrow{x}\right)={\overrightarrow{x}}^T.W.\overrightarrow{x};s.t.\overrightarrow{x}\in \left[0,1\right]|g:R^n\to R^m,m<n,m=238,n=300$$

(14)

We set an arbitrary initial point through MATLAB command “rand” [38]. Then, the RQP generates the exact solution after 36 iterations, as shown in

Table A3. Simulation results on underdetermined system of equations.

Iter		F-Count			f(x)			Feasibility			Steplength			Norm of Step			First-Order Optimality
0		1			1.032236 × 102			9.861 × 10−1									2.000
1		2			9.666889 × 101			9.984 × 10−1			1.000			4.379			4.059 × 102
2		3			9.931676 × 101			2.984 × 10−1			1.000			2.952			4.062 × 102
3		4			9.914983 × 101			1.361 × 10−1			7.000 × 10−1			1.644			4.062 × 102
4		5			1.032552 × 102			4.321 × 10−2			1.000			9.177 × 10−1			4.060 × 102
5		6			1.024552 × 102			1.324 × 10−2			1.000			1.406			4.056 × 102
6		7			1.023897 × 102			6.082 × 10−3			7.000 × 10−1			8.273 × 10−1			4.060 × 102
7		8			1.033093 × 102			6.327 × 10−4			1.000			9.285 × 10−1			4.062 × 102
8		9			1.022358 × 102			3.298 × 10−6			1.000			4.972 × 10−1			4.062 × 102
9		10			9.735171 × 101			1.030 × 10−7			1.000			1.702			4.062 × 102
10		11			9.510909 × 101			2.575 × 10−8			1.000			1.369			4.062 × 102
11		12			9.345127 × 101			6.438 × 10−9			1.000			8.949 × 10−1			4.062 × 102
12		13			9.241002 × 101			1.610 × 10−9			1.000			7.573 × 10−1			4.060 × 102
13		14			9.202713 × 101			4.024 × 10−10			1.000			6.289 × 10−1			4.062 × 102
14		15			9.200234 × 101			7.112 × 10−19			1.000			1.842 × 10−1			4.061 × 102
15		16			9.193331 × 101			0.000			1.000			2.631 × 10−2			4.061 × 102
16		17			9.157585 × 101			0.000			1.000			1.001 × 10−1			4.061 × 102
17		18			8.991064 × 101			0.000			1.000			5.182 × 10−1			4.059 × 102
18		19			8.738703 × 101			0.000			1.000			1.735			4.897 × 102
19		20			8.705728 × 101			1.110 × 10−16			1.000			6.643 × 10−1			4.931 × 102
20		21			8.701730 × 101			2.220 × 10−16			1.000			2.365 × 10−1			4.918 × 102
21		22			8.700852 × 101			2.220 × 10−16			1.000			9.617 × 10−2			4.923 × 102
22		23			8.700622 × 101			2.190 × 10−16			1.000			7.026 × 10−2			4.921 × 102
23		24			8.700109 × 101			2.220 × 10−16			1.000			6.787 × 10−2			4.915 × 102
24		25			8.700013 × 101			2.220 × 10−16			1.000			3.499 × 10−2			4.915 × 102
25		26			8.700002 × 101			2.220 × 10−16			1.000			1.208 × 10−2			4.915 × 102
26		27			8.700000 × 101			1.110 × 10−16			1.000			4.134 × 10−3			4.915 × 102
27		28			8.700000 × 101			1.110 × 10−16			1.000			1.391 × 10−3			4.914 × 102
28		29			8.700000 × 101			2.220 × 10−16			1.000			5.724 × 10−4			4.914 × 102
29		30			8.700000 × 101			1.110 × 10−16			1.000			3.275 × 10−4			4.915 × 102
30		31			8.700000 × 101			1.110 × 10−16			1.000			2.096 × 10−4			4.915 × 102
31		32			8.700000 × 101			2.220 × 10−16			1.000			1.244 × 10−4			4.915 × 102
32		33			8.700000 × 101			1.110 × 10−16			1.000			6.905 × 10−5			4.915 × 102
33		34			8.700000 × 101			1.110 × 10−16			1.000			4.039 × 10−5			4.104 × 102
34		35			8.700000 × 101			2.220 × 10−16			1.000			2.224 × 10−5			2.360 × 102
35		36			8.700000 × 101			1.110 × 10−16			1.000			7.175 × 10−6			1.499 × 101
36		37			8.700000 × 101			0.000			1.000			1.622 × 10−6			5.052 × 10−7
find(optimresults.x == 1.000)’
ans =
Columns 1 through 20
1	2	3	11	12	15	17	20	22	23	25	27	33	37	38	43	48	49	53	54
Columns 21 through 40
55	58	59	60	62	64	68	69	71	73	79	83	85	86	88	92	93	98	99	101
Columns 41 through 60
109	111	112	113	116	118	119	128	132	135	138	139	143	145	152	157	160	163	173	177
Columns 61 through 80
183	187	189	190	193	196	200	204	208	210	212	213	216	217	223	224	228	230	267	268
Columns 81 through 87
269	270	272	273	274	276	294

of the Appendix A. The most notable is that no constraint violation exists. The numerical results displayed in Table A3 include the number of iterations, the total number of function evaluations, the convergent sequence of points ${\left\{x_k\right\}}_{k=0}^{\infty }\to x^{*}$ to the optimum point and the optimal objective function value. The termination is succeeded based on the design criteria in terms of objective function evaluation, the measured first-order optimality at the solution point and the calculated constraint violation. Table A3 illustrates that the step-length is fully being taken to enforce global convergence to the optimum point. As a consequence of that, the unit step-length is accepted so that the Maratos effect does not occur, ensuring a superlinear convergence rate to that optimum point.

Also, the norm of step and the first-order optimality are presented. During the RQP’s iterations, the penalty function maintains the feasibility at the solution point. The objective function is minimized on the product $x^{*}$ in running time equal to $17.796910\sec$ whereas the solution point satisfies the constraint function. The nonlinear model is computationally efficient in finding the required PMUs for the IEEE-300 bus system, as shown in Table A3 of Appendix A and Figure 4.

The function evaluations lead to a feasible global solution point, whereas the constraints are satisfied within tolerances. The fmincon/RQP optimizes the tuning parameters i.e., TolX, TolFun, and TolCon to converge to global optimality whereas the binary restriction $\overrightarrow{x}\in {\left\{0,1\right\}}^n$ is satisfied.

The optimization is completed because the relative first-order optimality measure, 8.8015 × 10⁻¹¹, is less than the selected tolerance TolFun. Additionally, step-tolerance TolX specifies the termination tolerance for the design variable, as shown in Figure 4. Note that TolFun is a tolerance for both: the size of the latest change in the objective function value and the value of the first-order optimality measure [38]. The RQP detects a feasible solution satisfying all of the constraints in which the objective function takes it’s a minimal value, whereas the Euclidean norm of step is less than 5.50082 × 10⁻¹¹ (Figure 4). The norm of step is the current step-size, that is the last displayment in $x$. Therefore, the termination is succeeded based on the tolerance criteria in terms of objective evaluation, maximum constraint violation i.e., TolCon results in zero and first-order optimality [38].

The RQP identifies alternative solution points over the feasible region constituted by the design variable bounds and constraints, as shown in

Table A4. Simulation results using the Recursive Quadratic Programming (RQP) method.

Test System	Objective Value	Optimal PMU Placement
IEEE-14 bus	4	2, 8, 10, 13
		2, 6, 8, 9
		2, 7, 11, 13
		2, 7, 10, 13
		2, 6, 7, 9
IEEE-30 bus	10	1, 7, 8, 10, 11, 12, 18, 24, 26, 27
		1, 7, 8, 10, 11, 12, 18, 24, 25, 27
		1, 7, 8, 10, 11, 12, 18, 24, 26, 27
		1, 7, 8, 9, 10, 12, 18, 24, 26, 27
		1, 6, 7, 9, 10, 12, 18, 23, 26, 27
		1, 7, 8, 9, 10, 12, 15, 20, 25, 27
		1, 7, 8, 10, 11, 12, 18, 24, 25, 27
IEEE-57 bus	17	2, 6, 12, 19, 22, 25, 27, 29, 32, 36, 38, 41, 45, 46, 50, 54, 57
		2, 6, 12, 14, 19, 22, 25, 27, 32, 36, 41, 45, 47, 50, 52, 55, 57
		1, 4, 6, 10, 19, 22, 25, 27, 32, 36, 39, 41, 44, 46, 49, 52, 55
		1, 4, 6, 13, 20, 23, 25, 27, 32, 36, 41, 44, 47, 51, 52, 55, 57
		1, 4, 6, 10, 19, 22, 25, 27, 32, 36, 41, 44, 46, 49, 52, 55, 57
		1, 4, 9, 10, 19, 22, 25, 26, 29, 32, 36, 39, 41, 44, 46, 49, 53
		1, 4, 6, 10, 20, 23, 27, 30, 32, 36, 41, 44, 46, 49, 52, 55, 57
		1, 6, 9, 15, 19, 22, 25, 27, 32, 36, 38, 39, 41, 47, 50, 52, 55
		2, 6, 12, 14, 19, 22, 25, 27, 32, 36, 41, 44, 47, 50, 52, 54, 57
IEEE-118 bus	32	3, 5, 10, 12, 13, 17, 21, 25, 28, 34, 37, 41, 45, 49, 53, 56, 62, 64, 72, 73, 75, 77, 80, 85, 86, 91, 94, 102, 105, 110, 114, 116
		3, 5, 10, 12, 15, 17, 21, 24, 26, 28, 34, 37, 40, 45, 49, 53, 56, 62, 64, 73, 75, 77, 80, 85, 86, 90, 94, 102, 105, 110, 114, 116
		3, 5, 9, 12, 13, 17, 21, 25, 29, 34, 37, 41, 45, 49, 53, 56, 62, 64, 72, 73, 75, 77, 80, 85, 87, 90, 94, 102, 105, 110, 114, 116
		1, 5, 9, 11, 12, 17, 21, 24, 26, 28, 34, 37, 41, 45, 49, 53, 56, 62, 64, 73, 75, 77, 80, 85, 87, 90, 94, 102, 105, 110, 114, 116
		2, 5, 10, 11, 12, 17, 21, 23, 29, 30, 34, 37, 40, 45, 49, 53, 56, 62, 63, 68, 71, 75, 77, 80, 85, 87, 90, 94, 102, 105, 110, 115
		2, 5, 9, 12, 15, 17, 21, 24, 26, 28, 34, 37, 41, 45, 49, 53, 56, 62, 64, 68, 73, 75, 77, 80, 85, 87, 91, 94, 102, 105, 110, 114
		1, 5, 9, 11, 12, 17, 21, 24, 26, 28, 34, 37, 41, 45, 49, 53, 56, 62, 64, 68, 73, 75, 77, 80, 85, 87, 91, 94, 102, 105, 110, 114
		3, 5, 10, 12, 13, 17, 21, 25, 28, 34, 37, 41, 45, 49, 53, 56, 62, 63, 68, 70, 71, 76, 79, 84, 87, 89, 92, 96, 100, 105, 110, 114
		3, 5, 10, 12, 13, 17, 21, 25, 29, 34, 37, 40, 45, 49, 53, 56, 62, 63, 68, 70, 71, 78, 85, 86, 91, 92, 96, 100, 105, 110, 114, 118
		3, 5, 10, 12, 13, 17, 21, 25, 28, 34, 37, 40, 45, 49, 53, 56, 62, 63, 68, 70, 71, 78, 84, 86, 89, 92, 96, 100, 105, 110, 114, 118
		1, 5, 10, 12, 13, 17, 21, 25, 29, 34, 37, 40, 45, 49, 53, 56, 62, 63, 68, 70, 71, 78, 84, 86, 89, 92, 96, 100, 105, 110, 114, 118
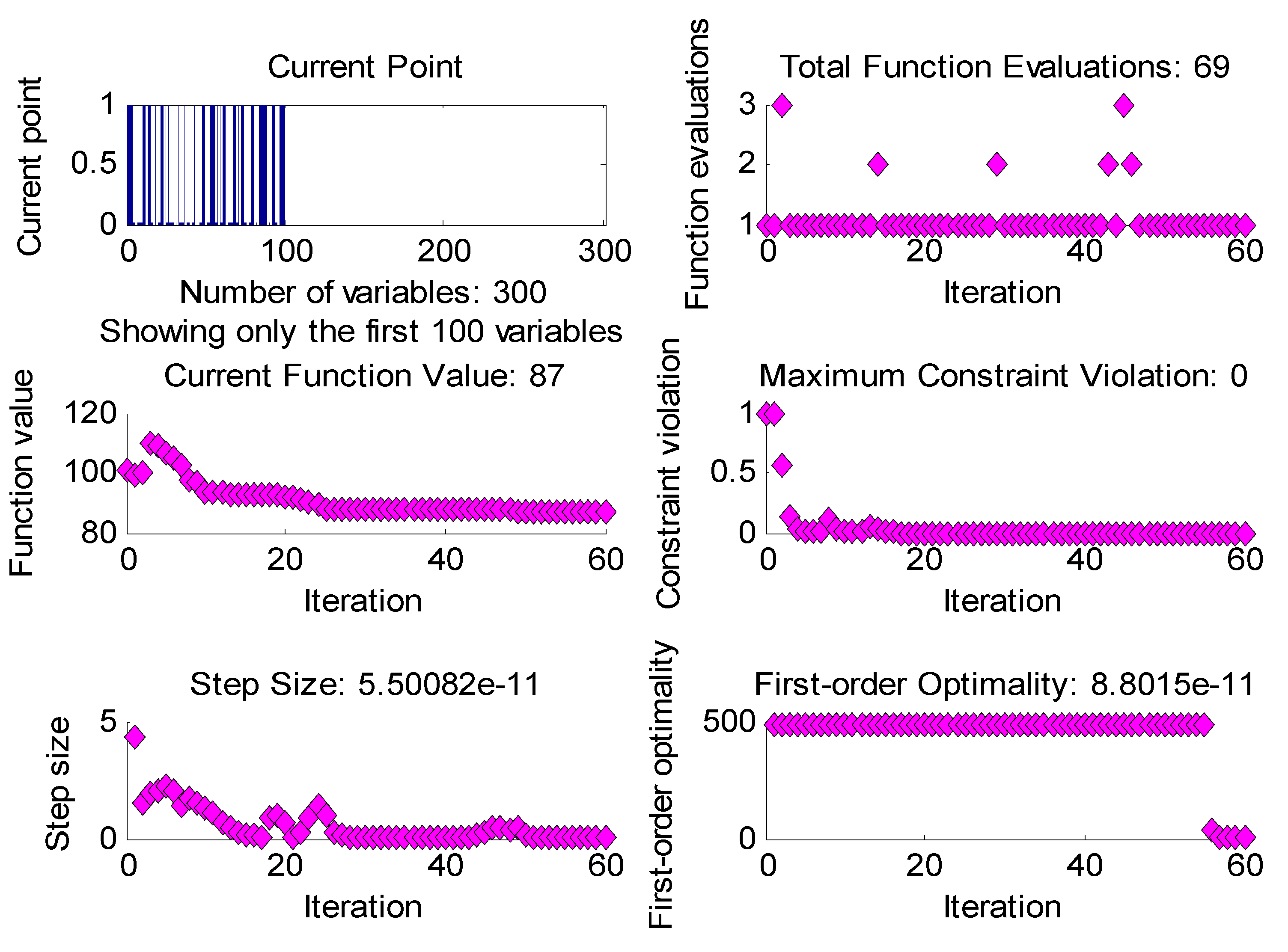
IEEE-300 bus	87	1, 2, 3, 11, 12, 15, 17, 20, 22, 23, 25, 27, 33, 37, 38, 43, 48, 49, 53, 54, 55, 58, 59, 60, 64, 68, 69, 71, 73, 79, 83, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 124, 132, 135, 138, 139, 143, 145, 152, 157, 163, 167, 173, 183, 187, 188, 189, 190, 193, 196, 202, 204, 208, 210, 212, 213, 216, 217, 219, 223, 226, 228, 240, 267, 268, 269, 270, 272, 273, 274, 276, 294
		1, 2, 3, 11, 12, 15, 17, 22, 23, 25, 26, 27, 33, 37, 38, 43, 48, 49, 53, 54, 55, 58, 59, 60, 62, 64, 65, 68, 71, 73, 79, 83, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 128, 132, 135, 138, 139, 143, 145, 152, 157, 163, 167, 173, 183, 187, 188, 189, 190, 193, 196, 202, 204, 208, 210, 212, 213, 216, 217, 223, 226, 228, 230, 267, 268, 269, 270, 272, 273, 274, 276, 294
		1, 2, 3, 11, 15, 17, 22, 23, 26, 27, 33, 37, 43, 48, 49, 53, 54, 55, 58, 59, 60, 62, 64, 68, 69, 71, 73, 78, 80, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 128, 132, 135, 138, 139, 143, 145, 152, 157, 160, 163, 173, 183, 187, 188, 189, 190, 193, 196, 200, 204, 208, 210, 212, 213, 216, 218, 221, 223, 228, 230, 232, 251, 256, 267, 268, 269, 270, 272, 274, 276, 299, 300
IEEE-300 bus	87	1, 2, 3, 11, 15, 17, 22, 23, 26, 27, 33, 37, 38, 43, 48, 49, 53, 54, 55, 58, 60, 62, 64, 68, 69, 71, 73, 78, 80, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 128, 132, 135, 138, 139, 143, 145, 152, 157, 160, 163, 173, 183, 187, 188, 189, 190, 193, 196, 200, 204, 208, 210, 212, 213, 216, 218, 221, 223, 228, 230, 232, 251, 262, 267, 268, 269, 270, 272, 274, 276, 299, 300
		1, 2, 3, 11, 12, 13, 15, 17, 22, 23, 25, 27, 33, 37, 38, 43, 48, 49, 53, 54, 58, 60, 62, 64, 65, 68, 71, 73, 78, 83, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 128, 132, 135, 138, 139, 143, 145, 152, 157, 163, 167, 173, 183, 187, 188, 189, 190, 193, 196, 202, 204, 208, 210, 212, 213, 216, 217, 221, 223, 228, 230, 236, 262, 267, 268, 269, 270, 272, 273, 274, 276, 300
		1, 2, 3, 11, 12, 15, 17, 22, 23, 25, 26, 27, 33, 37, 38, 43, 48, 49, 53, 54, 58, 60, 62, 64, 65, 68, 71, 73, 79, 83, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 128, 132, 135, 138, 139, 143, 145, 152, 157, 163, 167, 173, 183, 187, 188, 189, 190, 193, 196, 200, 204, 208, 210, 212, 213, 216, 217, 223, 226, 228, 230, 236, 262, 267, 268, 269, 270, 272, 273, 274, 276, 300
		1, 2, 3, 11, 12, 15, 17, 22, 23, 25, 26, 27, 33, 37, 38, 43, 48, 49, 53, 54, 58, 60, 62, 64, 65, 68, 71, 73, 78, 83, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 128, 132, 135, 138, 139, 143, 145, 152, 157, 164, 167, 173, 183, 187, 188, 189, 190, 193, 196, 202, 204, 209, 210, 212, 213, 216, 217, 221, 223, 228, 230, 236, 262, 267, 268, 269, 270, 272, 274, 276, 294, 299
		1, 2, 3, 11, 12, 15, 17, 22, 23, 26, 27, 33, 37, 38, 43, 48, 49, 53, 54, 59, 60, 62, 64, 65, 68, 71, 73, 79, 83, 85, 86, 88, 92, 93, 98, 99, 101, 109, 111, 112, 113, 116, 118, 119, 128, 132, 135, 138, 139, 143, 145, 152, 157, 164, 167, 173, 183, 187, 188, 189, 190, 193, 196, 202, 204, 208, 210, 212, 213, 216, 217, 223, 226, 228, 230, 232, 236, 237, 267, 268, 269, 270, 272, 275, 276, 294, 299

of Appendix A. The number of function evaluations measures the convergence rate [35]. Provided that the function evaluation is the most time-consuming part of the algorithm, this process characterizes the convergence speed [35]. Using approximations differences, the RQP detects the solution point but takes longer to achieve optimality as shown in

Table A5. Required PMU numbers and elapsed computational time.

IEEE System	Optimal Value	MIXED-INTEGER LINEAR PROGRAM				NONLINEAR PROGRAM
		Elapsed Time (s)				Average Elapsed Time (s)
		Gurobi	MOSEK	Intlinprog	SCIP	Analytically Gradients	Approximations Differences
14 bus	4	0.02417	0.11	0.050035	0.01873	0.087140	0.322370
30 bus	10	0.01506	0.08	0.018850	0.04615	0.151758	0.343953
57 bus	17	0.02302	0.17	0.038206	0.02890	0.493773	1.608577
118 bus	32	0.02459	0.16	0.036103	0.04214	0.249894	3.347825
300 bus	87	0.04447	0.17	0.458907	0.05359	2.703687	56.31137

of the Appendix A. The best performance would be obtained by combining analytically given gradient constraints with the RQP method [35].

The RQP requires only a small number of iterations and function evaluations to terminate successfully. The elapsed time overall outcomes by RQP are comparable to those spent by BBM, as shown in Table A5 of the Appendix A.

5. Performance Evaluation and Comparisons

In this paper, for unraveling the OPP problem, a minimization model is constructed in which the objective function is minimized under an underdetermined nonlinear system of equality constraints defined on a compact set. The proposed algorithm model is solved based on a hybrid-method coupling, a BBM and a gradient-based RQP method. The first phase of the optimization involves a static-BBM that achieves global optimality in solving the convex MILP model [39].

BBM is an efficient enumeration procedure for examining all possible integer feasible solutions. The pure ILP is relaxed to linear programming (LP), namely LP relaxations by removing the integrality conditions [39]. The concepts of branching, bounding, and fathoming are used to obtain the final solution in the process of building the enumeration tree [40]. If the LP optimum solution satisfies the integer requirement, the ΙP problem is solved. Otherwise, the LP objective value becomes the initial upper bound on the IP optimal value and the root node is partitioned into two successor nodes (subproblems) by two branches [39,40]. When a feasible binary integer solution is obtained via LP relaxations, an optimum point is displayed [39,40]. The main disadvantage is that each BBM has an alternative strategy to built the inherent-tree structure leading to a nonunique global minimum for the OPP [39,40]. The static strategies are best-first, depth-first, best-estimate, best-projection and breadth-first search strategy [39,40]. The number of LP relaxations being derived affects the PMU locations and the convergence speed justifying the differences among the derived running time by different MILP routines as shown in Table A5.

The second phase involves an RQP method, embedded in the fmincon optimizer, that generates a convergent sequence of estimated points to the global minimum point [38]. The RQP algorithm builds a sequence of non-strict global minima over the feasible region that constitutes by the objective function, the bound constraints and the constraint function.

Each optimum point satisfies the binary restriction as shown in Table A4. The RQP detects the solution point, whereas the first-order optimality measure is less than the selected tolerance without constraint violation. The objective is non-decreasing in feasible directions within the value of the function tolerance without constraint violation. Feasible directions are vectors from the current point that locally satisfy the constraints [35]. At a given point $\overrightarrow{x}$, not necessarily feasible, the algorithm generates a new point such that the first-order optimality is satisfied at the point and the step-length parameter is determined to minimize the penalty function [35]. The need for the penalty function stems from the fact that, that RQP algorithms do not maintain feasibility at each step performed by the underdetermined nonlinear programming model [35].

Starting from an arbitrary initial estimate, the step-length is required to enforce global convergence of the RQP method, i.e., the approximation of a point satisfying the necessary Karush–Kuhn–Tucker (KKT) optimality conditions [35]. The global convergence is included via a line-search requiring at each step the decrease of the penalty function whose reduction leads to optimality [35]. The fmincon optimizer computed the step-length to satisfy a certain Armijo condition to decrease the penalty function [38].

When the iterations are outsized, even if the iterative point is sufficiently close to the optimum point, the algorithm cannot guarantee that the step-length is $1$ [35]. As shown from the simulation results, the unit step- length is achieved so that the RQP does not suffer from slow convergence near to the solution point, ensuring a superlinear convergence rate.

Hence, the Maratos Effect, where the method makes slow progress because second-order changes in the constraints are magnified and outweigh reductions in the objective function, is avoided. It is observed the fast ultimate convergence due to the full accepted step-length by the algorithm for estimates remote from the optimum point. The RQP presents both global and local convergence properties concerned with the asymptotic rate of the convergence, which indicates the rapidity with which the discrepancy between the iterates and the solution goes to zero. The number of function evaluations measures the convergence rate [35].

Provided that the function evaluations are the most time-consuming part of the algorithm, this process characterizes the convergence speed [35]. Using approximations differences, the RQP detects the solution point but takes longer to achieve optimality. This suggests that the best performance would be obtained by combining analytical given gradient constraints with RQP. The RQP requires only a small number of iterations and function evaluations to terminate successfully.

The function evaluations are significantly reduced due to the fact that the gradients are given analytically to the optimizer avoiding finite-differencing of approximate derivatives [35]. As a result, the algorithm’s efficiency, measured by function, gradients evaluations and iterations, is improved concerning past studies [11,12,16]. Thus, the size-reducing transformation, which leads to an underdetermined nonlinear programming model, reduces the total run-time significantly as the power network size grows up regarding past studies [11,12,16].

6. Conclusions

This paper presents an underdetermined nonlinear programming model having fewer equality constraints than the design variables on a closed and bounded set for the solution of the optimal PMU placement problem. The proposed formulation leads to a simpler algorithm model ensuring complete power system observability compared to existing well-determined methods. The minimization model is tested on standard IEEE test systems. An RQP method is proposed to solve the proposed nonlinear model. The RQP produces a global as well as local convergence towards globally optimal solutions quickly with guaranteed accuracy. Each optimum point is a set of binary values assigned to the design variable. The strategic implications of our proposed method cover a wide range of methodological and applied contributions:

(1)

It delivers a fully functional solution for the OPP problem, with efficiency and increased effectiveness.

(2)

It serves as a first test best for a novel methodological approach for cost-efficient solutions to improve the monitoring of the power network across large geographic areas.

(3)

It has the potential to be integrated with sensor networks and 5G networks as well as advanced Data Miners in order to promote increased performance in energy management.

(4)

This approach can also be integrated with energy hardware solutions for advanced, low and middle scale smart home and smart city projects.

The items (3) and (4) above also define the future research directions for our research study. We intend to use this methodology for smart home power management applications as well as to analyze the impact of our approach for sophisticated data mining services for smart allocation and storage of energy resources over power grids. We understand that the computational sophistication of our approach and it’s technical character can also be very useful for other researchers that are dealing with the same research problems. Last but not least the issue of Smart Grids management will require more efforts in the near future with the evolution of smart homes and smart cities applications.