A Sliding Mode Control Strategy with Repetitive Sliding Surface for Shunt Active Power Filter with an LCLCL Filter
Abstract
1. Introduction
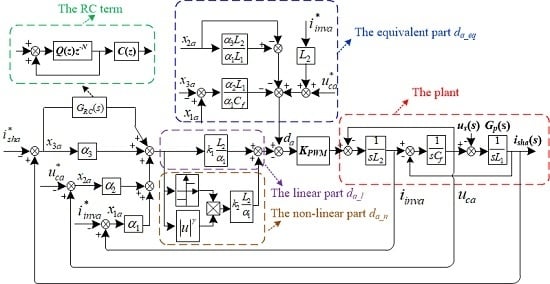
2. Sliding Mode Control Model Analysis
2.1. Sliding Mode Controller Design
2.2. Error Analysis of Sliding Mode Controller
- , ,, , .
3. Plug-in Repetitive Sliding Mode Controller Design
4. Simulation Results Analysis
4.1. Steady-State Characteristics
4.2. Dynamic Characteristics
4.3. Robustness Analysis
5. Analysis of Experimental Results
5.1. Steady-State Experimental Results
5.2. Dynamic Experimental Results
5.3. Robust Experimental Result
6. Conclusions
- (1)
- A sliding mode-switching function is established based on a linear combination of three error variables: inverter output current error, filter capacitor voltage error, and grid-connected harmonic current error. The control law is obtained through a fast exponential power reaching law. To address sliding mode surface drift caused by imperfect system modeling and system parameter uncertainty, the RC term of grid-connected harmonic current error are introduced into the sliding mode surface, and a plugin-repetitive sliding mode control strategy (RCSMC) is proposed. This strategy combines the advantages of RC and SMC to eliminate the harmonic current tracking error and suppress the grid current THD;
- (2)
- Simulation and experimental results on a 380 V, 3 kVA SAPF prototype show that, compared with SMC and MRSMC, the RCSMC has stronger robustness to perturbations, smaller tracking error, lower grid current THD and good dynamic response capabilities. The grid current THD can be reduced to 1.7% after compensation in experiment. The RCSMC is easier to realize in the discrete system, which has the advantage of simplicity and adaptability to SAPF.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. Frequency response analysis of current controllers for selective harmonic compensation in active power filters. IEEE Trans. Ind. Electron. 2009, 56, 337–347. [Google Scholar] [CrossRef]
- Trinh, Q.; Lee, H.; Member, S. An Advanced Current Control Strategy for Three-Phase Shunt Active Power Filters. IEEE Trans. Ind. Electron. 2013, 60, 5400–5410. [Google Scholar] [CrossRef]
- Zeng, Z.; Yang, J.Q.; Yu, N.C. Research on PI and repetitive control strategy for Shunt Active Power Filter with LCL-filter. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; pp. 2833–2837. [Google Scholar]
- Lu, W.; Li, C.; Xu, C. Sliding mode control of a shunt hybrid active power filter based on the inverse system method. Int. J. Electron. Power Energy Syst. 2014, 57, 39–48. [Google Scholar] [CrossRef]
- Alali, M.A.E.; Shtessel, Y.; Barbot, J.P. Grid-Connected Shunt Active LCL Control via Continuous Sliding Modes. IEEE Trans. Mechatron. 2019, 24, 729–740. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization, 1st ed.; Springer: Berlin, Germany, 1992. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation, 1st ed.; Birkhauser: Basel, Switzerland, 2014. [Google Scholar]
- Yu, X.H.; Kaynak, O. Sliding-Mode Control with Soft Computing: A Survey. IEEE Trans. Ind. Electron. 2009, 56, 3275–3285. [Google Scholar]
- Li, S.; Liang, X.; Fei, J. Dynamic Surface Adaptive Fuzzy Control of Three-Phase Active Power Filter. IEEE Access 2016, 4, 9451–9458. [Google Scholar]
- Fei, J.; Li, S. Adaptive Fractional High Order Sliding Mode Fuzzy Control of Active Power Filter. Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS). In Proceedings of the 2018 Joint 10th International Conference, Toyama, Japan, 5–8 December 2018; pp. 576–580. [Google Scholar]
- Liu, N.; Fei, J. Adaptive Fractional Sliding Mode Control of Active Power Filter Based on Dual RBF Neural Networks. IEEE Access 2017, 5, 27590–27598. [Google Scholar] [CrossRef]
- Utkin, V.; Shi, J. Integral sliding mode in systems operating under uncertainty conditions. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; Volume 4, pp. 4591–4596. [Google Scholar]
- Wai, R.J.; Wang, W.H. Grid-connected photovoltaic generation system. IEEE Trans. Circuits Syst. I Reg. Papers 2008, 55, 953–964. [Google Scholar]
- Levant, A. Higher-order sliding modes, differentiation and output feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Pradhan, R.; Subudhi, B. Double Integral Sliding Mode MPPT Control of a Photovoltaic System. IEEE Trans. Control Syst. Technol. 2016, 1, 285–292. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Cheng, J.; Fang, C. Altitude control for variable load quadrotor via learning rate based robust sliding mode controller. IEEE Access 2019, 7, 9736–9744. [Google Scholar] [CrossRef]
- Hao, X.; Yang, X.; Liu, T.; Huang, L.; Chen, W.A. Sliding-mode controller with multiresonant sliding surface for single-phase grid-connected VSI with an LCL filter. IEEE Trans. Power Electron. 2013, 28, 2259–2268. [Google Scholar] [CrossRef]
- Tang, Y.; Loh, P.C.; Wang, P.; Choo, F.H.; Gao, F. Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters. IEEE Trans. Power Electron. 2012, 27, 1433–1443. [Google Scholar] [CrossRef]
- Wang, J.; Yan, J.; Jiang, L. Pseudo-derivative-feedback current control for three-phase grid-connected inverters with LCL filters. IEEE Trans. Power Electron. 2016, 31, 3898–3912. [Google Scholar] [CrossRef]
- He, N.; Zhang, J.; Zhu, Y.; Shen, G.; Xu, D. Weighted average current control in three-phase grid inverter with LCL filter. IEEE Trans. Power Electron. 2013, 28, 2785–2797. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Gradshteyn, L.S.; Ryzhik, L.M. Table of Integrals, Series, and Products; Academic Press: San Diego, CA, USA, 2007; pp. 20–30. [Google Scholar]
- Zhu, M.Z.H.; Ye, Y.Q.; Zhao, Q. A design method of repetitive controller against variation of grid frequency. Proc. CSEE 2016, 36, 3857–3867. [Google Scholar]
- Gao, Y.G.; Jiang, F.Y.; Song, J.C.; Zheng, L.J.; Tian, F.Y.; Geng, P.L. A novel dual closed-loop control scheme based on repetitive control for grid-connected inverters with an LCL filter. ISA Trans. 2018, 74, 194–208. [Google Scholar] [CrossRef] [PubMed]


















| Symbol | Description | Value |
|---|---|---|
| Ls/L1/L2/Lh | inductor | 0.1 mH/0.7 mH/2 mH/0.3 mH |
| Cf/Ch | filter capacitor | 10 uF/1 uF |
| Rd | parasitic resistance of filter capacitor | 0.005 Ω |
| us | grid voltage | 380 V |
| udc | DC bus voltage | 750V |
| f | grid voltage frequency | 50 Hz |
| fc/fs | carrier frequency/sampling frequency | 9 kHz |
| S | system capacity | 3k VA |
| Parameters | Value |
|---|---|
| k1 | 5 × 104 |
| k2 | 105 |
| γ | 0.3 |
| α1 | 1 |
| α2 | 1 |
| α3 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Li, X.; Zhang, W.; Hou, D.; Zheng, L. A Sliding Mode Control Strategy with Repetitive Sliding Surface for Shunt Active Power Filter with an LCLCL Filter. Energies 2020, 13, 1740. https://doi.org/10.3390/en13071740
Gao Y, Li X, Zhang W, Hou D, Zheng L. A Sliding Mode Control Strategy with Repetitive Sliding Surface for Shunt Active Power Filter with an LCLCL Filter. Energies. 2020; 13(7):1740. https://doi.org/10.3390/en13071740
Chicago/Turabian StyleGao, Yunguang, Xiaofan Li, Wenjie Zhang, Dianchao Hou, and Lijun Zheng. 2020. "A Sliding Mode Control Strategy with Repetitive Sliding Surface for Shunt Active Power Filter with an LCLCL Filter" Energies 13, no. 7: 1740. https://doi.org/10.3390/en13071740
APA StyleGao, Y., Li, X., Zhang, W., Hou, D., & Zheng, L. (2020). A Sliding Mode Control Strategy with Repetitive Sliding Surface for Shunt Active Power Filter with an LCLCL Filter. Energies, 13(7), 1740. https://doi.org/10.3390/en13071740