Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part II—Simulations of Charge Transport
Abstract
1. Introduction
2. Physical Background and Formulation of the Model
2.1. Fundamentals of Charge Transport
2.2. Charge Transport Equations
2.3. Charge Injection
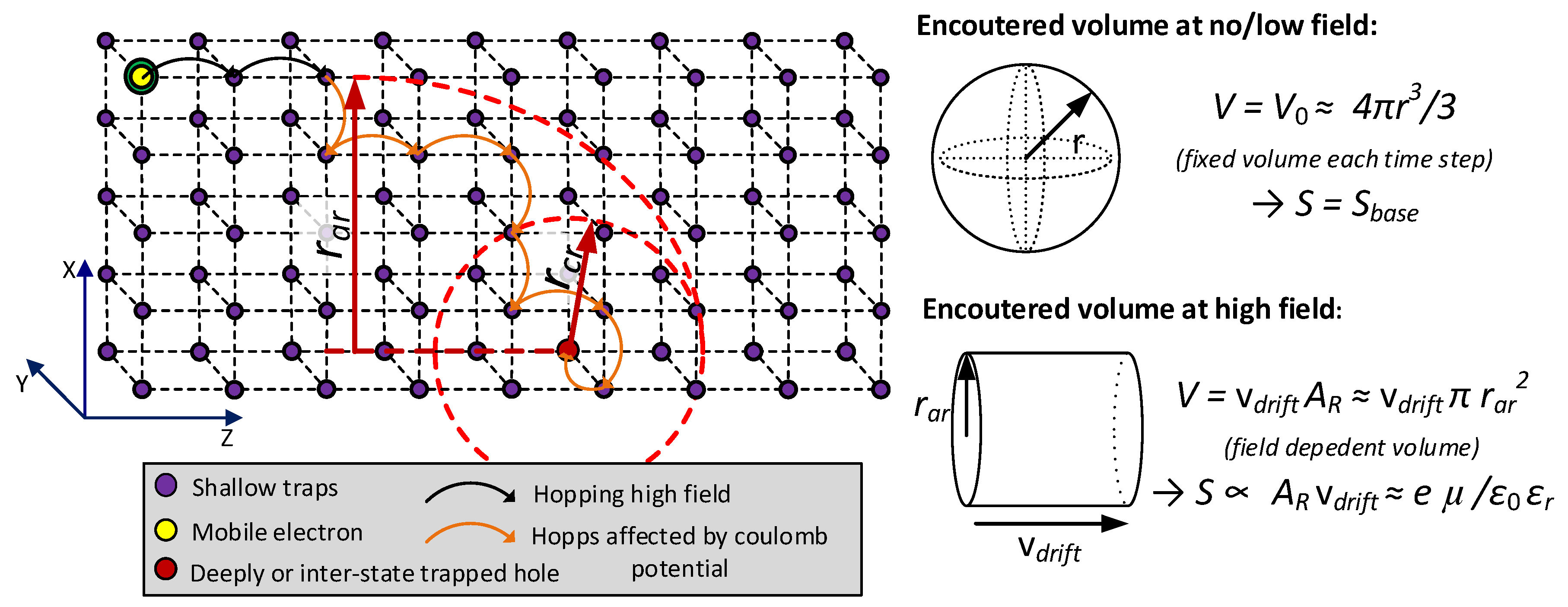
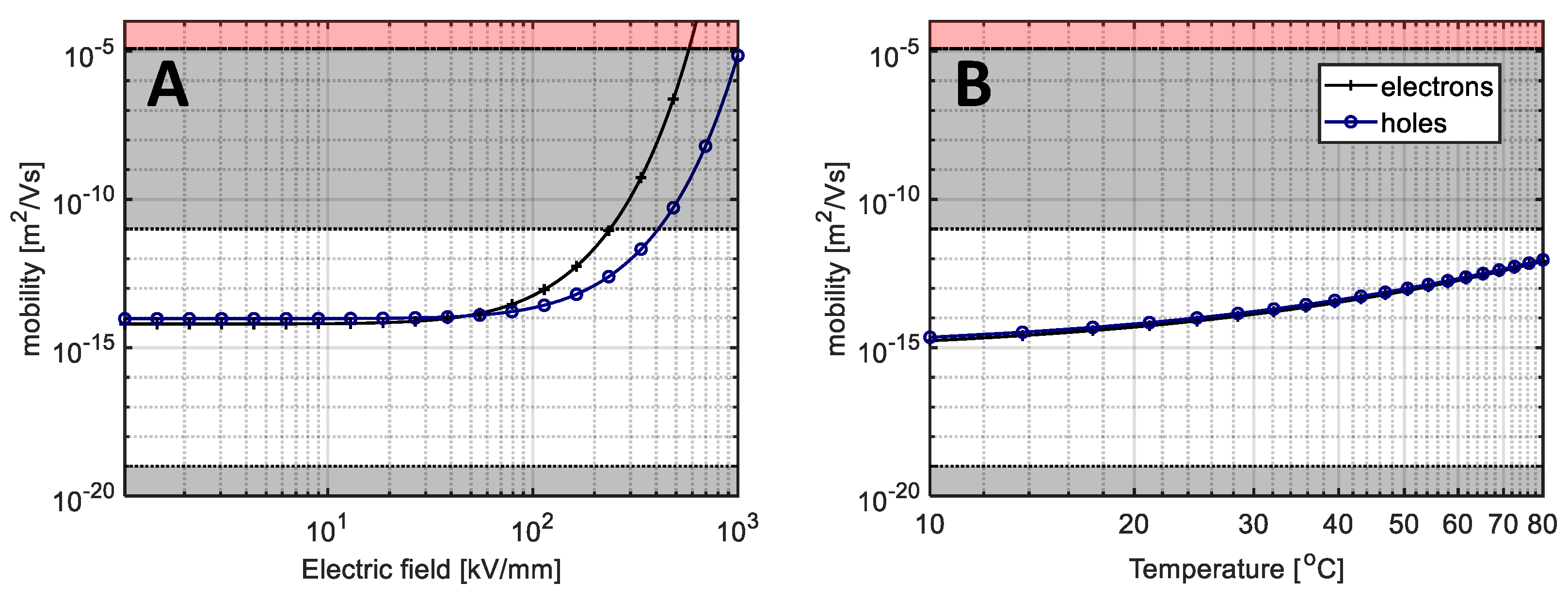
2.4. Field Dependent Mobility of Carriers
2.5. Field Dependent Trapping and Detrapping Rates
2.6. Field Dependent Recombination Rates
2.7. Model Implementation
3. Computational Results
3.1. Charge Transport Parameters
3.2. Charge Injection Parameters
3.3. Trapping and Detrapping Parameters
3.4. Recombination Parameters
4. Comparison of the Simulations and Measurement Results
4.1. Matching Results between the Model and the Measurements
4.2. Overall Performance of the Model
4.3. Limitations of the Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Johannes Rothfeld Nexans Successfully Qualifies a 525 kV HVDC Underground Cable System to German TSO Standards. Available online: https://www.nexans.com/newsroom (accessed on 3 December 2018).
- Doedens, E.H.; Frisk, N.B.; Jarvid, M.; Boyer, L.; Josefsson, S. Surface Preparations on MV-Sized Cable Ends for Ramped DC Breakdown Studies. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Toronto, ON, Canada, 16–19 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 360–362. [Google Scholar] [CrossRef]
- Le Roy, S.; Teyssedre, G.; Laurent, C.; Segur, P. Numerical Modeling of Space Charge and Electroluminescence in Polyethylene under dc Field. In Proceedings of the Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Cancun, Quintana Roo, Mexico, 20–24 October 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 172–175. [Google Scholar] [CrossRef]
- Le Roy, S.; Segur, P.; Teyssedre, G.; Laurent, C. Description of bipolar charge transport in polyethylene using a fluid model with a constant mobility: Model prediction. J. Phys. D Appl. Phys. 2004, 37, 298–305. [Google Scholar] [CrossRef]
- Laurent, C.; Teyssedre, G.; Le Roy, S. A Discussion on Charge Transport and Electroluminescence in Insulating Polymers. In Proceedings of the 2005 International Symposium on Electrical Insulating Materials, 2005. (ISEIM 2005), Kitakyushu, Japan, 5–9 June 2005; Volume 1, pp. 7–15. [Google Scholar]
- Le Roy, S.; Teyssedre, G.; Laurent, C. Charge transport and dissipative processes in insulating polymers: Experiments and model. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 644–654. [Google Scholar] [CrossRef]
- Le Roy, S.; Teyssedre, G.; Laurent, C.; Montanari, G.C.; Palmieri, F. Description of charge transport in polyethylene using a fluid model with a constant mobility: Fitting model and experiments. J. Phys. D Appl. Phys. 2006, 39, 1427–1436. [Google Scholar] [CrossRef]
- Boufayed, F.; Teyssèdre, G.; Laurent, C.; Le Roy, S.; Dissado, L.A.; Ségur, P.; Montanari, G.C. Models of bipolar charge transport in polyethylene. J. Appl. Phys. 2006, 100, 104–105. [Google Scholar] [CrossRef]
- Le Roy, S.; Miyake, H.; Tanaka, Y.; Takada, T.; Teyssedre, G.; Laurent, C. Simultaneous measurement of electroluminescence and space charge distribution in low density polyethylene under a uniform dc field. J. Phys. D Appl. Phys. 2005, 38, 89–94. [Google Scholar] [CrossRef]
- Hoang, A.T.; Serdyuk, Y.V.; Gubanski, S.M. Charge Transport in LDPE Nanocomposites Part II—Computational Approach. Polymers (Basel) 2016, 8, 103. [Google Scholar] [CrossRef] [PubMed]
- Boukhari, H.; Rogti, F. Simulation of Space Charge Dynamic in Polyethylene under DC Continuous Electrical Stress. J. Electron. Mater. 2016, 45, 5334–5340. [Google Scholar] [CrossRef]
- Teyssedre, G.; Laurent, C. Charge transport modeling in insulating polymers: From molecular to macroscopic scale. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 857–875. [Google Scholar] [CrossRef]
- Meunier, M.; Quirke, N.; Aslanides, A. Molecular modeling of electron traps in polymer insulators: Chemical defects and impurities. J. Chem. Phys. 2001, 115, 2876–2881. [Google Scholar] [CrossRef]
- Sato, M.; Kumada, A.; Hidaka, K.; Hirano, T.; Sato, F. Quantum chemical calculation of hole transport properties in crystalline polyethylene. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3045–3052. [Google Scholar] [CrossRef]
- Le Roy, S.; Teyssèdre, G.; Laurent, C. Modelling space charge in a cable geometry. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2361–2367. [Google Scholar] [CrossRef]
- Tsekmes, I.A.; van der Born, D.; Morshuis, P.H.F.; Smit, J.J.; Person, T.J.; Sutton, S.J. Space charge accumulation in polymeric DC mini-cables. In Proceedings of the IEEE International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 452–455. [Google Scholar] [CrossRef]
- Liu, N.; He, M.; Alghamdi, H.; Chen, G.; Fu, M.; Li, R.; Hou, S. An improved model to estimate trapping parameters in polymeric materials and its application on normal and aged low-density polyethylenes. J. Appl. Phys. 2015, 118, 064102. [Google Scholar] [CrossRef]
- Min, D.; Li, S. Simulation on the influence of bipolar charge injection and trapping on surface potential decay of polyethylene. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1627–1636. [Google Scholar] [CrossRef]
- Schroeder, H. Poole-Frenkel-effect as dominating current mechanism in thin oxide films—An illusion?! J. Appl. Phys. 2015, 117, 215103–215113. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® v. 5.3; www.comsol.com; COMSOL AB: Stockholm, Sweden, 2018.
- MATLAB Version 9.5.0.944444 (R2018b) 2018; The MathWorks Inc.: Natick, MA, USA, 2018.
- Dissado, L.A.; Fothergill, J.C. Electrical Degradation and Breakdown in Polymers, 1st ed.; Peter Peregrinus Ltd.: London, UK, 1992; ISBN 978-0-86341-196-0. [Google Scholar]
- Doedens, E.; Jarvid, M.; Serdyuk, Y.V.; Guffond, R.; Charrier, D. Local Surface Field- and Charge Distributions and Their Impact on Breakdown Voltage for HVDC Cable Insulation. In Proceedings of the International Conference on Insulated Power Cables (Jicable), Cigré, Versailles, France, 23–27 June 2019. [Google Scholar]
- Doedens, E.H. Characterization of Different Interface Types for HVDC Extruded Cable Applications. Lic. Thesis, Chalmers University of Technology, Göteborg, Sweden, 2018. [Google Scholar]
- Ieda, M.; Sawa, G.; Kato, S. A Consideration of Poole-Frenkel Effect on Electric Conduction in Insulators. J. Appl. Phys. 1971, 42, 3737. [Google Scholar] [CrossRef]
- Taleb, M.; Teyssedre, G.; Le Roy, S.; Laurent, C. Modeling of charge injection and extraction in a metal/polymer interface through an exponential distribution of surface states. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 311–320. [Google Scholar] [CrossRef]













| Description | Parameter | Min from Literature | Max from Literature | Parameter Values | Unit |
|---|---|---|---|---|---|
| Base level mobility e 1 | μe(E = 0) | 8·10−17 | 1.2·10−13 | 6.3·10−15 | m2/(V·s) |
| Base level mobility h 1 | μh(E = 0) | 4·10−16 | 2·10−13 | 9.5·10−15 | m2/(V·s) |
| Energetic hopping barrier e | whop,e | 0.608 | 1 | 0.76 | eV |
| Energetic hopping barrier h | whop,h | 0.532 | 0.83 | 0.74 | eV |
| Shallow trap spacing e | ash,e | 0.71 | 5.12 | 2.25 | nm |
| Shallow trap spacing h | ash,h | 0.71 | 6.23 | 1.25 | nm |
| Shallow trap density e 2 | N0shallow,e | - | - | 8.78·1025 | m−3 |
| Shallow trap density h 2 | N0shallow,h | - | - | 5.12·1026 | m−3 |
| Inter-level state spacing e | aint,e | - | - | 80 | nm |
| Inter-level state spacing h | aint,h | - | - | 100 | nm |
| Relative permittivity | εr | - | - | 2.3 | - |
| Description | Parameter | Min from Literature | Max from Literature | Parameter Values | Unit |
|---|---|---|---|---|---|
| Schottky injection barrier e | ϕBe | 1.1 | 1.27 | 0.905 | eV |
| Schottky injection barrier h | ϕBh | 1.1 | 1.27 | 1.148 | eV |
| Schottky correction factor e | λRe | 1 | 1 | 4.1·10−5 | none |
| Schottky correction factor h | λRh | 1 | 1 | 0.1 | none |
| High field barrier increase | Δϕs | - | - | 0.27 | eV |
| FN injection barrier e | ϕFNe | - | - | 2 (0.5) 1 | eV |
| FN injection barrier h | ϕFNh | - | - | 2 | eV |
| Ohmic field threshold | Eth | - | - | 5·106 | V/m |
| Spread parameter | Spr | - | - | 6·10−7 | m/V |
| Low field reduction factor | ƒs | 0 | 1 | 1 | none |
| Surface Type | Rough Abraded | Abraded | Smooth Abraded | Backside | Remolded | |
|---|---|---|---|---|---|---|
| Field (beta) parameters 1 | βs, βFN | 8 | 6.5 | 4.3 | 1.9 | 1.3 |
| Reduced beta, high field 2 | βhigh | 6 | 4.2 | 2.8 | 1.5 | 1.3 |
| Description | Parameter | Min from Literature | Max from Literature | Parameter Values | Unit |
|---|---|---|---|---|---|
| Base level trapping rate e 1 | B0,e(E = 0) | 1·10−3 | 0.1 | 3.2·10−4 | s−1 |
| Base level trapping rate h 1 | B0,h(E = 0) | 2·10−3 | 0.2 | 1.7·10−3 | s−1 |
| Trapping cross-section e and h | AT(e,h) | - | - | ash(h,e)2 | nm2 |
| Inter-level state density e | N0int,e | - | - | 1·1023 | m−3 |
| Inter-level state density h | N0int,h | - | - | 1·1023 | m−3 |
| Inter-level state depth e | wtr,int,e | 0.608 | 1 | 0.81 | eV |
| Inter-level state depth h | wtr,int,h | 0.532 | 0.83 | 0.79 | eV |
| Deep trap density, e | N0deep,e | 100/e | 200/e | 40/e | m−3 |
| Deep trap density, h | N0deep,h | 100/e | 200/e | 95/e | m−3 |
| Detrapping barrier e and h | wtr(e,h) | 0.9 | 1.05 | 1.03 | eV |
| Hop–detrap barrier e and h | wtr,hop(e,h) | - | - | 1.00 | eV |
| Trapping probability | PT | - | - | 100 | % |
| Description | Parameter | Min from Literature | Max from Literature | Parameter Values | Unit |
|---|---|---|---|---|---|
| Trapped h and trapped e | S0,base | 0 | 4·10−3 | 1·10−4 | m3/(C·s) |
| Trapped h and mobile e 1 | S1,base | 0 | 4·10−3 | 1·10−4 | m3/(C·s) |
| Mobile h and trapped e 1 | S2,base | 0 | 4·10−3 | 1·10−4 | m3/(C·s) |
| Mobile h and mobile e 1 | S3,base | 0 | 0 | 1·10−4 | m3/(C·s) |
| Recombination probability | PR | - | - | 100 | % |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doedens, E.; Jarvid, E.M.; Guffond, R.; Serdyuk, Y.V. Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part II—Simulations of Charge Transport. Energies 2020, 13, 1750. https://doi.org/10.3390/en13071750
Doedens E, Jarvid EM, Guffond R, Serdyuk YV. Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part II—Simulations of Charge Transport. Energies. 2020; 13(7):1750. https://doi.org/10.3390/en13071750
Chicago/Turabian StyleDoedens, Espen, E. Markus Jarvid, Raphaël Guffond, and Yuriy V. Serdyuk. 2020. "Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part II—Simulations of Charge Transport" Energies 13, no. 7: 1750. https://doi.org/10.3390/en13071750
APA StyleDoedens, E., Jarvid, E. M., Guffond, R., & Serdyuk, Y. V. (2020). Space Charge Accumulation at Material Interfaces in HVDC Cable Insulation Part II—Simulations of Charge Transport. Energies, 13(7), 1750. https://doi.org/10.3390/en13071750






