Modeling of Coal Mill System Used for Fault Simulation
Abstract
:1. Introduction
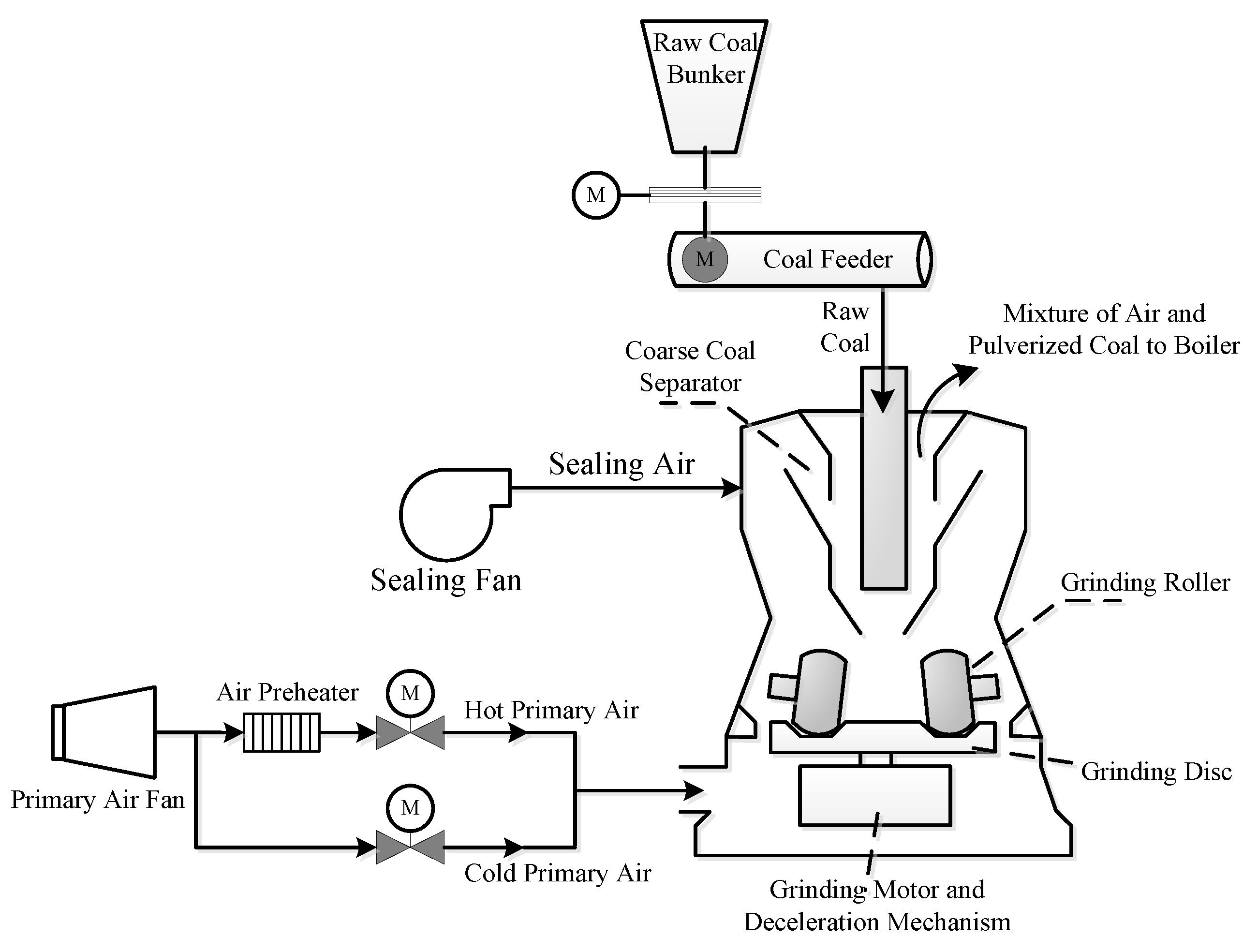
2. Working Principle of a Coal Mill System
3. Dynamic Model of a Coal Mill System
3.1. Primary Air System Model
3.2. Coal–Powder Storage Model
3.3. Outlet Temperature Model
3.4. Coal Powder Moisture Model
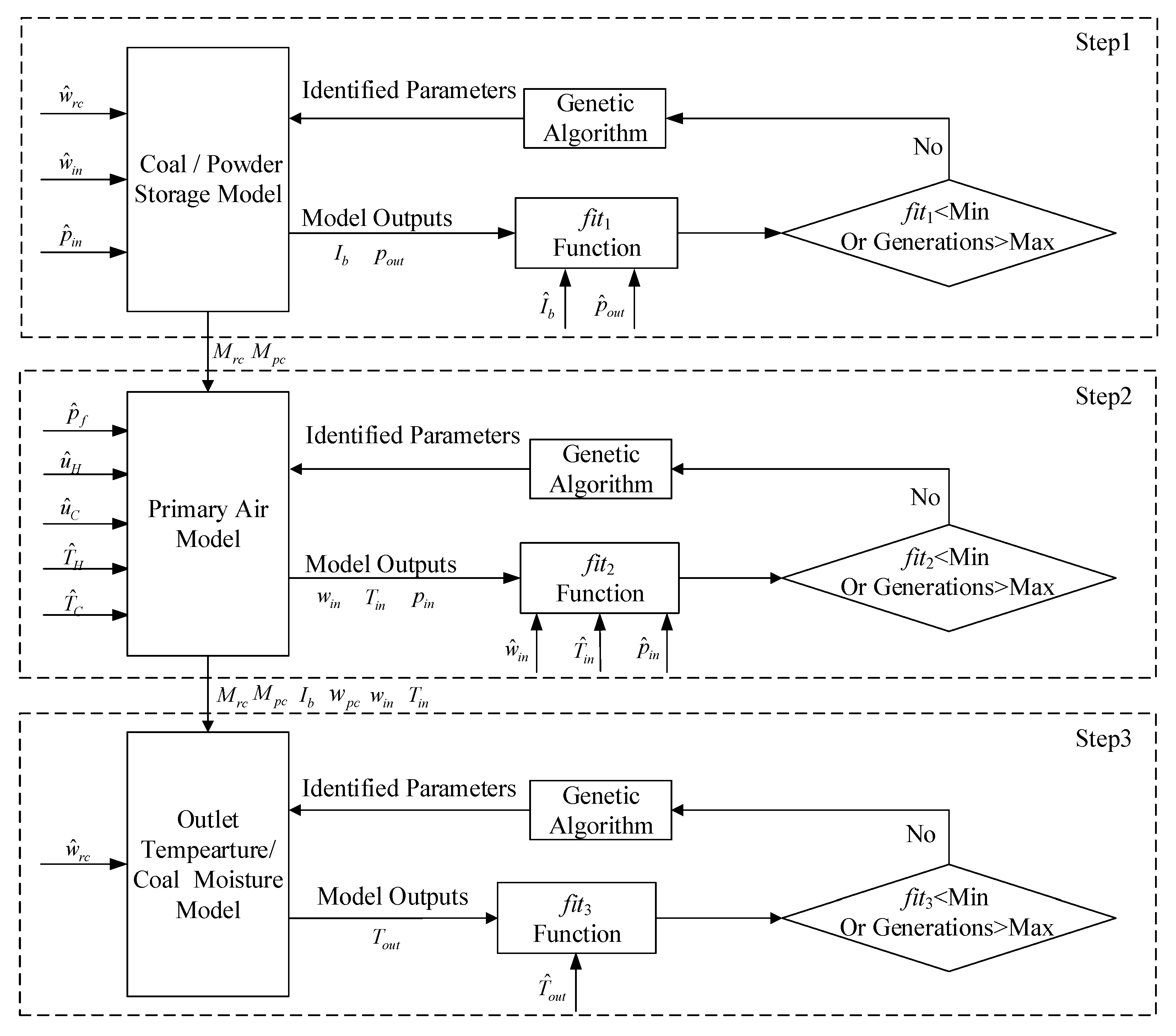
4. Model Parameter Identification and Verification
4.1. Model Parameter Identification
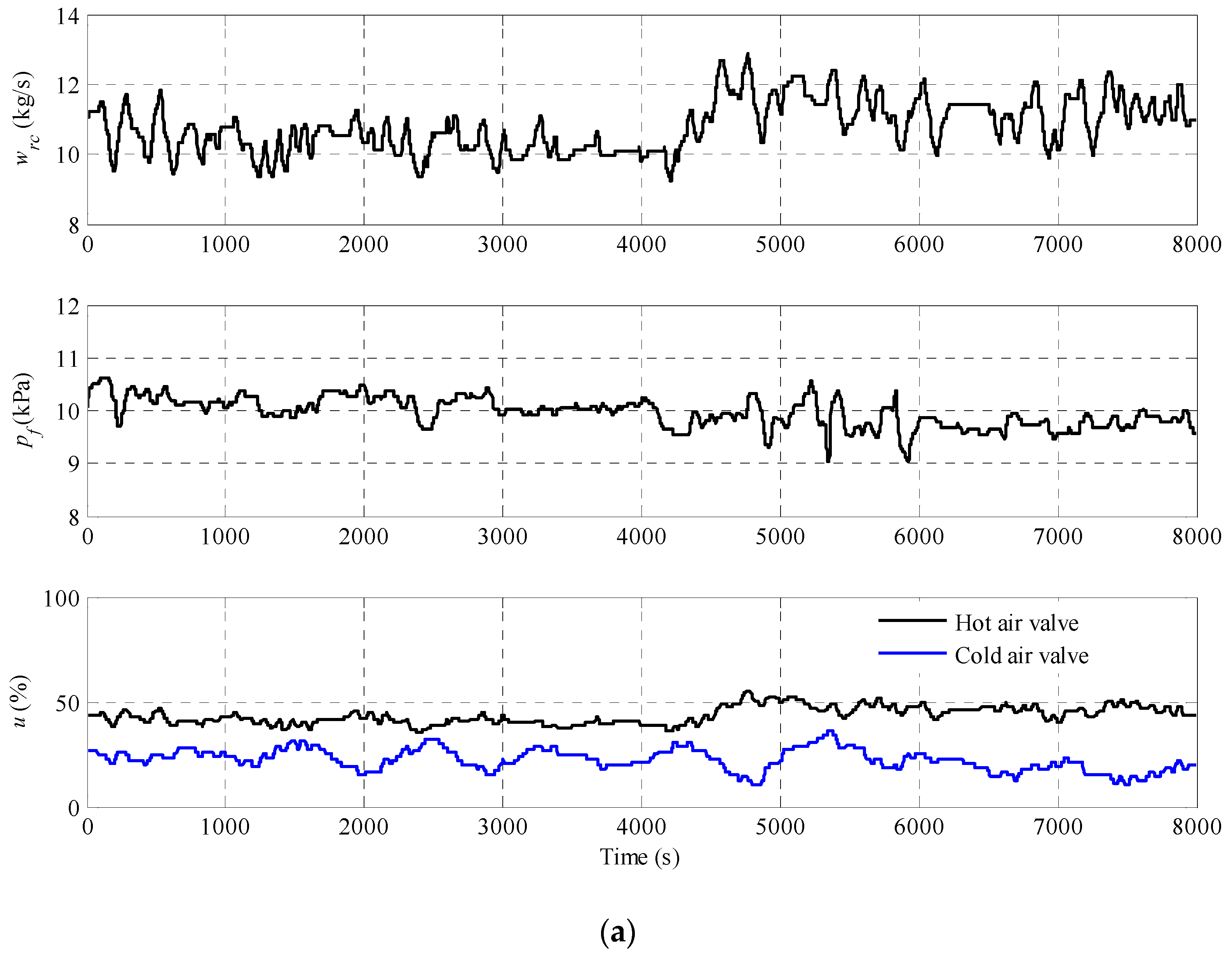
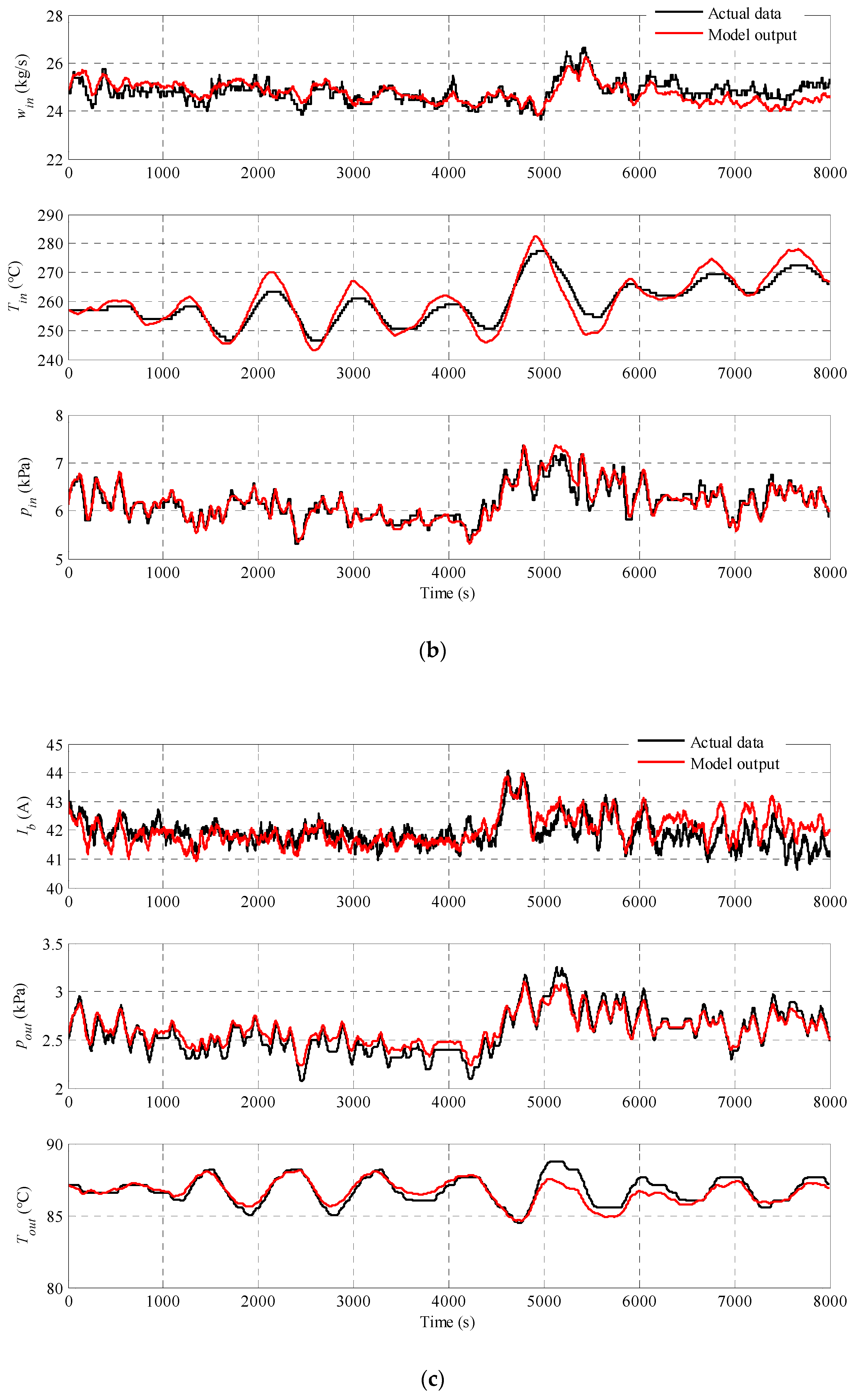
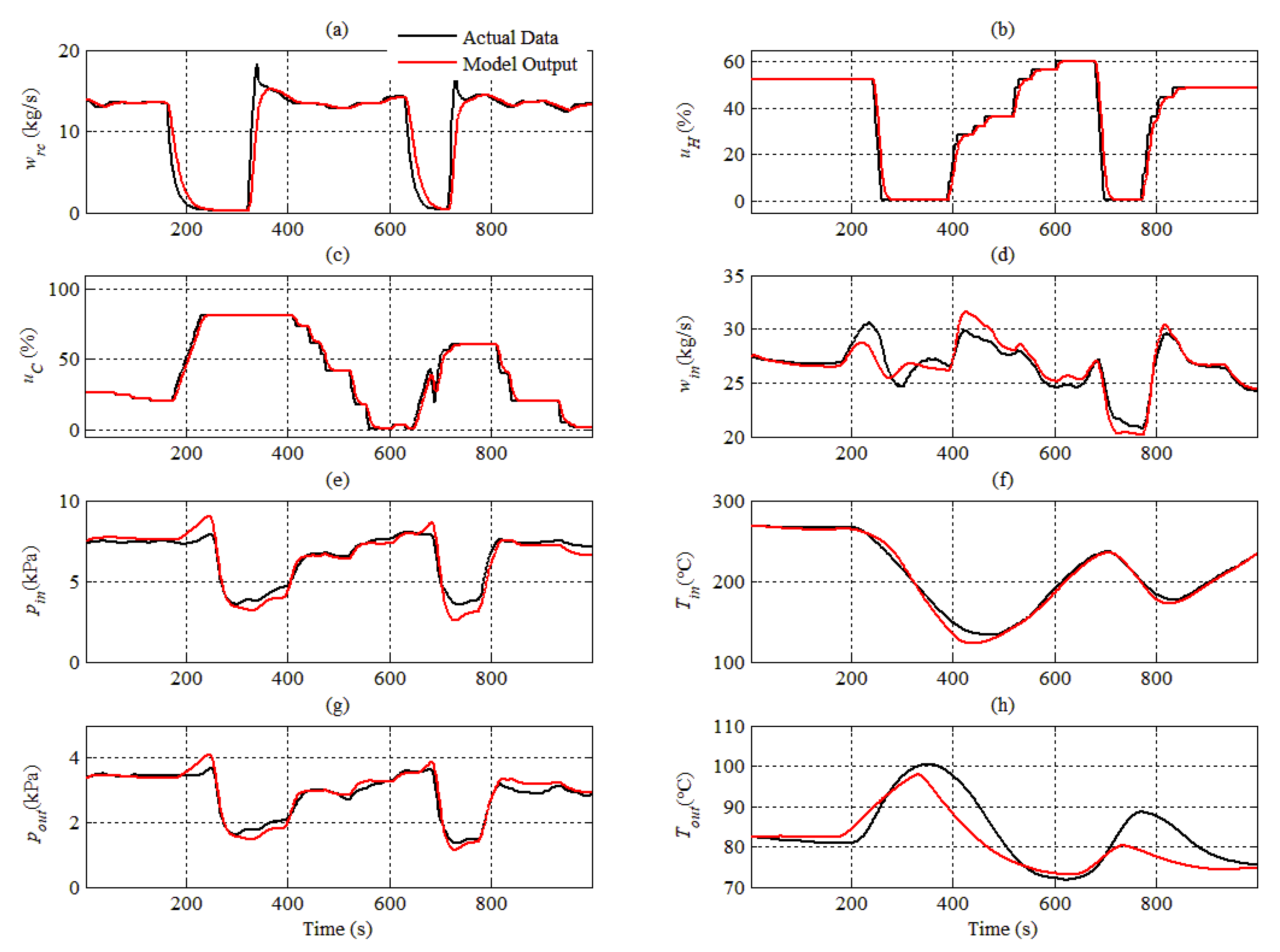
4.2. Model Validation
5. Typical Fault Simulation
5.1. Simulation of of Coal Interruption
5.2. Simulation of Coal Blockage
5.3. Simulation of Coal Self-Ignition
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Agrawal, V.; Panigrahi, B.; Subbarao, P. Review of control and fault diagnosis methods applied to coal mills. J. Process Control 2015, 32, 138–153. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Chen, Z.; Mauricio, A.; Li, W.; Gryllias, K. A deep learning method for bearing fault diagnosis based on Cyclic Spectral Coherence and Convolutional Neural Networks. Mech. Syst. Signal Process. 2020, 140, 106683. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Qi, Y.; Shen, C.; Wang, D.; Shi, J.; Jiang, X.; Zhu, Z. Stacked Sparse Autoencoder-Based Deep Network for Fault Diagnosis of Rotating Machinery. IEEE Access 2017, 5, 15066–15079. [Google Scholar] [CrossRef]
- Tamilselvan, P.; Wang, P. Failure diagnosis using deep belief learning based health state classification. Reliab. Eng. Syst. Saf. 2013, 115, 124–135. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep Convolutional Transfer Learning Network: A New Method for Intelligent Fault Diagnosis of Machines with Unlabeled Data. IEEE Trans. Ind. Electron. 2018, 66, 7316–7325. [Google Scholar] [CrossRef]
- Fan, G.; Rees, N.; Parker, D. Analysis of coal Mill Dynamic Characteristics under Normal and Abnormal Operating Conditions. IFAC Proc. Vol. 1997, 30, 451–457. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Mataji, B. Fault detection in coal mills used in power plants. IFAC Proc. Vol. 2006, 39, 177–182. [Google Scholar] [CrossRef]
- Niemczyk, P.; Bendtsen, J.D.; Ravn, A.P.; Andersen, P.; Pedersen, T.S. Derivation and validation of a coal mill model for control. Control Eng. Pract. 2012, 20, 519–530. [Google Scholar] [CrossRef]
- Cortinovis, A.; Mercangöz, M.; Mathur, T.; Poland, J.; Blaumann, M. Nonlinear coal mill modeling and its application to model predictive control. Control Eng. Pract. 2013, 21, 308–320. [Google Scholar] [CrossRef]
- Pradeebha, P.; Pappa, N.; Vasanthi, D.; Parameswaran, P.; Natarajan, P.; Vasanthi, D. Modeling and Control of Coal Mill. IFAC Proc. Vol. 2013, 46, 797–802. [Google Scholar] [CrossRef] [Green Version]
- Zeng, D.L.; Hu, Y.; Gao, S.; Liu, J.Z. Modelling and control of pulverizing system considering coal moisture. Energy 2015, 80, 55–63. [Google Scholar] [CrossRef]
- Zeng, D.; Wang, Y.; Gao, S.; Liu, J. Modeling and control of ball mill system considering coal moisture. Measurement 2016, 90, 43–51. [Google Scholar] [CrossRef]
- Gao, Y.; Zeng, D.; Liu, J. Modeling of a medium speed coal mill. Powder Technol. 2017, 318, 214–223. [Google Scholar] [CrossRef]
- Gao, Y.; Zeng, D.; Liu, J.; Jian, Y. Optimization control of a pulverizing system on the basis of the estimation of the outlet coal powder flow of a coal mill. Control Eng. Pract. 2017, 63, 69–80. [Google Scholar] [CrossRef]
- Bhatt, D.; Dadiala, V.; Barve, J. Industrial Coal Pulverizer Model Simulation and Parametric Investigation. IFAC PapersOnLine 2018, 51, 115–120. [Google Scholar] [CrossRef]


| k1 = 575.32 | k2 = 110.75 | k3 = 1.2001 | k4 = 0.3045 | k5 = 0.0095 | k6 = 0.4332 |
| k7 = 0.3746 | k8 = 22.139 | k9 = 0.0075 | k10 = 0.4704 | k11 = 0.0563 | k12 = −3.3664 |
| k13 = 28.155 | α1 = 15.269 | α2 = 210.62 | α3 = 8.1275 | α4 = 19.039 |
| Variables | win | Tin | pin | Ib | pout | Tout |
| Relative Error (%) | 1.09 | 0.97 | 1.45 | 0.77 | 2.53 | 0.39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Ping, B.; Zeng, D.; Niu, Y.; Gao, Y. Modeling of Coal Mill System Used for Fault Simulation. Energies 2020, 13, 1784. https://doi.org/10.3390/en13071784
Hu Y, Ping B, Zeng D, Niu Y, Gao Y. Modeling of Coal Mill System Used for Fault Simulation. Energies. 2020; 13(7):1784. https://doi.org/10.3390/en13071784
Chicago/Turabian StyleHu, Yong, Boyu Ping, Deliang Zeng, Yuguang Niu, and Yaokui Gao. 2020. "Modeling of Coal Mill System Used for Fault Simulation" Energies 13, no. 7: 1784. https://doi.org/10.3390/en13071784
APA StyleHu, Y., Ping, B., Zeng, D., Niu, Y., & Gao, Y. (2020). Modeling of Coal Mill System Used for Fault Simulation. Energies, 13(7), 1784. https://doi.org/10.3390/en13071784





