Mechanical Performances of Typical Robot Feet Intruding into Sands
Abstract
:1. Introduction
2. Materials and Methods
2.1. Design of Mechanical Feet
2.2. Intrinsic Parameter Tests and Virtual Parameter Calibrations
2.3. Mechanical Feet Intruding into Quartz Sand Tests
2.4. Discrete Element Simulation of Mechanical Feet Intruding into Quartz Sand
3. Results and Discussion
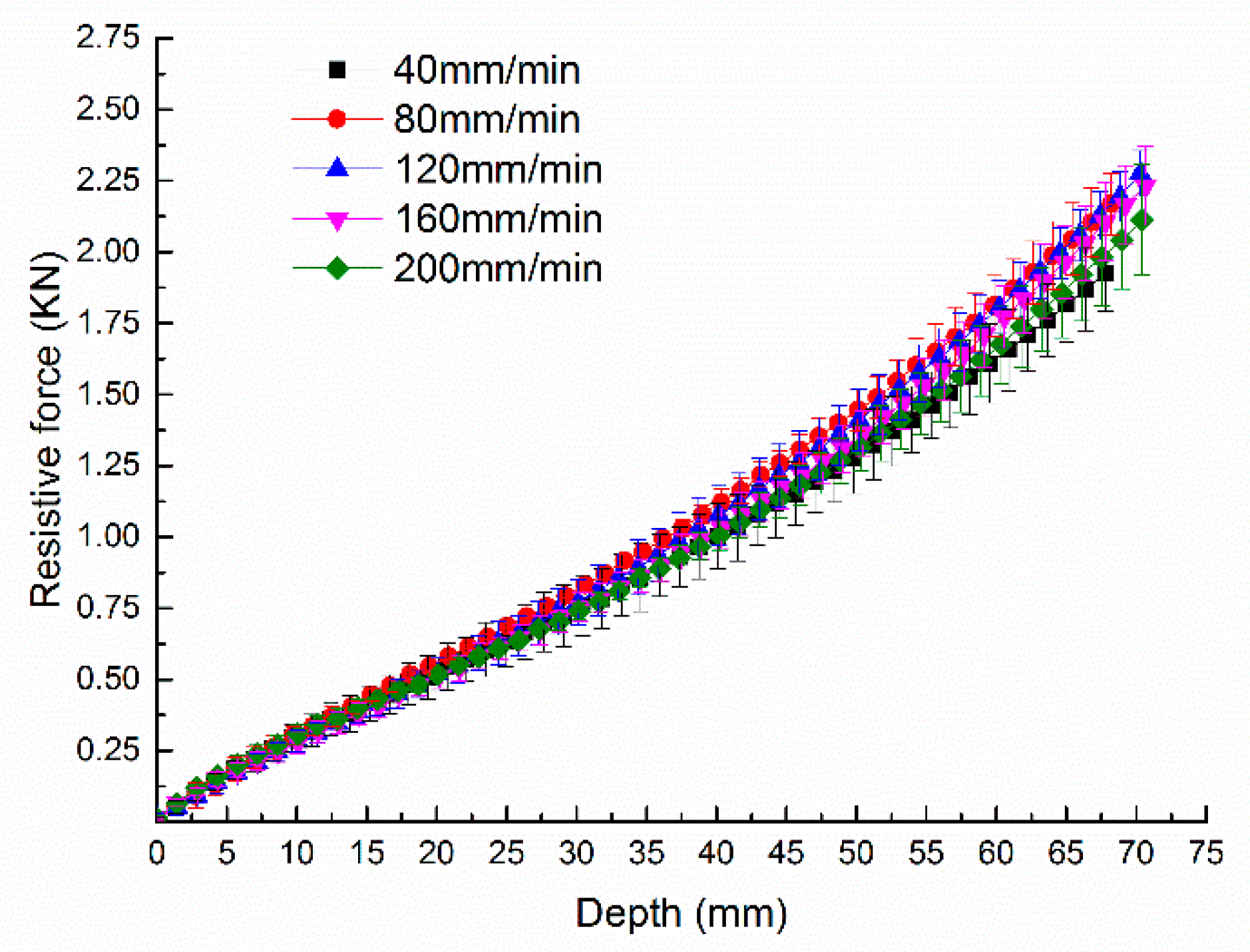
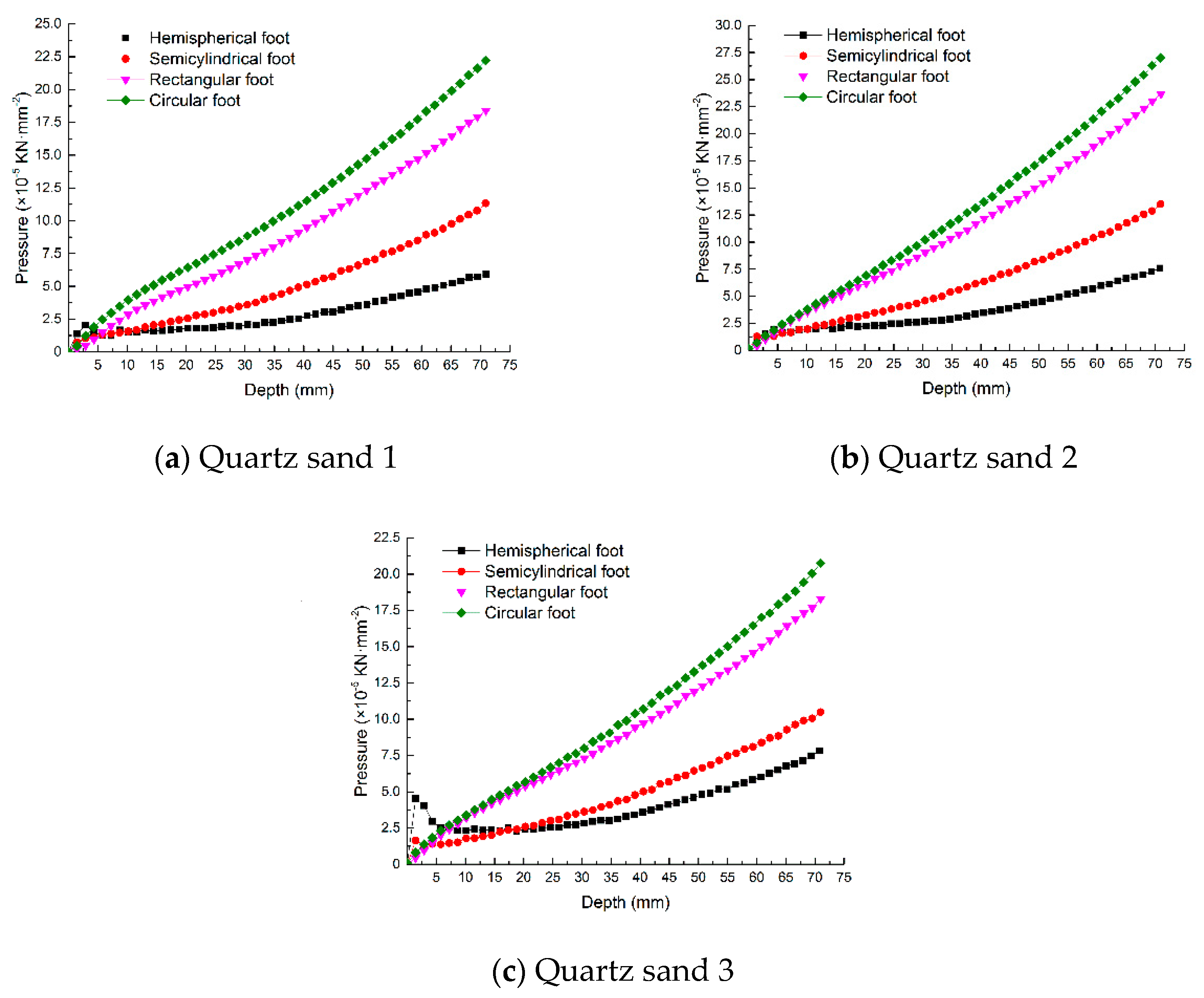
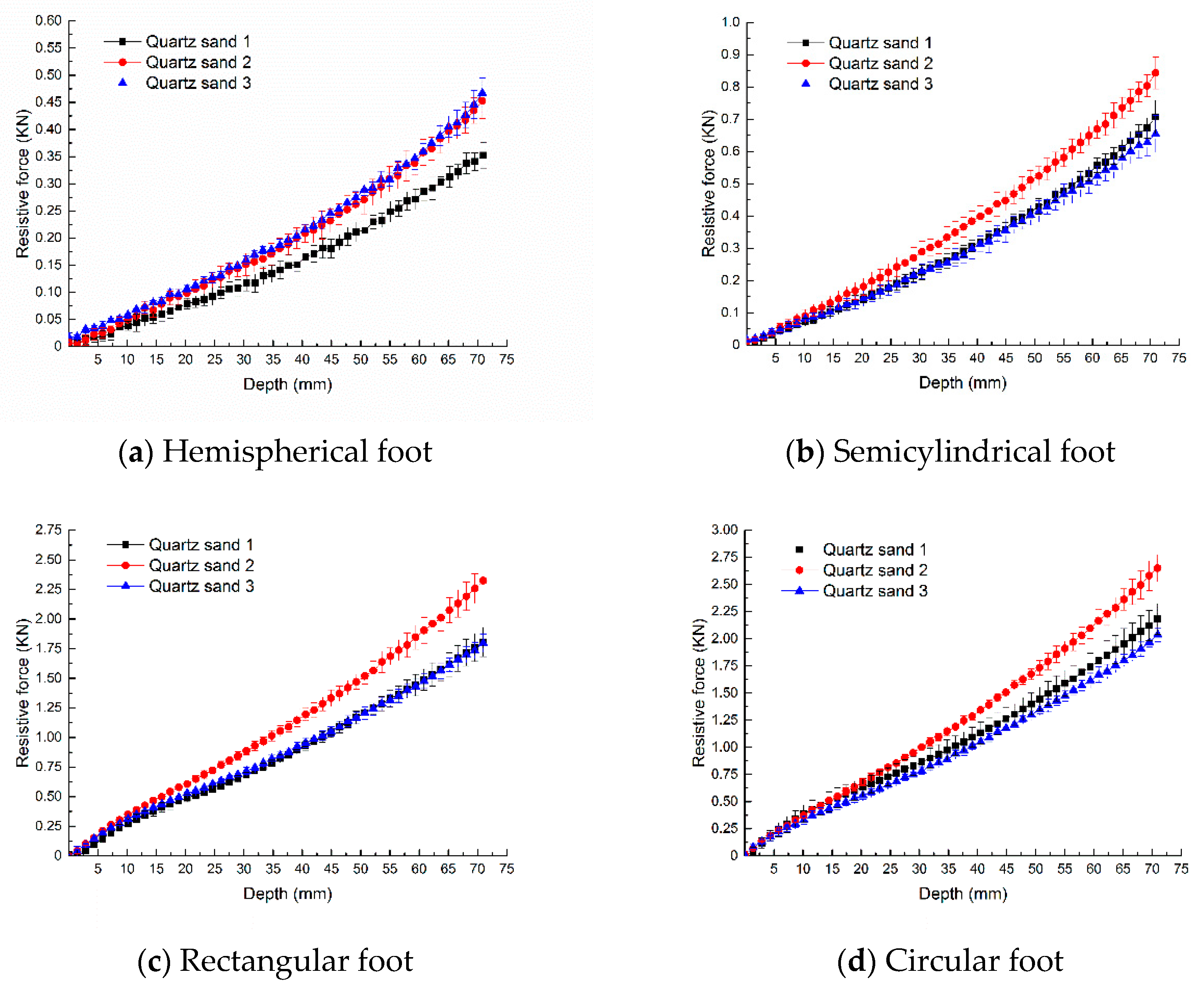
3.1. Comparisons of Intrusion Resistive Force and Pressure
3.2. Effect of Particle Size on Intrusion Resistive Force
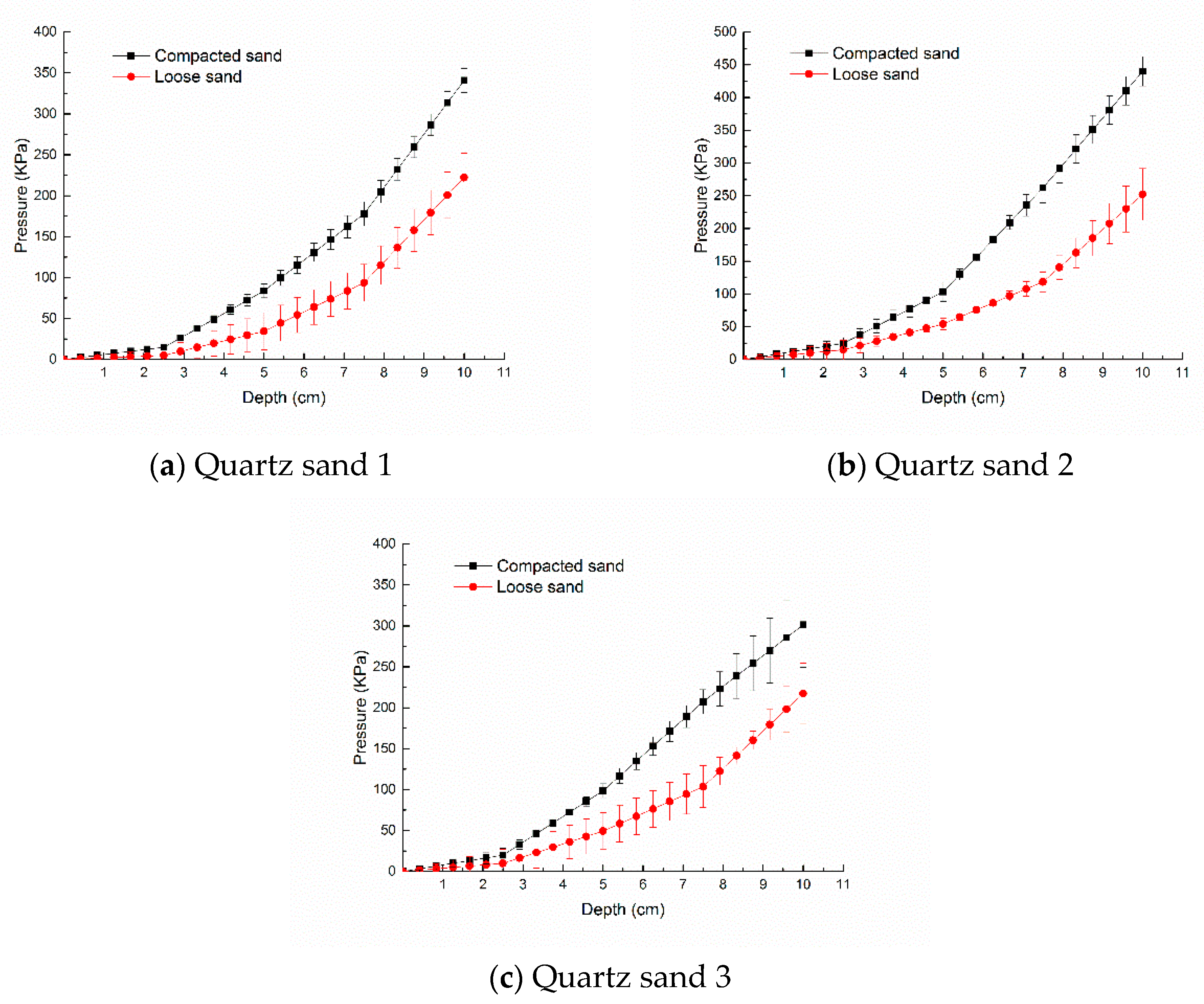
3.3. Effect of Compactness on Intrusion Resistive Force
3.4. Simulation Results of Mechanical Foot Intruding into Quartz Sand
3.4.1. Velocity Field Comparison
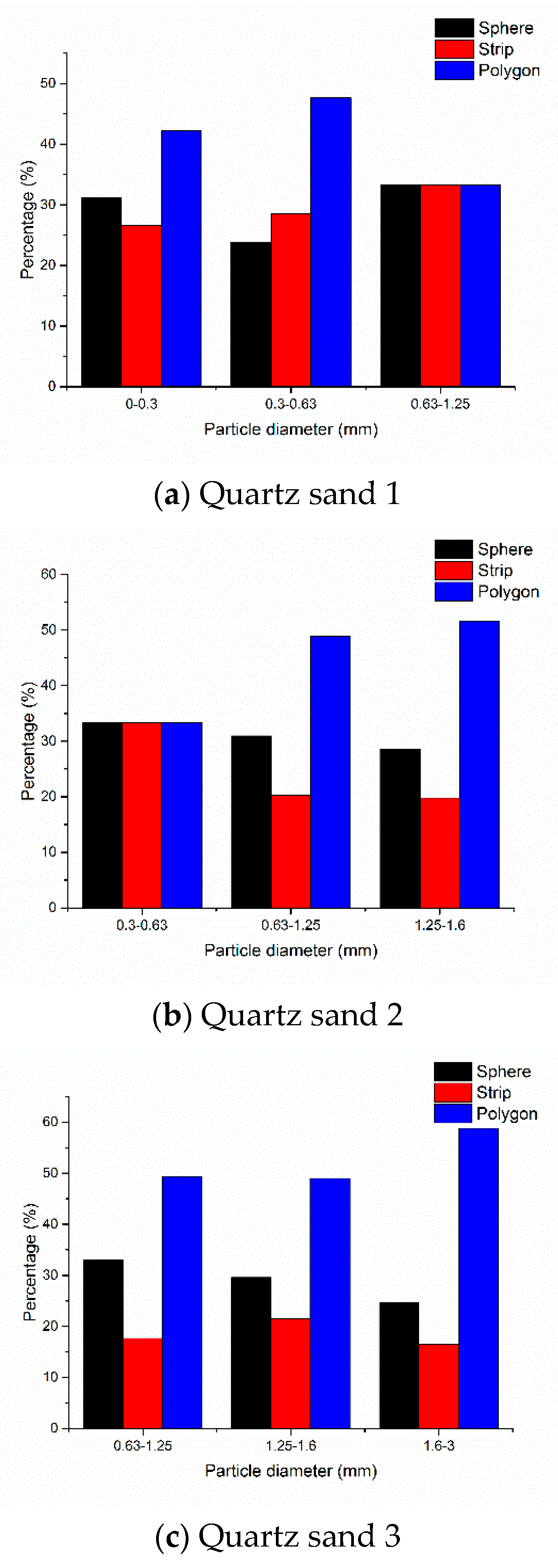
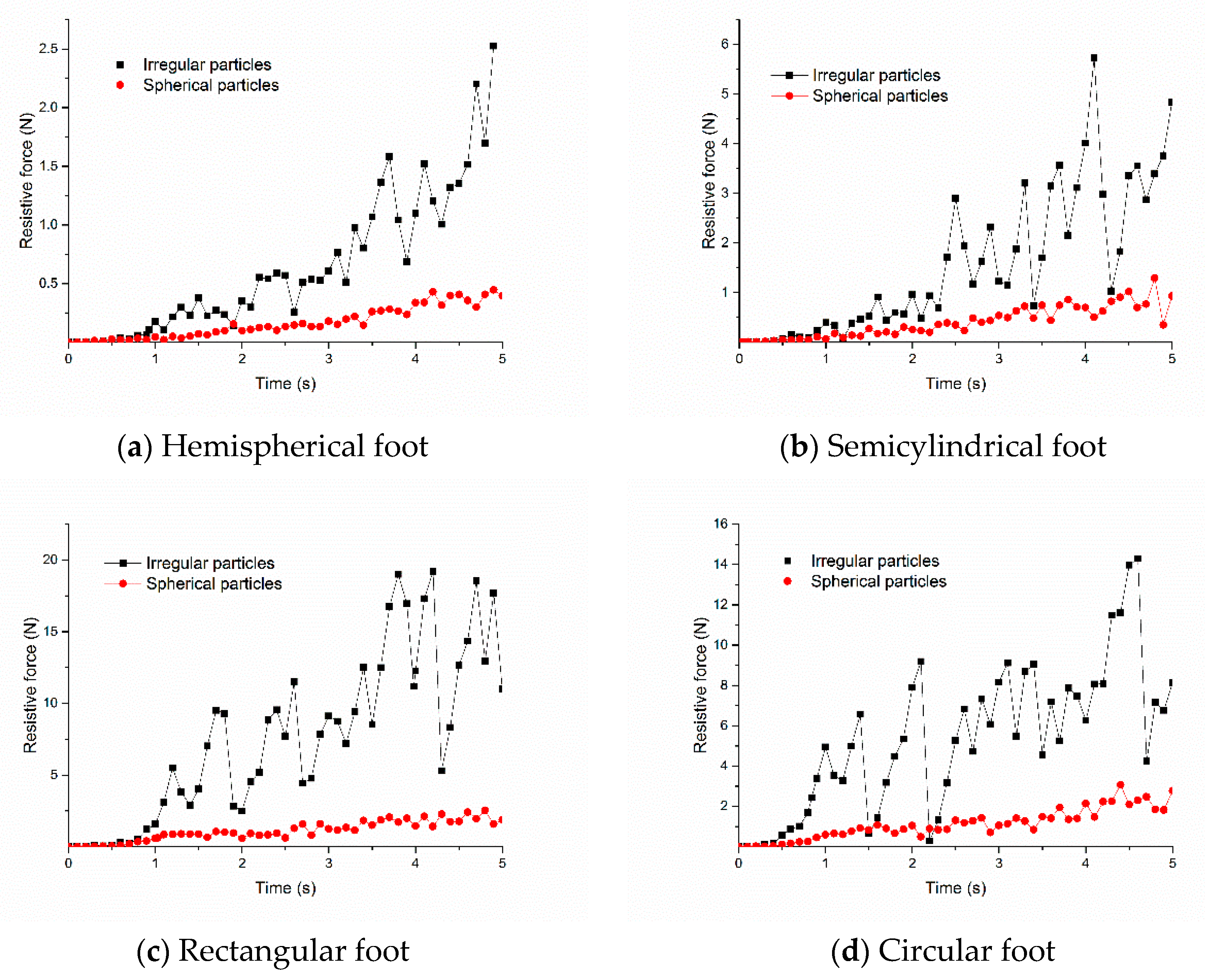
3.4.2. Effect of Particle Shape on Intrusion Resistive Force
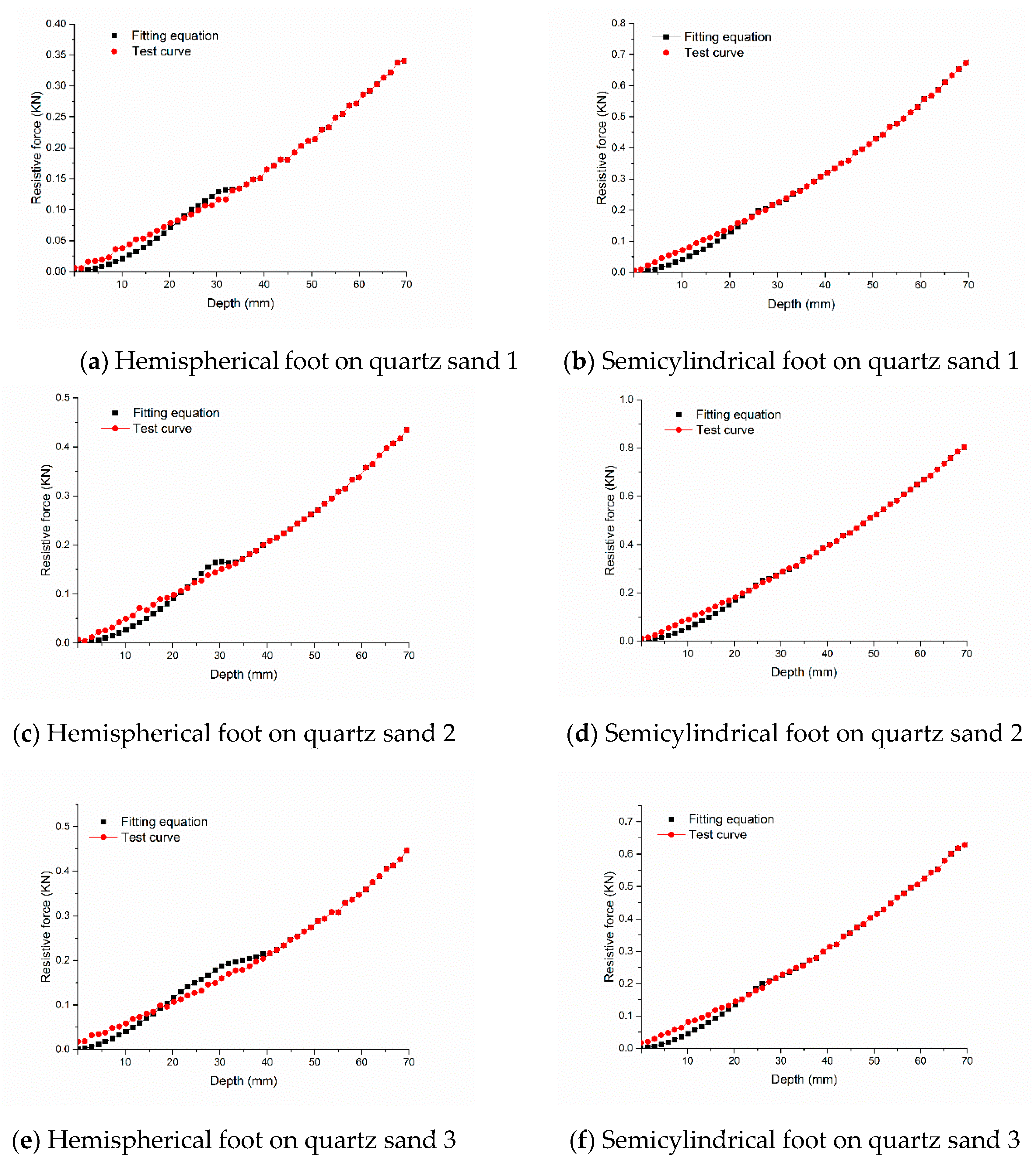
4. Mechanical Models of Robot Feet Intruding into Quartz Sand
5. Conclusions
- Granular media with smaller particle sizes have a higher bulk density and lower angle of stability, but no obvious rule is found for particle shapes of quartz sand with different sizes.
- The intrusion resistive force and pressure of the hemispherical foot are both less than those of the other three mechanical feet on all three kinds of quartz sand.
- The intrusion resistive forces of mechanical feet first increase and then decrease with the increasing particle sizes of quartz sand. The resistive force of intruding into spherical particles is less compared with irregular particles. The corresponding resistive forces of mechanical feet are characterized based on the compactness of quartz sand.
- Based on the intrusion test data, the classic pressure–sinkage model was modified, and a suitable relationship between the intrusion resistive force and the depth of mechanical feet was obtained.
Author Contributions
Funding
Conflicts of Interest
References
- Jaeger, H.M.; Nagel, S.R. Dynamics of granular material. Am. Sci. 1997, 85, 540–545. [Google Scholar]
- Hosoi, A.E.; Goldman, D.I. Beneath our feet: Strategies for locomotion in granular media. Annu. Rev. Fluid Mech. 2015, 47, 431–453. [Google Scholar] [CrossRef] [Green Version]
- Mehta, A.; Barker, G.C. The dynamics of sand. Rep. Prog. Phys. 1994, 57, 383–416. [Google Scholar] [CrossRef]
- Mazouchova, N.; Gravish, N.; Savu, A.; Goldman, D.I. Utilization of granular solidification during terrestrial locomotion of hatchling sea turtles. Biol. Lett. 2010, 6, 398–401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, C.; Zhang, T.; Goldman, D.I. A terradynamics of legged locomotion on granular media. Science 2013, 339, 1408–1412. [Google Scholar] [CrossRef] [Green Version]
- Albert, I.; Tegzes, P.; Kahng, B.; Albert, R.; Sample, J.G.; Pfeifer, M.; Barabasi, A.; Vicsek, T.; Schiffer, P. Jamming and fluctuations in granular drag. Phys. Rev. Lett. 2000, 84, 5122–5125. [Google Scholar] [CrossRef] [Green Version]
- Albert, I.; Sample, J.G.; Morss, A.J.; Rajagopalan, S.; Barabási, A.L.; Schiffer, P. Granular drag on a discrete object: Shape effects on jamming. Phys. Rev. E 2001, 64, 061303. [Google Scholar] [CrossRef] [Green Version]
- Qian, F.; Goldman, D.I. Anticipatory control using substrate manipulation enables trajectory control of legged locomotion on heterogeneous granular media. Proc. SPIE 2015, 9467, 94671U-1. [Google Scholar]
- Bergmann, P.J.; Pettinelli, K.J.; Crockett, M.E.; Schaper, E.G. It’s just sand between the toes: How particle size and shape variation affect running performance and kinematics in a generalist lizard. J. Exp. Biol. 2017, 220, 3706–3716. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Gao, H.; Deng, Z.; Song, J.; Liu, Y.; Liu, G.; Iagnemma, K. Foot-terrain interaction mechanics for legged robots: Modeling and experimental validation. Int. J. Robot Res. 2013, 32, 1585–1606. [Google Scholar] [CrossRef]
- Sakagami, Y.; Watanabe, R.; Aoyama, C.; Matsunaga, S.; Fujimura, K. The intelligent ASIMO: System Overview and Integration. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 2478–2483. [Google Scholar]
- Nelson, G.; Saunders, A.; Neville, N.; Swilling, B.; Bondaryk, J.; Billings, D.; Lee, C.; Playter, R.; Raibert, M. PETMAN: A Humanoid Robot for Testing Chemical Protective Clothing. J. Robot. Soc. Jpn. 2012, 30, 372–377. [Google Scholar] [CrossRef] [Green Version]
- Raibert, M.; Blankespoor, K.; Nelson, G.; Playter, R. Bigdog, the rough-terrain quadruped robot. IFAC Proc. Vol. 2008, 41, 10822–10825. [Google Scholar] [CrossRef] [Green Version]
- Michael, K. Meet Boston Dynamics’ LS3—the Latest Robotic War Machine. Available online: https://ro.uow.edu.au/cgi/viewcontent.cgi?referer=https://scholar.google.com/&httpsredir=1&article=3782&context=eispapers (accessed on 1 March 2020).
- Neuhaus, P.D.; Pratt, J.E.; Johnson, M.J. Comprehensive summary of the Institute for Human and Machine Cognition’s experience with LittleDog. Int. J. Robot. Res. 2011, 30, 216–235. [Google Scholar] [CrossRef]
- Gorner, M.; Wimbock, T.; Hirzinger, G. The DLR Crawler: Evaluation of gaits and control of an actively compliant six-legged walking robot. Ind. Robot 2009, 36, 344–351. [Google Scholar] [CrossRef]
- Krotkov, E.; Bares, J.; Kanade, T.; Mitchell, T.; Simmons, R.; Whittaker, R. Ambler: A Six-Legged Planetary Rover. In Proceedings of the Fifth International Conference on Advanced Robotics and Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991; IEEE: Piscataway, NJ, USA, 1991; pp. 717–722. [Google Scholar]
- Wettergreen, D.; Pangels, H.; Bares, J. Behavior-Based Gait Execution for the Dante II Walking Robot. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems and Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 274–279. [Google Scholar]
- Gilardi, G.; Sharf, I. Literature survey of contact dynamics modelling. Mech. Mach. Theory 2002, 37, 1213–1239. [Google Scholar] [CrossRef]
- Zhang, T.; Goldman, D.I. The effectiveness of resistive force theory in granular locomotion. Phys. Fluids 2014, 26, 2767–2780. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Umbanhowar, P.B.; Komsuoglu, H.; Koditschek, D.E.; Goldman, D.I. Sensitive dependence of the motion of a legged robot on granular media. Proc. Natl. Acad. Sci. USA 2009, 106, 3029–3034. [Google Scholar] [CrossRef] [Green Version]
- Qian, F.; Zhang, T.; Korff, W.; Umbanhowar, P.B.; Full, R.J.; Goldman, D.I. Principles of appendage design in robots and animals determining terradynamic performance on flowable ground. Bioinspir. Biomim. 2015, 10, 056014. [Google Scholar] [CrossRef]
- Ding, L.; Deng, Z.; Gao, H.; Nagatani, K.; Yoshida, K. Planetary rovers’ wheel–soil interaction mechanics: New challenges and applications for wheeled mobile robots. Intel. Serv. Robot. 2011, 4, 17–38. [Google Scholar] [CrossRef]
- Bekker, M.G. Introduction to Terrain–Vehicle Systems; The University of Michigan Press: Ann Arbor, MI, USA, 1969. [Google Scholar]
- Wong, J.Y.; Reece, A.R. Prediction of rigid wheel performance based on the analysis of soil-wheel stresses part I-performance of driven rigid wheels. J. Terramech. 1967, 4, 81–98. [Google Scholar] [CrossRef]
- Janosi, Z.; Hanamoto, B. Analytical Determination of Drawbar Pull as a Function of Slip for Tracked Vehicle in Deformable Soils. In Proceedings of the 1st International Conference of ISTVES, Turin, Italy, 1 June 1961; International Society for Terrain-Vehicle Systems: Ferrara, Italy, 1961; pp. 707–726. [Google Scholar]
- Kang, W.; Feng, Y.; Liu, C.; Blumenfeld, R. Archimedes’ law explains penetration of solids into granular media. Nat. Commun. 2018, 9, 1101. [Google Scholar] [CrossRef] [PubMed]
- Yeomans, B.; Saaj, C.M. Towards terrain interaction prediction for bioinspired planetary exploration rovers. Bioinspir. Biomim. 2014, 9, 016009. [Google Scholar] [CrossRef] [PubMed]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dynam. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]
- Gravish, N.; Goldman, D.I. Effect of volume fraction on granular avalanche dynamics. Phys. Rev. E 2014, 90, 032202. [Google Scholar] [CrossRef] [Green Version]
- Brzinski, T.A.; Mayor, P.; Durian, D.J. Depth-dependent resistance of granular media to vertical penetration. Phys. Rev. Lett. 2013, 111, 168002. [Google Scholar] [CrossRef] [Green Version]
- Stone, M.B.; Barry, R.; Bernstein, D.P.; Pelc, M.D.; Tsui, Y.K.; Schiffer, P. Local jamming via penetration of a granular medium. Phys. Rev. E 2004, 70, 041301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Han, D.L.; Ji, Q.L.; He, Y.; Li, J.Q. Calibration methods of sandy soil parameters in simulation of discrete element method. Trans. Chin. Soc. Agric. Mach. 2017, 48, 54–61. [Google Scholar]
- Shi, L.R.; Wu, J.M.; Zhao, W.Y.; Sun, W.; Zhang, F.W.; Sun, B.G. Establishment and parameter verification of farmland soil model in uniaxial compression based on discrete element method. J. China Agric. Univ. 2015, 20, 174–182. [Google Scholar]
- Zhang, R.; Han, D.L.; He, Y.; Wan, H.J.; Ma, S.S.; Li, J.Q. Drag reduction and wear resistance mechanisms of a bionic shovel by discrete element method simulation. Simul. Soc. Mod. Sim. 2019, 95, 231–239. [Google Scholar] [CrossRef]
- Aguilar, J.; Goldman, D.I. Robophysical study of jumping dynamics on granular media. Nat. Phys. 2016, 12, 278–283. [Google Scholar] [CrossRef] [Green Version]








| Particle Size Distributions (mm) | ||||||
|---|---|---|---|---|---|---|
| 0–0.3 | 0.3–0.63 | 0.63–1.25 | 1.25–1.6 | 1.6–3 | ||
| Quartz sand 1 | Mass (g) | 16 | 68 | 408 | ||
| Proportion (%) | 3.3 | 13.8 | 82.9 | |||
| Quartz sand 2 | Mass (g) | 14 | 324 | 160 | ||
| Proportion (%) | 2.8 | 65 | 32 | |||
| Quartz sand 3 | Mass (g) | 124 | 216 | 156 | ||
| Proportion (%) | 25 | 43.5 | 31.5 | |||
| Bulk Density (Kg·m−3) | Angle of Stability (°) | Elasticity Modulus (MPa) | Poisson Ratio | Shear Modulus (MPa) | |||
|---|---|---|---|---|---|---|---|
| Drawing Plate Method | Funnel Method | Mean ± S.D. | |||||
| Quartz sand 1 | 1464.44 ± 4.01 | 30.93 ± 0.45 | 31.80 ± 1.57 | 31.37 ± 1.14 | 23.97 | 0.48 | 8.12 |
| Quartz sand 2 | 1394.90 ± 4.78 | 31.47 ± 1.01 | 33.23 ± 0.91 | 32.35 ± 1.29 | 17.28 | 0.48 | 5.85 |
| Quartz sand 3 | 1294.59 ± 4.21 | 33.27 ± 0.40 | 34.37 ± 1.26 | 33.82 ± 1.03 | 15.59 | 0.48 | 5.28 |
| Coefficient of Restitution | Coefficient of Static Friction | Coefficient of Dynamic Friction | |
|---|---|---|---|
| Quartz sand 1 | 0.55 | 0.32 | 0.05 |
| Quartz sand 2 | 0.15 | 0.2 | 0.2 |
| Quartz sand 3 | 0.35 | 1.16 | 0 |
| Quartz Sand 1 | Quartz Sand 2 | Quartz Sand 3 | ||||
|---|---|---|---|---|---|---|
| K | n | K | n | K | n | |
| Hemispherical foot | 0.10536 | 0.91888 | 0.13966 | 0.90701 | 0.36103 | 0.67265 |
| R2 | 0.85962 | 0.89583 | 0.58719 | |||
| Semicylindrical foot | 0.06263 | 1.20465 | 0.09946 | 1.13823 | 0.08381 | 1.12071 |
| R2 | 0.98445 | 0.98547 | 0.97505 | |||
| Rectangular foot | 0.18920 | 1.06698 | 0.23688 | 1.07143 | 0.26057 | 0.98692 |
| R2 | 0.99601 | 0.99614 | 0.99464 | |||
| Circular foot | 0.30313 | 0.99680 | 0.24921 | 1.09116 | 0.25219 | 1.02336 |
| R2 | 0.99203 | 0.99652 | 0.99379 | |||
| Hemispherical foot (Z ≤ 0.035) | 0.1125 | 0.8409 |
| R2 | 0.9921 | |
| Semicylindrical foot (Z ≤ 0.035) | 0.0330 | 0.4576 |
| R2 | 0.9406 | |
| Intrusion Resistive Force Model | |
|---|---|
| Foot with variable cross-sectional area | where (Z ≤ 0.035) |
| where (Z > 0.035) | |
| Foot with constant cross-sectional area | where |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, D.; Zhang, R.; Zhang, H.; Hu, Z.; Li, J. Mechanical Performances of Typical Robot Feet Intruding into Sands. Energies 2020, 13, 1867. https://doi.org/10.3390/en13081867
Han D, Zhang R, Zhang H, Hu Z, Li J. Mechanical Performances of Typical Robot Feet Intruding into Sands. Energies. 2020; 13(8):1867. https://doi.org/10.3390/en13081867
Chicago/Turabian StyleHan, Dianlei, Rui Zhang, Hua Zhang, Zhenyu Hu, and Jianqiao Li. 2020. "Mechanical Performances of Typical Robot Feet Intruding into Sands" Energies 13, no. 8: 1867. https://doi.org/10.3390/en13081867
APA StyleHan, D., Zhang, R., Zhang, H., Hu, Z., & Li, J. (2020). Mechanical Performances of Typical Robot Feet Intruding into Sands. Energies, 13(8), 1867. https://doi.org/10.3390/en13081867







