Numerical Study of a Novel Concept for Manufacturing Savonius Turbines with Twisted Blades
Abstract
1. Introduction
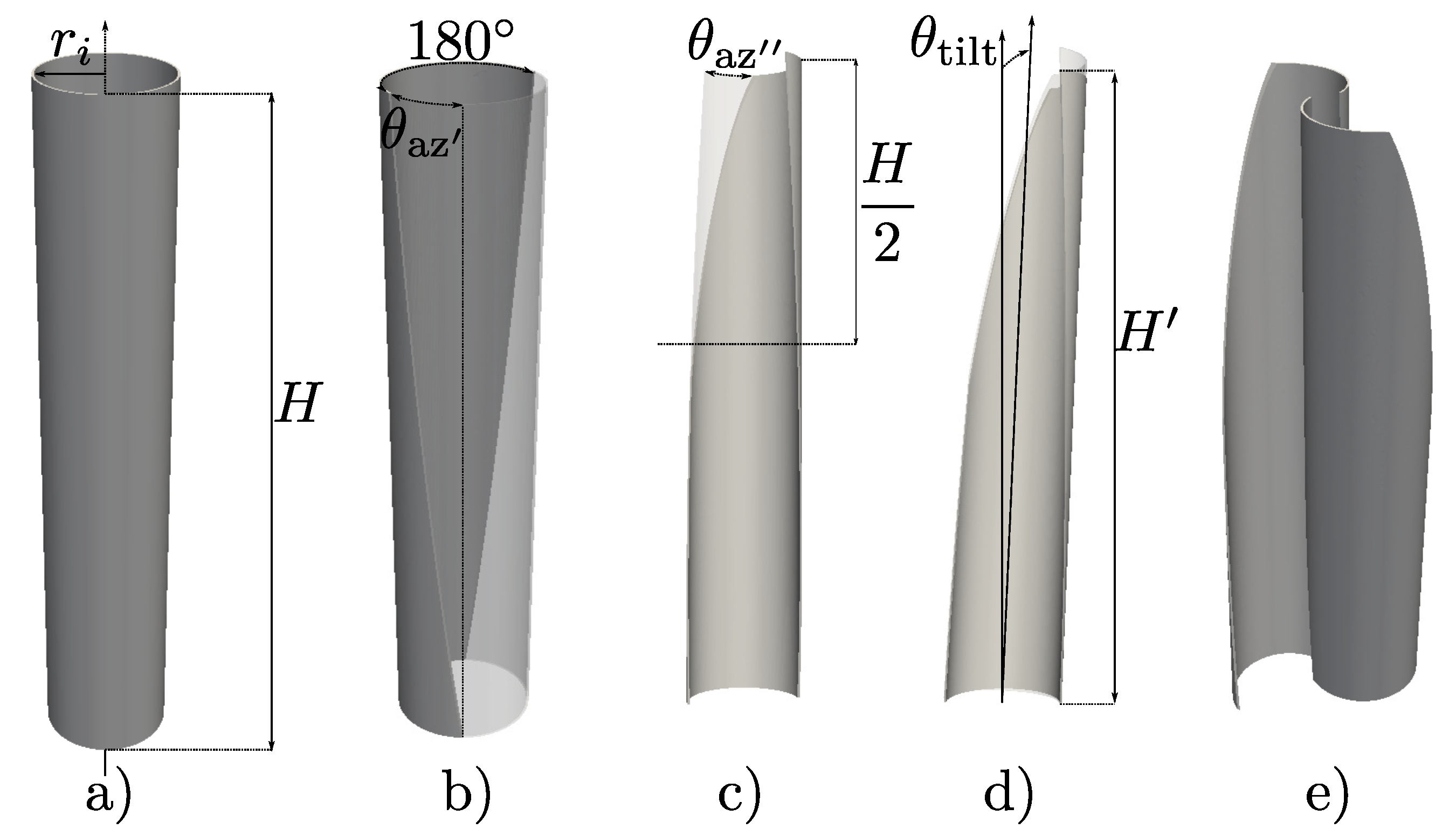
2. Description of the Novel Twisted Blades Manufacturing Concept
2.1. SAWINT: Savonius Turbine for Micro-Grid Systems
2.2. SAVANT: Savonius Turbine for Energy Production in Extremely Cold Conditions
3. Methodology
3.1. Numerical Model
3.2. Simulation Parameters: Validation Case
Mesh Spatial Sensitivity
4. Results and Discussion
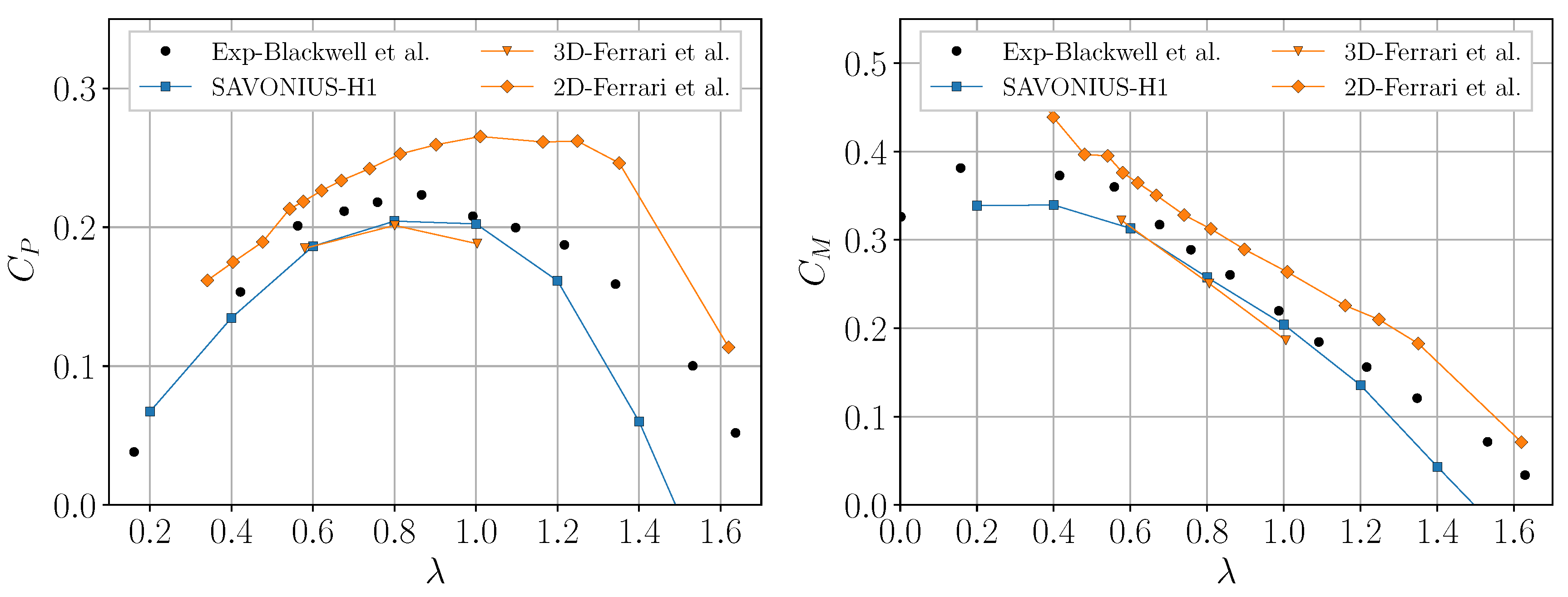
4.1. Power and Torque Coefficient Curves
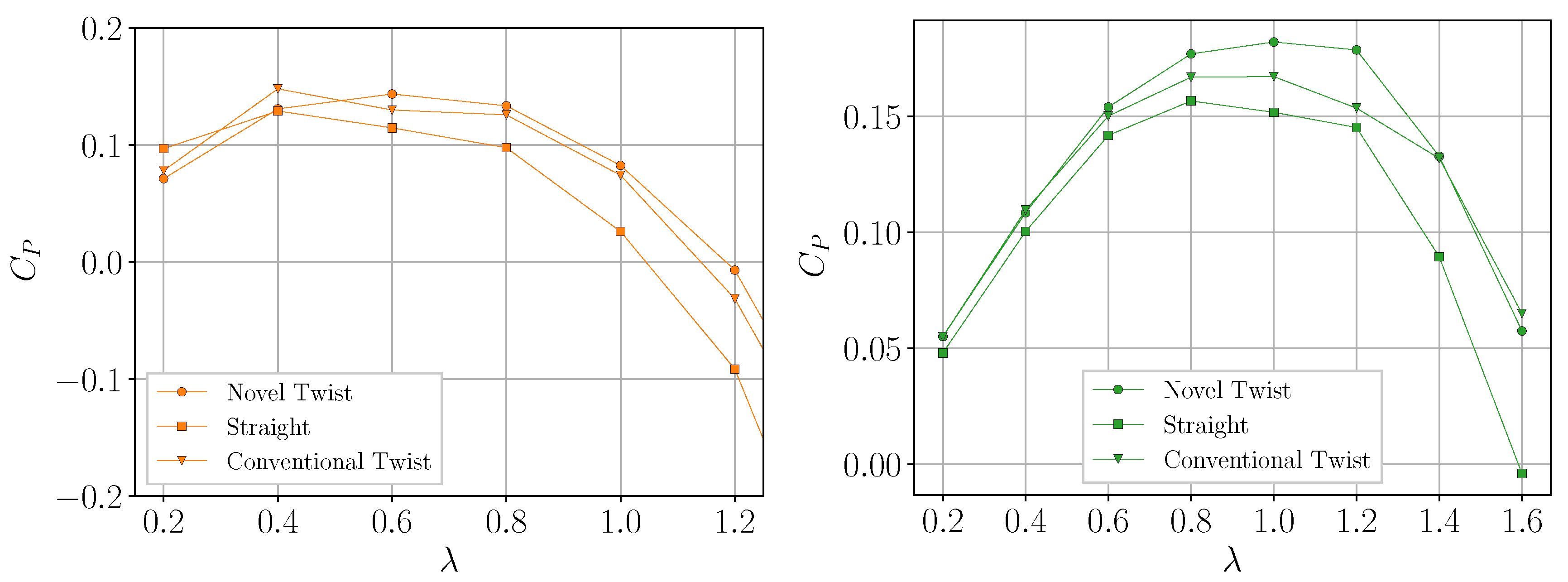
4.2. Aerodynamic Performance of SAWINT and SAVANT
4.2.1. Power Coefficient Curves
- a novel twisted blade obtained from manufacturing process presented in this work, which is based on the cutting of a hollow cylinder
- the conventional Savonius straight blade rotor with S-shaped cross section constructed by two semi circular buckets and
- the conventional twist blade with a cross section that changes to a certain degree in each step along the vertical axis (helical Savonius rotor).
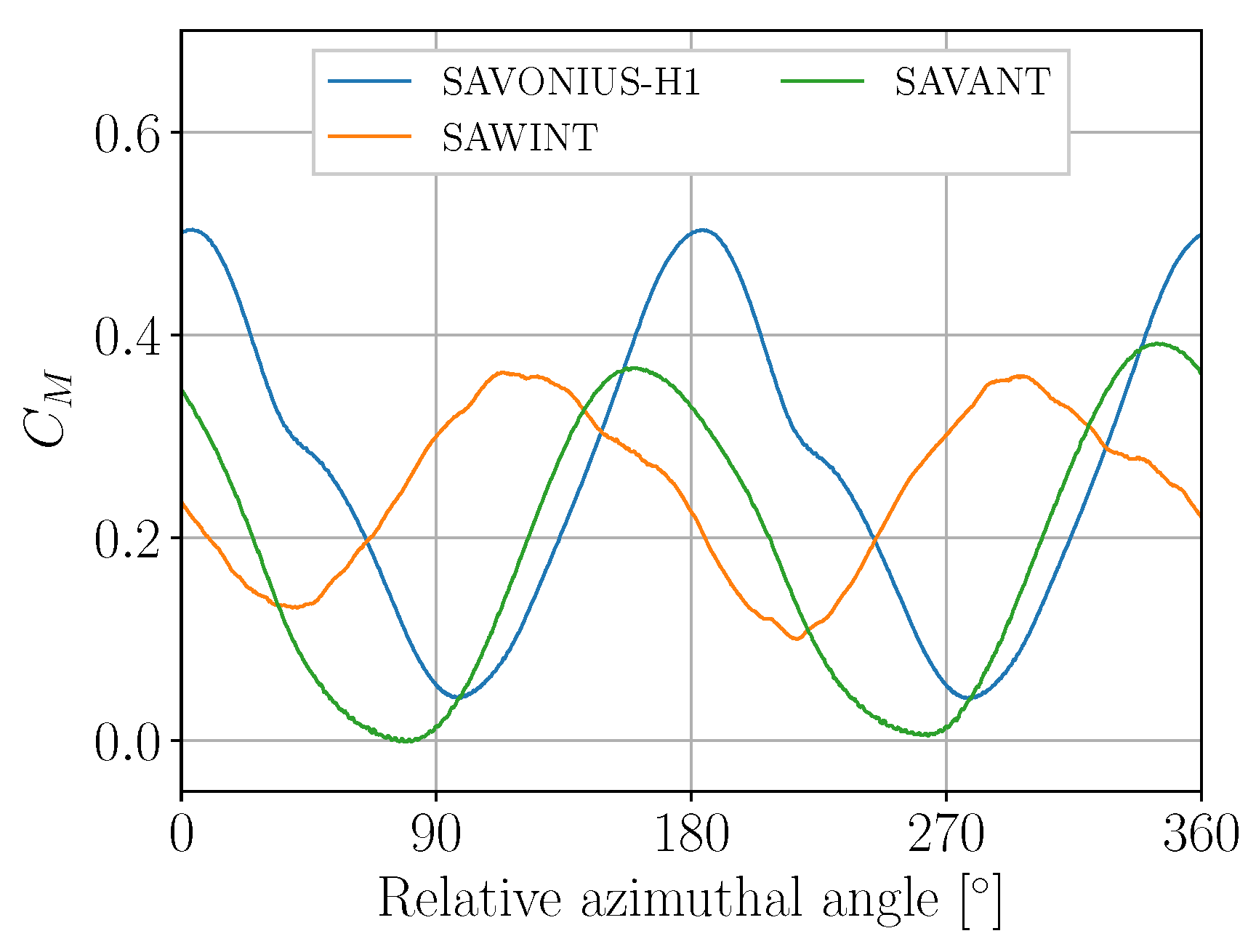
4.2.2. Torque Coefficient
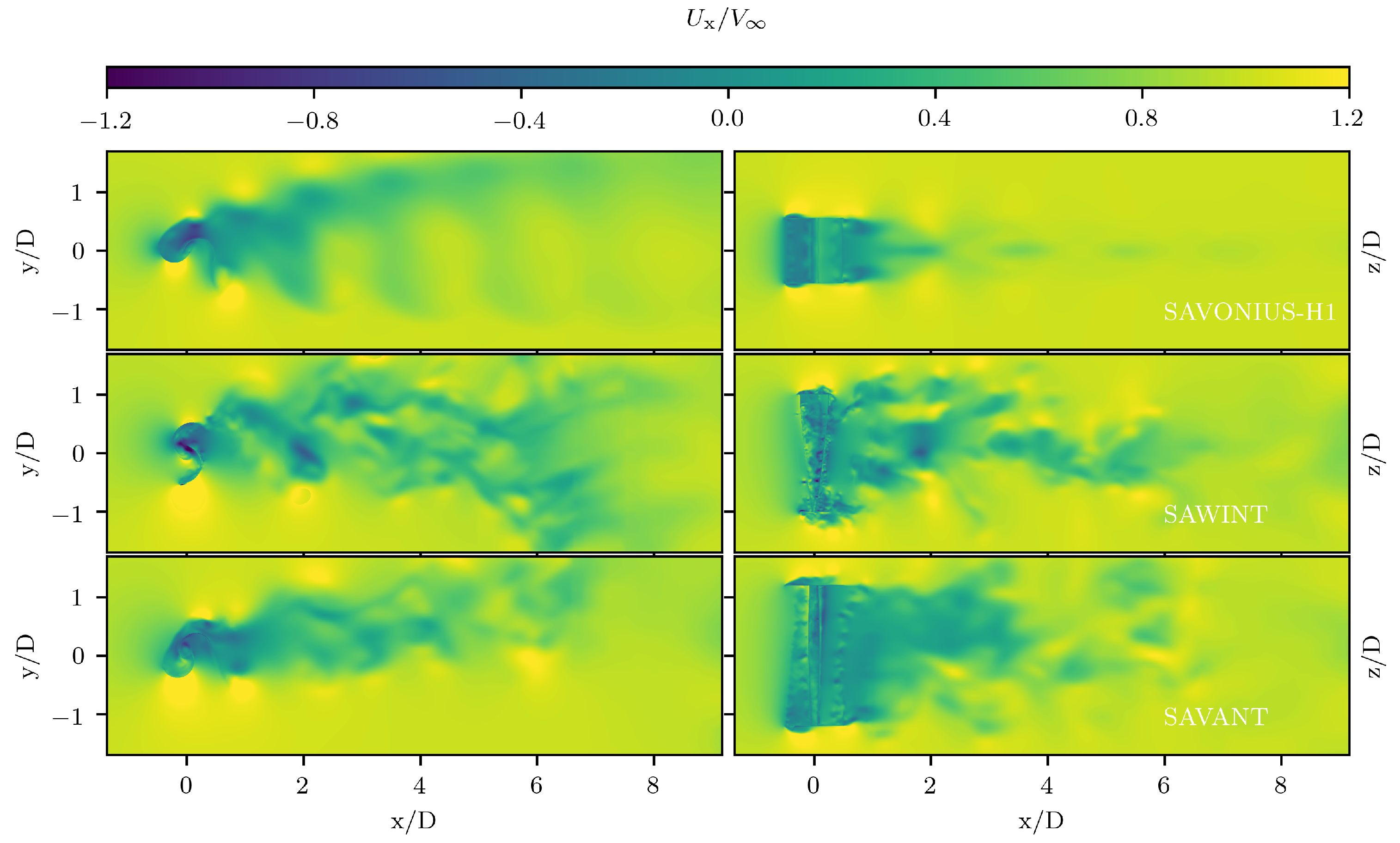
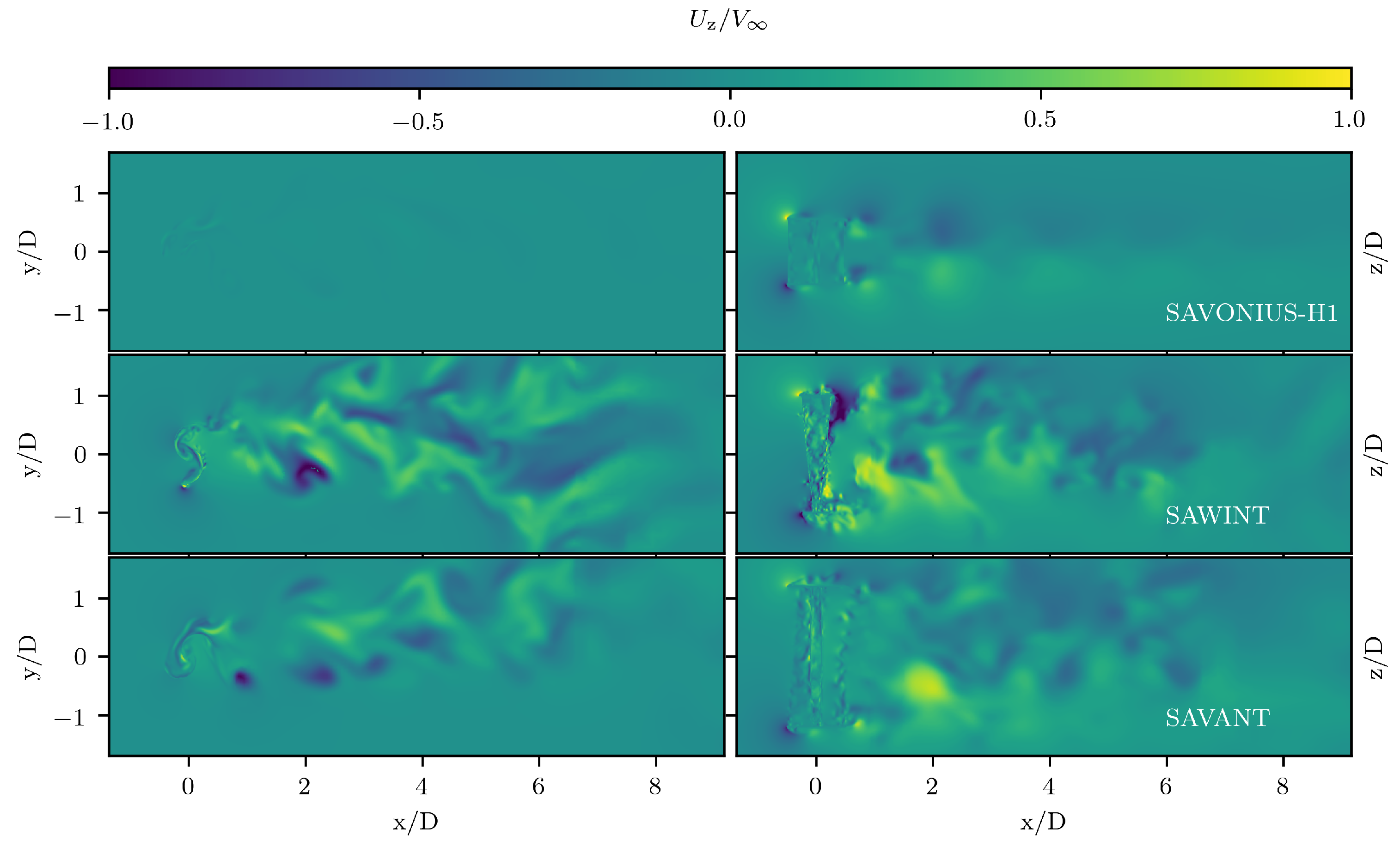
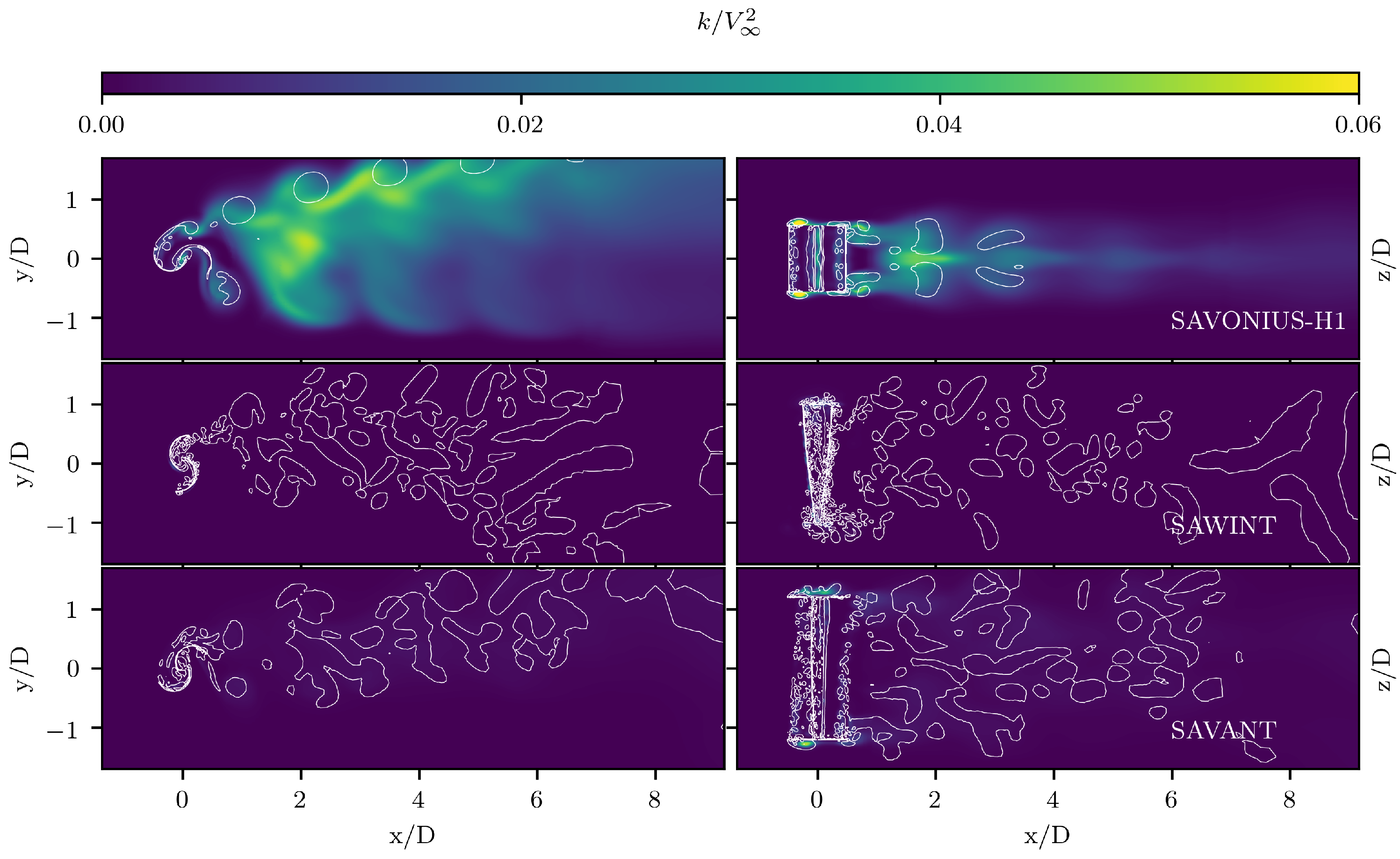
4.2.3. Resulting Flow Pattern
5. General Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Shikha; Bhatti, T.; Kothari, D. Wind energy conversion systems as a distributed source of generation. J. Energy Eng. 2003, 129, 69–80. [Google Scholar]
- Menet, J. A double-step Savonius rotor for local production of electricity: A design study. Renew. Energy 2004, 29, 1843–1862. [Google Scholar] [CrossRef]
- Kumara, E.; Hettiarachchi, N.; Jayathilake, R. Overview of the vertical axis wind turbines. Int. J. Sci. Res. Innov. Technol. 2017, 4, 56–67. [Google Scholar]
- Savonius, S.J. Wind Rotor. U.S. Patent 1,766,765, 24 June 1930. [Google Scholar]
- Kamoji, M.; Kedare, S.; Prabhu, S. Performance tests on helical Savonius rotors. Renew. Energy 2009, 34, 521–529. [Google Scholar] [CrossRef]
- Shankar, P. The Effects of Geometry and Reynolds Number on Savonius Type Rotors. In National Aeronautic Laboratory Bangalore 560017; Technical report, AE-TM-3-76; National Aeronautical Laboratory: Bangalore, India, 1976. [Google Scholar]
- Blackwell, B.F.; Sheldahl, R.F.; Feltz, L.V. Wind Tunnel Performance Data for Two-and Three-Bucket Savonius Rotors; Sandia Laboratories: Springfield, VA, USA, 1977. [Google Scholar]
- Jang, H.; Paek, I.; Kim, S.; Jeong, D. Performance Prediction and Validation of a Small-Capacity Twisted Savonius Wind Turbine. Energies 2019, 12, 1721. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, Y.T.; Lim, H.C. Effect of twist angle on the performance of Savonius wind turbine. Renew. Energy 2016, 89, 231–244. [Google Scholar] [CrossRef]
- Damak, A.; Driss, Z.; Abid, M. Experimental investigation of helical Savonius rotor with a twist of 180. Renew. Energy 2013, 52, 136–142. [Google Scholar] [CrossRef]
- Saha, U.; Rajkumar, M.J. On the performance analysis of Savonius rotor with twisted blades. Renew. Energy 2006, 31, 1776–1788. [Google Scholar] [CrossRef]
- Aliferis, A.D.; Jessen, M.S.; Bracchi, T.; Hearst, R.J. Performance and wake of a Savonius vertical-axis wind turbine under different incoming conditions. Wind Energy 2019, 22, 1260–1273. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, R. Performance analysis of a Savonius hydrokinetic turbine having twisted blades. Renew. Energy 2017, 108, 502–522. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, R. Performance analysis of a single stage modified Savonius hydrokinetic turbine having twisted blades. Renew. Energy 2017, 113, 461–478. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, R. Performance parameters of Savonius type hydrokinetic turbine–A Review. Renew. Sustain. Energy Rev. 2016, 64, 289–310. [Google Scholar] [CrossRef]
- Kamoji, M.; Kedare, S.; Prabhu, S. Experimental investigations on single stage, two stage and three stage conventional Savonius rotor. Int. J. Energy Res. 2008, 32, 877–895. [Google Scholar] [CrossRef]
- Saha, U.; Thotla, S.; Maity, D. Optimum design configuration of Savonius rotor through wind tunnel experiments. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1359–1375. [Google Scholar] [CrossRef]
- ARIANNA—Antarctic Ross Ice-Shelf ANtenna Neutrino Array. Available online: http://arianna.ps.uci.edu/ (accessed on 9 October 2019).
- Davidson, L. Fluid Mechanics, Turbulent Flow and Turbulence Modeling; Chalmers University of Technology: Goteborg, Sweden, 2016. [Google Scholar]
- Ferrari, G.; Federici, D.; Schito, P.; Inzoli, F.; Mereu, R. CFD study of Savonius wind turbine: 3D model validation and parametric analysis. Renew. Energy 2017, 105, 722–734. [Google Scholar] [CrossRef]
- Nasef, M.; El-Askary, W.; Abdel-Hamid, A.; Gad, H. Evaluation of Savonius rotor performance: Static and dynamic studies. J. Wind Eng. Ind. Aerodyn. 2013, 123, 1–11. [Google Scholar] [CrossRef]
- Shaheen, M.; El-Sayed, M.; Abdallah, S. Numerical study of two-bucket Savonius wind turbine cluster. J. Wind Eng. Ind. Aerodyn. 2015, 137, 78–89. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef]
- Pope, A.; Harper, J.J. Low Speed Wind Tunnel Testing; John Willy and Sons: New York, NY, USA, 1966. [Google Scholar]
- Chakraborty, P.; Balachandar, S.; Adrian, R.J. On the relationships between local vortex identification schemes. J. Fluid Mech. 2005, 535, 189–214. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 96–116. [Google Scholar]




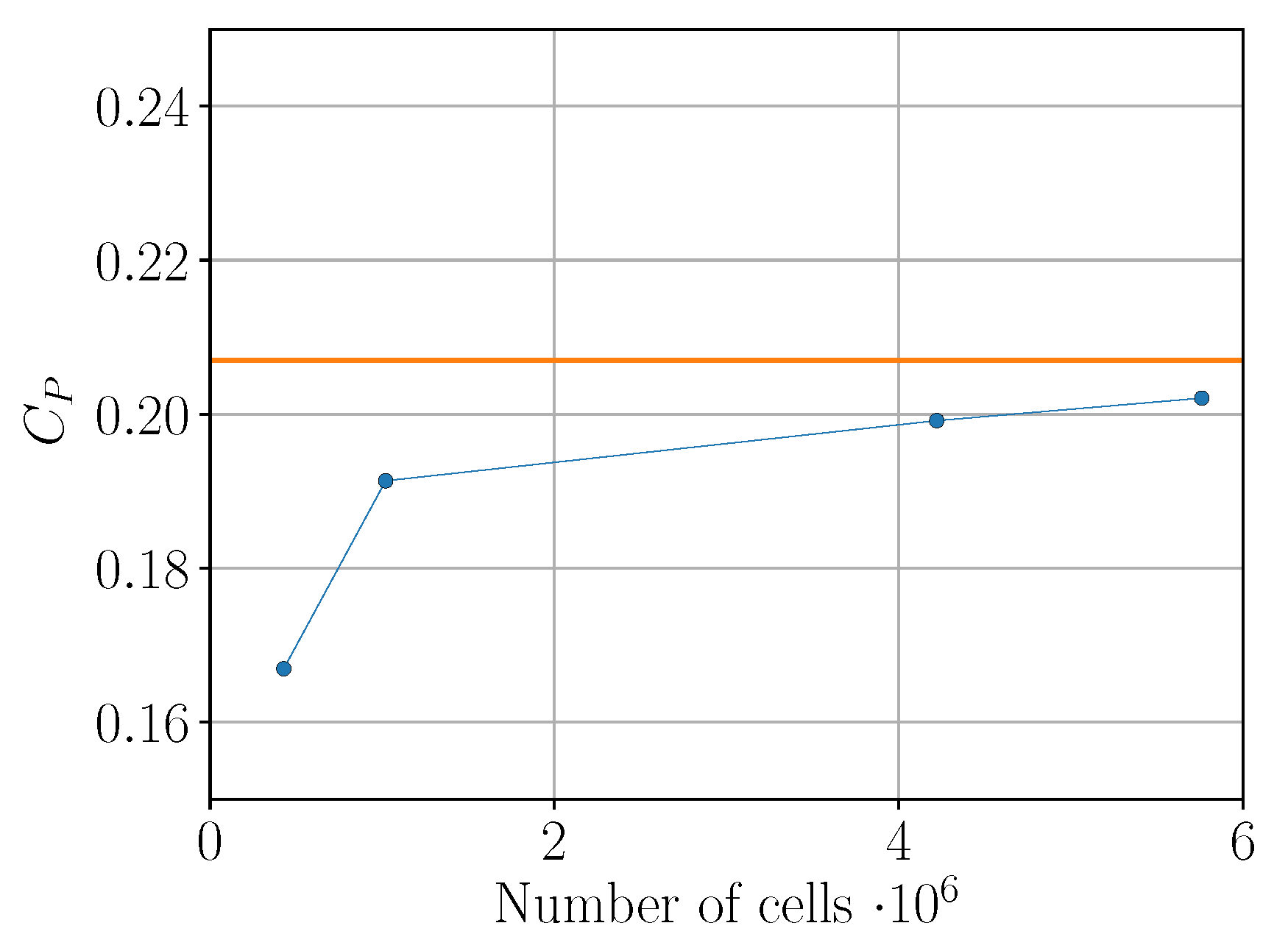

| Terms | Discretization Scheme |
|---|---|
| Temporal | First, order, Transient |
| Gradient ∇ | Second order, Gaussian integration |
| Divergence | Second order, Upwind-biased |
| Laplacian | Second order, Gaussian integration |
| Interpolation | Linear interpolation |
| Number of blades | 2 |
| 0.9024 m | |
| 0.9064 m | |
| H | 1 m |
| d | 0.5 m |
| s | 2 mm |
| o | 92.72 mm |
| Aspect ratio | 1.11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendoza, V.; Katsidoniotaki, E.; Bernhoff, H. Numerical Study of a Novel Concept for Manufacturing Savonius Turbines with Twisted Blades. Energies 2020, 13, 1874. https://doi.org/10.3390/en13081874
Mendoza V, Katsidoniotaki E, Bernhoff H. Numerical Study of a Novel Concept for Manufacturing Savonius Turbines with Twisted Blades. Energies. 2020; 13(8):1874. https://doi.org/10.3390/en13081874
Chicago/Turabian StyleMendoza, Victor, Eirini Katsidoniotaki, and Hans Bernhoff. 2020. "Numerical Study of a Novel Concept for Manufacturing Savonius Turbines with Twisted Blades" Energies 13, no. 8: 1874. https://doi.org/10.3390/en13081874
APA StyleMendoza, V., Katsidoniotaki, E., & Bernhoff, H. (2020). Numerical Study of a Novel Concept for Manufacturing Savonius Turbines with Twisted Blades. Energies, 13(8), 1874. https://doi.org/10.3390/en13081874







