Numerical Studies on Teeter Bed Separator for Particle Separation
Abstract
:1. Introduction
2. Model Description
2.1. Governing Equation for Liquid and Solid Phases
2.2. Simulation Conditions
3. Results and Discussion
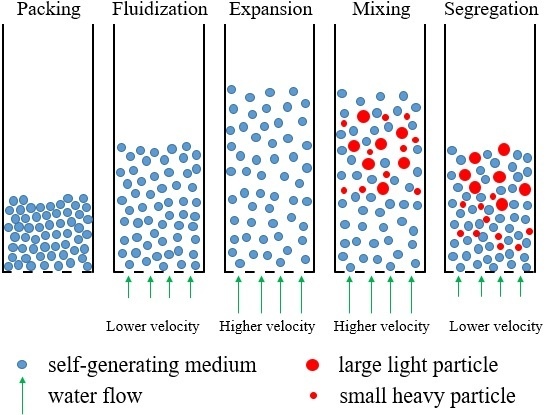
3.1. The Bed Expansion Characteristics
3.2. Settling Behavior of Foreign Particles in Bed
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| liquid density, kg/m3 | |
| volume fraction of liquid, dimensionless | |
| liquid velocity, m/s | |
| fluidized particles density, kg/m3 | |
| volume fraction of fluidized particles, dimensionless | |
| fluidized particle velocity, m/s | |
| drag force coefficient, dimensionless | |
| fluidized particle Reynolds number, dimensionless | |
| diameter of fluidized particle, m | |
| foreign particle density, kg/m3 | |
| foreign particle diameter, m | |
| foreign particle velocity, m/s | |
| gravity acceleration, m/s2 | |
| foreign particle slip velocity in indefinite medium, m/s | |
| bounded settling velocity for foreign particle, m/s | |
| mixture/pseudo-fluid density, kg/m3 | |
| fluidized particle velocity in indefinite medium, m/s | |
| pseudo-fluid viscosity, Pa·s | |
| liquid viscosity, Pa·s | |
| foreign particle classification velocity, m/s | |
| initial bed height, m | |
| R-Z index, dimensionless | |
| effective density, kg/m3 | |
| particle size, dimensionless | |
| friction factor, dimensionless | |
| number of displaced particles | |
| collision coefficient, dimensionless | |
| Greek letters | |
| μ | viscosity, Pa·s |
| ρ | density, kg/m3 |
| ε | volume fraction, dimensionless |
| ΔP | pressure drop, N/m2 |
| Subscripts | |
| L | liquid |
| S | fluidized particles |
| D | foreign particle |
| M | mixture |
| eff | effective |
| ∞ | infinite medium |
References
- Ma, T.; Fan, C.; Hao, L.; Li, S.; Jensen, P.A.; Song, W.; Lin, W.; Dam-Johansen, K. Biomass ash induced agglomeration in fluidized bed. Part 2: Effect of potassium salts in different gas composition. Fuel Process. Technol. 2018, 180, 130–139. [Google Scholar] [CrossRef]
- Zhu, X.; Dong, P.; Tu, Q.; Zhu, Z.; Yang, W.; Wang, H. Investigation of gas–solid flow characteristics in the cyclone dipleg of a pressurised circulating fluidised bed by ECT measurement and CPFD simulation. Meas. Sci. Technol. 2019, 30, 054002. [Google Scholar] [CrossRef]
- Jiang, H.; Huang, L.; Lu, Q.; Zhao, Y.; Luo, Z.; Duan, C.; Dong, L.; Chen, Z.; Lv, B.; Zhao, J.; et al. Separation performance of coal in an air dense medium fluidized bed at varying feeding positions. Fuel 2019, 243, 449–457. [Google Scholar] [CrossRef]
- He, J.; Zhao, Y.; Huang, G.; Liu, C. Evaluation of the separation performance of an air dense medium gas-solid fluidized bed for coal cleaning: Effect of the binary dense media. Adv. Powder Technol. 2018, 29, 3265–3273. [Google Scholar] [CrossRef]
- Sarkar, B.; Das, A.; Mehrotra, S.P. Study of separation features in floatex density separator for cleaning fine coal. Int. J. Miner. Process. 2008, 86, 40–49. [Google Scholar] [CrossRef]
- Tripathy, S.K.; Mallick, M.K.; Singh, V.; Murthy, Y.R. Preliminary studies on teeter bed separator for separation of manganese fines. Powder Technol. 2013, 239, 284–289. [Google Scholar] [CrossRef]
- Carpenter, J.L.; Iveson, S.M.; Galvin, K.P. Ultrafine desliming using a REFLUX (TM) classifier subjected to centrifugal G forces. Miner. Eng. 2019, 134, 372–380. [Google Scholar] [CrossRef]
- Sarkar, B.; Das, A.; Roy, S.; Rai, S.K. In depth analysis of alumina removal from iron ore fines using teetered bed gravity separator. Miner. Process. Extr. Metall. 2008, 117, 48–55. [Google Scholar] [CrossRef]
- Kohmuench, J.N.; Mankosa, M.J.; Honaker, R.Q.; Bratton, R.C. Applications of the CrossFlow teeter-bed separator in the US coal industry. Miner. Metall. Process. 2006, 23, 187–195. [Google Scholar]
- Nguyentranlam, G.; Galvin, K.P. Particle classification in the reflux classifier. Miner. Eng. 2001, 14, 1081–1091. [Google Scholar] [CrossRef]
- Xing, Y.; Gui, X.; Wang, Y.; Cao, Y.; Zhang, Y. Optimization of Teetered Bed Separator Using Pulsed Water. Int. J. Coal Prep. Util. 2015, 36, 283–292. [Google Scholar] [CrossRef]
- Fosu, S.; Awatey, B.; Skinner, W.; Zanin, M. Flotation of coarse composite particles in mechanical cell vs. the fluidised-bed separator (The HydroFloat™). Miner. Eng. 2015, 77, 137–149. [Google Scholar] [CrossRef]
- Das, A.; Sarkar, B. Advanced Gravity Concentration of Fine Particles: A Review. Miner. Process. Extr. Metall. Rev. 2018, 39, 359–394. [Google Scholar] [CrossRef]
- Mukherjee, A.K.; Kumar, A. Liquid/Solid Fluidization Its Role and Limitation in Fine Beneficiation—A Review. Miner. Process. Extr. Metall. Rev. 2009, 30, 280–306. [Google Scholar] [CrossRef]
- Tripathy, S.K.; Bhoja, S.K.; Kumar, C.R.; Suresh, N. A short review on hydraulic classification and its development in mineral industry. Powder Technol. 2015, 270, 205–220. [Google Scholar] [CrossRef]
- Kumar, C.R.; Tripathy, S.; Rao, D.S. Characterisation and Pre-concentration of Chromite Values from Plant Tailings Using Floatex Density Separator. J. Miner. Mater. Charact. Eng. 2009, 8, 367–378. [Google Scholar] [CrossRef]
- Ozcan, Ö.; Ergun, S.L. Performance of teetered bed separator for non-coal applications. Sep. Sci. Technol. 2017, 52, 1486–1495. [Google Scholar] [CrossRef]
- Roy, S.; Mandal, S.K.; Das, A. Segregation and Process Features in a Teeter Bed Separator as Revealed by High-Speed Videography and Image Processing. Miner. Process. Extr. Metall. Rev. 2013, 35, 15–22. [Google Scholar] [CrossRef]
- Kim, B.H.; Klima, M.S. Simulation of Hindered-Settling Column Separations When Processing Fine Anthracite Refuse. Coal Prep. 2004, 24, 261–275. [Google Scholar] [CrossRef]
- Xia, Y.K. CFD Simulation of Fine Particle Gravity Separation in Hindered-settling Bed Separators. Chem. Prod. Process. Model. 2007, 2, 1–21. [Google Scholar] [CrossRef]
- Das, A.; Sarkar, B.; Mehrotra, S.P. Prediction of separation performance of Floatex Density Separator for processing of fine coal particles. Int. J. Miner. Process. 2009, 91, 41–49. [Google Scholar] [CrossRef]
- Richardson, J.; Zaki, W. Sedimentation and fluidization: Part-1. Trans. Inst. Chem. Eng. 1954, 32, 35–53. [Google Scholar]
- Ergun, S.; Orning, A.A. Fluid Flow through Randomly Packed Columns and Fluidized Beds. Ind. Eng. Chem. 1949, 41, 1179–1184. [Google Scholar] [CrossRef]
- Wen, C.Y.; Yu, Y.H. Mechanics of fluidization. Chem. Eng. Prog. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Syamlal, M.; O’Brien, T.J. Computer simulation of bubbles in a fluidized bed. In Fluidization and Fluid Particle Systems: Fundamentals and Applications; AIChE: Washington, DC, USA, 1989; pp. 22–31. [Google Scholar]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Elsevier Inc.: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Huilin, L.; Gidaspow, D.; Lu, H. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures. Chem. Eng. Sci. 2003, 58, 3777–3792. [Google Scholar] [CrossRef]
- Grbavčić, Ž.B.; Vuković, D.V. Single-particle settling velocity through liquid fluidized beds. Powder Technol. 1991, 66, 293–295. [Google Scholar] [CrossRef]
- Grbavcic, Z.B.; Vuković, D.V.; Jovanović, S.D.; Littman, H. The effective buoyancy and drag on spheres in a water-fluidized bed. Chem. Eng. Sci. 1992, 47, 2120–2124. [Google Scholar] [CrossRef]
- Van Der Wielen, L.A.M.; Van Dam, M.H.H.; Luyben, K.C.A.M. On the relative motion of a particle in a swarm of different particles. Chem. Eng. Sci. 1996, 51, 995–1008. [Google Scholar] [CrossRef]
- Ghatage, S.V.; Sathe, M.J.; Doroodchi, E.; Joshi, J.B.; Evans, G.M. Effect of turbulence on particle and bubble slip velocity. Chem. Eng. Sci. 2013, 100, 120–136. [Google Scholar] [CrossRef]
- Ghatage, S.V.; Khan, S.M.; Peng, Z.; Doroodchi, E.; Moghtaderi, B.; Padhiyar, N.; Joshi, J.B.; Evans, G.M.; Mitra, S. Settling/rising of a foreign particle in solid-liquid fluidized beds: Application of dynamic mesh technique. Chem. Eng. Sci. 2017, 170, 139–153. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhu, J.-X. CFD Modelling and Simulation of Hydrodynamics in Liquid-Solid Circulating Fluidized Beds. Can. J. Chem. Eng. 2005, 83, 177–185. [Google Scholar] [CrossRef]
- Cornelissen, J.T.; Taghipour, F.; Escudié, R.; Ellis, N.; Grace, J.R. CFD modelling of a liquid–solid fluidized bed. Chem. Eng. Sci. 2007, 62, 6334–6348. [Google Scholar] [CrossRef]
- Reddy, R.K.; Joshi, J.B. CFD modeling of solid–liquid fluidized beds of mono and binary particle mixtures. Chem. Eng. Sci. 2009, 64, 3641–3658. [Google Scholar] [CrossRef]
- Syamlal, M.; O’Brien, T.J. Simulation of granular layer inversion in liquid fluidized beds. Int. J. Multiph. Flow 1988, 14, 473–481. [Google Scholar] [CrossRef]
- Doroodchi, E.; Galvin, K.P.; Fletcher, D.F. The influence of inclined plates on expansion behaviour of solid suspensions in a liquid fluidised bed—A computational fluid dynamics study. Powder Technol. 2005, 156, 1–7. [Google Scholar] [CrossRef]
- Lettieri, P.; Di Felice, R.; Pacciani, R.; Owoyemi, O. CFD modelling of liquid fluidized beds in slugging mode. Powder Technol. 2006, 167, 94–103. [Google Scholar] [CrossRef]
- Mukherjee, A.K.; Mishra, B.K. Experimental and simulation studies on the role of fluid velocity during particle separation in a liquid–solid fluidized bed. Int. J. Miner. Process. 2007, 82, 211–221. [Google Scholar] [CrossRef]
- Di Renzo, A.; Cello, F.; Di Maio, F.P. Simulation of the layer inversion phenomenon in binary liquid--fluidized beds by DEM–CFD with a drag law for polydisperse systems. Chem. Eng. Sci. 2011, 66, 2945–2958. [Google Scholar] [CrossRef]
- Peng, Z.; Joshi, J.B.; Moghtaderi, B.; Khan, M.S.; Evans, G.M.; Doroodchi, E. Segregation and dispersion of binary solids in liquid fluidised beds: A CFD-DEM study. Chem. Eng. Sci. 2016, 152, 65–83. [Google Scholar] [CrossRef]
- Vivacqua, V.; Vashisth, S.; Hébrard, G.; Grace, J.R.; Epstein, N. Characterization of fluidized bed layer inversion in a 191-mm-diameter column using both experimental and CPFD approaches. Chem. Eng. Sci. 2012, 80, 419–428. [Google Scholar] [CrossRef]
- Molaei, E.A.; Yu, A.B.; Zhou, Z.Y. Investigation of causes of layer inversion and prediction of inversion velocity in liquid fluidizations of binary particle mixtures. Powder Technol. 2019, 342, 418–432. [Google Scholar] [CrossRef]
- Peng, Z.; Ghatage, S.V.; Doroodchi, E.; Joshi, J.B.; Evans, G.M.; Moghtaderi, B. Forces acting on a single introduced particle in a solid–liquid fluidised bed. Chem. Eng. Sci. 2014, 116, 49–70. [Google Scholar] [CrossRef]
- Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 2005, 209, 448–476. [Google Scholar] [CrossRef] [Green Version]
- Ozel, A.; De Motta, J.C.B.; Abbas, M.; Fedea, P.; Masbernat, O.; Vincent, S.; Estivalezes, J.-L.; Simonin, O. Particle resolved direct numerical simulation of a liquid–solid fluidized bed: Comparison with experimental data. Int. J. Multiph. Flow 2017, 89, 228–240. [Google Scholar] [CrossRef] [Green Version]
- Mitra, S.; Doroodchi, E.; Pareek, V.; Joshi, J.B.; Evans, G.M. Collision behaviour of a smaller particle into a larger stationary droplet. Adv. Powder Technol. 2015, 26, 280–295. [Google Scholar] [CrossRef]
- Kunii, D.; Levenspiel, O. Fluidization Engineering; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Joshi, J.B. Solid-liquid fluidised beds: Some design aspects. Chem. Eng. Res. Des. 1983, 61, 143–161. [Google Scholar]
- Di Felice, R.; Foscolo, P.U.; Gibilaro, L.; Rapagna, S. The interaction of particles with a fluid—Particle pseudo—fluid. Chem. Eng. Sci. 1991, 46, 1873–1877. [Google Scholar] [CrossRef]
- Grbavcic, Z.B.; Arsenijevic, Z.L.; Garić-Grulović, R.V. Prediction of single particle settling velocities through liquid fluidized beds. Powder Technol. 2009, 190, 283–291. [Google Scholar] [CrossRef]
- Kozołub, P.; Klimanek, A.; Bialecki, R.A.; Adamczyk, W.P. Numerical simulation of a dense solid particle flow inside a cyclone separator using the hybrid Euler–Lagrange approach. Particuology 2017, 31, 170–180. [Google Scholar] [CrossRef]
- Sun, M.; Yu, C.; Lv, D.; Wei, L. Numerical studies of performance of various liquid-solid momentum exchange coefficient models for fluidization behavior of particles. J. Cent. South Univ. Sci. Technol. 2019, 50, 1–8. [Google Scholar]
- Zigrang, D.J.; Sylvester, N.D. An explicit equation for particle settling velocities in solid-liquid systems. AIChE J. 1981, 27, 1043–1044. [Google Scholar] [CrossRef]







| Source | Formulas |
|---|---|
| Richardson and Zaki [22] | |
| Kunii et al. [48] | |
| Joshi [49] | |
| Di Felice et al. [50] | |
| Van der Wielen et al. [30] | |
| Grbavcic et al. [51] | |
| Parameters | Values |
|---|---|
| Width of the column | 120 mm |
| Height of the column | 800 mm |
| Diameter of fluidized particle | 1 mm |
| Density of fluidized particle | 2607 kg/m3 |
| Diameter of foreign particle | 2, 4, 6 mm |
| Density of foreign particle | 2607 kg/m3, 8030 kg/m3 |
| Liquid density | 998.2 kg/m3 |
| Liquid viscosity | 0.001003 Pa·s |
| Operating pressure | 101,325 Pa |
| Grid size | 2 mm × 2 mm |
| Grid number | 24,000 |
| Turbulence model | standard κ-ε |
| Time step | 0.001 s |
| Max iterations/time step | 20 |
| Convergence criteria | 10−5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Liu, J.; Cao, C.; Dong, Y.; Wei, T. Numerical Studies on Teeter Bed Separator for Particle Separation. Energies 2020, 13, 2025. https://doi.org/10.3390/en13082025
Zhu X, Liu J, Cao C, Dong Y, Wei T. Numerical Studies on Teeter Bed Separator for Particle Separation. Energies. 2020; 13(8):2025. https://doi.org/10.3390/en13082025
Chicago/Turabian StyleZhu, Xueshuai, Junli Liu, Chao Cao, Yalin Dong, and Tao Wei. 2020. "Numerical Studies on Teeter Bed Separator for Particle Separation" Energies 13, no. 8: 2025. https://doi.org/10.3390/en13082025
APA StyleZhu, X., Liu, J., Cao, C., Dong, Y., & Wei, T. (2020). Numerical Studies on Teeter Bed Separator for Particle Separation. Energies, 13(8), 2025. https://doi.org/10.3390/en13082025