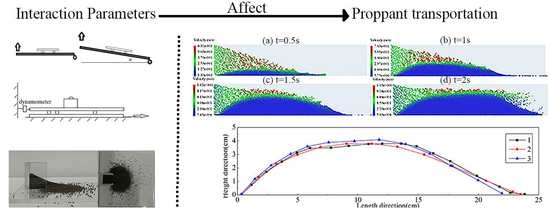
Calibration of the Interaction Parameters between the Proppant and Fracture Wall and the Effects of These Parameters on Proppant Distribution

Abstract

Saltation and reputation (creep) dominate proppant transport rather than suspension during slickwater fracturing, due to the low sand-carrying capacity of the slickwater. Thus, the interaction parameters between proppants and fracture walls, which affect saltation and reputation, play a more critical role in proppant transport. In this paper, a calibration method for the interaction parameters between proppants and walls is built. A three-dimensional coupled computational fluid dynamics–discrete element method (CFD–DEM) model is established to study the effects of the interaction parameters on proppant migration, considering the wall roughness and unevenly distributed diameters of proppants. The simulation results show that a lower static friction coefficient and rolling friction coefficient can result in a smaller equilibrium height of the sand bank and a smaller build angle and drawdown angle, which is beneficial for carrying the proppant to the distal end of the fracture. The wall roughness and the unevenly distributed diameter of the proppants increase the collision between proppant and proppant or the wall, whereas the interactions have little impact on the sandbank morphology, slightly increasing the equilibrium height of the sandbank.

1. Introduction

Slickwater is widely used during hydraulic fracturing in unconventional reservoirs to form complex fracture networks. It is used for its low cost and little damage it presents to reservoirs [1,2,3,4,5,6]. Proppants settle out of suspension more rapidly to form a bank in slickwater compared to conventional fracturing fluids, and the movement of the bank itself becomes an essential mechanism that dominates the proppant migration in the fracture [7]. As the proppant–proppant and proppant–wall interaction parameters affect the migration of the bedload layer, the study of the influences of the interaction parameters on proppant transport in slickwater is critical.

Experimental research over the years significantly contributed to our understanding of the mechanisms of proppant transport in low-viscosity fluids. Kern et al. [8] conducted the earliest work on slot flow experiments, and the results showed that the proppants would settle out of fluid and form a dune near the wellbore, and that proppants can be transported further into fractures only if the dune reaches the equilibrium height. More recent experimental works [9,10] on proppant transport in slickwater confirmed similar findings to Kern et al. [8]. Furthermore, Woodworth et al. [11] used the results of laboratory experiments to analyze the influences of fluid viscosity, fluid density, pump rate, proppant size and density, proppant concentration, and fracture width on proppant transport in a low-viscosity fluid. Moreover, experiments on proppant transport in fracture networks [10,12,13] were mostly carried out to answer the debatable question of whether slickwater can transport proppants into secondary fractures or not. In addition to experimental research, computational fluid dynamics (CFD) methods were widely used to study proppant transport in fractures. The most common approach for modeling proppant transport is the Eulerian–Eulerian method in which the interaction between the particles and fluid is fully coupled [14,15,16,17,18,19]. In a recent study, Han et al. [20] used the Eulerian granular model to track proppant movement in various fractures for a better understanding of how proppant transport is influenced by fracture viscosity, proppant density, and pump rate. The second method is the Eulerian–Lagrangian model, which tracks individual particle movement with time and location with the Lagrangian framework and describes fluid flow with the Eulerian framework [21,22,23]. The discrete element method (DEM) [24] is a useful tool to simulate the behavior of particles, and it can be coupled with CFD to model the interaction between particles and the surrounding fluid. In recent years, the coupled CFD–DEM model was used to study fracturing fluid flow in fractures for its advantages of considering proppant–proppant, proppant–boundary, and proppant–fracturing fluid interactions [25,26,27,28,29,30,31,32]. Blyton et al. [26] first used the coupled CFD–DEM model to simulate the motion of particles flowing with a fluid between fracture walls, and the simulations individually determined that particle trajectories such as particle-to-particle and particle-to-wall collisions occur. Zhang et al. [28] used a two-dimensional coupled CFD–DEM model to study the impacts of proppant diameter and density, fluid viscosity, and injection rate on proppant distribution. Kou et al. [31] used a three-dimensional coupled CFD–DEM model to investigate the effects of various proppant sizes and concentrations on bridging formation, and they quantified its impact by estimating the percentage of proppant reaching secondary fractures.

Although most of the numerical simulation studies on proppant transport in fractures considered the effects of the interaction between proppant and proppant or the wall, researchers stated the importance of the interaction parameters in two-phase flow [32,33], and the only work studying the effects of the interaction parameters on proppant distribution so far was conducted by Mack et al. [7]. As shown, the most critical proppant transport mechanisms in slickwater fracturing are saltation and reputation, and advanced ceramic proppants can be transported further into fractures as a result of the higher coefficient of restitution and a lower friction coefficient than other proppants. Furthermore, to the best of our knowledge, only the study of Mack et al. [7] calibrated some of the interaction parameters, including the friction coefficient and coefficient of restitution of the proppant, but without the interaction parameters between the proppant and wall.

Thus, in this paper, we intend to calibrate the interaction parameters between the proppant and proppant or the wall and study the effect of these parameters on proppant distribution in the fracture, considering the wall roughness and the uneven distribution of proppant size.

2. Calibration of the Interaction Parameters

The interaction parameters mainly include the static friction coefficient, rolling friction coefficient, and the coefficient of restitution. In this section, the interaction parameters between a conventional ceramic proppant and wall are measured. As the interaction parameters are related to the material, shape, and surface roughness of the proppant, and as they have little relationship with the particle size, a 20–40-mesh ceramic proppant is selected here as a research target for its large particle size, which is conducive to the experiments. A plexiglass plate, which is commonly used in experiments of proppant transport, and a cutting shale plate are selected here as research targets.

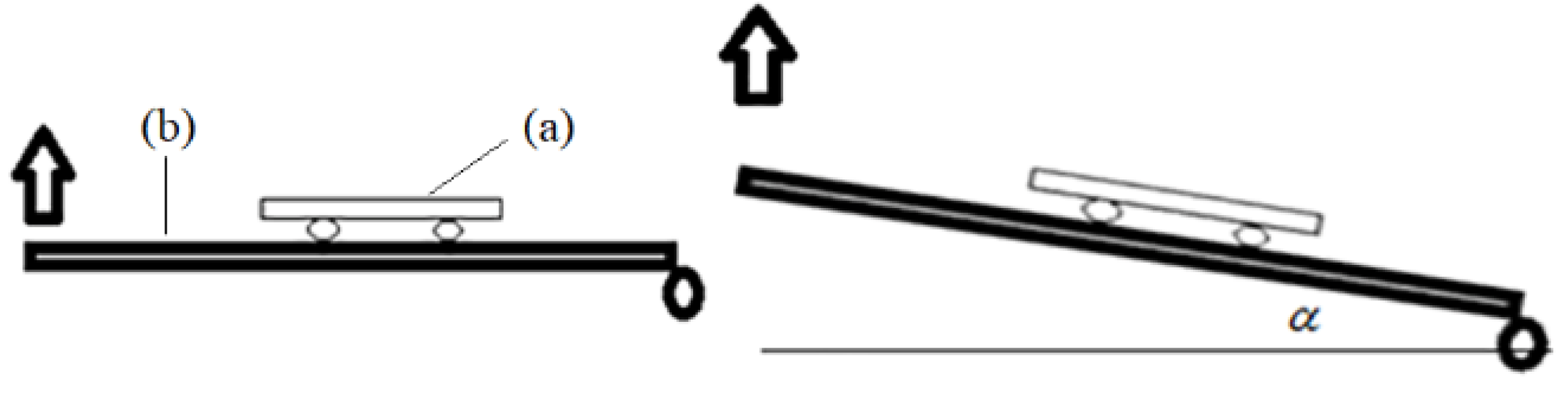
2.1. Methods for Calibrating the Interaction Parameters between Proppant and Wall

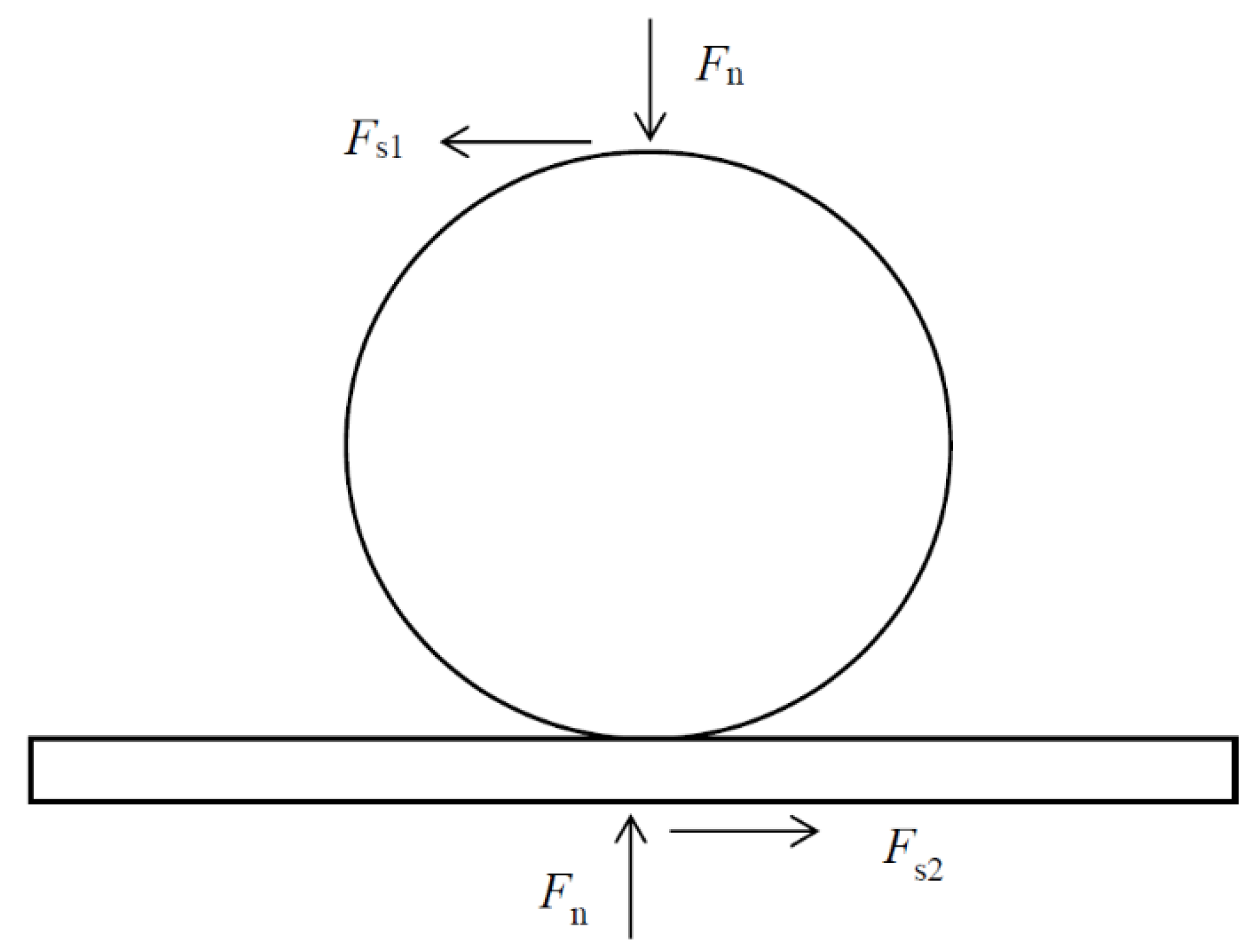
2.1.1. Static Friction Coefficient between the Proppant and Wall

Figure 1 shows the device for measuring the static friction coefficient between the proppant and wall. We fixed four proppant particles with the same diameter on a little glass plate (a) and placed the glass plate on the surface of either a plexiglass plate or a shale plate (b), which can be raised on one side. We slowly lifted one side of (b) and recorded the angle α between (b) and the horizontal direction when the glass plate (a) began to slide due to gravity. We repeated the experiment five times and took the average value of the experimental results. The static friction coefficient between proppant and wall can be calculated as $\tan \alpha$.

2.1.2. Rolling Friction Coefficient between Proppant and Wall

Figure 2 shows the device for measuring the rolling friction coefficient between the proppant and wall. Firstly, we balanced the upper glass plate (c) by placing three proppant particles (equilateral triangles) between plates (c) and (d). We connected the left side of the top plate (c) with a force sensor. We slowly pulled the lower plate (d) to the right side at a constant speed, and the proppants began to move due to the tangential force of the lower plate (d). In the horizontal direction, the upper plate (c) was affected by the sliding friction force on the contact surface of the proppants and the horizontal binding force of the dynamometer. The proppants were in quasi-static equilibrium during the experiment.

Figure 3 shows the forces acting on proppant particles. $F_{s1}$ and $F_{s2}$ are the rolling friction forces on the upper and lower plates caused by the proppant, respectively. At the initial stage, as the tangential force increased, the proppants were in quasi-static equilibrium under the effect of the rolling friction torque and the rolling friction forces. Then, the proppants started to move from their rest position, affected by the increasing external force. The normal forces of the proppant acting on the upper and lower plates ($F_n$) are equal when the weight of the proppant is neglected, and $F_{s1}=F_{s2}=F_s$ can be obtained by the balance equation of force when the proppants are in a stationary state or the critical state when the motion occurs. The friction torque between the proppant and the upper contact surface or the lower contact surface is equal because of the same contact condition when the proppants are regular spheres. The rolling friction coefficient can be calculated using Equation (1).

$$u_r=\frac{F_s}{2F_n},$$

(1)

where $u_r$ is the rolling friction coefficient (dimensionless).

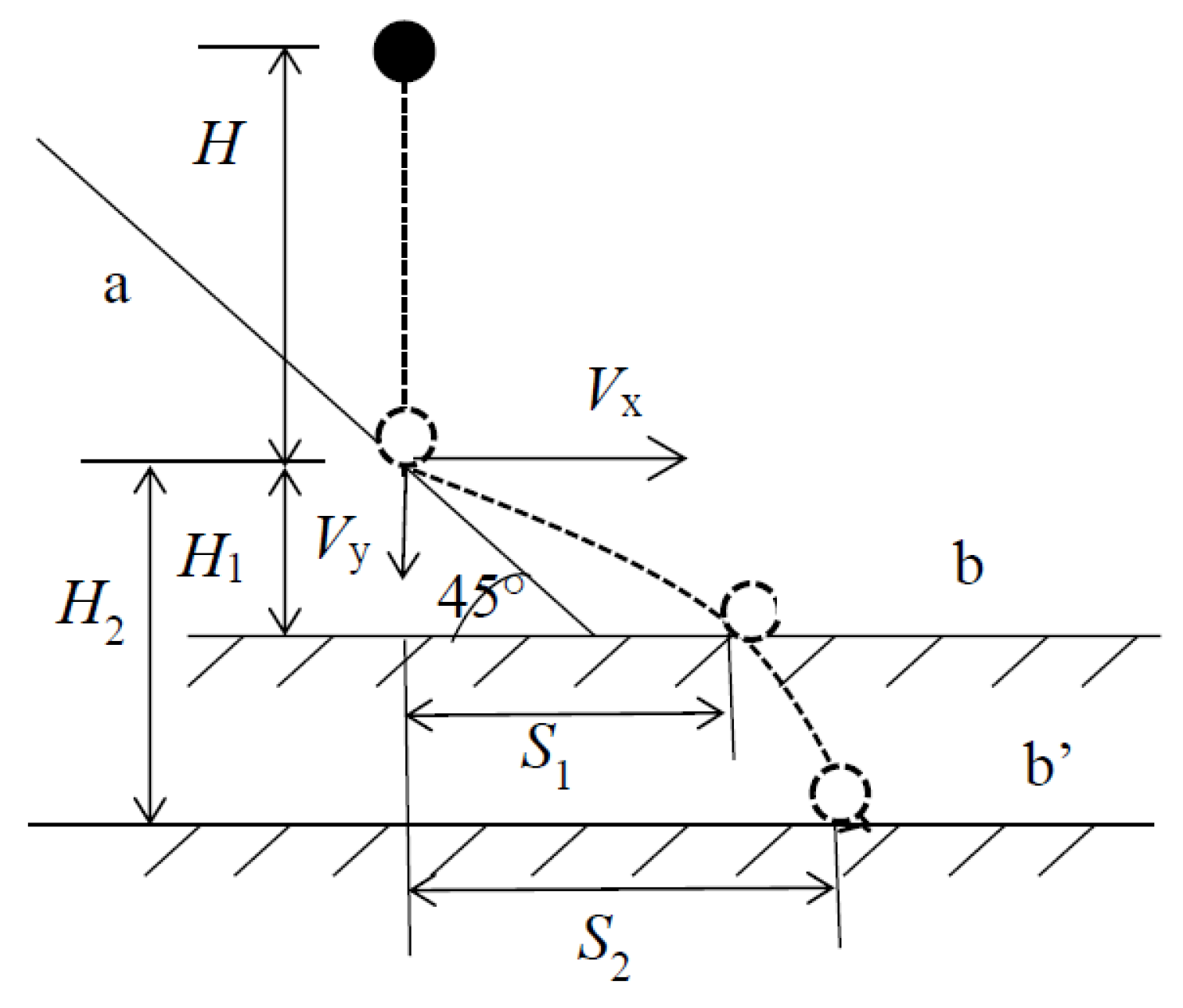
2.1.3. Coefficient of Restitution

The free-fall method is usually used to measure the coefficient of restitution. Mack et al. [7] used a 28-FPS (frames per second) video camera to record the proppant trajectory for measuring the maximum rebound height after the first collision between the proppant and wall. Since the equipment required with the free-fall method is expensive, a simple experimental device was used in this paper to measure the coefficient of restitution between the proppant and wall in air, and the coefficient of restitution in slickwater is 40% of the value in the air [34,35,36]. As shown in Figure 4, the angle between the plexiglass plate or the shale plate (a) and the horizontal direction was 45°. We let the proppant particle fall onto the surface (a) from a fixed initial height (H), and then the proppant bounced onto the surface (b). We covered a layer of butter on the surface of the plate (b) to accurately record the collision position of proppant with the plate (b). We carried out experiments for the distance between the plate (b) and the collision position of the proppant with the plate (a), denoted as H₁ and H₂, respectively, and we measured the displacement of the proppant in the horizontal direction (S₁ and S₂). The following formulae can be obtained without considering the effects of air resistance:

$$\{\begin{array}{c}{V}_0=gt\\ H=\frac{1}{2}g{t}^2\end{array}\to V_0=\sqrt{2gH},$$

(2)

$$\{\begin{array}{c}{S}_1=V_x{t}_1\\ S_2=V_x{t}_2\\ H_1=V_y{t}_1+\frac{1}{2}g{t}_1^2\\ H_2=V_y{t}_2+\frac{1}{2}g{t}_2^2\end{array}\to \{\begin{array}{c}{V}_x=\sqrt{\frac{g{S}_1{S}_2(S_1-S_2)}{2(H_1{S}_2-H_2{S}_1)}}\\ V_y=\frac{H_1{V}_x}{S_1}-\frac{g{S}_1}{2V_x}\end{array},$$

(3)

where $V_0$ is the instantaneous velocity of the proppant before the proppant collides with the plate (a), given in m/s. $V_x$ and $V_y$ are the horizontal and vertical velocities of the proppant after the collision with the plate (a), respectively, given in m/s.

The coefficient of restitution is defined as the ratio of the normal relative velocity with which the particle leaves a collision to the normal relative velocity with which it enters the collision, and it can be calculated using Equation (4).

$$e=\frac{V_n}{V_{n0}}=\frac{\sqrt{V_x^2+V_y^2}\cdot \cos \left[{45}^{\circ }+{\tan }^{-1}\left(\frac{V_y}{V_x}\right)\right]}{V_0\sin {45}^{\circ }}$$

(4)

2.1.4. The Results of the Interaction Parameters between the Proppant and Wall

According to the above experiments, the interaction parameters between the proppant and wall could be obtained. The results are shown in

Table 1. Results of the interaction parameters between the proppant and wall.

Case	$\mathit{e}$ (air)	$\mathit{e}$ (Slickwater)	${\mathit{\mu }}_{\mathbf{s}}$	${\mathit{\mu }}_{\mathbf{r}}$
Proppant–plexiglass wall	0.6	0.24	0.1944	6.5 × 10−4
Proppant–shale wall	0.36	0.144	0.84	0.24

${\mu }_{\mathrm{s}}$ denotes the static friction coefficient.

.

2.2. Interaction Parameters between Proppants

The coefficient of restitution between proppants was not calculated in this paper, and the results of Mack et al. [7] were used, where e (air) = 0.53 and e (slickwater) = 0.21. Due to the tiny size of proppants, it was difficult to directly measure the static friction coefficient and the rolling friction coefficient between proppant particles in the experiments. Therefore, the angle of repose was studied by combining experiment and numerical simulation to obtain the friction coefficient between proppants.

(1)

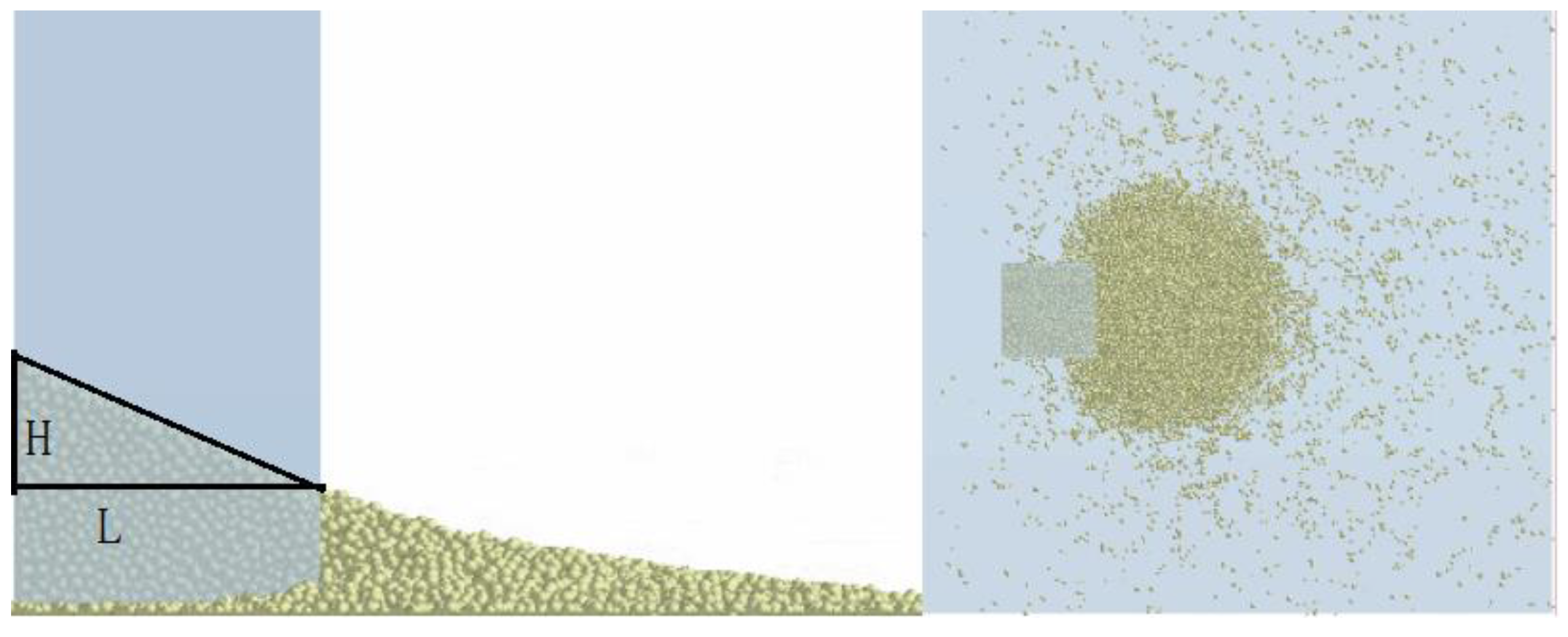
Experimental measurement of the angle of repose

The funnel method [37,38,39,40] and the hollow cylinder method (collapse test method) [41,42,43] are commonly used to measure the angle of repose of particles. In this study, the principle of the collapse test method was applied in the experimental device, shown in Figure 5. We put proppant particles with a height of 0.02 m into a cell made of plexiglass plates, and then quickly removed the baffle plate. The proppant began to move due to gravity until it stopped. Figure 6 shows the result. The angle of repose can be calculated using Equation (5), and the result was determined to be 24.22°.

$$\alpha ={\tan }^{-1}\frac{H}{L}.$$

(5)

(2)

Numerical simulation of the angle of repose

Using the median sieving diameter of the proppants may affect the simulation results because of the size difference of proppant of the same mesh. Therefore, in this study, the 20–40-mesh proppants were sieved into four groups, as shown in

Table 2. Proppant subdivision standard.

Group	1	2	3	4
The sieving diameter (10−6 m)	425–500	500–600	600–710	>710

. We randomly selected 40 proppants from each group and measured the diameter of these proppants separately (average of length and width) with a microscope. The average diameter of the 40 proppants was taken as the actual particle diameter of the group. Figure 7 shows the linear relationship between the sieving diameter and the actual diameter of the proppants, and the actual proppant diameter can be calculated using Equation (6).

$$d_a=0.9525d_s+0.1253,$$

(6)

where $d_a$ and $d_s$ are the actual diameter and sieving diameter of proppants, respectively, given in m.

The mass fractions of the 20–40-mesh proppants in each group after sieving refinement are shown in

Table 3. The mass fractions of the proppants in each group after sieving refinement.

Group	1	2	3	4
Mass fraction (%)	10	32	38	20

, and the other essential parameters for the simulation are listed in

Table 4. Parameters for the simulation.

Parameters	Value
Proppant density (kg/m3)	3223
The density of plexiglass (kg/m3)	1130
The static friction coefficient between proppant and wall	0.1944
The rolling friction coefficient between proppant and wall	0.00065
The coefficient of restitution between proppants	0.53

.

Various static friction coefficients and rolling friction coefficients between proppants were preset, and the results are shown in

Table 5. Simulation results.

Case #	Static Friction Coefficient (Proppant–Proppant)	Rolling Friction Coefficient (Proppant–Proppant)	Angle of Repose (°)	The Difference in the Angle of Repose with Experimental Results (%)
1	0.6	0.005	17.05	29.626878
2	0.5	0.005	16.69	31.1127621
3	0.4	0.005	15.99	34.0019812
4	0.3	0.005	15.64	35.4465907
5	0.6	0.01	18.43	23.9309889
6	0.5	0.01	18.09	25.3343239
7	0.4	0.01	17.74	26.7789335
8	0.3	0.01	17.05	29.626878
9	0.6	0.05	24.39	−0.6686478
10	0.5	0.05	23.75	1.9729239
11	0.4	0.05	23.43	3.2937098
12	0.3	0.05	23.11	4.6144956

. Figure 8 shows one simulation result of the angle of repose. By comparing the simulation results with the experimental results, the static friction coefficient and the rolling friction coefficient between proppants were 0.6 and 0.05, respectively.

3. Effects of the Interaction Parameters on Proppant Migration

3.1. Coupled CFD–DEM Model

3.1.1. Fluid Control Equations

As a high displacement is generally used during slickwater fracturing, turbulence is the normal state of sand-carrying fluid, which is accounted for by using the standard k–ε turbulence model [19,30,44]. Only the fluid phase is solved by the CFD code (Euler–Euler model) [30,45].

(1)

Mass conservation equation

$$\frac{\partial }{\partial t}\left({\epsilon }_f{\rho }_f\right)+\nabla \cdot \left({\epsilon }_f{\rho }_f{v}_f\right)=0.$$

(7)

(2)

Momentum conservation equation

$$\frac{\partial }{\partial t}\left({\epsilon }_f{\rho }_f{v}_f\right)+\nabla \cdot \left({\epsilon }_f{\rho }_f{v}_f{v}_f\right)=-{\epsilon }_f\nabla p+{\epsilon }_f\nabla \cdot {\tau }_f+{\epsilon }_f{\rho }_{f}g-\frac{1}{V_{cell}}{\displaystyle \sum _{i=1}^k{F}_{di}}.$$

(8)

Here, ${\rho }_f$ is the fluid density (kg/m³), ${\epsilon }_f$ is the volume fraction of the fluid in the computational cell (dimensionless), $v_f$ is the average velocity of a fluid cell (m/s), $t$ is the time (s), $g$ is the acceleration due to gravity (m/s²), ${\tau }_f$ is the fluid stress tensor (N), $k$ is the number of particles in the corresponding fluid cell (dimensionless), and $F_{di}$ is the force of the particles acting on the fluid (N).

3.1.2. Particle Control Equations

In the flow field, a variety of forces act on the particles, including the gravity force, collision contact force, buoyancy force, and drag force. The movement of particles is predominantly translational and rotational, and, according to Newton’s second law, the expressions are given as Equations (9) and (10) [46].

$$m_i\frac{d{v}_i}{dt}=m_{i}g+{\displaystyle \sum _{i=1}^n{F}_{ci}+}{F}_{di}+F_b,$$

(9)

$$I_i\frac{d{w}_i}{dt}={\displaystyle \sum _{i=1}^n{T}_{ij}},$$

(10)

where $v_i$ is the translational velocity of particle i (m/s), $w_i$ is the angular velocity of particle i (rad/s), $m_i$ is the mass of particle i (kg/m³), $I_i$ is the moment of inertia of the particle i (kg·m²), ${\displaystyle \sum _{i=1}^n{F}_{ci}}$ is total contact force acting on particle i (N), ${\displaystyle \sum _{i=1}^n{T}_{ij}}$ is total torque acting on particle i (N·m), $F_{di}$ is the drag force of the fluid acting on particle (N), $F_b$ is the buoyancy force (N), and n is the number of total contacts for the particle i (N).

The collisions between particle and particle or the boundaries are critical parts in the solid–liquid two-phase flow. In this paper, we apply the Hertz–Mindlin (no slip) model [30,47,48] to analyze the particle moving pattern.

$$F_{ci}=F_{cni}+F_{cti}+F_{dni}+F_{dti},$$

(11)

where $F_{cni}$ and $F_{cti}$ are the contact forces along the normal and tangential directions, respectively (N). Terms $F_{dni}$ and $F_{dti}$ are the damping forces in the normal and tangential directions, respectively (N).

$$F_{cni}=\frac{4}{3}{E}^{*}{\left(R^{*}\right)}^{1/2}{\alpha }^{3/2},$$

(12)

$$\frac{1}{E^{*}}=\frac{1-v_1^2}{E_1}+\frac{1-v_2^2}{E_2},$$

(13)

$$R^{*}=\frac{1}{R_1}+\frac{1}{R_2},$$

(14)

where $E^{*}$ is the effective Young’s modulus (N/m²), $R^{*}$ is the effective particle radius (m), $\alpha$ is the displacement of the amount of normal overlap (m), $E_1$ and $E_2$ are the Young’s moduli of particles 1 and 2, respectively (N/m²), $v_1$ and $v_2$ are the Poison ratios of particles 1 and 2, respectively (dimensionless), and $R_1$ and $R_2$ denote the radii of particles 1 and 2, respectively (m).

$$F_{dni}=-2\sqrt{\frac{5}{6}}\lambda \sqrt{S_n{m}^{*}}{v}_n^{rel},$$

(15)

$$m^{*}=\frac{m_1{m}_2}{m_1+m_2},$$

(16)

$$\lambda =\frac{\ln e}{\sqrt{{\ln }^{2}e+{\pi }^2}},$$

(17)

$$S_n=2E^{*}\sqrt{R^{*}\alpha },\alpha =R_1+R_2-\overrightarrow{r_1}-\overrightarrow{r_2},$$

(18)

$$v_n^{rel}=\left(\overrightarrow{v_1}-\overrightarrow{v_2}\right)\cdot \overrightarrow{n},\overrightarrow{n}=\frac{\overrightarrow{r_1}-\overrightarrow{r_2}}{|\overrightarrow{r_1}-\overrightarrow{r_2}|},$$

(19)

where $m^{*}$ is the equivalent mass (kg), $S_n$ is the stiffness in the normal direction (N/m), $v_n^{rel}$ is the component of relative velocity in the normal direction (m/s), m is the mass of the particle (kg), $e$ is the coefficient of restitution (dimensionless), $\overrightarrow{v}$ is the particle velocity before the collision (m/s), $\overrightarrow{n}$ is the normal unit vector at collision (dimensionless), and $\overrightarrow{r_1}$ and $\overrightarrow{r_2}$ are the position vectors of the two ball centers, respectively (m/s).

$$F_{cti}=-S_t\zeta ,$$

(20)

$$S_t=8G^{*}\sqrt{R^{*}\alpha },G^{*}=\frac{2-v_1^2}{G_1}+\frac{2-v_2^2}{G_2},$$

(21)

where $S_t$ is the stiffness in the tangential direction (N/m), $\zeta$ is the overlap in the tangential direction (m), $G^{*}$ is the effective shear modulus (Pa), and $G_1$ and $G_2$ are the shear moduli of particles 1 and 2, respectively (Pa).

$$F_{dti}=-2\sqrt{\frac{5}{6}}\lambda \sqrt{S_n{m}^{*}}{v}_t^{rel},v_t^{rel}=\left(\overrightarrow{v_1}-\overrightarrow{v_2}-v_n^{rel}\right)\cdot \overrightarrow{n},$$

(22)

where $v_t^{rel}$ is the relative velocity in the tangential direction (m/s).

The rolling friction is essential in the simulation and can be illustrated by the torque on the friction surface using Equation (23).

$$T_{ij}=-{\mu }_r{F}_{cni}{R}_i\overrightarrow{w_i},$$

(23)

where ${\mu }_r$ is the rolling friction coefficient (dimensionless), $R_i$ is the distance between the mass center and the contact point (m), and $\overrightarrow{W_i}$ denotes the unit angular velocity vector of the object at the point of contact.

The calculation of the drag forces of the fluid acting on the particles is significant for the coupling of the CFD and DEM parts.

$$F_{di}=\frac{V\beta }{{\epsilon }_s}\left(\overrightarrow{v_s}-\overrightarrow{v_f}\right),$$

(24)

where $V$ is the volume of the proppant particles (m³), $\beta$ given by the Gidaspow drag model (kg/(m³·s)) [27,49], as per Equation (25), and the fluid–particle drag coefficient $C_D$ (dimensionless) can be calculated using Equation (26).

$$\beta =\{\begin{array}{l}150\frac{{\epsilon }_s^2{\mu }_f}{{\epsilon }_f{d}_p^2}+1.75\frac{{\rho }_f{\epsilon }_s|\overrightarrow{v_s}-\overrightarrow{v_f}|}{d_p}\mathrm{when}{\epsilon }_f\le 0.8\\ \frac{3}{4}{C}_D\frac{{\rho }_f{\epsilon }_s|\overrightarrow{v_s}-\overrightarrow{v_f}|}{d_p}{\epsilon }_f^{-1.65}\hspace{1em}\mathrm{when}{\epsilon }_f>0.8\end{array},$$

(25)

$$C_D=\{\begin{array}{l}\frac{24}{{\epsilon }_f{\mathrm{Re}}_s}\left[1+0.15{\left({\epsilon }_f{\mathrm{Re}}_s\right)}^{0.687}\right]\mathrm{when}{\mathrm{Re}}_s<1000\\ 0.44\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{when}{\mathrm{Re}}_s\ge 1000\end{array},$$

(26)

where ${\epsilon }_f$ and ${\epsilon }_s$ denote the volume fraction of fluid and particles, respectively (dimensionless), and ${\mu }_f$ is the fluid viscosity (Pa·s).

3.1.3. Initial and Boundary Conditions

Figure 9 shows the geometric model of the vertical well and the horizontal well, and the size of the fracture model was 0.25 m (L) × 0.006 m (W) × 0.05 m (H).

(1)

CFD initial and boundary conditions

Fluid flowed from the inlet (IN) to the outlet (OUT). For the horizontal well, the location of the perforation was in the middle of the left boundary, and the size of the perforation was 0.006 m × 0.006 m. We applied a velocity boundary and a constant pressure boundary on the inlet and outlet, respectively. The boundaries in the y-direction and z-direction were rigid walls with the no-slip condition.

(2)

DEM initial and boundary conditions

Randomly located particles were created through the particle factory, which was built at the inlet boundary, at a fixed rate, to ensure a constant concentration of injected particles. Furthermore, the injected particles had the same horizontal speed as the injected fluid.

(3)

Coupling of CFD and DEM

We set the timestep of the CFD and DEM solver. The timestep used in the DEM solver was 5 × 10⁻⁶ s (21% of the Rayleigh times), and the timestep used in the CFD solver was 5 × 10⁻⁴ s. The data exchange for coupling the CFD and DEM solver mainly includes three steps:

• Solving the pressure and velocity fields of the liquid phase with the CFD part without considering the particles.
• The velocities of particles are exerted on the CFD grid blocks where they are “covered” by the particles. As a result of this process, the flow field violates the conservation of mass requirements and is corrected to ensure this condition is once more satisfied.
• The force exerted on each particle by the fluid is calculated and sent to the DEM code.

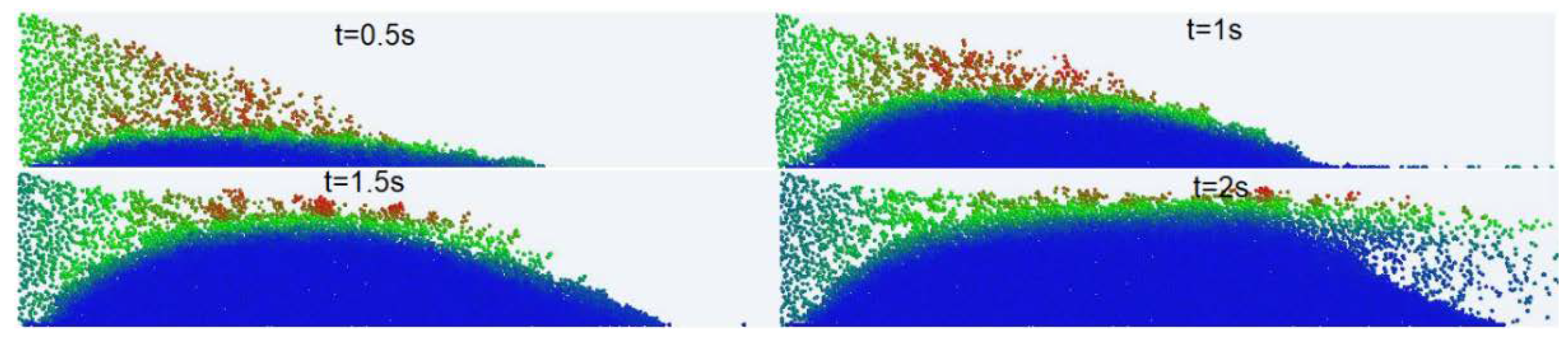
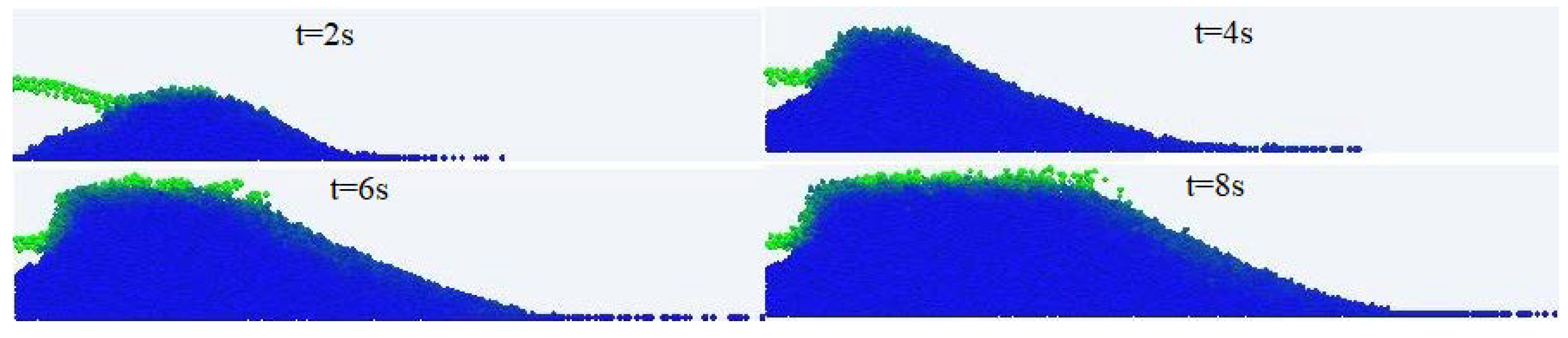
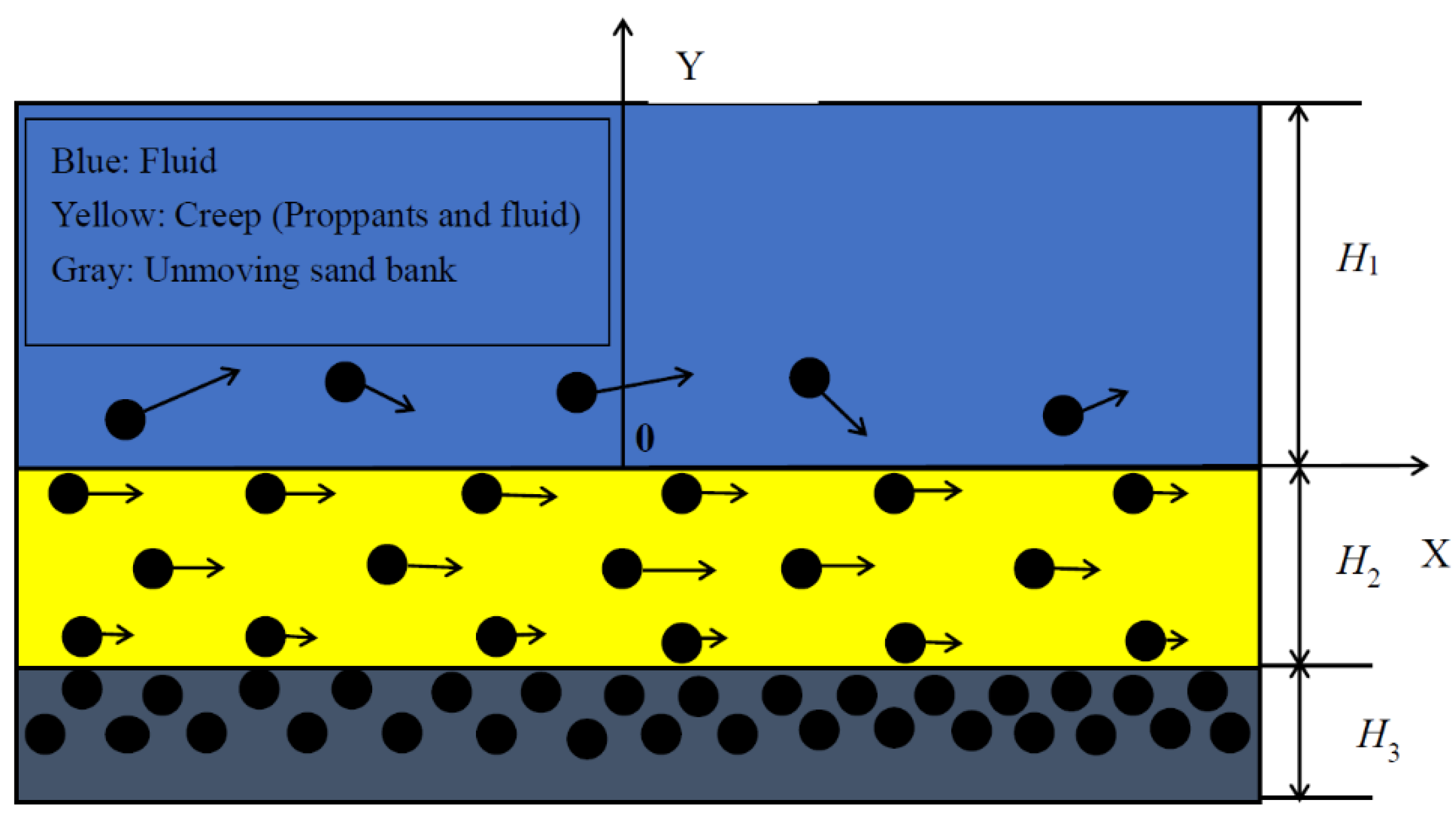
3.2. Mechanisms of Proppant Transport in the Fracture

The mechanisms of proppant transport in the low-viscosity fluid along the fracture were studied first. The proppant–proppant and proppant–wall interaction parameters are shown in

Table 6. The interaction parameters between proppant and fracture wall.

Parameters	Coefficient of Restitution	Static Friction Coefficient	Rolling Friction Coefficient
Proppant–proppant	0.21	0.6	0.05
Proppant–wall	0.24	0.1944	0.005

, and the other necessary settings in the simulation are shown in

Table 7. Necessary parameters in the simulation.

Parameters	Value	Parameters	Value
Injection rate	0.3 m/s	Fracturing fluid viscosity	1 mPa·s
Particle diameters	1.4 mm	Sand ratio	20%

According to actual real-life hydraulic fracturing, the injection rate is about 2–6 m³/min, W = 0.006 m, H = 20 m; then, in the initial stage of fracturing, the velocity of the fracturing fluid in the fracture will be in the range of 0.26–1 m/s. The injection rate in the simulation can reflect the actual flow rate of the fracturing fluid.

. As the mechanisms of the proppant migration are only analyzed in this section, the proppant diameter and sand ratio were bigger than those used during fracturing to reduce the time cost in the simulation, and this did not affect the mechanism of proppant migration.

Figure 10 and Figure 11 show the phenomenon of proppant transport in the fracture of the vertical well and horizontal well, respectively. As can be seen from them, whether for the vertical or for the horizontal well, in the early stage, the proppants settled down rapidly near the wellbore under the action of gravity and formed the proppant dune because of the low viscosity of the fracture fluid, and the suspension was the primary mechanism of proppant migration. With the injection of the fracturing fluid, a bedload layer formed on the surface of the proppant due to the dragging effects of the fracturing fluid on proppants, and the flow rate of the fracturing fluid increased with the decrease of the flow area in the upper part of the sand bed. Therefore, the drag force acting on the surface of the sand bed increased until the height of the sand bed stopped increasing to reach the equilibrium height, and the build angle and the drawdown angle were also maintained constant. The proppants were transported to the distal end of the fracture. At this stage, fluidization and resuspension at the distal end of the sand bed dominated the proppant migration. Due to the erosion of the fracturing fluid, a sizeable non-filled area formed near the wellbore, which influenced the hydraulic fracturing as a consequence. The study of proppant migration mechanisms showed that bedload transport was the main form of proppant transport during slickwater fracturing, and the process of proppant migration with saltation and creep can be shown in Figure 12. The mass flux of the creeping layer can be expressed as per Equation (21) [50,51].

$$Q_{creep}=\frac{{\rho }_f^2}{2{\rho }_s\overline{\epsilon }g{\mu }_m^2}\sqrt{\frac{{\mu }_m-{\mu }_d}{c{d}_{p}g}}\cdot U_{*}^4,$$

(27)

where $Q_{creep}$ is the mass flux of the creeping layer per unit width (kg/(s·m)), ${\rho }_s$ is the density of the proppant (kg/m³), $\overline{\epsilon }$ is the volume fraction of the proppant in the creep layer (dimensionless), ${\mu }_m$ and ${\mu }_d$ are the coefficient of static friction and coefficient of rolling friction between the proppant, respectively (dimensionless), $U_{*}$ is the shear velocity of the fluid acting on the creeping layer (m/s), and $c$ is a constant of 1.5.

As can be seen from Equation (27), the coefficient of static friction and the coefficient of rolling friction between proppants affect the mass flux of the creeping layer, which further affect the distribution of proppants in the fracture. Moreover, the interaction between the proppant and fracture walls can also affect the migration in the fracture. Therefore, it is significant to calibrate the parameters of the proppant–proppant and proppant–wall interactions. Figure 13 shows the surface morphology of the sand bed with time, through which the growth process of the sand bed can be better observed.

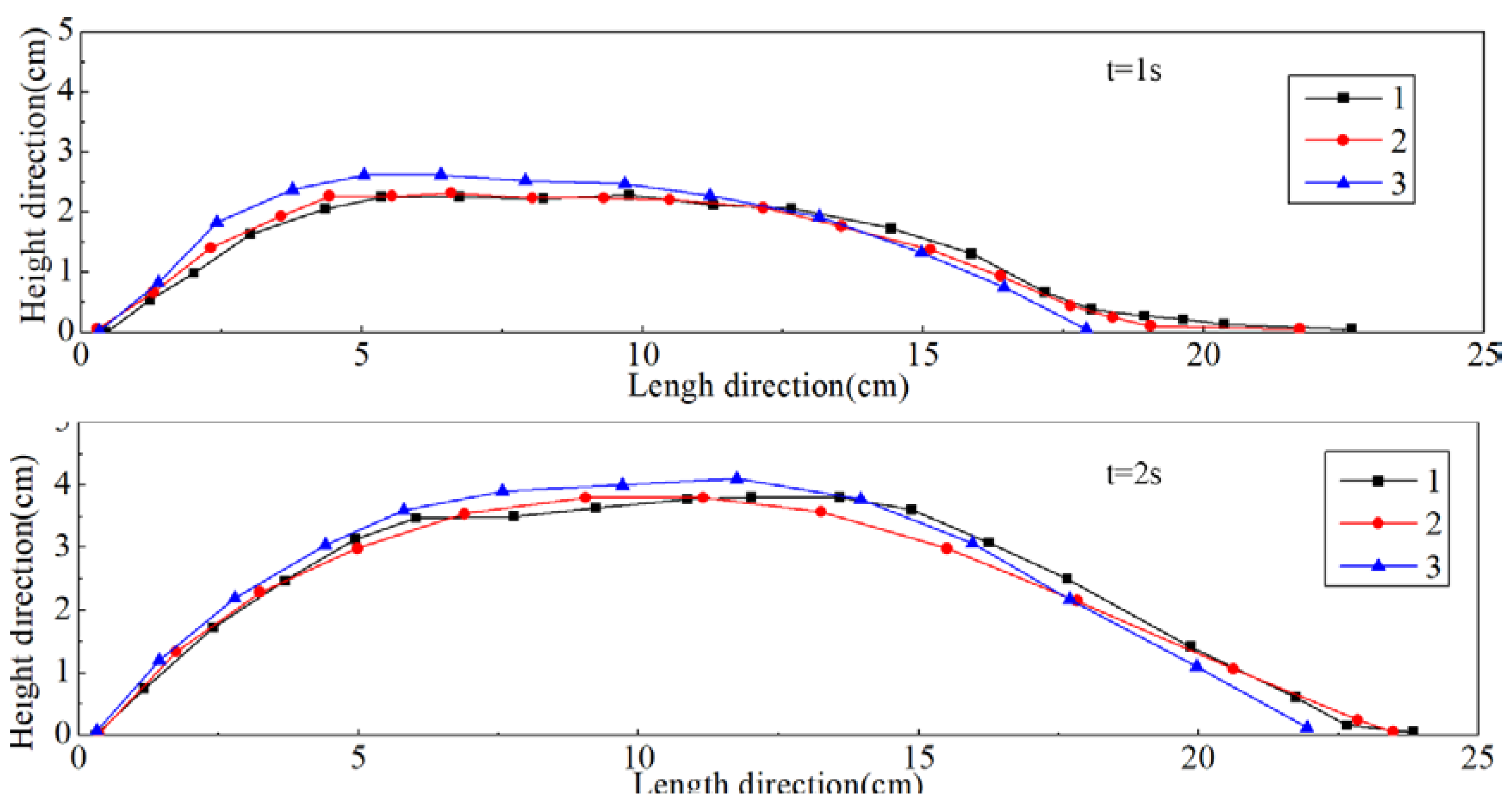
3.3. Effects of Interaction Parameters on Proppant Distribution in the Fracture

The wall roughness and the uneven distribution of proppant diameter increase the interaction between proppants and walls, and the interaction parameters between the proppants and walls affect the sand bed morphology. Therefore, in this section, the effects of the interaction parameters of the proppants and walls on proppant distribution are studied, considering the wall roughness and unevenly distributed proppant diameter. As can be seen from the previous study, the mechanism of proppant migration in fractures of vertical or horizontal wells is the same. Therefore, fracture of vertical wells was analyzed when studying the influence of interaction parameters on proppant migration. The underlying simulation parameters are listed in Table 7. The rough fracture model was established based on the experiment data of Barton (JRC = 10) [52], as shown in Figure 14.

Table 8. The contact parameters of different models.

Case	The Contact Parameters (Proppant–Proppant)			The Contact Parameters (Proppant–Wall)
	Coefficient of Restitution	Static Friction Coefficient	Rolling Friction Coefficient	Coefficient of Restitution	Static Friction Coefficient	Rolling Friction Coefficient
1	0.21	0.6	0.05	0.24	0.19	0.005
2	0.27	0.6	0.05	0.31	0.3	0.005
3	0.21	0.8	0.1	0.24	0.26	0.01

shows the contact parameters of different cases for the simulation. Case 2 had a larger coefficient of restitution than case 1, while the static friction coefficient and rolling friction coefficient of the two models were the same. Case 3 had a larger static friction coefficient and rolling friction coefficient of proppant–proppant and proppant–wall interaction than case 1, while the coefficients of restitution of the two models were the same.

(1)

The sand bed morphology with single-diameter proppants

Figure 15 shows the distribution of single-diameter proppants in a smooth fracture, and, as can be seen, the coefficient of restitution had little effect on the equilibrium height, build angle, and drawdown angle due to less interaction between the proppant and proppant or the wall. When the static friction coefficient and the rolling friction coefficient were smaller, the equilibrium height, build angle, and drawdown angle of the sand bank were lower, enabling the proppants to be transported into the distal end of the fracture. When the sandbank reached the equilibrium height, all the proppant injected could be calculated as the bedload layer. From Equation (27), it can be calculated that the shear velocity of the fluid acting on the sandbank in case 3 was 1.1236 times that of the shear velocity in case 1. Therefore, the equilibrium height of the sandbank in case 3 would be higher than that in case 1 for a higher shear velocity.

(2)

The effects of a rough fracture on proppant distribution

Figure 16 shows the distribution of proppants with a single diameter in smooth and rough fractures. As shown, the roughness of the fracture had little effect on proppant distribution, and the equilibrium height of the sandbank in the rough fracture was slightly larger than that in the smooth fracture, while the build and the drawdown angles were similar. This result indicates that the interaction between the proppants and walls had little impact on the morphology of the sandbank, although the wall roughness increased proppant–proppant and proppant–wall collisions.

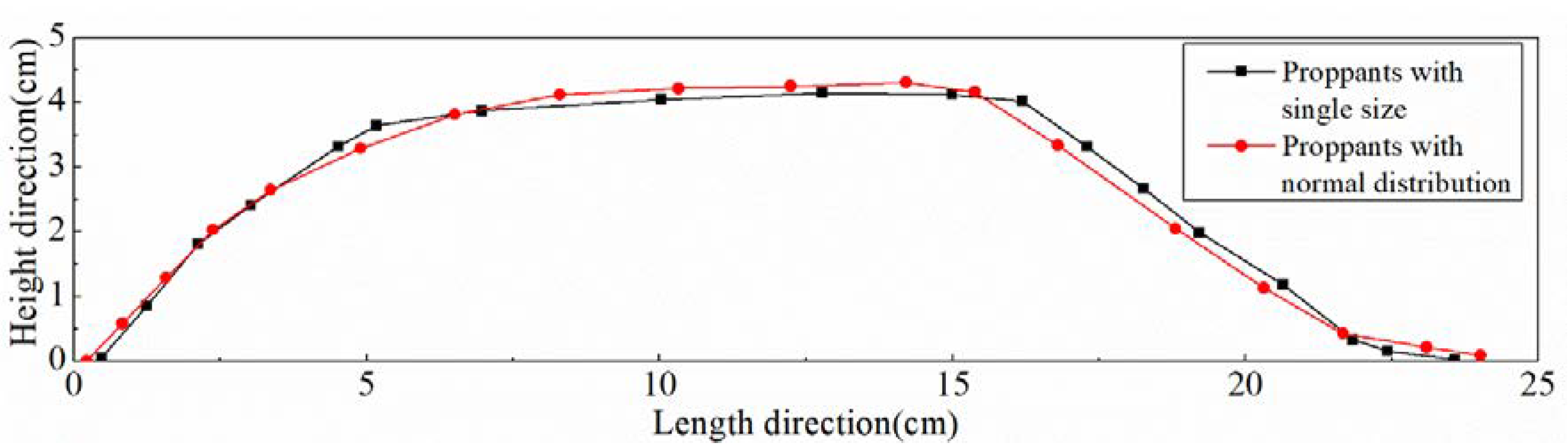
(3)

The effects of an unevenly distributed proppant diameter on proppant distribution

Figure 17 shows the comparison of the distribution of proppants with a single diameter and proppants with a normally distributed diameter in fractures. In the early stage of the injection, the nonuniformity of the proppant size increased the interaction between the suspended particles and made the particle movement more complicated. However, when the sandbank reached the equilibrium height, the primary mechanisms which dominated the proppant migration were fluidization and resuspension at the distal end of the fracture. Thus, the proppant–proppant collision and proppant–wall collision had little impact on proppant distribution, slightly increasing the equilibrium height of the sandbank, while they had no influence on the buildup and drawdown angles.

4. Discussion

In conventional fracturing fluids, the mechanism of proppant transport is mainly suspension, and most of the proppant remains in suspension until the fracture is reclosed. Thus, the study of proppant transport is mostly about the settling velocity of proppants in fracturing fluids with various viscosities, and the wall-retardation effect is also a significant research direction. As the interactions between the proppant and proppant or the wall affect the settling velocity and horizontal velocity of the proppant, and since the sand ratio and unevenly distributed diameter of the proppant increase the complexity of suspended proppant movement, the proppant distribution in the fracture will be greatly influenced by the interactions. Since the coupled CFD–DEM model used in this paper greatly reduced the calculation efficiency with the increase in the number of particles, a small fracture size was used in the simulation, and the proppant was in suspension for a short time. Therefore, although the results obtained in this paper show little effect of the fracture roughness and unevenly distributed diameter of the proppant on proppant distribution, this result only reflects the effects of the factors on bedload proppant transport but without the suspension proppant transport. In slickwater, the proppant settles out of suspension near the wellbore rapidly to form a dune, and the bedload layer becomes the main patten of proppant transport. Thus, we believe that the study of the settling velocity and wall retardation is not as important as the bedload proppant transport affected by various factors during slickwater hydraulic fracturing. Thus, the effects of the interaction parameters on suspended proppant transport are no longer conducted here.

Many researchers [7,11,28,30] studied the effects of various factors, including the proppant diameter, proppant density, the viscosity of the fracturing fluid, injection rate, and sand ratio on the proppant distribution and equilibrium height of the sand bank. However, they did not consider the effects of the interaction parameters. However, from the research in this paper, we can see that, when the sandbank reaches the equilibrium height, the shear stress of the fluid acting on the bedload layer needed for carrying the injected proppant to the further end of the fracture will increase with an increase of the static friction coefficient and rolling friction coefficient between proppants, and this will lead to the increase in the equilibrium height of the sandbank. The experimental results of Mack et al. [7] also showed similar results. As shown, advanced ceramic proppants can be transported further into fractures as a result of the higher coefficient of restitution and a lower friction coefficient than conventional ceramic proppant and sand. However, many of the bedload transport models, including the model used in the paper of Mack et al. [7], cannot consider the influence of interaction parameters, although the experimental and numerical simulation results show that the interaction parameters have an impact on the bedload proppant transport and proppant distribution. Thus, it is of great significance to calibrate the interaction parameters between proppant and further studies on the bedload proppant transport for further study of the proppant distribution in the fracture during slickwater hydraulic fracturing.

As can be seen from the study above, the impacts of proppant physical parameters on suspended proppant transport and bedload proppant transport should be considered when selecting the proppant during slickwater hydraulic fracturing. Moreover, further research and discussion can be done. In this paper, the influences of the interaction parameters on suspended proppant transport were not studied, and the effects of the interaction parameters on proppant migration were analyzed only from the phenomena observed, but not quantitatively analyzed. All the factors that affect the movement of the bedload layer will affect the equilibrium height of the sand bank, such as the injection rate, the density of the proppant, density of the fluid, rolling friction coefficient, static friction coefficient, and so on. To the best of our knowledge, the equations for calculating the equilibrium height of the sandbank cannot consider the influence of all of the factors. Thus, in future research, we will establish a new model for calculating the equilibrium height based on the analysis of the forces acting on the bedload layer, and we will make some progress by doing so.

5. Conclusions

In this paper, a method for calibrating the interaction parameters between proppant and proppant or the wall was proposed. The coupled CFD–DEM model was established considering the interaction between proppants and walls to study the mechanisms of proppant transport in fracture and to analyze the impacts of the interaction parameters on proppant distribution considering the wall roughness and unevenly distributed diameter of proppants. The following conclusions can be drawn from the research:

(1)

A lower static friction coefficient and rolling friction coefficient between the proppant and proppant or the wall can result in a smaller equilibrium height of sandbank and a smaller build angle and drawdown angle, which is beneficial for transporting the proppant to the distal end of fractures.

(2)

The wall roughness increases the collision between the proppant and proppant or the wall, whereas the interactions have little impacts on the sandbank morphology. Wall roughness slightly increases the equilibrium height of the sandbank, while it does not have any influence on the build angle or drawdown angle.

(3)

In the early stage of fracturing, an uneven particle size increases the complexity of the movement of the suspended proppant. However, when the sand bed reaches the equilibrium height, it has little impact on the sandbank morphology, only slightly increasing the equilibrium height.