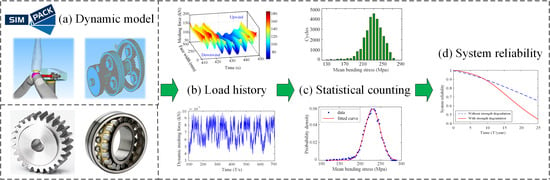
Fatigue Reliability Analysis of Wind Turbine Drivetrain Considering Strength Degradation and Load Sharing Using Survival Signature and FTA
Abstract
:1. Introduction
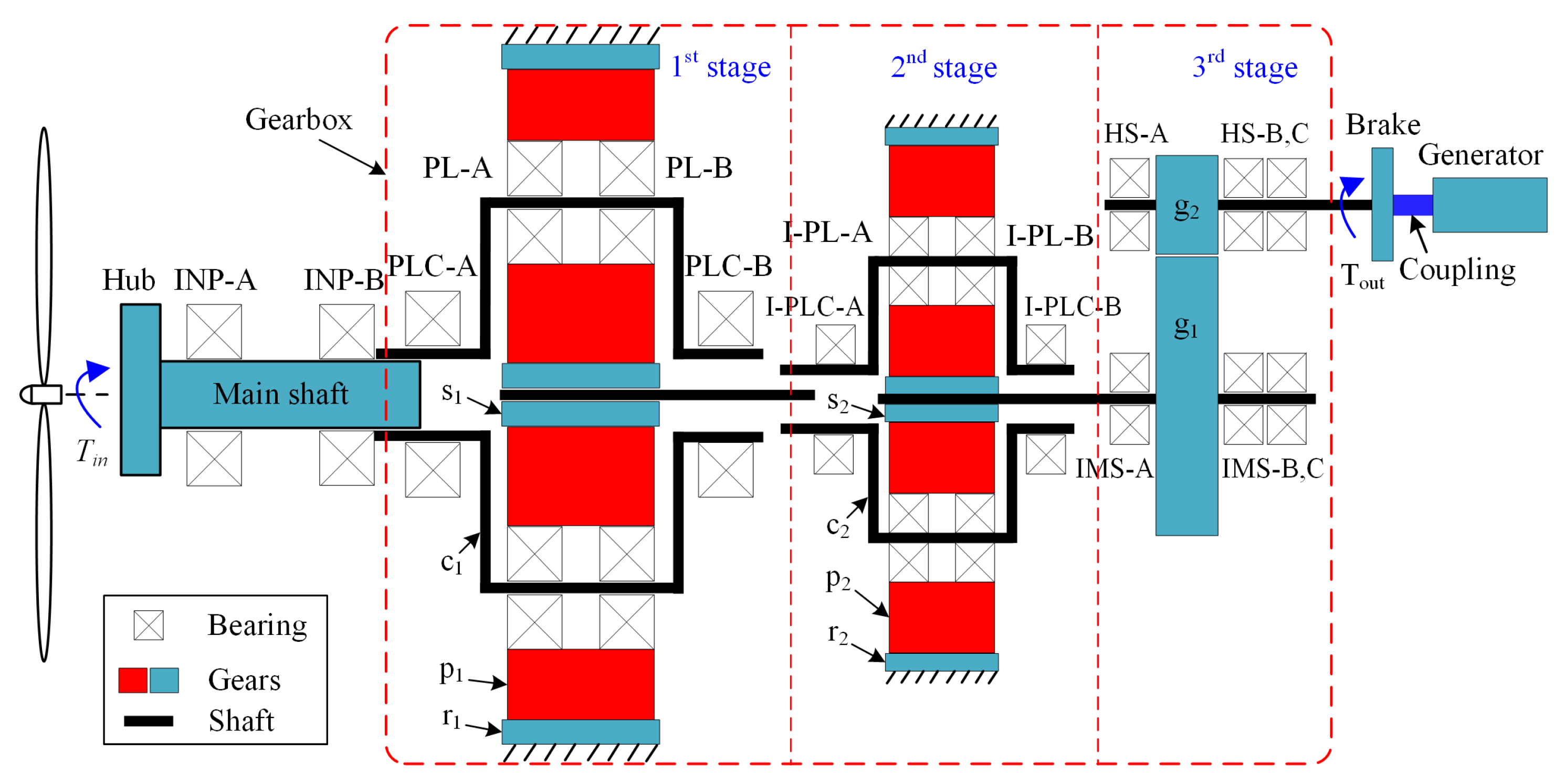
2. Structure and Transmission Principles of Wind Turbine Drivetrain
3. Electromechanical Coupling Dynamic Model of Wind Turbines
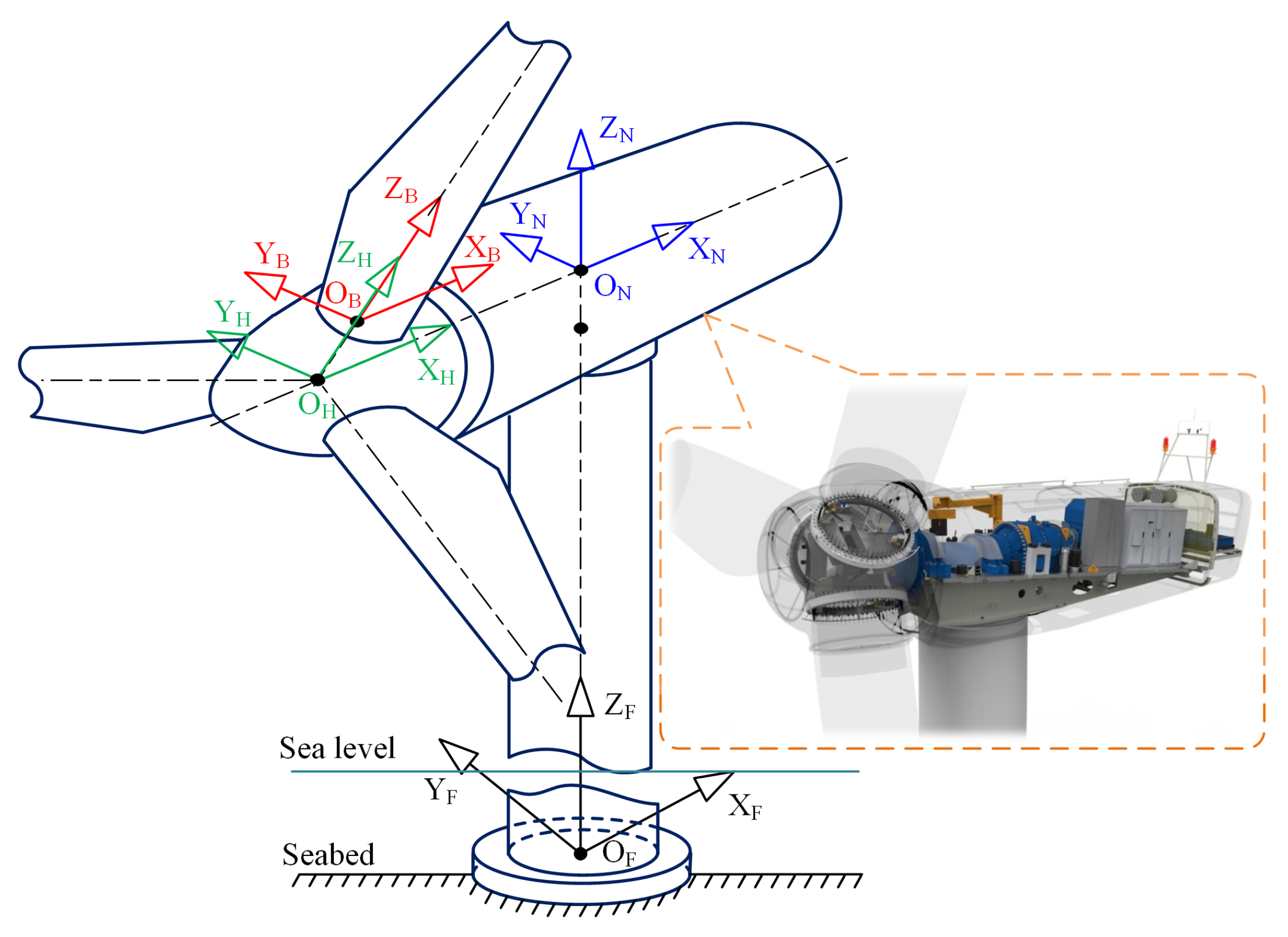
3.1. Coordinate System Definition
3.2. Aerodynamic and Wave Model
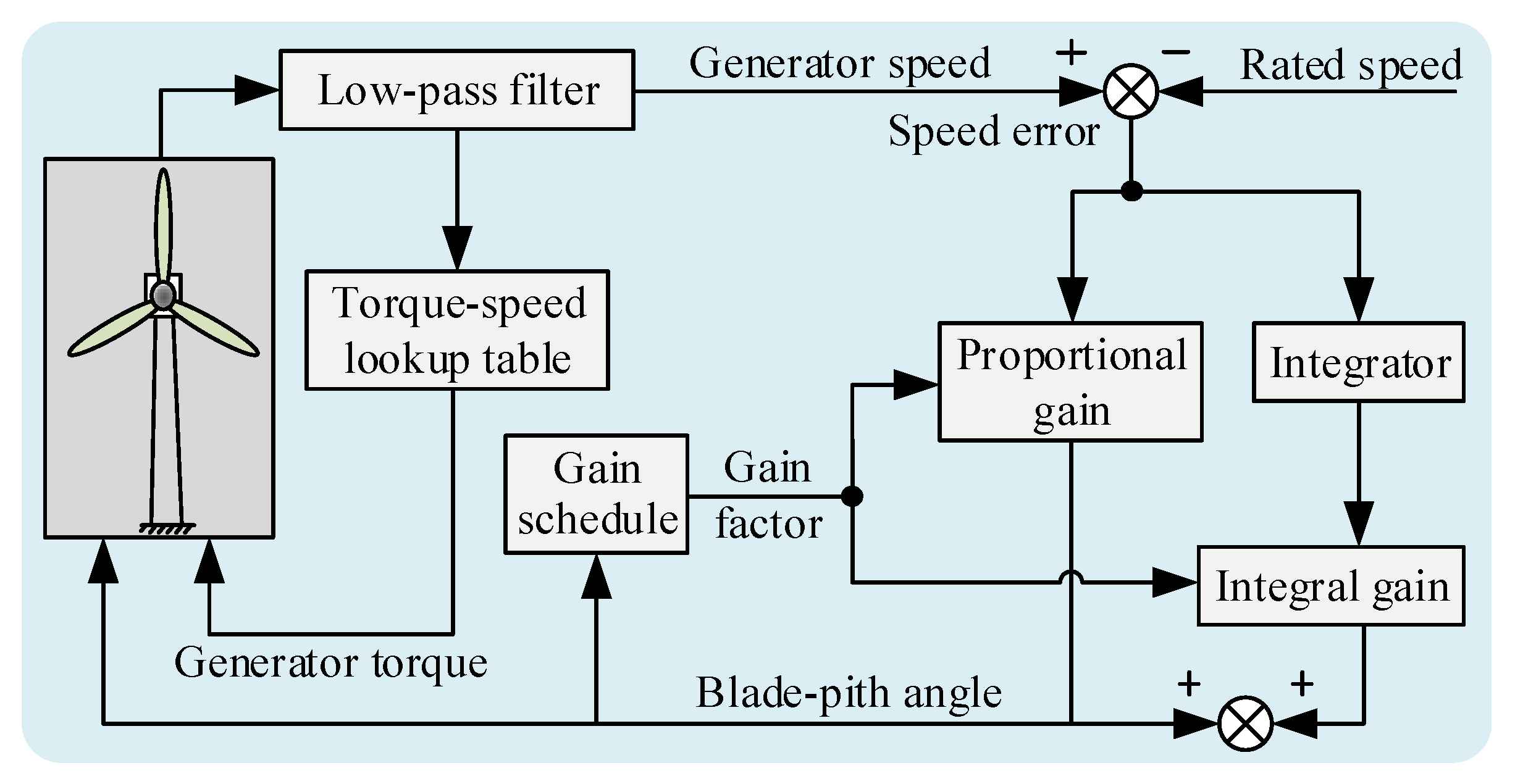
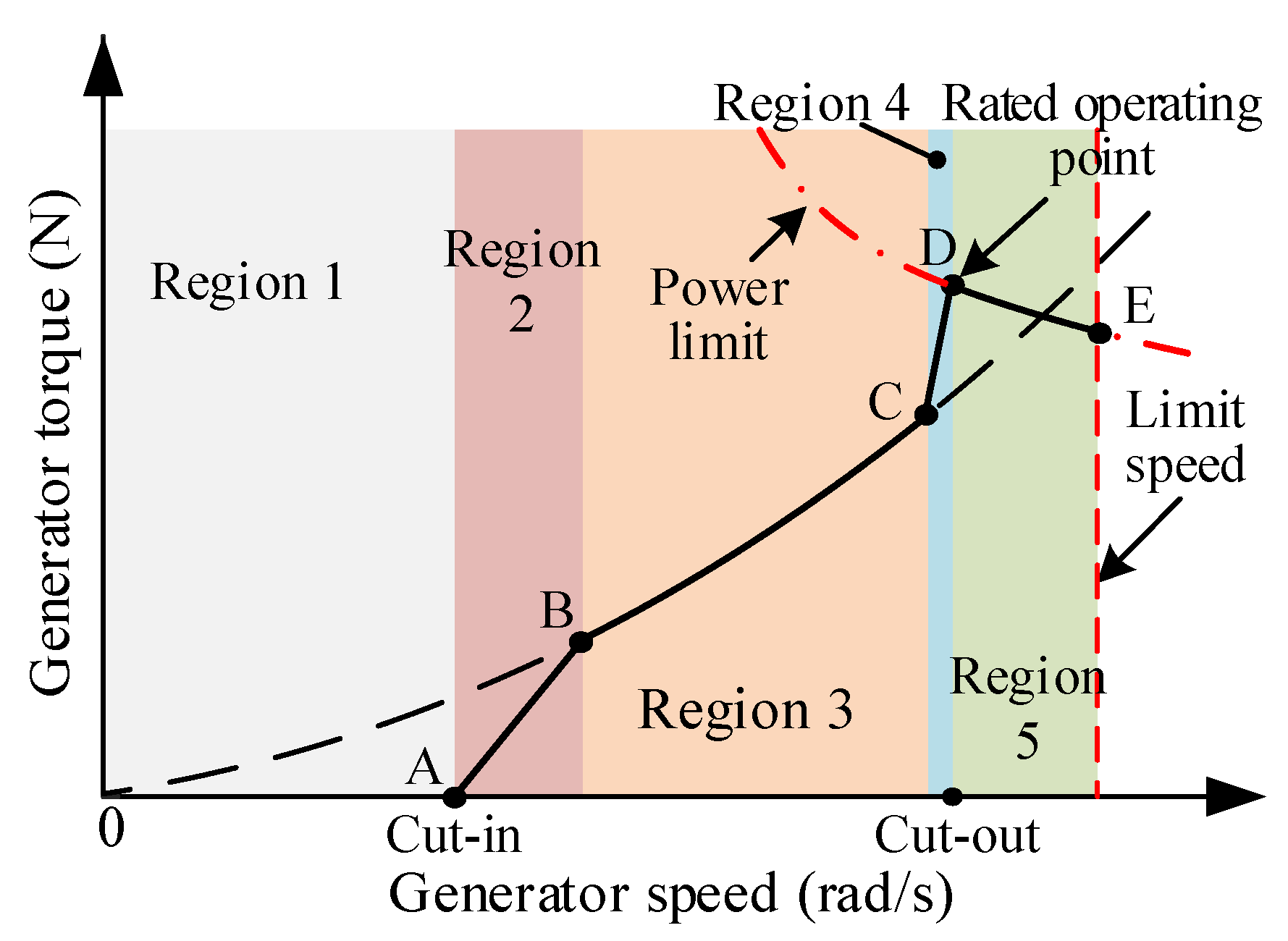
3.3. Control System
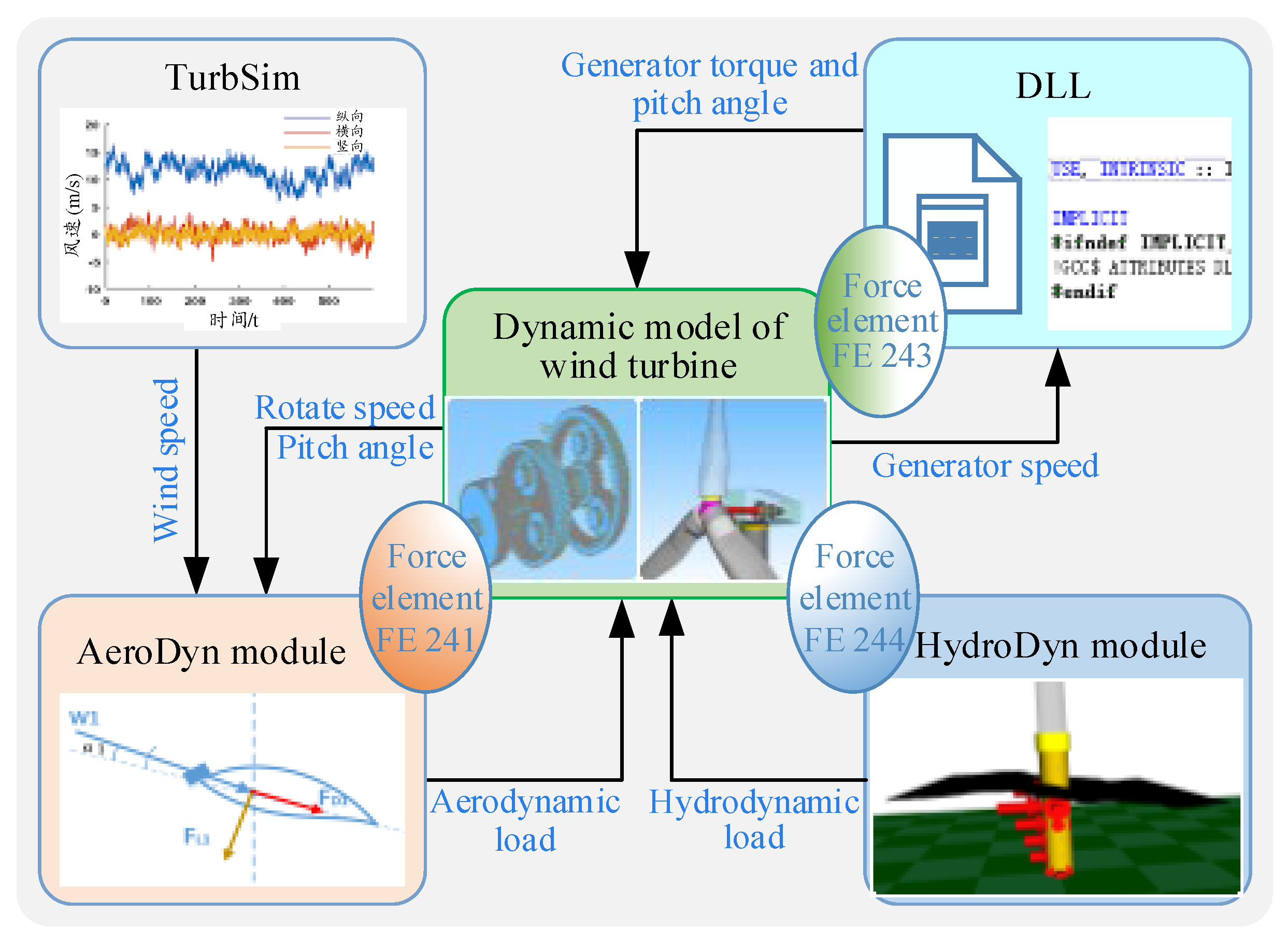
3.4. Dynamic Model of the Wind Turbine Drivetrain
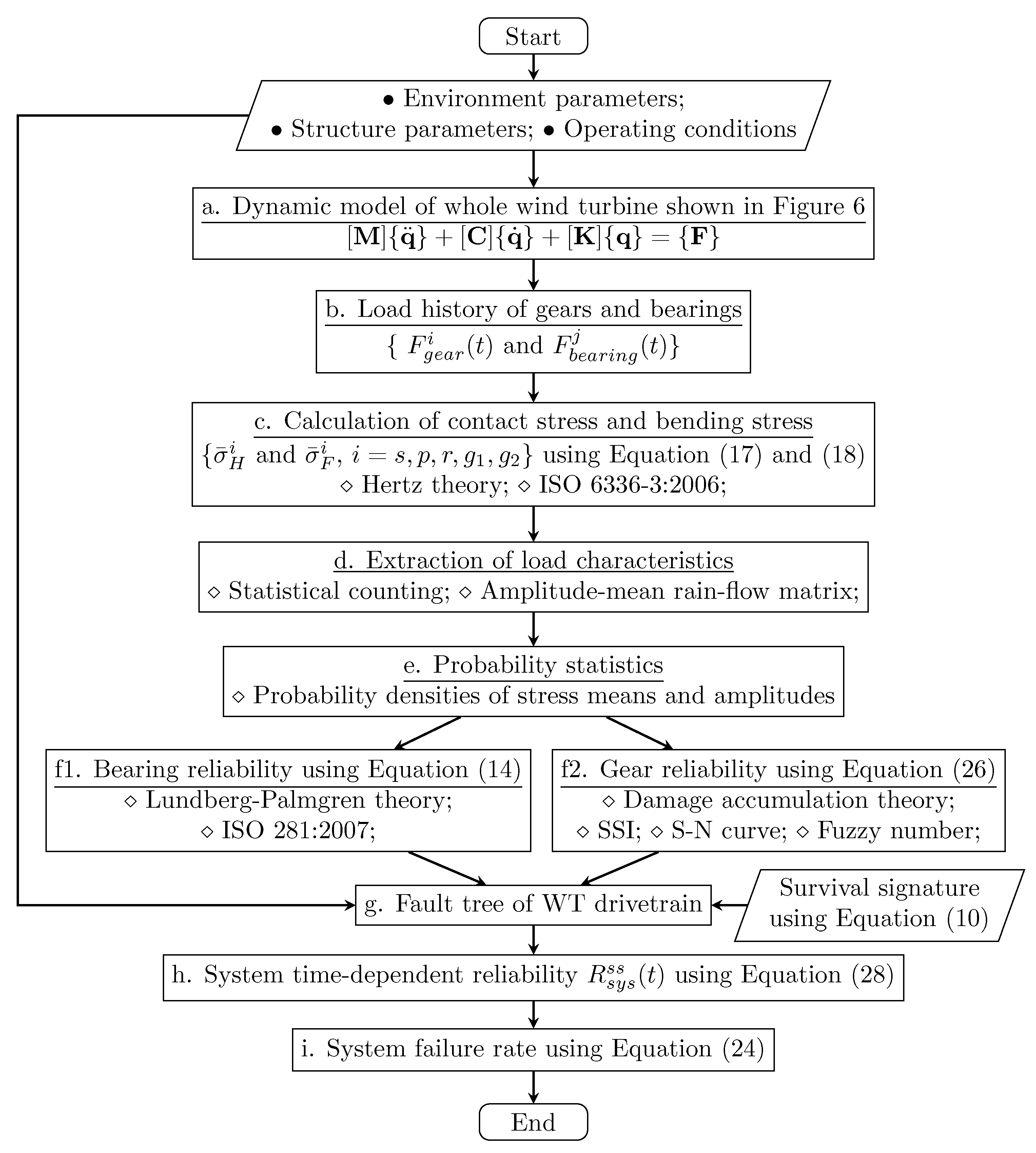
4. Dynamic Reliability Model of the Wind Turbine Drivetrain
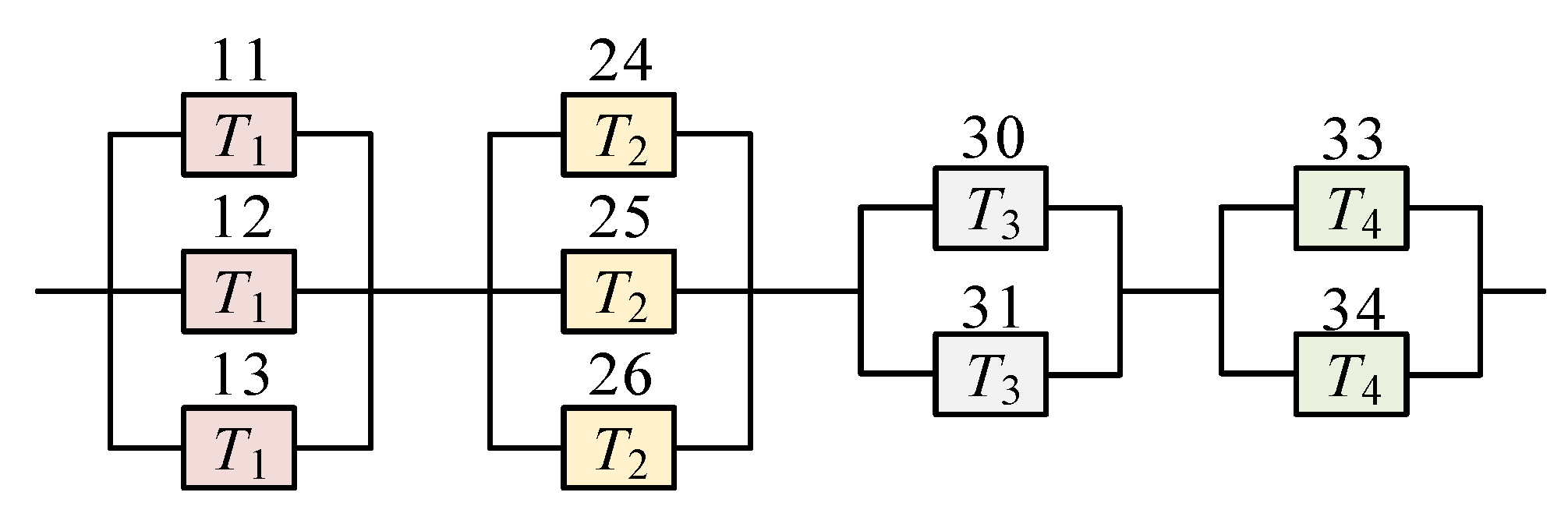
4.1. Survival Signature
4.2. Bearing Reliability
4.3. Gear Reliability Considering Fatigue Damage Accumulation
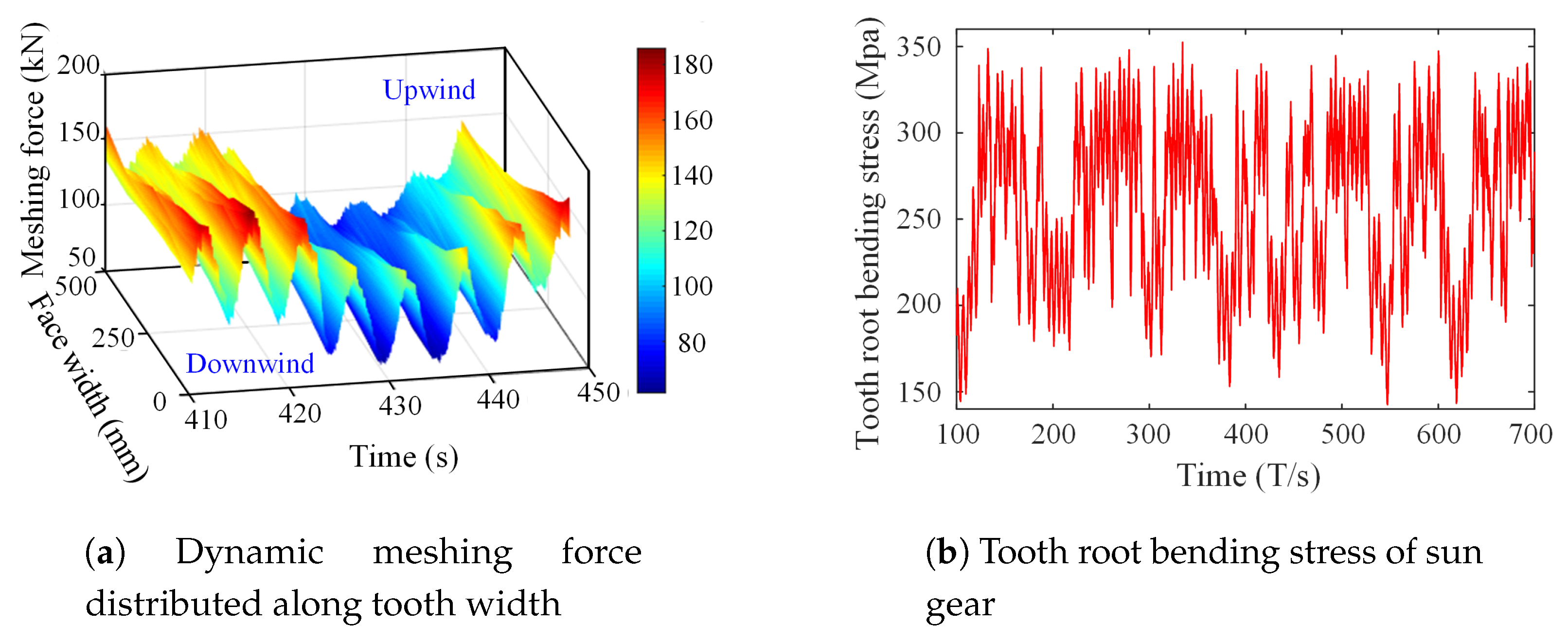
4.3.1. Gear Stresses Calculation
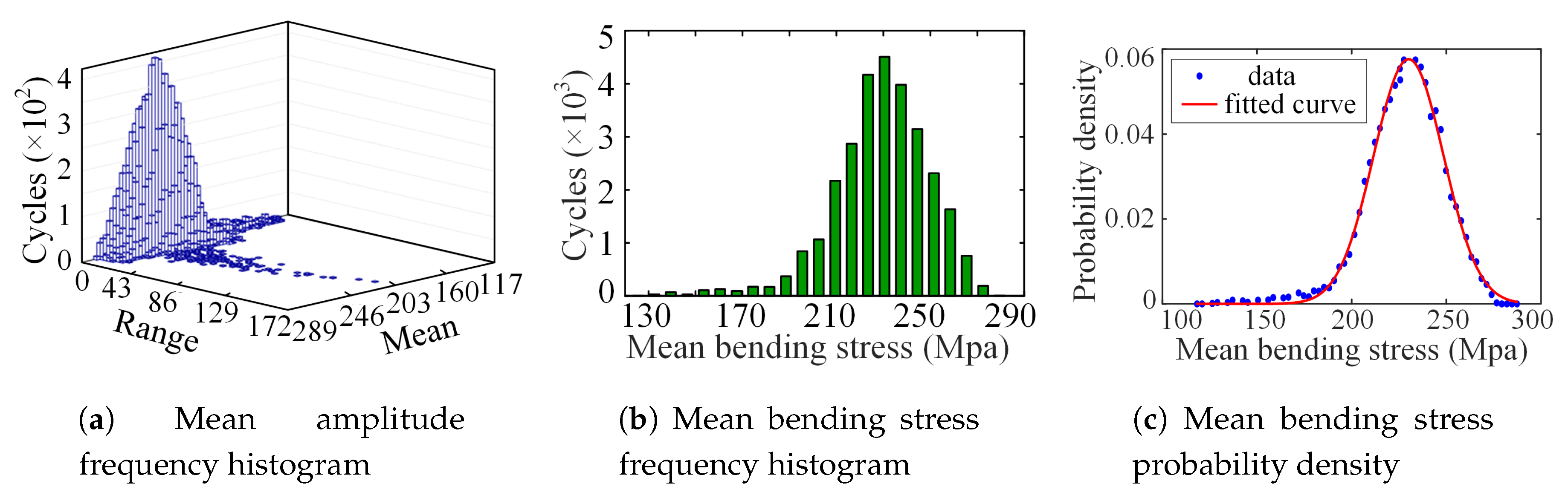
4.3.2. Fuzzy Reliability Model
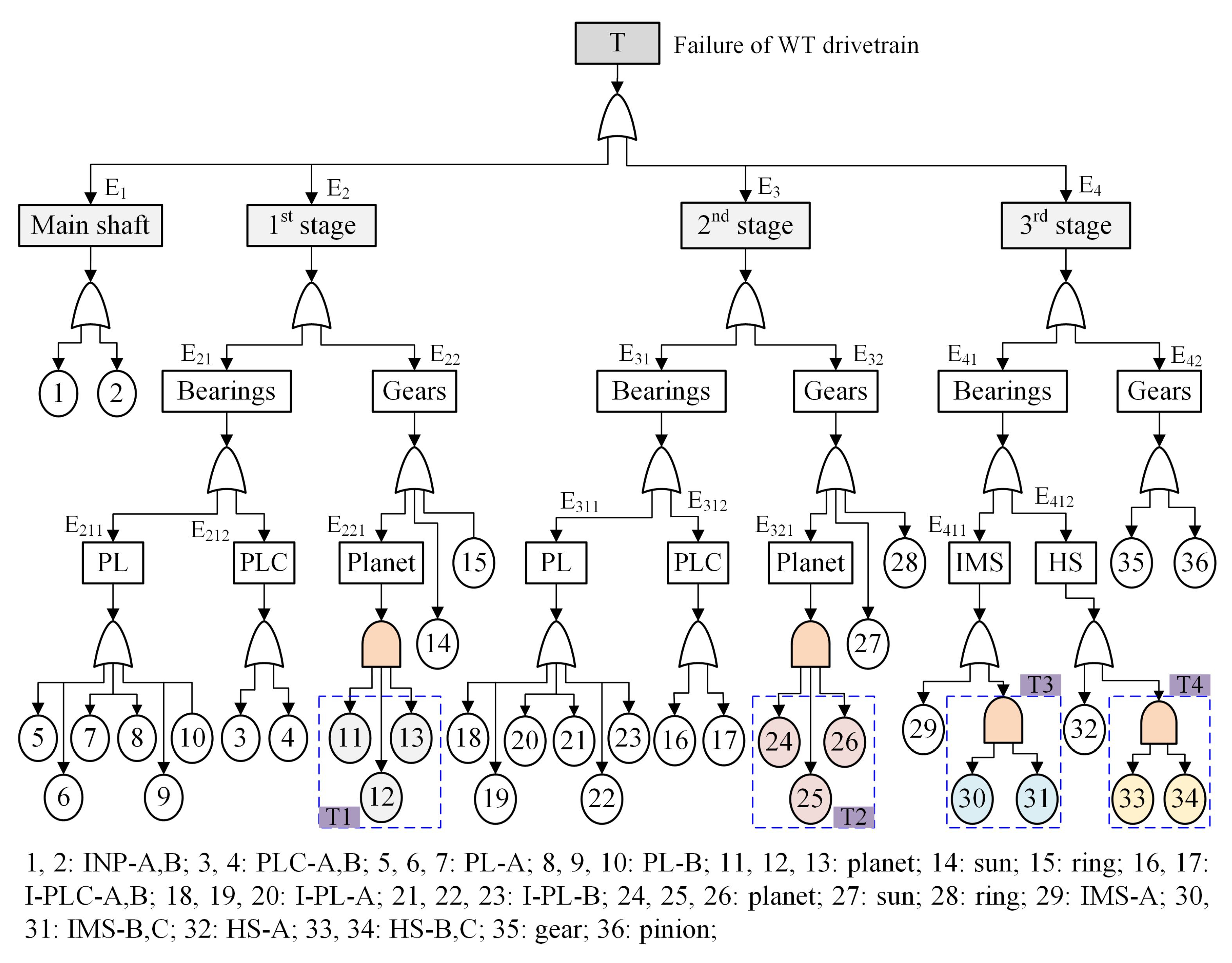
4.4. System Reliability Model
- T:
- {E,E,E,E}, E: {}
- E:
- {}, {}, {}
- E:
- {16,17,18,19,20,21,22,23,24,27,28}, {16,17,18,19,20,21,22,23,25,27,28},{16,17,18,19,20,21,22,23,26,27,28}
- E:
- {29,30,32,33,35,36}, {29,31,32,33,35,36}, {29,30,32,34,35,36}, {29,31,32,34,35,36}
5. Reliability Analysis
5.1. Survival Signature
5.2. Fatigue Damage Accumulation
5.3. Load Distribution
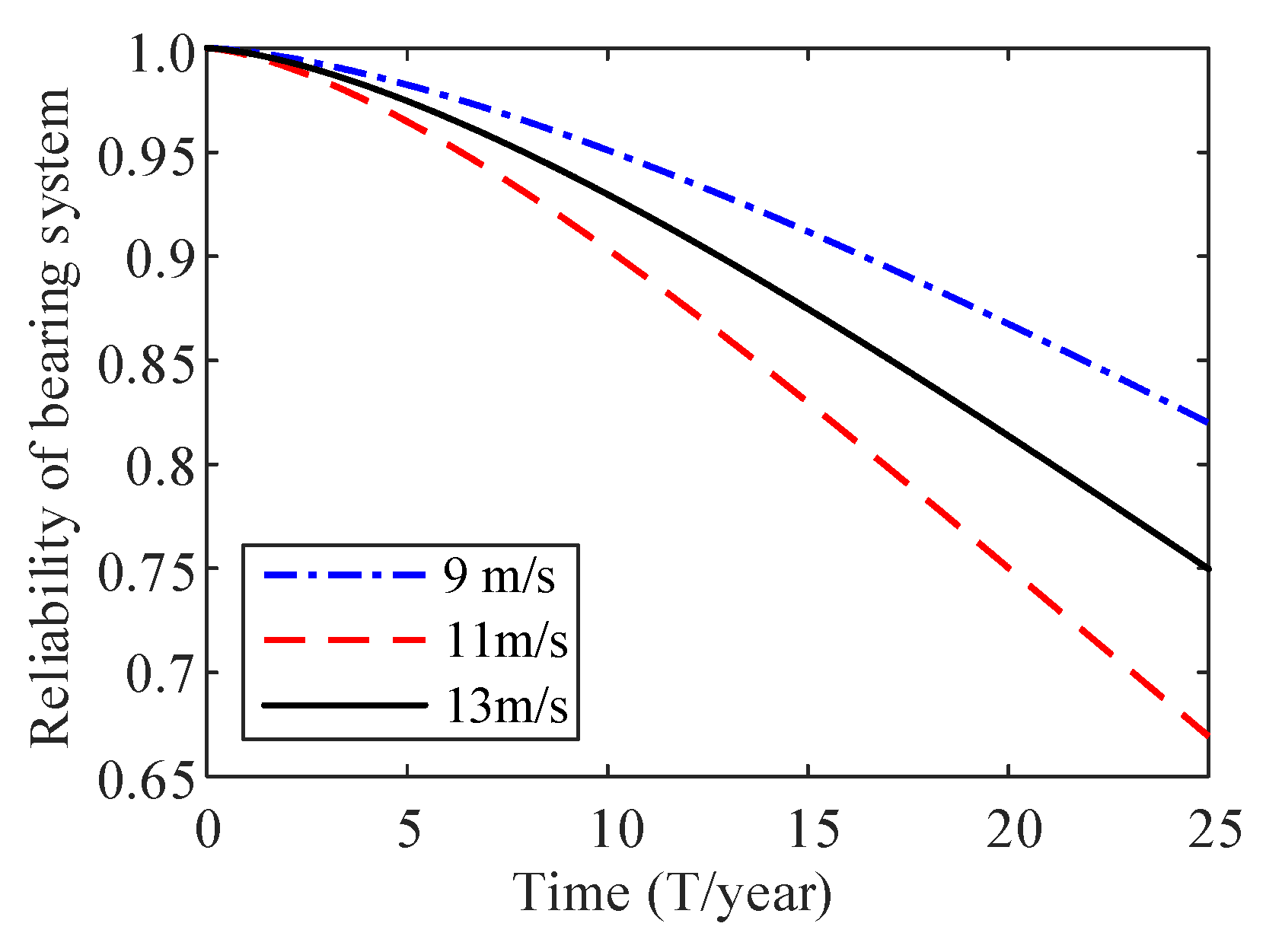
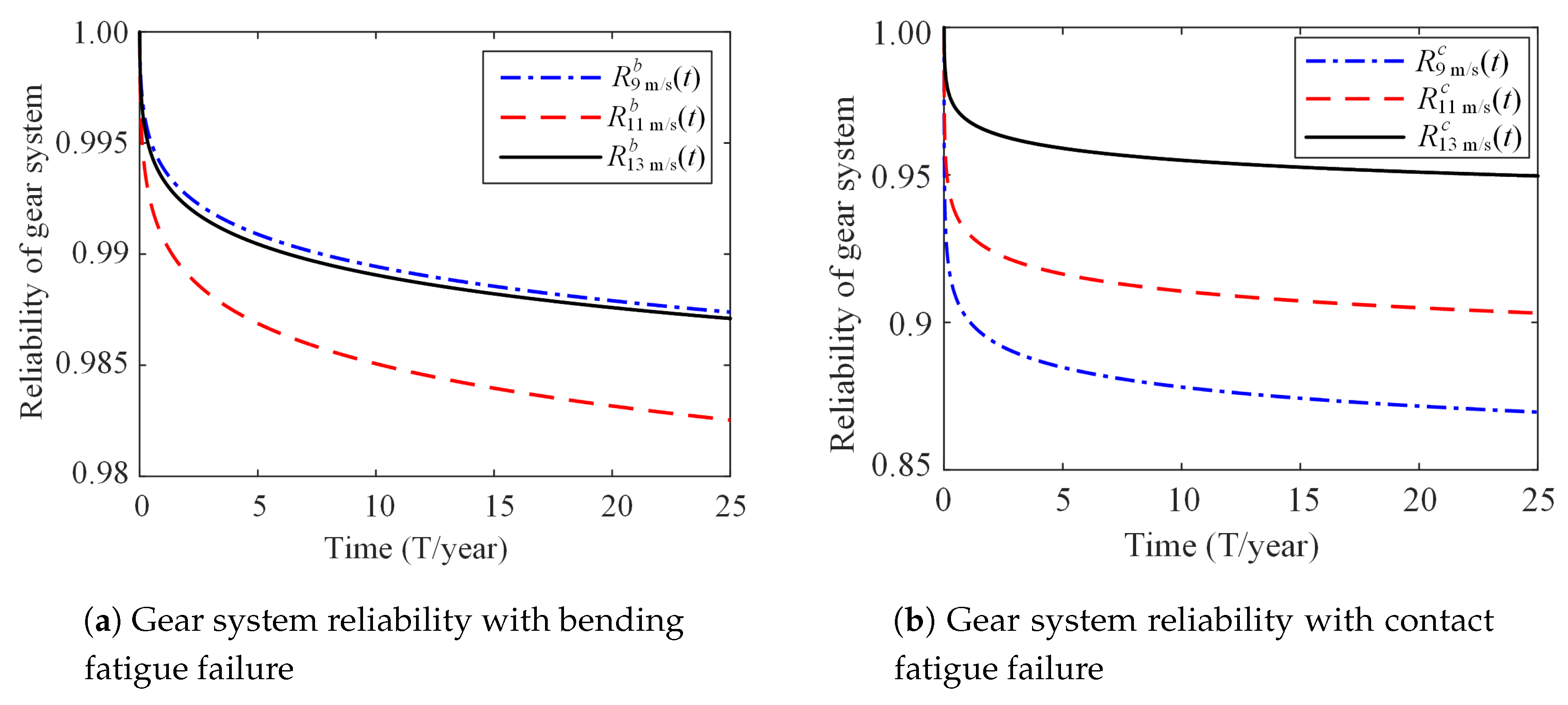
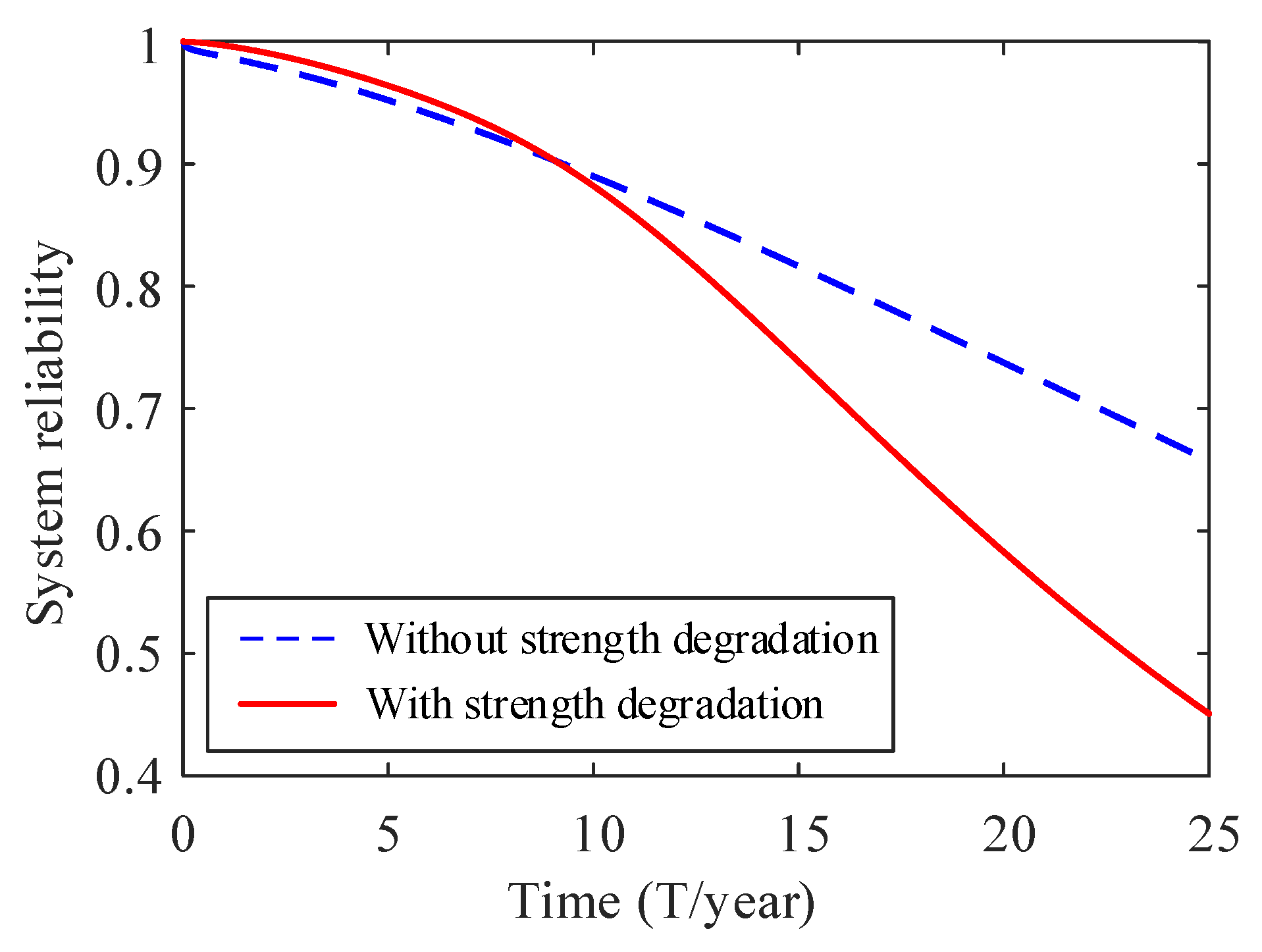
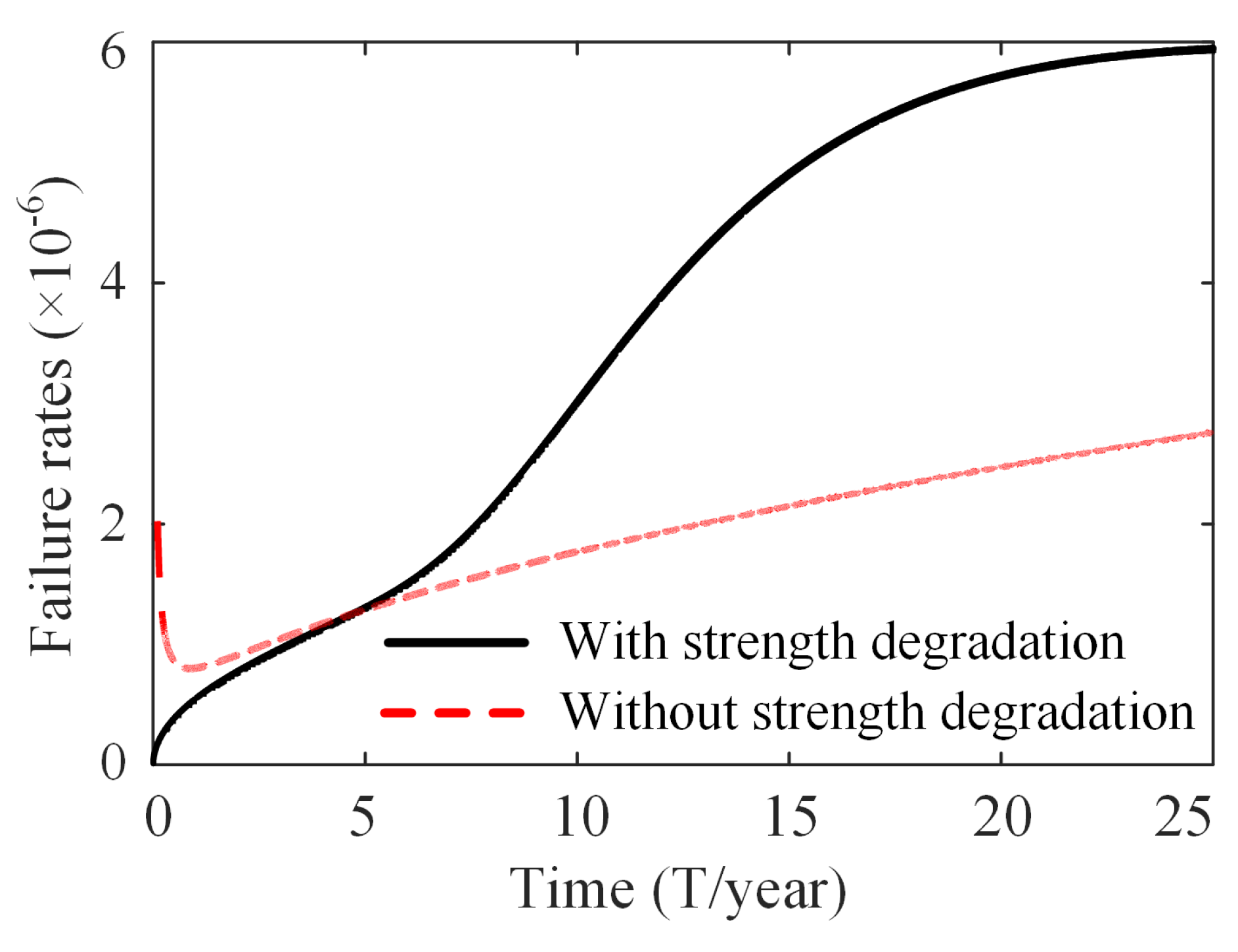
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FTA | fault tree analysis |
| SSI | stress and strength interference |
| NREL | national renewable energy laboratory |
| DLL | dynamic link library |
| MBS | multi-body system |
| WT | wind turbine |
| DoFs | degrees of freedom |
| T1, T2, T3, T4 | four types of load-sharing components |
Nomenclature
| v, , | mean wind speed, wave height, and spectral peak period |
| , , | the wind speed at the hub height, the wind profile, and the hub height |
| , | the dynamic meshing force of gear i and the supporting force of bearing j at time t |
| , | contact stress and bending stress of the gear |
| , | the number of components of type k and the survival components’ number of type k |
| the failure rate of components or system | |
| survival signature of the system with m components of type K | |
| the reliability of the rolling bearing | |
| the fuzzy reliability of the component | |
| , | the system’s reliability without and with using the survival signature |
| the system’s reliability with respect to the mean wind speed of i | |
References
- International Electrotechnical Commission. IEC 61400-1: Wind Turbines Part 1: Design Requirements; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Helsen, J.; Heirman, G.; Vandepitte, D.; Desmet, W. The influence of flexibility within multibody modeling of multi-megawatt wind turbine gearboxes. In Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 15–17 September 2008; Volume 4, pp. 2045–2072. [Google Scholar]
- Zhang, S.; Zhu, C.; Song, C.; Tan, J.; Chen, X. Natural characteristic analysis of wind turbine drivetrain considering flexible supporting. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 842–856. [Google Scholar]
- Zhu, C.; Chen, S.; Liu, H.; Huang, H.; Li, G.; Ma, F. Dynamic analysis of the drive train of a wind turbine based upon the measured load spectrum. J. Mech. Sci. Technol. 2014, 28, 2033–2040. [Google Scholar] [CrossRef]
- Guo, Y.; Keller, J.; LaCava, W. Combined Effects of Gravity, Bending Moment, Bearing Clearance, and Input Torque on Wind Turbine Planetary Gear Load Sharing; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2012. [Google Scholar]
- Wang, S.; Zhu, C.; Song, C.; Liu, H.; Tan, J.; Bai, H. Effects of gear modifications on the dynamic characteristics of wind turbine gearbox considering elastic support of the gearbox. J. Mech. Sci. Technol. 2017, 31, 1079–1088. [Google Scholar] [CrossRef]
- Girsang, I.P.; Dhupia, J.S.; Muljadi, E.; Singh, M.; Pao, L.Y. Gearbox and drivetrain models to study dynamic effects of modern wind turbines. IEEE Trans. Ind. Appl. 2014, 50, 3777–3786. [Google Scholar] [CrossRef]
- Li, Y.; Castro, A.M.; Martin, J.E.; Sinokrot, T.; Prescott, W.; Carrica, P.M. Coupled computational fluid dynamics/multibody dynamics method for wind turbine aero-servo-elastic simulation including drivetrain dynamics. Renew. Energy 2017, 101, 1037–1051. [Google Scholar] [CrossRef] [Green Version]
- Nejad, A.R.; Jiang, Z.; Gao, Z.; Moan, T. Drivetrain load effects in a 5-mw bottom-fixed wind turbine under blade-pitch fault condition and emergency shutdown. J. Physics: Conf. Ser. 2016, 753, 112011. [Google Scholar] [CrossRef]
- Huang, X.; Coolen, F.P.A. Reliability sensitivity analysis of coherent systems based on survival signature. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2018, 232, 627–634. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Xie, L.; Ding, L. Load sharing analysis and reliability prediction for planetary gear train of helicopter. Mech. Mach. Theory 2017, 115, 97–113. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, X.; Lim, T.C.; Du, X.; Liu, M. Effect of flexible pin on the dynamic behaviors of wind turbine planetary gear drives. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 74–86. [Google Scholar] [CrossRef]
- Qin, D.; Zhou, Z.; Yang, J.; Chen, H. Time-dependent reliability analysis of gear transmission system of wind turbine under stochastic wind load. Jixie Gongcheng Xuebao (Chin. J. Mech. Eng.) 2012, 48, 1–8. [Google Scholar] [CrossRef]
- Huang, X.; Hu, S.; Zhang, Y.; Xu, Y. A method to determine kinematic accuracy reliability of gear mechanisms with truncated random variables. Mech. Mach. Theory 2015, 92, 200–212. [Google Scholar] [CrossRef]
- Xiao, N.; Yuan, K.; Zhou, C. Adaptive kriging-based efficient reliability method for structural systems with multiple failure modes and mixed variables. Comput. Methods Appl. Mech. Eng. 2019, 359, 112649. [Google Scholar] [CrossRef]
- Nejad, A.R.; Gao, Z.; Moan, T. On long-term fatigue damage and reliability analysis of gears under wind loads in offshore wind turbine drivetrains. Int. J. Fatigue 2014, 61, 116–128. [Google Scholar] [CrossRef] [Green Version]
- Nejad, A.R.; Gao, Z.; Moan, T. Fatigue Reliability-Based Inspection and Maintenance Planning of Gearbox Components in Wind Turbine Drivetrains. Energy Procedia 2014, 53, 248–257. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Xing, Y.; Guo, Y.; Moan, T.; Gao, Z. Long-term contact fatigue analysis of a planetary bearing in a land-based wind turbine drivetrain. Wind Energy 2015, 18, 591–611. [Google Scholar] [CrossRef]
- Gallego-Calderon, J.; Natarajan, A.; Cutululis, N.A. Ultimate design load analysis of planetary gearbox bearings under extreme events. Wind Energy 2017, 20, 325–343. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-mw Reference Wind Turbine for Offshore System Development; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Nejad, A.R.; Guo, Y.; Gao, Z.; Moan, T. Development of a 5 mw reference gearbox for offshore wind turbines. Wind Energy 2016, 19, 1089–1106. [Google Scholar] [CrossRef] [Green Version]
- Rulka, W. Simpack-a computer program for simulation of large-motion multibody systems. In Multibody Systems Handbook; Springer: Berlin/Heidelberg, Germany, 1990; pp. 265–284. [Google Scholar]
- Zhu, C.; Chen, S.; Song, C.; Liu, H.; Bai, H.; Ma, F. Dynamic analysis of a megawatt wind turbine drive train. J. Mech. Sci. Technol. 2015, 29, 1913–1919. [Google Scholar] [CrossRef]
- Johannessen, K.; Meling, T.S.; Haver, S. Joint Distribution for Wind and Waves in the Northern North Sea. Available online: https://www.onepetro.org/journal-paper/ISOPE-02-12-1-001 (accessed on 20 February 2020).
- IEC 61400-1. Wind Turbines, Part 1: Design Requirements; International Electrotechnical Commission: Geneva, Switzerland, 2005.
- Shabana, A.A. Dynamics of Multibody Systems; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Jonkman, J.M.; Hayman, G.J.; Jonkman, B.J.; Damiani, R.R.; Murray, R.E. Aerodyn v15 User’s Guide and Theory Manual; National Renewable Energy Laboratory: Golden, CO, USA, 2015. [Google Scholar]
- Jonkman, J.M.; Robertson, A.; Hayman, G.J. Hydrodyn User’s Guide and Theory Manual; National Renewable Energy Laboratory: Golden, CO, USA, 2014. [Google Scholar]
- Jonkman, J.M.; Buhl, M.L., Jr. Fast User’s Guide; National Renewable Energy Laboratory: Golden, CO, USA, 2005; Volume 365, p. 366. [Google Scholar]
- Coolen, F.P.A.; Coolen-Maturi, T. Generalizing the signature to systems with multiple types of components. In Complex Systems and Dependability; Springer: Berlin/Heidelberg, Germany, 2013; pp. 115–130. [Google Scholar]
- Xia, X.; Xu, Y.; Jin, Y.; Shang, Y.; Chen, L. Assessment of optimum confidence interval of reliability with three-parameter weibull distribution using bootstrap weighted-norm method. J. Aerosp. Power 2013, 28, 481–488. [Google Scholar]
- Chiu, Y.P.; Tallian, T.E.; McCool, J.I.; Martin, J.A. A mathematical model of spalling fatigue failure in rolling contact. ASLE Trans. 1969, 12, 106–116. [Google Scholar] [CrossRef]
- Organización Internacional de Normalización. Rolling Bearings: Dynamic Load Ratings and Rating Life; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- Zaretsky, E.V.; Poplawski, J.V.; Peters, S.M. Comparison of life theories for rolling-element bearings. Tribol. Trans. 1996, 39, 237–248. [Google Scholar] [CrossRef] [Green Version]
- Dong, W.; Xing, Y.; Moan, T.; Gao, Z. Time domain-based gear contact fatigue analysis of a wind turbine drivetrain under dynamic conditions. Int. J. Fatigue 2013, 48, 133–146. [Google Scholar] [CrossRef] [Green Version]
- Standard and ISO. 6336-2: 2003, Calculation of Load Capacity of Spur and Helical Gears—Part 2: Calculation of Surface Durability (Pitting); International Organization for Standardization: Geneva, Switzerland, 2006. [Google Scholar]
- Standard, British; ISO, BS. Calculation of Load Capacity of Spur and Helical Gears—Part 3: Calculation of Tooth Bending Strength; International Organization for Standardization: Geneva, Switzerland, 2006; Volume 6336, p. 1996. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometrics 1985, 27, 251–261. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Zhang, Y.; Zhang, X. A new direct second-order reliability analysis method. Appl. Math. Model. 2018, 55, 68–80. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, X.; Lu, B.; Song, C. Fuzzy reliability optimization for transmission system of high-power marine gearbox. J. Ship Mech. 2010, 14, 915–921. [Google Scholar]
- Li, Y.; Coolen, F.P.A. Time-dependent reliability analysis of wind turbines considering load-sharing using fault tree analysis and markov chains. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2019, 233, 1074–1085. [Google Scholar] [CrossRef] [Green Version]
- Aslett, L.J.M. Reliabilitytheory: Tools for structural reliability analysis. R package 2012. Available online: https://github.com/louisaslett/ReliabilityTheory (accessed on 12 September 2016).
- Batsoulas, N.D. Cumulative fatigue damage: Cdm-based engineering rule and life prediction aspect. Steel Res. Int. 2016, 87, 1670–1677. [Google Scholar] [CrossRef]
- Rege, K.; Pavlou, D.G. A one-parameter nonlinear fatigue damage accumulation model. Int. J. Fatigue 2017, 98, 234–246. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative fatigue damage. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar]
- Zhang, Y.; Wang, G.; Wang, J.; Jia, H.; Zhang, E. Compilation method of power train load spectrum of engineering vehicle. Trans. Chin. Soc. Agric. Eng. 2011, 27, 179–183. [Google Scholar]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rating (MW) | 5.0 | Nacelle mass (kg) | 240,000 |
| Cut-in wind speed (m/s) | 3 | Rotor mass (kg) | 110,000 |
| Rated wind speed (m/s) | 11.4 | Hub height (m) | 90 |
| Cut-out wind speed (m/s) | 25 | Rated rotor speed (r/min) | 12.1 |
| Rotor diameter (m) | 126 | Gearbox ratio | 97:1 |
| Cut-in rotor speed (r/min) | 6.9 | Maximum absolute blade pitch rate (∘/s) | 8 |
| Tower mass (kg) | 347,460 | High-speed shaft brake torque (N·m) | 28,116.3 |
| Power control system | Pitch |
| 1 | [1,2,3] | [1,2] | [1,2] | 1 |
| 2 | [1,2,3] | [1,2] | [1,2] | 1 |
| 3 | [1,2,3] | [1,2] | [1,2] | 1 |
| 0 | [1,2,3] | [1,2] | [1,2] | 0 |
| [1,2,3] | 0 | [1,2] | [1,2] | 0 |
| [1,2,3] | [1,2,3] | 0 | [1,2] | 0 |
| [1,2,3] | [1,2,3] | [1,2] | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhu, C.; Chen, X.; Tan, J. Fatigue Reliability Analysis of Wind Turbine Drivetrain Considering Strength Degradation and Load Sharing Using Survival Signature and FTA. Energies 2020, 13, 2108. https://doi.org/10.3390/en13082108
Li Y, Zhu C, Chen X, Tan J. Fatigue Reliability Analysis of Wind Turbine Drivetrain Considering Strength Degradation and Load Sharing Using Survival Signature and FTA. Energies. 2020; 13(8):2108. https://doi.org/10.3390/en13082108
Chicago/Turabian StyleLi, Yao, Caichao Zhu, Xu Chen, and Jianjun Tan. 2020. "Fatigue Reliability Analysis of Wind Turbine Drivetrain Considering Strength Degradation and Load Sharing Using Survival Signature and FTA" Energies 13, no. 8: 2108. https://doi.org/10.3390/en13082108
APA StyleLi, Y., Zhu, C., Chen, X., & Tan, J. (2020). Fatigue Reliability Analysis of Wind Turbine Drivetrain Considering Strength Degradation and Load Sharing Using Survival Signature and FTA. Energies, 13(8), 2108. https://doi.org/10.3390/en13082108