A Novel Technique for Load Frequency Control of Multi-Area Power Systems
Abstract
:1. Introduction
- An adaptive type-2 fuzzy control system is proposed for frequency control of the two-area power system.
- PD controller is added to the controller to increase stability and robustness.
- Two re-heating and non re-heating areas are considered.
- Plant dynamics are assumed to be uncertain.
- Unlike similar methods, the Jacobian of the plant is not required.
- The center-of-set (COS) is used to order-reduction.
- The controller performance is evaluated on a larger-scale power system.
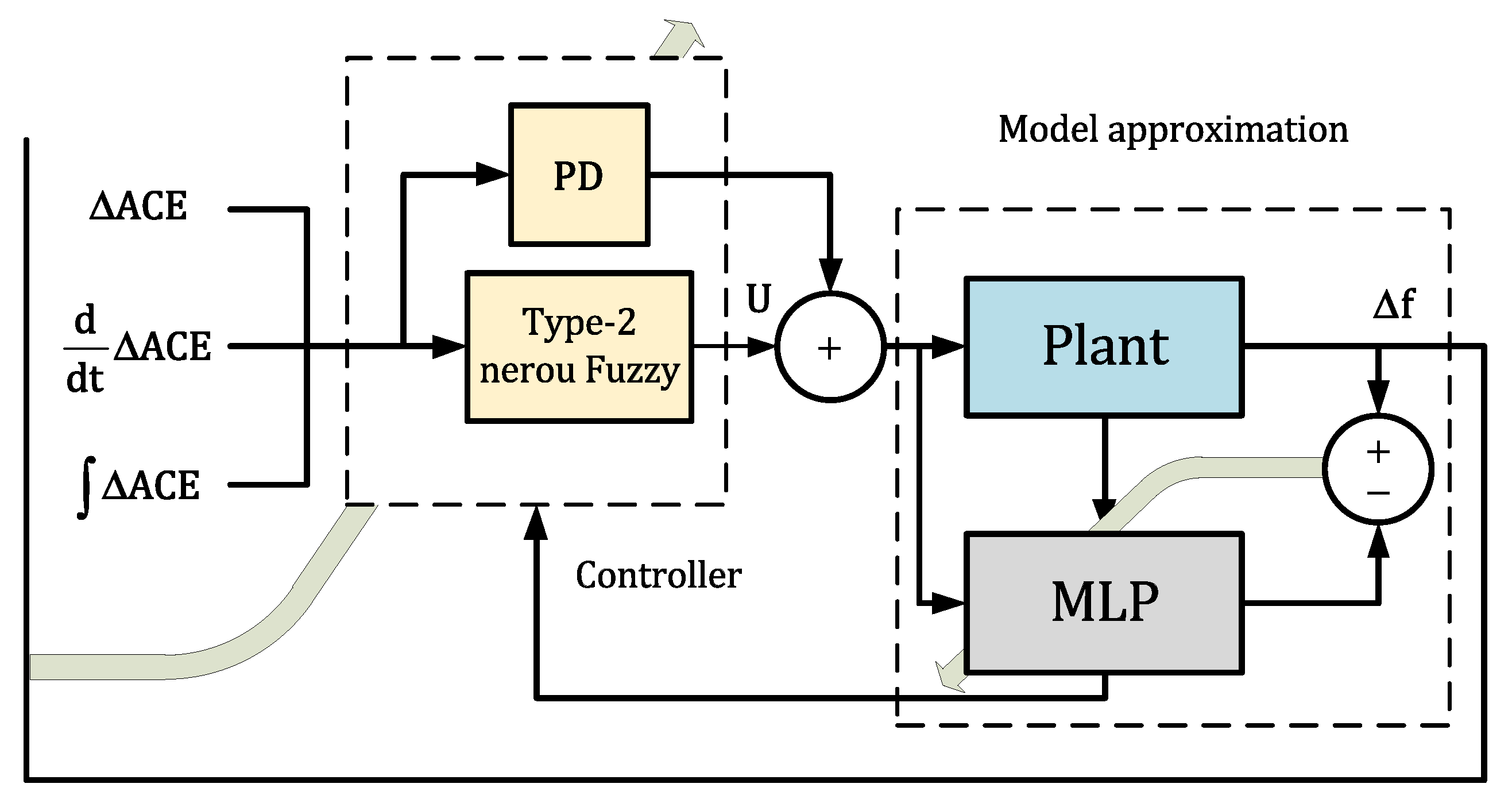
2. Theory of the Proposed Structure
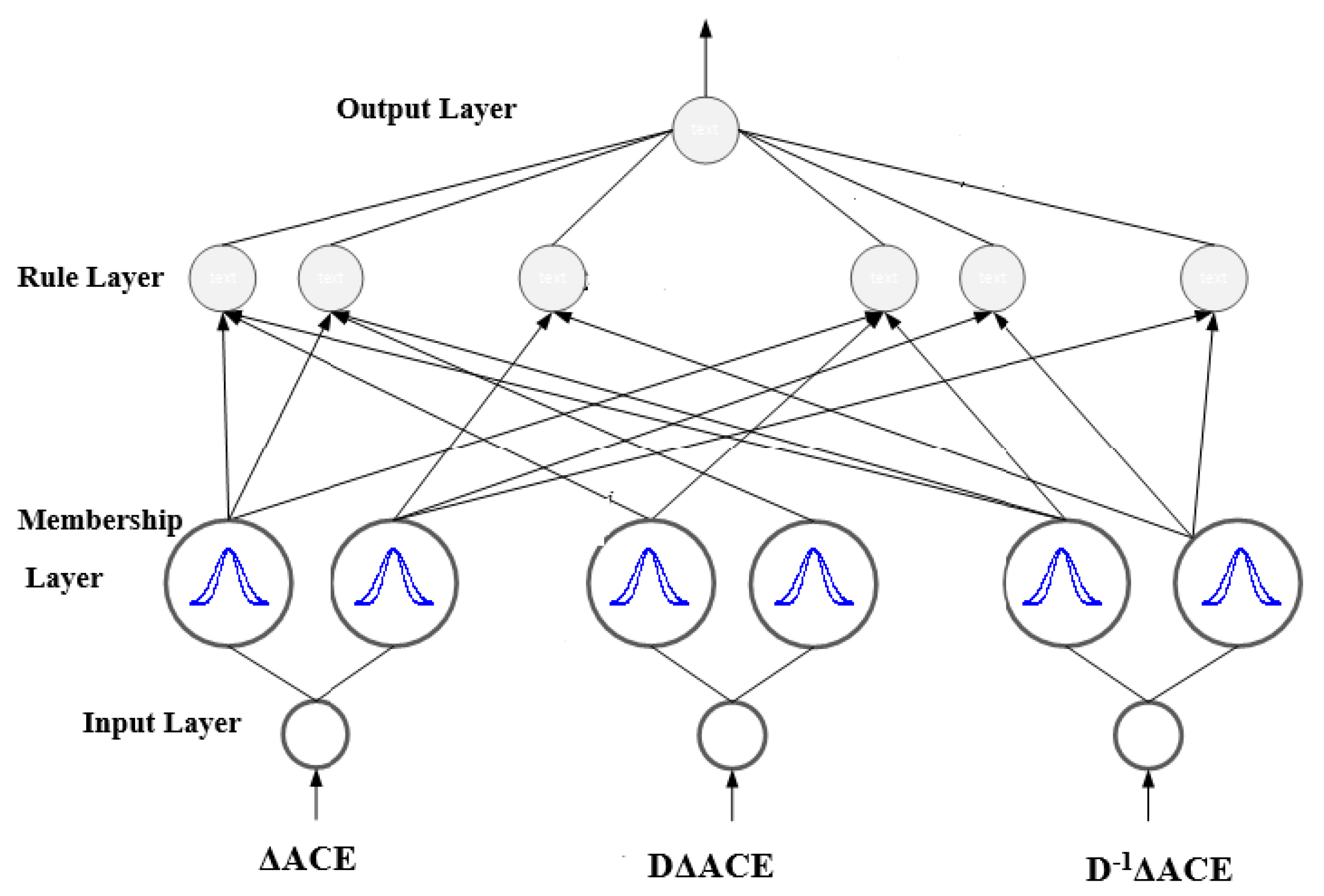
2.1. Structure of the MLP Neural Network
2.2. System Jacobian
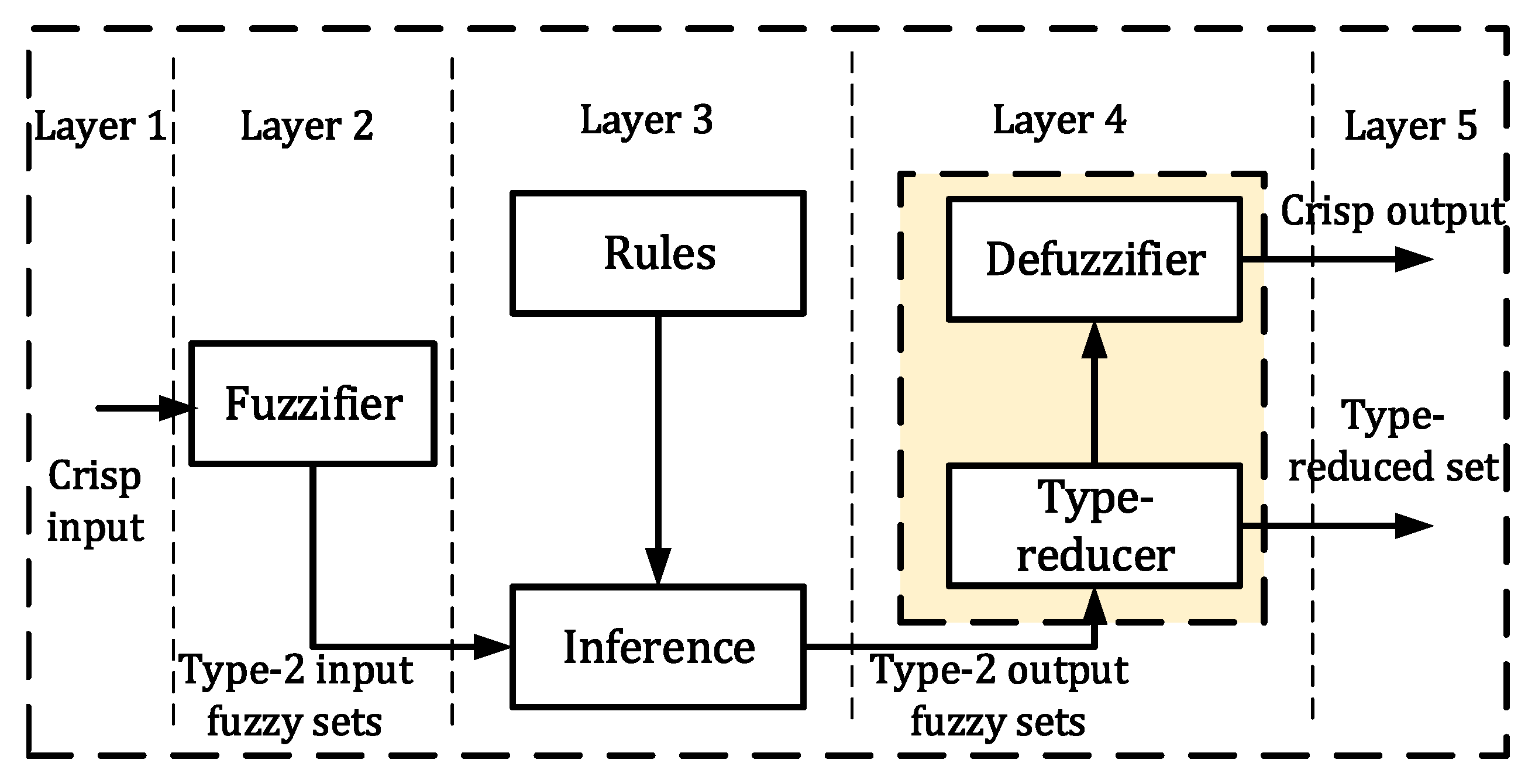
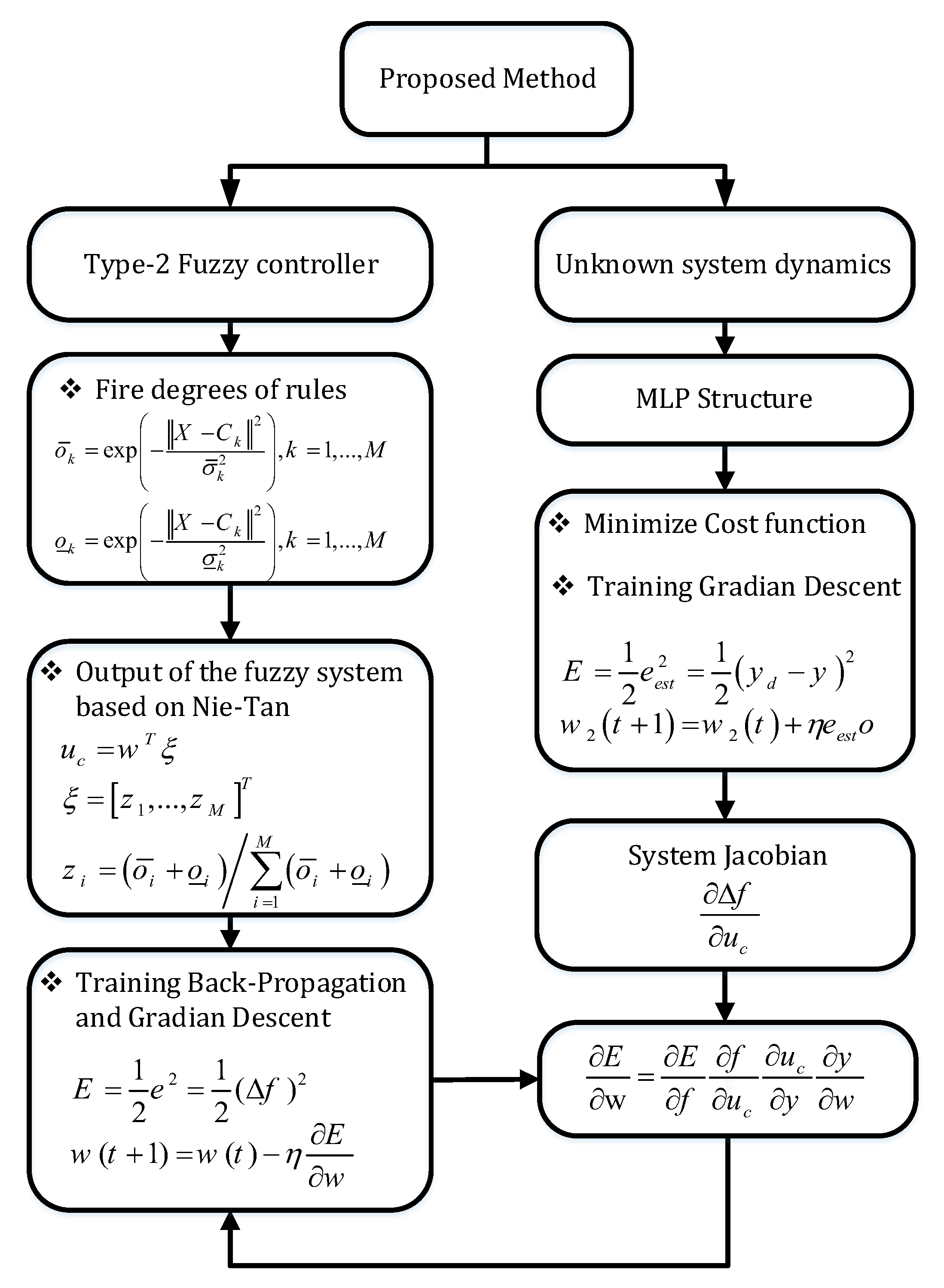
2.3. Type 2 Fuzzy-Neural Controller Structure
2.4. Learning by Descending Gradient and Error Back-Propagation
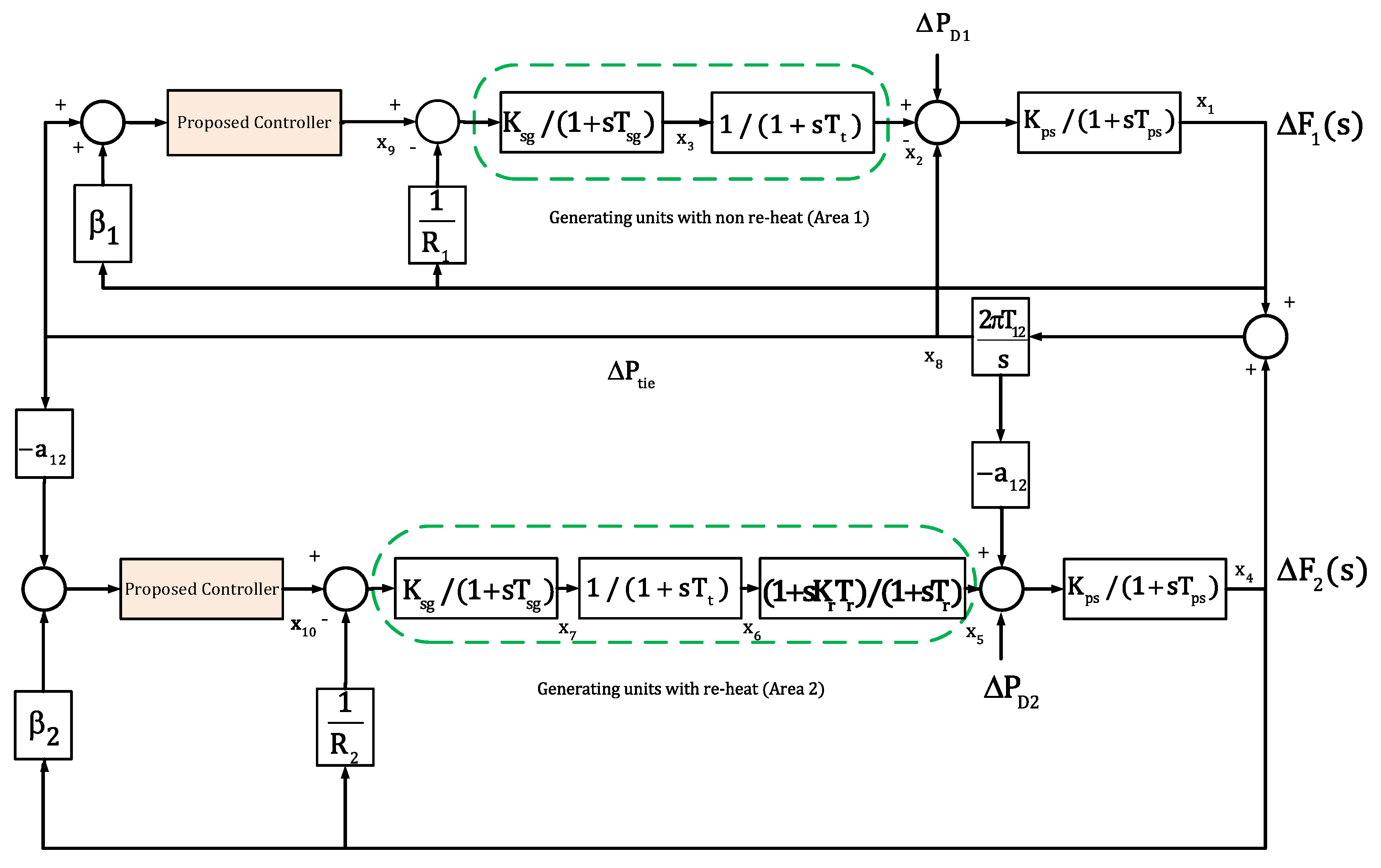
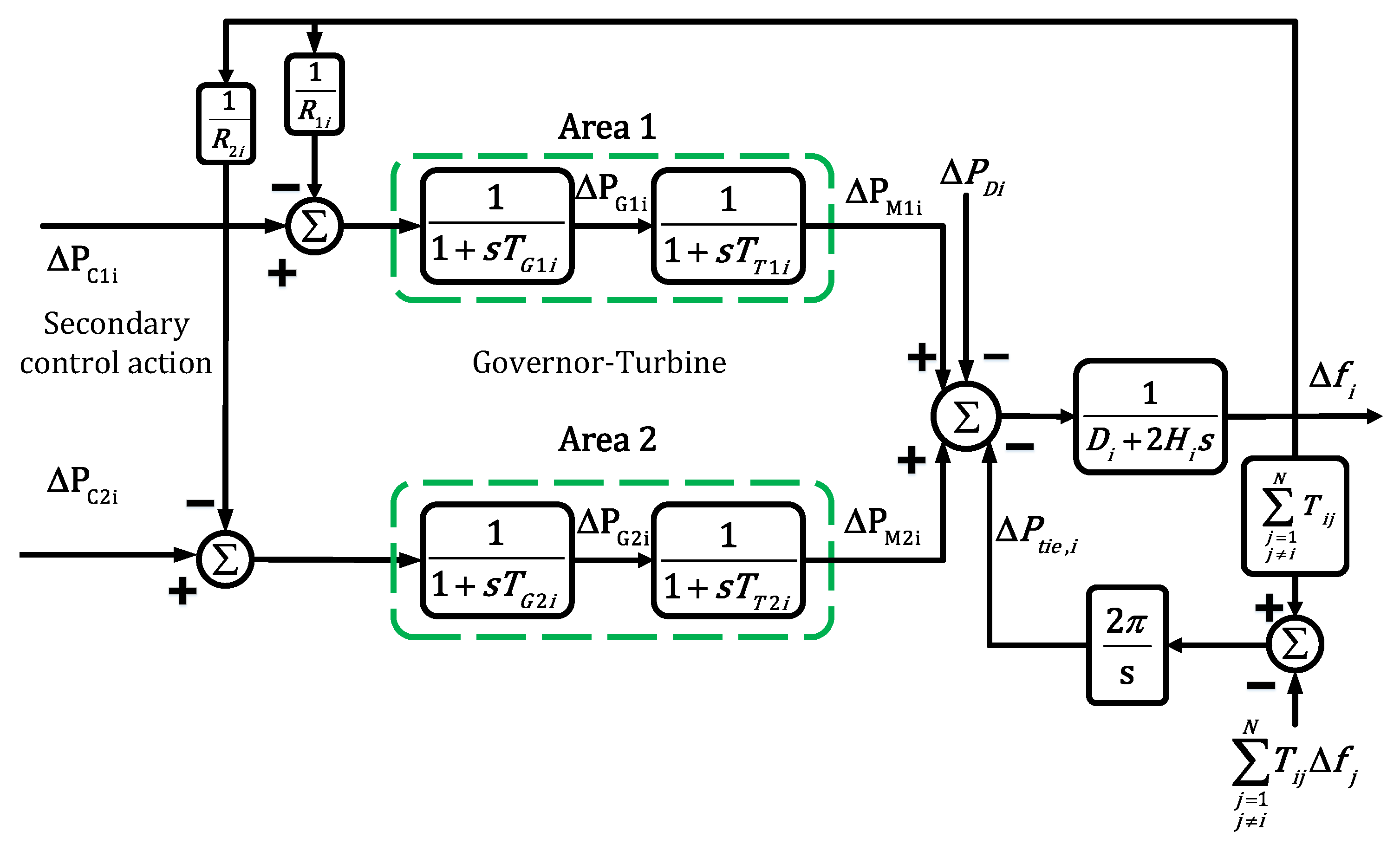
3. Dynamic Model of Power System
4. Simulation Results
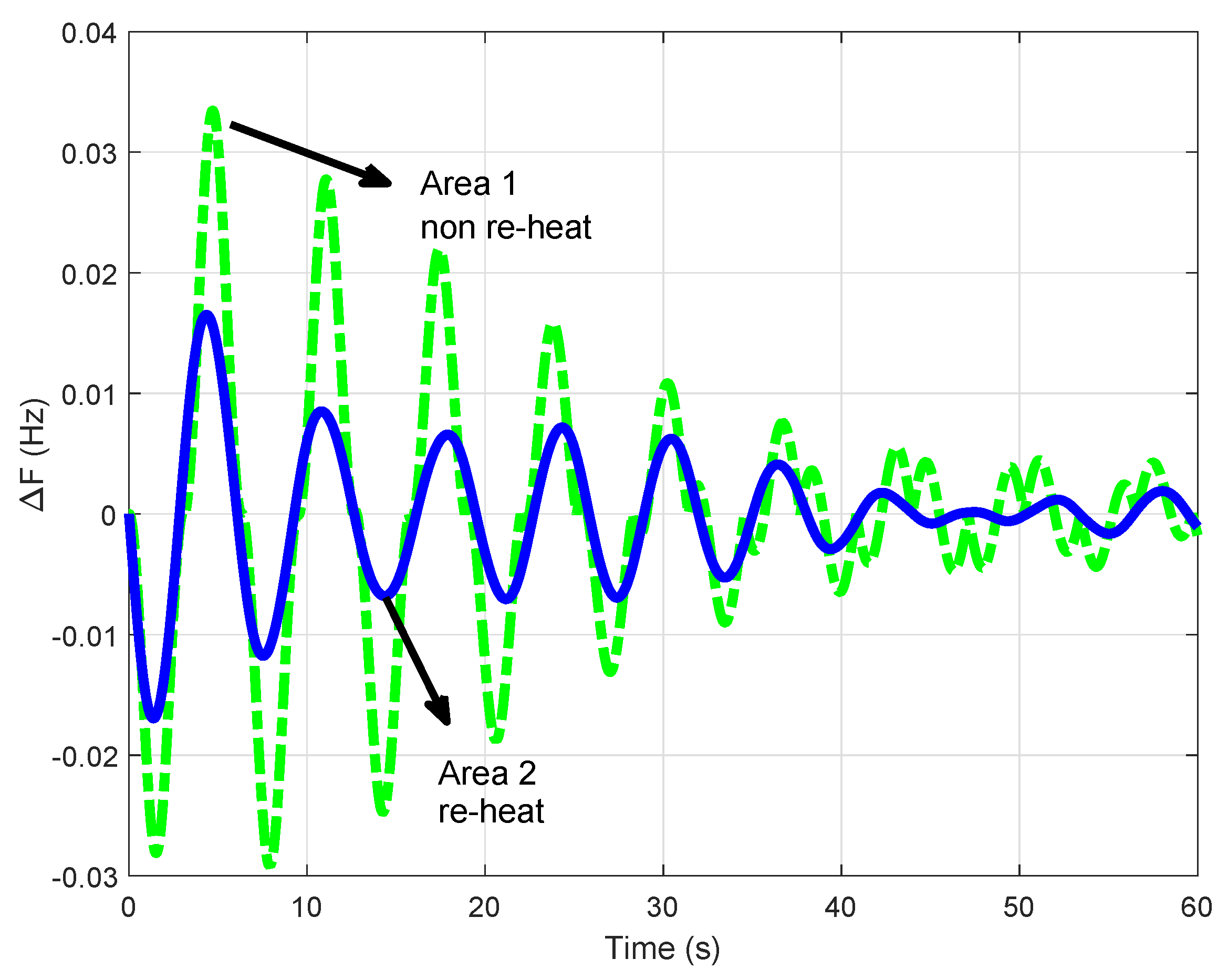
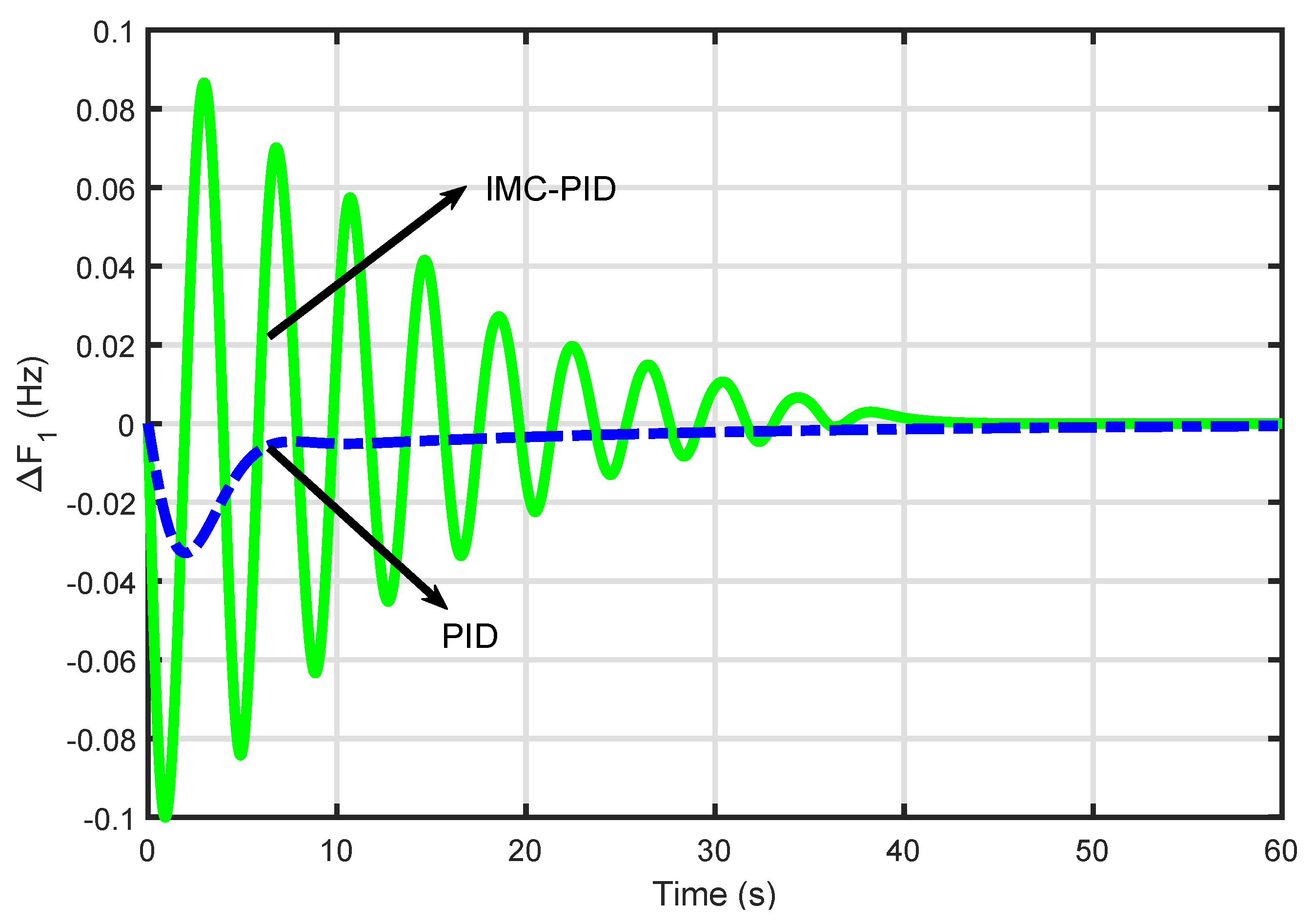
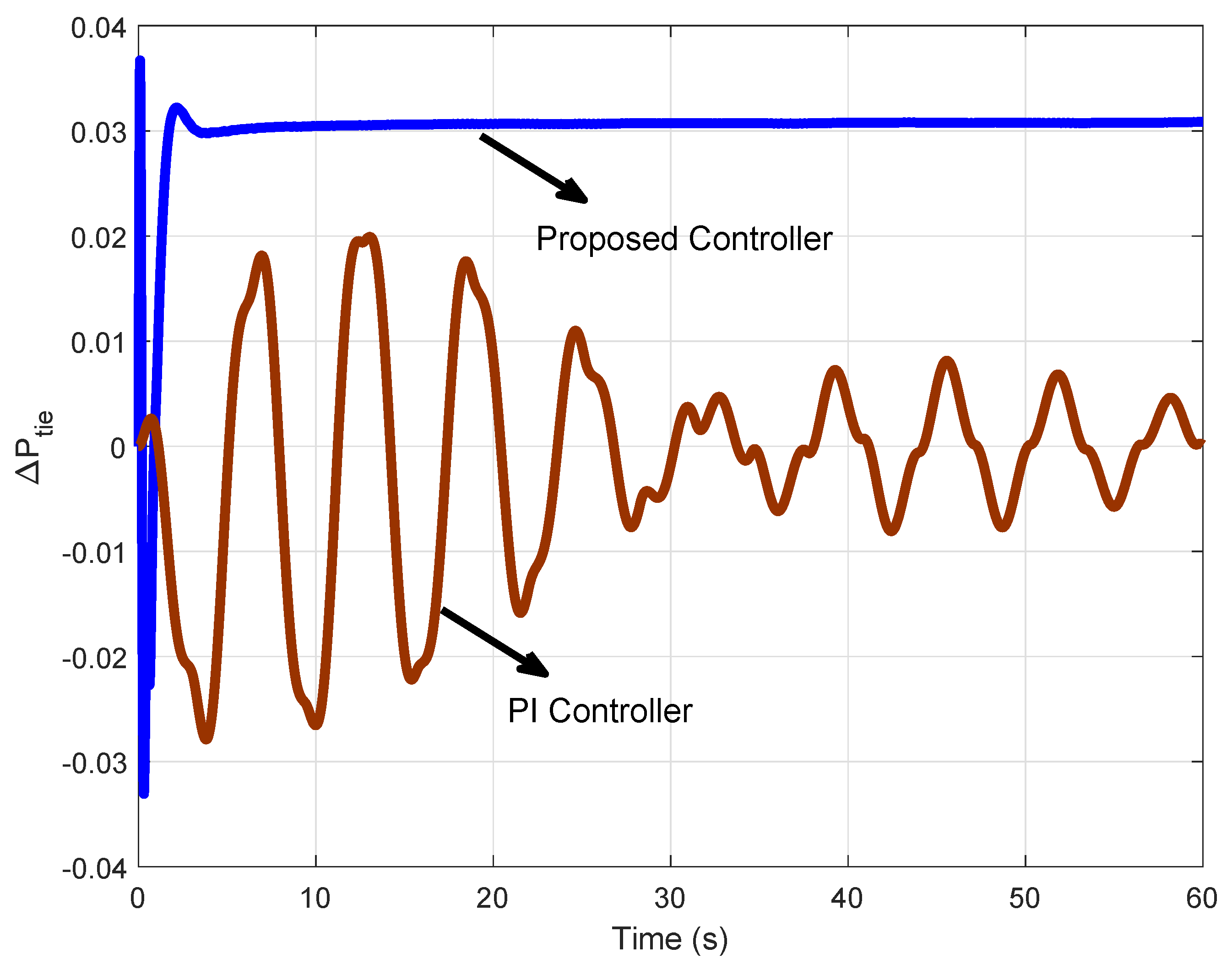
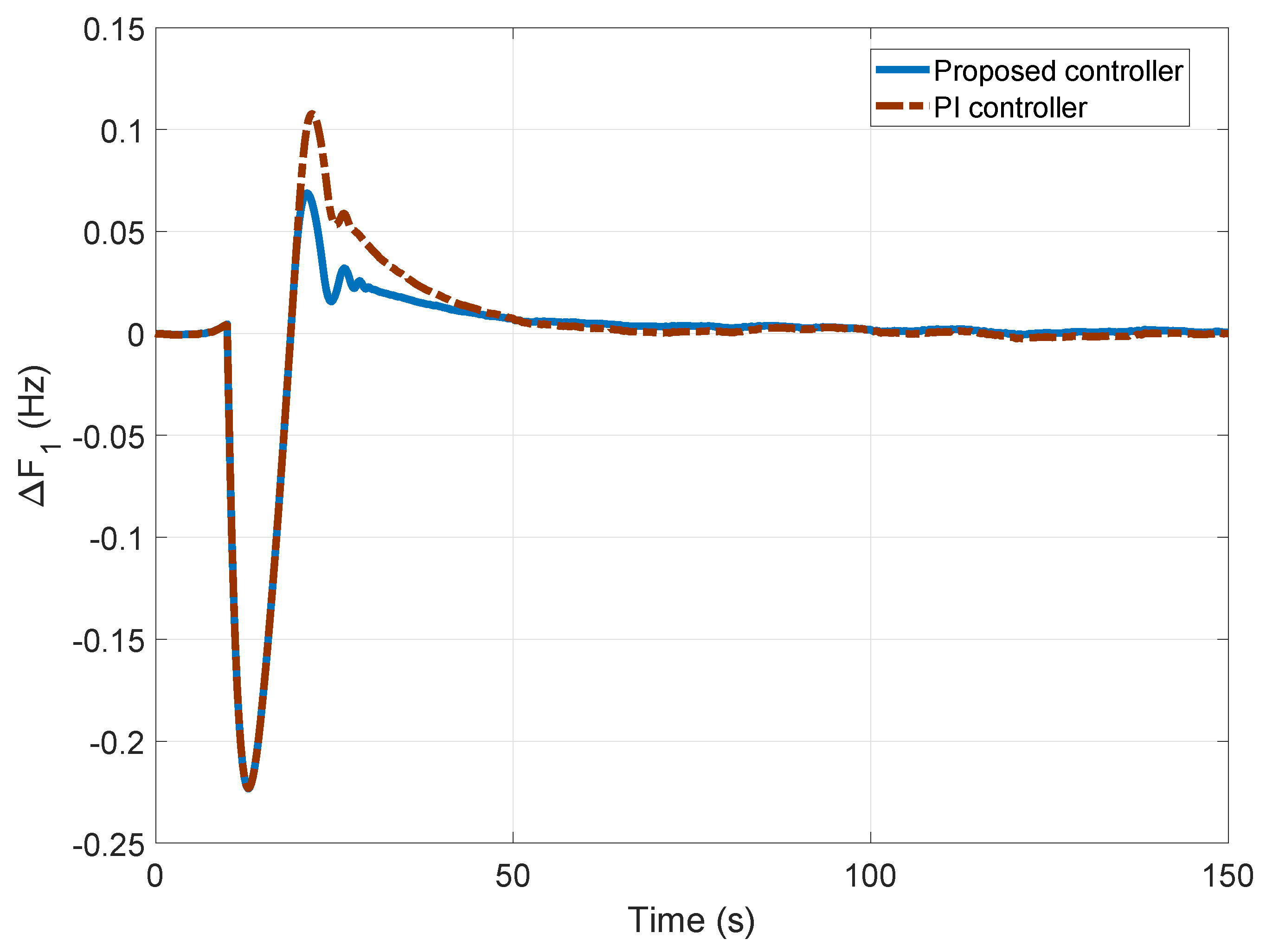
4.1. First Test System: Two-Area Power System
- Divide the system model into two parts:where is the minimum-phase part, and is the non-minimum-phase part.
- Design IMC controller for setpoint-tracking as follows:where is a tuning parameter and n is the relative degree of .
- Design the IMC controller for disturbance-rejecting as follows:where is a tuning parameter for disturbance rejection, m is the number of poles of and should satisfy:where are the poles to be omitted.
- The Feedback controller is obtained using:
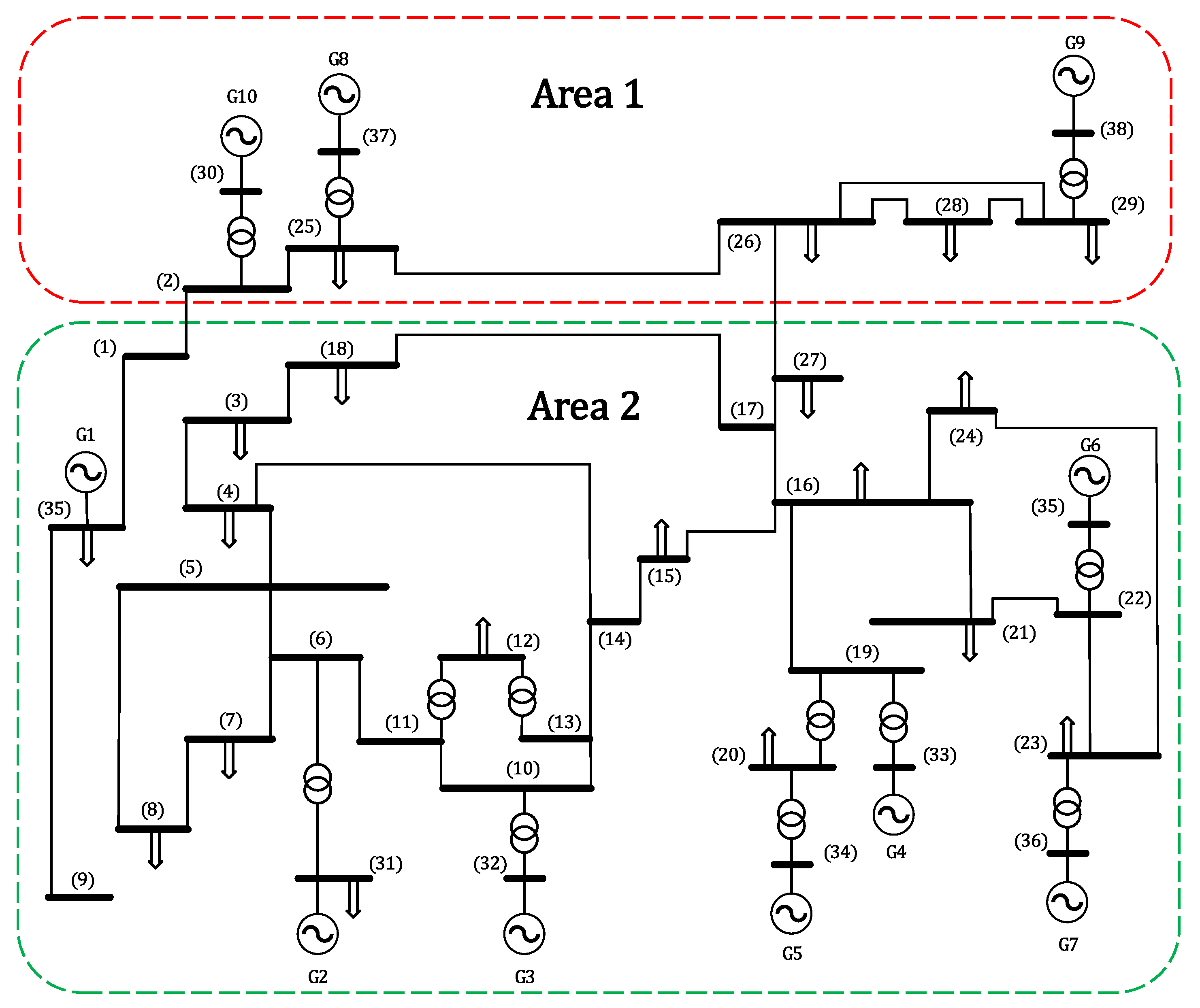
4.2. Second Test System: 39-Bus New England Test System
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Notations | Full Name |
|---|---|
| i | Subscript referring to area i. |
| Rating of ith generator in MW. | |
| Time constant of turbine in s. | |
| Time constant of speed governor in s. | |
| Time constant and gain of power system, respectively. | |
| Re-heat coefficient and time constant, respectively. | |
| Synchronizing coefficient. | |
| Governor speed regulation parameter in Hz per p.u. MW. | |
| The tie-line power deviation. | |
| Frequency deviation. | |
| Load demand deviation. | |
| Re-heat output deviation. | |
| Frequency bias constant. |
References
- Kumar, A.; Kumar, V. A novel interval type-2 fractional order fuzzy PID controller: Design, performance evaluation, and its optimal time domain tuning. ISA Trans. 2017, 68, 251–275. [Google Scholar] [CrossRef] [PubMed]
- Bhavanisankar, C.; Sudha, K.R. An adaptive technique to control the load frequency of hybrid distributed generation systems. Soft Comput. 2019, 23, 12385–12400. [Google Scholar] [CrossRef]
- Sabahi, K.; Ghaemi, S.; Pezeshki, S. Gain Scheduling Technique using MIMO Type-2 Fuzzy Logic System for LFC in Restructure Power System. Int. J. Fuzzy Syst. 2017, 19, 1464–1478. [Google Scholar] [CrossRef]
- Zeng, G.-Q.; Xie, X.-Q.; Chen, M.-R. An Adaptive Model Predictive Load Frequency Control Method for Multi-Area Interconnected Power Systems with Photovoltaic Generations. Energies 2017, 10, 1840. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Zhang, J.; He, Y.; Liu, M.; Zhang, Y.; Chen, C.; Gu, Y.; Ren, Y. Load-Frequency Control of Multi-Area Power System Based on the Improved Weighted Fruit Fly Optimization Algorithm. Energies 2020, 13, 437. [Google Scholar] [CrossRef] [Green Version]
- Khuntia, S.R.; Panda, S. Simulation study for automatic generation control of a multi-area power system by ANFIS approach. Appl. Soft Comput. 2012, 12, 333–341. [Google Scholar] [CrossRef]
- Khezri, R.; Oshnoei, A.; Oshnoei, S.; Bevrani, H.; Muyeen, S.M. An intelligent coordinator design for GCSC and AGC in a two-area hybrid power system. Appl. Soft Comput. 2019, 76, 491–504. [Google Scholar] [CrossRef]
- Babahajiani, P.; Shafiee, Q.; Bevrani, H. Intelligent Demand Response Contribution in Frequency Control of Multi-Area Power Systems. IEEE Trans. Smart Grid. 2018, 9, 1282–1291. [Google Scholar] [CrossRef]
- Chibuikem Nnadozie, E.; Ukachukwu Oparaku, O. Adaptation of a Novel Fuzzy Logic Controller to a Hybrid Renewable Energy System. J. Energy Res. Rev. 2018, 1, 1–10. [Google Scholar] [CrossRef]
- Hoonchareon, N.; Ong, C.; Kramer, R.A. Implementation of an ACE1 decomposition method. IEEE Trans. Power Syst. Rev. 2002, 22, 757–761. [Google Scholar] [CrossRef]
- Yousef, H.A.; AL-Kharusi, K.; Albadi, M.H. Load Frequency Control of a Multi-Area Power System: An Adaptive Fuzzy Logic Approach. IEEE Trans. Power Syst. 2016, 29, 1822–1830. [Google Scholar] [CrossRef]
- Guha, D.; Prasad, P.K. Problem analysis in MW frequency control of an Interconnected Power system using sampled data technique. IJLTET 2013, 2, 54–62. [Google Scholar]
- Velusami, S.; Chidambaram, I.A. Decentralized biased dual mode controllers for load frequency control of interconnected power systems considering GDB and GRC non-linearities. Energy Convers. Manag. 2007, 48, 1691–1702. [Google Scholar] [CrossRef]
- Talaq, J.; Al-Basri, F. Adaptive fuzzy gain scheduling for load frequency control. IEEE Trans. Power Syst. 1999, 14, 145–150. [Google Scholar] [CrossRef]
- Juang, C.-F.; Lu, C.-F. Load-frequency control by hybrid evolutionary fuzzy PI controller. Proc. Inst. Electr. Eng. Gener. Trans. Distrib. 2006, 153, 196–204. [Google Scholar] [CrossRef]
- Liu, X.J.; Kong, X.B.; Deng, X.Z. Power system model predictive load frequency Control. In Proceedings of the American Control Conference, Monteal, QC, Canada, 27–29 June 2012; pp. 6602–6607. [Google Scholar]
- Rajesh, K.S.; Dash, S.S.; Rajagopal, R. Hybrid improved firefly-pattern search optimized fuzzy aided PID controller for automatic generation control of power systems with multi-type generations. Swarm Evol. Comput. 2019, 44, 200–211. [Google Scholar] [CrossRef]
- Niknam, T.; Khooban, M.H. Fuzzy sliding mode control scheme for a class of nonlinear uncertain chaotic systems. IET Sci. Meas. Technol. 2013, 7, 249–255. [Google Scholar] [CrossRef]
- Khooban, M.H.; Alfi, A.; Nazari Maryam Abadi, D. Teaching–learning-based optimal interval type-2 fuzzy PID controller design: A nonholonomic wheeled mobile robots. Robotica 2013, 31, 1059–1071. [Google Scholar] [CrossRef]
- Khooban, M.H.; Alfi, A.; Nazari Maryam Abadi, D. Control of a class of nonlinear uncertain chaotic systems via an optimal type-2 fuzzy PID controller. IET Sci. Meas. Technol. 2013, 7, 50–58. [Google Scholar] [CrossRef]
- Tan, T. Tuning of PID load frequency controller for power systems. Energy Convers. Manag. 2009, 50, 1465–1472. [Google Scholar] [CrossRef]
- Zhao, X.; Lin, Z.; Fu, B.; He, L.; Fang, N. Research on Automatic Generation Control with Wind Power Participation Based on Predictive Optimal 2-Degree-of-Freedom PID Strategy for Multi-area Interconnected Power System. Energies 2018, 11, 3325. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, P.C.; Kumar Sahu, R.; Panda, S. Firefly algorithm optimized fuzzy PID controller for AGC of multi-area multisource power systems with UPFC and SMES. Eng. Sci. Technol. 2016, 19, 338–354. [Google Scholar]
- Khooban, M.H.; Niknam, T. A new intelligent online fuzzy tuning approach for multi-area load frequency control: Self adaptive modified bat algoritm. Electr. Power Energy Syst. 2015, 71, 254–261. [Google Scholar] [CrossRef]
- Zeynelgil, H.L.; Demiroren, A.; Sengor, N.S. The application of ANN technique to automatic generation control for multi-area power system. Electr. Power Energy Syst. 2002, 24, 345–354. [Google Scholar] [CrossRef]
- Rinaldi, G.; Cucuzzella, M.; Ferrara, A. Third order sliding mode observer-based approach for distributed optimal load frequency control. IEEE Control Syst. Lett. 2017, 1, 215–220. [Google Scholar] [CrossRef]
- Pappachen, A.; Peer Fathima, A. Load frequency control in deregulated power system integrated with SMES–TCPS combination using ANFIS controller. Electr. Power Energy Syst. 2016, 82, 519–534. [Google Scholar] [CrossRef]
- Cong, S.; Li, G.; Ji, B. A Novel PID-LIKE Neural Network Controller. IFAC Proc. Vol. 2005, 38, 121–126. [Google Scholar] [CrossRef]
- Jin, W.; Wenzhong, G.; Shusheng, G.; Fuli, W. PID-like controller using a modified neural network. Int. J. Syst. Sci. 1997, 28, 809–815. [Google Scholar] [CrossRef]
- Lutfy, O.F.; Mohd Noor, S.B.; Marhaban, M.H.; Abbas, K.A. A Simplified PID-like ANFIS Controller Trained by Genetic Algorithm to Control Nonlinear Systems. Aust. J. Basic Appl. Sci. 2010, 4, 6331–6345. [Google Scholar]
- Dokht Shakibjoo, A.; Moradzadeh, M.; Moussavi, S.Z.; Afrakhte, H. Online Adaptive Type-2 Fuzzy Logic Control for Load Frequency of Multi-Area Power System. J. Intell. Fuzzy Syst. 2019, 37, 1033–1042. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Teshnehlab, M.; Kayacan, E.; Kaynak, O. A novel type-2 fuzzy membership function: Application to the prediction of noisy data. In Proceedings of the IEEE International Conference on Computational Intelligence for Measurement Systems and Applications, Taranto, Italy, 6–8 September 2010. [Google Scholar]
- Sabahi, K.; Ghaemi, S.; Pezeshki, S. Application of type-2 fuzzy logic system for load frequency control using feedback error learning approaches. Appl. Soft Comput. 2014, 21, 1–11. [Google Scholar] [CrossRef]
- John, R.; Castillo, O.; Hagras, H. Type-2 Fuzzy Logic and Systems; Springer: London, UK, 2018. [Google Scholar]
- Tan, W. Unified tuning of PID load frequency controller for power systems via IMC. IEEE Trans. Power Syst. 2010, 25, 341–350. [Google Scholar] [CrossRef]
- Report, I.C. Dynamic Models for Steam and Hydro Turbines in Power System Studies. IEEE Trans. Power Appar. Syst. 1973, 92, 1904–1915. [Google Scholar] [CrossRef]
- Bevrani, H.; Daneshfar, F.; Daneshmand, R.P. Intelligent Power System Frequency Regulations Concerning the Integration of Wind Power Units. In Wind Power Systems. Green Energy and Technology; Wang, L., Singh, C., Kusiak, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]






| Notations | Numerical Value |
|---|---|
| 2000 MW | |
| 0.3 s | |
| 0.08 s | |
| 120 s, 20 s | |
| 0.5 s, 10 s | |
| 0.545/2 | |
| 1/2.4 | |
| 0.425 | |
| 0.4 | |
| 1 | |
| −0.81 |
| Full Name | Value |
|---|---|
| Governor time constant () [s] | 0.07 |
| Turbine time constant () [s] | 0.001 |
| Load change in area i ( | 0.9 |
| Load damping coefficient () | 1 |
| Equivalent inertia constant () | 2.35 |
| Tie-Line synchronizing torque coefficient () [s] | 0.02 |
| Speed-droop charateristic (R) | 0.05 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dokht Shakibjoo, A.; Moradzadeh, M.; Moussavi, S.Z.; Vandevelde, L. A Novel Technique for Load Frequency Control of Multi-Area Power Systems. Energies 2020, 13, 2125. https://doi.org/10.3390/en13092125
Dokht Shakibjoo A, Moradzadeh M, Moussavi SZ, Vandevelde L. A Novel Technique for Load Frequency Control of Multi-Area Power Systems. Energies. 2020; 13(9):2125. https://doi.org/10.3390/en13092125
Chicago/Turabian StyleDokht Shakibjoo, Ali, Mohammad Moradzadeh, Seyed Zeinolabedin Moussavi, and Lieven Vandevelde. 2020. "A Novel Technique for Load Frequency Control of Multi-Area Power Systems" Energies 13, no. 9: 2125. https://doi.org/10.3390/en13092125
APA StyleDokht Shakibjoo, A., Moradzadeh, M., Moussavi, S. Z., & Vandevelde, L. (2020). A Novel Technique for Load Frequency Control of Multi-Area Power Systems. Energies, 13(9), 2125. https://doi.org/10.3390/en13092125







