Parallel Power Flow Computation Trends and Applications: A Review Focusing on GPU
Abstract
:1. Introduction
2. Background
2.1. GPU
2.2. Numerical Analysis of Power Systems
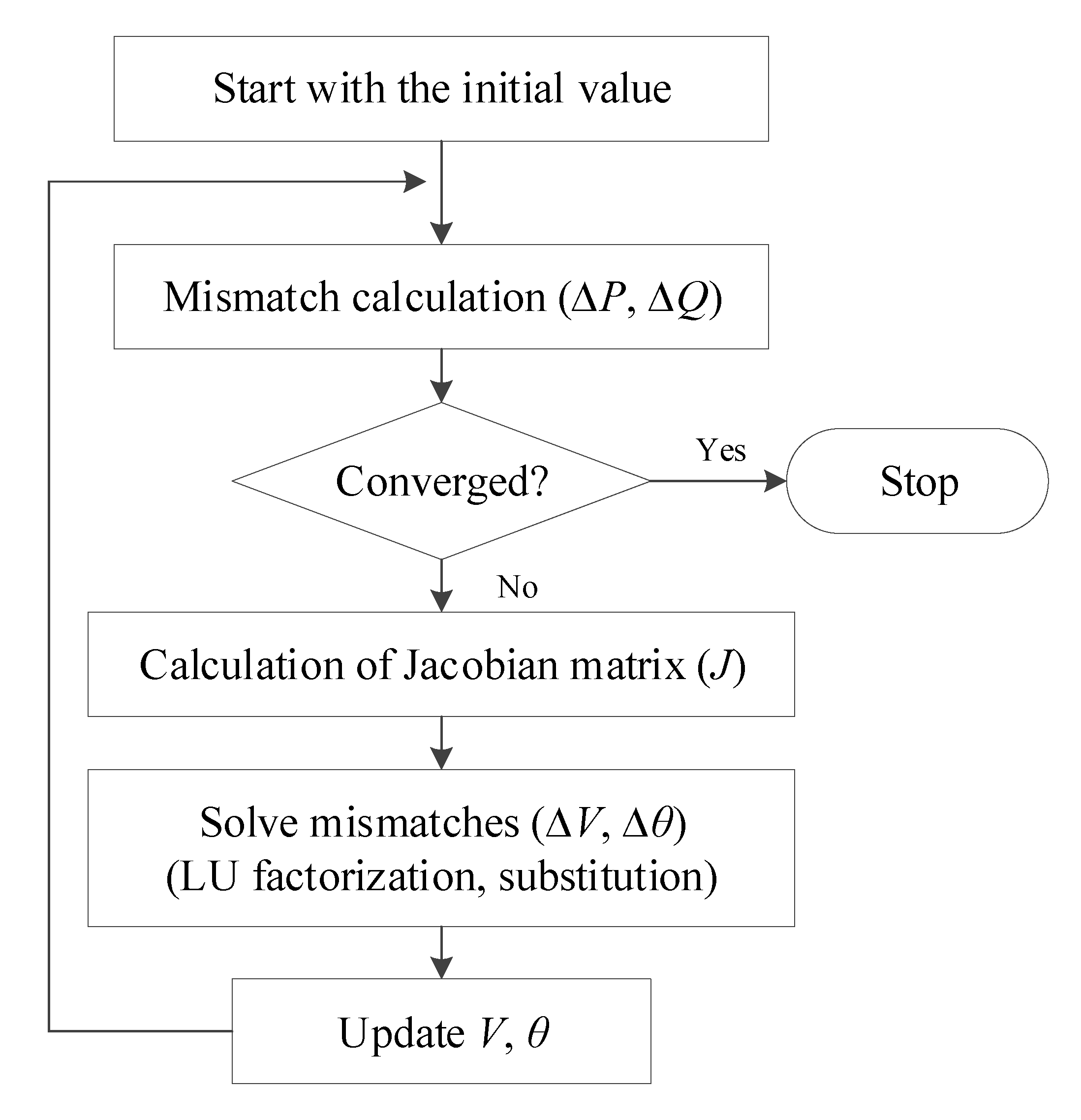
2.2.1. Power Flow Analysis
2.2.2. LU Decomposition
2.2.3. QR Decomposition
2.2.4. Conjugate Gradient Method
3. GPU Application Trend in Power Flow Computation
3.1. Conventional Parallel Processing in PF Studies
3.2. Advantages of GPU-Based PF Computation
3.3. GPU Applications Trends in PF Studies
4. Typical GPU-Based PF Studies
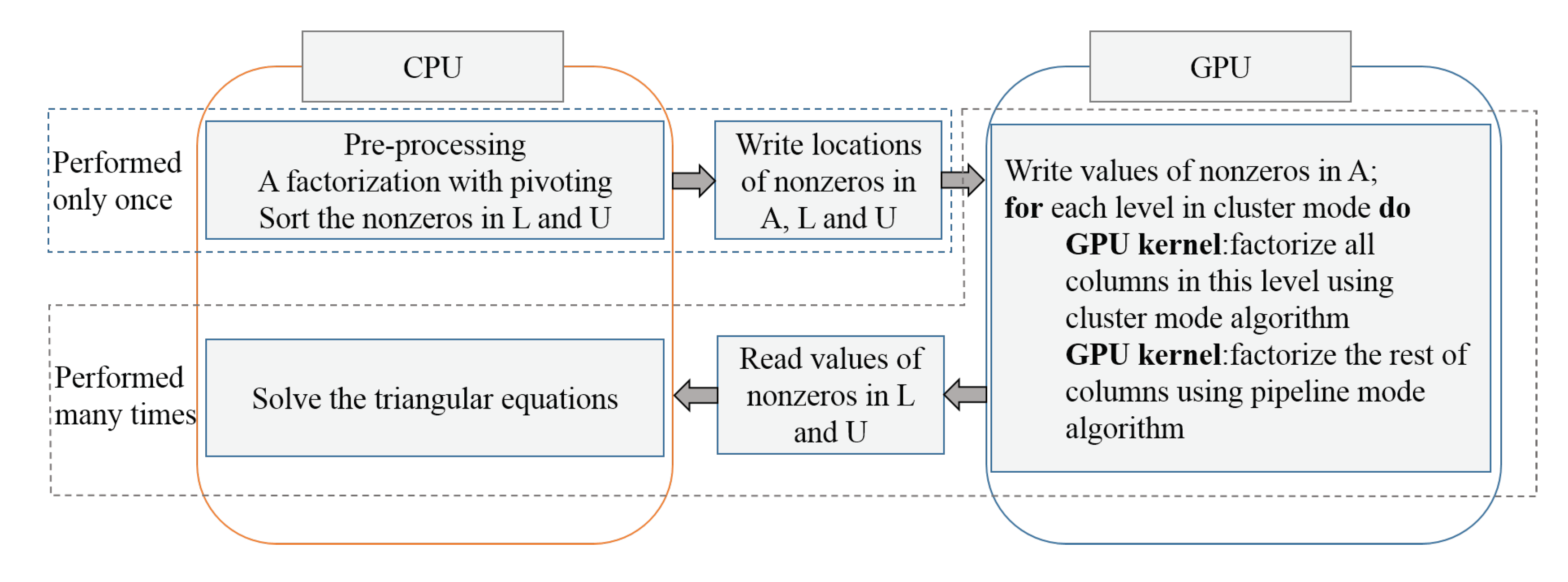
4.1. A Study Based on LU Decomposition
| Algorithm 1 left-looking LU factorization (GPU-based) [45,55,64]. |
| INPUTA: an input matrix to be LU factorized OUTPUT : lower and upper triangular matrices factorized from A
|
| Algorithm 2 GPU-based batch LU factorization [55]. |
| INPUTA: an input matrix to be LU factorized OUTPUT : lower and upper triangular matrices factorized from A
|
- Unifying sparsity pattern: All SLSs must have a uniform sparsity pattern.
- Performing reordering and symbolic analysis only once: can be performed only once.
- Achieving extra inter-SLS parallelism: We have achieved N (N = batch size) times parallelism automatically by packaging a large number of LU decomposition subtasks into a new large-scale batch computation task. First, the decompositions on the same indexed columns, which belong to different subtasks of LU decomposition, are designated to a single thread block. In the algorithm, , , and mean the input matrix, output lower and upper triangular matrices, respectively, that are accessed by the t-th thread block. Second, the data of the same indexed columns are located in the adjacent address of a GPU device memory.
- Preventing thread divergence: Lines four to six in Algorithm 2 (updated warp thread operation) will execute the same branch and it does not diverge due to the identical sparsity pattern and aforementioned thread-allocation type.
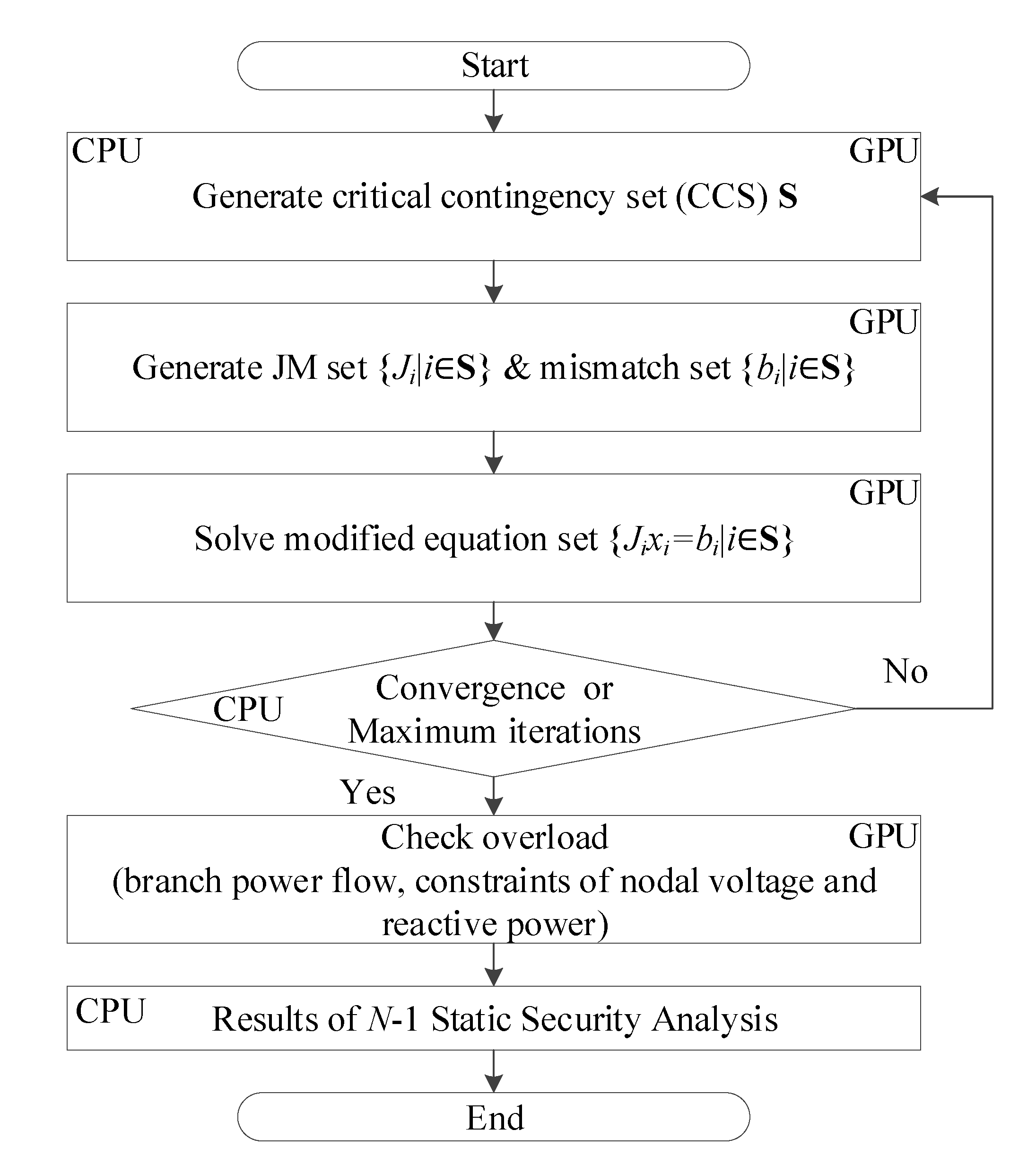
4.2. A Study Based on QR Decomposition
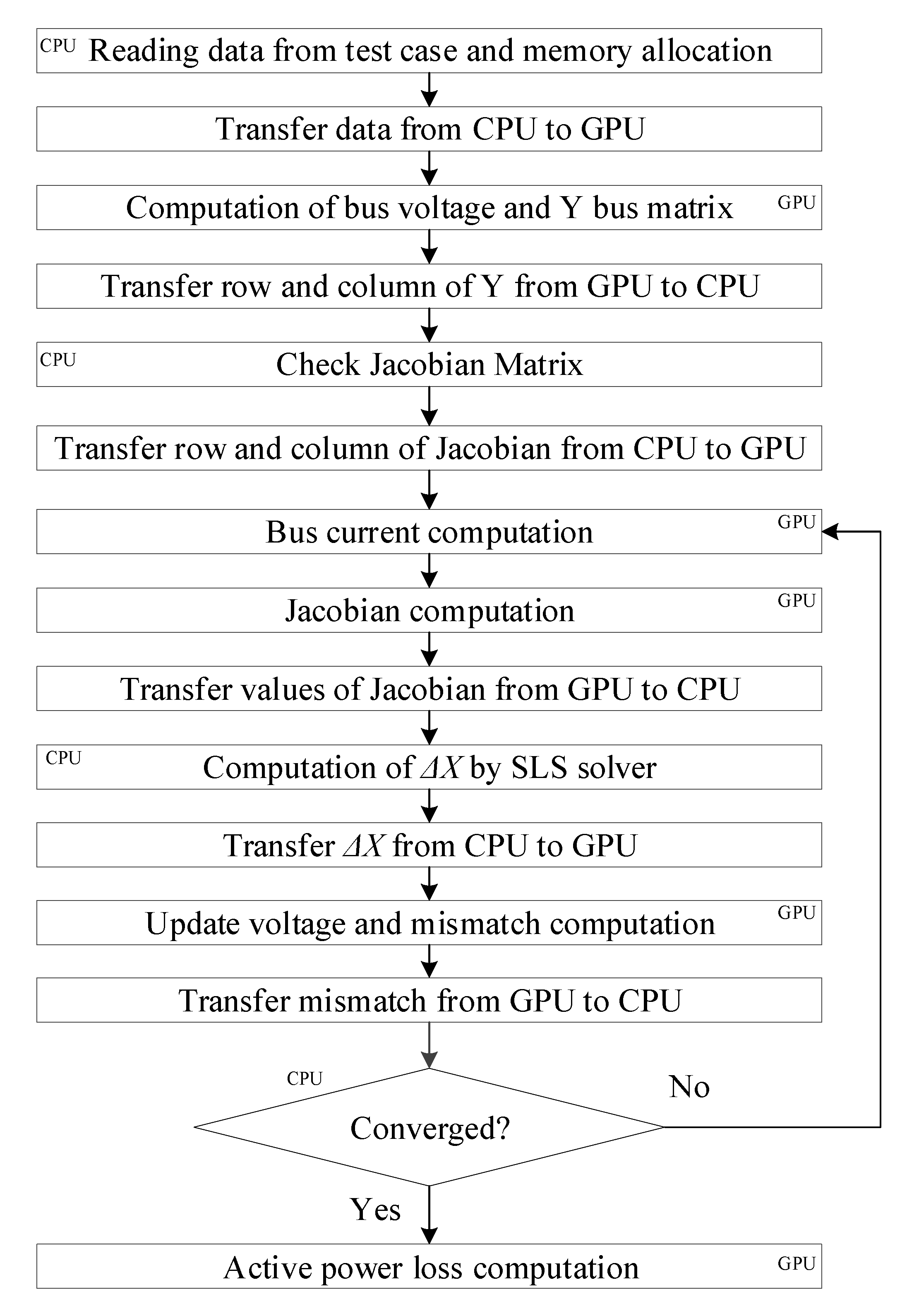
4.3. Computation Time Reduction of GPU-Based Parallel Processing
4.4. Results and Comparison
5. Conclusions
- The basic concepts of PF computation methods and matrix handling are described.
- Conventional approaches of parallel processing technology in PF studies are summarized.
- Representative studies are reviewed to describe how to achieve parallel processing using GPUs in PF studies.
- The main features and speedup results are summarized for each study as a table form.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| PF | Power flow |
| NR | Newton–Raphson |
| GS | Gauss–Seidel |
| EV | Electric vehicle |
| FDPF | Fast decoupled power flow |
| CG | Conjugate gradient |
| RTOPF | Real-time optimal power flow |
| SLS | Sparse linear system |
| CUDA | Compute Unified Device Architecture |
| OpenCL | Open Computing Language |
| HPC | High performance computing |
| CPU | Central processing unit |
| GPU | Graphics Processing Units |
| GPGPU | General-Purpose computing on Graphics Processing Units |
| SM | Streaming multiprocessor |
| TLP | Thread-level parallelism |
| PPF | Probabilistic power flow |
References
- Falcão, D.M. High performance computing in power system applications. In International Conference on Vector and Parallel Processing; Springer: Berlin, Germany, 1996; pp. 1–23. [Google Scholar]
- Ramesh, V. On distributed computing for on-line power system applications. Int. J. Electr. Power Energy Syst. 1996, 18, 527–533. [Google Scholar] [CrossRef]
- Baldick, R.; Kim, B.H.; Chase, C.; Luo, Y. A fast distributed implementation of optimal power flow. IEEE Trans. Power Syst. 1999, 14, 858–864. [Google Scholar] [CrossRef]
- Li, F.; Broadwater, R.P. Distributed algorithms with theoretic scalability analysis of radial and looped load flows for power distribution systems. Electr. Power Syst. Res. 2003, 65, 169–177. [Google Scholar] [CrossRef]
- Green, R.C.; Wang, L.; Alam, M. High performance computing for electric power systems: Applications and trends. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Tournier, J.C.; Donde, V.; Li, Z. Potential of general purpose graphic processing unit for energy management system. In Proceedings of the 2011 Sixth International Symposium on Parallel Computing in Electrical Engineering, Luton, UK, 3–7 April 2011; pp. 50–55. [Google Scholar]
- Huang, Z.; Nieplocha, J. Transforming power grid operations via high performance computing. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar]
- Wu, Q.; Spiryagin, M.; Cole, C.; McSweeney, T. Parallel computing in railway research. Int. J. Rail Trans. 2018, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Santur, Y.; Karaköse, M.; Akin, E. An adaptive fault diagnosis approach using pipeline implementation for railway inspection. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 987–998. [Google Scholar] [CrossRef]
- Nitisiri, K.; Gen, M.; Ohwada, H. A parallel multi-objective genetic algorithm with learning based mutation for railway scheduling. Comput. Ind. Eng. 2019, 130, 381–394. [Google Scholar] [CrossRef]
- Zawidzki, M.; Szklarski, J. Effective multi-objective discrete optimization of Truss-Z layouts using a GPU. Appl. Soft Comput. 2018, 70, 501–512. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Xu, K.; Yu, H.; Ren, F. A GPU-Outperforming FPGA Accelerator Architecture for Binary Convolutional Neural Networks. Available online: https://dl.acm.org/doi/abs/10.1145/3154839 (accessed on 10 February 2020).
- Choi, K.H.; Kim, S.W. Study of Cache Performance on GPGPU. IEIE Trans. Smart Process. Comput. 2015, 4, 78–82. [Google Scholar] [CrossRef]
- Oh, C.; Yi, Y. CPU-GPU2 Trigeneous Computing for Iterative Reconstruction in Computed Tomography. IEIE Trans. Smart Process. Comput. 2016, 5, 294–301. [Google Scholar] [CrossRef] [Green Version]
- Burgess, J. RTX on—The NVIDIA Turing GPU. IEEE Micro 2020, 40, 36–44. [Google Scholar] [CrossRef]
- Wittenbrink, C.M.; Kilgariff, E.; Prabhu, A. Fermi GF100 GPU Architecture. IEEE Micro 2011, 31, 50–59. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Stott, B.; Alsac, O. Fast decoupled load flow. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 859–869. [Google Scholar] [CrossRef]
- Glover, J.D.; Sarma, M.S.; Overbye, T. Power System Analysis & Design, SI Version. Available online: https://books.google.co.kr/books?hl=ko&lr=&id=XScJAAAAQBAJ&oi=fnd&pg=PR7&dq=Power+System+Analysis+%26+Design,+SI+Version&ots=QEYUnLwXnN&sig=fofumZoNynEPX0YuRaKiO2glnA8#v=onepage&q=Power%20System%20Analysis%20%26%20Design%2C%20SI%20Version&f=false (accessed on 16 February 2020).
- Alvarado, F.L.; Tinney, W.F.; Enns, M.K. Sparsity in large-scale network computation. Adv. Electr. Power Energy Convers. Syst. Dyn. 1991, 41, 207–272. [Google Scholar]
- Zhou, G.; Zhang, X.; Lang, Y.; Bo, R.; Jia, Y.; Lin, J.; Feng, Y. A novel GPU-accelerated strategy for contingency screening of static security analysis. Int. J. Electr. Power Energy Syst. 2016, 83, 33–39. [Google Scholar] [CrossRef]
- Wu, J.Q.; Bose, A. Parallel solution of large sparse matrix equations and parallel power flow. IEEE Trans. Power Syst. 1995, 10, 1343–1349. [Google Scholar]
- Lau, K.; Tylavsky, D.J.; Bose, A. Coarse grain scheduling in parallel triangular factorization and solution of power system matrices. IEEE Trans. Power Syst. 1991, 6, 708–714. [Google Scholar] [CrossRef]
- Amano, M.; Zecevic, A.; Siljak, D. An improved block-parallel Newton method via epsilon decompositions for load-flow calculations. IEEE Trans. Power Syst. 1996, 11, 1519–1527. [Google Scholar] [CrossRef]
- El-Keib, A.; Ding, H.; Maratukulam, D. A parallel load flow algorithm. Electr. Power Syst. Res. 1994, 30, 203–208. [Google Scholar] [CrossRef]
- Fukuyama, Y.; Nakanishi, Y.; Chiang, H.D. Parallel power flow calculation in electric distribution networks. In Proceedings of the 1996 IEEE International Symposium on Circuits and Systems, Circuits and Systems Connecting the World (ISCAS 96), Atlanta, GA, USA, 15 May 1996; Volume 1, pp. 669–672. [Google Scholar]
- Davis, T.A. Direct Methods for Sparse Linear Systems. Available online: https://books.google.co.kr/books?hl=ko&lr=&id=oovDyJrnr6UC&oi=fnd&pg=PR1&dq=Direct+Methods+for+Sparse+Linear+Systems&ots=rQcLPxz3GE&sig=jYD7MDkkW_KGkK6rU6AWOstk3j8#v=onepage&q=Direct%20Methods%20for%20Sparse%20Linear%20Systems&f=false (accessed on 20 February 2020).
- Zhou, G.; Feng, Y.; Bo, R.; Chien, L.; Zhang, X.; Lang, Y.; Jia, Y.; Chen, Z. GPU-accelerated batch-ACPF solution for N-1 static security analysis. IEEE Trans. Smart Grid 2017, 8, 1406–1416. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations. Available online: https://books.google.co.kr/books?hl=ko&lr=&id=5U-l8U3P-VUC&oi=fnd&pg=PT10&dq=Matrix+Computations&ots=7_JDJm_Lfp&sig=FP_n3ws8CRIxseHwoh97znxmpmE#v=onepage&q=Matrix%20Computations&f=false (accessed on 1 March 2020).
- Dag, H.; Semlyen, A. A new preconditioned conjugate gradient power flow. IEEE Trans. Power Syst. 2003, 18, 1248–1255. [Google Scholar] [CrossRef]
- Garcia, N. Parallel power flow solutions using a biconjugate gradient algorithm and a Newton method: A GPU-based approach. In Proceedings of the Power and Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–4. [Google Scholar]
- Li, X.; Li, F. GPU-based power flow analysis with Chebyshev preconditioner and conjugate gradient method. Electr. Power Syst. Res. 2014, 116, 87–93. [Google Scholar] [CrossRef]
- Rafian, M.; Sterling, M.; Irving, M. Decomposed Load-Flow Algorithm Suitable for Parallel Processor implementation. In IEE Proceedings C (Generation, Transmission and Distribution). Available online: https://digital-library.theiet.org/content/journals/10.1049/ip-c.1985.0047 (accessed on 3 March 2020).
- Wang, L.; Xiang, N.; Wang, S.; Huang, M. Parallel reduced gradient optimal power flow solution. Electr. Power Syst. Res. 1989, 17, 229–237. [Google Scholar] [CrossRef]
- Enns, M.K.; Tinney, W.F.; Alvarado, F.L. Sparse matrix inverse factors (power systems). IEEE Trans. Power Syst. 1990, 5, 466–473. [Google Scholar] [CrossRef]
- Huang, G.; Ongsakul, W. Managing the bottlenecks in parallel Gauss-Seidel type algorithms for power flow analysis. IEEE Trans. Power Syst. 1994, 9, 677–684. [Google Scholar] [CrossRef]
- Ezhilarasi, G.A.; Swarup, K.S. Parallel contingency analysis in a high performance computing environment. In Proceedings of the 2009 International Conference on Power Systems, Kharagpur, India, 27–29 December 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, Y.; Nieplocha, J. Massive contingency analysis with high performance computing. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Smith, S.; Van Zandt, D.; Thomas, B.; Mahmood, S.; Woodward, C. HPC4Energy Final Report: GE Energy; Technical Report; Lawrence Livermore National Laboratory (LLNL): Livermore, CA, USA, 2014.
- Konstantelos, I.; Jamgotchian, G.; Tindemans, S.H.; Duchesne, P.; Cole, S.; Merckx, C.; Strbac, G.; Panciatici, P. Implementation of a massively parallel dynamic security assessment platform for large-scale grids. IEEE Trans. Smart Grid 2017, 8, 1417–1426. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.; Jiang, B.; Yuan, H.; Yang, Z.; Wang, L.; Ren, S. Performance comparisons of parallel power flow solvers on GPU system. In Proceedings of the 2012 IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, Seoul, Korea, 19–22 August 2012; pp. 232–239. [Google Scholar]
- Demmel, J.W.; Eisenstat, S.C.; Gilbert, J.R.; Li, X.S.; Liu, J.W. A supernodal approach to sparse partial pivoting. SIAM J. Matrix Anal. Appl. 1999, 20, 720–755. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. Solving unsymmetric sparse systems of linear equations with PARDISO. Future Gener. Comput. Syst. 2004, 20, 475–487. [Google Scholar] [CrossRef]
- Christen, M.; Schenk, O.; Burkhart, H. General-Purpose Sparse Matrix Building Blocks Using the NVIDIA CUDA Technology Platform. In First Workshop on General Purpose Processing on Graphics Processing Units. Available online: https://scholar.google.co.kr/scholar?hl=ko&as_sdt=0%2C5&q=General-purpose+sparse+matrix+building+blocks+using+the+NVIDIA+CUDA+technology+platform&btnG= (accessed on 10 March 2020).
- Ren, L.; Chen, X.; Wang, Y.; Zhang, C.; Yang, H. Sparse LU factorization for parallel circuit simulation on GPU. In Proceedings of the 49th Annual Design Automation Conference, San Francisco, CA, USA, 3–7 June 2012; ACM: New York, NY, USA, 2012; pp. 1125–1130. [Google Scholar]
- Jalili-Marandi, V.; Zhou, Z.; Dinavahi, V. Large-scale transient stability simulation of electrical power systems on parallel GPUs. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–11. [Google Scholar]
- Chen, D.; Li, Y.; Jiang, H.; Xu, D. A parallel power flow algorithm for large-scale grid based on stratified path trees and its implementation on GPU. Autom. Electr. Power Syst. 2014, 38, 63–69. [Google Scholar]
- Gnanavignesh, R.; Shenoy, U.J. GPU-Accelerated Sparse LU Factorization for Power System Simulation. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar]
- Roberge, V.; Tarbouchi, M.; Okou, F. Parallel Power Flow on Graphics Processing Units for Concurrent Evaluation of Many Networks. IEEE Trans. Smart Grid 2017, 8, 1639–1648. [Google Scholar] [CrossRef]
- Li, X.; Li, F.; Yuan, H.; Cui, H.; Hu, Q. GPU-based fast decoupled power flow with preconditioned iterative solver and inexact newton method. IEEE Trans. Power Syst. 2017, 32, 2695–2703. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, D.; Li, Y.; Zheng, R. A Fine-Grained Parallel Power Flow Method for Large Scale Grid Based on Lightweight GPU Threads. In Proceedings of the 2016 IEEE 22nd International Conference on Parallel and Distributed Systems (ICPADS), Wuhan, China, 13–16 December 2016; pp. 785–790. [Google Scholar]
- Liu, Z.; Song, Y.; Chen, Y.; Huang, S.; Wang, M. Batched Fast Decoupled Load Flow for Large-Scale Power System on GPU. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; pp. 1775–1780. [Google Scholar]
- Zhou, G.; Feng, Y.; Bo, R.; Zhang, T. GPU-accelerated sparse matrices parallel inversion algorithm for large-scale power systems. Int. J. Electr. Power Energy Syst. 2019, 111, 34–43. [Google Scholar] [CrossRef]
- Huang, S.; Dinavahi, V. Performance analysis of GPU-accelerated fast decoupled power flow using direct linear solver. In Proceedings of the Electrical Power and Energy Conference (EPEC), Saskatoon, SK, Canada, 22–25 October 2017; pp. 1–6. [Google Scholar]
- Zhou, G.; Bo, R.; Chien, L.; Zhang, X.; Shi, F.; Xu, C.; Feng, Y. GPU-based batch LU factorization solver for concurrent analysis of massive power flows. IEEE Trans. Power Syst. 2017, 32, 4975–4977. [Google Scholar] [CrossRef]
- Eigen. Eigen 3 Documentation. Available online: http://eigen.tuxfamily.org (accessed on 12 April 2020).
- Li, X.; Li, F.; Clark, J.M. Exploration of multifrontal method with GPU in power flow computation. In Proceedings of the Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- MATPOWER. MATPOWER User’s Manual. Available online: http://matpower.org (accessed on 3 February 2020).
- MathWorks Inc. MATLAB. Available online: http://www.mathworks.com (accessed on 15 March 2020).
- Huang, S.; Dinavahi, V. Fast batched solution for real-time optimal power flow with penetration of renewable energy. IEEE Access 2018, 6, 13898–13910. [Google Scholar] [CrossRef]
- Zhou, G.; Bo, R.; Chien, L.; Zhang, X.; Yang, S.; Su, D. GPU-accelerated algorithm for online probabilistic power flow. IEEE Trans. Power Syst. 2018, 33, 1132–1135. [Google Scholar] [CrossRef]
- Su, X.; He, C.; Liu, T.; Wu, L. Full Parallel Power Flow Solution: A GPU-CPU Based Vectorization Parallelization and Sparse Techniques for Newton-Raphson Implementation. IEEE Trans. Smart Grid 2019, 11, 1833–1844. [Google Scholar] [CrossRef]
- Araújo, I.; Tadaiesky, V.; Cardoso, D.; Fukuyama, Y.; Santana, Á. Simultaneous parallel power flow calculations using hybrid CPU-GPU approach. Int. J. Electr. Power Energy Syst. 2019, 105, 229–236. [Google Scholar] [CrossRef]
- Chen, X.; Ren, L.; Wang, Y.; Yang, H. GPU-accelerated sparse LU factorization for circuit simulation with performance modeling. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 786–795. [Google Scholar] [CrossRef]
- Davis, T. SUITESPARSE: A Suite OF Sparse Matrix Software. Available online: http://faculty.cse.tamu.edu/davis/suitesparse.html (accessed on 1 April 2020).
- Schenk, O.; Gärtner, K. User Guide. Available online: https://www.pardiso-project.org/ (accessed on 15 April 2020).
- Wang, M.; Xia, Y.; Chen, Y.; Huang, S. GPU-based power flow analysis with continuous Newton’s method. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- Yoon, D.H.; Kang, S.K.; Kim, M.; Han, Y. Exploiting Coarse-Grained Parallelism Using Cloud Computing in Massive Power Flow Computation. Energies 2018, 11, 2268. [Google Scholar] [CrossRef] [Green Version]

| Major Procedures (>30 ms) | Time (ms) | Speedup | |
|---|---|---|---|
| CPU | GPU | ||
| Build admittance matrix | 154.285 | 2.820 | 54.7× |
| Build Jacobian matrix | 61.308 | 2.925 | 21.0× |
| Solve linear system | 972.043 | 55.104 | 17.6× |
| Compute S and losses on all lines | 69.094 | 0.971 | 71.2× |
| No. | SSA Solution | Analysis Time (s) | Speedup |
|---|---|---|---|
| 1 | CPU SSA with a single-threaded UMFPACK [65] | 144.8 | - |
| 2 | CPU SSA with 12-threaded PARDISO [66] | 33.6 | 4.3× |
| 3 | CPU SSA with 12-threaded KLU [56] | 9.9 | 14.6× |
| 4 | GPU SSA with Batch-ACPF solver [28] | 2.5 | 57.6× |
| References | Main Features (Solver or Method) | Speedup (Comparison Target) | Year | Hardware Specification |
|---|---|---|---|---|
| [46] | LU decomposition | 10.4× (in-house code) | 2012 | CPU: Phenom 9850 (4 cores) GPU: Tesla S1070 |
| [45] | 7.90× (1-core CPU) 1.49× (8-core CPU) | 2012 | CPU: Xeon X5680 (24 cores) GPU: GTX 580 | |
| [54] | 4.16× (Matlab counterpart) | 2017 | CPU: Xeon E5-2620 (6 cores) GPU: GeForce Titan Black | |
| [55] | 76.0× (KLU library) | 2017 | CPU: Xeon E5-2620 (24 cores) GPU: Tesla K40 | |
| [63] | LU decomposition, hybrid CPU-GPU | Only graphs (MATPOWER) | 2019 | CPU: Xeon E5-2620 (6 cores) GPU: Tesla K20c |
| [32] | CG method | 4.7× (Matlab CG) | 2014 | CPU: Xeon E5607 (8 cores) GPU: Tesla M2070 |
| [28] | Batch-QR | 64× (UMFPACK) | 2014 | CPU: Xeon E5-2620 (24 cores) GPU: Tesla K20c |
| [50] | GPU-based FDPF with Inexact Newton method | 2.86× (traditional FDPF) | 2017 | CPU: Xeon E5607 (8 cores) GPU: Tesla M2070 |
| [49] | Parallel GS, NR | GS: 45.2×, NR: 17.8× (MATPOWER) | 2017 | CPU: Xeon E5-2650 (32 cores) GPU: Telsa K20c |
| [67] | Continuous NR | 11.13× (CPU) | 2017 | CPU: Xeon E5-2620 (6 cores) GPU: Tesla K20Xm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, D.-H.; Han, Y. Parallel Power Flow Computation Trends and Applications: A Review Focusing on GPU. Energies 2020, 13, 2147. https://doi.org/10.3390/en13092147
Yoon D-H, Han Y. Parallel Power Flow Computation Trends and Applications: A Review Focusing on GPU. Energies. 2020; 13(9):2147. https://doi.org/10.3390/en13092147
Chicago/Turabian StyleYoon, Dong-Hee, and Youngsun Han. 2020. "Parallel Power Flow Computation Trends and Applications: A Review Focusing on GPU" Energies 13, no. 9: 2147. https://doi.org/10.3390/en13092147
APA StyleYoon, D.-H., & Han, Y. (2020). Parallel Power Flow Computation Trends and Applications: A Review Focusing on GPU. Energies, 13(9), 2147. https://doi.org/10.3390/en13092147





