Enhanced Quadratic V/f-Based Induction Motor Control of Solar Water Pumping System

Abstract

In rural and remote areas, solar photovoltaic energy (PV) water pumping systems (SPWPSs) are being favored over diesel-powered water pumping due to environmental and economic considerations. PV is a clean source of electric energy offering low operational and maintenance cost. However, the direct-coupled SPWPS requires inventive solutions to improve the system’s efficiency under solar power variations while producing the required amount of pumped water concurrently. This paper introduces a new quadratic V/f (Q V/f) control method to drive an induction motor powered directly from a solar PV source using a two-stage power converter without storage batteries. Conventional controllers usually employ linear V/f control, where the reference motor speed is derived from the PV input power and the dc-link voltage error using a simple proportional–integral (PI) controller. The proposed Q V/f-based system is compared with the conventional linear V/f control using a simulation case study under different operating conditions. The proposed controller expectedly enhances the system output power and efficiency, particularly under low levels of solar irradiance. Some alternative controllers rather than the simple PI controller are also investigated in an attempt to improve the system dynamics as well as the water flow output. An experimental prototype system is used to validate the proposed Q V/f under diverse operating conditions.

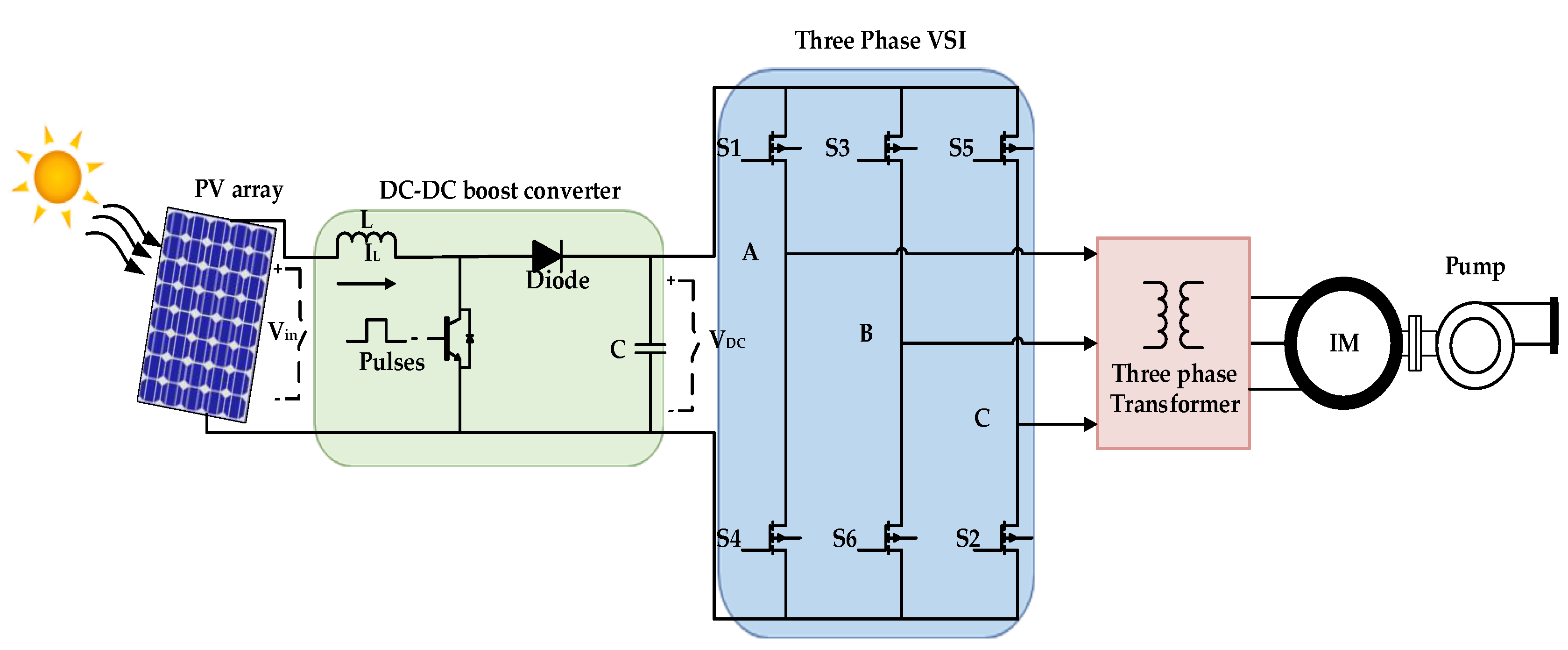
1. Introduction

In developing countries, electrical and diesel-powered water pumping systems are widely used in agriculture. Diesel powered water pumping is typically utilized in remote locations without electrical grid access; however, the associated cost is high. Moreover, environmental considerations have also placed significant focus on exploiting renewable energy sources such as photovoltaics, wind energy, and biomass sources to power water pumping systems [1]. The combination of renewable energy sources and water pumps is recommended by many researchers as a mean to satisfy the energy demands and eliminate the detrimental effect on the environment.

Among the possible renewable energy resources, photovoltaic energy (PV) is particularly suited for water pumping in remote desert locations. It is naturally available, environment friendly, and has low maintenance cost. In remote areas, particularly in arid regions, solar radiation is abundantly available, which makes PV a favorable solution to supply water demand [2].

Usually, solar photovoltaic water pumping systems (SPWPSs) can be classified into two types, namely, battery-coupled SPWPSs and direct-coupled SPWPSs [3]. In battery-coupled SPWPS, the excess energy from the PV panels is stored in batteries which can be used to extend the duration of supplying electricity to water pumps or operate the water pumps during night and cloudy days. Whereas the generated electricity from the PV panels is directly utilized to drive the water pumps in direct-coupled SPWPS. This system has many advantages such as simplicity, lower cost due to lack of storage batteries, requiring less maintenance, and operating with high efficiency on sunny days. Additionally, a storage water tank can be used to cover the water demand in the evening or when the PV array is unable to produce sufficient power to drive the pump.

To design an efficient direct-coupled SPWPS, the main challenge is the operation under significant power oscillations, which defies the regulation of the DC link voltage. Consequently, this system requires creative solutions in order to concurrently extract the maximum PV power and the desired quantity of pumped water [4]. There are several efficient methods for tracking the maximum power point (MPP) that can be utilized to obtain the peak power from PV. The most commonly used MPP tracking techniques are the perturb and observe (P&O) [5] and incremental conductance (INC) methods [6].

In the solar PV water pumping system (SPWPS), various types of motors can be used to drive the water pump such as permanent magnet [7], induction motors [8], and synchronous reluctance motors [9]. However, induction motors are preferred in practical grounds, due to their rugged construction, which results in a reliable, maintenance free and productive solar PV water pumping system [10].

Commonly, there is no crucial need for high dynamic response in solar PV water pumping systems. Subsequently, the conventional V/f control can sufficiently be applied in the majority of practical systems [11]. The traditional linear (or constant) V/f control is commonly utilized in almost all existing systems. Simply, the main principle of scalar control of induction motor is to maintain the stator flux constant by keeping the ratio of the voltage by frequency (V/f) linearly constant. The scalar V/f control is generally applied with induction motor drives since it is simple and can be easily implemented, compared to vector control and direct torque control (DTC) techniques that require higher computational effort and are parameter dependent [12,13,14,15]. Moreover, scalar control has the advantage of low cost, low steady-state error [16], and does not depend on motor parameters [17]. Although, the linear V/f has many advantageous, it suffers from a main limitation which is the low performance at low-speed operation [18]. A linear scalar V/f control method is utilized in [19,20] for induction motor drives where the machine parameters are used to determine the boosting voltage value. A two-stage solar PV water pumping system with a simple scalar V/f control is used in [21,22,23]. Note how the DC-link voltage is relatively unstable. In [24], a simple linear V/f control method is presented with no need for additional sensors for motor’s current nor speed. The proposed control technique is used to drive induction motors in a direct-coupled solar PV water pumping system while maintaining the voltage at the DC link at a constant level.

In general, the torque of a pump driven motor is proportional to the square of the speed. Thus, employing linear V/f control to maintain a constant rated stator flux at low speeds will result in a relatively low torque/RMS current ratio due to the magnetizing current component. This deteriorates the machine efficiency under low speed (low discharge rates) operation. For that reason, it is more suitable to use a quadratic V/f control in this case, where the relation between the voltage magnitude and the operating frequency is parabolic. This resembles a lower stator current magnitude under lower speeds and hence, a higher motor efficiency will likely be achieved. This technique has been presented in [25] for induction motors employed in variable speed pumps but a thorough comparison with linear v/f has not been introduced so far in direct-coupled SPWPS. An initial simulation study introduced in [26] has proved the effectiveness of employing quadratic V/f over linear V/f to improve the system efficiency and to increase the pump discharge.

In this paper, a quadratic V/f is proposed to control the induction motor in a two-stage directly-coupled solar PV water pumping system. First, proportional–integral (PI) control is used with the proposed quadratic V/f to maintain a constant DC-link voltage and regulate the input inductor current of the DC-DC boost converter. The proposed method is compared with the linear V/f control at selected scenarios. Then, other alternative controllers based on fuzzy logic and sliding mode control techniques have been proposed with the quadratic V/f to replace to the conventional PI controller in order to improve the system performance.

The main highlights of this paper can be summed up as follows:

• Performance of the two-stage solar PV water pumping system with quadratic V/f control compared to linear V/f control.
• The dynamic response and the system efficiency due to a sudden change in the input power under the proposed quadratic V/f control.
• Replacing the conventional PI control with fuzzy logic and sliding mode controllers in order to improve the system performance.

The paper is organized as follows: Section 2 presents the system design. The design of the control system is described in Section 3 including the proposed quadratic V/f control, sliding mode control, and the fuzzy logic control. Section 4 shows the MATLAB/Simulink simulation results and the associated discussion. Section 5 presents the experimental validation of the proposed control system under diverse operating conditions. Finally, the main conclusions that can be derived from the presented work are discussed in Section 6.

2. SPWPS Layout and Design

The power circuit of a two-stage solar photovoltaic water pumping system (SPWPS) is composed of a PV array, DC-DC boost converter, three phase voltage source inverter (VSI), three phase transformer, induction motor (IM) and pump, as shown in Figure 1 [24]. In the following section, the selection of different system components is briefly described.

2.1. Pump Selection

An existing three-phase, 380 V, 430 W, 50 Hz induction motor-based water pump is used to validate the proposed controller.

Table 1. Motor Pump Specifications and Parameters.

Parameter	Value
Rated line voltage	380 V
Rated phase current	2.7 A
Rated frequency	50 Hz
Rated speed	2850 rpm
Stator resistance	12.6 Ω
Stator leakage inductance	5 mH
Rotor resistance	12.1 Ω
Rotor leakage inductance	5 mH
Magnetizing inductance	250 mH

shows the motor pump specifications and parameters. Convectional no load and blocked rotor tests are used to estimate the machine parameters which are required to build the simulation model.

2.2. PV Array Design

Based on the rated pump output power of 430 W and rated efficiency of 56%, the required capacity of the PV array should be 730 W (2 series modules × 2 parallel module).

Table 2. PV Array Specifications (SFK185-S).

Parameter	Value
Module maximum power (Pm)	185 W
Module open Circuit Voltage (VOC)	121 V
Module Short Circuit Current (ISC)	2.19 A
Module MPP voltage (Vm)	95 V
Module MPP current (Im)	1.95 A
Array maximum power (Pm)	740 W
Array open Circuit Voltage (VOC)	242 V
Array Short Circuit Current (ISC)	4.38 A
Array MPP voltage (Vm)	190 V
Array MPP current (Im)	3.9 A

shows the specification of the selected PV array.

The output voltage and current of the PV array are affected by temperature and solar irradiation. The effect of temperature on voltage is more significant as shown in Figure 2a, while current is more sensitive to changes in solar irradiation, as depicted by Figure 2b. Figure 2a shows the I-V and P-V characteristic curves of the employed PV array at different atmospheric temperature values and constant solar irradiation. Figure 2b shows the I-V and P-V characteristics curves of the PV array exposed to different solar irradiation levels at constant atmospheric temperature.

If the effect of the temperature is discarded, the PV module can be represented by a constant DC voltage source for the sake of simplicity, especially under experimental validation. The different solar irradiation effect can be represented by changing the input current level. In the experimental prototype system, a programable dc voltage source is used to emulate the PV array. Hence, the first stage DC-DC converter is alternatively controlled based on a certain reference DC current corresponding to a specified solar irradiance level, while the programmable supply voltage is set to 200 V.

2.3. Design of System Passive Elements

The selected system has two passive elements, the inductor of the DC-DC boost converter and the DC link capacitor. In this section, the design of these passive elements is addressed. The required DC link voltage is calculated from (1).

$$m\times \frac{V_{DC}}{2\sqrt{2}}=\frac{V_L}{\sqrt{3}}$$

(1)

where

• $m$ is the modulation index.
• $V_L$ is the motor line to line voltage = 380 V and the step-up transformer turns ratio is 1:2, so that the inverter RMS line voltage output is 190 V.
• $V_{DC}$ is the DC link voltage. From (1), it is selected to be 300 V.

The DC link capacitor is calculated from using (2) [27]:

$$\frac{1}{2}C\left[V_{DC}^{*2}-V_{DC}{}^2\right]=3\alpha \times V\times I\times t$$

(2)

where

• $V_{DC}^{*}$ is the set value of the DC link voltage = 300 V.
• $V_{DC}$ is the acceptable lower voltage at the DC link during transients.
• α is an overloading factor and $t$ is the duration of transient.
• $V$ and $I$ are the phase RMS voltage and current, respectively.

From (2), a 2000 µF DC-link capacitor seems to be sufficient. An available 4700µF has, however, been used in the experimental validation.

The inductor of the DC-DC boost converter can be designed using (3)

$$L=\frac{V_{in}\times D}{\Delta I_L\times f_s}$$

(3)

where

• $V_{in}$ is the input DC voltage = 200 V.
• $D$ is the duty cycle = 0.3333.
• $\Delta I_L$ is the value of the input current ripple, which is set to 20% of the rated PV current.
• $f_s$ is the switching frequency, which is set to 10 kHz.

Thus, the boost inductor is selected to be 3 mH.

3. Two-Stage SPWPS Control

The two-stage SPWPS control consists of two cascaded parts: the control of the DC-DC boost converter and the control of the voltage source inverter (VSI) using the proposed quadratic V/f control. The DC-DC boost converter is responsible for extracting maximum power form the PV array by controlling the input current at a certain level corresponding the maximum possible extracted power. On the other hand, the VSI drives the induction motor a certain speed such that the pump output power will maintain zero power balance over the intermediate DC-link capacitor. In this section, the theoretical formulation of the proposed quadratic V/f with the conventional PI controller is first discussed and then alternative controllers combined with the proposed quadratic V/f control are also introduced.

3.1. Quadratic V/f Combined with PI Controller

In the proposed system, there are two main controllers: the current controller of the boost converter inductor and the DC-link voltage controller. The simplest controller that is commonly employed is the conventional PI controller. Two PI controllers are, therefore, needed for the two control loops.

The first PI controller is used to maintain the inductor current of the DC-DC boost converter at a certain reference value. The output from this PI controller is the duty ratio of the DC-DC boost converter. In practice, the DC-DC boost converter is controlled based on an MPPT algorithm. The second part of the system control is the DC-link capacitor voltage control based on the proposed quadratic V/f control of the induction motor. The final output of this control loop is the switching pulses to drive the VSI using conventional sinusoidal pulse-width modulation (SPWM), as shown in Figure 3 [24]. The capacitor voltage is controlled to maintain power balance between the injected solar power and the pump output power. The difference between the input and output powers simply represents the power losses of both motor as well as the two-stage power converter. The control action can be explained as follows.

According to centrifugal pump characteristics, load torque is related to the speed as in (4).

$$T_L=K_{pump} {\omega }^2$$

(4)

where $T_L$ is the load torque of the water pump, $K_{pump}$ is the pump constant, and $\omega$ is the rotor rotational speed in rad/s.

The required pump power, $P_L$, can, therefore, be calculated based on (5).

$$P_L=K_{pump} {\omega }^3$$

(5)

The PV array power can be estimated from its terminal voltage and current. Assuming zero system power losses, the required reference motor speed can be calculated from (6) by assuming that $P_L=P_{in}$.

$$\omega =K \sqrt[3]{P_{in}}$$

(6)

where $K=1/\sqrt[3]{K_{pump}}$.

Assuming also a neglected motor slip, this reference speed is then used to estimate the required reference operating frequency from (7).

$$f=p \frac{\omega }{2\pi }$$

(7)

where $p$ is the motor number of pole-pairs.

Since $P_{in}>P_L$ and motor slip cannot be zero, especially under full loading conditions, the calculated reference frequency from (7) will be higher than the correct value. This mismatch can be compensated for by subtracting a compensating term, $\Delta f$, obtained from the DC-link voltage error using another PI controller. The term $\Delta f$ compensates for the motor losses to ensure a power balance over the DC-link capacitor. Hence, the required motor reference frequency can finally be calculated from (7).

$$f_{ref}=p\frac{K}{2\pi } \sqrt[3]{P_{in}}-\Delta f$$

(8)

The open-loop V/f control is recognized by its simplicity and low cost because no speed feedback sensor is required. In linear V/f control, the amplitude of the stator flux is proportional to the stator voltage and inversely proportional to the frequency ($\phi \propto V/f$). Hence, ensuring a constant V/f ratio will yield a constant airgap flux amplitude, which is the case for linear V/f-based control. On the other hand, in the proposed quadratic V/f control, the magnitude of the stator voltage changes with the square of the reference frequency $V\propto f^2$. Hence, that flux magnitude will be proportional to that frequency ($\phi \propto f$). The linear and quadratic V/f characteristics are shown in Figure 4, where V_n and f_n represents the values of the rated voltage and the rated frequency, respectively.

The input to the proposed quadratic V/f control is only the reference frequency which is then used to generate the required modulation index of the three sinusoidal voltage references. Conventional SPWM is finally used to produce the switching signals of the voltage source inverter.

3.2. Quadratic V/f Combined with Other Alternative Controllers

In order to improve the system performance, two alternative controllers are suggested with the proposed quadratic V/f and are shown in Figure 5. The first controller is denoted as Q V/f PI-FLC based controller. In this proposed controller, a PI controller is used to control the inductor current, while a fuzzy logic controller (FLC) is used in the DC-link voltage control loop. The second controller is denoted as (Q V/f SM-FLC), where the PI controller of the inductor current is replaced by a sliding mode controller.

3.2.1. Sliding Mode Control (SMC)

Sliding Mode Control is a nonlinear control technique which is suitable to control the dynamics of a nonlinear system. Sliding Mode control uses a discontinuous control signal to impose the system to slide along a cross-section of the system’s normal behavior [28]. By forcing the system to follow a predetermined path in the state space, called the sliding surface, the sliding mode control makes the controlled system dynamically stable [29].

In this study, the sliding mode is used to control the boost converter duty cycle based on both inductor current and capacitor voltage errors. In other words, the error of the output voltage and the input current are employed as state variables, as given by the following equations [30]

$$x_1=V_{ref,DC}-V_{DC}$$

(9)

$$x_2=I_{ref,L}-I_L$$

(10)

where $x_1$ and $x_2$ are the system states variables, and $V_{ref,DC}$ and $I_{ref,L}$ are the references of the output voltage and the input current, respectively.

The sliding surface (S) is defined as the summation of the state variables multiplied by the sliding surface coefficients as follows:

$$S=K_V{x}_1+K_I{x}_2$$

(11)

where $K_V$ and $K_I$ are the sliding surface coefficients which are chosen in order to ensure zero DC Link voltage and input current errors.

3.2.2. Fuzzy Logic Control (FLC)

Fuzzy logic control is another form of control commonly used with nonlinear systems because it does not need the system’s mathematical model, simply the human linguistic concepts are converted to an automatic control strategy [31]. Since PV water pumping system may be operating over a wide range of input power levels, the FLC is expected to better perform during severe transients than classical PID controllers.

In fuzzy logic control, Mamdani fuzzy interference is utilized, triangular membership functions denoted by NB (Negative Big), NS (Negative small), Z (Zero), PS (Positive Small), and PB (Positive Big) are used in the input and output surfaces. Figure 6 shows the selected inputs and output membership functions, respectively.

Table 3. Fuzzy Logic Control Rule Table.

E/CE	NB	NS	Z	PS	PB
NB	NB	NB	NB	NS	Z
NS	NB	NB	NS	Z	PS
Z	NB	NS	Z	PS	PB
PS	NS	Z	PS	PB	PB
PB	Z	PS	PB	PB	PB

shows the rules table for the fuzzy logic control, which is a set of relations between the specified inputs to determine the output. The number of membership functions defines the number of rules. In case of five membership functions, the table has 25 rules.

4. Simulation Results

The MATLAB/SIMULINK simulation program is used to design, model, and simulate the proposed two-stage solar PV water pumping system. In order to validate the performance of the proposed quadratic V/f control method, the input power is changed in steps. To simulate the solar irradiation variation, the input reference current is changed to certain selected values, while the input voltage is assumed constant at 200 V, representing the maximum voltage of the PV array, because the voltage is not affected with the variation of the solar radiation as explained in Section 2.2.

4.1. Comparsion between Q V/f and L V/f-Based Controllers

In this simulation case, the inductor current and the DC-link voltage are kept constant using proportional–integral PI controllers. All PI controllers are tuned by trial-and-error technique. The dynamic response of the proposed quadratic V/f (Q V/f PI-PI) control is compared with the linear V/f (L V/f PI-PI) control in each step change of the input power.

The input power is changed in three steps by changing the reference input current. First, the input current is set to 3.65 A (rated PV module current) for the first five seconds. Then, the input current is changed to 2.74 A from 5 to 10 s, so that the input power is reduced by 25%. After that, the input current becomes 1.825 A from 10 to 15 s and the input power is decreased to 50% of rated output. From 15 to 20 s, the input power is recovered to full rated power. The simulation results for both the conventional linear V/f and the proposed quadratic V/f are shown in Figure 7.

Table 4. Simulation results for both Q V/f and L V/f.

Time (S)	Type of Control	Inductor Current (A)	DC Link Voltage (V)	Motor Speed (rpm)	Motor Torque (N.m)	RMS Phase Current (A)	Efficiency (%)
0–5	Quadratic V/f	3.65	300	2840	1.376	2.54	56.04
	Linear V/f	3.65	300	2836	1.372	2.54	55.79
5–10	Quadratic V/f	2.74	300	2544	1.104	2.302	53.649
	Linear V/f	2.74	299.6	2379	0.9655	2.52	43.88
10–15	Quadratic V/f	1.825	300	2169	0.802	1.91	49.917
	Linear V/f	1.825	299.5	1757	0.5269	2.461	26.567

shows the steady-state values of the input inductor current, DC link voltage, motor speed, RMS value of the motor stator current, and system efficiency (η) for both linear and quadratic V/f at each interval of the input power variations. The system efficiency is calculated using (12)

$$\eta =\frac{P_L}{P_{in}}$$

(12)

For both linear and quadratic V/f control methods, the average inductor current is kept constant at the selected reference value, while the DC-link voltage is held constant at 300 V regardless the change in the machine input power. From the simulation results, it is observed that the settling time to reach the steady-state is less under quadratic V/f control. Thus, the dynamic response under quadratic V/f control is much better. When the input power is reduced to very low levels, the dynamic response of the dc-link voltage becomes much worse under linear V/f.

It is also clear that the motor speed is higher under the quadratic V/f control, which indicates a consequent higher output power. When the input power is reduced by 50% at time 10 s, the motor speed under the linear V/f control is 20% less than the proposed quadratic V/f control and eventually, the corresponding system efficiency is reduced by approximately 50% under linear V/f control.

The main enhancement in system response is owing to the fact that induction motors will be more efficient under low-speed operation at low levels of air gap flux in pump load applications, where torque production is comparatively small. As a matter of fact, the motor torque increases as the motor speed increases, which entails higher level of air-gap flux to minimize the torque/current ratio. Since there is a direct relationship between the stator reactive current component and the V/f ratio, the motor current will be less under quadratic V/f for a specific motor speed, resulting in higher motor efficiency.

4.2. Simulation Results of the Other Alternative Controller Combined with the Q V/f

The MATLAB/SIMULINK simulation program is also used to model and simulate the other proposed Q V/f-based controllers in order to improve the system dynamic response and steady-state output. The same input power profile will be used with the (Q V/f PI-FLC) and (Q V/f SM-FLC) controllers shown in Figure 5.

The simulation results for all cases are compared in Figure 8. From the obtained results, the inductor current and the motor speed values are the same for all controllers at different cases. However, the sliding mode control of the inductor current corresponds to a faster dynamic response and at the steady state it is observed that the inductor current has lower ripples. This will, in turn, correspond to lower inductor copper losses in the boost converter stage. The dynamic response of the DC link voltage shown in Figure 8b is improved when employing a fuzzy logic controller over a classical PI controller. The fuzzy logic controller achieves faster transient response and less overshoot. The value of the DC link voltage is nearly the same for all controllers at nearly 300 V, as shown in Figure 8.

Table 5. Simulation results for Q V/f PI-FLC and Q V/f SM-FLC compared to Q V/f PI-PI.

Time (S)	Type of Control	Inductor Current (A)	DC Link Voltage (V)	Motor Speed (rpm)	Efficiency (%)
0–5	Q V/f PI-PI	3.65	300	2840	56.04
	Q V/f PI-FLC	3.65	298.8	2840	56.08
	Q V/f SM-FLC	3.652	299.1	2837	55.72
5–10	Q V/f PI-PI	2.74	300	2544	53.649
	Q V/f PI-FLC	2.74	298.9	2554	54.32
	Q V/f SM-FLC	2.743	298.9	2554	54.21
10–15	Q V/f PI-PI	1.825	300	2169	49.917
	Q V/f PI-FLC	1.825	299	2173	50.24
	Q V/f SM-FLC	1.822	299	2169	50.05

summarizes the steady-state simulation results for the inductor current, DC link voltage, motor speed, and system efficiency for all controllers. To sum up, although the controller type has nothing to do with the average inductor current and motor speed, employing a sliding mode control to the inductor current will slightly improve the total efficiency due to the relative reduction in the inductor ripple current component. However, this slight improvement may be assumed insignificant to justify employing these complex controllers.

5. Experimental Results

An experimental prototype system has been constructed to validate the performance of the proposed quadratic V/f control. The laboratory setup is composed of a DC power supply (to emulate the PV array), a boost converter, a three-phase VSI, a DSP board (TMS320F28379D), and a three-phase induction motor coupled to a pump. A 600 V, 20 A IRAMY20UP60B inverter module operating at 10 kHz switching frequency is used to construct the two-level three-phase inverter. The PV array is emulated with a 300 V, 17 A TDK-Lambda programmable supply. The Code Composer Studio software EDI under Simulink/MATLAB platform is used to run the proposed controller.

In order to represent the lower and upper heads of water, two tanks are used as shown in Figure 9. The pump draws water from the lower tank to the upper tank through connecting pipes and then, a returning pipe is connected from the upper tank to the lower one to ensure water continuity to the lower tank. Two sensors are used to measure the inductor current, and the DC link voltage. The DSP board is opto-isolated using fast switching opto-couplers 6N137.

Based on simulation results given in Section 4, the classical PI-based control seems sufficient in this application. The experimental validation is, therefore, limited to this case. Both linear and quadratic V/f control will be compared under both transient and steady state cases. Since it was not possible with the employed prototype system to measure the pump speed, the steady-state frequency is alternatively used to compare the pump running speed under different cases (higher frequency indicates a higher rotor speed).

The voltage of the DC power supply is set to 150 V and the inductor current of the DC-DC boost converter is changed from 2 A to 4 A. The PI controller is used to regulate the inductor current and the DC link voltage. All PI controllers are tuned by trial-and-error technique. The same controller values are then reserved for both V/f characteristics.

Figure 10 and Figure 11 show the inductor current, DC link voltage and the stator phase current of the motor at 4 A and 2 A inductor current for the quadratic V/f and the linear V/f control, respectively. For both the quadratic and linear V/f, the DC link voltage is kept constant at 300 V. The stator phase current under quadratic V/f control is smaller than linear V/f control, especially with lower level of input power (inductor current), which means that the system is more efficient when using the quadratic V/f control. In addition, the frequency in case of quadratic V/f control is higher, its percentage increases at lower input power than the conventional V/f control.

Table 6. Experimental results for Q V/f PI-PI compared to L V/f PI-PI.

Type of Control	Inductor RMS Current (A)	DC Link Voltage (V)	Frequency (HZ)	RMS Phase Current (A)
Quadratic V/f	2.05	298	37.2	1.91
Linear V/f	2.04	298	35.07	2.25
Quadratic V/f	4.33	304	46.54	2.46
Linear V/f	4.27	300	42.26	2.64

summarizes the steady-state values for both cases.

Figure 12 shows the dynamic response of the inductor current, DC link voltage and the stator phase current for a step change of the inductor current from 2 A to 4 A for both the proposed quadratic V/f and the conventional linear V/f control, respectively. Not much difference can be claimed between the two cases for this relatively low-power scale prototype system.

6. Conclusions

A quadratic V/f control is proposed to drive an induction motor for a solar PV direct-coupled water pumping system. Quadratic torque-speed curves are the characteristic of pumping loads, and hence a matching V/f-Quadratic-control approach was, therefore, utilized. In comparison to the classical linear V/f control, the quadratic control has guaranteed higher performance over the whole operating speed range. To verify the performance of the proposed quadratic V/f control method, a case study was simulated to examine the system behavior under different levels of input power. Moreover, a prototype system was built in a laboratory to validate the proposed control method. Both simulation and the experiments have complied with the theoretical findings and entirely confirm the supremacy of the quadratic V/f-based control over classical linear V/f-based control, especially under steady-state operation. The performance enhancement was shown in terms of lower phase current magnitude, higher pump speed, and higher efficiency for the same input power. Simulations has also confirmed a relative improvement in the system dynamic response under quadratic V/f-based control. Furthermore, sliding mode and the fuzzy logic controllers were proposed to replace the conventional PI controller with the proposed quadratic V/f. Although these control techniques have shown a slight improvement in the system dynamic response, the obtained gain in the machine efficiency (around 0.3–0.7% based on input power level) does not justify this complexity while arguing in favor of employing a classical PI controller in water pumping applications where dynamic response may not be that important.