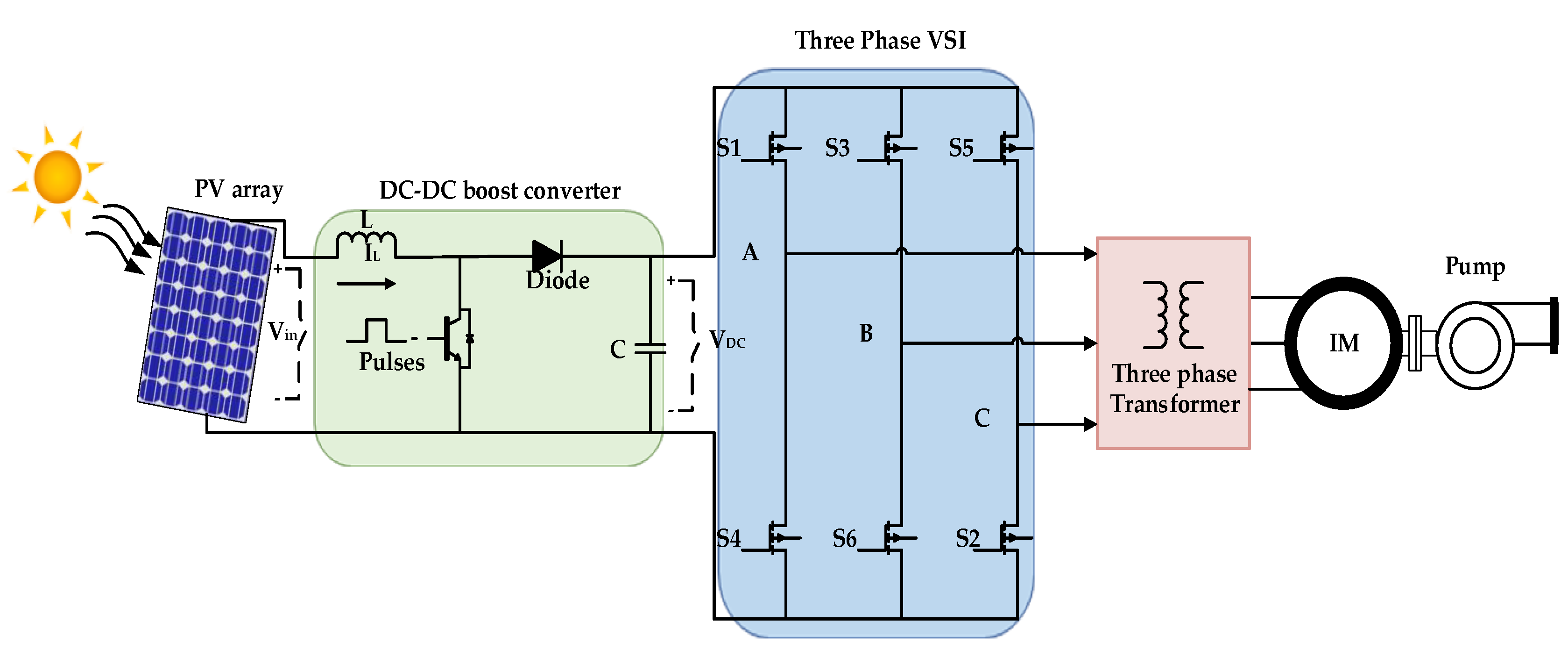
1. Introduction
In developing countries, electrical and diesel-powered water pumping systems are widely used in agriculture. Diesel powered water pumping is typically utilized in remote locations without electrical grid access; however, the associated cost is high. Moreover, environmental considerations have also placed significant focus on exploiting renewable energy sources such as photovoltaics, wind energy, and biomass sources to power water pumping systems [
1]. The combination of renewable energy sources and water pumps is recommended by many researchers as a mean to satisfy the energy demands and eliminate the detrimental effect on the environment.
Among the possible renewable energy resources, photovoltaic energy (PV) is particularly suited for water pumping in remote desert locations. It is naturally available, environment friendly, and has low maintenance cost. In remote areas, particularly in arid regions, solar radiation is abundantly available, which makes PV a favorable solution to supply water demand [
2].
Usually, solar photovoltaic water pumping systems (SPWPSs) can be classified into two types, namely, battery-coupled SPWPSs and direct-coupled SPWPSs [
3]. In battery-coupled SPWPS, the excess energy from the PV panels is stored in batteries which can be used to extend the duration of supplying electricity to water pumps or operate the water pumps during night and cloudy days. Whereas the generated electricity from the PV panels is directly utilized to drive the water pumps in direct-coupled SPWPS. This system has many advantages such as simplicity, lower cost due to lack of storage batteries, requiring less maintenance, and operating with high efficiency on sunny days. Additionally, a storage water tank can be used to cover the water demand in the evening or when the PV array is unable to produce sufficient power to drive the pump.
To design an efficient direct-coupled SPWPS, the main challenge is the operation under significant power oscillations, which defies the regulation of the DC link voltage. Consequently, this system requires creative solutions in order to concurrently extract the maximum PV power and the desired quantity of pumped water [
4]. There are several efficient methods for tracking the maximum power point (MPP) that can be utilized to obtain the peak power from PV. The most commonly used MPP tracking techniques are the perturb and observe (P&O) [
5] and incremental conductance (INC) methods [
6].
In the solar PV water pumping system (SPWPS), various types of motors can be used to drive the water pump such as permanent magnet [
7], induction motors [
8], and synchronous reluctance motors [
9]. However, induction motors are preferred in practical grounds, due to their rugged construction, which results in a reliable, maintenance free and productive solar PV water pumping system [
10].
Commonly, there is no crucial need for high dynamic response in solar PV water pumping systems. Subsequently, the conventional V/f control can sufficiently be applied in the majority of practical systems [
11]. The traditional linear (or constant) V/f control is commonly utilized in almost all existing systems. Simply, the main principle of scalar control of induction motor is to maintain the stator flux constant by keeping the ratio of the voltage by frequency (V/f) linearly constant. The scalar V/f control is generally applied with induction motor drives since it is simple and can be easily implemented, compared to vector control and direct torque control (DTC) techniques that require higher computational effort and are parameter dependent [
12,
13,
14,
15]. Moreover, scalar control has the advantage of low cost, low steady-state error [
16], and does not depend on motor parameters [
17]. Although, the linear V/f has many advantageous, it suffers from a main limitation which is the low performance at low-speed operation [
18]. A linear scalar V/f control method is utilized in [
19,
20] for induction motor drives where the machine parameters are used to determine the boosting voltage value. A two-stage solar PV water pumping system with a simple scalar V/f control is used in [
21,
22,
23]. Note how the DC-link voltage is relatively unstable. In [
24], a simple linear V/f control method is presented with no need for additional sensors for motor’s current nor speed. The proposed control technique is used to drive induction motors in a direct-coupled solar PV water pumping system while maintaining the voltage at the DC link at a constant level.
In general, the torque of a pump driven motor is proportional to the square of the speed. Thus, employing linear V/f control to maintain a constant rated stator flux at low speeds will result in a relatively low torque/RMS current ratio due to the magnetizing current component. This deteriorates the machine efficiency under low speed (low discharge rates) operation. For that reason, it is more suitable to use a quadratic V/f control in this case, where the relation between the voltage magnitude and the operating frequency is parabolic. This resembles a lower stator current magnitude under lower speeds and hence, a higher motor efficiency will likely be achieved. This technique has been presented in [
25] for induction motors employed in variable speed pumps but a thorough comparison with linear v/f has not been introduced so far in direct-coupled SPWPS. An initial simulation study introduced in [
26] has proved the effectiveness of employing quadratic V/f over linear V/f to improve the system efficiency and to increase the pump discharge.
In this paper, a quadratic V/f is proposed to control the induction motor in a two-stage directly-coupled solar PV water pumping system. First, proportional–integral (PI) control is used with the proposed quadratic V/f to maintain a constant DC-link voltage and regulate the input inductor current of the DC-DC boost converter. The proposed method is compared with the linear V/f control at selected scenarios. Then, other alternative controllers based on fuzzy logic and sliding mode control techniques have been proposed with the quadratic V/f to replace to the conventional PI controller in order to improve the system performance.
The main highlights of this paper can be summed up as follows:
Performance of the two-stage solar PV water pumping system with quadratic V/f control compared to linear V/f control.
The dynamic response and the system efficiency due to a sudden change in the input power under the proposed quadratic V/f control.
Replacing the conventional PI control with fuzzy logic and sliding mode controllers in order to improve the system performance.
The paper is organized as follows:
Section 2 presents the system design. The design of the control system is described in
Section 3 including the proposed quadratic V/f control, sliding mode control, and the fuzzy logic control.
Section 4 shows the MATLAB/Simulink simulation results and the associated discussion.
Section 5 presents the experimental validation of the proposed control system under diverse operating conditions. Finally, the main conclusions that can be derived from the presented work are discussed in
Section 6.
4. Simulation Results
The MATLAB/SIMULINK simulation program is used to design, model, and simulate the proposed two-stage solar PV water pumping system. In order to validate the performance of the proposed quadratic V/f control method, the input power is changed in steps. To simulate the solar irradiation variation, the input reference current is changed to certain selected values, while the input voltage is assumed constant at 200 V, representing the maximum voltage of the PV array, because the voltage is not affected with the variation of the solar radiation as explained in
Section 2.2.
4.1. Comparsion between Q V/f and L V/f-Based Controllers
In this simulation case, the inductor current and the DC-link voltage are kept constant using proportional–integral PI controllers. All PI controllers are tuned by trial-and-error technique. The dynamic response of the proposed quadratic V/f (Q V/f PI-PI) control is compared with the linear V/f (L V/f PI-PI) control in each step change of the input power.
The input power is changed in three steps by changing the reference input current. First, the input current is set to 3.65 A (rated PV module current) for the first five seconds. Then, the input current is changed to 2.74 A from 5 to 10 s, so that the input power is reduced by 25%. After that, the input current becomes 1.825 A from 10 to 15 s and the input power is decreased to 50% of rated output. From 15 to 20 s, the input power is recovered to full rated power. The simulation results for both the conventional linear V/f and the proposed quadratic V/f are shown in
Figure 7.
Table 4 shows the steady-state values of the input inductor current, DC link voltage, motor speed, RMS value of the motor stator current, and system efficiency (
η) for both linear and quadratic V/f at each interval of the input power variations. The system efficiency is calculated using (12)
For both linear and quadratic V/f control methods, the average inductor current is kept constant at the selected reference value, while the DC-link voltage is held constant at 300 V regardless the change in the machine input power. From the simulation results, it is observed that the settling time to reach the steady-state is less under quadratic V/f control. Thus, the dynamic response under quadratic V/f control is much better. When the input power is reduced to very low levels, the dynamic response of the dc-link voltage becomes much worse under linear V/f.
It is also clear that the motor speed is higher under the quadratic V/f control, which indicates a consequent higher output power. When the input power is reduced by 50% at time 10 s, the motor speed under the linear V/f control is 20% less than the proposed quadratic V/f control and eventually, the corresponding system efficiency is reduced by approximately 50% under linear V/f control.
The main enhancement in system response is owing to the fact that induction motors will be more efficient under low-speed operation at low levels of air gap flux in pump load applications, where torque production is comparatively small. As a matter of fact, the motor torque increases as the motor speed increases, which entails higher level of air-gap flux to minimize the torque/current ratio. Since there is a direct relationship between the stator reactive current component and the V/f ratio, the motor current will be less under quadratic V/f for a specific motor speed, resulting in higher motor efficiency.
4.2. Simulation Results of the Other Alternative Controller Combined with the Q V/f
The MATLAB/SIMULINK simulation program is also used to model and simulate the other proposed Q V/f-based controllers in order to improve the system dynamic response and steady-state output. The same input power profile will be used with the (Q V/f PI-FLC) and (Q V/f SM-FLC) controllers shown in
Figure 5.
The simulation results for all cases are compared in
Figure 8. From the obtained results, the inductor current and the motor speed values are the same for all controllers at different cases. However, the sliding mode control of the inductor current corresponds to a faster dynamic response and at the steady state it is observed that the inductor current has lower ripples. This will, in turn, correspond to lower inductor copper losses in the boost converter stage. The dynamic response of the DC link voltage shown in
Figure 8b is improved when employing a fuzzy logic controller over a classical PI controller. The fuzzy logic controller achieves faster transient response and less overshoot. The value of the DC link voltage is nearly the same for all controllers at nearly 300 V, as shown in
Figure 8.
Table 5 summarizes the steady-state simulation results for the inductor current, DC link voltage, motor speed, and system efficiency for all controllers. To sum up, although the controller type has nothing to do with the average inductor current and motor speed, employing a sliding mode control to the inductor current will slightly improve the total efficiency due to the relative reduction in the inductor ripple current component. However, this slight improvement may be assumed insignificant to justify employing these complex controllers.
5. Experimental Results
An experimental prototype system has been constructed to validate the performance of the proposed quadratic V/f control. The laboratory setup is composed of a DC power supply (to emulate the PV array), a boost converter, a three-phase VSI, a DSP board (TMS320F28379D), and a three-phase induction motor coupled to a pump. A 600 V, 20 A IRAMY20UP60B inverter module operating at 10 kHz switching frequency is used to construct the two-level three-phase inverter. The PV array is emulated with a 300 V, 17 A TDK-Lambda programmable supply. The Code Composer Studio software EDI under Simulink/MATLAB platform is used to run the proposed controller.
In order to represent the lower and upper heads of water, two tanks are used as shown in
Figure 9. The pump draws water from the lower tank to the upper tank through connecting pipes and then, a returning pipe is connected from the upper tank to the lower one to ensure water continuity to the lower tank. Two sensors are used to measure the inductor current, and the DC link voltage. The DSP board is opto-isolated using fast switching opto-couplers 6N137.
Based on simulation results given in
Section 4, the classical PI-based control seems sufficient in this application. The experimental validation is, therefore, limited to this case. Both linear and quadratic V/f control will be compared under both transient and steady state cases. Since it was not possible with the employed prototype system to measure the pump speed, the steady-state frequency is alternatively used to compare the pump running speed under different cases (higher frequency indicates a higher rotor speed).
The voltage of the DC power supply is set to 150 V and the inductor current of the DC-DC boost converter is changed from 2 A to 4 A. The PI controller is used to regulate the inductor current and the DC link voltage. All PI controllers are tuned by trial-and-error technique. The same controller values are then reserved for both V/f characteristics.
Figure 10 and
Figure 11 show the inductor current, DC link voltage and the stator phase current of the motor at 4 A and 2 A inductor current for the quadratic V/f and the linear V/f control, respectively. For both the quadratic and linear V/f, the DC link voltage is kept constant at 300 V. The stator phase current under quadratic V/f control is smaller than linear V/f control, especially with lower level of input power (inductor current), which means that the system is more efficient when using the quadratic V/f control. In addition, the frequency in case of quadratic V/f control is higher, its percentage increases at lower input power than the conventional V/f control.
Table 6 summarizes the steady-state values for both cases.
Figure 12 shows the dynamic response of the inductor current, DC link voltage and the stator phase current for a step change of the inductor current from 2 A to 4 A for both the proposed quadratic V/f and the conventional linear V/f control, respectively. Not much difference can be claimed between the two cases for this relatively low-power scale prototype system.