Building Energy Management for Passive Cooling Based on Stochastic Occupants Behavior Evaluation

Abstract

The common approach to model occupants behaviors in buildings is deterministic and consists of assumptions based on predefined fixed schedules or rules. In contrast with the deterministic models, stochastic and agent based (AB) models are the most powerful and suitable methods for modeling complex systems as the human behavior. In this paper, a co-simulation architecture is proposed with the aim of modeling the occupant behavior in buildings by a stochastic-AB approach and implementing an intelligent Building Energy Management System (BEMS). In particular, optimized control logics are designed for smart passive cooling by controlling natural ventilation and solar shading systems to guarantee the thermal comfort conditions and maintain energy performance. Moreover, the effects of occupant actions on indoor thermal comfort are also taken into account. This study shows how the integration of automation systems and passive techniques increases the potentialities of passive cooling in buildings, integrating or replacing the conventional efficiency strategies.

1. Introduction

In recent years, moving towards a Nearly Zero Energy Building (NZEB) target, increasing attention has been paid to the development of innovative strategies and technology solutions for the energy efficiency of building components and Heating, Ventilation, Air Conditioning (HVAC) systems [1].

NZEB standard requires a sophisticated dynamic control of the building-HVAC system to minimize the wastes that can be generated by an incorrect management by users [2,3]. In particular, occupants are considered as one of the major source of microclimate alteration in building environment, being “passive agents” that generates sensible and latent energy emissions and pollutants. Moreover, they can be considered as “active agents” interacting with the building systems e.g., by activating thermostats and artificial lighting, opening, closing and shading windows, etc. [4]. Hence, the modeling of occupant behaviors should take into account the effects of users actions in buildings. In Kim [5] an optimal occupant behavior is established that can simultaneously reduce total energy consumption and improve the Indoor Environmental Quality (IEQ), using an energy simulation and optimization tool.

Furthermore, even though the occupants actions in the building have a significant impact on the energy consumption and the indoor environment, only recent studies focus on this topic, modeling and simulating occupant actions by stochastic models. In [6,7] the modeling of occupant behaviors is performed in a realistic way by means of an Agent-Based (AB) approach, where the occupant actions are ruled by Predicted Mean Vote (PMV) analysis. Other papers, like [8,9,10,11] analyze individual occupant behavior by means of statistical models, analyzing questionnaires surveys and monitoring campaigns for several years. In contrast to the deterministic methods, stochastic and AB models are the most powerful and suitable methods for modeling the complex human behavior [7,12].

Despite the increasing attention to the development of strategies and innovative technology solutions for the energy efficiency of building components and HVAC systems [13,14,15,16] few studies analyze the building-HVAC integrated system management. Building Energy Management Systems (BEMSs) are generally devoted to the control of active systems, such as the HVAC systems ([17,18,19]). For example, the authors in [20] design an intelligent controller for determining the optimal ventilation rate, guaranteeing the required indoor $C{O}_2$ concentration and minimizing energy consumption. In addition, the authors in [21] propose a complex predictive control system to guarantee the thermal comfort and Indoor Air Quality (IAQ) by using HVAC systems and natural ventilation. Sun et al. [22] present an integrated control system aiming at the minimization of the total energy costs. Differently from [20,21,22], in this study, passive strategies are studied with the goal of reducing thermal discomfort conditions according to adaptive thermal comfort theory [23].

One of the research areas on building automation, in rapid development, concerns the harmonization between the concepts of intelligent building and bioclimatic building. This topic comes out from the integration of active and automation systems with passive systems, in order to make the building-HVAC system able to adapt to internal and external changes. From this point of view, some studies [24,25,26] show that it is possible to achieve a significant reduction of energy consumption through the adoption of natural ventilation strategies as an alternative to Air Conditioning (AC) systems. The use of building automation systems is progressivly diffusing and it reserves potential of great interest both in residential and office buildings [27]. The work in [28] presents the effects of efficient exterior shades for a mixed residential and office building: external shades are designed to significantly reduce the cooling loads.

The aim of this paper is proposing a methodology for passive cooling such as natural ventilation and solar shading for indoor thermal comfort in buildings, based on stochastic occupant behavior. Moreover the case study refers to a building located in warm climate and only cooling conditions are evaluated. Even if no mechanical ventilation, such as ventilating ducts or fans, is employed, we consider the additional use of the AC system in the case that the passive cooling strategies are not enough to guarantee the thermal comfort. The control procedure is implemented by a BEMS that opens/closes windows and blinds on the basis of optimized decision variables. The paper starts by the results of investigations carried out by the authors in previous studies [29,30,31]. In the aforementioned studies, natural ventilation control strategies for passive cooling are proposed and thermal comfort analysis and energy needs for cooling are evaluated only on the most discomfortable room. Moreover, the occupant behavior impacting the control decision is evaluated in a deterministic way by predefined schedules. Indeed, the understanding of occupant behavior in buildings results often simplified, leading to inaccurate expectations of building energy performance. The human dimension, especially regarding the occupant interaction with the building-HVAC system, is often neglected. In most cases, it causes a significant discrepancy between the expected use of energy and the real energy consumptions in buildings.

In this context, one of the contributions of this work is to consider and simulate the human behavior in buildings as a stochastic phenomenon that has a certain probability of occurrence depending on specific conditions. In particular, the occupant behavior is evaluated through three possible actions concerning the opening/closing of windows and blinds and the switching on/off the AC system. Each of the considered action can occur with a specific probability that depends on the environmental conditions. As far as we know, this is the first time that the passive cooling strategies are analyzed also considering the impact of the human stochastic actions for controlling windows, blinds and AC system that are modeled and integrated in a complex building co-simulation architecture implemented by different tools.

Then, the thermal comfort is evaluated by the Long-term Percentage of Dissatisfied (LPD) index defined in [32,33] and the occupant behaviors are modeled by a stochastic-AB approach.

Comparing the methods presented in the related literature to design BEMS [18,20,21,22,34,35,36], we point out that generally the BEMS aims to minimize the energy needs with low attention on occupants comfort and interaction. In particular, the novelty of this paper can be summarized as follows:

• With particular reference to the summer season, an intelligent BEMS is designed in order to minimize indoor thermal discomfort and energy needs using passive cooling strategies such as natural ventilation and solar shading, through windows and blinds opening/closing.
• The control actions are determined by an optimization procedure based on a co-simulation architecture that integrates optimization tools, building, HVAC, air flows and day-lighting simulation models and occupant interactions.
• The occupant behaviors are modeled and simulated by a stochastic-AB approach that combines for the first time the stochastic control actions of windows, blinds and AC system implementing these actions in a building co-simulation architecture.

The rest of the paper is organized as follows. Section 2 introduces the building energy and thermal management problem and Section 3 describes the Co-Simulation architecture. In addition, Section 4 presents the occupant behavior model and Section 5 proposes the BEMS control strategy. In Section 6 the case study and the simulation results are presented and Section 7 reports conclusions and future perspectives.

2. The Building Energy and Thermal Management Problem

Modern buildings are facing the challenge to become smart buildings, where intelligent control systems needs to interact with occupants and to adapt to their needs in order to guarantee the comfort, minimizing the energy consumption.

In particular, thermal and visual comfort are very important for building occupants. In this context, this paper aims at designing a management architecture to deal with stochastic occupant behavior in buildings, optimizing BEMS control rules in order to reduce thermal discomfort conditions and minimizing the use of energy consuming systems such as HVAC.

To this purpose, the proposed architecture should include a resilient and intelligent BEMS able to manage the comfort of the users, according to the adaptive thermal comfort theory, by favouring the use of passive solutions [23].

In this work, the management architecture takes into account the occupant interactions with the building-HVAC system in an AB approach. In detail, the agent (i.e., the occupant) can autonomously open/close windows and solar shading systems and activate the AC for cooling (no interaction among agents is considered).

In the stochastic AB approach, the interactions of a single autonomous agent with the building system are driven by the thermal stimuli and based on the adaptive thermal comfort theory [23]. Indoor and outdoor temperatures are considered as driven factors, although there are other parameters like $C{O}_2$ concentration, wind speed and direction, RH and rainfall that influence the occupant behavior in a building [8,10,37].

On the other hand, the BEMS is designed to optimize the natural ventilation and solar radiation control, managing the interactions with the users and avoiding conflicts. In particular, BEMS control logics are designed to minimize thermal discomfort, by interacting with an optimizer. The building energy and thermal performances are evaluated on the basis of the LPD index [32,33]. We assume the so-called “adaptive approach” [23] to evalutate the thermal comfort conditions in buildings, which states that “if a change occurs such as to produce discomfort, people react in ways which tend to restore their comfort”. Recent studies [38,39] highlighted that in mixed-mode buildings the adaptive comfort theory fits better than the static theory (based on PMV and PPD indices) when the inhabitants use AC only in peak conditions, i.e., the natural ventilation does not guarantee the thermal comfort. In particular, the LPD index assumes real values in the range $[0,1]$ and quantifies predicted thermal discomfort in a specified time period in the building rooms/zones, according to the following equation:

$$LPD=\frac{{\sum }_{t=1}^{\theta }{\sum }_{z=1}^Z{r}_z\ast L{D}_z}{{\sum }_{t=1}^{\theta }{\sum }_{z=1}^Z{r}_z}$$

(1)

where

• t is the time step of the considered time period;
• $\theta$ is the last time step of the considered time period;
• z is the generic zone of the building;
• Z is the total number of zones;
• $r_z$ is the occupancy rate of zone z at time t;
• $L{D}_z$ is the Likelihood of Dissatisfied (LD) inside zone z at time t.

It is remarked that $LPD=1$ means maximum discomfort, $LPD=0$ means no discomfort.

The $LD$ is an analytical function that estimates “the severity of the deviations from the thermal comfort conditions, given certain outdoor and indoor conditions at specified time and space location” [32]. The LD index is computed as follows:

$$L{D}_z=\frac{e^{0.008\ast \Delta T^2+0.406\ast \Delta T-3.050}}{1+e^{0.008\ast \Delta T^2+0.406\ast \Delta T-3.050}}$$

(2)

where $\Delta T=T_{in}-T_c$ is the absolute value of the difference between the indoor operative temperature and the optimal comfort temperature calculated accordingly to EN 16798, at time t [23].

3. The Co-Simulation Architecture

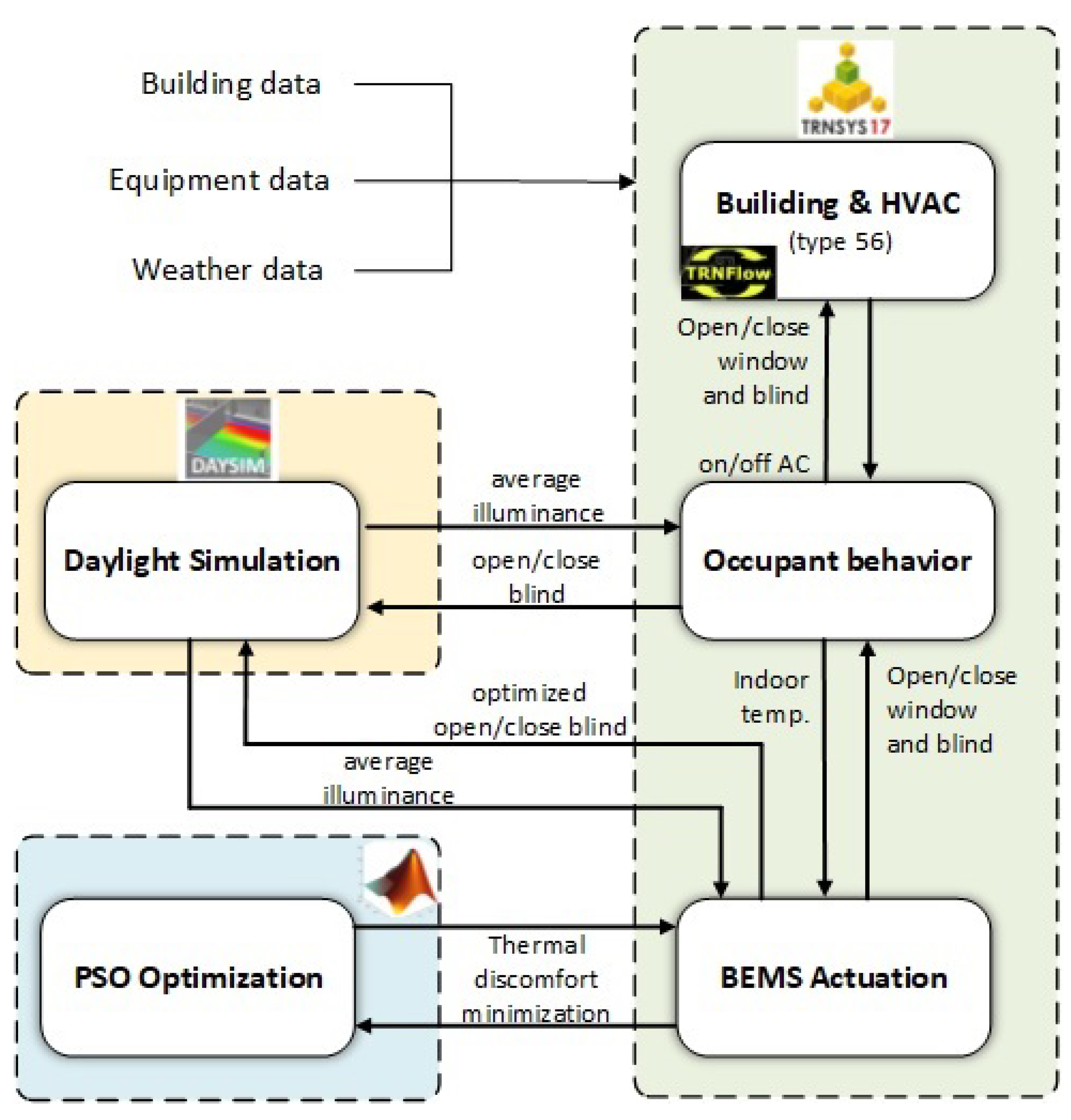
The proposed co-simulation architecture is shown in Figure 1. Five main model components, realized by means of different tools, and their interactions are depicted:

• the building and HVAC model that includes the air flow network (TRNSYS, Type 56), [40];
• the day-lighting model (DAYSIM);
• the Particle Swarm Optimization (PSO) module (MATLAB);
• the BEMS actuation module (TRNSYS);
• the occupant behavior model (TRNSYS).

In particular, as it is shown in Figure 1, the building-HVAC system includes all the building and HVAC features. It is realized by TRNSYS v.17, which is a tool for simulating the energy flows in buildings, taking into account the weather and indoor conditions, the indoor loads and the HVAC systems.

TRNSYS is based on an architecture that is modular and flexible and the Dynamic-Link Library (DLL) allows the creation of new component models. In particular, TRNSYS is composed by two parts: (1) the engine (kernel), able to process the input data and files, simulate the system, determine the system convergence, and plot the variables; (2) an extensive library that includes the components commonly found in electric and thermal systems, and other routines to manage weather and time-dependent data.

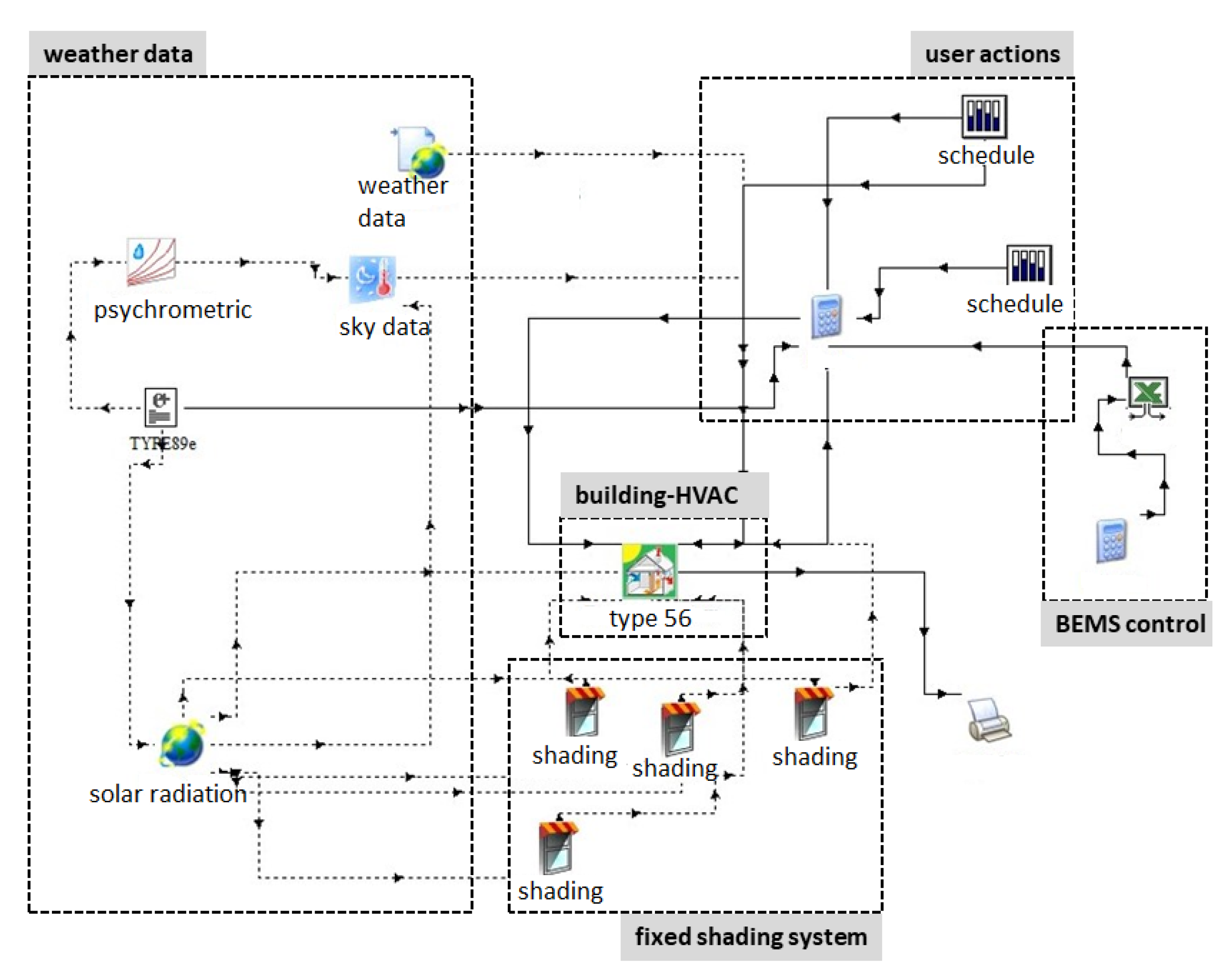
The graphic user interface is Simulation Studio, where building envelope and HVAC components can be used to model the system. Figure 2 depicts the building-HVAC integrated system. The type 56 block integrates the building model and the TRNFLOW tool that is used to provide the multi-zone air flow model. Furthermore, complex computations are possible in TRNSYS thanks to the calculator blocks.

Moreover, with TRNSYS is possible to simulate the occupant behavior i.e., manually closing/opening the windows and the blinds and activating the AC system. Notably, the outdoor and indoor air temperatures affect the occupant behavior in buildings: the individuals turn the HVAC on/off, open/close windows and open/close blinds depending on the outdoor and indoor temperatures. In addition, the BEMS module is activated according to indoor temperature and interacts with an optimization module that minimizes the LPD index. It is remarked that, in this paper, the BEMS action is auxiliary and the humans act independently based on the personal comfort sensation.

The optimization module implements the Particle Swarm Optimization (PSO) algorithm [41,42]. The PSO is a metaheuristic algorithm based on the simulation of the birds flocking behavior. With respect to other evolutionary algorithms, the PSO algorithm is preferrable for the following reasons: it is efficient, robust, proper to handle non-linear problems and generally needs less function evaluations than genetic algorithms. At the same time, the PSO leads to better results than other comparable algorithms or at least to results of the same quality. In the PSO the particles are placed in the search space and are candidate solutions with respect to the optimization problem. More in detail, in the swarm, each particle is composed of three vectors of dimension D (search space dimension): The current position $x_i$, the previous best position $p_i$, and the velocity $v_i$. Each particle of the swarm evaluates the objective function at its current location $x_i$ as a possible solution of the problem. If $x_i$ improves the previous positions, according to the objective function evaluation, then the coordinates of $x_i$ are stored in the vector $p_i$. Moreover, the resulting best function is stored in the variable $pbes{t}_i$, for comparison on later iterations. Therefore, each particle has the objective of finding better positions and updating the vectors $p_i$ and $pbes{t}_i$, accordingly. Afterwards, the PSO solve Equations (3) and (4) to iteratively update the velocity $v_i$ of each particle and determines the new positions $x{p}_i$, also based on the best global location ($gbest$):

$$v_i(k+1)=w{v}_i\left(k\right)+c_1{r}_1^{\left(k\right)}[pbes{t}_i\left(k\right)-x{p}_i\left(k\right)]+c_2{r}_2^{\left(k\right)}[gbest\left(k\right)-x{p}_i\left(k\right)]$$

(3)

$$x{p}_i(k+1)=x{p}_i\left(k\right)+v_i(k+1)$$

(4)

where w is the inertia weight, k is the iteration number, $c_1$ and $c_2$ are the cognitive and social weight, respectively, $r_1$ and $r_2$ are vectors of random numbers sampled from a uniform distribution in the range $[0,1]$.

Finally, a day-lighting model is realized by DAYSIM tool to check that indoor average illuminance (a.i.) is higher than the minimum threshold of 200 lux [23].

4. Modeling Occupant Behavior by Stochastic-AB Approach

In this section the occupant behaviors are modelled and evaluated starting from the probability of making actions defined by field studies in the related literature [43,44,45]. In particular, the equation-based modelling approach is used to simulate occupant behaviors in buildings. We consider naturally ventilated buildings where mechanical systems such as ventilating ducts or fans are not used. However, we assume that the AC system is only activated when an auxiliary action is needed in the case of the passive cooling strategies are not enough to guarantee the thermal comfort. More precisely, the implemented occupant behaviors include the following actions:

• opening/closing windows;
• opening/closing blinds;
• tuning on/off the AC.

On the basis of the results in [43,44,45], the occupant behaviors are governed by the following variables:

• $B_1=T_{in}-T_{out}$, difference between indoor temperature and outdoor temperature;
• $B_2=R{H}_{in}$, indoor relative humidity;
• $B_3$, wind speed;
• $B_4$, solar radiation incident on window;
• $B_5$, indoor $C{O}_2$ concentration;
• $B_6$, solar altitude.

The sign of the variables indicates the direction of correlation, positive or negative.

4.1. Window Control by Occupants

We recall that paper [43] is the only study that presents an inhabitant behavior model taking into account several variables that can affect the window operations in living rooms of residential buildings. Here we implement the occupants window control model presented in [43]. In particular, the multivariate logistic regression is deployed to evaluate how the outdoor and indoor variables affect the occupant actions for the windows control. In order to determine the probability for windows opening and closing a set of coefficients are evaluated with different values for the two actions.

Table 1. Coefficients of the multivariate logistic regression model for window human control.

	${\mathit{a}}_{1,\mathit{k}}$	${\mathit{a}}_{2,\mathit{k}}$	${\mathit{a}}_{3,\mathit{k}}$	${\mathit{a}}_{4,\mathit{k}}$	${\mathit{a}}_{5,\mathit{k}}$
win. open. ($k=o$)	7.772	0.048	−0.063	−0.038	0.002
win. clos. ($k=c$)	1.090	−0.031	0.029	−0.459	0.001

shows the coefficients $a_{i,k}$ associated to each variable $B_i$ for $i=1,\cdots ,5$, where $k=o$ refers to windows opening and $k=c$ refers to windows closing. In particular, the probabilities of window opening ($k=o$) or closing ($k=c$), at time t, are obtained by the following logistic regression formula:

$$p_{w,k}=\frac{e^{(a_{1,k}\ast B_1+\cdots +a_{5,k}\ast B_5)}}{1+e^{(a_{1,k}\ast B_1+\cdots +a_{5,k}\ast B_5)}}.$$

(5)

4.2. Blind Control by Occupants

The study of Zhang [44] statistically shows that the solar altitude and radiation are the most influencing factors to predict lowering and/or raising behaviors performed by occupants on blinds. We adopt the Zhang model based on the logit analysis to compute the probability of blind opening and closing actions. In particular, solar altitude and radiation are the two variables that have the strongest correlation with the blind action.

Therefore, the probability for blinds opening and closing are defined and treated separately on the basis of the cited variables. Hence, the probabilities of blind opening ($k=o$) or closing ($k=c$), at time t, on the basis of the solar radiation are obtained by the following logistic regression formula:

$$p_{b1,k}=\frac{e^{(a_{4,k}+b_{4,k}{B}_4)}}{1+e^{(a_{4,k}+b_{4,k}{B}_4)}}.$$

(6)

Analogously, the probabilities of blind opening ($k=o$) or closing ($k=c$), at time t, on the basis of the solar altitude are obtained by:

$$p_{b2,k}=\frac{e^{(a_{6,k}+b_{6,k}{B}_6)}}{1+e^{(a_{6,k}+b_{6,k}{B}_6)}}.$$

(7)

Note that

Table 2. Coefficients of the multivariate logistic regression model for blind human control.

	${\mathit{a}}_{4,\mathit{k}}(\mathit{Std}.\mathit{error})$	${\mathit{b}}_{4,\mathit{k}}(\mathit{Std}.\mathit{error})$	${\mathit{a}}_{6,\mathit{k}}(\mathit{Std}.\mathit{error})$	${\mathit{b}}_{6,\mathit{k}}(\mathit{Std}.\mathit{error})$
blind open.	−3.330 (0.035)	0.003 (0.001)	−3.446 (0.049)	0.019 (0.001)
($k=o$)
blind clos.	−3.170 (0.034)	0.002 (0.001)	−3.424 (0.049)	0.018 (0.001)
($k=c$)

shows the coefficients $a_{4,k},a_{6,k},b_{4,k}$ and $b_{6,k}$ reported in formulas (6) and (7) and the relative standard error values.

4.3. Air Conditioner Activation by Occupants

The AC system is activated by occupants when feeling hot. The stochastic function proposed in [37,45,46] is used to describe the probability of activating AC as a function of indoor air temperature.

It is remarked that when the room is unoccupied, the AC is always off. The probability to turn on/off the AC ($p_{AC}$) depends on the indoor air temperature: The more the indoor air temperature is high, the more the probability to turn on the AC is high. The probability $p_{AC}$ is defined as follows:

$$p_{AC}=1-e^{\frac{-{(T_{in}-T_u)}^8}{L}}$$

(8)

where:

• $T_u$ is the temperature upper bound, assumed equal to the overheating temperature according to EN16798, i.e., $T_u=T_c+3{}^{\circ }\mathrm{C}$; furthermore we set $T_l=T_c-3{}^{\circ }\mathrm{C}$ as lower bound;
• L represents the difference between the upper and lower bounds ($T_u-T_l$), assumed equal to 6, obtained considering the comfort range according to the adaptive thermal comfort theory, i.e., $T_l<T_{in}<T_u$.

4.4. The Occupant Behavior Model

The thermal comfort status of zone z at time t is described by the variable $Y_z\in \{0,1\}$: $Y_z=1$ means that there are thermal discomfort conditions in zone z according to EN 16798, $Y_z=0$ means that the temperature of zone z is comfortable and no action is necessary. More in detail, thermal comfort conditions are defined as follows:

$$Y_z=\left\{\begin{array}{c}1,\mathrm{if}{T}_{in}>T_u\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(9)

Furthermore, if the AC is on, it is assumed that the occupant closes the window to avoid the warm air inlet.

In each room, $T_{in}$ is calculated and if thermal discomfort is detected ($Y_z\left(t\right)=1$), then the occupant can react in different ways operating on windows, blinds and AC system. It is worth noting that there is no a fixed order of occurrence for occupant actions on windows, blinds and AC system. More specifically, the occupant actions will occur according to the steps of Algorithm Algorithm 1 that is executed at each time window of 15 min.

At Step 2 the set of probabilities $S_p=\{p_{w,o},p_{w,c},p_{b1,o},p_{b1,c},p_{b2,o},p_{b2,c},p_{AC}\}$ are computed and a real number $p_r\in [0, 1]$ is generated at random, with uniform probability, at each time step. In order to determine if the occupant actions on windows, blinds and AC take place or not in the next 15 min, the value of $p_r$ is compared to Equation (5), (6) and (8), respectively. Afterwards, at STEP 3 the highest probability $p^{\ast }$ of $S_p$ is selected. In STEPs 4, 5, 6, 7, 8, 9 and 10 Algorithm 1 identifies the highest probability $p^{\ast }$ and verifies that it is greater than the random generated number $p_r$. If it is true, the action associated with the identified probability is performed by the occupant, else no action is taken. Moreover, if the highest probability is $p^{\ast }=p_{AC}$, then at Step 10 $p_{AC}$ is compared with $p_r$: if $p_{AC}\ge p_r$ then the AC is turned on else it is turned off. We point out that each action is performed if it is possible: for instance the window can be opened if it is closed at the beginning of the considered time window. It should be assumed that the aforementioned probabilities of actions by occupants are only possible when there is occupancy in the rooms. If no occupancy is detected, the BEMS optimizes the operation of windows and blinds by maximizing the potential of passive cooling for natural ventilation and solar radiation.

Algorithm 1 Occupant behavior.

5. The BEMS Control Strategy

This section presents the BEMS control strategy that is based on the optimization of windows, blinds and AC activation by minimizing thermal discomfort conditions. Hence, the windows and blinds are opened and closed by the BEMS at suitable time interval, when particular indoor thermal conditions are detected, by avoiding, if it is possible, the activation of the high-consumption AC system.

5.1. Windows Control Strategy

The decision real variables $\delta 1{[}^{\circ }\mathrm{C}]$ and $\delta 2{[}^{\circ }\mathrm{C}]$ are introduced to control the activation of windows in order to minimize thermal discomfort conditions.

In detail, the window opening is defined by the following control variable:

$$x\left(t\right)=\left\{\begin{array}{c}1,\mathrm{if}{T}_{in}>T_c+\delta 1\mathrm{and}{T}_{in}+\delta 2<T_{out}<T_{in}\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

(10)

where $x\left(t\right)=1$ corresponds to windows opening and $x\left(t\right)=0$ means that no action will be done by BEMS. Once the window is open, it will be closed by BEMS when the indoor temperature is lower than $T_l$.

The values of the variables $\delta 1$ and $\delta 2$ are determined by solving the following optimization problem:

$$F_{obj}=mi{n}_{\delta 1,\delta 2}LPD(\delta 1,\delta 2)$$

(11)

with:

• $\delta 1\in \mathbb{R}$ and $\delta 1\in [-10{}^{\circ }\mathrm{C},10{}^{\circ }\mathrm{C}]$;
• $\delta 2\in \mathbb{R}$ and $\delta 2\in [-10{}^{\circ }\mathrm{C},0{}^{\circ }\mathrm{C}]$;

The PSO algorithm is applied to minimize the objective function LPD($\delta 1$, $\delta 2$). The current position of particles is a two-elements vector $x{p}_i\left(k\right)={\left[\delta 1\left(k\right)\delta 2\left(k\right)\right]}^T$ formed by the values that $\delta 1$ and $\delta 2$ assume at the iteration k. The range values of $\delta 1$ and $\delta 2$ are defined so that indoor temperature is in the comfort range at time t.

Several studies focused on the convergence analysis of the classic PSO and its variants. In particular, paper [47] suggests to set the PSO coefficients as $w=0.7298$, $c_1=c_2=1.49618$ in order to lead the PSO algorithm to convergence behavior. Moreover, according to [48,49,50], these settings ensure the best tradeoff between exploration and exploitation and a good convergence rate. Therefore, it is a common choice to set the three aforementioned parameters in order to have at least local convergence [48]. In addition, it is proved that small population size should be avoided and setting the size of the population equal to about 20 particles prevent stagnation of the PSO algorithm with each of the test functions [47]. Hence, after an experimental simulation campaign, we come to the conclusion that a population of 20 particles provides an effective convergence in the considered optimization problem.

Moreover, we performed a large set of tests to determine the stop criterion based on the number of $M\in {\mathbb{N}}^{+}$ consecutive iterations that provide the same value of the best location $g_{best}$. The results show that after $M=5$ consecutive iterations the objective function $F_{obj}=g_{best}$ reaches a stationary value (optimal values of [$\delta 1,\delta 2$]).

5.2. Blinds Control Strategy

The second control action of the BEMS is the blinds control that is defined by the following real control variable:

$$y\left(t\right)=\left\{\begin{array}{c}\beta ,\mathrm{if}{T}_{in}>T_c+\delta 1\mathrm{and}{T}_{in}+\delta 2<T_{out}<T_{in}\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

(12)

where $\beta =\{0.25,0.5,0.75,1\}$ is the shading factor representing the ratio between the shaded windowed area and the windowed area and $\beta =1$ means total shading. If conditions (12) are not satisfied, then $y\left(t\right)=0$ and no action will be done by the BEMS. This control on the blinds can be activated only during the daytime hours (from 6 a.m. to 5 p.m.) and when the incident solar radiation is higher than 150 W/m${}^2$.

Moreover, the shading activation and $\beta$ value are determined by applying Algorithm 2 that is described in the following. At Step 2 the thermal comfort conditions are checked and if thermal discomfort is detected then the total shading is applied $y\left(t\right)=1$ by Step 3, otherwise Algorithm 2 goes to an end. At Step 4, the a.i. level is checked in order to regulate the value of $\beta$: if the minimum a.i. level is not guaranteed and $y\left(t\right)\ne 0$, Algorithm 2 goes to Step 5, otherwise ends. Afterwards, at Step 5, $y\left(t\right)$ is decreased by 0.25, to decrease the shading level of $25\%$. Finally, Algorithm 2 goes back to Step 4 until the condition of minimum a.i. level is not met and $y\left(t\right)\ne 0$, otherwise ends.

Algorithm 2 Blinds control actions.

5.3. BEMS Control Actions

Table 3. Control logics of window, blind and Air Conditioning (AC) applied by Building Energy Management System (BEMS) if occupancy is detected.

Status		Condition
		$T_{in}\left(t\right)>T_c\left(t\right)+\delta 1$
1. window	$x\left(t\right)=1$	$T_{in}\left(t\right)+\delta 2<T_{out}\left(t\right)<T_{in}\left(t\right)$
	$x\left(t\right)=0$	otherwise
		$T_{in}\left(t\right)>T_c\left(t\right)+\delta 1$
2. blind	$y\left(t\right)=\beta$	$T_{in}\left(t\right)+\delta 2<T_{out}\left(t\right)<T_{in}\left(t\right)$
	$y\left(t\right)=0$	otherwise
3. AC	$z\left(t\right)=1$	$T_{in}\left(t\right)>T_u\left(t\right)$
	$z\left(t\right)=0$	otherwise

reports the BEMS control actions of windows and blinds. More precisely, the PSO module receives the indoor temperatures from the BEMS and computes the values of $\delta 1$ and $\delta 2$ to minimize the LPD index (see Figure 3). Such values are then sent back to the BEMS that implements the control strategy of windows and blinds (10) and (12). Iteratively, the PSO algorithm evaluates the two decision variables $\delta 1$ and $\delta 2$. The control of AC system is defined by the following control variable:

$$z\left(t\right)=\left\{\begin{array}{c}1,\mathrm{if}{T}_{in}>T_u\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

(13)

where $z\left(t\right)=1$ corresponds to AC activation and $z\left(t\right)=0$ means that no action will be done by the BEMS. In detail, if thermal discomfort is detected, then the BEMS operates on windows, blinds and AC in function of the room occupancy, as described in Table 3 and

Table 4. Control logics of window and blind by BEMS if no occupancy is detected.

Status		Condition
		$T_{in}\left(t\right)>T_c\left(t\right)+\delta 1$
1. blind	$y\left(t\right)=1$	$T_{in}\left(t\right)+\delta 2<T_{out}\left(t\right)<T_{in}\left(t\right)$
	$y\left(t\right)=0$	otherwise
		$T_{in}\left(t\right)>T_c\left(t\right)+\delta 1$
2. window	$x\left(t\right)=1$	$T_{in}\left(t\right)+\delta 2<T_{out}\left(t\right)<T_{in}\left(t\right)$
	$x\left(t\right)=0$	otherwise

.

More precisely, if occupancy is detected, the BEMS operates at first on windows and then on blinds to emphasize the free cooling positive effects (see Table 3). If thermal discomfort conditions are still detected, it turns on the AC. When the BEMS activates the AC, the windows are automatically closed to avoid energy wastes. If no occupancy is detected (see Table 4), the BEMS operates at first on blinds by totally shading the window to avoid solar radiation inlet and then open the windows. In this case, no action will be performed on the AC as no occupant is present.

5.4. Occupant-BEMS Interaction

Finally, the control system procedure is specified as depicted in Figure 3, and the interaction among occupant and BEMS is described and modeled by a flow-chart diagram (see Figure 4). In presence of thermal discomfort situations according to Table 3, the following two scenarios (named a and b) are possible (see Figure 4).

(a) If room occupancy is detected, two cases can occurr: (i) the occupant agrees with the BEMS activation, (ii) the occupant does not agree with the BEMS activation. To simulate this behavior, we assume that the occupant agrees if the LPD index is greater than $0.4$. The value LPD = 0.4 comes out from the analysis of simulations performed to evaluate the interaction human–BEMS. In particular, we perform a simulation campaign, considering different values of the LPD index in each simulation: LPD = 0.2, LPD = 0.4, LPD = 0.6 and LPD = 0.8. It results that if LPD > 0.4, then the user is not able to maintain the comfort and, therefore, the BEMS action is needed and the user consensus is given to the BEMS. The BEMS starts the automatic procedure and interacts with PSO module to optimize $\delta 1$ and $\delta 2$. After that, the BEMS commands the Building-HVAC system to open/close windows and blinds to minimize the thermal discomfort, guaranteeing visual comfort. If thermal discomfort is still detected, the BEMS activates the AC. On the contrary, the BEMS waits for 15 min and, if thermal discomfort is still detected, the process is repeated.

(b) If no occupancy is detected, the BEMS directly starts the automatic procedure by only implementing passive strategies (if AC is on, it turned off by the BEMS; if the AC is off no action is taken).

In consequence of occupant and BEMS actions, indoor environmental conditions change and are checked iteratively until comfort conditions are satisfied.

6. Case Study

This section presents a case study to show the effectiveness of the proposed architecture and strategies applied to a residential building. In particular, several simulations have been performed on a 12 GB RAM, i5 core CPU machine equipped with all the needed tools.

6.1. Building Description and Usage Schedules Specification

The building is located in Southern Italy (Bari—Italy, ${41.09}^{\circ }\mathrm{N},{16.44}^{\circ }\mathrm{E},6\mathrm{m}$ above sea level). It has a surface area of about 100 m${}^2$ and is situated at the intermediate floor (Figure 5). Figure 6 shows the three dimensional model of the building. The main thermal characteristics of the building opaque envelope and of the windows are indicated in

Table 5. Thermal characteristics of building envelope.

	U-Value	Surface Mass	Decrement	Thermal	Periodic
	(W/m${}^2$K)	(kg/m${}^2$)	Factor	Lag (h)	Trasmit.
					(W/m${}^2$K)
Ceiling	0.47	382	0.1	12	0.033
floor
External	0.31	296	0.08	16	0.026
wall
Partition	0.51	311	0.1	13	0.034
wall

and

Table 6. Thermal and optical properties of windows.

Glass Type	U-Value	Solar Heat	Visual
	(W/m${}^2$K)	Gain Coeff.	Transmission
Window	1.7	0.62	0.75
(insul.glass low-Ar)

, respectively. These data are taken from the construction documents of the building. We consider a tilt-turn window, with possible automated bottom-hinged opening. Moreover, automated PVC roller shutters are considered as blinds.

The indoor thermal loads are scheduled as follows: artificial lighting activation time (4 p.m.–8 p.m.); electric appliances activation time (9 a.m.–1 p.m.; 3 p.m.– 8 p.m.). In addition,

Table 7. Scheduled daily occupancy of each room.

Room	Occupacy Daily Time Slots
Room 1-2-3	9 a.m.–1 p.m.; 3 p.m.–8 p.m.
Dining room	7 a.m.–9 a.m.; 1 p.m.–3 p.m.; 8 p.m.–10 p.m.
Living room	9 a.m.–10 a.m.; 4 p.m.–5 p.m.; 9 p.m.–12 a.m.

shows the scheduled daily occupancy of each room, in function of the forecasted occupancy. It is remarked that the proposed schedules are active from Monday to Friday. Moreover, an activity level of 70 W/m${}^2$ that is a metabolic activity of 1.2 met is set as occupancy gains, according to [51].

6.2. Simulated Cases

This section presents different simulation scenarios in order to assess the benefits of the designed architecture on the building thermal comfort and energy consumption by applying the proposed control strategy.

In particular, four cases are considered, where the occupant behaviors models are evaluated by stochastic-AB approach. More in detail, the four cases are specified as follows:

• Case 1: The AC is off, BEMS is not activated and only the occupant can change the status of windows and blinds, as described in Section 4;
• Case 2: The AC is off and BEMS is activated for controlling windows and blinds, and the interaction occupant-BEMS is managed according to Section 5.4;
• Case 3: The AC can be turned on, the BEMS is not activated and only the occupant can change the status of windows, blinds and AC, as described in Section 4;
• Case 4: The AC can be turned on and BEMS is activated for controlling windows, blinds and AC, as described in Section 5. The interaction occupant-BEMS is managed according to the procedure of Section 5.4.

Table 8. Simulated Cases.

Case	AC	BEMS			OCCUPANT
		Window	Blind	AC	Window	Blind	AC
Case 1	N	N	N	N	Y	Y	N
Case 2	N	Y	Y	N	Y	Y	N
Case 3	Y	N	N	N	Y	Y	Y
Case 4	Y	Y	Y	Y	Y	Y	Y

shows the four evaluated cases by summarizing the considered assumptions. In particular, “Y” (i.e., Yes) and “N” (i.e., not) terms identify the actions that can or can not be performed by occupants or BEMS.

More in detail, in Cases 1 and 2, where the AC system is off, the thermal comfort is evaluated by computing the LPD index in order to assess the benefits of BEMS control logics. In Case 3 and Case 4, where the AC system can be activated by the occupants (Case 3) or by the optimized BEMS control action (Case 4), the energy consumptions for cooling are evaluated. Therefore, since occupant models are stochastic and depend on random numbers, a simulation campaign is performed to take into account different occupant actions and the BEMS control. In particular, in Case 1 and Case 3, the occupant behavior is simulated in the period June–July for 35 times (i.e., the results do not change significantly when a number of simulations greater than 35 is chosen). In Case 2, for each of the 35 simulated occupant behaviors we perform a set of 40 simulations to evaluate the BEMS control action on the indoor thermal condition. Then, during the 40 simulations, the values of $\delta 1$ and $\delta 2$ can vary according to the PSO optimization, while the occupant behavior does not change. The results reported for Case 2 are obtained by applying the optimal pair ($\delta 1$,$\delta 2$) provided by the 40 simulations. In Case 4, by considering the 35 optimal values ($\delta 1$,$\delta 2$) obtained in Case 2, we perform 35 simulations to evaluate the AC energy consumption in the period June–July.

6.3. Results

The stocahistc occupant behaviors models on window, blind and AC is showed in Figure 7, Figure 8 and Figure 9. In particular, the statistical distribution of the aforementioned actions are depicted. The red lines respresent the trend lines of each probability distributions. In particular, the following outcomes are pointed out:

• the probability of window opening increases for higher values of the difference between the indoor and outdoor temperature (Figure 7);
• the probability of blind closing increases for higher solar radiation values (Figure 8);
• the probability of AC activation increases for higher values of indoor temperatures with respect to those for window opening and blind closing. In detail, the window opening and blind closing actions are possible if $T_{in}>20{}^{\circ }\mathrm{C}$, while the AC is activated if $T_{in}>26{}^{\circ }\mathrm{C}$ (Figure 9).

By the analysis of the LPD index in Cases 1 and 2 of Figure 10, a significant reduction of total discomfort conditions results from Case 1 to Case 2. In Case 1, the LPD index varies from $0.41$ to $0.55$, while in Case 2 it is between $0.25$ and $0.38$ due to the BEMS actions. Note that the average LPD index value decreases of about $33\%$ in Case 2. In particular, the LPD index values of Case 2 are obtained by the PSO optimal values ($\delta 1$, $\delta 2$) for each of the 35 simulations. As example, referring to simulation 1 of Figure 10, Figure 11 shows how the LPD index varies in Case 2 as consequence of the optimization procedure: The optimal values ($\delta 1$, $\delta 2$) that determine the minimum values of the LPD index are obtained at iterations 22, 25, 30, 32, 36–40. In simulation 1 of Case 2 the optimal values of $\delta 1$ and $\delta 2$ that minimize the thermal discomfort conditions are the following: $\delta 1=-2.37{}^{\circ }\mathrm{C}$ and $\delta 2=-5.75{}^{\circ }\mathrm{C}$. In order to compare the effects of the actions performed by the occupants and/or by BEMS on LPD index, Figure 12 and Figure 13 show the number of actions performed for the windows opening and the blinds closing, respectively, by the occupants in Case 1 and both by occupants and by BEMS in Case 2. It results that the BEMS improves the thermal comfort by allowing the reduction of the occupant actions that can negatively affect the indoor conditions. The BEMS actions replace the actions made by the occupants, and comparing Cases 1 and 2, a significant reduction of actions by occupant occurs.

In accordance with thermal comfort analysis outcomes, the BEMS control allows a significant decreasing of the energy needs for cooling: in Cases 3 and 4, the average energy for cooling is about 55 kWh/m${}^2$ and 32 kWh/m${}^2$, respectively. In particular, as shown in Figure 14 an optimal pair ($\delta 1$,$\delta 2$) corresponds to each of the 35 simulations in Case 4. Therefore, by comparing Cases 3 and 4 results, the proposed passive strategies for natural ventilation and solar shading lead to an average energy consumption reduction by $42\%$.

Furthermore, Figure 15 show the number of AC activation by the occupant and the BEMS in the simulations. In particular, the proposed BEMS allows a significant reduction of the occupant actions, by optimizing the activation times. In particular, it results how the BEMS replaces the user actions and the possible negative effects of occupant. The obtained results demonstrate the validity of the proposed co-simulation architecture that is able to take into account the unpredictable occupant behaviors in different operating conditions. Indeed the occupant behaviors actions can be compensated by the control actions of the intelligent BEMS allowing at significantly reduce thermal discomfort and the use of active cooling system.

6.4. Discussion

Towards the NZEB standard, this work focuses on resilient and intelligent BEMSs able to adapt to the human action randomness and maintain high level of thermal and energy performance. In order to better evaluate the occupant behavior in buildings, and thus its implication on energy and thermal performance, an intelligent BEMS is proposed to maintain the energy performance at the desired level despite the different operations by occupants, climate and environmental conditions. Aiming at energy conservation and thermal comfort, the paper analyzes the occupants role since it is a key issue for building-HVAC design optimization, performance evaluation, and building energy simulation.

In particular, differently from the work [52] that analyzes five different climate conditions, in this paper the performed analysis focuses on summer season where there is high interaction of occupants with the building components (adjusting windows, blinds status, thermostat set-point). On the contrary, in winter season, typically the occupants have less interaction with the building components [53].

In addition, while [52] evaluates the influence of solar reflectance and renewable energies on residential heating and cooling demand in sustainable architecture, this work proposes the application of passive cooling strategies via an intelligent BEMS by taking into account the stochastic occupant behavior. In particular, the stochastic approach allows evaluating the effects of the occupants interaction with the building. As a result, it is necessary to integrate the building automation systems to balance the effect of the non-optimized occupant actions, minimizing the use of high-consumption systems.

Moreover, while [54] adopt only Matlab Simulink to design the building thermal model and a BEMS aims at minimizing the energy costs and reducing the peak load by adjusting the operation time of the HVAC system, we propose a complex co-simulation architecture integrating three different tools: TRNSYS that is suitable to accurately model the building, the envelope and thermodynamical systems including the HVAC system; MATLAB to implement the optimal BEMS control actions on passive systems to guarantee the thermal comfort; DAYSIM for the day-lighting modeling. In addition, the authors in [54] do not investigate the use of passive cooling strategies as well as in [35,55]. In [55], they study how the policy measures can improve the building-level energy efficiency compared to a smart BEMS with dynamic temperature set points. Among the policy measures no passive strategies for heating/cooling are analyzed for thermal comfort. In [35], a Multiple Power-Based Building Energy Management System (MPBEMS) is proposed for the energy management, by controlling the power consumption equipment of the building.

As remarked in [56], data analytics and simulation need to be integrated for improving the applicability of data analytics and simulation tools. To this scope, in this paper, starting from the real studies of data analytics conducted in [43,44,45], we integrate these data in the modeling of occupant behaviors to increase the accuracy, the implications for energy performance and reduce the limited understanding and inappropriate over-simplification of the occupant behaviors models. Finally, compared to [43,44,45] that take into account only single occupant action for window, blind and AC control, we simulate and analyze the combination of the three actions.

A comparison of the results obtained in this paper can be done with the works of [30,31]. In these studies, natural ventilation control strategies for passive cooling are proposed for thermal comfort and are evaluated without taking into account the unpredictibility of occupant behaviors and they are tested only on the most discomfortable room. In this paper, by considering the stochastic occupant behaviors, we obtained different results by the optimization algorithm leading to an improved BEMS control action that significantly reduces the discomfort conditions.

7. Conclusions

This paper proposes a co-simulation architecture that integrates an intelligent BEMS to optimize the control of windows and blinds actions for guaranteeing thermal comfort through passive strategies. The proposed co-simulation architecture is based on five main components, implemented through different tools. The building, the HVAC system, the BEMS and the occupant behavior are modelled by TRNSYS. The day-lighting model is evaluated by DAYSIM and the optimization strategy based on PSO is performed in MATLAB.

More specifically, the main outcomes of this work can be resumed as follows: (i) the proposed co-simulation architecture allows a consistent model of the building energy and thermal characteristics, taking into account the occupant-BEMS interaction; (ii) the designed approach evaluates the stochastic effect of the occupant actions on building energy and thermal performances; (iii) the application of the optimized passive strategies, i.e., natural ventilation and solar shading, allows a significant reduction of energy consumption for cooling and at the same time guarantees high levels of thermal comfort; (iv) the optimization strategies determine the optimal time intervals to close and open windows and blinds with the aim of minimizing thermal discomfort conditions; (v) the BEMS action does not conflict with human actions and the interaction human–BEMS shows that the occupant actions on the buildings components are significantly reduced. It is demonstrated that the application of suitable control logics increases the potentialities of passive cooling in buildings, by integrating or replacing the conventional efficiency strategies.

Future developments will concern the modeling of multioccupant behaviors based on complex agent-based oriented approach, by assuming different stimuli as driven forces for occupant actions, considering the interaction of agents. In order to enhance high performance of future buildings (nZEB), the BEMS control rules will be designed according to the Internet of Energy paradigm by proposing a more complex architecture that can handle real components. This new architecture will be tested in an equipped dwelling aiming at minimizing energy consumption and guaranteeing adequate comfort conditions, at the same time.