Downward Annular Flow of Air–Oil–Water Mixture in a Vertical Pipe
Abstract
:1. Introduction
| No. | Author | Mixture Components | Channel Diameter | Oil Properties | Scope of Experiment | |
|---|---|---|---|---|---|---|
| Density | Viscosity | |||||
| mm | kg/m3 | mPas | ||||
| 1 | Poettmann et al. [13] (1952) | paraffin–water–air | boreholes | - | - | pressure drop |
| 2 | Tek [14] (1961) | paraffin–water–air | borehole | - | - | pressure drop, void fraction |
| 3 | Foreman [15] (1975) | paraffin–water–air | 19 | 810 | 1.5 | void fraction |
| 4 | Shean [16] (1976) | oil–water–air | 19 | 889 | 71.8 | flow patterns, void fraction, pressure drop |
| 5 | Pleshko et al. [17] (1990) | oil–water–air | 51 | 814 | 7.48 | flow patterns, gas void fraction, frictional pressure drops |
| 6 | Woods et al. [18] (1998) | oil–water–air | 26 | 829 | 12 | flow patterns, void fraction, pressure drop |
| 7 | Spedding et al. [19] (2000) | oil–water–air | 26 | 829 | 11 | flow patterns, void fraction, pressure drop |
| 8 | Oddie et al. [20] (2003) | paraffin–water–nitrogen | 152 | 810 | 1.5 | flow patterns, void fraction |
| 9 | Huang et al. [30] (2003) | oil–water–air | 40 | 870 | 117 | flow patterns for pipe inclination of −30° (upward and downward) |
| 10 | Shi et al. [21] (2004) | paraffin–water–nitrogen | 15 | 810 | 1.5 | void fraction |
| 11 | Descamps et al. [22] (2006) | oil–water–air | 82.8 | 830 | 7.5 | effect of gas injection on critical concentration of oil and water at phase inversion point, pressure drop |
| 12 | Nowak [24] (2007) | oil–water–air | 30 | 860 | 20 | flow patterns, void fraction, pressure drop |
| 13 | Bannwart et al. [29] (2009) | oil–water–air | 28.4 | 970 | 3.4 | flow patterns, pressure drop |
| 14 | Wang et al. [28] (2012) | oil–water–natural gas | 52.5 | - | 150–570 | flow patterns, gas void fraction, frictional pressure drop |
| 15 | Brandt [32] (2015) | oil–water–air | 12.5 | 860–880 | 16–2000 | flow patterns, void fraction, liquid film thickness |
| 16 | Pietrzak et al. [26] (2017) | oil–water–air | 30 | 856 | 29 | flow patterns, void fraction of phases, pressure drop |
| 17 | Hanafizadeh et al. [31] (2017) | oil–water–air | 20 | 840 | 4.5 | flow patterns for pipe inclination of −45° to +45° (upward and downward) |
| 18 | Colmanetti et al. [27] (2018) | oil–water–air | 50, 95 | 900 | 70–280 | flow patterns, pressure drop |
2. Materials and Methods
Scope of Experiment
3. Results and Discussion
3.1. Flow Patterns
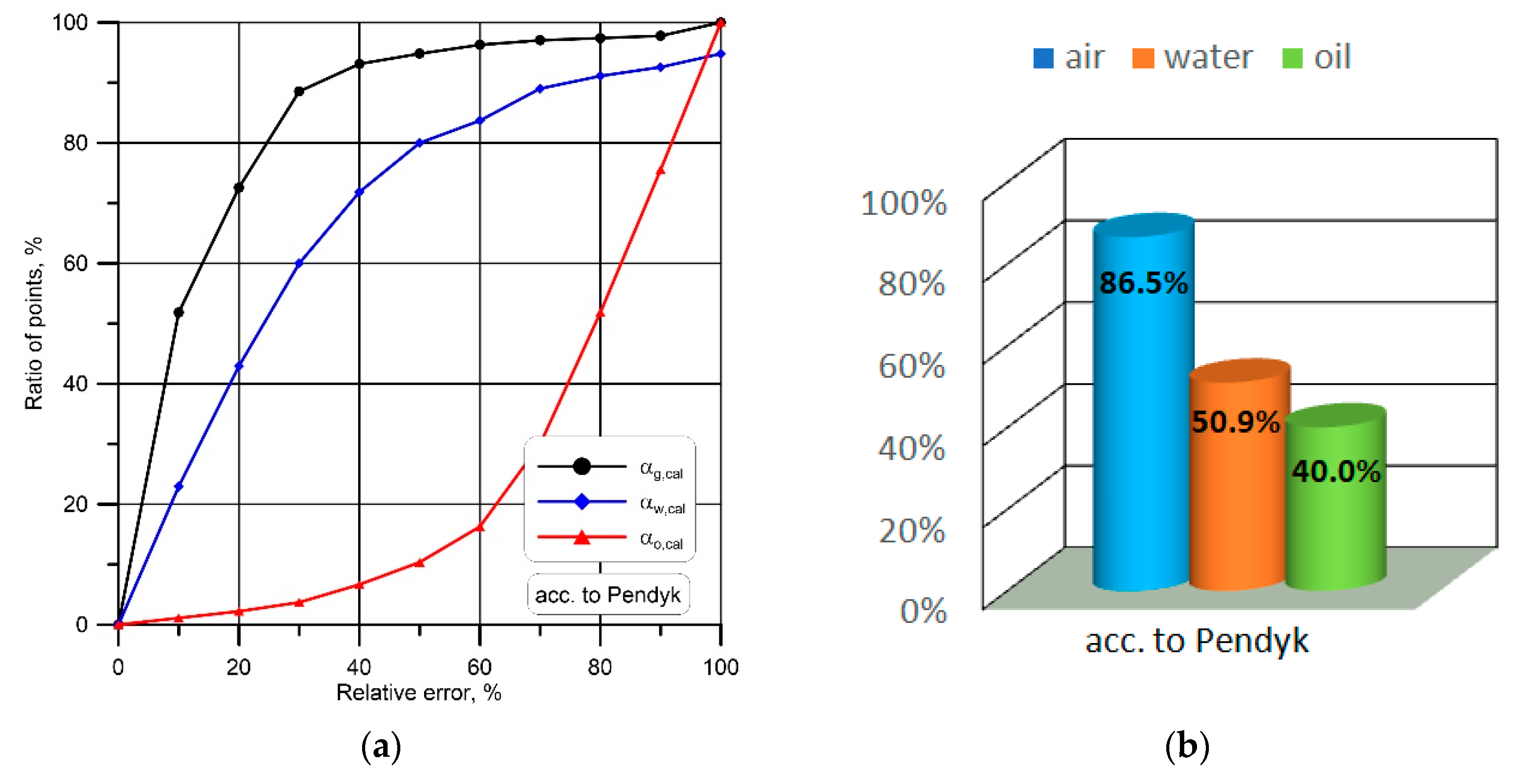
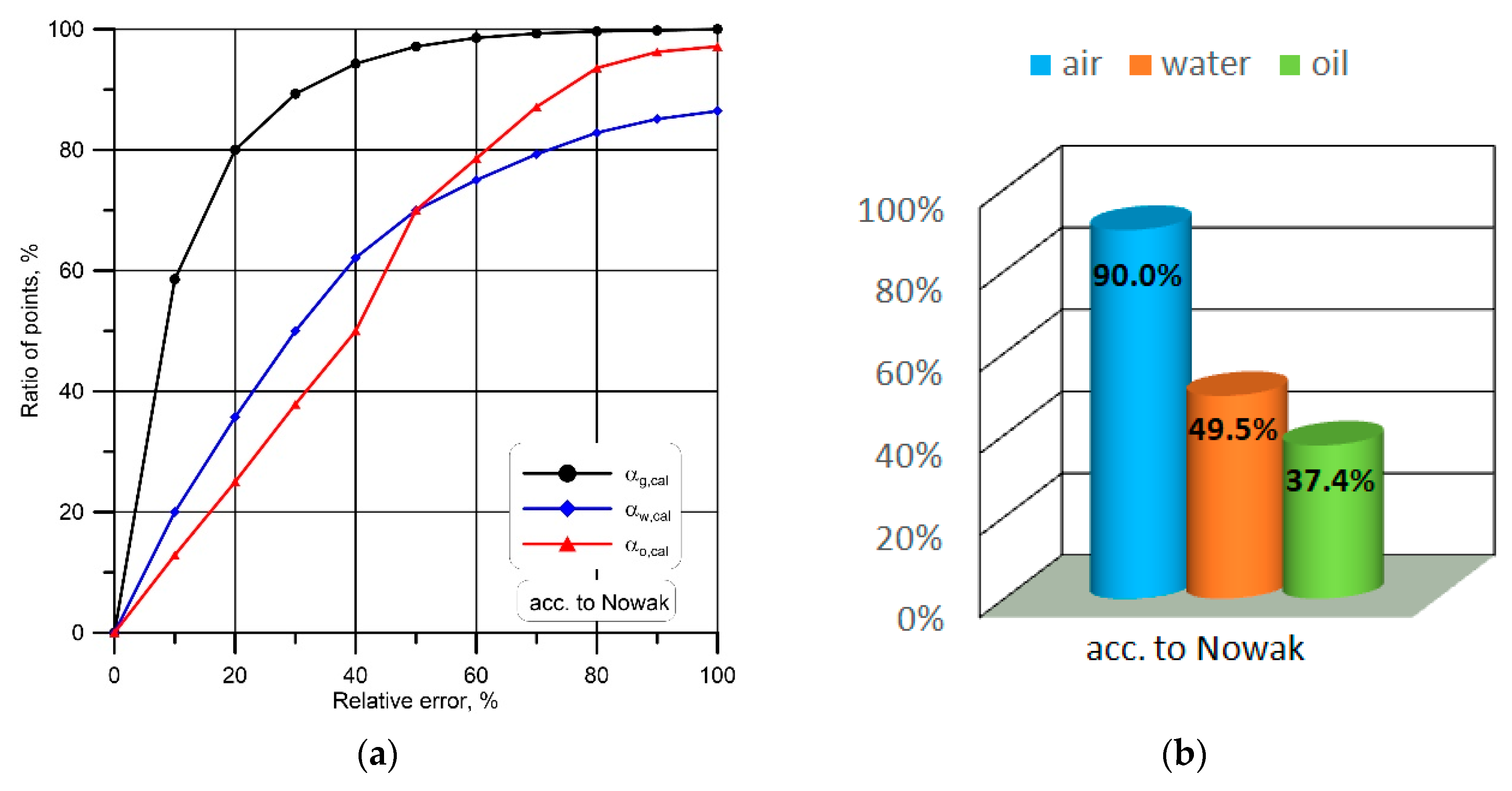
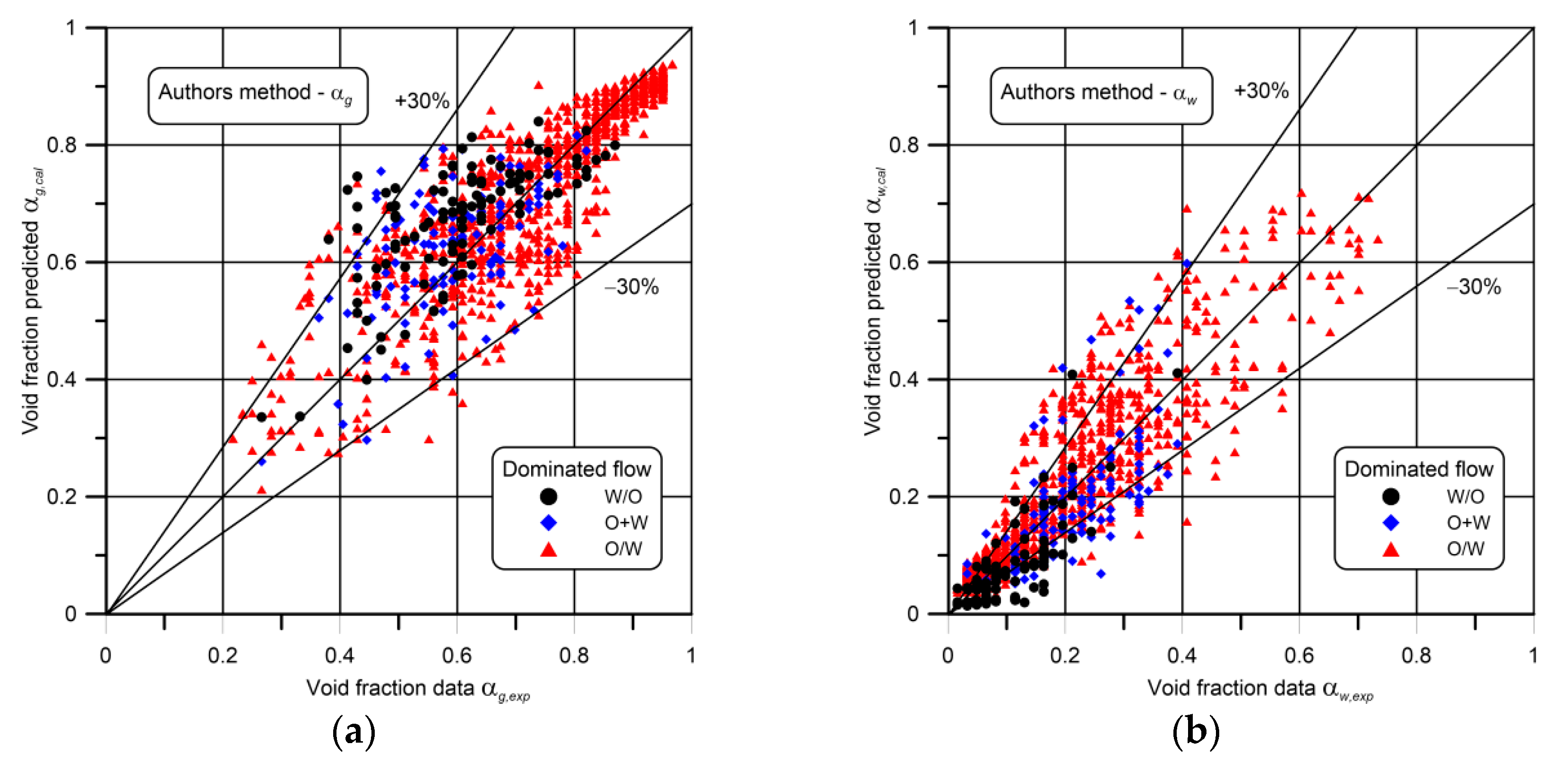
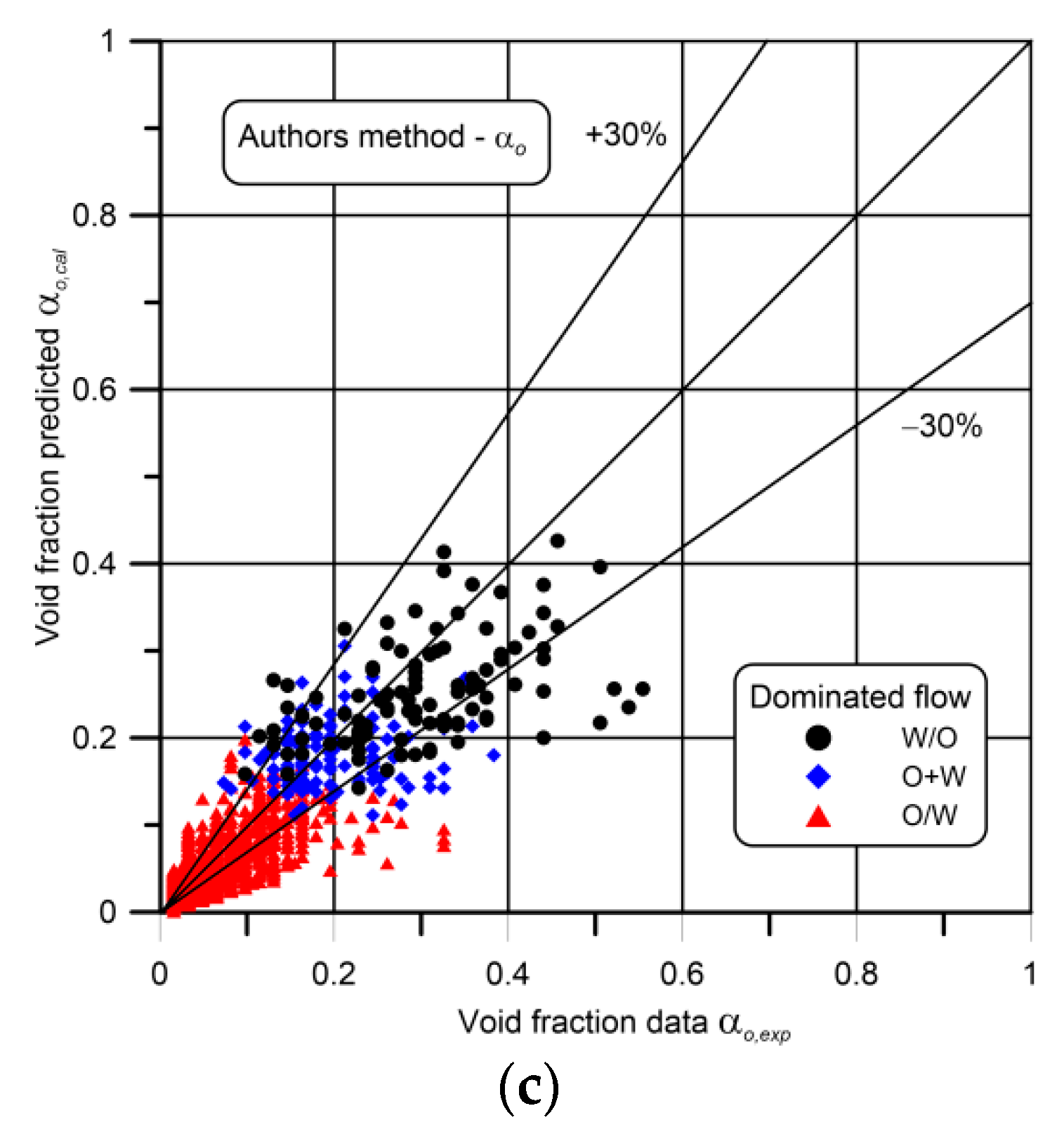
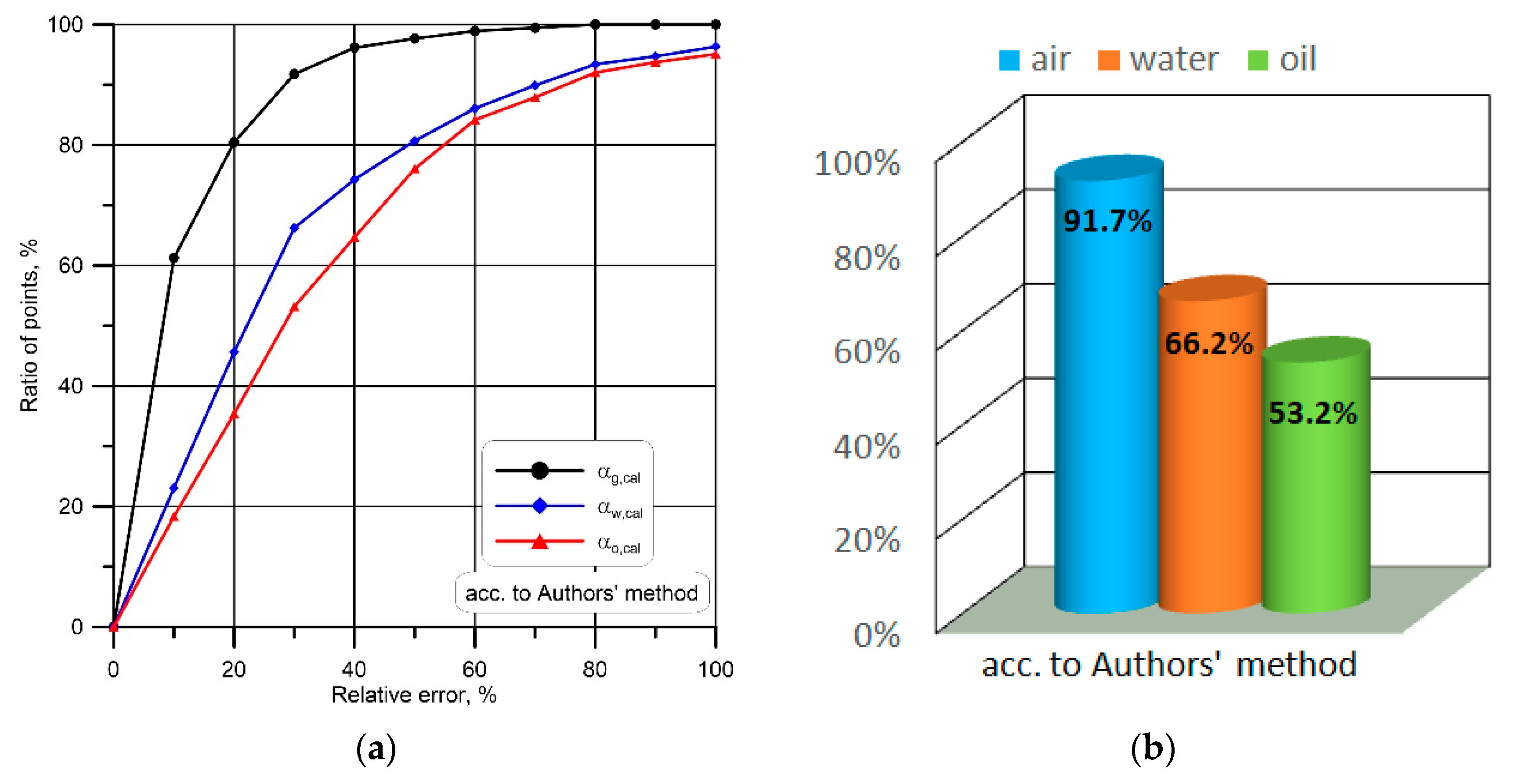
3.2. Void and Volume Fraction
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| d | internal diameter of pipe (m) |
| Fr | Froude number (-) |
| g | acceleration of gravity (m/s2) |
| j | superficial velocity (m/s) |
| Re | Reynolds number (-) |
| t | temperature (°C) |
| Q | volumetric flow rate (m3/s) |
| x | mass fraction (-) |
| Greek Symbol | |
| α | in situ average void/volume fraction (-) |
| β | input void fraction (-) |
| β * | input volume fraction of liquid in three-phase flow (-) |
| η | dynamic viscosity (Pas) |
| ϑz | equivalent linear dimension (m) |
| ρ | density (kg/m3) |
| σ | surface tension (N/m) |
| Subscripts | |
| 2P | two-phase flow |
| 3P | three-phase flow |
| cal | calculated value |
| cr | critical value |
| exp | measured value |
| g | gas |
| g-3P | relation between gas and three-phase mixture |
| i | i-phase |
| inv | inversion phenomena |
| l | liquid |
| o | oil |
| w | water |
| w-l | relation between water and liquid |
References
- Cyklis, P. Industrial scale engineering estimation of the heat transfer in falling film juice evaporators. Appl. Therm. Eng. 2017. [Google Scholar] [CrossRef]
- Czernek, K.; Płaczek, M. Hydrodynamics of two-phase flow in tubular reactor. Czas. Tech. 2017, 8, 101–114. [Google Scholar] [CrossRef]
- Nagavarapu, A.K.; Garimella, S. Experimentally validated models for falling-film absorption around microchannel tube banks: Heat and mass transfer. Int. J. Heat Mass Transf. 2019. [Google Scholar] [CrossRef]
- Witczak, S.; Troniewski, L.; Filipczak, G. Influence of oil concentration on heat transfer conditions during pool boiling of water-oil mixtures. Chem. Process. Eng. Inz. Chem. Proces. 2008, 29, 859–867. [Google Scholar]
- Czernek, K.; Witczak, S. Non-invasive evaluation of wavy liquid film. Chem. Process. Eng. Inz. Chem. Proces. 2013, 34. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Hibiki, T. Correlation of heat transfer coefficient for two-component two-phase slug flow in a vertical pipe. Int. J. Multiph. Flow 2018, 108. [Google Scholar] [CrossRef]
- Hamidi, M.J.; Karimi, H.; Boostani, M. Flow patterns and heat transfer of oil-water two-phase upward flow in vertical pipe. Int. J. Therm. Sci. 2018, 127, 173–180. [Google Scholar] [CrossRef]
- Guichet, V.; Jouhara, H. Condensation, evaporation and boiling of falling films in wickless heat pipes (two-phase closed thermosyphons): A critical review of correlations. Int. J. Thermofluids 2020, 1–2, 100001. [Google Scholar] [CrossRef]
- Sobolewski, M.; Fuchs, L. Consistency issues of Lagrangian particle tracking applied to a spray jet in crossflow. Int. J. Multiph. Flow 2007, 33, 394–410. [Google Scholar] [CrossRef] [Green Version]
- Edwards, L.; Jebourdsingh, D.; Dhanpat, D.; Chakrabarti, D.P. Hydrodynamics of air and oil–water dispersion/emulsion in horizontal pipe flow with low oil percentage at low fluid velocity. Cogent Eng. 2018, 5, 1494494. [Google Scholar] [CrossRef]
- Edwards, L.; Darryan, D.; Chakrabarti, D.P. Hydrodynamics of three phase flow in upstream pipes. Cogent Eng. 2018, 5, 1433983. [Google Scholar] [CrossRef]
- Edwards, L.; Keeran, W.; Chakrabarti, D.P. Phase inversion in liquid phase for air-liquid horizontal flow. Cogent Eng. 2020, 7, 1782622. [Google Scholar] [CrossRef]
- Poettmann, F.H.; Carpenter, P.G. The Multiphase Flow of Gas, Oil, and Water Through Vertical Flow Strings with Application to the Design of Gas-lift Installations. In Proceedings of the Drilling and Production Practice, New York, NY, USA, 1 January 1952; American Petroleum Institute: Washington, DC, USA, 1952. [Google Scholar]
- Tek, M.R. Multiphase Flow of Water, Oil and Natural Gas Through Vertical Flow Strings. J. Pet. Technol. 1961. [Google Scholar] [CrossRef]
- Foreman, F.J.; Woods, P.H. Void fraction calculations for three phase flow in a vertical pipe. Proj. Rep. Course 1975, 2. [Google Scholar]
- Shean, A.R. Pressure drop and phase fraction in oil-water-air vertical pipe flow. Mech. Eng. 1976. Available online: https://dspace.mit.edu/handle/1721.1/30976 (accessed on 14 August 2020).
- Pleshko, A.; Sharma, M.P. An experimental study of vertical three-phase (oil-water-air) upward flows. Winter Annu. Meet. ASME Dallas 1990, 97–108. [Google Scholar]
- Woods, G.S.; Speddeng, P.L.; Watterson, J.K.; Raghunathan, R.S. Three-phase oil/water/air vertical flow. Chem. Eng. Res. Des. 1998. [Google Scholar] [CrossRef]
- Spedding, P.L.; Woods, G.S.; Raghunathan, R.S.; Watterson, J.K. Flow pattern, holdup and pressure drop in vertical and near vertical two- and three-phase upflow. Chem. Eng. Res. Des. 2000. [Google Scholar] [CrossRef]
- Oddie, G.; Shi, H.; Durlofsky, L.J.; Aziz, K.; Pfeffer, B.; Holmes, J.A. Experimental study of two and three phase flows in large diameter inclined pipes. Int. J. Multiph. Flow 2003. [Google Scholar] [CrossRef]
- Shi, H.; Holmes, J.A.; Diaz, L.R.; Durlofsky, L.J.; Aziz, K. Drift-flux parameters for three-phase steady-state flow in wellbores. SPE J. 2005, 10, 130–137. [Google Scholar] [CrossRef]
- Descamps, M.; Oliemans, R.V.A.; Ooms, G.; Mudde, R.F.; Kusters, R. Influence of gas injection on phase inversion in an oil-water flow through a vertical tube. Int. J. Multiph. Flow 2006. [Google Scholar] [CrossRef]
- Descamps, M.N.; Oliemans, R.V.A.; Ooms, G.; Mudde, R.F. Experimental investigation of three-phase flow in a vertical pipe: Local characteristics of the gas phase for gas-lift conditions. Int. J. Multiph. Flow 2007. [Google Scholar] [CrossRef]
- Nowak, M. Void Fractions and Three-Phase Pressure Drop in Vertical Pipe. Ph.D. Thesis, Opole University of Technology, Opole, Poland, 2007. (In Polish). [Google Scholar]
- Nowak, M.; Troniewski, L.; Witczak, S. Prediction of void fraction in three-phase air–water–oil upflow. In Proceedings of the 5th International Conference on Transport Phenomena in Multiphase Systems, HEAT 2008, Bialystok, Poland, 30 June–3 July 2008; Bialystok Technical University: Bialystok, Poland, 2008; Volume 1, pp. 349–356. [Google Scholar]
- Pietrzak, M.; Płaczek, M.; Witczak, S. Upward flow of air–oil–water mixture in vertical pipe. Exp. Therm. Fluid Sci. 2017. [Google Scholar] [CrossRef]
- Colmanetti, A.R.A.; de Castro, M.S.; Barbosa, M.C.; Rodriguez, O.M.H. Phase inversion phenomena in vertical three-phase flow: Experimental study on the influence of fluids viscosity, duct geometry and gas flow rate. Chem. Eng. Sci. 2018. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, H.; Sarica, C.; Pereyra, E.J. Experimental Study of High-Viscosity Oil/Water/Gas Three-Phase Flow in Horizontal and Upward Vertical Pipes. SPE Prod. Oper. 2013, 28, 306–316. [Google Scholar] [CrossRef]
- Bannwart, A.C.; Rodriguez, O.M.H.; Trevisan, F.E.; Vieira, F.F.; de Carvalho, C.H.M. Experimental investigation on liquid–liquid-gas flow: Flow patterns and pressure-gradient. J. Pet. Sci. Eng. 2009. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, B.; Lu, J.; Wang, D. Study on flow pattern maps in hilly-terrain air–water–oil three-phase flows. Exp. Therm. Fluid Sci. 2013. [Google Scholar] [CrossRef]
- Hanafizadeh, P.; Shahani, A.; Ghanavati, A.; Akhavan-Behabadi, M.A. Experimental investigation of air-water-oil three-phase flow patterns in inclined pipes. Exp. Therm. Fluid Sci. 2017. [Google Scholar] [CrossRef] [Green Version]
- Brandt, A. The Annular Flow of Multiphase Mixture in Pipes of Film-Type Evaporators. Ph.D. Thesis, Opole University of Technology, Opole, Poland, 2015. (In Polish). [Google Scholar]
- Goshika, B.K.; Majumder, S.K. Entrainment and holdup of gas–liquid–liquid dispersion in a downflow gas–liquid–liquid contactor. Chem. Eng. Process. Process. Intensif. 2018. [Google Scholar] [CrossRef]
- Stomma, Z. Two-Phase Flows-Void Fraction Values Determination; No. INR--1818/9/R; Institute of Nuclear Research: Kyiv, Ukraine, 1979; Volume 12. [Google Scholar]
- Chisholm, D. A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow. Int. J. Heat Mass Transf. 1967. [Google Scholar] [CrossRef]
- Armand, A.A. Resistance to two-phase flow in horizontal tubes. Izv. Vsa. Tepl. Inst. 1946, 15, 16–23. [Google Scholar]
- Zivi, S.M. Estimation of steady-state steam void-fraction by means of the principle of minimum entropy production. J. Heat Transf. 1964. [Google Scholar] [CrossRef]
- Zhao, T.S.; Bi, Q.C. Co-current air-water two-phase flow patterns in vertical triangular microchannels. Int. J. Multiph. Flow 2001. [Google Scholar] [CrossRef]
- Harrison, R.F. Methods for the Analysis of Geothermal Two-Phase Flow. Master’s Thesis, University of Auckland, Aucklan, New Zealand, 1975. [Google Scholar]
- Zuber, N.; Findlay, J.A. Average volumetric concentration in two-phase flow systems. J. Heat Transf. 1965. [Google Scholar] [CrossRef]
- Hughmark, G.A. Holdup and heat transfer in horizontal slug gas–liquid flow. Chem. Eng. Sci. 1965. [Google Scholar] [CrossRef]
- Punches, W.C. MAYU04: A Method to Evaluate Transient Thermal Hydraulic Conditions in Rod Bundles; General Electric Co.: Schenectady, NY, USA, 1977. [Google Scholar]
- Bonnecaze, R.H.; Erskine, W.; Greskovich, E.J. Holdup and pressure drop for two-phase slug flow in inclined pipelines. AIChE J. 1971. [Google Scholar] [CrossRef]
- Lahey, R.T.; Açikgöz, M.; França, F. Global volumetric phase fractions in horizontal three-phase flows. AIChE J. 1992. [Google Scholar] [CrossRef]
- Pendyk, B. Void Fraction of Gas–liquid–liquid Flow in Horizontal Pipes. Ph.D. Thesis, Opole University of Technology, Opole, Poland, 2002. (In Polish). [Google Scholar]
- Witczak, S.; Pendyk, B. The method of the hold-up calculation during the three-phase flow. Chem. Process. Eng. Inz. Chem. Proces. 2004, 25, 75–86. [Google Scholar]
- Czernek, K. Hydrodynamic Aspects of Thin-Film Apparatus Design for Very Viscous Liquids; Oficyna Wydawnicza Politechniki Opolskiej: Opole, Poland, 2013; ISBN 8364056158. [Google Scholar]
- Czernek, K.; Okoń, P. Verification of methods for calculating the gas volume fraction in the vertical descending flow of two-phase gas–liquid mixtures. J. Mech. Energy Eng. 2018. [Google Scholar] [CrossRef] [Green Version]


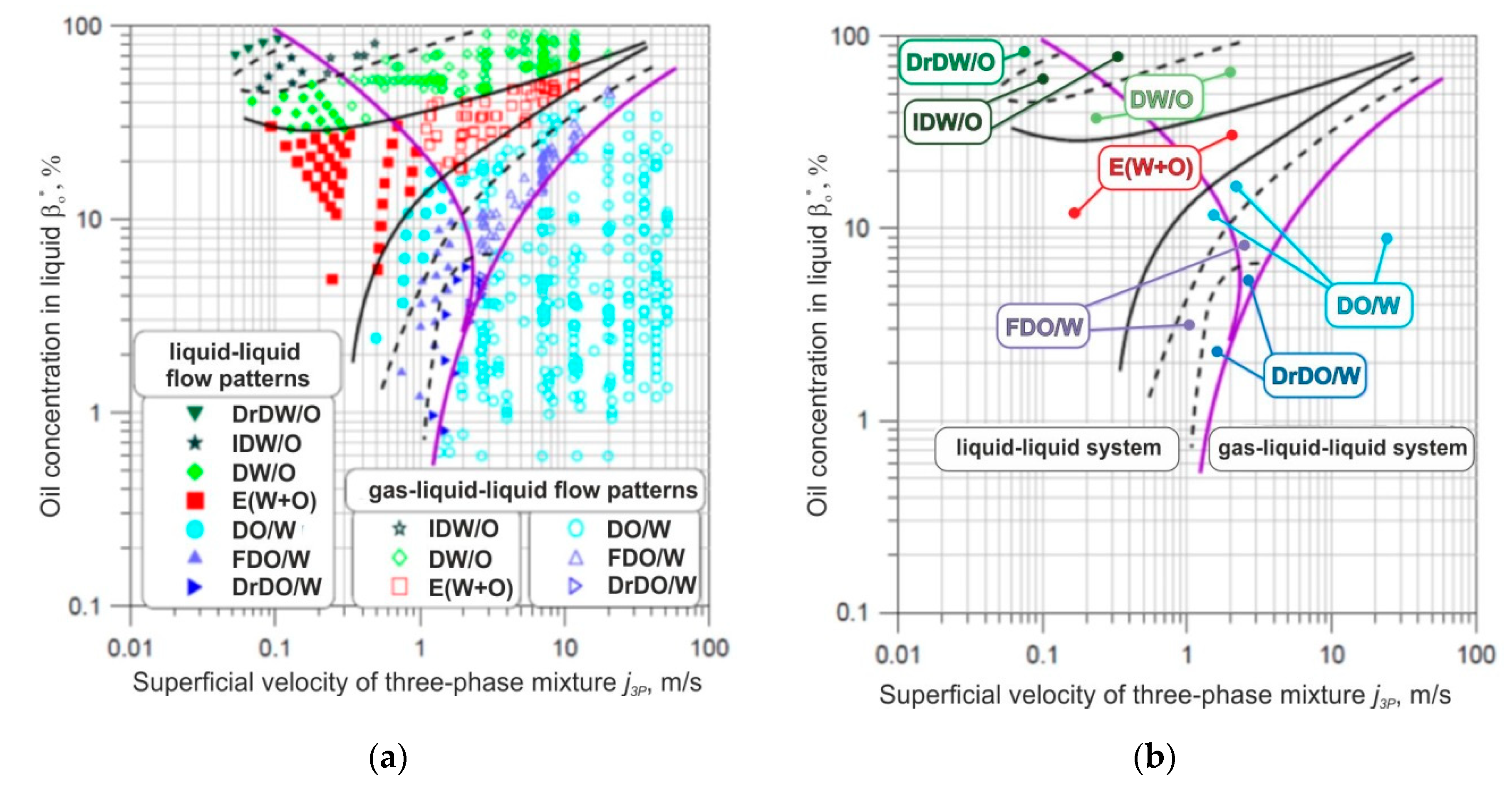




| Mixture Component | Flow Rate | Superficial Velocity | Reynolds Number | Inlet Void Fraction | ||
| Qi, m3/h | ji, m/s | Rei, - | βi, - | |||
| Air | 0.15–23.2 | 0.34–52.5 | 271–43,870 | 0.1–0.99 | ||
| Water | 0.007–1.1 | 0.02–2.5 | 181–32,632 | 0.095–0.98 | ||
| L-AN 15 oil | 0.012–0.33 | 0.028–0.75 | 11–300 | 0.027–0.94 | ||
| Iterm 6 Mb oil * | 0.00096–0.33 | 0.0022–0.75 | 0.3–110 | 0.024–0.9 | ||
| Iterm 12 oil | 0.001–0.17 | 0.0028–0.22 | 0.12–20 | 0.0086–0.94 | ||
| Iterm 30MF oil | 7.31 × 10−5–0.022 | 0.000165–0.05 | 0.0007–12 | 0.0017–0.7 | ||
| Physical Properties of Oils at Temperature of 20 °C | ||||||
| Oil | Density, kg/m3 | Viscosity, mPas | Surface Tension, mN/m | |||
| L-AN 15 | 859.8 | 29 | 32.47 | |||
| Iterm 6 Mb | 860.7 | 83 | 35.85 | |||
| Iterm 12 | 881.5 | 37 | 61.43 | |||
| Iterm 30 MF | 880.8 | 2190 | 91.23 | |||
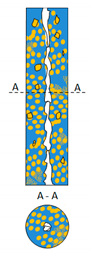
| Water Dominated Flow (O/W) | Emulsified Flow (O + W) | Oil Dominated Flow (W/O) | ||||
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
| A-DrDO/W | A-FDO/W | A-DO/W | A-E(W+O) | A-IDW/O | A-DW/O | DrDW/O |
| jg = 2.485 | 3.457 | 11.32 | 2.485 | 3.887 | 8.432 | 0.982 m/s |
| jw = 0.141 | 0.742 | 0.742 | 0.230 | 0.110 | 0.110 | 0.186 m/s |
| jo = 0.036 | 0.120 | 0.094 | 0.210 | 0.158 | 0.158 | 0.210 m/s |
| Water Dominated Flow (O/W) | Emulsified Flow (O + W) | Oil Dominated Flow (W/O) | ||||
|---|---|---|---|---|---|---|
 | 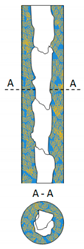 | 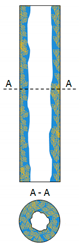 | 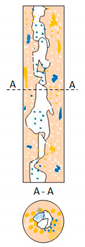 | 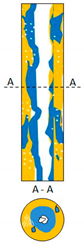 | 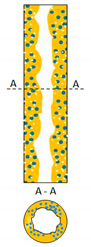 | 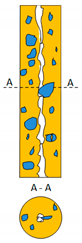 |
| A-DrDO/W | A-FDO/W | A-DO/W | A-E(W+O) | A-IDW/O | A-DW/O | A-DrDW/O |
| Characteristics of Flow Patterns with Water Phase Domination | |
| A-DrDO/W | Annular with dispersed drops of oil in water |
| The water phase occupied a significant part of the measuring channel and remained in constant contact with the channel wall. The gas flowed with a significant velocity through the center of the channel, forming a core that intensified the flow of the very dispersed liquid mixture along the walls of the channel. The flowing liquid mixture formed an annulus of varying thickness and surface waves. The oil flowed (depending on the concentration in the liquid mixture) in the form of individual smaller or larger drops. | |
| A-F-DO/W | Annular with foam-dispersed oil in water |
| The water formed the dominant phase in the flow and was displaced by the gas phase flowing at high velocity through the middle of the channel, towards the channel wall. The water contained tiny oil droplets. The liquid phase formed a characteristic annulus with waves on the surface. The liquid film was of varying thickness along the length of the channel wall.Due to the intensive and oscillating nature of the flow of the liquid mixture, it assumed the characteristics of a dynamic foam. Waves of varying length and amplitude were formed on the surface of the thin film of water near the channel wall. | |
| A-DO/W | Annular with oil dispersed in water |
| The dispersed mixture of oil in water was on the surface of the channel wall. The gas–liquid mixture flowed at high velocity, which increased the degree of dispersion of oil droplets in water. The liquid mixture generated an annulus in the channel with different thickness. The waves created on the mixture surface with a geometry that could be described in terms of a specific wavelength and amplitude depend on the gas flow velocity and the flow rates of both liquid phases. With increasing water and oil flow rates and at high gas velocities, the nature and form of the created waves change and the liquid film becomes thinner. | |
| A-E(W+O) | Annular with emulsified water and oil |
| Emulsified flow forms the type of flow in which it cannot be clearly stated which of the phases is dominant in the flow. This type of flow pattern was initiated at large water and oil flow rates and comparable values of their void fraction. In the gravitational flow of liquids and their flow with low velocity, there was often an alternate flow of differently shaped portions of water and oil. However, as the gas velocity increased, the flow took on dynamic characteristics and there was a strong emulsification of the gas–liquid mixture. The liquid phase took the form of “liquid butter”. | |
| Characteristics of Flow Patterns with Oil Phase Domination | |
| A-IDW/O | Annular with dispersed drops of oil in water |
| This pattern was formed at low flow rates of the continuous oil phase and a small void fraction of water present in the form of numerous small droplets. The emerging regions occupied by water and oil were repeatedly recorded on the channel wall. Clearly delimited areas of individual phase on the channel wall, i.e., oil and water, were observed. The liquid mixture formed an annulus with a varying thickness and with different types of surface waves. | |
| A-DW/O | Annular with intermittently dispersed water in oil |
| The dispersed water-in-oil mixture flows along the wall of the experimental channel section. The liquid mixture became almost opaque, reminiscent of a liquid butter emulsion. Along with an increase in the flow velocities of both liquid phases and the high flow velocity of the gas phase, the resulting liquid annulus was characterized by a different level of surface waves, and its thickness was significantly decreased as the velocity of the gas phase increased. | |
| A-DrDW/O | Annular with dispersed drops of water in oil |
| Oil flow occurred along the wall of the channel, considerably filling its entire cross-section. The oil also contained water droplets with various dimensions, which were entrained by the continuous oil phase during the flow. The gas phase flowed at a significant velocity through the center of the channel forming a core that intensified the flow of the highly dispersed liquid mixture along the wall of the channel. The flowing liquid mixture formed an annulus of varying thickness and surface wave characteristics. Depending on the concentration of water in the multiphase mixture, the water flowed in the form of individual drops or irregular clusters of various dimensions. | |
| Author | Equation |
|---|---|
| Methods for Gas–liquid Two-Phase Flow | |
| ; ; ; | |
| Stomma [34], (1979) | |
| Chisholm [35], (1967) | , |
| Armand [36], (1946) | ; |
| Zivi [37], (1964) | |
| Zhao et al. [38], (2001) | |
| Harrison et al. [39], (1975) | |
| Zuber-Findlay [40], (1965) | ; |
| Hughmark [41], (1965) | |
| GE RAMP [42], (1977) | for or for for for |
| Bonnecaze et al. [43], (1971) | |
| Methods for Gas–Liquid–Liquid Three-Phase Flow | |
| Lahey [44], (1992) | ; ; . |
| Pendyk [45], (2002) | ; ; . |
| Nowak [24], (2007) | for for ; ; |
| No | Author | Value of Statistical Quantities, % | ||
|---|---|---|---|---|
| MRE | MAE | Percent Ratio of Points for MAE <30% | ||
| Methods for two-phase gas–liquid flow | ||||
| 1. | Stomma [34] | 21.91 | 23.26 | 74.6 |
| 2. | Chisholm [35] | 14.58 | 16.73 | 82.2 |
| 3. | Armand [36] | 3.12 | 11.99 | 87.7 |
| 4. | Zivi [37] | −12.95 | 21.80 | 71.0 |
| 5. | Zhao et al. [38] | 10.59 | 17.74 | 82.3 |
| 6. | Harrison et al. [39] | −17.46 | 21.18 | 69.9 |
| 7. | Zuber-Findlay [40] | 4.89 | 14.60 | 86.7 |
| 8. | Hughmark [41] | 11.26 | 16.99 | 82.9 |
| 9. | GE RAMP [42] | 10.53 | 15.59 | 87.2 |
| 10. | Bonnecaze et al. [43] | 7.94 | 15.42 | 86.8 |
| Methods for three-phase gas–liquid–liquid flow | ||||
| 11. | Lahey [44] | 4.53 | 13.54 | 88.0 |
| 12. | Pendyk [45] | 9.61 | 14.80 | 86.9 |
| 13. | Nowak [24] | 4.32 | 12.96 | 90.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandt, A.; Czernek, K.; Płaczek, M.; Witczak, S. Downward Annular Flow of Air–Oil–Water Mixture in a Vertical Pipe. Energies 2021, 14, 30. https://doi.org/10.3390/en14010030
Brandt A, Czernek K, Płaczek M, Witczak S. Downward Annular Flow of Air–Oil–Water Mixture in a Vertical Pipe. Energies. 2021; 14(1):30. https://doi.org/10.3390/en14010030
Chicago/Turabian StyleBrandt, Agata, Krystian Czernek, Małgorzata Płaczek, and Stanisław Witczak. 2021. "Downward Annular Flow of Air–Oil–Water Mixture in a Vertical Pipe" Energies 14, no. 1: 30. https://doi.org/10.3390/en14010030
APA StyleBrandt, A., Czernek, K., Płaczek, M., & Witczak, S. (2021). Downward Annular Flow of Air–Oil–Water Mixture in a Vertical Pipe. Energies, 14(1), 30. https://doi.org/10.3390/en14010030







