1. Introduction
The general idea of the flywheel (FW) system is based on the inertia variation of wind turbine (WT) rotor blades. This is done by shifting a fluid mass between two-piston accumulators in the rotor blade of a WT. The physical description of such an energy storage system is presented in previous works of Jauch et al. and this covers the kinetic [
1] and hydraulic [
2] aspects.
The initial application of the FW system was developed to allow a certain variation of the electrical power of the WT, independent of the prevailing wind conditions [
3]. Meanwhile, the impact of the FW system on the vibratory behavior of the WT and on the natural frequencies of the rotor blades has become one of the most important applications of this system, because of its influence on the operation life of the WT [
4].
In order to analyze the impact of the FW system on the vibratory behavior of the WT components, the dynamic behavior of the FW system should be first implemented in the load simulation tool. Due to the fact that all state-of-the-art load simulation tools for WTs are unable to represent variable rotor blade inertias as they happen in the FW system, the dynamic behavior of the FW system cannot be represented without changing the source code of these load simulation tools. Therefore, all the previous mechanical load simulations, either for the conventional steel FW accumulators design [
5] or for the flexible carbon fiber-reinforced plastics (CFRP) FW accumulators design [
4], could only be done under two conditions: the FW statically fully charged and the FW statically fully discharged.
The previous load simulations were done for several FW configurations. These configurations were derived via a methodology, which was used to determine the positions and dimensions of the FW accumulators into the rotor blades [
6]. However, since the goal of this paper is not to analyze the load impact of all the CFRP FW configurations published in previous work by the author [
4], the load analysis is limited in this paper to only one relevant FW configuration. This configuration is the same one used by the first eigenmodes simulation tool of a WT [
7]. This tool is developed for control algorithm design at the Wind Energy Technology Institute (WETI) of Flensburg University of Applied Sciences, Germany. In the following, the considered FW configurations are named “types” and are identified with Roman numerals, as introduced in Hippel et al. [
6]. Hence, the properties of the CFRP position accumulators of the FW type VI, mentioned in
Table 1, are used to implement the variable blade inertia.
The stationary masses in
Table 1 are added to the distributed mass densities of the rotor blade regarding the total length of the root and tip accumulators. For the Sandia 61.5 m rotor blade design (Sandia National Lab., Albuquerque, USA) [
8] that is used in this paper, where the mechanical properties of the rotor blades are distributed over 17 elements, the stationary masses of the root and tip accumulators are added to the first two elements and to the 11th, 12th, and 13th elements, respectively. Whereas the stationary masses of the tip and root accumulators are considered as constant masses, the fluid mass is the mass that is varying along the root and tip elements. Varying the fluid mass is determined by so-called charge-index-factors (
K). These factors can be steplessly varied between the limit values of 0 and 1 for the discharged and charged states, respectively. If
K in one blade equals 0, the FW is fully discharged and the total fluid mass is added to the root elements of this blade and, if
K equals 1, the FW is fully charged and the total fluid mass is added to the tip elements of the same blade.
Due to the public availability of the 5 megawatt (MW) reference WT, and the extensive use of its data in studies by the wind energy research community as a system that represents the current and future state-of-the-art offshore systems, the FW system was adapted to this WT. The Sandia 61.5 m rotor blade design is also applied in the original design of the 5 MW reference WT developed by the National Renewable Energy Laboratory (NREL), USA [
9].
First of all, before discussing the code adjustment of a load simulation tool to implement the dynamic behavior of the FW system, it must be decided in which load simulation tool this adjustment should be performed. FLEX5 [
10], FAST [
11], and Bladed [
12] are all recognized WT load simulation tools which are used by the WT industry. However, in this paper, OpenFAST is selected because of it is free, publicly available, and well documented. OpenFAST is a computer-aided engineering tool, which is developed by NREL for simulating the coupled dynamic response of WTs [
13]. This software is also used by thousands of WT designers, manufactures, consultants, certifiers, researchers, students, and educators all over the world [
11]. Moreover, OpenFAST has the advantages of a self-sustaining community-developed software by working with OpenFAST on a GitHub repository. This feature offers a good opportunity to communicate with the NREL OpenFAST team and other developers throughout the OpenFAST community [
14]. All of these advantages make it obvious that OpenFAST is a suitable load simulation tool to implement the dynamic behavior of the FW system in WT. However, the high complexity of the structure of OpenFAST requires a good understanding of the architecture of this program before any modifications to its source code. Hence, the architecture of OpenFAST is briefly introduced in the next section. More details about the program are described in a previous project report of the author [
15].
This paper begins with the introduction about the program structure, which helps to understand where and how the variable blade inertias are implemented in the source code of OpenFAST. Subsequently, the computation and integration of the resulting loads from the change in rotor blade inertia are discussed in two following sections. Consequently, the modified code is tested using a simple simulation scenario of a WT without aerodynamic loads and controllers. This test aims to verify the implementation correctness of the modified code and to illustrate the impact of the variable blade inertia on the WT rotor speed behavior. Finally, the applicability of the FW system to correct a rotor mass imbalance is tested during the WT operation with enabled aerodynamic and controller modules.
2. Architecture of OpenFAST
OpenFAST is a multi-physics, multi-fidelity tool for simulating the coupled dynamic response of wind turbines. The theory of OpenFAST is based on the coupled interactions of several computational modules which are responsible for structural dynamics, aerodynamics, control and electrical system dynamics, and hydrodynamics for offshore structures to enable coupled nonlinear aero-hydro-servo-elastic simulation in the time domain [
16].
Basically, the architecture of OpenFAST consists of a driver program (glue code), which couples several individual submodules together, see
Figure 1. These submodules (AeroDyn, SevoDyn, ElastoDyn, BeamDyn, etc.) correspond to different physical domains of the coupled aero-hydro-servo-elastic solution [
16].
ElastoDyn and BeamDyn in
Figure 1 are those submodules that are responsible for the blade structural dynamics. The major difference between these two modules lies in the implementation of beam theory. The model underlining BeamDyn is based on the geometrically exact representation of the beam theory (GEBT), whereas ElastoDyn uses Bernoulli-Euler beam theory under bending [
16].
ElastoDyn uses Kane’s method [
17] to set up equations of motion, which can be put into Newton’s Second Law (see Equation (1)).
This method simplifies the equation of motion, which makes the equations easier to solve than the method of GEBT.
The GEBT used by BeamDyn makes no approximation on the geometries in formulating the equation of motions (see Equation (2))
where
and
are the distributed moment and force applied to the beam structure, respectively;
and
are the angular and linear moment resolved in the inertial coordinate system, respectively;
and
are the beam’s sectional moment and force, respectively;
and
are the one-dimensional displacement and the position vector of a point along the beam’s reference line, respectively; the notation
and
indicates a derivative with respect to beam axis
and to time, respectively; the tilde operator
defines a skew-symmetric tensor corresponding to the given vector [
16].
Since the goal of this paper is not to support a full geometric nonlinearity solution or to simulate a large deflection of an anisotropic composite material of a rotor blade with a pre-bended reference axis, it is obvious to choose ElastoDyn to implement the dynamic behavior of the FW system in OpenFAST. Although ElastoDyn uses a simpler mathematical theory than BeamDyn, the exact solutions of ElastoDyn meet the needs in this paper. A detailed comparison between ElastoDyn and BeamDyn is introduced in a previous project report of the author’s [
15].
Figure 1 shows that the implementation of variable blade inertia takes place within the module of ElastoDyn, whereas the additional variables of the FW system are defined into the glue code of OpenFAST. This enables the FW variables to be passed through the local and external modules of OpenFAST, as discussed later in the next sections.
The executable files, as well as the configuration libraries of the program, are available online on the homepage of OpenFAST [
18]. Since variable rotor blade inertias are not considered in the original source code of OpenFAST, the currently available executable cannot be used for the proposed tasks in this paper. Hence compiling from the source code must be done in order to obtain an executable, which includes the add-on of variable blade inertias in its code.
Different methods to obtain the OpenFAST executable from the source code are presented on the homepage of OpenFAST [
18]. One of these methods uses Visual Studio (VS) to build OpenFAST on Windows. Building OpenFAST on Windows with VS gives Windows users better options for developing and debugging the source code because of its streamlined manner in solving and maintaining programing errors.
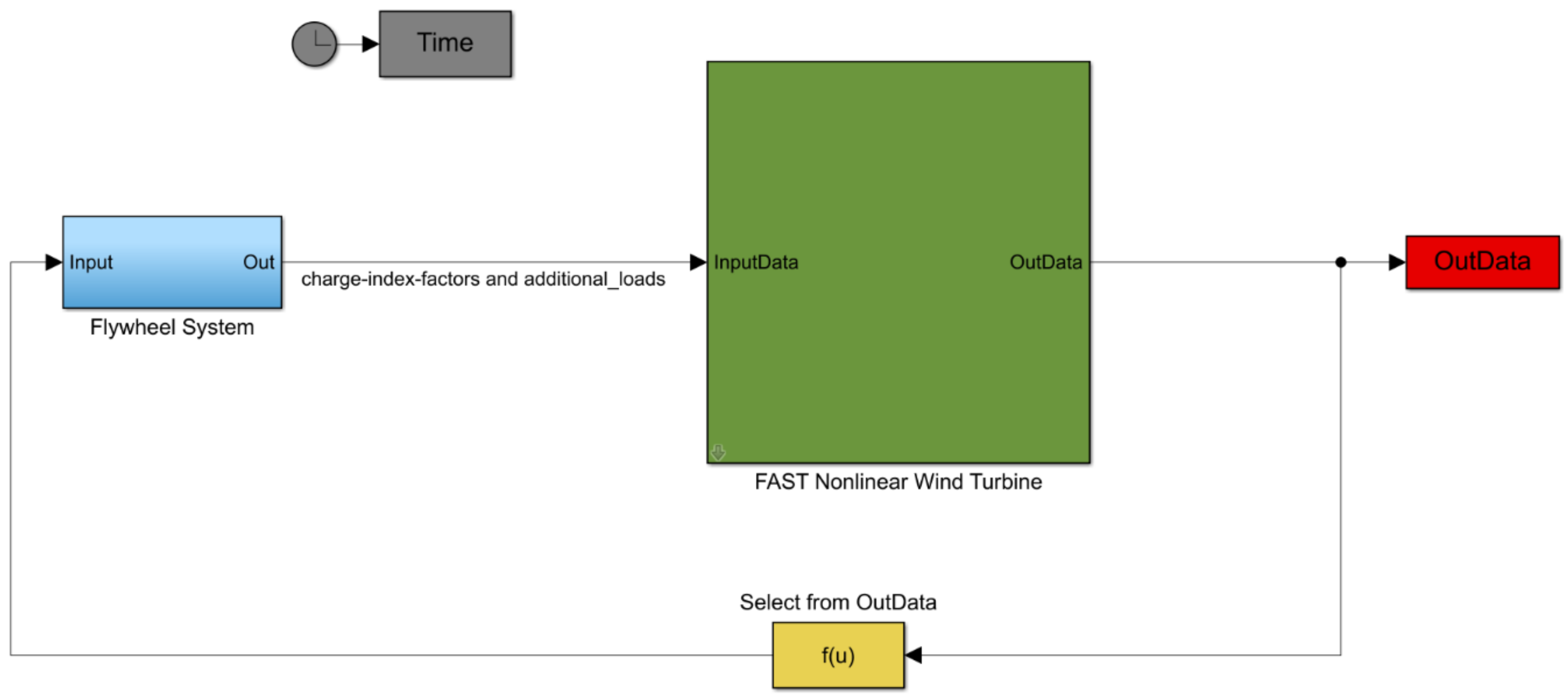
4. Integration of Flywheel System in OpenFAST Simulink Interface
As Simulink is a popular simulation tool for the design and development of control algorithms, OpenFAST has also been implemented as a library that can be called from a Simulink S-Function block, using predefined inputs from Simulink. Therefore, modules such as Generator torque control, nacelle yaw control, pitch control, high-speed shaft brake, and other external modules can be designed in the Simulink environment and, meanwhile, they can use the complete nonlinear aeroelastic wind turbine equations of motion available in OpenFAST [
19].
The wind turbine sample model, as shown in
Figure 3, contains the S-Function block with the OpenFAST equations of motion. It also contains the control signals that are implanted in the above-mentioned control models. These models are deactivated in the Flywheel_System.mdl model in
Figure 4, as the focus is only on the implementation of the FW system.
Figure 4 shows the FW system block, which includes the equations of the additional loads and the charge-index-factors for each rotor blade. The next section will discuss in detail which loads are generated by the FW system and not considered in the OpenFAST equations of motion. The function block
f(u) shown in
Figure 4 is used to select certain data from OpenFAST outputs, which are required for the equations in the FW system model.
However, since the OpenFAST Simulink interface is currently set up to receive only the control signals as inputs, as shown in
Figure 3, both the OpenFAST glue code and Simulink Interface must be modified. This modification is needed, in order to pass the outputs of the FW system model through the Simulink interface, and then to use them in OpenFAST glue code. Moreover, it must be noted that the largest array of inputs that can be accepted from Simulink interface and passed to OpenFAST glue code must not be more than 11 elements, otherwise, a segmentation fault is transmitted. Both of these issues are discussed in detail on OpenFAST GitHub [
20]. Moreover, all source code modifications of OpenFAST that are performed in this paper are available on ResearchGate [
21]. However, compiling from the source code is needed in order to obtain an OpenFAST executable with the add-on of variable blade inertia. For compiling from the source code, the NREL OpenFAST team has developed an approach that uses CMake to generate build files for all platforms [
18].
5. Impact of the Variable Blade Elements’ Masses on Wind Turbine Loads
In general, the theory basics of ElastoDyn blade structural dynamics does account for the blade loads in two main categories: generalized inertia forces,
; and generalized active forces,
; including the external forces acting on the body, such as blade aerodynamic forces, blade and tower elastic bending forces, gravity, and drive train forces. These are described in Equations (3) and (4) [
16].
Consequently, the resulting velocities and accelerations due to the blade and tower deflections are expressed as partials in the main kinematics and kinetics routines in ElastoDyn. Hence, every force that is based on the acceleration of the blade body is intrinsic to the kinematics and kinetics. This means that the additional loads resulting from the FW system due to the stationary change of the blade elements’ masses are intrinsically included in the kinematics and kinetics of ElastoDyn. However, the load that is resulting from the portable mass between two blade elements in a certain time is not considered in the structural dynamics of ElastoDyn. This is because variations in the inertia of the rotor do not happen in state-of-the-art WTs.
This load is already explained in the previous work of Jauch [
1] as an additional torque, which is resulting from the change in angular momentum. The law of the conservation of the angular momentum presented in Equations (5)–(7) describes the fact that a torque, T, results if the angular momentum, L, changes, in order to keep the kinetic energy,
, constant.
where
is the mass moment of inertia, and
is the rotational speed.
Equation (8) expresses the FW torque,
, in one blade in terms of change in the FW inertia in a rotor blade,
.
The inertia of the FW in one blade,
, changes if the centre of gravity,
, of the FW fluid,
, changes.
The value of the rotational speed,
, in Equation (8) is derived from the outputs of OpenFAST using the select function
f(u), as shown in
Figure 4. However, before any outputs are generated in OpenFAST, the FW torque must be implanted correctly in the dynamic calculation of OpenFAST. It must be ensured that the added load does not double count terms that are already added by the change in the masses of the blade elements in the source code of ElastoDyn. This can be accomplished by implementing the FW torque as an external additional torque at the hub since ElastoDyn has a model-level input point mesh for external loads applied at the hub. The FW torque is already calculated in the FW system model in Simulink (see
Figure 4) by using Equations (8) and (9), therefore, the value of this additional torque can be used to set the value of the external loads at the hub. Normally, this load is set to zero, in case no external loads have been applied at the hub.
In order to verify the implementation correctness of the FW system in the structural dynamics of the load simulation tool, load simulations are performed for a WT with a deactivated control system and without the impact of the aerodynamic loads. This allows clarification of the impact of variable blade inertia on the behavior of the WT rotor speed independent of any influences from aerodynamic loads and controllers. Therefore, in the following simulation scenario, the aerodynamic, as well as the control modules of OpenFAST are disabled. However, in the next section, these modules are enabled again to cover the impact of the FW system on the behavior of the WT during its power production.
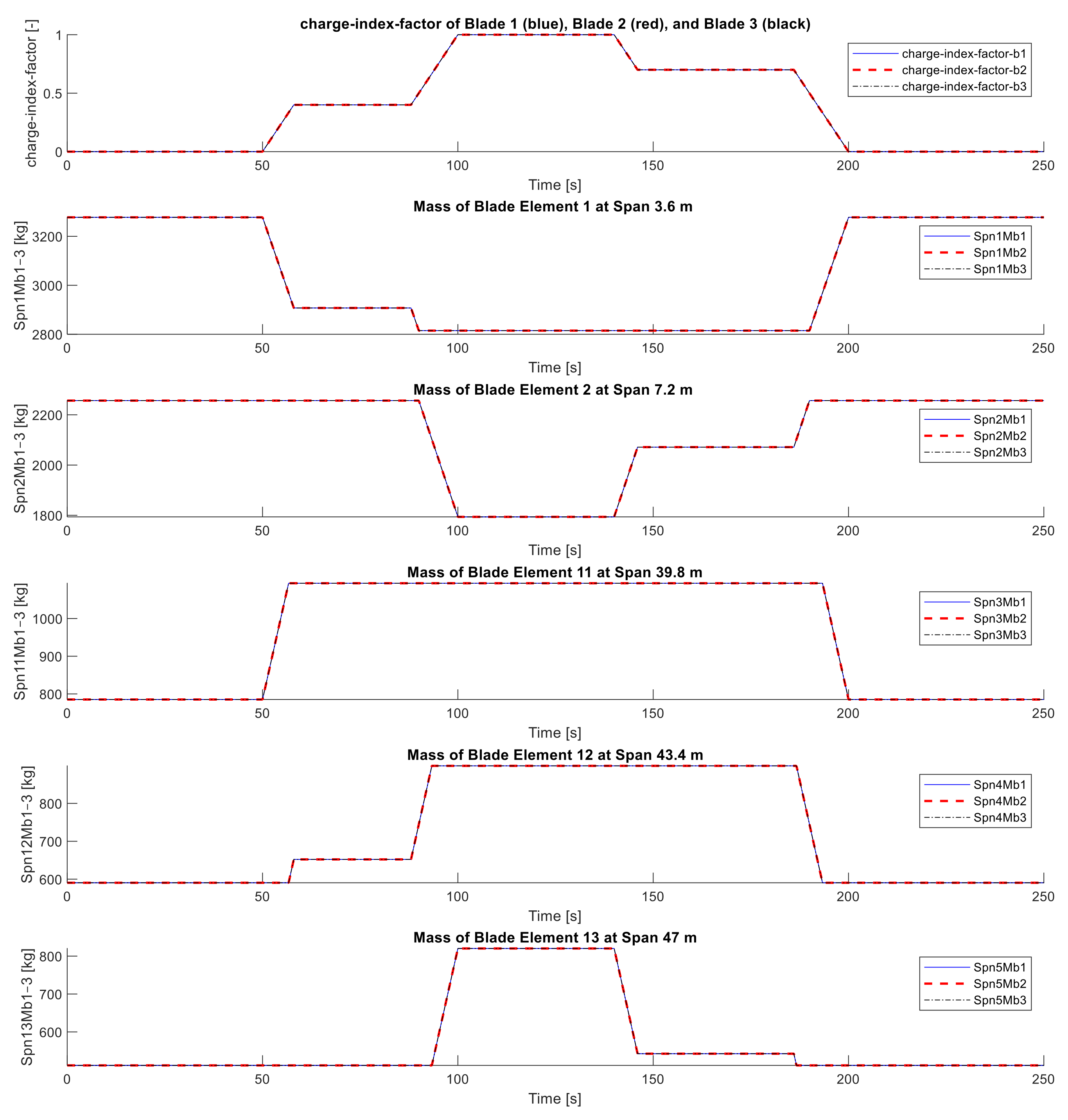
As mentioned in the introduction, blade spans, those that are close to the location of the blade root and tip accumulators of the FW type VI, are selected according to the Sandia 61.5 m rotor blade design. Therefore, blade elements 1 and 2 as well as blade elements 11, 12, and 13 are selected to represent the positions of the root and tip accumulators of the FW type VI, respectively.
Figure 5 shows the span locations and the mass of these elements. The definition of the mechanical properties of the blade elements in the source code of ElastoDyn is based on the distributed sectional properties of the Sandia 61.5 m blade design. This design follows the characteristics of the NREL 5 MW reference turbine blade. The NREL 5 MW reference WT has three blades. The structural properties of each blade are distributed in sectional properties along the blade pitch-axis [
9]. The distributed blade section mass is based on the geometry and the material selection for each blade section. Regarding the Sandia 61.5 m blade design, the dimensions of the blade root sections are much bigger than the geometry of the blade body and the blade tip sections. Therefore, most of the blade mass is concentrate near to the blade root. This difference in the mass distribution along the rotor blade can also be seen in the difference between the mass of the blade elements in
Figure 5, where blade element 1 at a span location of 3.6 m is much heavier than blade element 13 at a span location of 47 m.
Figure 5 also shows a fluid mass of 925.46 kg, which is corresponding to the total fluid mass of the FW type VI (see
Table 1), which is shifted between the root and tip accumulator. The charge-index-factors determine when and where how much fluid mass must be shifted and which is baled. For the simulation scenario in
Figure 5, the FW is charged and discharged simultaneously in the rotor, therefore, the charge-index-factors of the three blades are identical. Unsynchronized charging/discharging is discussed in the next section.
The FW starts to charge at 50 s and it is fully charged at 100 s, whereas discharging starts at 140 s and ends at 200 s. Meanwhile, the charge/discharge process is interrupted twice: at 58 s as the FW is 40% charged, and at 146 s as the FW is 30% discharged, see subplot 1 in
Figure 5. As a response to the changes in the charge-index-factors subplots, 2–6 in
Figure 5 show the change in the masses of the above-selected blade elements.
The resulting total FW torque from the three blades,
, and its relation to the change in the FW inertia,
are illustrated in
Figure 6.
Figure 6 also shows the change in the value of the variable center of gravity,
, of the FW type VI in relation to the values of the charge-index-factors in
Figure 5.
The impact of variable blade inertia on the rotor speed of the WT due to the application of the FW system is illustrated in
Figure 7. Where it is obvious that the increase of the blade inertia by charging the FW system leads to slowing down the rotor speed on the one hand and, on the other hand, the decrease of the blade inertia by discharging the FW system leads to speed up the rotor speed. As mentioned above, since the control system and the aerodynamic loads of the WT are deactivated, the decrease of the rotor speed is not recovered by the aerodynamics or by pitching the rotor blades. This can be obviously seen in
Figure 7 as the pitch angle is still unchanged during the whole simulation time, even when the rotor speed changes due to the change in the blade inertia.
As the response of the rotor speed to the change in the rotor blade inertia shown in
Figure 7 meets the physical basics of the law of the conservation of the angular momentum [
22], this verifies that the implementation of the FW system in the structural dynamics of OpenFAST is correct. Hence, the modified code can be applied on a WT model during its power production.
6. Analysis of Rotor Imbalance of Wind Turbine with Flywheel System
A rotating system is imbalanced when its center of mass is out of alignment with the center of rotation [
23]. In WT, rotor imbalance may be the result of aerodynamic imbalances which could be caused by pitch misalignment of one blade with respect to the other blades, or it may be the result of mass imbalance due to a number of causes, for example, ice accretion, blade damage, poor blade manufacturing tolerances, etc. [
24]. Vibrations resulting from rotor imbalances significantly affect WT fatigue, which may reduce the efficiency and the operation life of a WT.
Therefore, there is a need to correct rotor imbalances depending on their causes as soon as possible. Different literature sources contain detailed descriptions on the determination and correction of aerodynamic [
25] as well as mass imbalances [
24,
26]. The rotor imbalance correction methods are generally based on the adjustment of the pitch angle of WT rotor blades, which leads to a reduction in the power output of the WT. Since the FW system has the ability to operate variable blade inertias, this advantage can be applied to correct rotor mass imbalances without the need to adjust the pitch angle. This ability is illustrated in the next simulation scenario.
At first, if the applicability of the FW system to correct mass imbalances to be simulated, the rotor imbalance needs to be represented in a simulated WT model. Therefore, the 5 MW reference WT model presented in the following simulation scenario contains one rotor blade with an additional mass at a certain span location. Since The Sandia 61.5 m blade design is used to implement the FW type VI, this design is also used to represent the rotor imbalance.
Figure 8 shows the rotor imbalance in terms of additional mass of circa 191 kg in blade 1 element 11 at a span location of 39.8 m (see subplot 4 in
Figure 8 Spn3Mb1 in blue). The additional mass weight and location are set to those values in order to generate a mass imbalance for this simulation scenario, and they can be varied for other simulation scenarios. This mass difference in blade 1 from the other two blade masses leads to rotor imbalance. In the following simulation scenario, the WT model starts with fully charged FW tip accumulators and with a rotor imbalance simulation time of 150 s. From that time, the FW system is set to discharge not simultaneously in all blades until the three blades have the same inertia. This is done by stopping the FW to discharge in blades 2 and 3 at a simulation time of 163 s, whereas the discharging process is continuing in blade 1 until the mass of blade element 11 in all blades is equal, which is achieved at a simulation time of 167 s. At this point, the total additional mass of blade 1 is shifted from the blade body at a span of 39.8 m to the blade root at a span of 3.6 m. This is how the rotor imbalance is corrected using the FW system, which allows the minimization of the lever arm of the additional mass in one or more blades, and thus, reduces the impact of the mass imbalance on WT behavior. However, since the rotor blades are balanced, the tip FW accumulators in blades 2 and 3 are not allowed to be fully discharged, in order to keep the balance in blade element 11 of all blades.
For the above simulation scenario of rotor imbalance, the WT runs under rated steady wind conditions with a constant horizontal wind speed of 12 m/s. The FW system is initially fully charged in the rotor and is discharged not simultaneously in the three blades, see
Figure 9. Such initial rotor imbalance is a 1p excitation, which excites the tower to a later vibration.
Figure 9 shows this vibration in terms of side-to-side deflection of the tower top, where the vibration amplitudes of the tower top side-to-side deflections are obviously much greater within the period of the rotor imbalance than the period after the imbalance correction at a simulation time of 167 s. The reason for this is essentially that there is a grater tower-top yaw bearing roll moment before rather than after the correction of rotor imbalance.
In
Section 5 it is shown how the WT behaves with the FW system when its aerodynamic loads and control system are disabled. By contrast with
Figure 7,
Figure 10 shows the impact of the FW system on the WT behavior with enabled aerodynamics and controller modules. Moreover, the presented WT in this section gets excited with a 1p excitation, due to the previously mentioned rotor imbalance. This excitation obviously affects the behavior of rotor speed, pitch angle, and generator power in the first 150 s, where continuous oscillations in the signals are seen in this period. After that, the rotor imbalance correction procedure starts by discharging the FW system asymmetrically in the three blades. The FW torque,
, generated by discharging the FW speeds up the rotor over the rated value of rotor speed, and thus, the power production increases over the rated value of 5 MW. Consequently, the pitch controller raises the pitch angle in order to slow down the rotor to the rated rotor speed again. The original pitch controller of the NREL 5 MW reference WT is designed to maintain the balance between power generation and rotor speed at rated conditions. Therefore, such changes in the rotor speed due to the change in blade inertia are immediately maintained by the pitch controller, and thus, the released kinetic energy by discharging the FW system is wasted through the pitch control.
Hence, in future, a controller has to be designed that uses the stored kinetic energy, for example, to support grid frequency. The developed controller should also consider the power consumption of the FW system since its tip accumulators are charged with electric pumps, which are supplied from the power production of the WT.
7. Conclusions
In the present paper, variable blade inertia was implemented in the source code of the load simulation tool OpenFAST, in order to integrate an FW system in WT rotor blades. The FW configurations used to represent the change in blade inertia are those corresponding to the FW type VI. The stationary masses of the root and tip accumulators are added at the respective location of the FW type VI within the blade mechanical properties of the Sandia 61.5 m rotor blade design, whereas the fluid mass of the FW type VI is implanted in the source code of the blade’s structural dynamic module of OpenFAST to be shifted in- and outboard.
ElastoDyn and BeamDyn are those two modules that are represented by OpenFAST to implement the structural dynamics of rotor blades. Since the goals of this paper are not to support a full geometric nonlinearity solution, or to simulate a large deflection of a rotor blade, which is supported by BeamDyn, ElastoDyn is used for implanting the variable blade inertia. Moreover, the exact solutions of ElastoDyn fulfill the requirements of the simulated WT scenarios.
However, such implementation needs a good understanding of the source code of the load simulation program. Therefore, an algorithm is prepared to illustrate the major modifications of the source code. The code that the algorithm is based on is described in detail in a previous research project of the author [
15], and it is available on ResearchGate [
21].
Since OpenFAST is also implemented as a dynamic library that can be called from MATLAB/Simulink, this feature is used to implement the mathematical operations of the FW system as a Simulink model. However, passing outputs from the FW model through the Simulink interface of OpenFAST needs to modify both OpenFAST glue code and Simulink Interface.
The outputs of the FW Simulink models includes inter alia, the FW torque, , This torque represents the additional rotor torque that results from the change in angular momentum. Although this additional load is not considered in the structural dynamics of ElastoDyn, ElastoDyn offers a model-level input point mesh for external loads to be applied at the hub. This model is used to apply the FW toque to the hub.
As the source code, modifications are done. It is, therefore, necessary to verify the implementation correctness of the FW system in the structural dynamics of OpenFAST. This verification is done by simulating a WT with the integrated FW system and without the interaction of the aerodynamic loads and controllers. This simulation scenario aims to illustrate that the implemented variable blade inertia can lead to speeding up the rotor when the FW discharges, and to slowing down the rotor when the FW charges, as provided by the law of the conservation of the angular momentum.
Finally, as one of the several FW system advantages, the change of the blade inertia is applied to correct a rotor mass imbalance. The simulated mass imbalance is produced by adding an additional mass to one blade at a certain span location. The impact of the 1p excitation of rotor imbalance on the vibratory behavior of the WT is shown before and after the imbalance correction by using the FW system.
The impact of the FW system on the WT during its power production is also illustrated, where it was clear that future works should focus on developing control designs which manage the energies that are released and consumed by the FW system. Moreover, it is advantageous to validate the implementation of variable blade inertia in BeamDyn or in different load simulation tools, which will be the focus of future works.