PV Modules Interfacing Isolated Triple Active Bridge for Nanogrid Applications
Abstract
1. Introduction
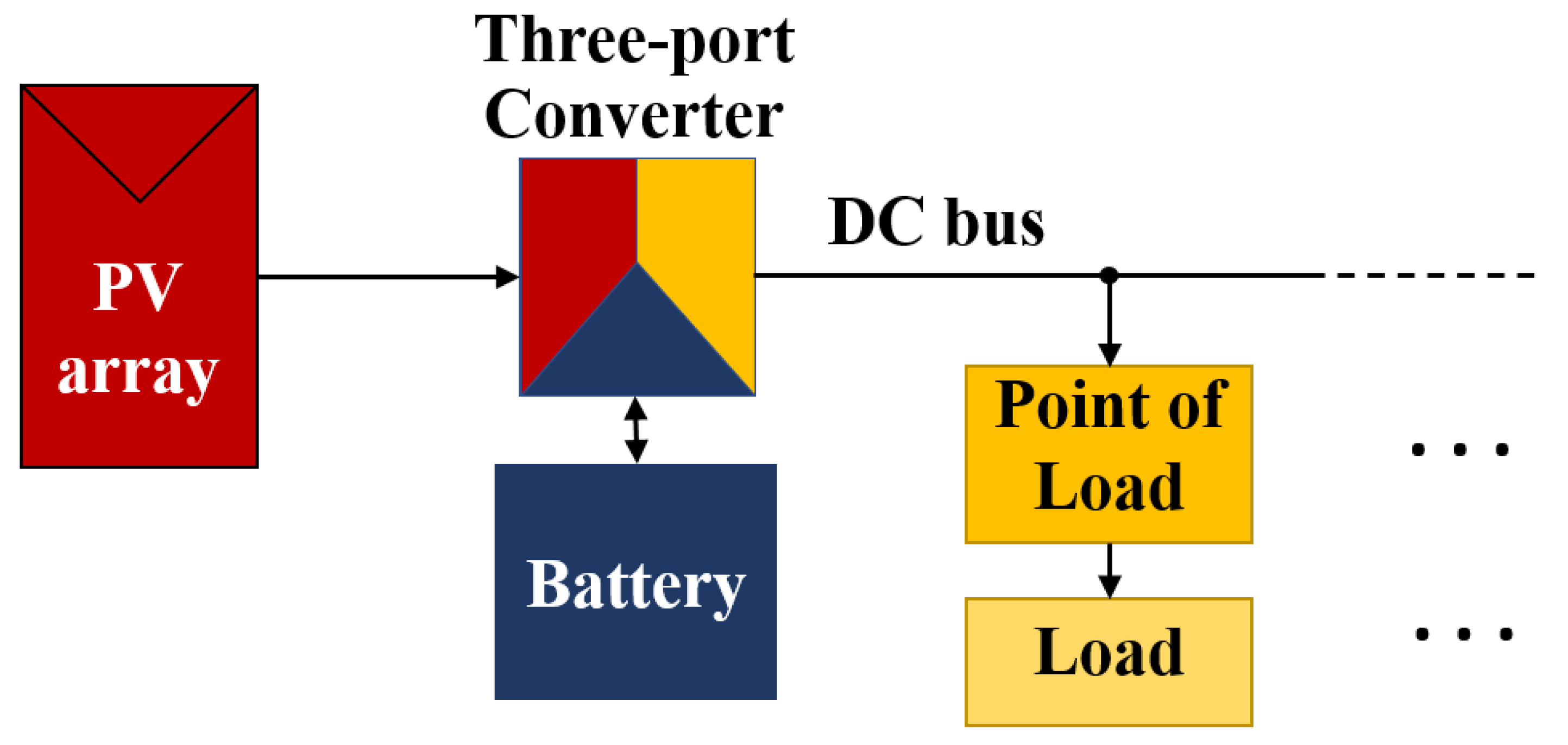
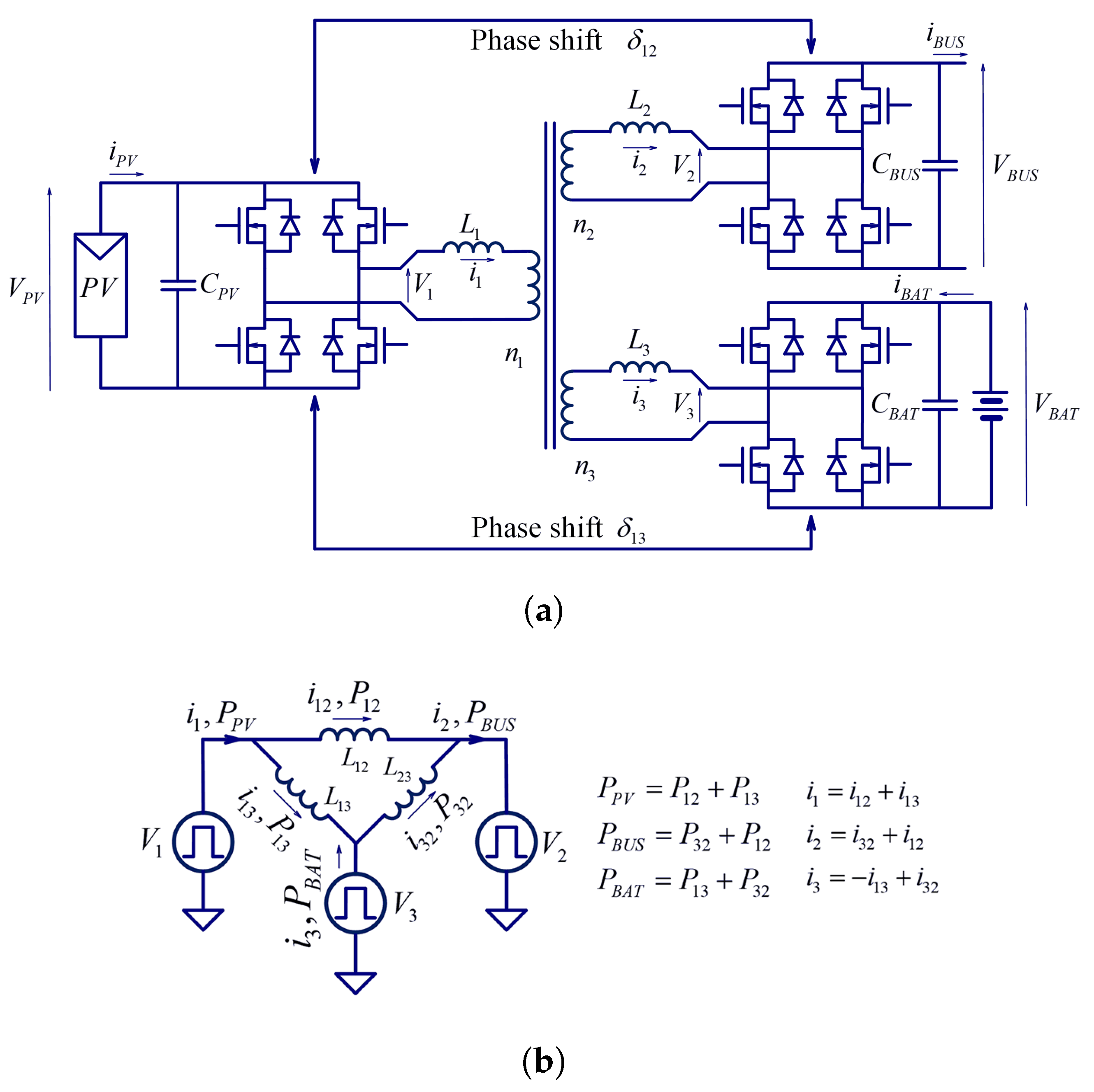
2. TAB and Analyzed Nanogrid Architecture
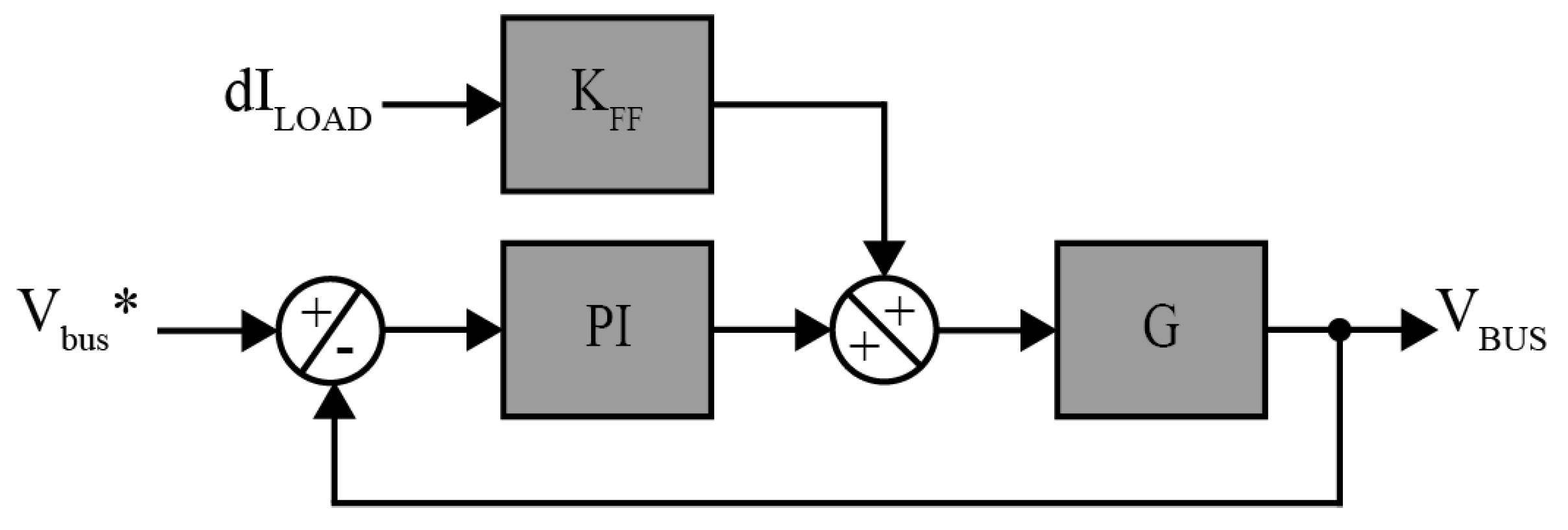
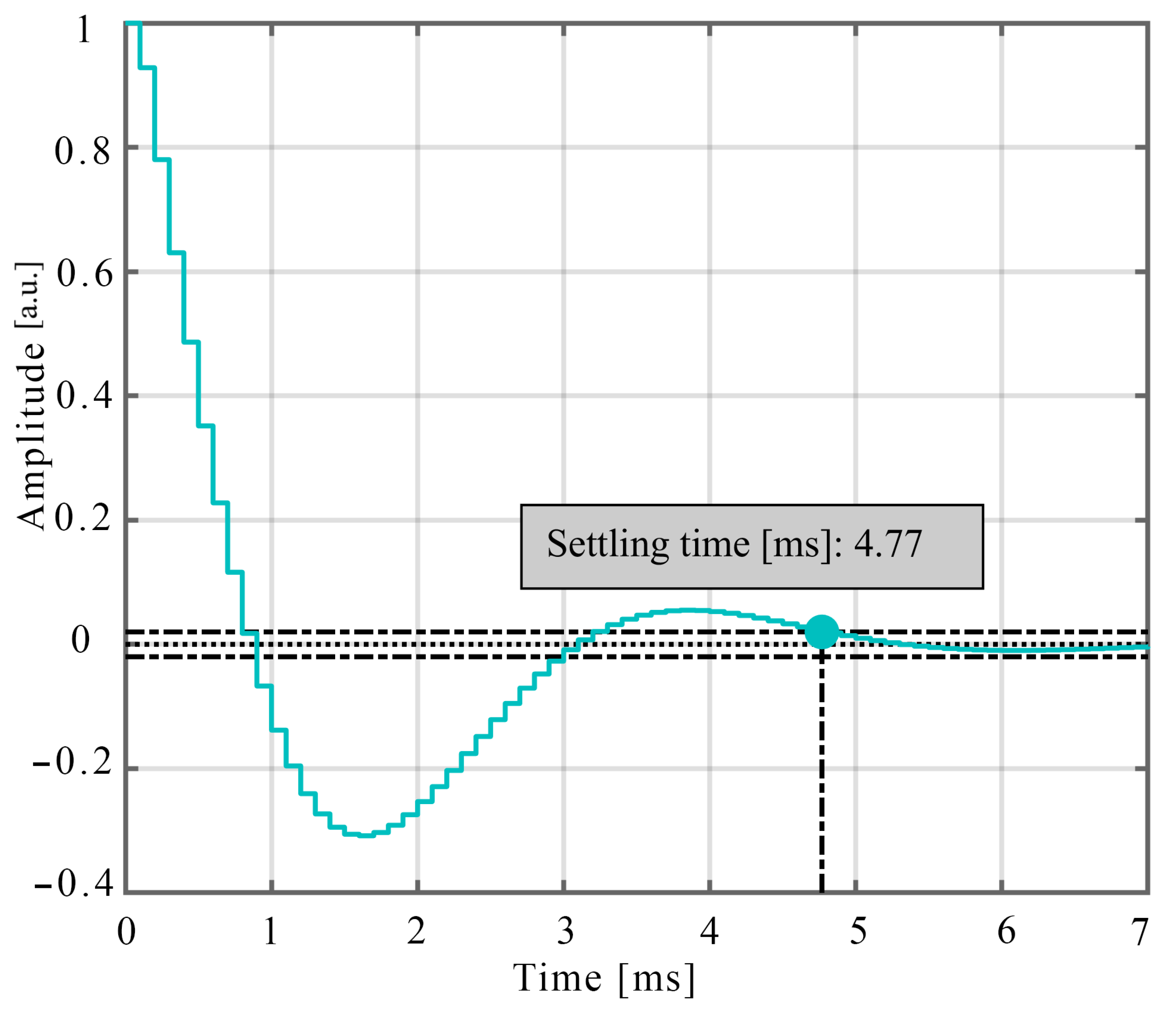
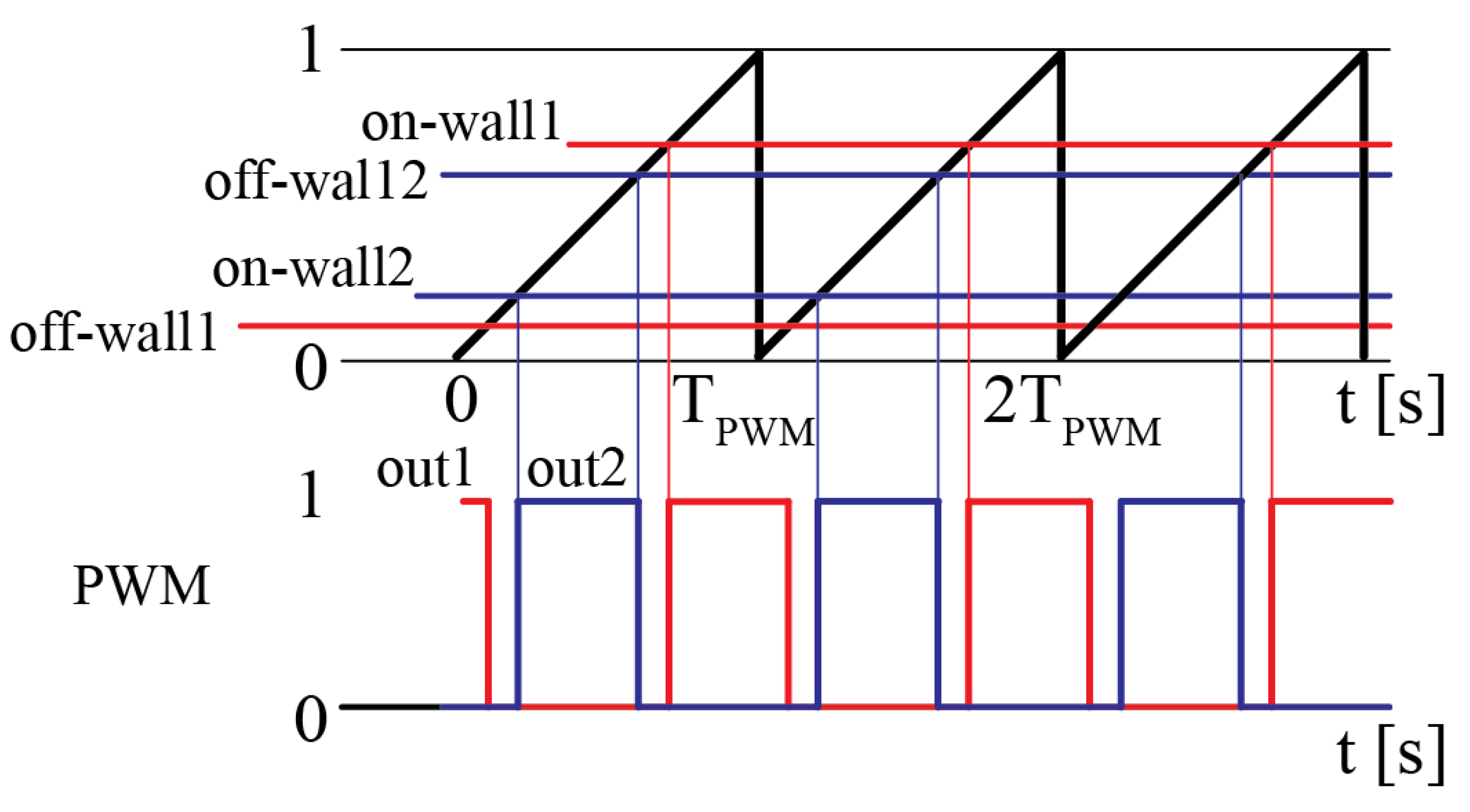
3. Bus Control Loop
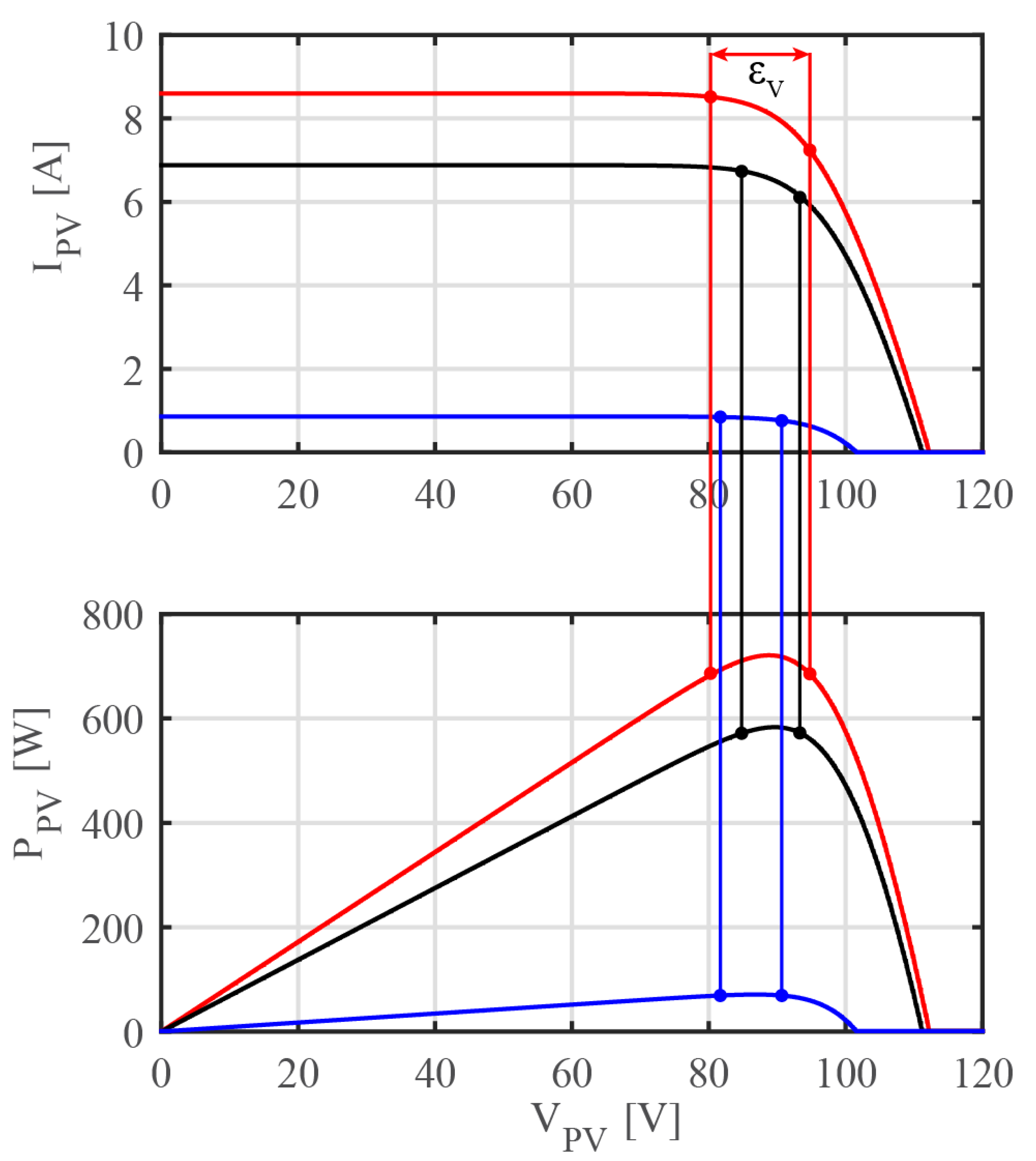
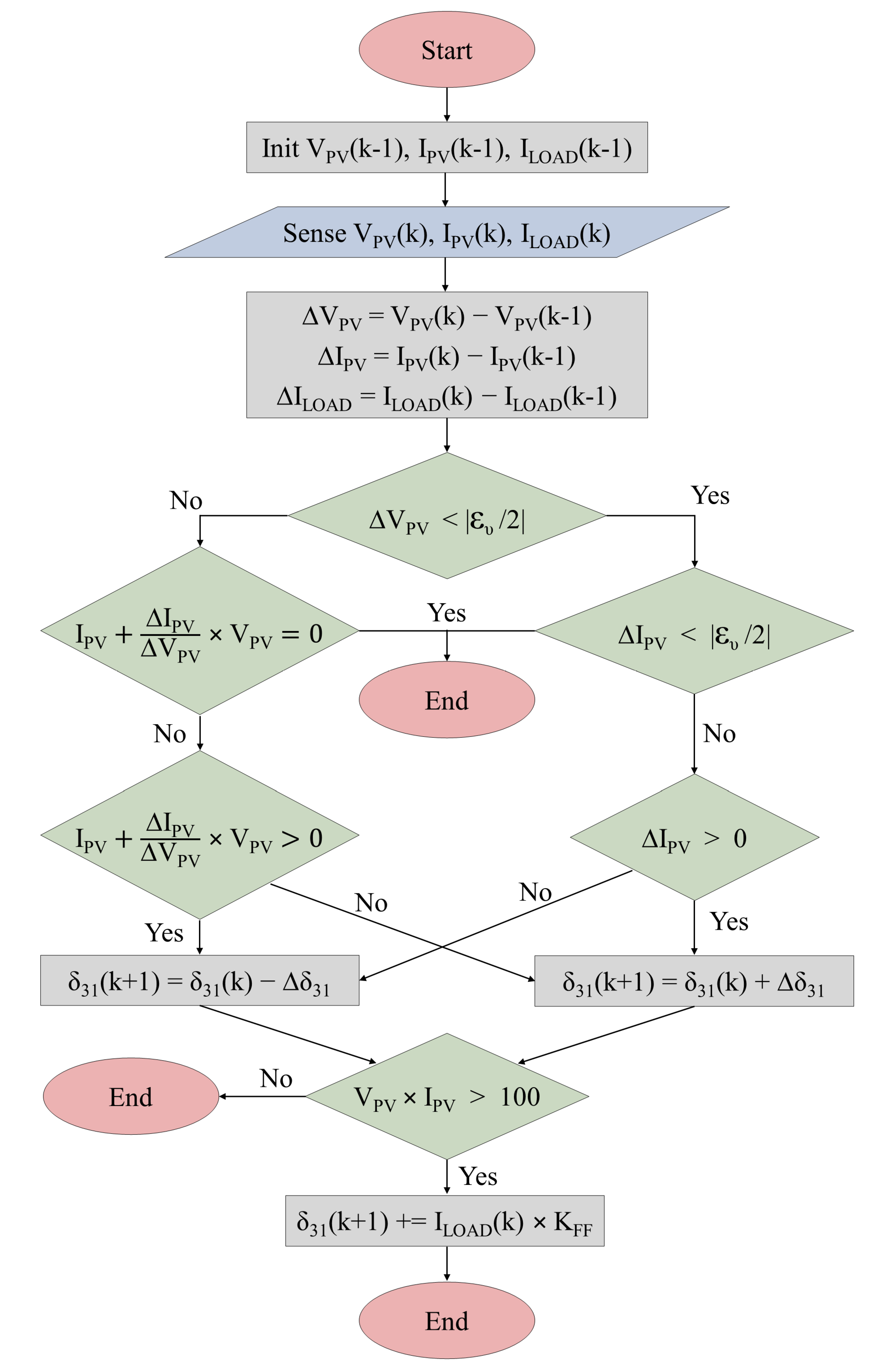
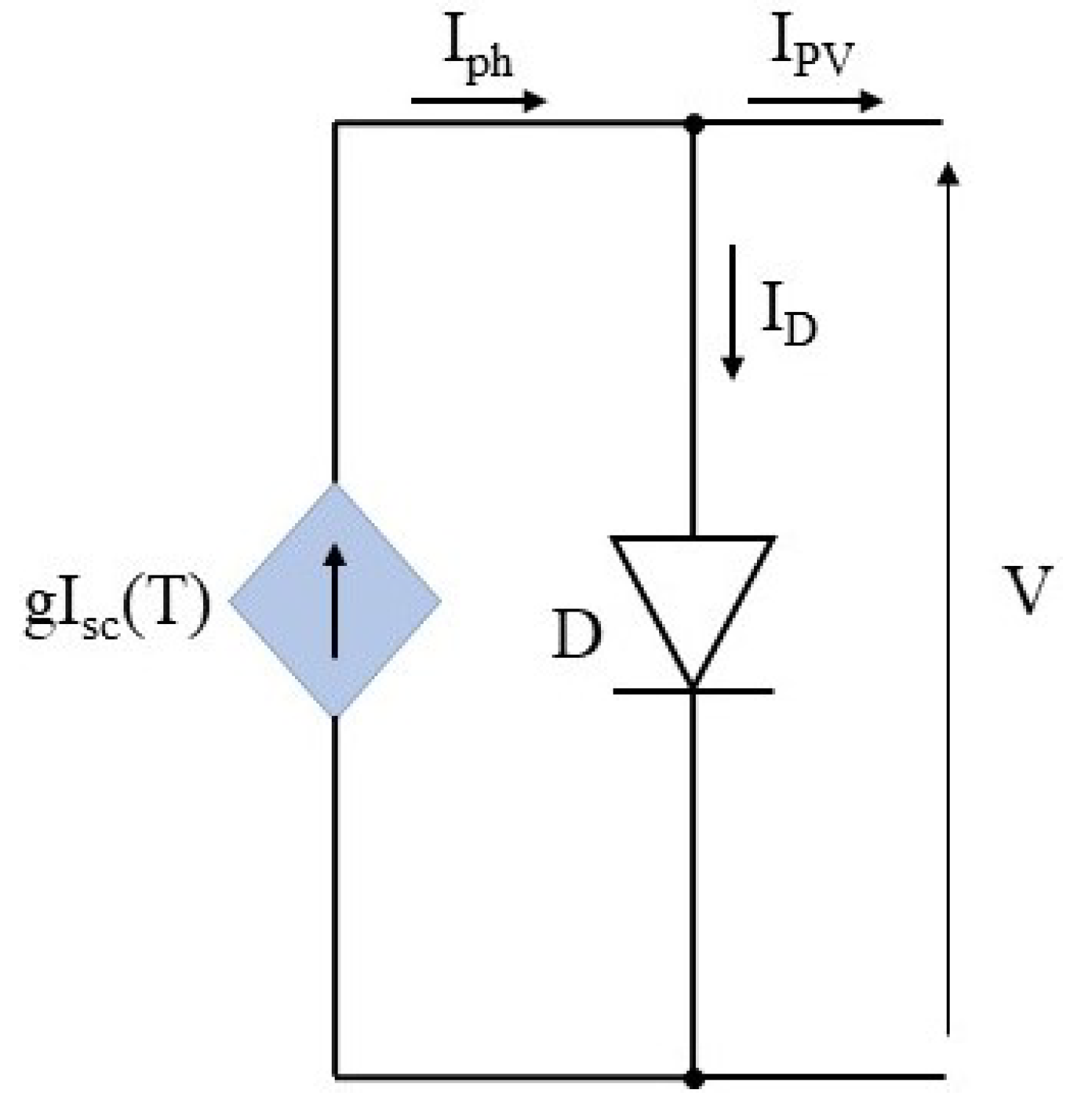
4. MPPT Control Loop
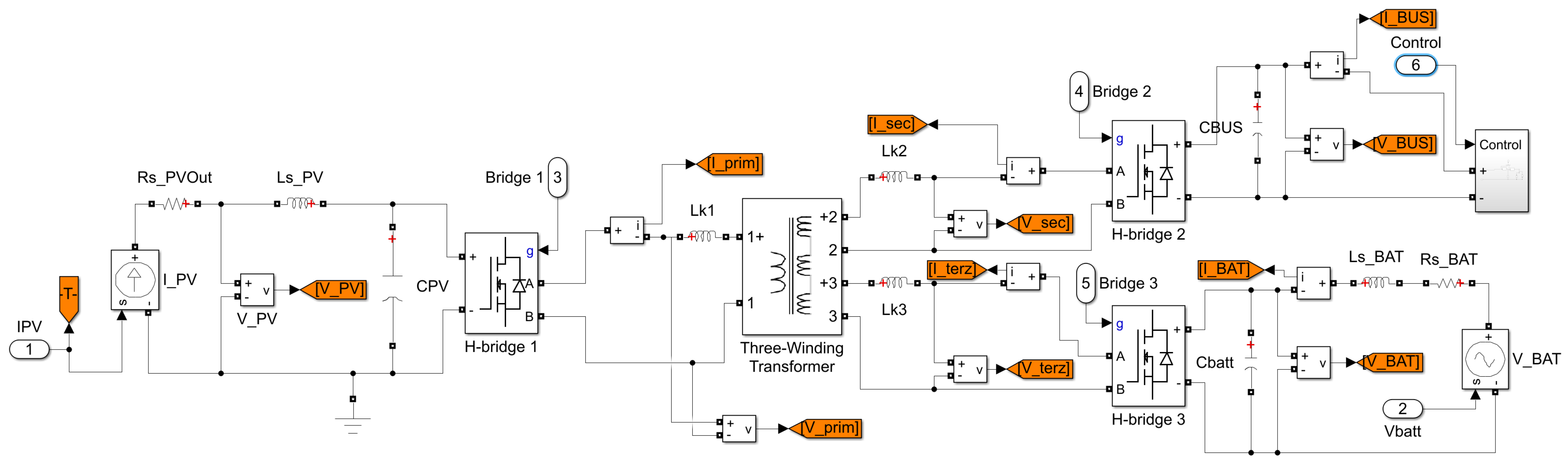
5. Simulated Model
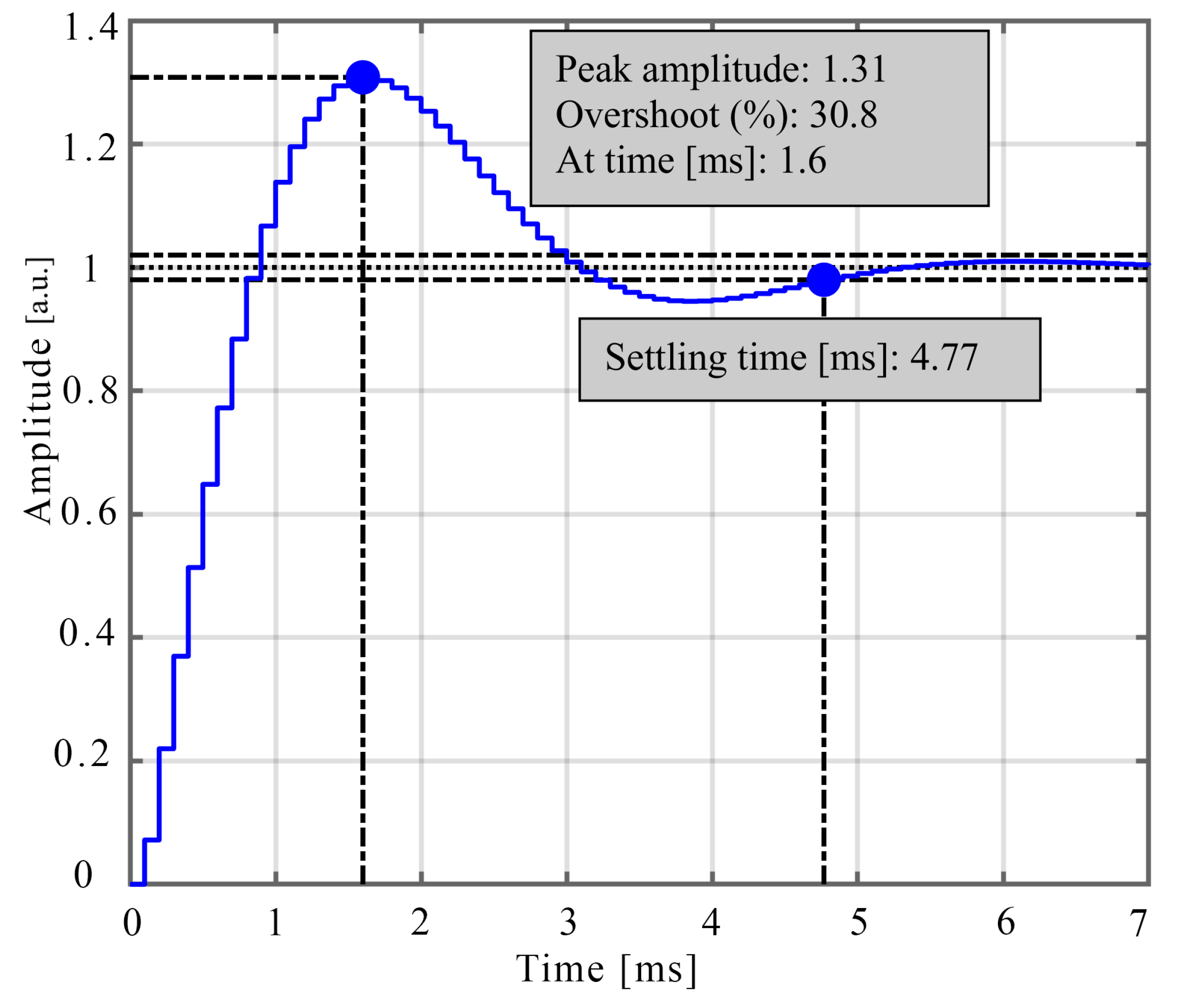
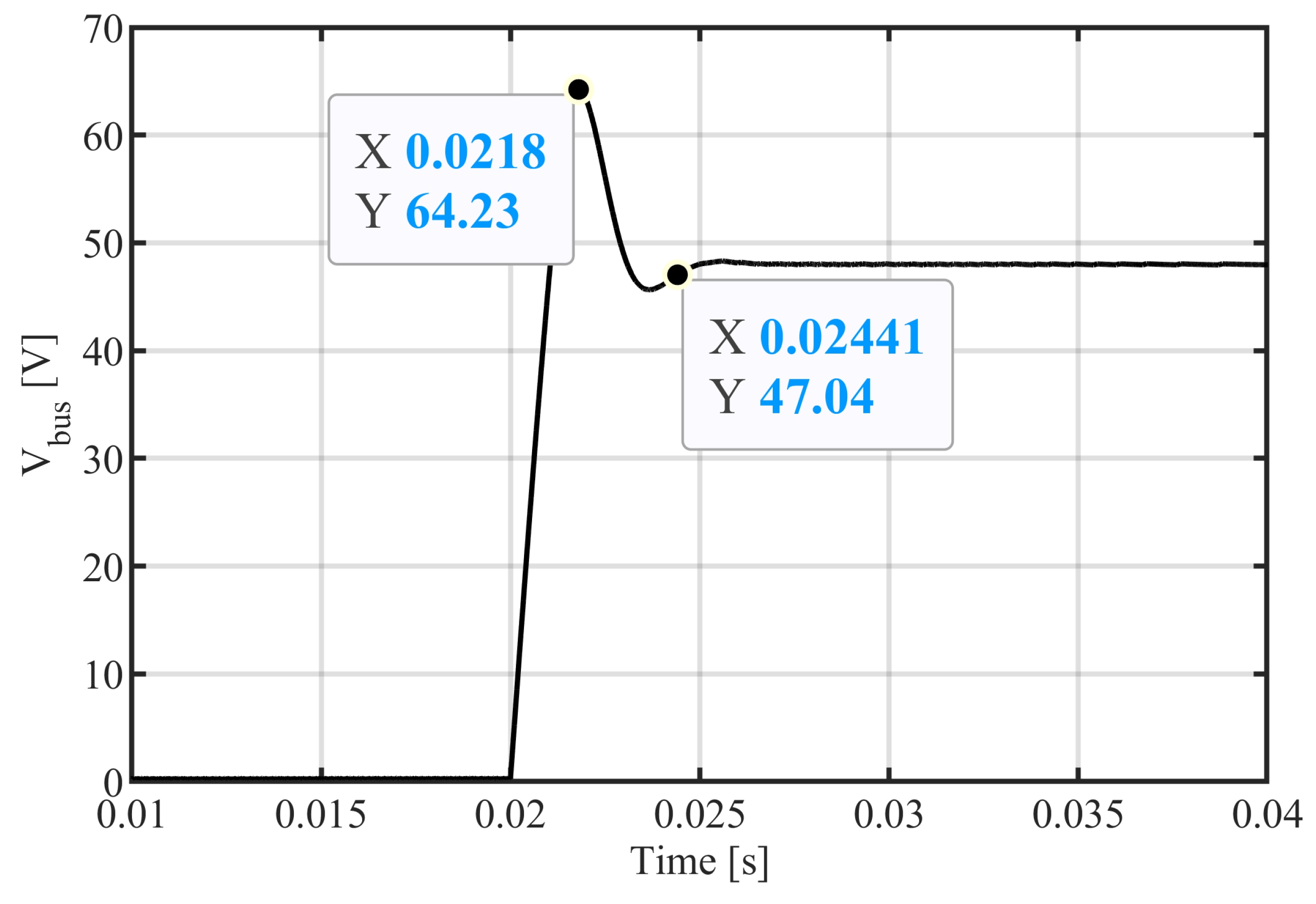
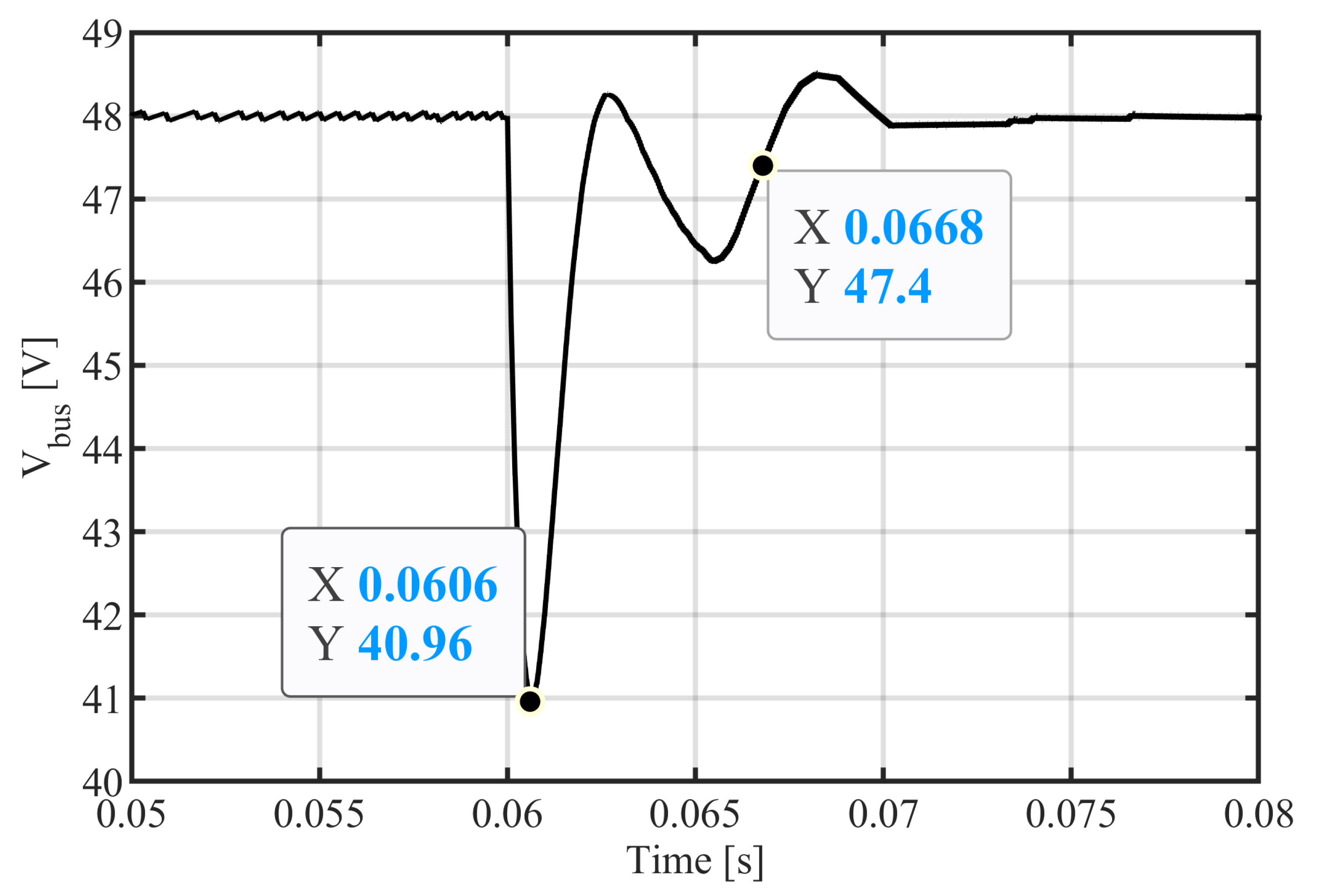
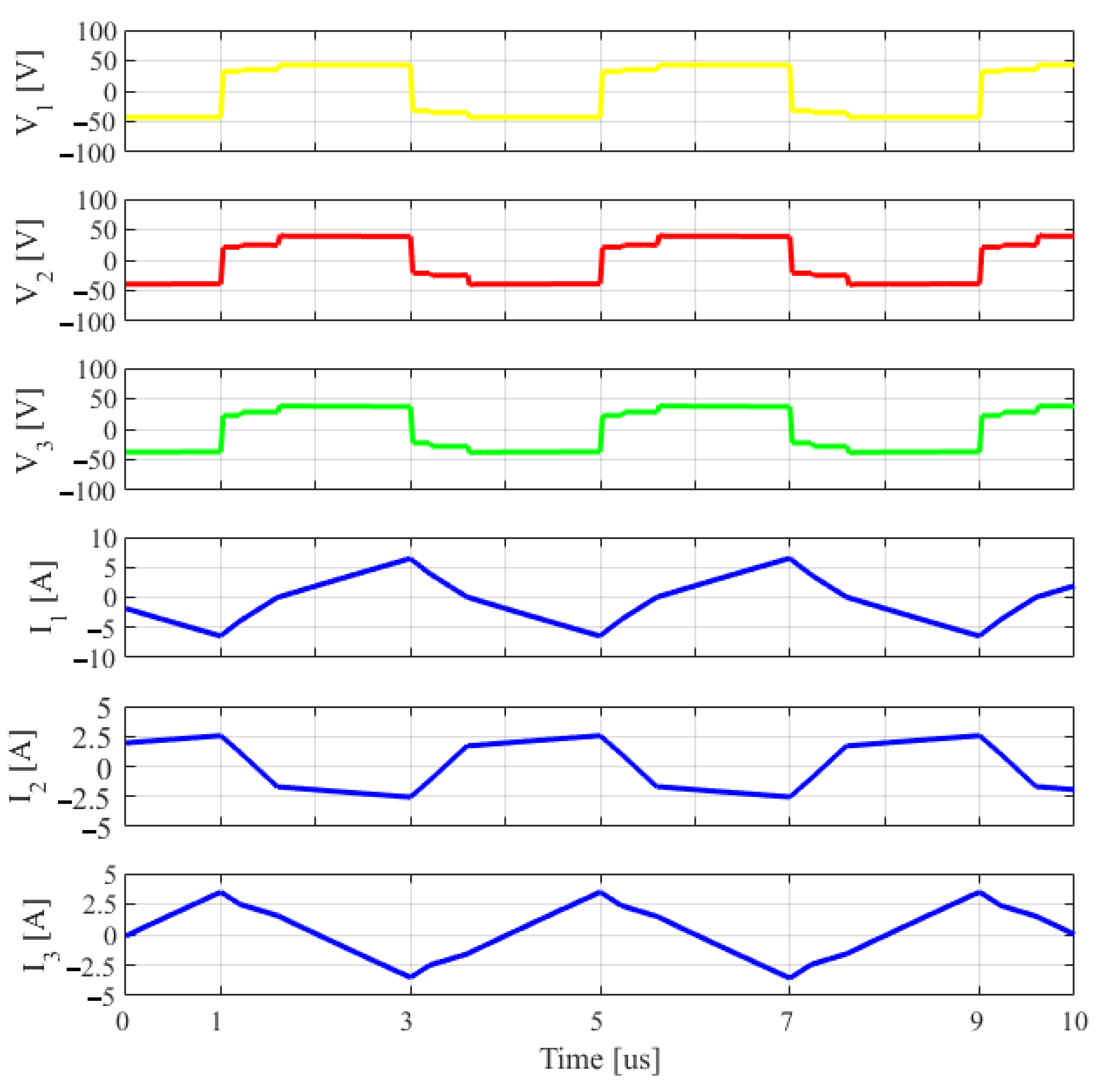
6. Model Validation with Early Experimental Results
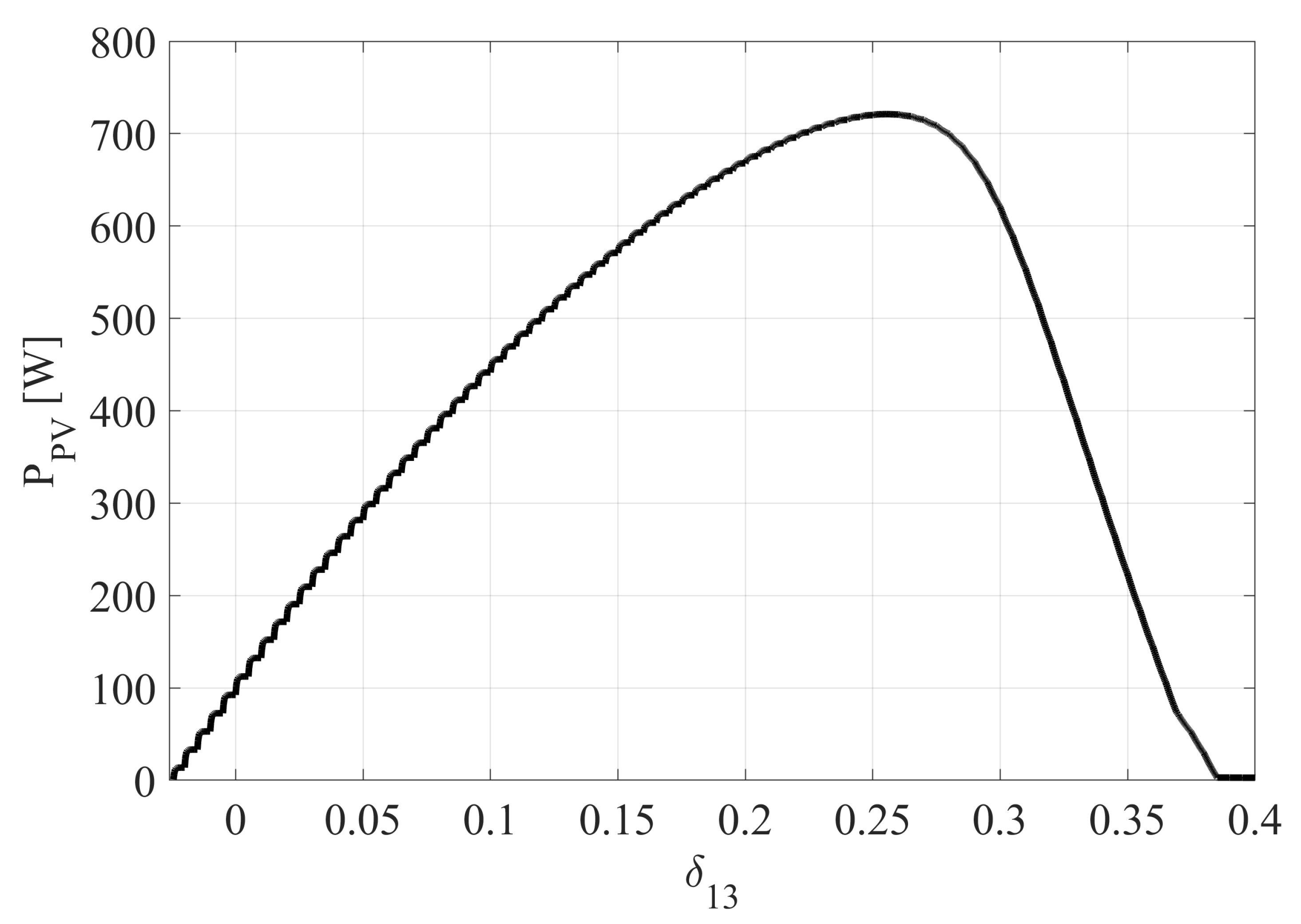
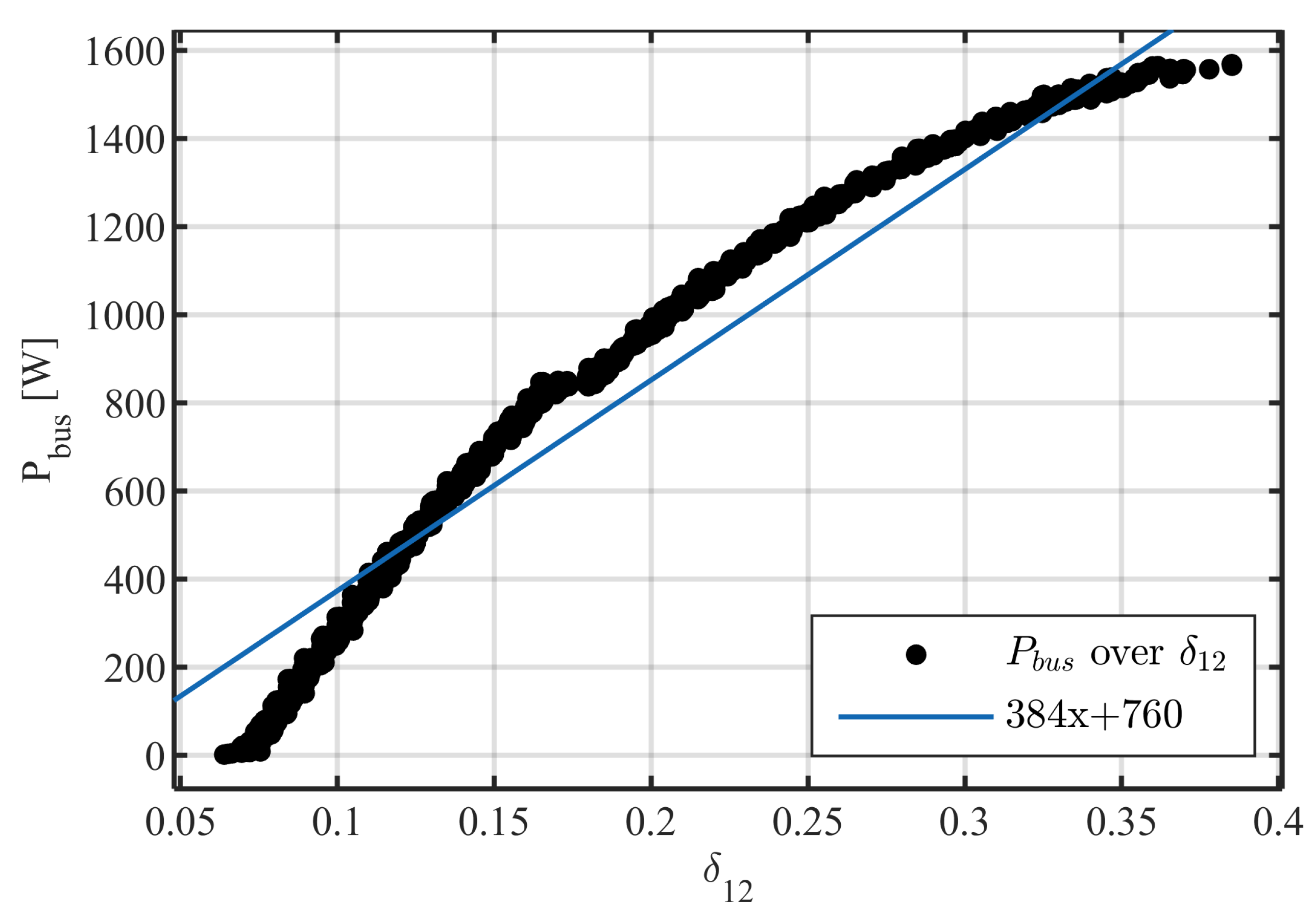
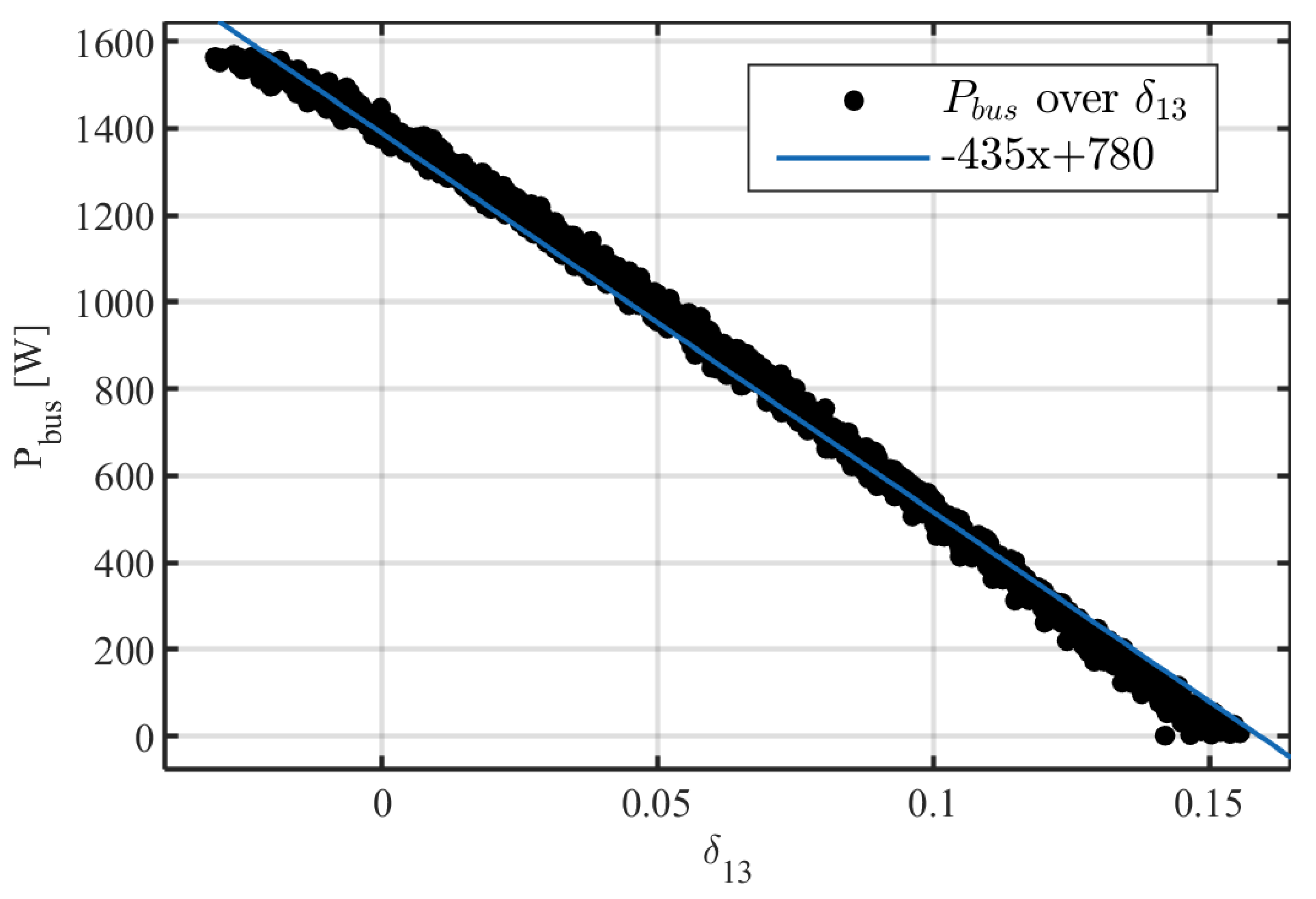
7. Simulation Results and Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Boroyevich, D.; Cvetković, I.; Dong, D.; Burgos, R.; Wang, F.; Lee, F. Future electronic power distribution systems—A contemplative view. In Proceedings of the International Conference on Optimisation of Electrical and Electronic Equipment, Brasov, Romania, 20–22 May 2010. [Google Scholar]
- Goikoetxea, A.; Canales, J.M.; Sanchez, R.; Zumeta, P. DC versus AC in residential buildings: Efficiency comparison. In Proceedings of the International Conference IEEE EuroCon 2013, Zagreb, Croatia, 1–4 July 2013. [Google Scholar]
- Burmester, D.; Rayudu, R.; Seah, W.; Akinyele, D. A review of nanogrid topologies and technologies. Renew. Sustain. Energy Rev. 2017, 67, 760–775. [Google Scholar] [CrossRef]
- Yu, Y.; Wada, K.; Masumoto, K.; Kado, Y. A DC power distribution system In a data center using a triple active bridge DC-DC converter. IEEJ J. Ind. Appl. 2018, 7, 202–209. [Google Scholar] [CrossRef]
- Liu, R.; Xu, L.; Kang, Y.; Hui, Y.; Li, Y. Decoupled TAB converter with energy storage system for HVDC power system of more electric aircraft. J. Eng. 2018, 13, 593–602. [Google Scholar] [CrossRef]
- Wang, Z.; Castellazzi, A. SiC-based Triple Active Bridge Converter for Shipboard Micro-grid Applications with Efficient Energy Storage. In Proceedings of the 6th IEEE International Conference on Smart Grid icSmartGrids, Nagasaki, Japan, 4–6 December 2018. [Google Scholar]
- Giuliani, F.; Buticchi, G.; Liserre, M.; Delmonte, N.; Cova, P.; Pignoloni, N. GaN-based Triple Active Bridge for Avionic Application. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017. [Google Scholar]
- Michon, M.; Duarte, J.L.; Hendrix, M.; Simões, M.G. A three-port bi-directional converter for hybrid fuel cell systems. In Proceedings of the International Conference PESC Record—IEEE Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004. [Google Scholar]
- Duarte, J.L.; Hendrix, M.; Simões, M.G. Three-port bidirectional converter for hybrid fuel cell systems. IEEE Trans. Power Electron. 2007, 22, 480–487. [Google Scholar] [CrossRef]
- Zou, S.; Lu, J.; Khaligh, A. Modelling and control of a triple-activebridge converter. IET Power Electron. 2020, 13, 961–969. [Google Scholar] [CrossRef]
- Dos Santos, W.M.; Marcon, R.C.; Martins, D.C. Application of the voltage fed TAB converter as energy source coupler. IEEE Lat. Am. Trans. 2011, 9, 510–515. [Google Scholar] [CrossRef]
- Chattopadhyay, R.; Acharya, S.; Gohil, G.; Bhattacharya, S. One switching cycle current control strategy for Triple Active Bridge phaseshifted DC-DC converter. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–8. [Google Scholar]
- Zhao, C.; Round, S.D.; Kolar, J.W. An isolated three-port bidirectional dc-dc converter with decoupled power flow management. IEEE Trans. Power Electron. 2008, 23, 2443–2453. [Google Scholar] [CrossRef]
- Ilango, S.; Viju Nair, R.; Chattopadhyay, R.; Bhattacharya, S. Photovoltaic and energy storage grid integration with fully modular architecture using triple port active bridges and cascaded H-bridge inverter. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar]
- Nair, R.V.; Gulur, S.; Chattopadhyay, R.; Beddingfield, R.; Mathur, S.; Bhattacharya, S.; Gohil, G.; Ohodnicki, P. Large Scale Grid Integration of Photovoltaic and Energy Storage Systems Using Triple Port Dual Active Bridge Converter Modules. In Proceedings of the International Conference IEEE Power and Energy Society General Meeting, Portland, OR, USA, 5–10 August 2018. [Google Scholar]
- Chao, K.H.; Huang, C.H. Bidirectional DC-DC soft-switching converter for stand-alone photovoltaic power generation systems. IET Power Electron. 2014, 7, 1557–1765. [Google Scholar] [CrossRef]
- Delmonte, N.; Cova, P.; Santoro, D.; Toscani, A. Development of a GaN based triple-active-bridge for DC nanogrid. In Proceedings of the 20th European Conference on Power Electronics and Applications, EPE 2018 ECCE Europe, Riga, Latvia, 17–21 September 2018. [Google Scholar]
- De Doncker, R.W.; Divan, D.M.; Kheraluwala, M.H. A Three-Phase Soft-Switched High-Power-Density DC/DC Converter for High-Power Applications. IEEE Trans. Ind. Appl. 1991, 27, 63–73. [Google Scholar] [CrossRef]
- Pham, V.L.; Wada, K. Design of Series Inductances in Triple Active Bridge Converter Using Normalization Procedure for Integrated EV and PV System. In Proceedings of the ICPE 2019—ECCE Asia-10th International Conference on Power Electronics, Bexco, Busan, Korea, 27–30 May 2019. [Google Scholar]
- Tao, H.; Duarte, J.L.; Hendrix, M.A. Three-port triple-half-bridge bidirectional converter with zero-voltage switching. IEEE Trans. Power Electron. 2008, 23, 782–792. [Google Scholar]
- Luo, S.; Wu, F.; Wang, G. Improved TPS control for DAB DC-DC converter to eliminate dual-side flow back currents. IET Power Electron. 2020, 13, 32–39. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Li, H. Asymmetrical duty cycle control and decoupled power flow design of a three-port bidirectional DC-DC converter for fuel cell vehicle application. IEEE Trans. Power Electron. 2012, 27, 891–904. [Google Scholar] [CrossRef]
- Sim, J.; Lee, J.; Choi, H.; Jung, J.-H. High Power Density Bidirectional Three-port DC-DC Converter for Battery Applications in DC microgrids. In Proceedings of the ICPE 2019—ECCE Asia—10th International Conference on Power Electronics, Bexco, Busan, Korea, 27–30 May 2019. [Google Scholar]
- Yang, J.; Buticchi, G.; Gu, C.; Gunter, S.; Yan, H.; Wheeler, P. Transfer Function Based Input Impedance Determination of Triple Active Bridge Converter. In Proceedings of the ECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar]
- Mahmoud, Y.; El-Saadany, E. Accuracy improvement of the ideal PV Model. IEEE Trans. Sustain. Energy 2015, 6, 909–911. [Google Scholar] [CrossRef]
- Elkholy, A.; Abou El-Ela, A.A. Optimal parameters estimation and modelling of photovoltaic modules using analytical method. Heliyon 2019, 5, 7. [Google Scholar] [CrossRef] [PubMed]
- Carter, R.; Cruden, A.; Hall, P.J.; Zaher, A.S. An improved lead-acid battery pack model for use in power simulations of electric vehicles. IEEE Trans. Energy Convers. 2012, 27, 21–28. [Google Scholar] [CrossRef]
- Transphorm. TDHBG2500P100: 2.5kW Half-bridge Evaluation Board. User Guide. 2017. Available online: https://www.transphormusa.com/en/document/tdhbg2500p100-user-guide/ (accessed on 1 March 2021).
- Kado, Y.; Katagiri, K. Autonomous Distributed Power Network Consisting of Triple Active Bridge Converters. In Proceedings of the International Conference Energy and Sustainability in Small Developing Economies, Funchal, Portugal, 9–12 July 2018. [Google Scholar]
- Katagiri, K.; Nakagawa, S.; Kado, Y. Analysis on Load-Factor Dependence of Triple Active Bridge Converter’s Transmission Efficiency for Autonomous Power Networks. In Proceedings of the International Conference IEEE Region 10 Conference (TENCON), Penang, Malaysia, 5–8 November 2017. [Google Scholar]



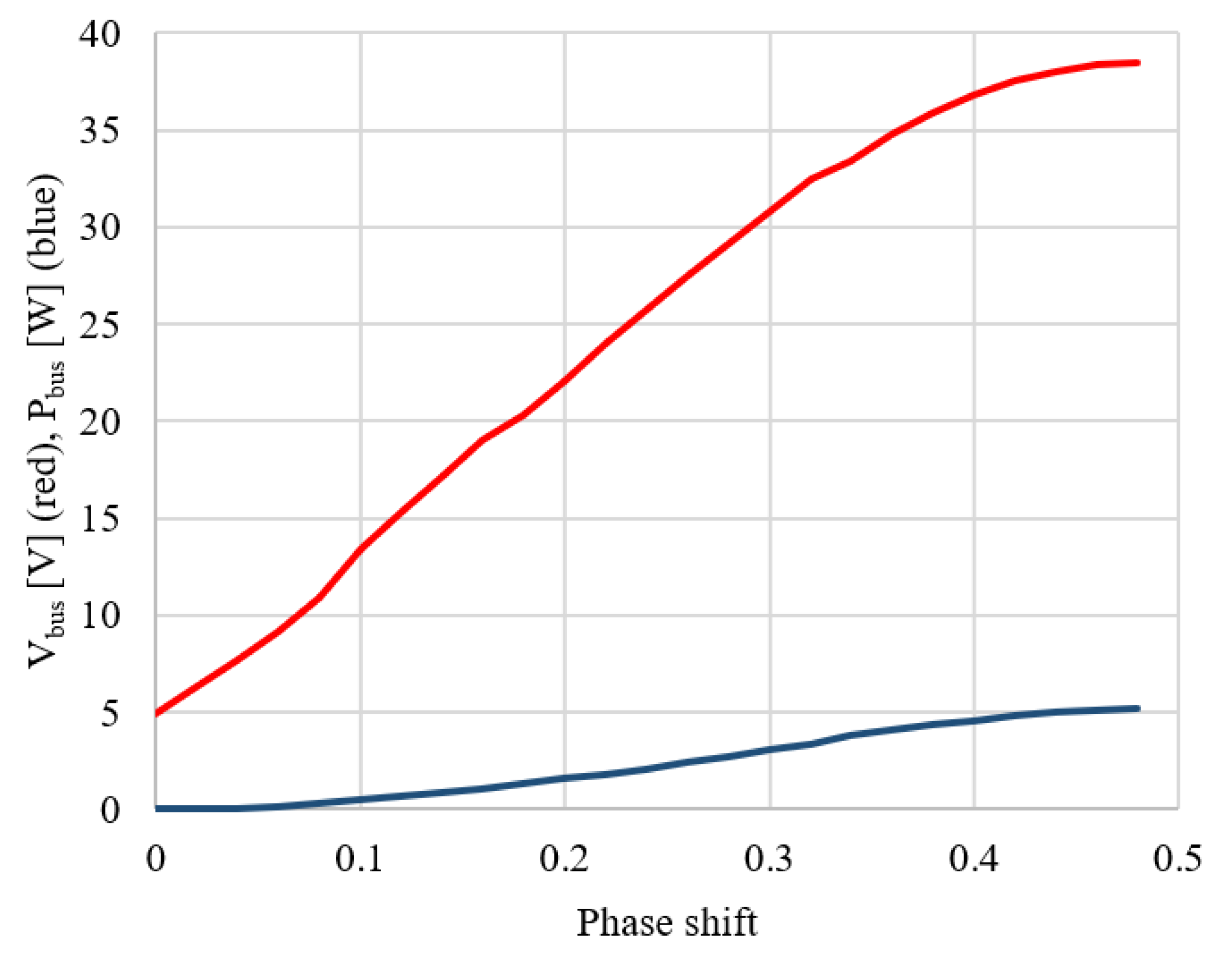
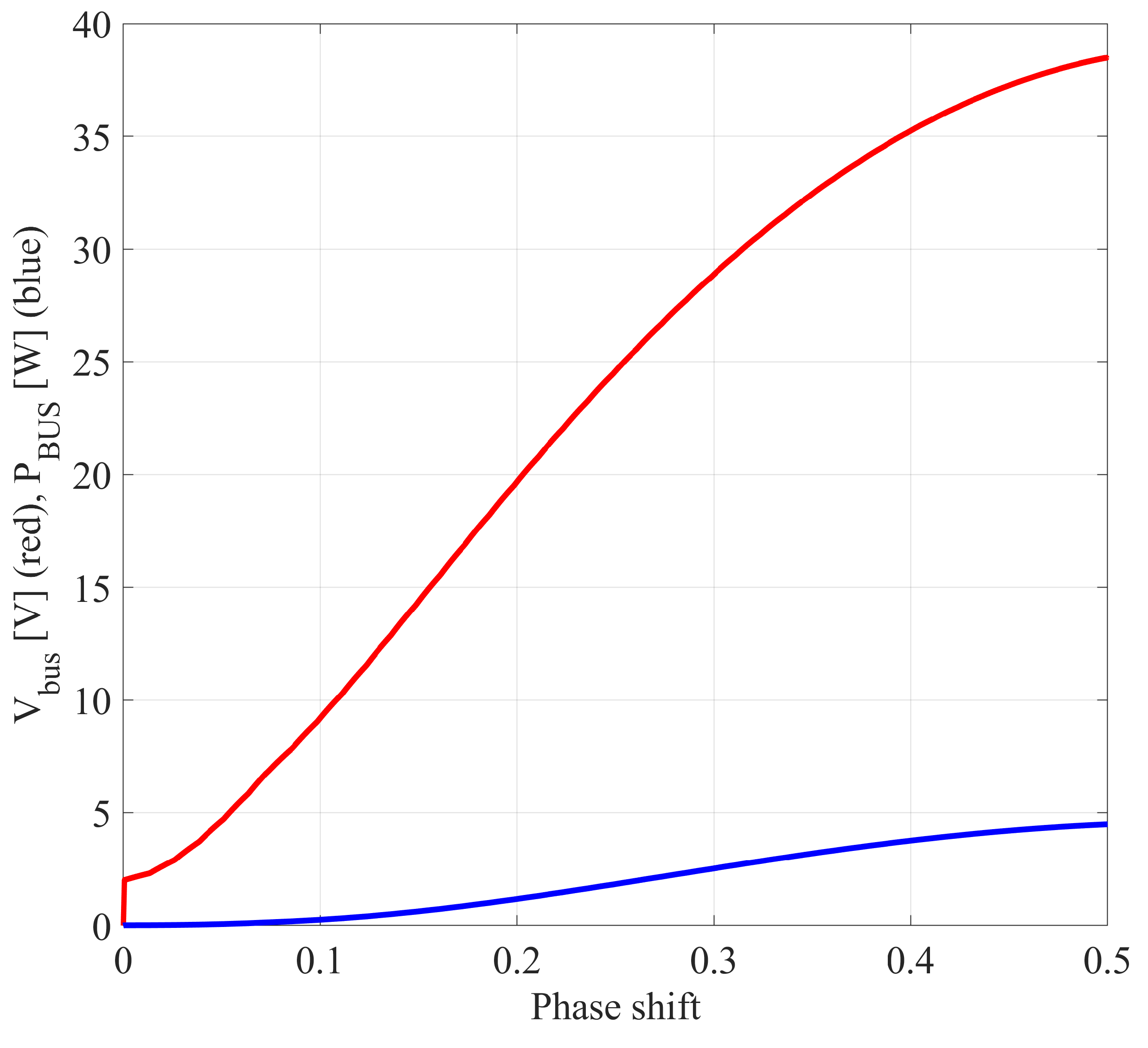
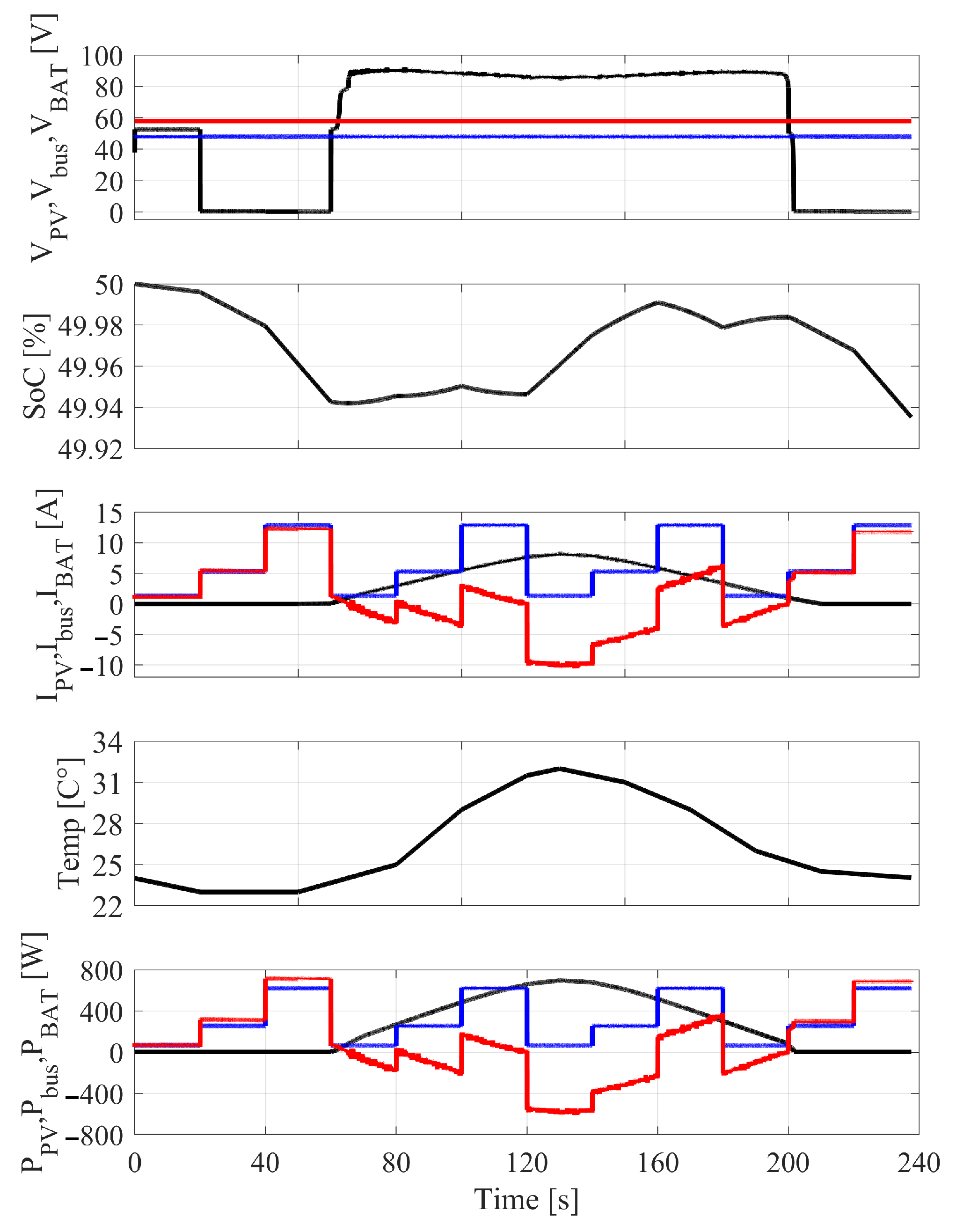
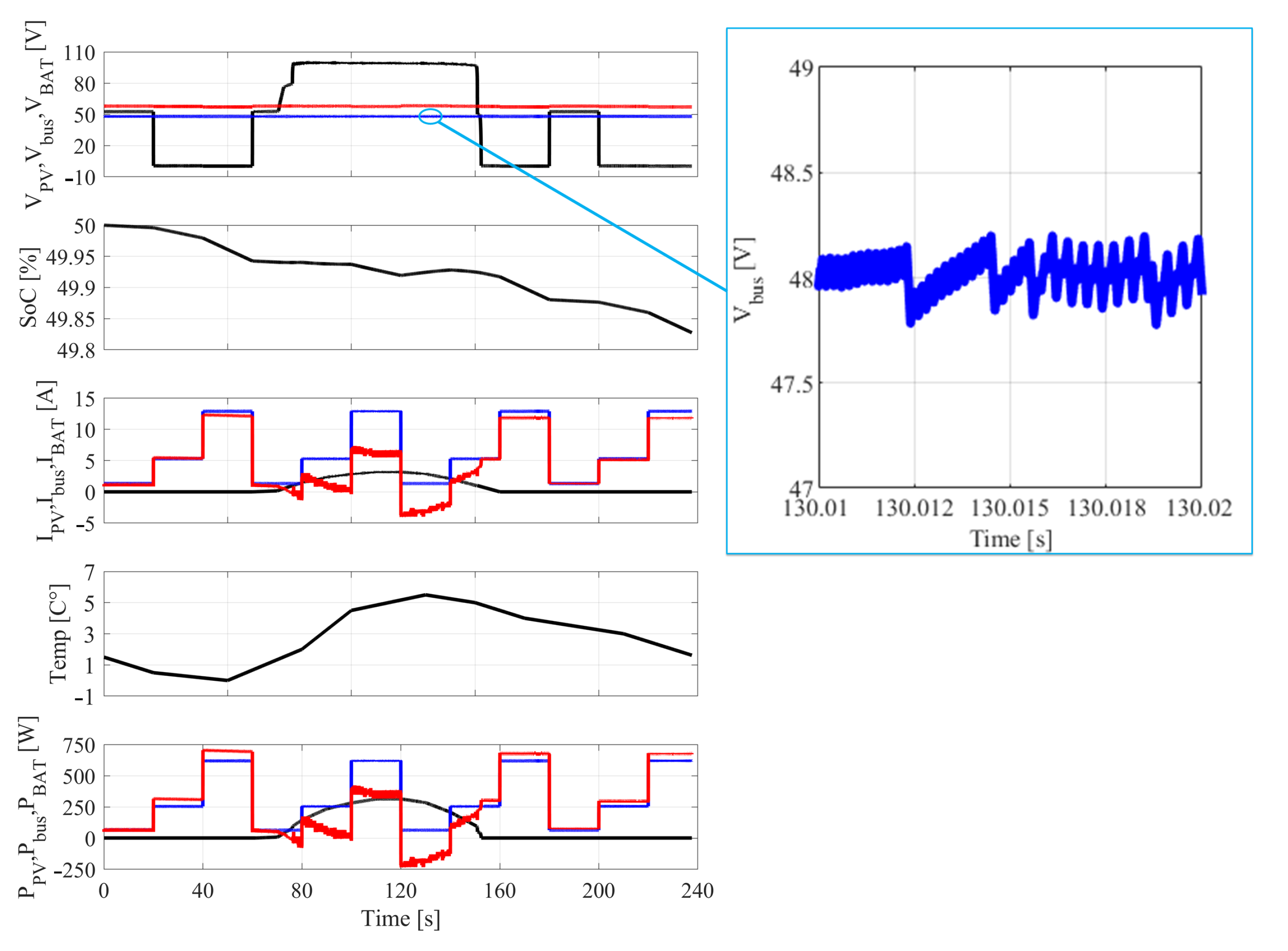
| (a) PV Parameters | |||
|---|---|---|---|
| Max [W] | [V] | [A] | [F] |
| 721 | 112.2 | 8.6 | 470 |
| (b) Bus parameters | |||
| Max [W] | [V] | [F] | |
| 1570 | 48 | 470 | |
| (c) Battery parameters | |||
| Capacity [Ah] | [V] | [F] | [A] |
| 200 | 48 | 470 | 450 |
| (d) Transformer parameters | |||
| [kHz] | [mH] | ||
| 100 | 1:1:1 | 0.2 | |
| [H] | [H] | [H] | |
| 2.8 | 1.4 | 1.6 | |
| Simulation [ns] | Control [μs] | Control MPPT [ms] |
|---|---|---|
| 25 | 100 | 1 |
| Feed Forward | Step | |
| Feed Forward | ||
| 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santoro, D.; Kortabarria, I.; Toscani, A.; Concari, C.; Cova, P.; Delmonte, N. PV Modules Interfacing Isolated Triple Active Bridge for Nanogrid Applications. Energies 2021, 14, 2854. https://doi.org/10.3390/en14102854
Santoro D, Kortabarria I, Toscani A, Concari C, Cova P, Delmonte N. PV Modules Interfacing Isolated Triple Active Bridge for Nanogrid Applications. Energies. 2021; 14(10):2854. https://doi.org/10.3390/en14102854
Chicago/Turabian StyleSantoro, Danilo, Iñigo Kortabarria, Andrea Toscani, Carlo Concari, Paolo Cova, and Nicola Delmonte. 2021. "PV Modules Interfacing Isolated Triple Active Bridge for Nanogrid Applications" Energies 14, no. 10: 2854. https://doi.org/10.3390/en14102854
APA StyleSantoro, D., Kortabarria, I., Toscani, A., Concari, C., Cova, P., & Delmonte, N. (2021). PV Modules Interfacing Isolated Triple Active Bridge for Nanogrid Applications. Energies, 14(10), 2854. https://doi.org/10.3390/en14102854











