Diagnosis and Robust Design Optimization of SPMSM Considering Back EMF and Cogging Torque due to Static Eccentricity
Abstract
:1. Introduction
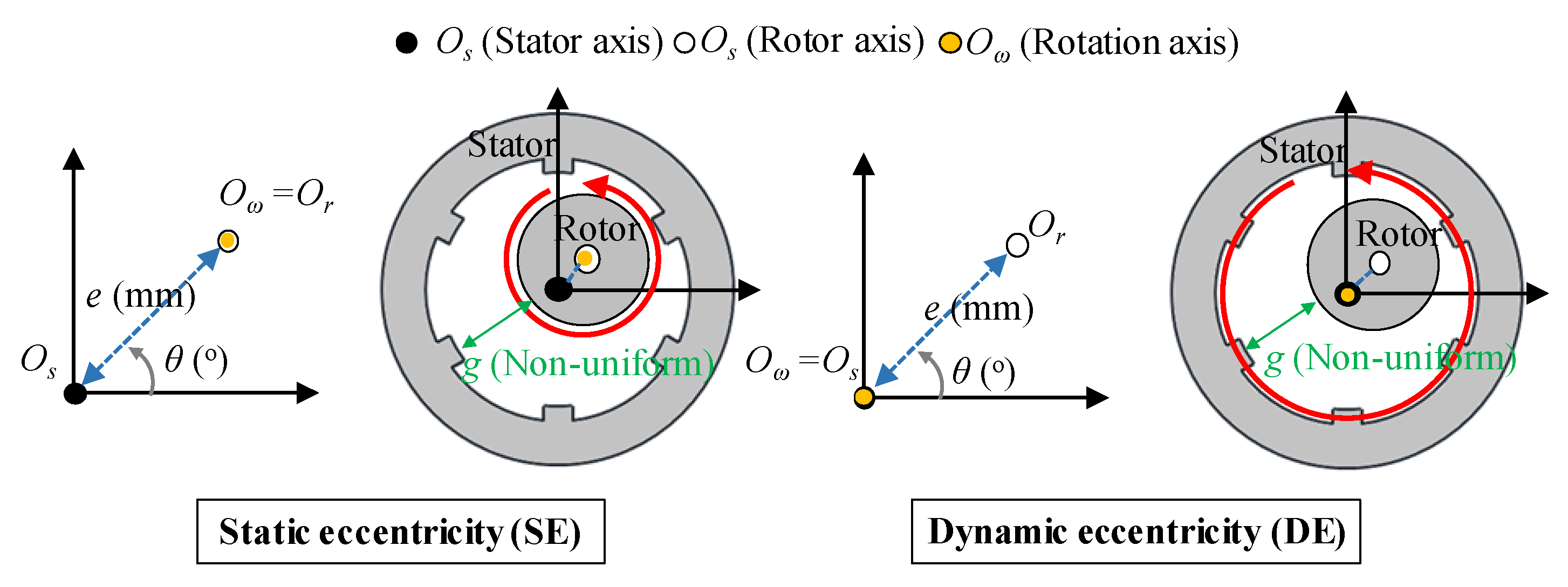
2. Static and Dynamic Eccentricity
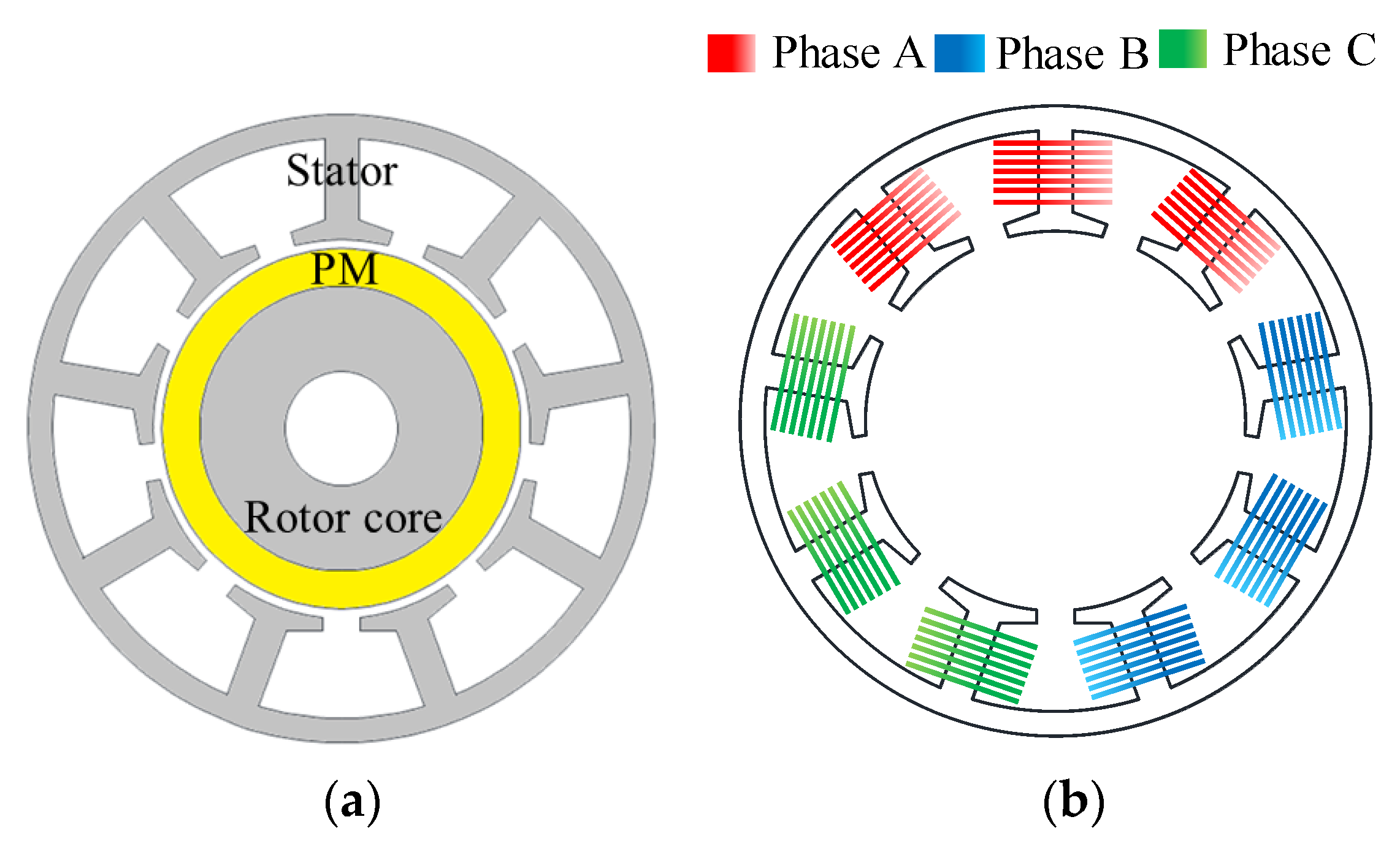
3. Diagnosis and Analysis of Base Model
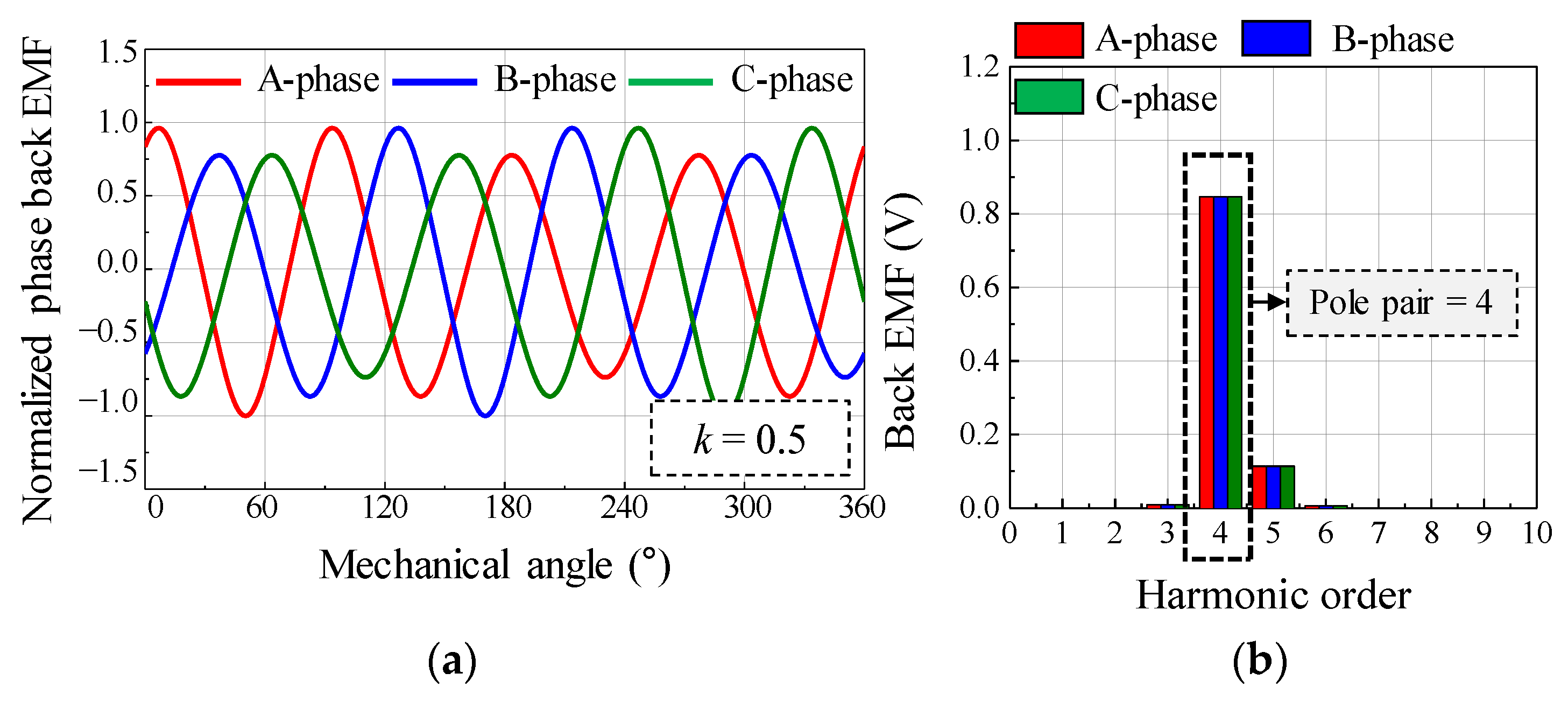
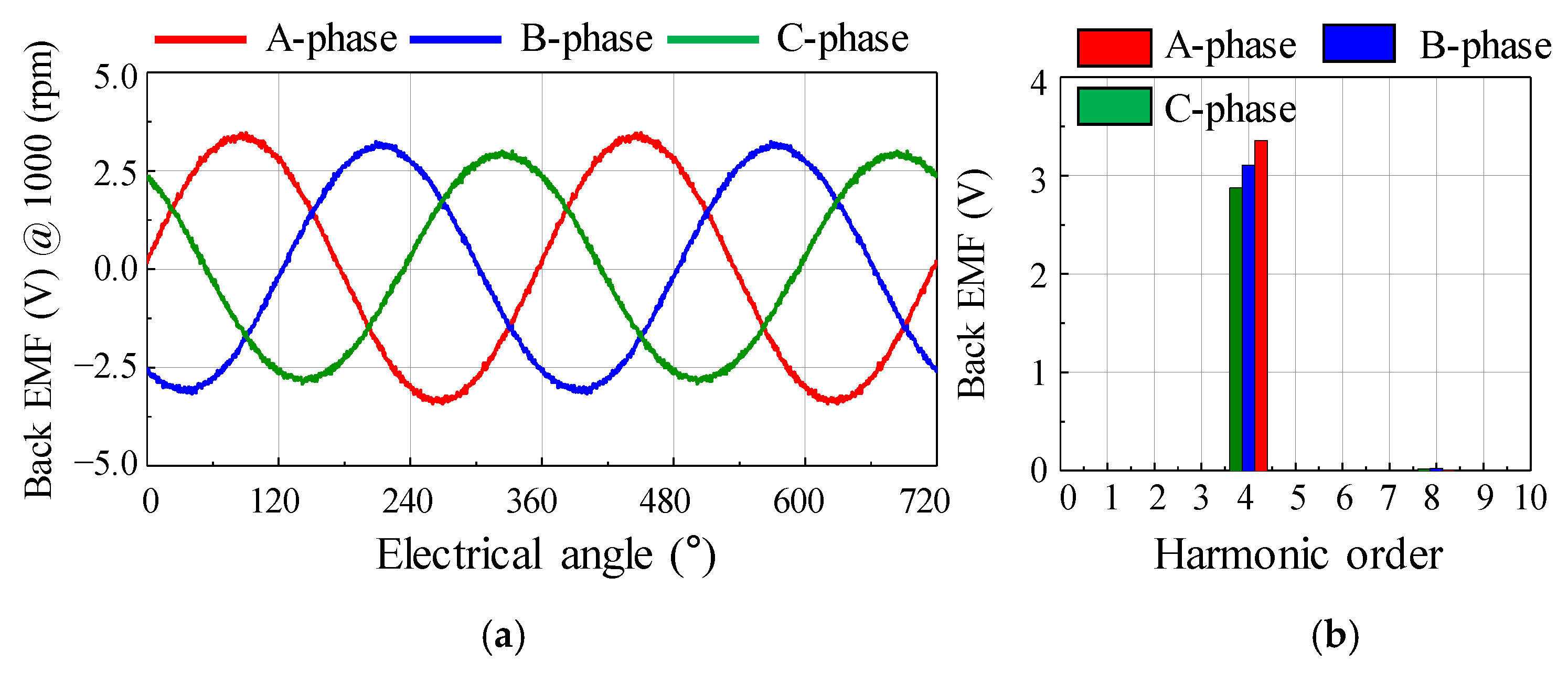
3.1. Back EMF Analysis to Diagnose Rotor Eccentricity
3.2. Cogging Torque Analysis to Diagnose Rotor Eccentricity
4. Robust Design Optimization Considering Static Eccentricity
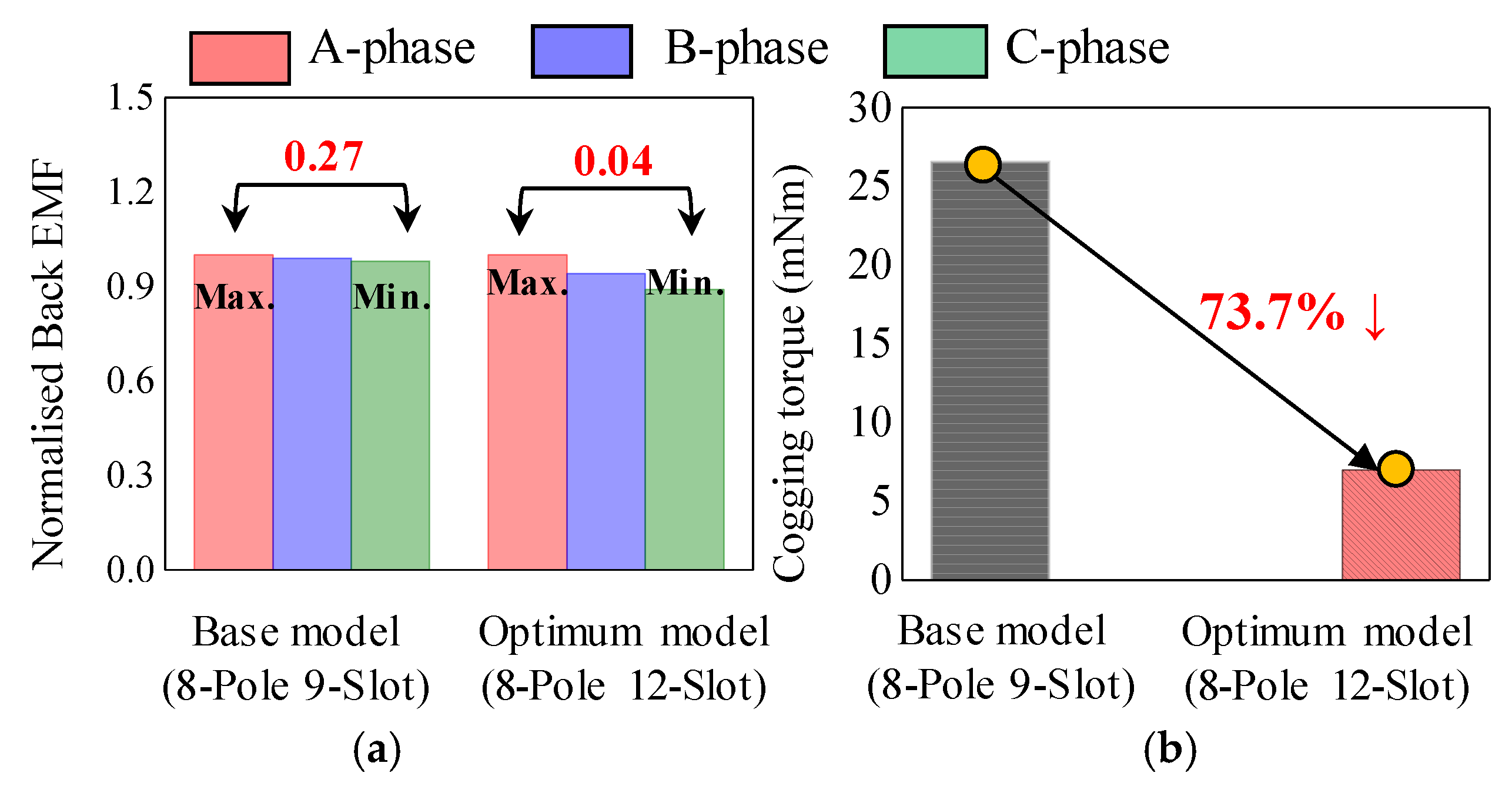
4.1. Selection for the Number of Slots
4.2. Robust Design Optimization
4.2.1. Definition of the Design and Cogging Torque Variables
4.2.2. Kriging Surrogate Model and Determination of the Optimum Design Point
4.2.3. Optimum Model
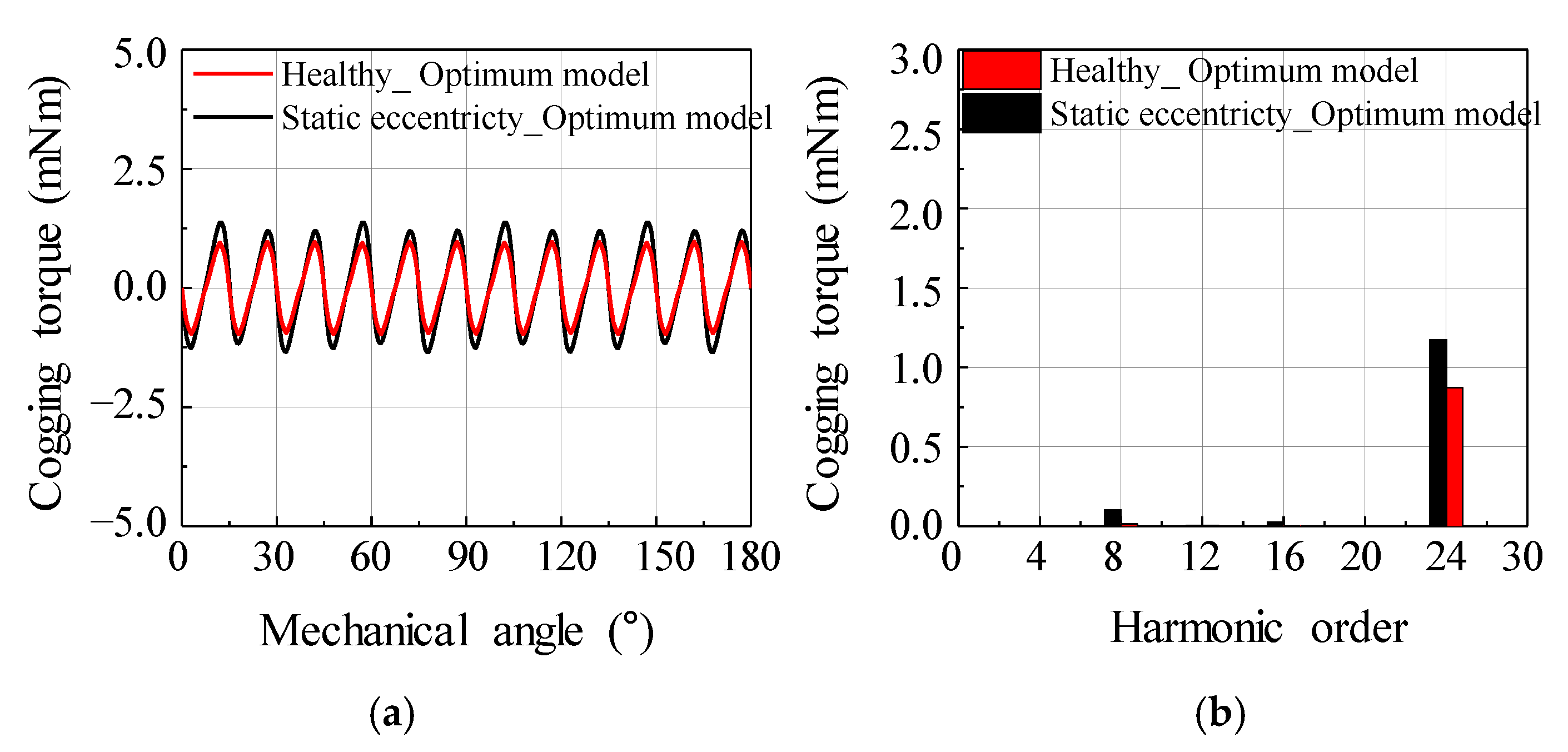
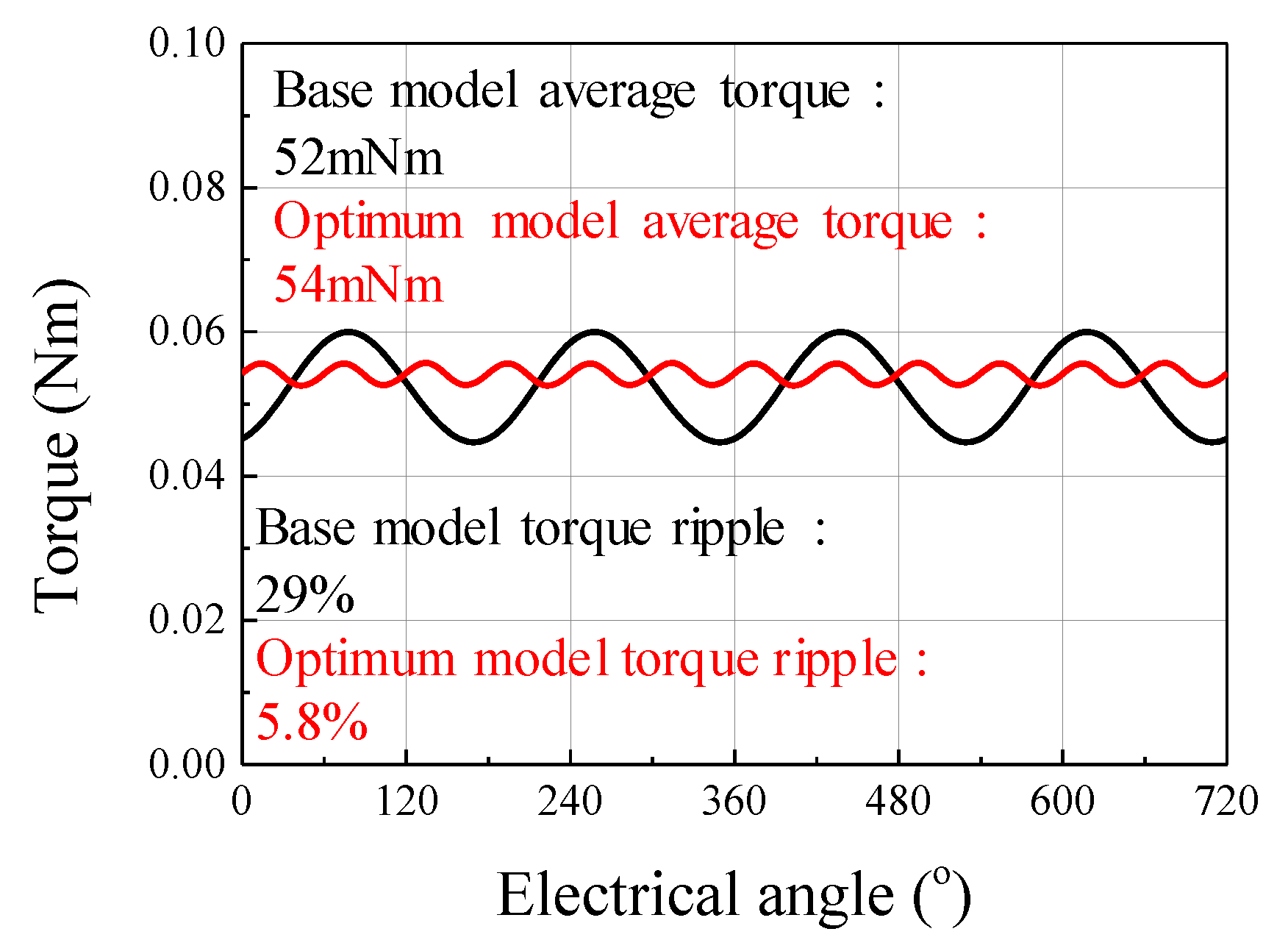
5. Design Result and Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lee, C.-S.; Cha, K.-S.; Park, J.-C.; Lim, M.-S. Tolerance-Insensitive Design of the Magnet Shape for a Surface Permanent Magnet Synchronous Motor. Energies 2020, 13, 1311. [Google Scholar] [CrossRef] [Green Version]
- Song, B.-K.; Kim, D.-K.; Kim, S.-I.; Park, H.-J.; Lee, G.-H.; Lim, M.-S. Comparative Study on Surface-Mounted Permanent Magnet Motors With Segmented and Connected Core for Brake System. IEEE Access 2020, 8, 167930–167938. [Google Scholar] [CrossRef]
- Park, S.-H.; Park, J.-C.; Hwang, S.-W.; Kim, J.-H.; Park, H.-J.; Lim, M.-S. Suppression of Torque Ripple Caused by Misalignment of the Gearbox by Using Harmonic Current Injection Method. IEEE/ASME Trans. Mechatron. 2020, 25, 1990–1999. [Google Scholar] [CrossRef]
- Tong, W.; Li, S.; Pan, X.; Wu, S.; Tang, R. Analytical Model for Cogging Torque Calculation in Surface-Mounted Permanent Magnet Motors with Rotor Eccentricity and Magnet Defects. IEEE Trans. Energy Convers. 2020, 35, 2191–2200. [Google Scholar] [CrossRef]
- Lee, H.-K.; Shin, K.-H.; Bang, T.-K.; Nah, J.-H.; Choi, J.-Y. Experimental Verification and Analytical Study of Influence of Rotor Eccentricity on Electromagnetic Characteristics of Permanent Magnet Machine. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Le Roux, W.; Habetler, T.G.; Harley, R.G. Dynamic Eccentricity and Demagnetized Rotor Magnet Detection in Trapezoidal Flux (Brushless DC) Motors Operating Under Different Load Conditions. IEEE Trans. Power Electron. 2007, 22, 2061–2069. [Google Scholar] [CrossRef]
- Goktas, T.; Zafarani, M.; Akin, B. Discernment of Broken Magnet and Static Eccentricity Faults in Permanent Magnet Synchronous Motors. IEEE Trans. Energy Convers. 2016, 31, 578–587. [Google Scholar] [CrossRef]
- Ajily, E.; Ardebili, M.; Abbaszadeh, K. Magnet Defect and Rotor Eccentricity Modeling in Axial-Flux Permanent-Magnet Machines via 3-D Field Reconstruction Method. IEEE Trans. Energy Convers. 2015, 31, 486–495. [Google Scholar] [CrossRef]
- Faiz, J.; Ebrahimi, B.; Akin, B.; Toliyat, H. Comprehensive Eccentricity Fault Diagnosis in Induction Motors Using Finite Element Method. IEEE Trans. Magn. 2009, 45, 1764–1767. [Google Scholar] [CrossRef]
- Ogidi, O.O.; Barendse, P.S.; Khan, M.A. Influence of Rotor Topologies and Cogging Torque Minimization Techniques in the Detection of Static Eccentricities in Axial-Flux Permanent-Magnet Machine. IEEE Trans. Ind. Appl. 2016, 53, 161–170. [Google Scholar] [CrossRef]
- Barmpatza, A.C.; Kappatou, J.C. Study of a Combined Demagnetization and Eccentricity Fault in an AFPM Synchronous Generator. Energies 2020, 13, 5609. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Faiz, J.; Roshtkhari, M.J. Static-, Dynamic-, and Mixed-Eccentricity Fault Diagnoses in Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2009, 56, 4727–4739. [Google Scholar] [CrossRef]
- Del Pizzo, A.; Di Noia, L.P.; Fedele, E. A Simple Analytical Model of Static Eccentricity for PM Brushless Motors and Validation through FEM Analysis. Energies 2020, 13, 3420. [Google Scholar] [CrossRef]
- Faiz, J.; Nejadi-Koti, H. Eccentricity fault diagnosis indices for permanent magnet machines: State-of-the-art. IET Electr. Power Appl. 2019, 13, 1241–1254. [Google Scholar] [CrossRef]
- Madariaga, C.; Jara, W.; Riquelme, D.; Bramerdorfer, G.; Tapia, J.A.; Riedemann, J. Impact of Tolerances on the Cogging Torque of Tooth-Coil-Winding PMSMs with Modular Stator Core by Means of Efficient Superposition Technique. Electronics 2020, 9, 1594. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, M.; Hong, J.; Kim, S. Analysis of cogging torque caused by manufacturing tolerances of surface-mounted permanent magnet synchronous motor for electric power steering. IET Electr. Power Appl. 2016, 10, 691–696. [Google Scholar] [CrossRef]
- Gasparin, L.; Cernigoj, A.; Markic, S.; Fiser, R. Additional Cogging Torque Components in Permanent-Magnet Motors Due to Manufacturing Imperfections. IEEE Trans. Magn. 2009, 45, 1210–1213. [Google Scholar] [CrossRef]
- Coenen, I.; Van Der Giet, M.; Hameyer, K. Manufacturing Tolerances: Estimation and Prediction of Cogging Torque Influenced by Magnetization Faults. IEEE Trans. Magn. 2011, 48, 1932–1936. [Google Scholar] [CrossRef]
- Ou, J.; Liu, Y.; Qu, R.; Doppelbauer, M. Experimental and Theoretical Research on Cogging Torque of PM Synchronous Motors Considering Manufacturing Tolerances. IEEE Trans. Ind. Electron. 2018, 65, 3772–3783. [Google Scholar] [CrossRef]
- Islam, R.; Husain, I. Analytical Model for Predicting Noise and Vibration in Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Appl. 2010, 46, 2346–2354. [Google Scholar] [CrossRef]
- Salah, A.A.; Dorrell, D.G.; Guo, Y. A Review of the Monitoring and Damping Unbalanced Magnetic Pull in Induction Machines Due to Rotor Eccentricity. IEEE Trans. Ind. Appl. 2019, 55, 2569–2580. [Google Scholar] [CrossRef]
- Veras, F.C.; Lima, T.L.V.; Souza, J.S.; Ramos, J.G.G.S.; Filho, A.C.L.; Brito, A.V. Eccentricity Failure Detection of Brushless DC Motors from Sound Signals Based on Density of Maxima. IEEE Access 2019, 7, 150318–150326. [Google Scholar] [CrossRef]
- Vaseghi, B.; Nahid-Mobarakh, B.; Takorabet, N.; Meibody-Tabar, F. Inductance Identification and Study of PM Motor with Winding Turn Short Circuit Fault. IEEE Trans. Magn. 2011, 47, 978–981. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, G. Anti-Interference and Location Performance for Turn-to-Turn Short Circuit Detection in Turbo-Generator Rotor Windings. Energies 2019, 12, 1378. [Google Scholar] [CrossRef] [Green Version]
- Aggarwal, A.; Strangas, E.G. Review of Detection Methods of Static Eccentricity for Interior Permanent Magnet Synchronous Machine. Energies 2019, 12, 4105. [Google Scholar] [CrossRef] [Green Version]
- Lasjerdi, H.; Nasiri-Gheidari, Z.; Tootoonchian, F. Online Static/Dynamic Eccentricity Fault Diagnosis in Inverter-Driven Electrical Machines Using Resolver Signals. IEEE Trans. Energy Convers. 2020, 35, 1973–1980. [Google Scholar] [CrossRef]
- Park, J.-K.; Hur, J. Detection of Inter-Turn and Dynamic Eccentricity Faults Using Stator Current Frequency Pattern in IPM-Type BLDC Motors. IEEE Trans. Ind. Electron. 2015, 63, 1771–1780. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Faiz, J. Feature Extraction for Short-Circuit Fault Detection in Permanent-Magnet Synchronous Motors Using Stator-Current Monitoring. IEEE Trans. Power Electron. 2010, 25, 2673–2682. [Google Scholar] [CrossRef]
- Park, J.-K.; Jeong, C.-L.; Lee, S.-T.; Hur, J. Early Detection Technique for Stator Winding Inter-Turn Fault in BLDC Motor Using Input Impedance. IEEE Trans. Ind. Appl. 2014, 51, 240–247. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Sen, B. Experimental Assessments of a Triple Redundant Nine-Phase Fault-Tolerant PMA SynRM Drive. IEEE Trans. Ind. Electron. 2019, 66, 772–783. [Google Scholar] [CrossRef] [Green Version]
- Shakouhi, M.; Mohamadian, M.; Afjei, E. Fault-Tolerant Control of Brushless DC Motors Under Static Rotor Eccentricity. IEEE Trans. Ind. Electron. 2015, 62, 1400–1409. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, Z.Q.; Wu, Z.; Liu, T.; Li, Y. Analysis and Suppression of Rotor Eccentricity Effects on Fundamental Model Based Sensorless Control of Permanent Magnet Synchronous Machine. IEEE Trans. Ind. Appl. 2020, 56, 4896–4905. [Google Scholar] [CrossRef]
- Xia, C.L.; Xiao, Y.W.; Chen, W.; Shi, T.N. Torque ripple Reduction in Brushless DC drives Based on Reference Current Opti-mization Using Integral Variable Structure Control. IEEE Trans. Ind. Electron. 2014, 61, 738–752. [Google Scholar] [CrossRef]
- Park, G.-J.; Lee, T.-H.; Lee, K.H.; Hwang, K.-H. Robust Design: An Overview. AIAA J. 2006, 44, 181–191. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.-G.; Kim, J.-M.; Lee, T.H.; Lim, M.-S. Robust Design Optimization of Surface-Mounted Permanent Magnet Synchronous Motor Using Uncertainty Characterization by Bootstrap Method. IEEE Trans. Energy Convers. 2020, 35, 2056–2065. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.-G.; Kim, J.-M.; Lee, T.H.; Hong, J.-P. Uncertainty identification method using kriging surrogate model for industrial electromagnetic device. In Proceedings of the Tenth International Conference on Computational Electromagnetics (CEM 2019), Edinburgh, UK, 19–20 June 2019; Volume 14. [Google Scholar] [CrossRef]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Tucker, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.-G.; Kim, S.; Park, J.-C.; Park, M.-R.; Lee, T.H.; Lim, M.-S. Robust Design Optimization of SPMSM for Robotic Actuator Considering Assembly Imperfection of Segmented Stator Core. IEEE Trans. Energy Convers. 2020, 35, 2076–2085. [Google Scholar] [CrossRef]





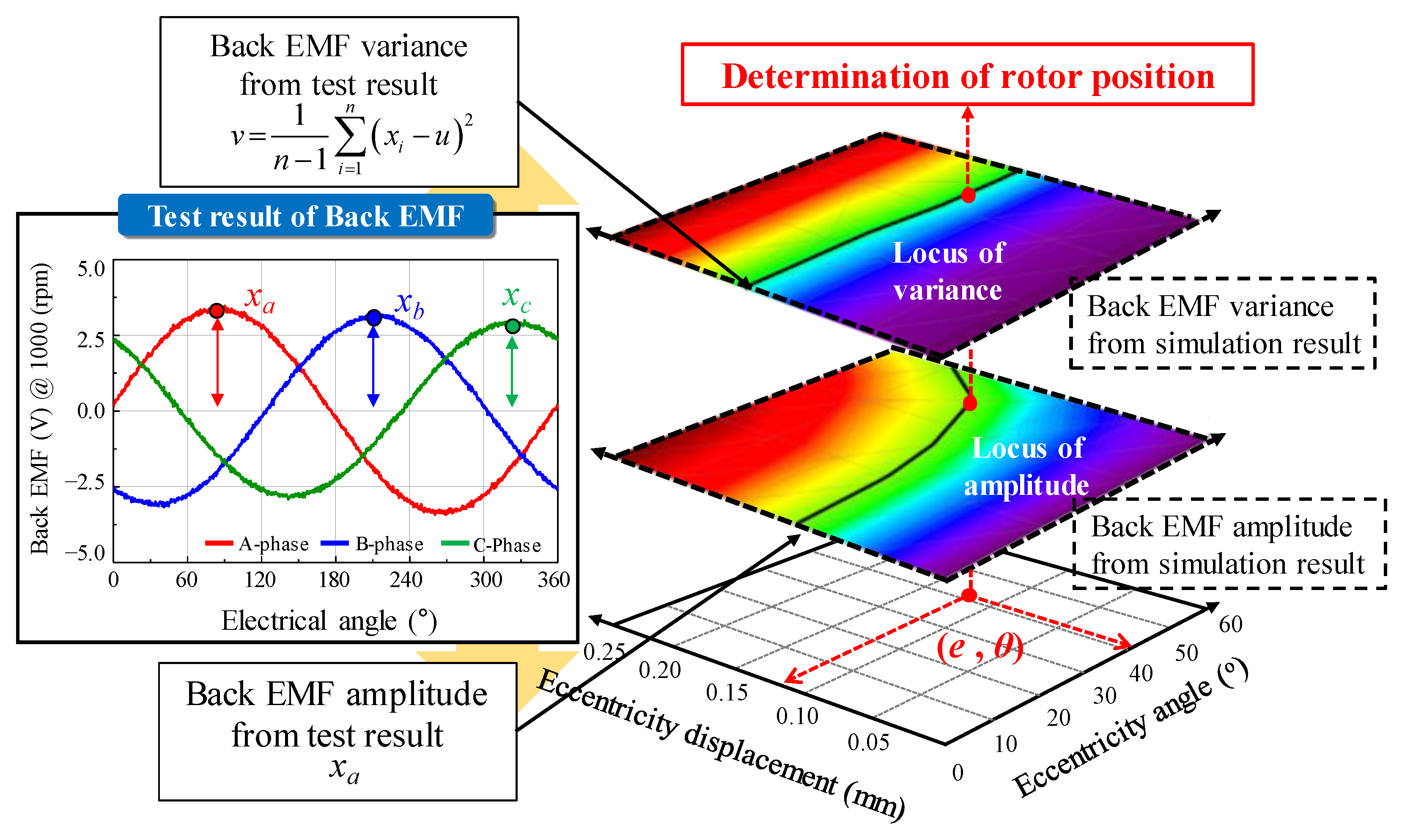
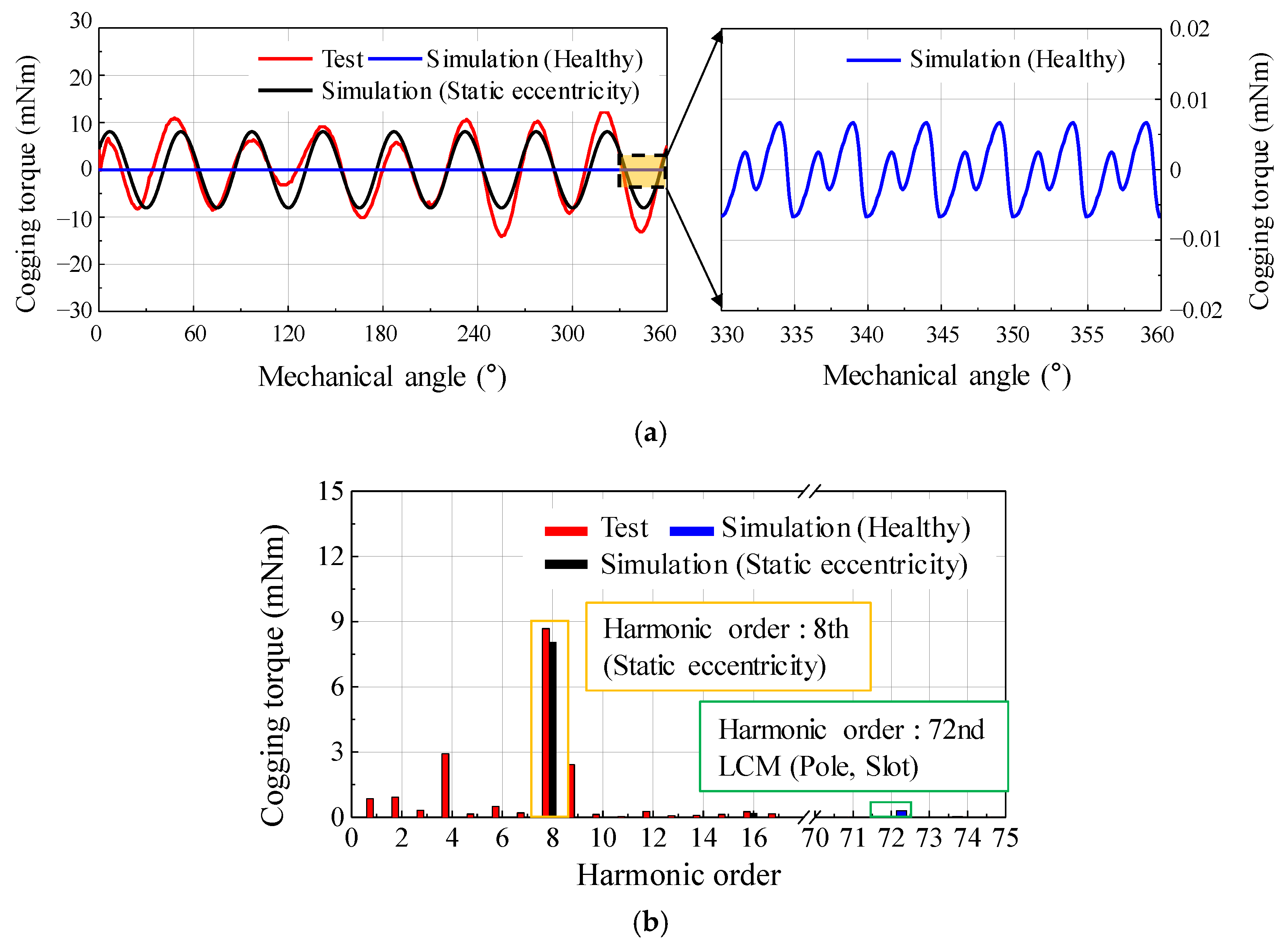
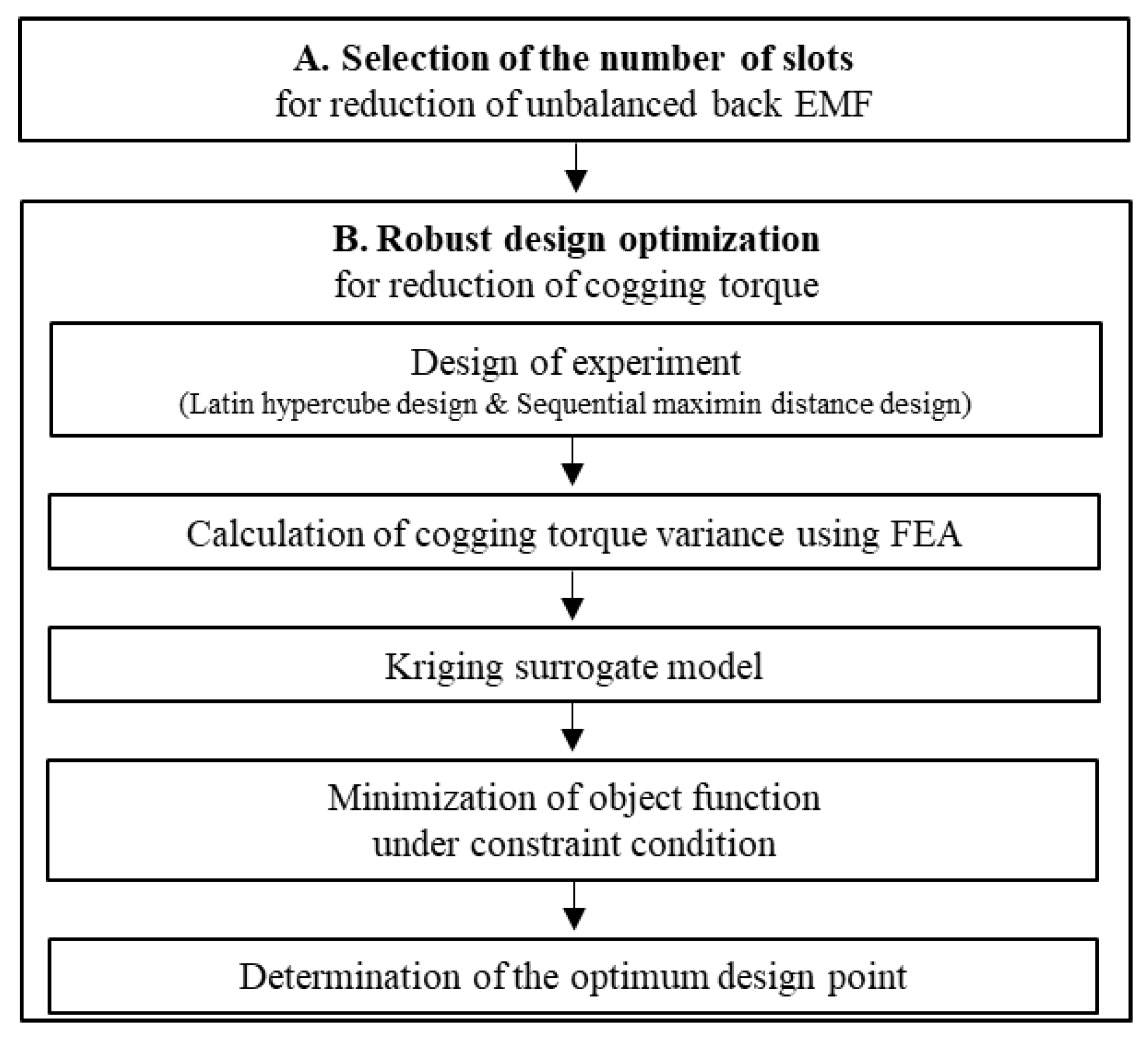
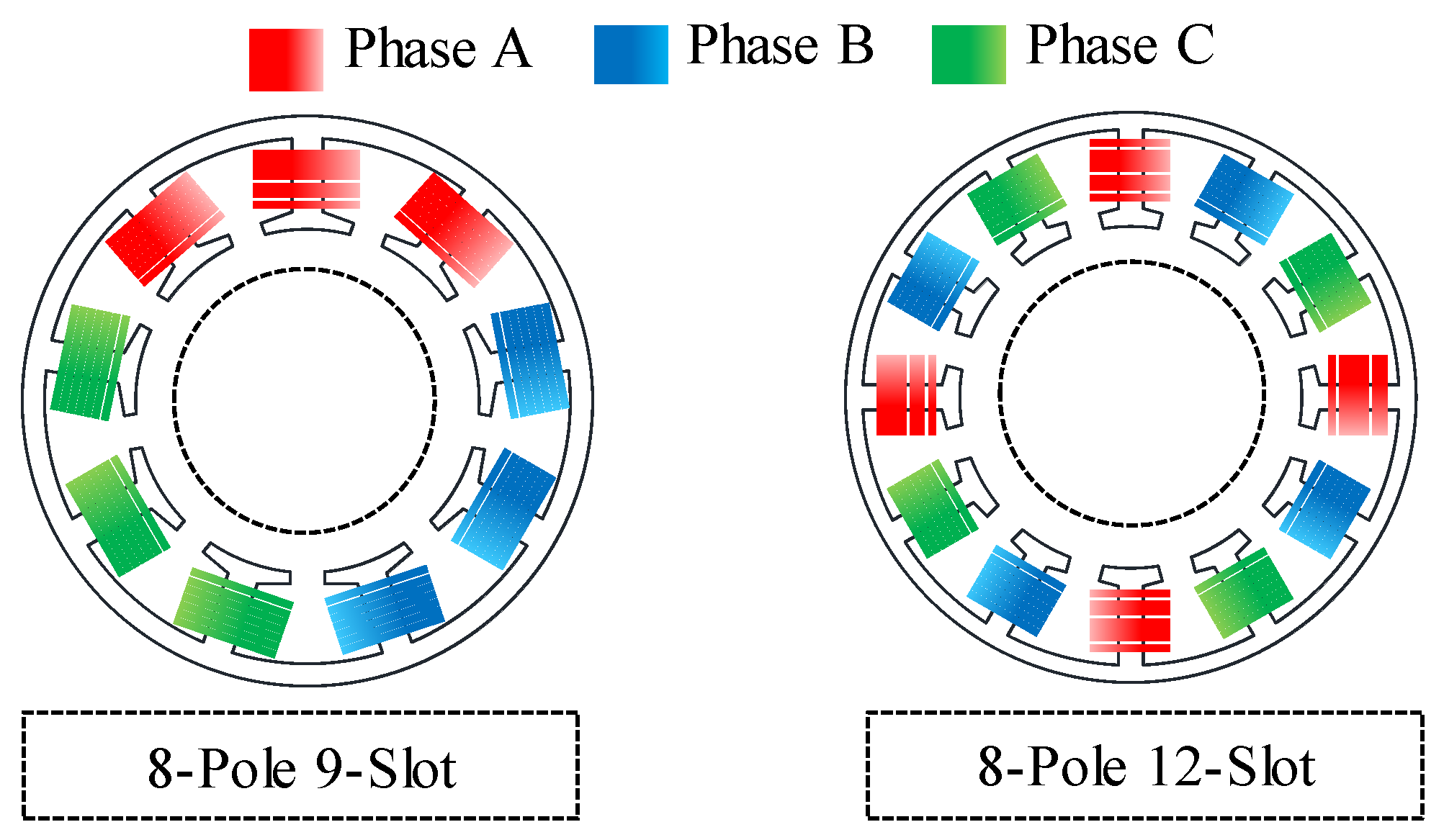
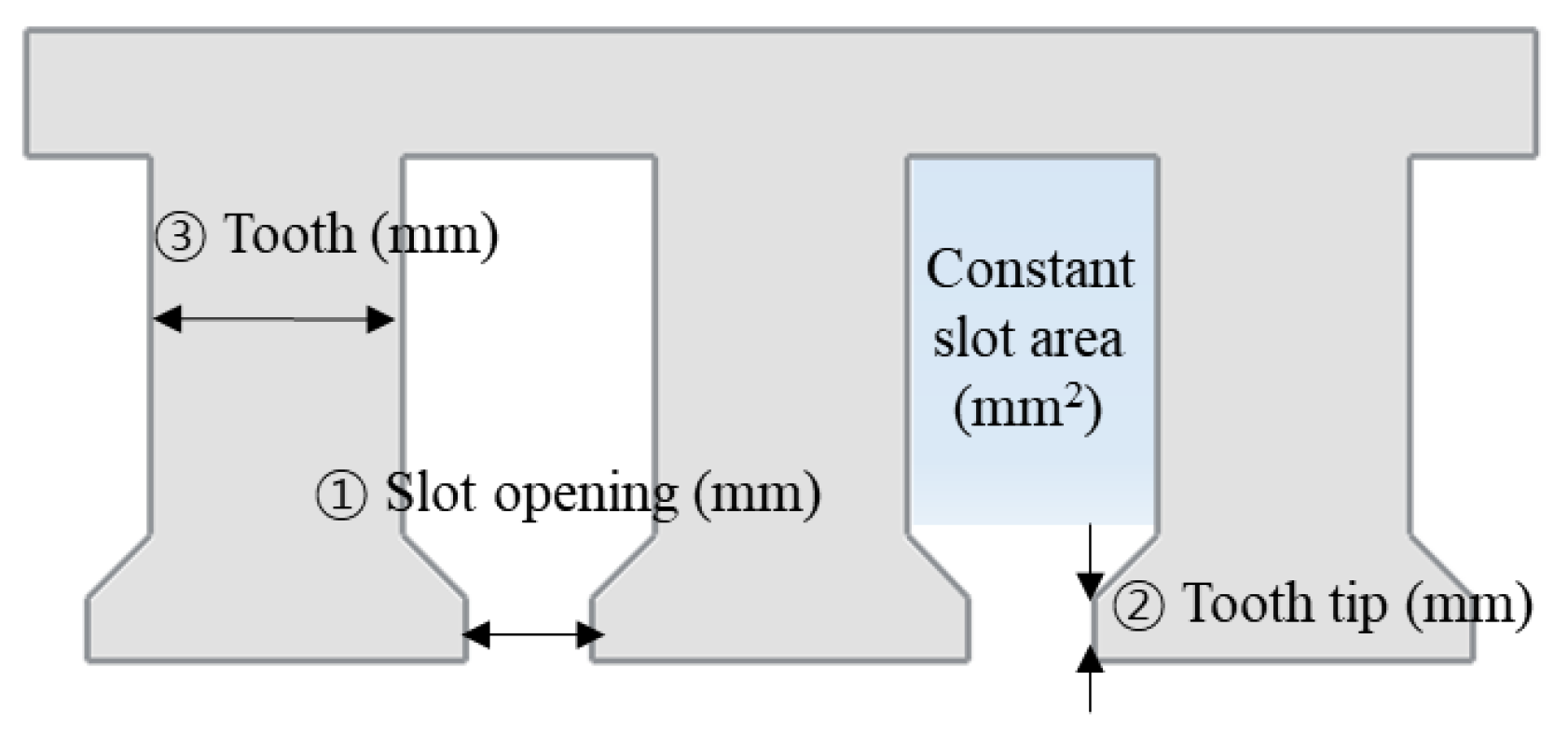

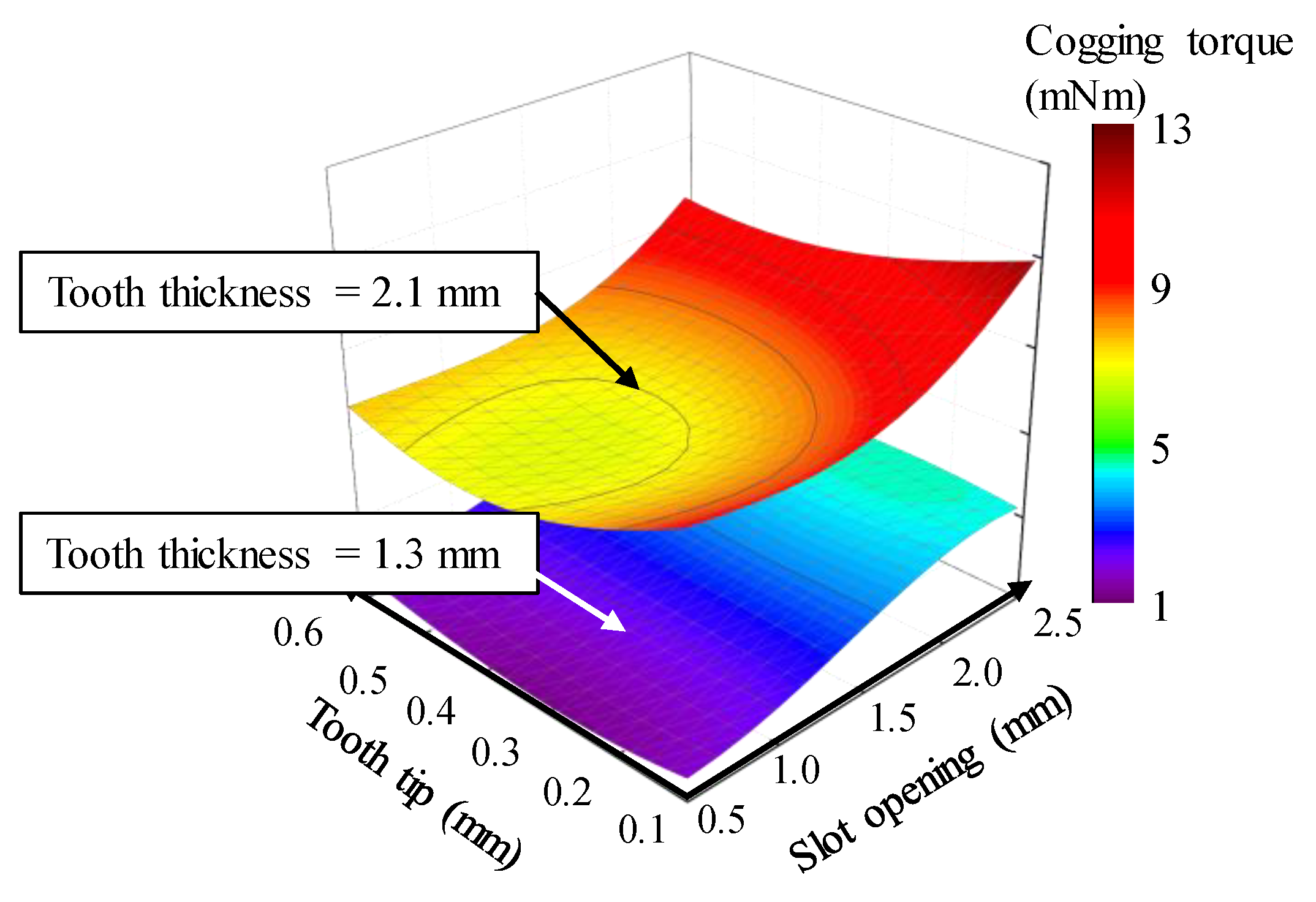

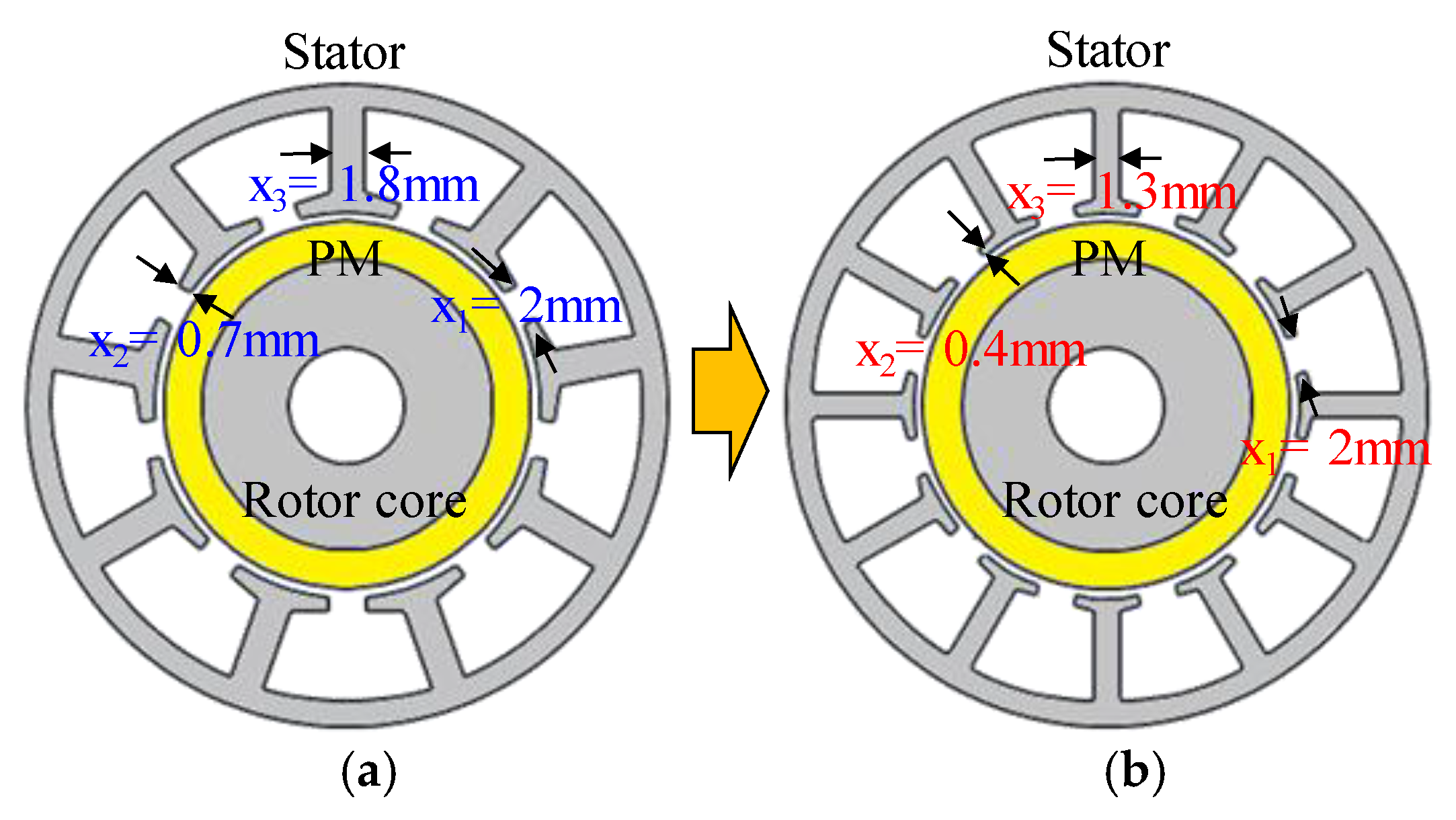
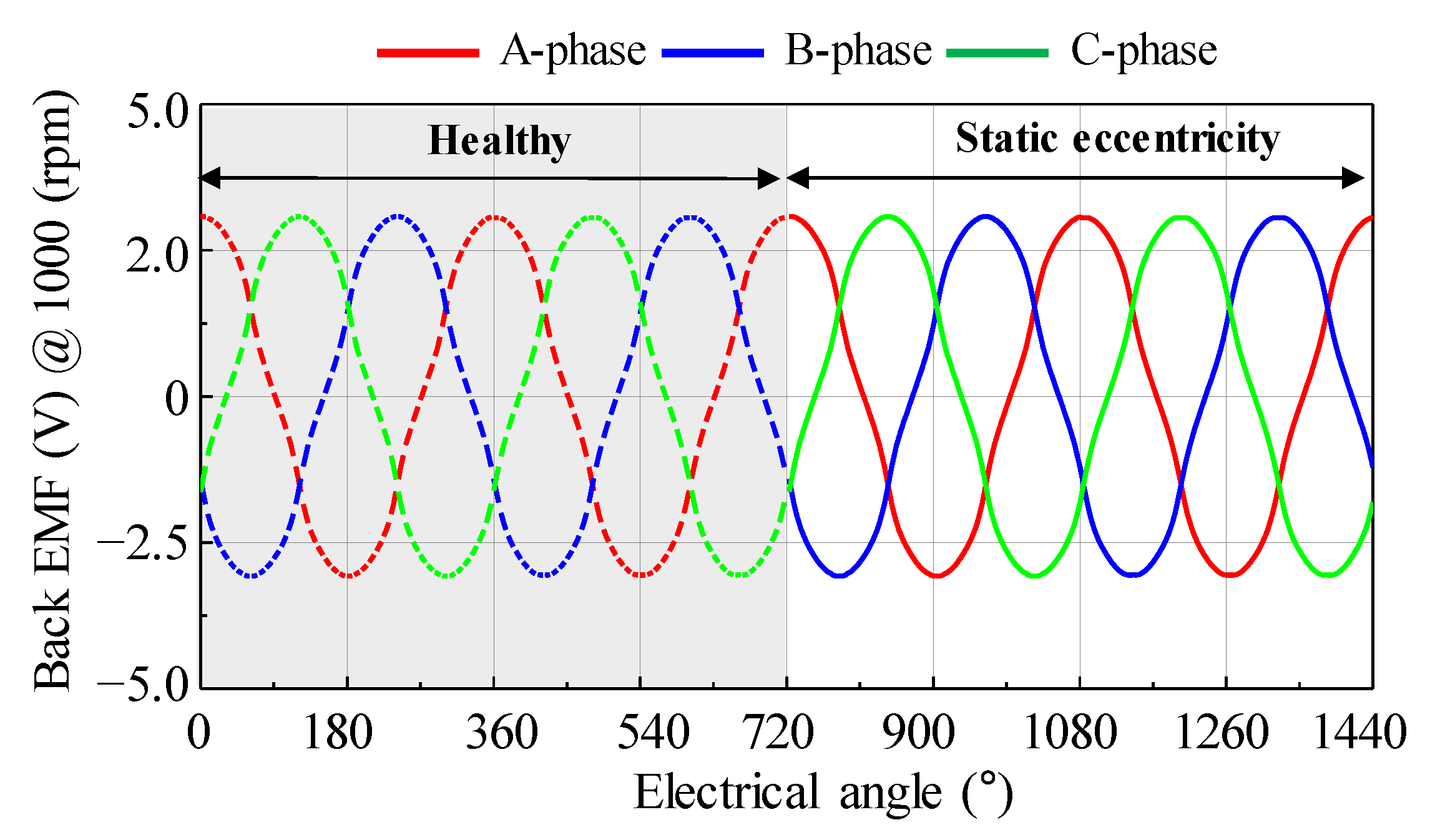



| Item | Unit | Value |
|---|---|---|
| Motor type | - | SPMSM |
| Number of Poles | - | 8 |
| Number of Slots | - | 9 |
| Stator diameter | mm | 33.2 |
| Rotor diameter | mm | 19 |
| Stack length | mm | 30 |
| Air-gap length | mm | 0.5 |
| Core material | - | 50PN470 |
| DC link voltage | V | 24 |
| PM type | - | Ring magnet |
| PM thickness | mm | 2 |
| PM material | - | Bonded NdFeB |
| Item | A Phase | B Phase | C Phase |
|---|---|---|---|
| Back EMF (V1st) | 3.32 | 3.12 | 2.94 |
| Unit | Min. | Max. | ||
|---|---|---|---|---|
| Design variables | Slot opening | mm | 0.5 | 2.5 |
| Tooth tip | 0.1 | 0.6 | ||
| Tooth thickness | 0.5 | 2.6 | ||
| Design parameters with uncertainties | Eccentricity angle | deg. | 0 | 60 |
| Eccentricity displacement | mm | 0 | 0.025 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.-C.; Park, S.-H.; Kim, J.-H.; Lee, S.-G.; Lee, G.-H.; Lim, M.-S. Diagnosis and Robust Design Optimization of SPMSM Considering Back EMF and Cogging Torque due to Static Eccentricity. Energies 2021, 14, 2900. https://doi.org/10.3390/en14102900
Park J-C, Park S-H, Kim J-H, Lee S-G, Lee G-H, Lim M-S. Diagnosis and Robust Design Optimization of SPMSM Considering Back EMF and Cogging Torque due to Static Eccentricity. Energies. 2021; 14(10):2900. https://doi.org/10.3390/en14102900
Chicago/Turabian StylePark, Jin-Cheol, Soo-Hwan Park, Jae-Hyun Kim, Soo-Gyung Lee, Geun-Ho Lee, and Myung-Seop Lim. 2021. "Diagnosis and Robust Design Optimization of SPMSM Considering Back EMF and Cogging Torque due to Static Eccentricity" Energies 14, no. 10: 2900. https://doi.org/10.3390/en14102900
APA StylePark, J.-C., Park, S.-H., Kim, J.-H., Lee, S.-G., Lee, G.-H., & Lim, M.-S. (2021). Diagnosis and Robust Design Optimization of SPMSM Considering Back EMF and Cogging Torque due to Static Eccentricity. Energies, 14(10), 2900. https://doi.org/10.3390/en14102900







