1. Introduction
Mathematical models of complex electric power and electromechanical systems for transients simulation can be derived directly on the basis of mathematical descriptions of physical phenomena occurring in the elements of these systems or on the basis of equivalent diagrams containing the fundamental (ideal) elements of electrical circuits, including: resistors, inductors, capacitors, and sources. From the transients analysis point of view, the mathematical models consist of a set of first-order differential equations based on Kirchhoff’s laws. This is a well-documented subject in electrical engineering texts.
The tensorial analysis of networks was developed in [
1]. Rather than using nodes and edges in graphs to describe the circuit topology, the developed circuit definition using the space of the meshes was proposed. This approach was justified through topology considerations.
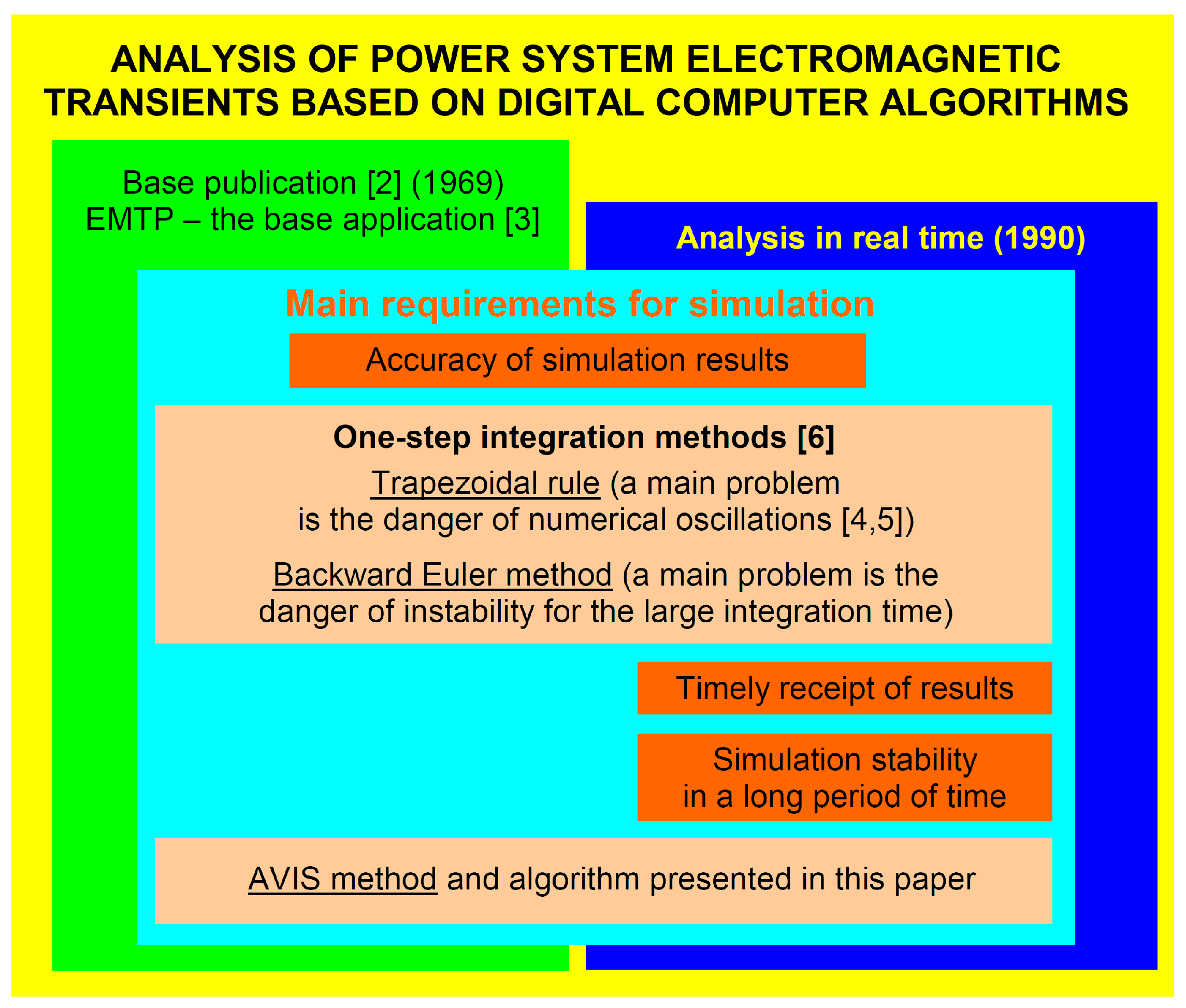
The application of efficient computational techniques to the solution of electromagnetic transient problems in systems of any size and topology is the actual scientific problem. The electric power system variables are continuous. The digital simulation is of course discrete. The main task in digital simulation is still the development of suitable methods for the solution of the differential and algebraic equations at discrete points. The diagram presented in
Figure 1 shows the place of one-step integration methods in the analysis of the dynamics of electrical systems. The following publications were listed there: basic Dommel’s book [
2], EMTP Theory Book [
3], Araujo’s Ph.D. thesis [
4], Marti’s publication [
5] and Crow’s book [
6].
The selection of an integration method and an algorithm is, in particular for the real-time mathematical modeling, an important and current scientific problem. The integration method for real-time simulation must be numerically stable, computationally efficient, and accurate enough for practical purposes.
The book [
7] can be distinguished especially in the area of the parallel calculation in the real-time simulation of power system dynamics. The book [
8] has a chapter on real-time simulation. A number of Ph.D. Thesis on real-time simulation were carried out, including [
9,
10,
11].
The use of parallel calculations can significantly reduce the computation time. It is especially important in the case of real-time simulation and also simulation realized faster than real time (for example, the prediction of power system operating states). Real-time systems are widely used in the simulation of complex electric circuits [
12]. In these kinds of systems, calculations for the given iteration of the discrete mathematical model of electrical system have to be done in the given integration time step [
13]. This is an indispensable condition to be met with the requirements related to operation in real-time. Extracting individual processes is not a trivial problem. This subject in relation to electrical systems has been discussed in the literature. Methods such as wave relaxation [
14] and domain decomposition [
15,
16] were used here. The main issue that occurs in the first case is the lack of guaranteed convergence for a general electric circuit. This caused the inhibition of using this method in simulating software of electrical systems. Scalability for algorithms based on the domain decomposition method is strictly limited in the case of increasing numbers of interface variables between extracted parts of the equation system [
17].
The explanation of the parallelization of long-running power system simulations using existing desktop computer technology is presented in the book [
7]. The topic of partitioning and evaluating runtime as a power system model with partitioned numerous times was discussed in this book. This book provides a fresh perspective on power system simulation to embrace multicore technology, including, among others: the power system model, time domain simulation, discretization, power apparatus models, network formulation, partitioning, and multithreading. In the topic of interest to us, from the point of view of this paper, tunable integration and root-matching were used in the book [
7]. Tunable integration was used for stand-alone electrical branches and control blocks, and root-matching was used for electrical branch pairs. Let us pay attention to a certain context of the solution proposed in this book. The choice of integration method typically depends on which power apparatus is included in the model. For example, the trapezoidal rule is recommended for networks where the voltages and currents are expected to be sinusoidal; the backward Euler method is recommended for networks where the voltages and currents are expected to be piecewise linear such as when power converters are present. Tunable integration was defined in [
8], and it is an effective approach that benefits from the accuracy of trapezoidal integration and the stability of backward Euler integration. Therefore, it is expedient to look for new integration methods that will avoid the use of the tunable integration.
The answer to these problems is the new numerical one-step integration method and the resulting new mathematical models and new simulation algorithms that are used in the research carried out at the Institute of Electrical Engineering UTP University of Science and Technology in Bydgoszcz (Poland). Previously, no one wrote about this method, mathematical models, and algorithms in any of the above-mentioned publications. The essence of the new method is the use of the numerical discretization of electrical circuit equations, formulated for average voltage values [
18]. The proposed method was successfully developed and used by the authors from IEE UTP for issues related to the analysis of complex power systems [
19,
20,
21,
22]. A survey of power systems analysis programs presented above did not mention the method based on average voltages in the integration step (AVIS method) even once.
The goal of this paper was the presentation of the scientifically acceptable general method for the mathematical modeling of the dynamics of linear electrical systems using parallel calculations. The new method for the mathematical modeling has an advantage over others known from the literature in that it allows for a stable simulation with a relatively large integration time step without losing the accuracy of the results. The original contributions of the author of this paper were the method of determining the areas of application of the proposed integration method, in which it has an advantage over other methods and the theory of mathematical modeling of dynamics of linear electrical systems using parallel calculations.
The organization of the article is as follows: (1) we present in detail the derivation and physical basis of the mathematical models of individual structural elements and the mathematical model of the generalized electrical system; (2) we present the method of separating the fragments of the mathematical model of the generalized electrical system into computational threads that can be implemented in parallel; and (3) we present, on a relatively simple example, the application of the mathematical modeling method proposed in this paper.
Section 1 of this paper presents the Introduction, which justifies the need to search for effective methods of the mathematical modeling of complex electrical systems, especially those that are to be used in real-time simulators. It has been shown that not everything is solved today in the area of the real-time simulation of the dynamics of power systems. The search for new stable simulation methods with a relatively large integration time step without losing the accuracy of the results is a current issue from the scientific point of view. The ability to perform computations in parallel is a way to speed up computation as expected in a real-time simulation.
Section 2 defines the generalized electrical system and provides the basic terms and definitions used in the proposed method for the mathematical modeling of electrical systems. Mathematical relationships between physical quantities characteristic of a generalized electrical system are also presented. The mathematical model of the generalized branch of the electric circuit, based on the AVIS method, is presented in
Section 3. The mathematical model of the generalized branch of the electric circuit was used to create mathematical models of the interconnecting structural elements, in which the terminals of the branches extend outside the structural element (a multi-term element). The advantage of the applied integration method (AVIS method) over others (backward Euler and trapezoidal rule) recommended in the literature is demonstrated in
Section 4. The derivation and physical justification of the mathematical models of structural elements with any internal structure are presented in
Section 5. The mathematical basis for aggregating three structural elements into one equivalent element is presented in the
Section 6. This is an example of the aggregation of multiple structural elements for which the external characteristics are known (the internal structure of the element does not have to be known) into one equivalent structural element. This manner is often used in modeling complex power structures. The mathematical bases and physical justifications presented in
Section 2,
Section 3,
Section 5, and
Section 6 form the basis of the formulation of the algorithm of the mathematical modeling of linear electrical systems with parallel calculations. This algorithm is presented in
Section 7. In
Section 8, on a very simple example, the practical application of the algorithm resulting from the method proposed in this paper is shown. The conclusions are at the end of the paper.
The paper does not provide the implementation of the proposed method in a specific hardware solution of the simulator. A detailed description of the implementation of the proposed mathematical modeling method of electrical systems, due to its specificity (PC, DSP, FPGA, GPU), is beyond the scope of this paper.
2. Basic Terms and Definitions
The concept of a generalized electrical system is introduced here. Any electrical system consists of all of the elements needed to generate, distribute, and consume electrical energy. This system can be simplified as shown in
Figure 2.
Definition 1. A generalized electrical system is an abstract object, consisting of abstract elements, that is characterized by suitable physical (electrical) and mathematically exact relationships among these elements.
The word “abstract” is understood in the sense of being a product of abstraction. That is, extracting characteristics or relations, i.e., formal relationships in a real object or event, or in a set of objects or events.
Generalized electrical system can be interpreted as the connection of
n multi-terminal elements
in
+ 1 nodes (0, 1, 2, 3, …,
), as shown for example in
Figure 2.
Physical (electrical) relationships, resulting directly from Definition 1, imply identifying physical quantities characteristic of nodes (black points in
Figure 2) of this generalized electrical system as electric potentials. An electric potential of one of the nodes is taken as a reference (
). Based on that, it is possible to introduce the vector of node electric potentials of the generalized electrical system, as follows:
where
is the vector of the node electric potentials of the generalized electrical system,
is the electric potential of node
x (where:
x = 1, 2, 3, …,
), and the symbol “T” in the superscript of the matrix notation means the transposition operation.
The essence of the new method of the integration of differential equations, which will be presented in detail in the next section, is to write down the equations for the average voltages in the integration step. Hence, in the mathematical models, the matrix of average electric potentials is used. Thus, the vector of average electric potentials in the integration step
h for discrete time
has the following form:
where
is the average electric potentials in the integration step of node
x (where:
x = 1, 2, 3, …,
and
).
Electrical systems naturally consist of separate multi-terminal elements interconnected with each other. Alternatively, it is also possible to carry out artificial extraction (decomposition) of the electrical system on the separate elements. Separate elements can be called structural elements of the analyzed electrical system (structural elements).
Definition 2. The poles of each separate multi-terminal element (structural element) are the terminals (nodes) of this element that are available outside and allow direct electrical connection with other elements.
These multi-terminal elements (structural elements) are known from electrical circuit theory as electric multipoles. Multipoles are introduced as elements with ordered external terminals (poles) consisting of a network and a family of terminal classes. The terminal classes are disjoint subsets of the node set of the corresponding network [
23]. The rest of the nodes (after extraction of poles) in the structure of each structural element are named internal nodes of this element. Each structural element
in the general case is composed of
g number of branches that are interconnected with each other. The branch is a set of interconnected ideal elements of electric circuits, which has only two terminals on the outside. Branches of the structural element
are interconnected in
E
k number of poles (see
Figure 2) and
w number of internal nodes. Two vectors of external physical quantities are introduced for each structural element
, as follows:
where
and
are the vectors of the node (pole) potentials and currents of the external branches of structural element
(current directions in external branches of the structural elements are always oriented from inside the elements to the poles) and
and
are the electric potential of pole
x and the current of the branch with pole
x (where
x = 1, 2, …,
, …,
) of structural element E
k (see
Figure 2), respectively.
We consistently introduce the vector of average electric potentials of poles of structural element
in the integration step for discrete time
, as follows:
where
is the average electric potentials in the integration step of pole
x of structural element E
k (where:
x = 1, 2, …,
, …,
).
Definition 3. The external equation of the structural element is an equation in the following form (formulated for element ): Equation (
6) is composed of matrices for which
is a square matrix of size
and
is the column matrix with
number of elements. Those matrices are described by parameters and physical quantities, which occur inside structural element
. The methods of the calculations of those matrices elements are introduced in next parts of this paper.
Dependencies between the pole potentials of structural element
and the nodal potentials of the analyzed electric system are described by equation:
where
is the incidence matrix of structural element
.
The same relationship is valid for the average pole potentials of the structural element
(Equation (
5)) and the average nodal potentials of the analyzed electric system (Equation (
2)), as follows:
Definition 4. The incidence matrix of the structural element is a matrix in which the number of rows is equal to the number (ζ) of independent nodes of the generalized electrical system and the column number is equal to the number (ξ) of poles of this structural element. The matrix element upon crossing the individual row and individual column is equal to one if the node with the number the same as the number of the row is connected to the pole with the number the same as the column number. In other cases, the matrix element is equal to zero.
Based on Kirchhoff’s current law for all independent nodes of the generalized system, the equation was obtained:
Substituting vectors of external branches’ currents determined from Equation (
6) for each structural element into Equation (
9) and taking into account Equation (
8), we obtained the equation:
where:
From Equation (
11), it follows that the size of the matrix
is
, and matrix
has
number of elements.
Taking into account Definition 2, which is related to the poles of structural element
, for the internal nodes (1, 2, …,
w) of this element, a vector of internal nodal potentials is written in the form of:
where
is the vector of internal nodes potentials of structural element
(the symbol “i” indicates that it is about the internal value of the element) and
is an electric potential of internal node
x (where:
x = 1, 2, …,
w) of structural element
.
We consistently introduce for the internal nodes (1, 2, …,
w) of structural element
a vector of internal nodal average potentials, in the following form:
where
is the average electric potentials in the integration step of internal node
x (where:
x = 1, 2, …,
w).
For each branch (
g) of structural element
, the branch’s voltages (as the differences of the electric potentials of the respective nodes of the branch) are written in the following vector:
where
is the vector of the branch’s voltages of structural element
(the symbol “b” indicates that it is about the branches of the element) and
is a voltage of branch
x (where:
x = 1, 2, …,
g) of structural element
.
We consistently introduce for each branch (
g) of structural element
the branch’s average voltages in integration step (as the differences of the average electric potentials of the respective nodes of the branch) the following form:
where
is the branch’s average voltages in integration step of branches
x (where:
x = 1, 2, 3, …,
g).
The relation between the vector of branch voltages (
14) and the vector of internal nodal potentials (
12), as well as the vector potential of poles (
3) of structural element
is given in the following equation:
where
is the incidence matrix for internal nodes of structural element
and
is the incidence matrix for poles of structural element
.
The same relationship is valid for average voltages and electric potentials in the integration step, as follows:
Definition 5. The incidence matrix for internal nodes of the structural element is a matrix in which the number of rows is equal to the number of internal nodes (w) and the column number is equal to the number of its branches (g). The matrix element in the n-th row and the m-th column is equal to: 0 if the terminals of the m-th branch are not connected with the n-th node, or −1 if the terminal of the m-th branch to which the branch current is supplied is connected to the n-th node, or 1 if the terminal of the m-th branch, from which the branch current flows, is connected to the n-th node.
Definition 6. The incidence matrix for poles of the structural element is a matrix in which the number of rows is equal to the number of poles (ξk) and the column number is equal to the number of its branches (g). The matrix element in the n-th row and the m-th column is equal to: 0 if the terminal of the m-th branch is not connected with the n-th pole, or −1 if the terminal of the m-th branch to which the branch current is supplied is connected to the n-th pole, or 1 if the terminal of the m-th branch, from which the branch current flows, is connected to the n-th pole.
Similar to the case of branch average voltages (
15), also for each branch (
g) of structural element
, branch currents are written in the following vector:
where
is the vector of the branch currents of structural element
(the symbol “b” indicates that it is about the branches of the element) and
is a current of branch
x (where:
x = 1, 2, …,
g) of structural element
.
Therefore, for structural element
treated as an element of the generalized electric system, we can write the following matrix equations:
Formula (
21) is a characteristic of the individual branches as a vector relationship between current and average voltage.
Definition 7. The state equation system of the structural element is created using the following Equations (17) and (19)–(21). The solution of the state equation system of structural element is a set of values of the following vectors: , , and , which meets all of the equations and describes the state of this structural element at given excitations, in this case the average values of the potentials of the poles of this element (matrix ).
Definition 8. The structural element, the branches of which are described by the linear current–average voltage characteristic (21), is the linear structural element. 4. Accuracy of the Integration Rules
The formulas for the AVIS method, presented in
Section 3, and the commonly known formulas for the backward Euler and trapezoidal methods are the basis for assessing the accuracy of these integration methods. It should be noted here that we were interested in the integration methods proposed for real-time simulation. Therefore, many different integration methods used in the general approach to mathematical modeling of electrical systems were omitted here (this will be the subject of other publications).
For the purposes of this paper, the accuracy of an integration rule was assessed by considering its frequency response [
3,
5,
9,
24]. The frequency response of the integration for three rules in the discrete-time system
H(
z) was compared with the exact frequency response of an integrator in the continuous-time system
H(
s). Additionally, the results of the frequency responses comparison are illustrated with example waveforms for the selected branch of the electrical circuit.
For example, we considered the branch consisting of the following elements connected in series: a resistor, an inductor, and a capacitor, with the known parameters, respectively: resistance
R, inductance
L, and capacitance
C. The branch was powered by a sinusoidal voltage source
. Taking the supplying voltage as the input and the current as the output,
H(
z) is the transfer function of the discrete time system, where
(
h is integration time step). Applying the above-mentioned three numerical integration methods to the integrator, appropriate transfer functions
H(
z) were determined, which are listed in
Table 1.
The transfer function H(s) of the consideration continuous-time system equals .
Figure 4 and
Figure 5 show the accuracy as a function of frequency for the integration rules in
Table 1 with the parameters presented in
Table 2. Two sets of data were adopted, labeled as (1) and (2), respectively. The frequency axis is labeled in units of
up to the Nyquist frequency
.
The “teeth” visible in the figures appear near the resonance frequencies (531 Hz for the first set and 130 Hz for the second set). The plots in
Figure 4 show that the AVIS method gave very accurate magnitude responses for frequencies in the whole considered range. In addition, the AVIS method produced no phase distortion (excluding frequencies close to the resonance frequency for the first data set). This is clearly visible in the plots in
Figure 5. The AVIS method was the best for the two sets of parameters considered here.
Figure 6 shows the current waveforms in the considered branch as the simulation results using three methods: backward Euler, trapezoidal, and AVIS, for the two data sets (see
Table 2). These results are perfectly illustrated in the plots presented in
Figure 4 and
Figure 5. For the second data set, it can be seen that the discrete values obtained from the simulation using the AVIS method (
Figure 6c,d) coincided very precisely with the exact solution. Very good accuracy was also maintained at a frequency of 150 Hz (
Figure 6c), close to the resonance frequency. For the first set, especially near the resonance frequency (
Figure 6a), the phase and amplitude shifts in the solution using the AVIS method are visible. However, the results obtained were acceptable in terms of accuracy. Taking into account the proximity of frequency to the resonance frequency, we achieved a satisfactory result when the difference of the simulation result with the exact solution did not exceed 20%. This difference should be determined close to the maximum values. It should be noted here that the most important effect of the real-time simulation near the resonance frequencies was the maintenance of stability. An error value greater than 20% can make the simulation unstable. The other two methods gave much worse results and were unacceptable in the context of real-time simulators.
The results presented in this section show the advantage of the proposed integration method in a real-time simulation over the other two proposed in the literature. Therefore, it is advisable to develop a new approach to the method of the mathematical modeling of the dynamics of linear electrical systems, with the possibility of parallel calculations. This is what is considered and proposed in the following sections of this paper.
5. External Equation of the Linear Electric Structural Element (Associated with the AVIS Rule)
First, an example of a three-phase structural element was considered, the schematic diagram of which is shown in
Figure 7. The current–average voltage characteristic (Formula (
21)) of this element takes the following form:
where:
It should be noted that matrix
(Equation (
29)) contains values of individual physical quantities determined for the time
(so it is known from the previous integration step or initial conditions) and also values for time
, but there are values of voltage sources and current sources that are given by known algebraic equations.
Substitution Equation (
17) into Equation (
27) gives the following expression:
which substituted into Formula (
19) derives the following equation:
Equation (
33) was transformed into the following form:
It should be noted that matrix
is a nonsingular matrix with dimension
. Taking this into account, it is possible to calculate the matrix of internal nodal average voltages of the structural element as follows:
Expression (
32) gives the current vector of the internal branches of the structural element, so substitution of (
36) into (
32) derives the new form of Equation (
32):
where:
The Formula (
28) is substituted into (
20), directly giving external matrix Equation (
6) of the structural element in the following form:
Based on the matrices from Equation (
6), it has the following form:
The method of determining the external Equation (
6) of a linear structural element with a general internal structure can be carried out on the example of a structural element with the schematic diagram shown in
Figure 8.
Using the derived Formula (
23) for the generalized linear branch of the electric circuit using the AVIS method for the considered structural element
, the characteristic (
21) is described by Equation (
27), so:
where:
By using Formulas (
34) and (
38), respectively, it is possible to get the matrices (
40) and also Equation (
6), which is the external equation of considered structural element
.
6. External Equation of the Structural Element as the Internal Connection of the Structural Elements with Known External Equations
In the real-time simulation of the operating states of complex electrical systems, it is useful to apply parallel computing in order to speed up the results of the calculations, without degrading the accuracy. The structural element extraction of the complex electrical system and using the previously described mathematical modeling method give the possibility to apply parallel computing in some parts of the computing process. At some stage of the calculations, it is necessary to solve the system of linear Equation (
10) for the analyzed electrical system. Matrix
in Equation (
10) is a sparse matrix for electrical systems with a high number of nodes (
). Even that feature does not enable a significant solving speedup of that equation system. This is due to issues with the effective parallelization of the procedure of solving systems of linear equations. The author of this paper proposed on the particular stage of the calculation process the aggregation of some structural elements’ groups. This tends to replace a few structural elements in the given group by one structural element. This gives the opportunity to significantly reduce the electrical system nodes and reduce the number of equations in Equation (
10), so it can speed up solving (even if the calculations are carried out sequentially in this part).
It was assumed that the considered electrical system consisted of structural elements for which the external equations of the form (
6) were known. In the general case, the internal structures of the structural elements are not known. Due to that, the extraction of the internal branches of the structural elements being a product of aggregation was impossible. In this case, using only the pole average potentials of the aggregated structural elements and the currents of their external branches was required.
The method of determining the external Equation (
6) of a linear structural element resulting from the aggregation of three structural elements, for which external equations are known, was considered on the example of a fragment of the electrical system with the schematic diagram shown in
Figure 9.
The external equations of aggregated structural elements are known and have the form of Formula (
6). The equivalent structural element E (including the aggregation of three
,
, and
structural elements) will have three poles and five internal nodes (
Figure 9, right side). The vectors of the pole average potentials and currents of the external branches of the equivalent structural element E have the form of Formulas (
5) and (
4), respectively.
For five internal nodes (
w = 5), based on Formula (
13), the vector of average potentials of these nodes is written as:
Formula (
17) is written for branch average voltages, and in the aggregation of structural elements, it does not apply, because there is no reason to recognize, e.g., terminals
and
as terminals of the same branch. In the case of the aggregation of structural elements, the average potentials of their nodes (poles of aggregated structural elements) should be associated with the average potentials of the poles and internal nodes (Equation (
44)) of the equivalent structural element, as follows:
where the incidence matrix of internal nodes and the incidence matrix of poles are determined according to Definitions 5 and 6, respectively.
In this case, the vector of currents of the internal branches of the equivalent structural element E have the form:
and taking into account the characteristics of aggregated structural elements, the following equation is obtained:
where:
Substituting Equation (
45) into Formula (
47), the following formula is obtained:
which, after substitution into Formula (
19), gives exactly the same form as Equation (
33). Using the same reasoning in the sequence of Formulas (
33)–(
40), we obtained formulas for matrices appearing in the external equation of the equivalent structural element E.
8. The Example of Using the Proposed Method
The application of the method for the mathematical modeling of linear electric systems with parallel calculations proposed in this paper is shown on the example of a fragment of a MV power distribution network with distributed generation in one phase.
The equivalent diagram of the modeled electrical system is shown in
Figure 12. The
structural element is a substitute voltage source representing the power system, in the form of three independent branches (three phases), consisting of three series-connected ideal elements: voltage source, resistor, and inductor (based on Thevenin’s theorem).
The system nodes, marked in bold by 5, 6, and 7, represent busbars in the MV power substation. The
structural element is an equivalent electric power receiver that contains a fragment of the network that is not modeled in detail. The
structural element is a representation of a MV power line section that is derived from the power substation (from Busbars 5, 6, and 7). Element
represents an unconventional electric power receiver, whose equivalent diagram is shown in
Figure 8. The ideal current source in this element represents a single-phase generating unit (as a distributed generation) that uses renewable energy sources (e.g., a series of single-phase PV installations). The
structural element is a representation of another section of the medium voltage power line that connects the
load with the
and
loads. Structural elements
and
are representations of concentrated loads. The parameters of individual structural elements are summarized in
Table 3.
Let us apply the algorithm proposed in
Section 7 of this paper. The initial conditions are: the current value for each inductor and voltage on each capacitor. Thus, the following vectors are given:
The nodes of the modeled electrical system are marked in
Figure 9 in bold:
(where
= 0). Based on Equation (
2), we have:
For individual structural elements, we write matrices based on Equations (
4) and (
5), respectively:
The potentials of internal nodes, the voltage at branch terminals, and the branch currents for the
structural element are identical to the formulas presented in
Section 5.
The incidence matrices (based on Definition 6) for poles of individual structural elements , , , , , and are the same. These matrices and incidence matrices (based on Definition 4) for individual structural elements of the modeled electrical system are easy to determine and are not presented here.
Then, the process of mathematical modeling of the states of operation of the analyzed electrical system proceeds in accordance with the algorithms shown in
Figure 10 and
Figure 11.
Figure 13 presents examples of the simulation results of the analyzed electrical system (where:
f = 50.0 Hz and
h = 0.2 ms).
Figure 13a,b shows the waveforms of the currents of structural element
in a transient state caused by switching on (
t = 0) of the three-phase supply voltage system. All initial conditions equal zero (all elements of vectors in (
50) equal zero).
Figure 13a shows the simulation results using the AVIS method and
Figure 13b the results using the trapezoidal method. There were clear differences in the accuracy of the results, of course in favor of the AVIS method.
Figure 13c also shows the waveforms of the currents of structural element E1 characterizing a different transient operating state (using the AVIS method only). This state arose as a result of a simultaneous, significant reduction of the parameters values in two phases (L1 and L2) of the structural element
(see
Table 3). In this case, there was a short circuit (low impedance) between the system nodes:
9,
10, and
12. The short circuit occurred at
t = 50 ms and ended at
t = 98 ms. This is a kind of transient short circuit. At the end of the short circuit event, all parameters of the analyzed electrical system returned to their pre-short circuit values.
The same results can be obtained using the aggregation of structural elements, as described in
Section 6 of this paper, with respect to elements
,
, and
(as equivalent element
;
Figure 9) and
,
, and
(as equivalent element
;
Figure 9).
The given results for the example system are only to illustrate the mathematical modeling method proposed in this paper. This simple example was deliberately chosen to achieve a clear effect. A detailed analysis of this example is not the subject of this paper.