Power Distribution Optimization Based on Demand Respond with Improved Multi-Objective Algorithm in Power System Planning
Abstract
1. Introduction
2. The Problem Formulation
2.1. Proposed Multi-Objective Problem
2.2. Constrains
- (i)
- Power balance
- (ii)
- Generation boundary
- (iii)
- Ramp-up and Ramp-down
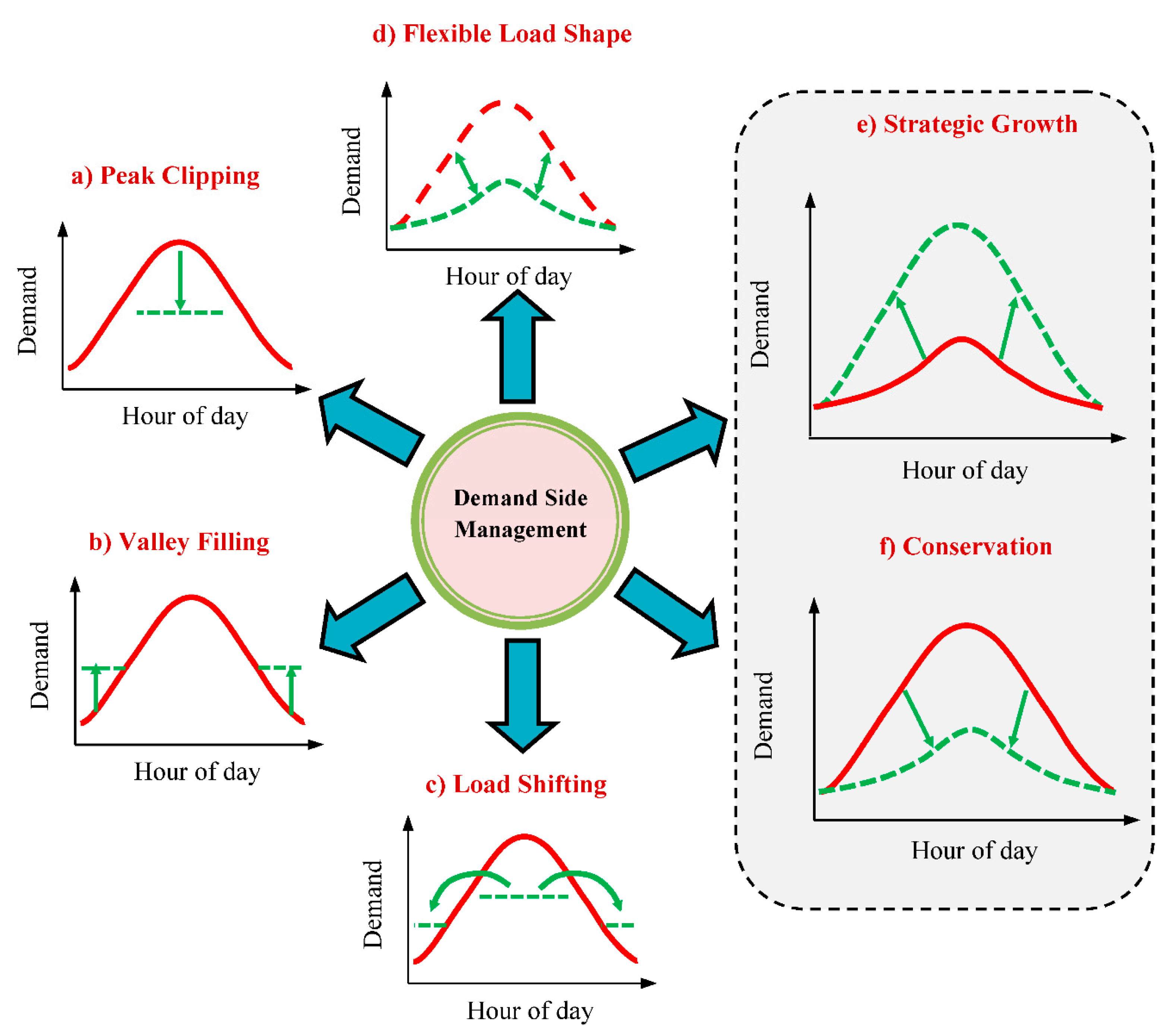
2.3. Problem of Demand Side Management
3. Utility Energy Modeling of DSM
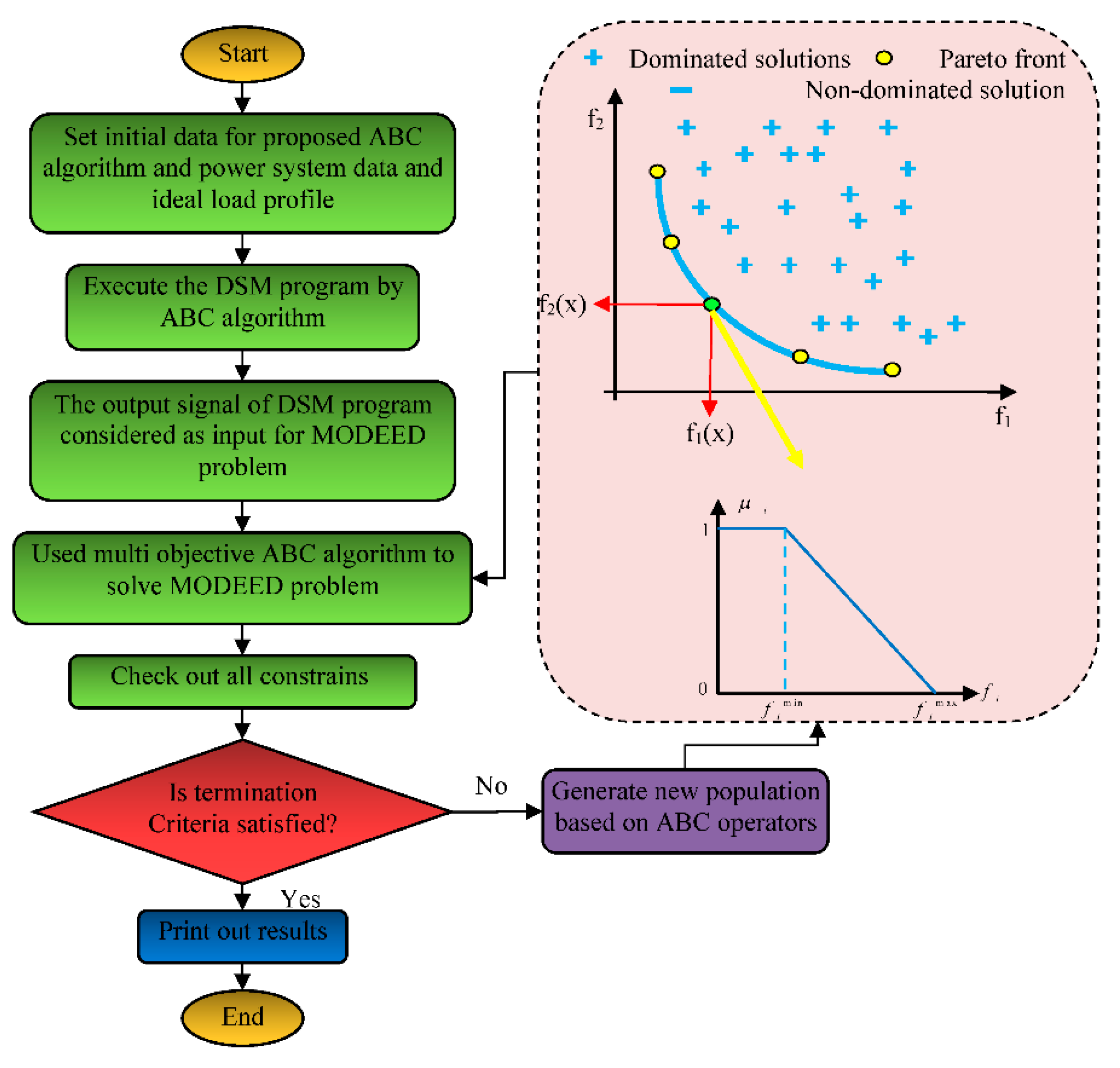
4. Improved Multi-Objective Artificial Bee Colony Algorithm
- Unlike other traditional methods, this method does not need differentiation.
- Less sensitivity to the nature of the objective function means that it has convexity and continuity.
- Unlike other methods, it needs less adjustment of parameters.
- Has the ability to escape from local solutions.
- It is easily implemented and planned with other mathematical and logical operations.
- For objective function with random nature, it could be applied.
- Generate the initial solutions Xij
- Compute the initial solutions in objective function
- Initial iteration circle =1
- Supply new solutions based on Equation (26)
- Select the best resource or best answer between Xij and Vij
- Calculate the possibility rate for Xij solutions based on:
- 7.
- Generate new solutions Vi based on ABC operator from solutions Xi and determine their possibility rate Pi.
- 8.
- Select the best solutions between the answers of Xij and Vij.
- 9.
- Determine the distorted resources and substitute the random resources with created random resources by scout bee Xi by:
- 10.
- Save the best solution (the most qualified resource) that is obtained in this stage.
- 11.
- Cycle = cycle + 1.
- 12.
- Repeat the previous stages until arriving at the stop criterion.
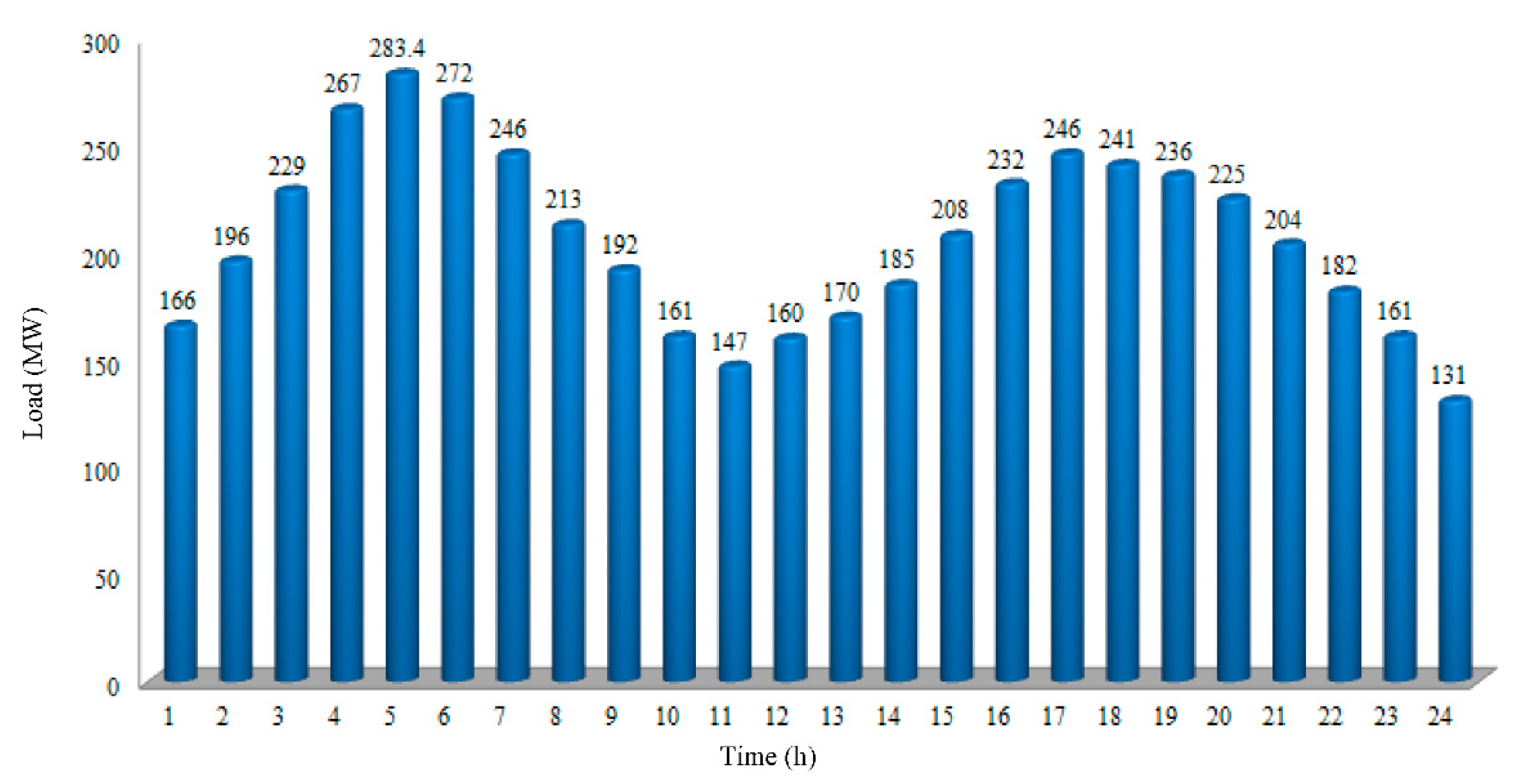
5. Simulation Test Systems
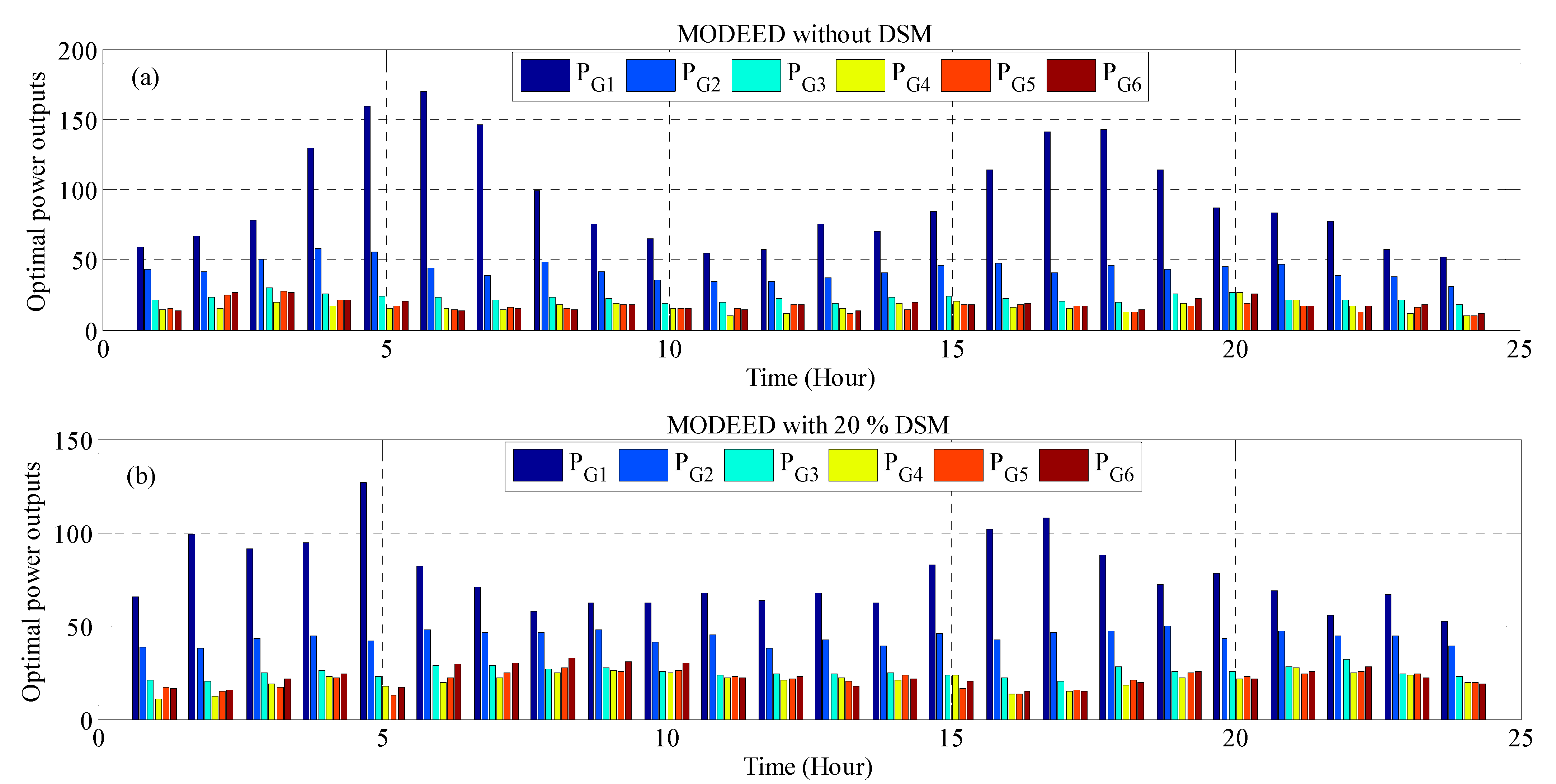
6. The Results of Simulation and Discussion
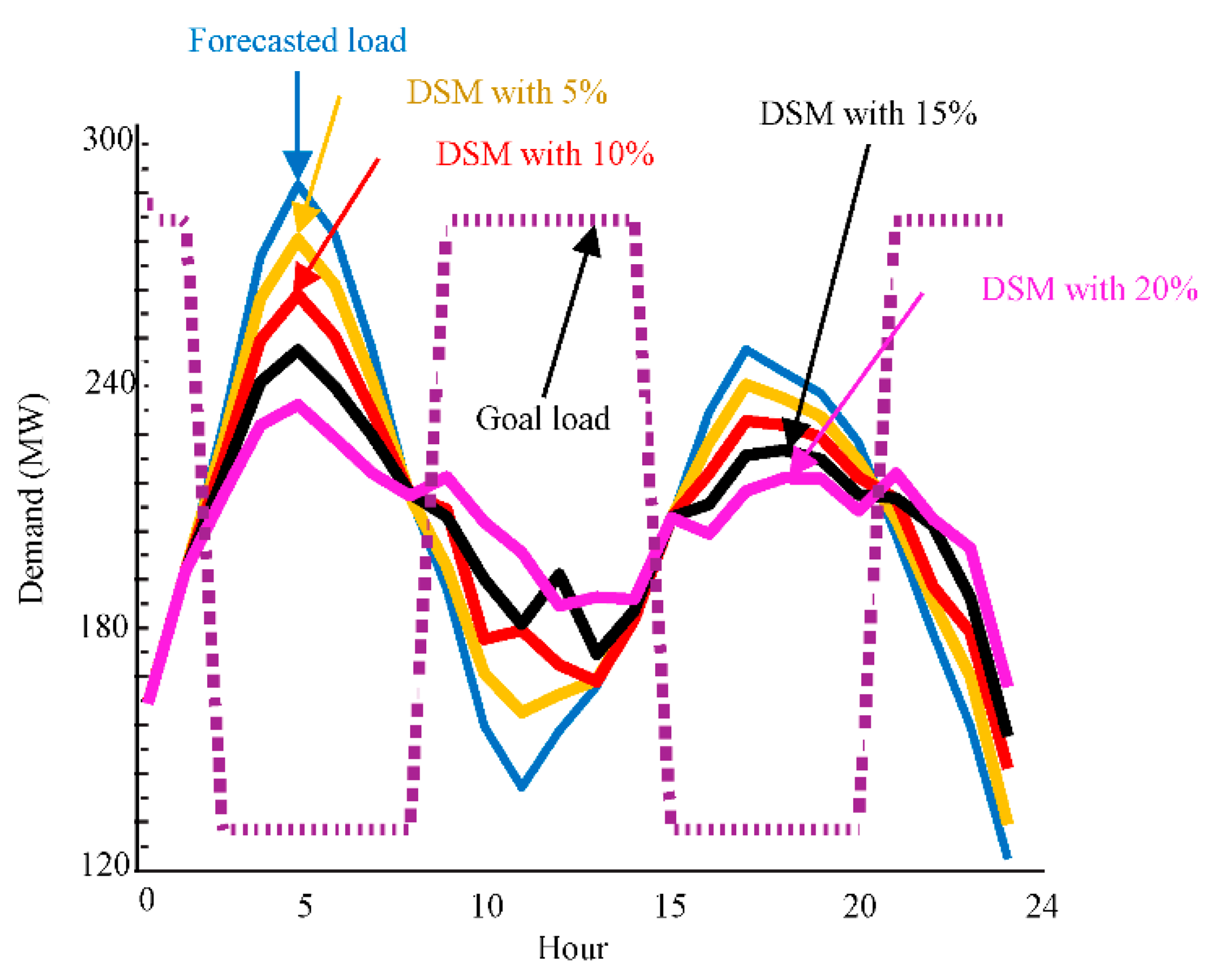
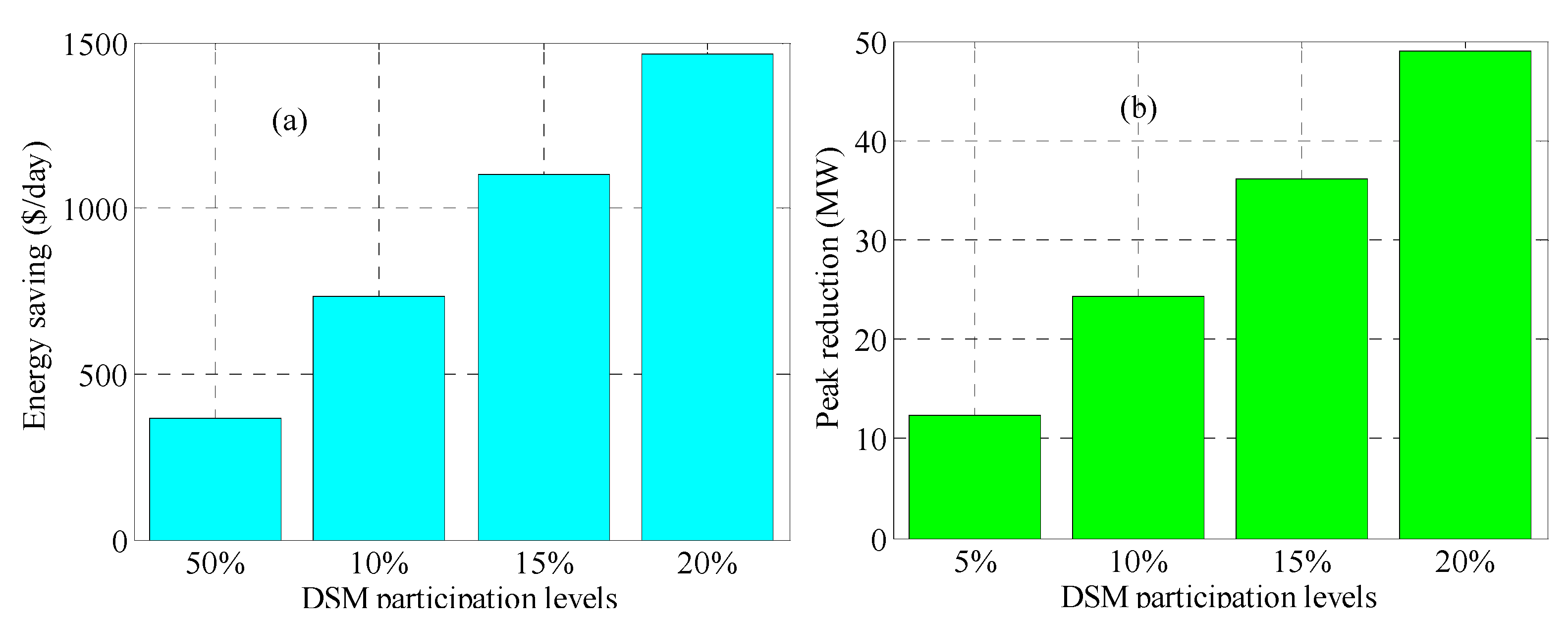
6.1. The Effects of DSM on the Public Facility Side
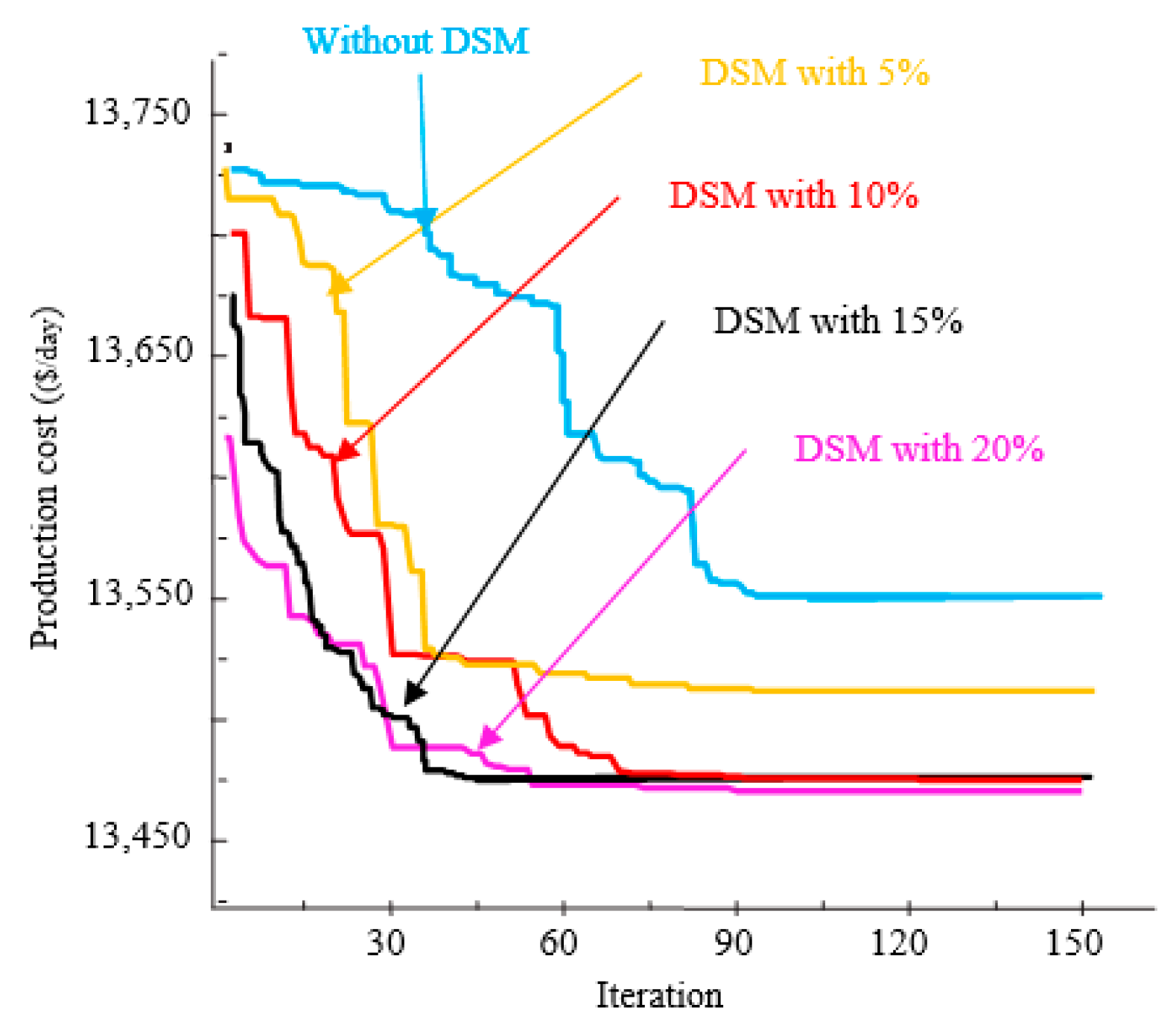
6.2. Case 1: DSM Bundled with Dynamic Economic Dispatch
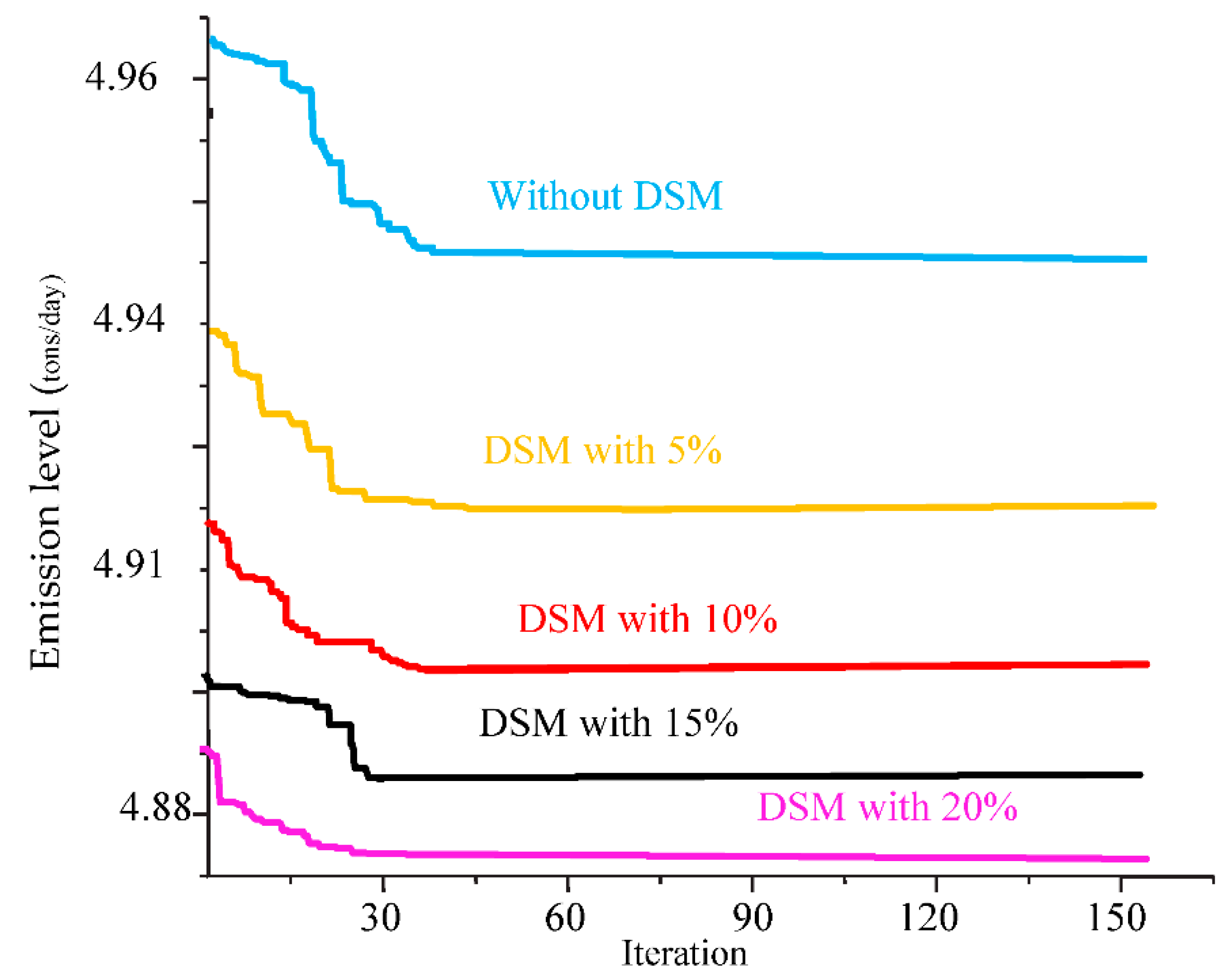
6.3. Case 2: DSM Bundled with Dynamic Emission Distribution
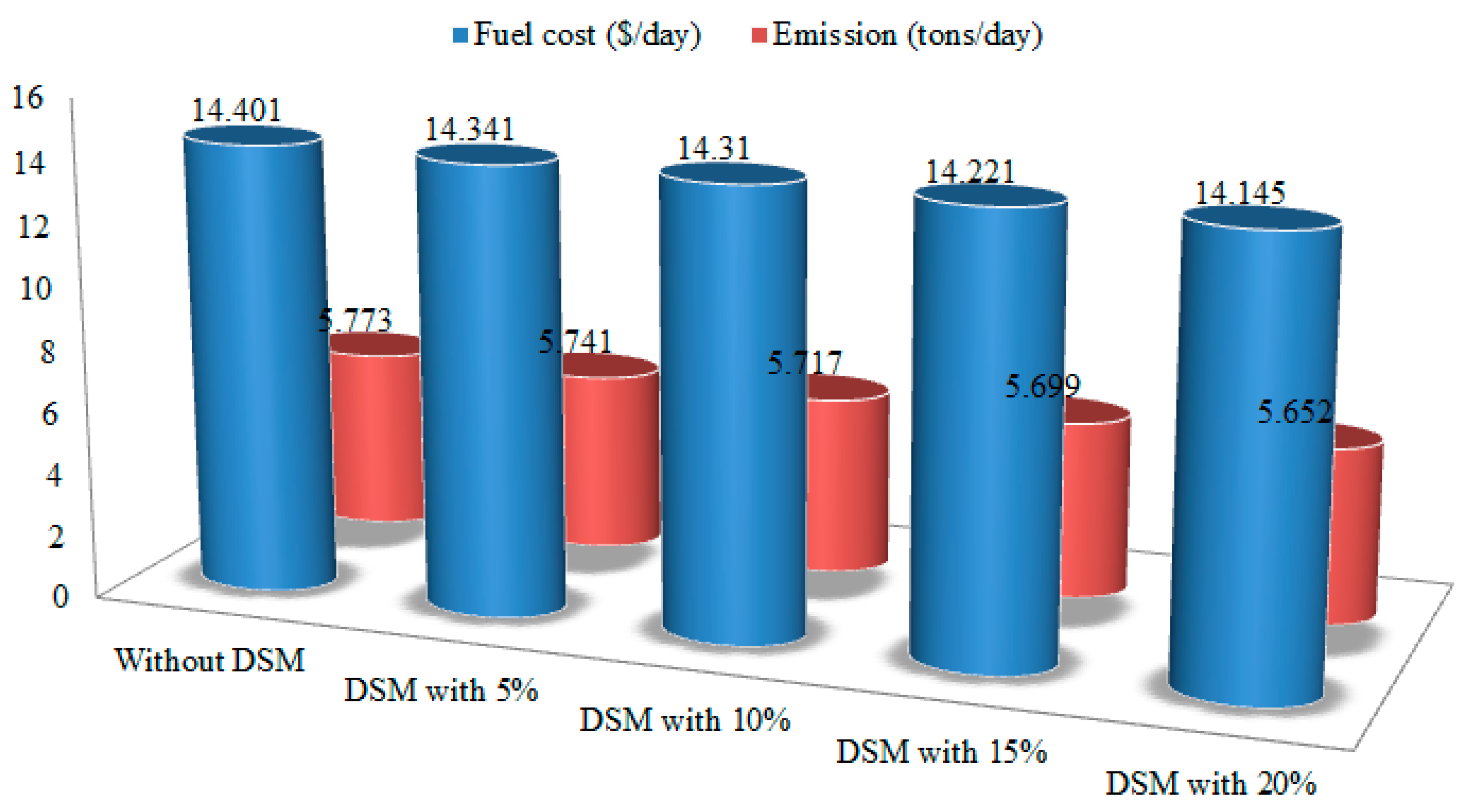
6.4. Case 3: DSM Bundled with Economical and Emission Dispatch
6.5. Test Function for Multi-Objective Algorithm
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Coninx, K.; Deconinck, G.; Holvoet, T. Analysis of Activation Constraints and their Effect on Demand-Side Flexibility Allocations. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Institute of Electrical and Electronics Engineers (IEEE), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–5. [Google Scholar]
- Yilmaz, S.; Chambers, J.; Patel, M. Comparison of clustering approaches for domestic electricity load profile characterisation Implications for demand side management. Energy 2019, 180, 665–677. [Google Scholar] [CrossRef]
- De Craemer, K.; Vandael, S.; Claessens, B.; Deconinck, G. An Event-Driven Dual Coordination Mechanism for Demand Side Management of PHEVs. IEEE Trans. Smart Grid 2013, 5, 751–760. [Google Scholar] [CrossRef]
- Sobhani, S.O.; Sheykhha, S.; Azimi, M.R.; Madlener, R. Two-Level Distributed Demand-Side Management Using the Smart Energy Hub Concept. Energy Procedia 2019, 158, 3052–3063. [Google Scholar] [CrossRef]
- van de Meerssche, B.; van Ham, G.; van Hertem, D.; Deconinck, G. Balancing renewables by demand side man-agement: Local and global potential. Int. J. Distrib. Energy Resour. 2013, 9, 383–397. [Google Scholar]
- Tang, R.; Wang, S.; Li, H. Game theory based interactive demand side management responding to dynamic pricing in price-based demand response of smart grids. Appl. Energy 2019, 250, 118–130. [Google Scholar] [CrossRef]
- Essiet, I.; Sun, Y.; Wang, Z. Scavenging differential evolution algorithm for smart grid demand side management. Procedia Manuf. 2019, 35, 595–600. [Google Scholar] [CrossRef]
- Kuiken, D.; Más, H.F. Integrating demand side management into EU electricity distribution system operation: A Dutch ex-ample. Energy Policy 2019, 129, 153–160. [Google Scholar] [CrossRef]
- Craparo, E.; Sprague, J. Integrated supply- and demand-side energy management for expeditionary environmental control. Appl. Energy 2019, 233–234, 352–366. [Google Scholar] [CrossRef]
- Lokeshgupta, B.; Sivasubramani, S. Multi-objective dynamic economic and emission dispatch with demand side management. Int. J. Electr. Power Energy Syst. 2018, 97, 334–343. [Google Scholar] [CrossRef]
- Mellouk, L.; Boulmalf, M.; Aaroud, A.; Zine-Dine, K.; Benhaddou, D. Genetic Algorithm to Solve Demand Side Management and Economic Dispatch Problem. Procedia Comput. Sci. 2018, 130, 611–618. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand Side Management in Smart Grid Using Heuristic Optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Ma, K.; Hu, G.; Spanos, C.J. Distributed Energy Consumption Control via Real-Time Pricing Feedback in Smart Grid. IEEE Trans. Control. Syst. Technol. 2014, 22, 1907–1914. [Google Scholar] [CrossRef]
- Ma, K.; Hu, G.; Spanos, C.J. Energy Management Considering Load Operations and Forecast Errors with Application to HVAC Systems. IEEE Trans. Smart Grid 2018, 9, 605–614. [Google Scholar] [CrossRef]
- Altinoz, O.T. The distributed many-objective economic/emission load dispatch benchmark problem. Swarm Evol. Comput. 2019, 49, 102–113. [Google Scholar] [CrossRef]
- Alham, M.; Elshahed, M.; Ibrahim, D.; Zahab, E.E.D.A.E. A dynamic economic emission dispatch considering wind power uncertainty incorporating energy storage system and demand side management. Renew. Energy 2016, 96, 800–811. [Google Scholar] [CrossRef]
- Dehnavi, E.; Abdi, H. Optimal pricing in time of use demand response by integrating with dynamic economic dispatch problem. Energy 2016, 109, 1086–1094. [Google Scholar] [CrossRef]
- Zaman, F.; Elsayed, S.M.; Ray, T.; Sarker, R.A. Configuring two-algorithm-based evolutionary approach for solving dynamic economic dispatch problems. Eng. Appl. Artif. Intell. 2016, 53, 105–125. [Google Scholar] [CrossRef]
- Aghaei, J.; Niknam, T.; Azizipanah-Abarghooee, R.; Arroyo, J.M. Scenario-based dynamic economic emission dispatch con-sidering load and wind power uncertainties. Int. J. Electr. Power Energy Syst. 2013, 47, 351–367. [Google Scholar] [CrossRef]
- Qiao, B.; Liu, J. Multi-objective dynamic economic emission dispatch based on electric vehicles and wind power integrated system using differential evolution algorithm. Renew. Energy 2020, 154, 316–336. [Google Scholar] [CrossRef]
- Zou, Y.; Zhao, J.; Ding, D.; Miao, F.; Sobhani, B. Solving dynamic economic and emission dispatch in power system integrated electric vehicle and wind turbine using multi-objective virus colony search algorithm. Sustain. Cities Soc. 2021, 67, 102722. [Google Scholar] [CrossRef]
- Gul, R.N.; Ahmad, A.; Fayyaz, S.; Sattar, M.K.; Haq, S.S.U. A Hybrid Flower Pollination Algorithm with Sequential Quadratic Programming Technique for Solving Dynamic Combined Economic Emission Dispatch Problem. Mehran Univ. Res. J. Eng. Technol. 2021, 40, 371–382. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Wang, H.; Wu, J.; Fan, X.; Xu, Q. Dynamic environmental economic dispatch of hybrid renewable energy systems based on tradable green certificates. Energy 2020, 193, 116699. [Google Scholar] [CrossRef]
- Kaboli, A.; Abdullah, S.H.; Alqallaf, K. Solving non-convex economic load dispatch problem via artificial cooperative search algorithm. Expert Syst. Appl. 2019, 128, 14–27. [Google Scholar] [CrossRef]
- Armaghani, S.; Amjady, N.; Abedinia, O. Security constrained multi-period optimal power flow by a new enhanced artificial bee colony. Appl. Soft Comput. 2015, 37, 382–395. [Google Scholar] [CrossRef]
- Abedinia, O.; Wyns, B.; Ghasemi, A. Robust fuzzy PSS design using ABC. In Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering, Institute of Electrical and Electronics Engineers (IEEE), Rome, Italy, 8–11 May 2011; pp. 1–4. [Google Scholar]
- Niknam, T.; Narimani, M.; Aghaei, J.; Azizipanah-Abarghooee, R. Improved particle swarm optimisation for multi-objective optimal power flow considering the cost, loss, emission and voltage stability index. IET Gener. Transm. Distrib. 2012, 6, 515. [Google Scholar] [CrossRef]
- Simon, S.; Padhy, N.; Anand, R. Ant colony system based unit commitment problem with Gaussian load distribution. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 16 October 2006; Volume 8. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.R.; Abarghooee, R.A. A new hybrid algorithm for optimal power flow considering pro-hibited zones and valve point effect. Energy Convers Manag. 2012, 58, 197–206. [Google Scholar] [CrossRef]



| Thermal Unites | Power Limits | Fuel Cost Coefficients | Emission Coefficients | Ramp Rate Limits | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pmin (MW) | Pmax (MW) | ag | bg | cg | dg | eg | γg | βg | αg | ξg | λg | URg (MW/h) | DRg (MW/h) | |
| Unit 1 | 50 | 200 | 0.00375 | 2 | 0 | 18 | 0.037 | 0.0649 | −0.05554 | 0.04091 | 0.0002 | 2.857 | 50 | 50 |
| Unit 2 | 20 | 80 | 0.0175 | 1.75 | 0 | 16 | 0.038 | 0.05638 | −0.06047 | 0.02543 | 0.0005 | 3.333 | 16 | 16 |
| Unit 3 | 15 | 50 | 0.0625 | 1 | 0 | 14 | 0.040 | 0.04586 | −0.05094 | 0.04258 | 0.000001 | 8 | 10 | 10 |
| Unit 4 | 10 | 35 | 0.00834 | 3.25 | 0 | 12 | 0.045 | 0.0338 | −0.0355 | 0.05326 | 0.002 | 2 | 7 | 7 |
| Unit 5 | 10 | 30 | 0.025 | 3 | 0 | 13 | 0.042 | 0.04586 | −0.05094 | 0.04258 | 0.000001 | 8 | 6 | 6 |
| Unit 6 | 12 | 40 | 0.025 | 3 | 0 | 13.5 | 0.041 | 0.05151 | −0.05555 | 0.06131 | 0.000001 | 6.667 | 8 | 8 |
| Participation Level | Without DSM | DSM with 5% | DSM with 10% | DSM with 15% | DSM with 20% |
|---|---|---|---|---|---|
| Fuel cost ($/day) | 13.554 | 13.513 | 13.469 | 13.456 | 13.413 |
| Emission (tons/day) | 7.500 | 7.343 | 7.301 | 7.286 | 7.284 |
| Participation Level | Method | Without DSM | DSM with 5% | DSM with 10% | DSM with 15% | DSM with 20% |
|---|---|---|---|---|---|---|
| Fuel cost ($/day) | NSGA | 17.53 | 17.56 | 17.65 | 17.75 | 18.53 |
| Emission (tons/day) | 6.784 | 6.753 | 6.689 | 6.624 | 6.124 | |
| Fuel cost ($/day) | MOPSO | 17.03 | 17.04 | 17.23 | 17.28 | 17.35 |
| Emission (tons/day) | 6.241 | 6.211 | 6.165 | 6.021 | 6.001 | |
| Fuel cost ($/day) | Proposed | 15.943 | 15.962 | 15.976 | 15.991 | 15.981 |
| Emission (tons/day) | 4.936 | 4.911 | 4.879 | 4.881 | 4.859 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abedinia, O.; Bagheri, M. Power Distribution Optimization Based on Demand Respond with Improved Multi-Objective Algorithm in Power System Planning. Energies 2021, 14, 2961. https://doi.org/10.3390/en14102961
Abedinia O, Bagheri M. Power Distribution Optimization Based on Demand Respond with Improved Multi-Objective Algorithm in Power System Planning. Energies. 2021; 14(10):2961. https://doi.org/10.3390/en14102961
Chicago/Turabian StyleAbedinia, Oveis, and Mehdi Bagheri. 2021. "Power Distribution Optimization Based on Demand Respond with Improved Multi-Objective Algorithm in Power System Planning" Energies 14, no. 10: 2961. https://doi.org/10.3390/en14102961
APA StyleAbedinia, O., & Bagheri, M. (2021). Power Distribution Optimization Based on Demand Respond with Improved Multi-Objective Algorithm in Power System Planning. Energies, 14(10), 2961. https://doi.org/10.3390/en14102961






