Pore-Scale Investigation of Microscopic Remaining Oil Variation Characteristic in Different Flow Rates Using Micro-CT

Abstract

The main means of secondary oil recovery is water flooding, which has been widely used in various oilfields. Different flow rates have a great impact on the recovery ratio and the occurrence of remaining oil. Scholars have carried out extensive research on it, but mostly on the macro scale, and research on the three-dimensional micro scale is also limited by accuracy and a lack of accurate understanding. In this paper, micro-CT and core displacement experiments are used to intuitively show the occurrence state of remaining oil under different flow rates. Through a series of quantitative image processing methods and remaining oil classification methods, the occurrence characteristics of remaining oil under different flow rates are systematically evaluated and studied. The results show that: (1) As the displacement rate increases, the remaining oil saturation decreases (61%; 35%; 23%), but the remaining oil is more evenly distributed along the slice; (2) Two lower displacement speeds (0.003 mL/min; 0.03 mL/min) can reduce the volume of huge oil clusters under oil-saturated conditions, and the highest displacement speed (0.3 mL/min) can completely break up large oil clusters into small oil droplets. At the same time, the shape factor of the oil clusters also gradually increases; (3) The proportion of continuous remaining oil volume decreases, and the proportion of discontinuous remaining oil increases. Discontinuous remaining oil is the main production target of EOR; (4) After water flooding, the microscopic remaining oil is more inclined to the middle and corner parts of the larger pores.

1. Introduction

The oil production from subsurface reservoirs is initially driven by the formation pressure and expansion of oil and rock [1,2], and then the secondary oil production is carried out by means of water injection [3,4]. Due to the heterogeneity of the formation and the existence of fractures, it is easy to form a stable water flow channel [5]. As the production progresses, it enters the high water cut stage, with water cut reaching 90% and even higher [6]. A large amount of remaining oil becomes trapped in oil reservoirs and is difficult to recover. Increasing the flow rate is a common method in the field to enhance oil recovery [7]. However, oil production by waterflooding can only reach 30%~50% of the original oil saturation in a water-wet reservoir [8]. The micro-structure of rock and the nature of fluid are fundamental and the macro-feature is a surface phenomenon [9]. Therefore, studying the location and form of microscopic remaining oil under different flow rates at pore-scale can provide new insights for enhanced oil recovery.

With the advancement of technology, CT technology has been applied to the field of petroleum engineering [10,11,12]. The physical properties of porous media and fluid distribution can be determined by the use of micro-CT on the submillimeter level, which provides a new method for pore-scale mechanism research [13]. During decades of research, micro-CT has been used to study reservoir properties [14], multi-phase flow [15] and CO₂ sequestration [16], etc., and more specifically, the characterization of relative permeability changes [17], measurement of contact angle [18], calculation of capillary pressure [19], enhanced oil recovery by low salinity recovery [20] and distribution of fluids during the water flooding [21]. For the occurrence of microscopic remaining oil, scholars have studied various controlling factors including reservoir factors and development factors.

The reservoir factors, such as pore-throat structure, reservoir heterogeneity and wettability in real rock systems have been focused on with the aid of micro-CT. Guo et al. analyzed the pore structures of four samples by fractal dimension and quantified and classified the microscopic remaining oil into five categories, which indicated that large connected oil clusters can be more easily broken into smaller segments in high permeability samples while all distribution patterns coexist with low permeability and complex pore structure [22]. The weaker the heterogeneity, the higher the pore sweep efficiency is, and the remaining oil clusters are mainly trapped in the form of non-continuous phase [9]. Li et al. found a lower S_or, 19.8%, for the oil-wet plug than for water-wet plug (25.2%) and that the trapped oil tends to occupy the center of the larger pores in the water-wet plug while it tends to occupy the pores corner and attach to the walls of the pores in the oil-wet plug [23]. The study of reservoir factors can help in the understanding of the distribution characteristics of microscopic remaining oil in different types of reservoirs.

The development factors, such as waterflooding PVs, flow rate and EOR, are more important than the reservoir factors, which can help to further explore how different types of microscopic remaining oil can be recovered. With the waterflooding PV increases, the volume fraction of the cluster microscopic remaining oil decreases significantly while the other four kinds of microscopic remaining oil show different increases [24]. Khishvand et al., (2016) found that an increase in capillary number produced significantly different pore-scale fluid distributions during imbibition by using pore-scale displacement mechanisms, in-situ wettability characteristics and pore size distribution information [25]. The volume of each oil cluster against its surface area follows the linear relationship, and the volume of each discontinuous oil cluster against its cumulative contribution to total oil volume follows the logarithmic relationship by the performance of HPF synergy with SPF [26]. Although the research on the occurrence and location of microscopic remaining oil under the influence of different factors has been thorough, there are still two main problems. One is that there are too many types of remaining oil classification, which leads to unclear analysis of the formation mechanism of various types of remaining oil. The other is that due to the limitation of scanning accuracy, some micropores and their internal fluids cannot be identified.

In this paper, we study the size and distribution of microscopic remaining oil under different flow rates in water-wet sandstone plugs by using the in-situ micro-CT scanning experiment. We propose a new classification standard of microscopic remaining oil to analyze the change law of microscopic remaining oil. In addition, the calculation method of oil saturation in micropores is further derived on the basis of the calculation method of micropores [27]. Based on the above method, this research is conducted to explore: (1) the morphology changes of microscopic remaining oil changes; (2) the production of microscopic remaining oil in pores of different radius; (3) the production mechanism of microscopic remaining oil in different flow rates.

2. Experimental Methodology

2.1. Rock Samples and Fluid Properties

The rock sample, which comes from Jiangsu Oilfield, is a cylinder 8 mm in diameter and 50 mm in length. The physical parameters of the sample are shown in

Table 1. Parameters of the sample.

Permeability/mD	Helium Porosity/%	Macro Porosity/%	Micro Porosity/%	Wettability
80.5	20.6	14.2	5.9	Water-wet

. The total of macro porosity and micro porosity based on CT scanning is less than the helium porosity, which indicates that some micro-porosity is not captured. The experimental fluids are No. 32 White Oil and KI solution with a mass fraction of 30%, where KI solution is used to increase the contrast of the oil–water gray value and extract the micro-pores in the sandstone core. The oil–water interfacial tension is 0.0074 N/m, and the oil viscosity and density at room temperature and pressure are 8.6 mPa·s and 828 kg/m³.

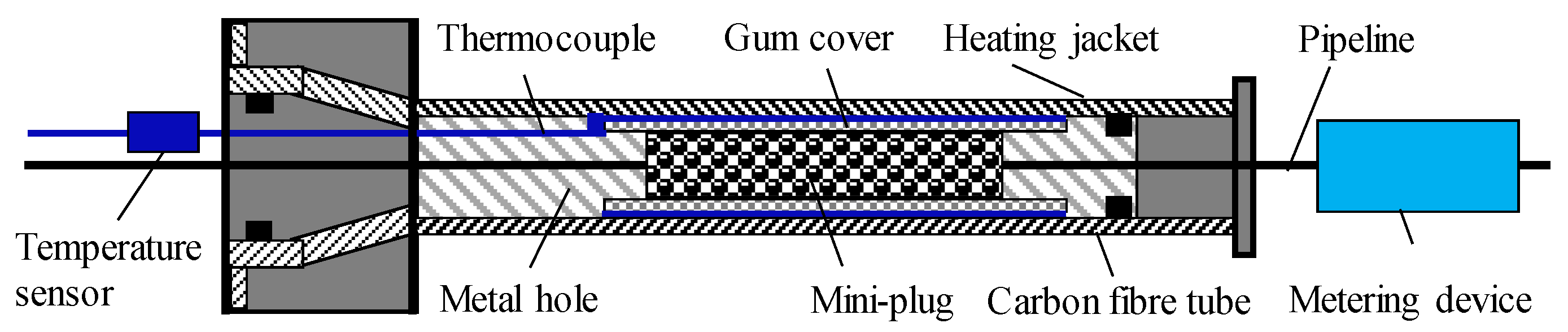
2.2. Experimental Procedure

The micro-CT scanner is a nanoVoxel-3502E series of Tianjing Sanying Precision Instrument CO., Ltd. (28 Siwei Road, Dongli District, Tianjin). The carbon fiber core holder has the function of maintaining high temperature and high pressure on-line in situ CT scanning (Figure 1). The experimental device diagram is shown in Figure 2. Before each CT scan, the pump is turned off to stop fluid injection. All scans are in-situ CT scans. The scan position is the center of the sample, and the scan resolution is 3 μm.

The specific experimental steps are as follows:

(1)

Core was placed in the core holder and subjected to a confining pressure of 12 MPa for 5 h, and then the first scanning was performed to obtain a reference dry scan. The confining pressure of 8 MPa was applied during all experiments.

(2)

The core was vacuumed and completely saturated with water phase and left for 12 h until the water phase and the core reached a chemical equilibrium, and the second scanning was performed.

(3)

Fifty PVs(Pore Volume) of oil was flushed through the plug at an injection rate of 0.03 mL/min to establish irreducible water condition. The third CT scanning was performed at the end of the saturation state called Exp. 0.

(4)

Fifty PVs of water displacement at an injection rate of 0.003 mL/min were conducted to establish residual oil state. Then the fourth CT scanning of the sandstone was conducted called Exp. 1.

(5)

Step 4 was repeated at an injection rate of 0.03 and 0.3 mL/min. Then the fifth and sixth CT scanning were performed called Exp. 2 and 3.

2.3. Data Process

After three-dimensional reconstruction, the software of Avizo and ImageJ were used for image processing and analysis. The images were subjected to pre-processing such as correction of edge hardening and removal of ring artifacts before segmentation. Then the images were filtered using a non-local mean to eliminate noise and enhance the contrast between each phase. Because of the limitation of the scanning accuracy (3 μm), micropores below the scanning accuracy could not be identified. The differential imaging method was used to identify the micropores. As shown in Figure 3a,b, they are cross-sectional views of the dried sample and the sample saturated with 30 wt% KI brine, respectively. The use of high-concentration KI brine can make the water phase have strong X-ray absorption capacity, making the area containing water brighter. As we can see, the solid grains appear saturated after the use of KI brine. However, the solid grains area with micropores appear gray because of the presence of KI brine. The different image was obtained by subtracting the dry scanning image from the saturated brine scanning image, where the black area is the solid grains, the white area is the macropores, and the gray area is the micropores, which makes the micropore area easier to distinguish (Figure 3c).

The method of distinguishing the solid grains, macropores and micropores is different from the previous method, which was to directly perform three-phase segmentation on the differential image and could cause certain errors. The method used in this paper is to extract the macropores using the watershed algorithm on the dry scanning image (Figure 4a). The macropores part of the mask was removed from the differential image, and the watershed algorithm method was used again to distinguish the solid grains and micropores in the remaining part (Figure 4b,c). The CT gray values distribution map of the three phases was obtained from the dry scanning image, and the peak values of the three phases were taken as the CT gray values of solid grains, macropores and micropores to calculate the porosity of the micropores (Figure 5), calculated as follows:

$$C{T}_{micro}^{dry}=C{T}_{grain}\times (1-{\varphi }_{micro})+C{T}_{macro}^{dry}\times {\varphi }_{micro},$$

(1)

$${\varphi }_{micro}=\frac{C{T}_{micro}^{dry}-C{T}_{grain}}{C{T}_{macro}^{dry}-C{T}_{grain}},$$

(2)

where $C{T}_{grain}$ is the CT gray value for solid grain, $C{T}_{mirco}^{dry}$ and $C{T}_{marco}^{dry}$ are the CT gray value for micropores and macropores in dry scanning image and ${\varphi }_{micro}$ is the porosity of micropores. After the porosity of micropores was obtained, the initial oil saturation of the micropores was obtained by adding the image of the saturated oil state. The oil-water distribution map in the saturated oil state was obtained by using the macropores as a mask. The above method was used to calculate the CT gray value of the oil phase, the water phase and the micropores in the saturated oil image after the oil and water phases were segmented by using watershed algorithm. The oil saturation of the micropores in different flow rates can be obtained by changing to images under the corresponding states, calculated as follows:

$$C{T}_{micro}^{oil}=C{T}_{grain}\times (1-{\varphi }_{micro})+C{T}_{brine}\times {\varphi }_{micro}\times (1-S_{o\_micro})+C{T}_{oil}\times {\varphi }_{micro}\times S_{o\_micro},$$

(3)

$$S_{o\_micro}=\frac{C{T}_{micro}^{oil}-C{T}_{grain}\times (1-{\varphi }_{micro})-C{T}_{brine}\times {\varphi }_{micro}}{C{T}_{oil}\times {\varphi }_{micro}-C{T}_{brine}\times {\varphi }_{micro}},$$

(4)

where $C{T}_{mirco}^{oil}$ is the CT gray value for micropores in the scanning image under the saturated oil state, $C{T}_{brine}$ and $C{T}_{oil}$ are the CT gray values for water phase and oil phase and $S_{o\_micro}$ is the oil saturation of the micropores.

3. Results and Discussion

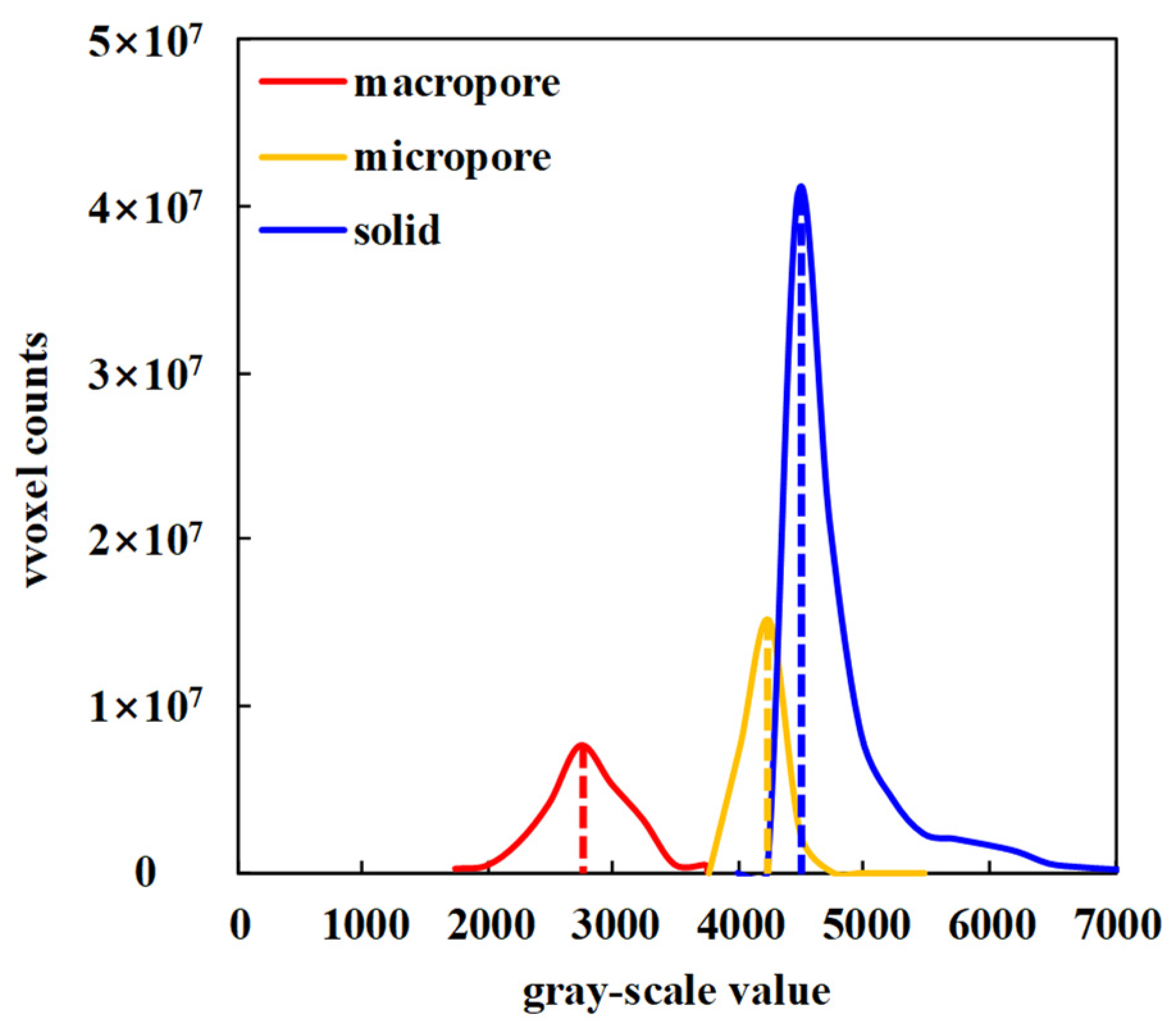
3.1. Representative Elementary Volume

The larger the volume of the data, the more possible it was that the image represented the characteristics of the core, but the computing power of the computer may not have met the computational requirements. Therefore, to meet the computing power of the computer, we needed to choose the representative elementary volume of the core, that is, the smallest volume of data that could characterize the basic characteristics and physical properties of the core. Taking the porosity and saturation as parameters and the segmented data volume as the research object, a series of cube data bodies with different side lengths were cut out, and the macro-porosity and micro-porosity of each data volume were calculated. Taking the macro- and micro-porosity as parameters and the segmented data as the object, a series of data cubes with different lengths were cut out, and the macro- and micro-porosity of each cube was calculated. The length of cube gradually increased from 50 to 500 pixels. As shown in Figure 6, as the data volume increased, the curve change of each parameter gradually tended to be horizontal, indicating that the scanning field of view was larger than the representative elementary volume of the core, so it was determined that the studied area was a cube with a side length of 500 pixels.

3.2. Cluster Morphologies and Classification

Two parameters were used to classify the remaining oil. One was the Euler Number ($E_N$) and the other was the Average Oil Thickness ($T$). The Euler Number was used to describe the topological properties of the residual oil clusters. The Euler Number can be expressed as follows:

$$E_N=1-b_1+b_2,$$

(5)

where $E_N$ is the Euler Number of the oil cluster, $b_1$ is the number of connectivity and $b_2$ is the enclosed cavities.

Average Oil Thickness was used to describe the morphology properties of the residual oil clusters. It is computed as follows:

$$T=\frac{2*V}{S},$$

(6)

where $V$ is the volume of the residual oil cluster, μm³, and $S$ is the surface area of the oil cluster, μm². In the definition of oil thickness, the surface area of the side of the oil cluster is ignored.

Combining the Euler Number and Oil Thickness, the remaining oil was divided into three categories. The classification standard of the remaining oil is listed in

Table 2. This is a table. Tables should be placed in the main text near to the first time they are cited.

Remaining Oil Type	Euler Number	Oil Thickness/Voexl
Clustered Flow (Continuous phase)	En ≤ −1	T ≥ 5
Membranous Flow ((Continuous phase)	En ≤ −1	T < 5
Discontinuous phase	En > −1	/

. Following are the characteristics of the three remaining oil categories:

(1)

Clustered Flow (Continuous phase) occupied multiple pores, causing its Euler Number to be less than or equal to −1. Different from the Membranous Flow, the Oil Thickness of the Clustered Flow was larger, which was determined to be greater than or equal to 5 μm through analysis and comparison.

(2)

Membranous Flow (Continuous phase) occupied multiple pores, and its Euler Number was the same as Clustered Flow. The Oil Thickness of Membranous Flow was less than that of Clustered Flow, which was determined to be less than 5 μm.

(3)

Discontinuous phase only occupied single or a few pores, which was the remaining oil with discrete distribution after water flooding. The Euler Number of the Discontinuous phase was greater than −1.

3.3. Research on Microscopic Remaining Oil

In this section, we first calculated the oil saturation of each stage and each slice in the data volume based on the CT scanning. Then the occurrence state and distribution of microscopic remaining oil in different flow rates were counted. Finally, the mobilization of different flow rates on the microscopic remaining oil was summarized.

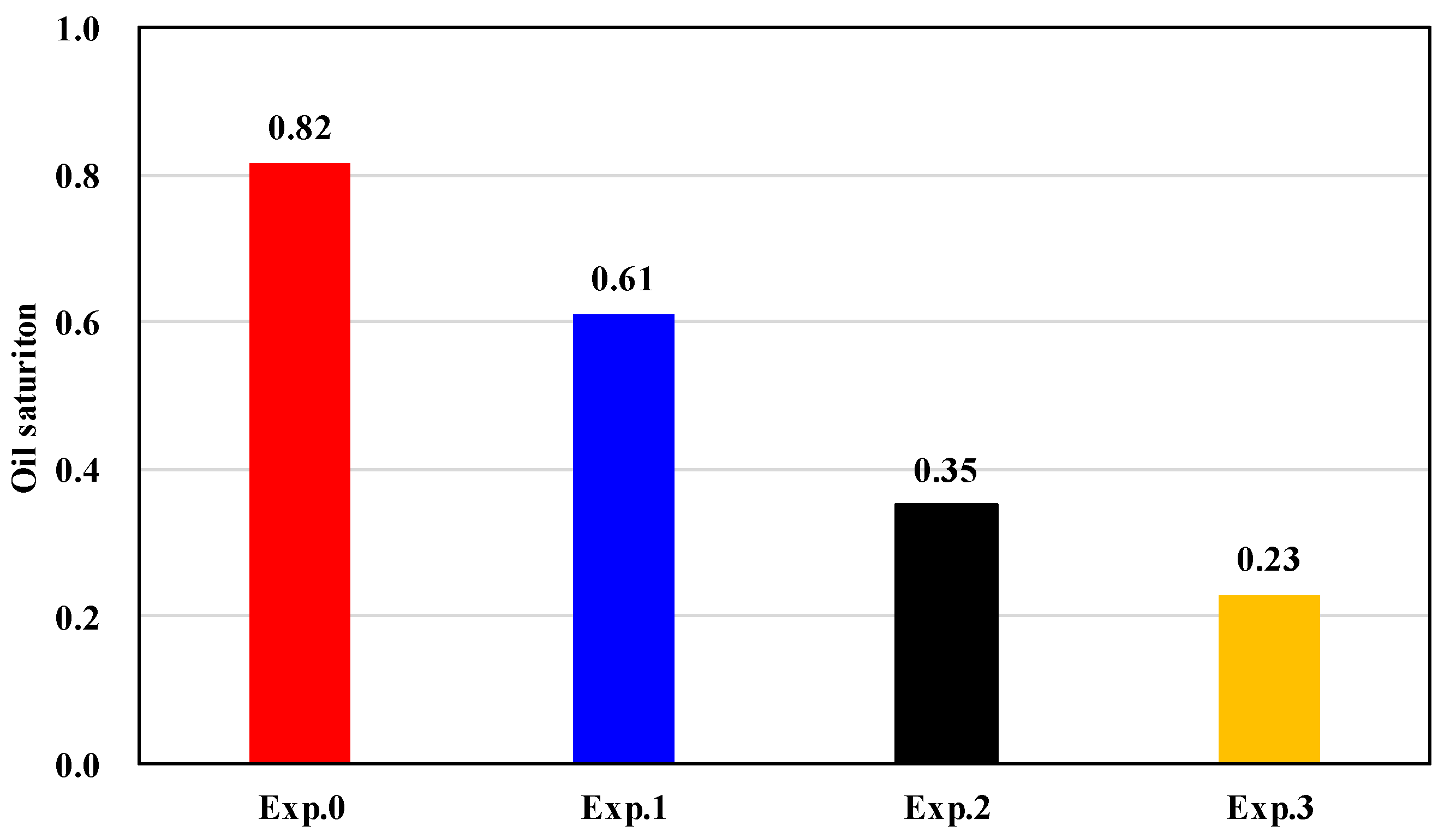
3.3.1. Oil Saturation

According to the change of oil saturation, increasing the flow rate has a great effect on enhanced oil recovery, see Figure 7. In order to observe the change oil saturation along the core, we calculated the micro- and macro-porosity (Figure 8) and the oil saturation along the longitudinal direction of the core after each displacement state (Figure 9). The porosity in the slice numbers 0–45, 213–376 and 458–500 was high, but the overall distribution was relatively uniform from the slice map of porosity. The initial oil saturation distribution along the core was uniform because of the uniform porosity distribution, with a standard deviation of 2.59. After water flooding, the standard deviation of oil saturation at each stage was 4.92, 4.87 and 4.35 respectively. Although the porosity and the initial oil saturation distribution was homogeneous, the heterogeneity of the distribution of oil saturation along the core increased after water flooding. At the same time as the flow rate increased, the heterogeneity decreased. After water flooding three times with different flow rates, four lower saturation points appeared at the same locations, which corresponded to the higher points of the porosity. Along the displacement direction, the remaining oil tended to be less where the porosity was higher, and it did not change with the increase of the flow rate.

By segmenting images, we obtained the distribution of oil and water in macropores at each stage, as shown in Figure 10. As observed, the oil phase inside the pores was well connected and remained in the center of pores or even occupied the entire pores at the initial stage. After the first displacement at 0.003 mL/min, the oil phase was broken up, but it was still continuous. From the two-dimensional images, when the flow rate reached 0.03 mL/min, the microscopic remaining oil was basically no longer continuous, but existed in the center or corner of the pores in an isolated state. The isolated oil phase further shrunk or was broken up into smaller oil droplets when the flow rate increased to 0.3 mL/min.

3.3.2. The Morphological Characteristics of Microscopic Remaining Oil

To obtain more information about the morphological characteristics of the microscopic remaining oil, it was reconstructed in three dimensions to count the surface area, volume, shape factor and other parameters. The classification method in Section 3.2 was used for classification analysis. Figure 11 shows the oil cluster volume against its contribution to total oil volume at each state. There is a large oil cluster that accounts for more than 90% of the total oil volume in the initial oil saturation state. After the first water flooding at a flow rate of 0.003 mL/min, the largest oil cluster was stripped out of several medium oil clusters, but the largest oil cluster still accounted for 74%. The dominance of the volume of the largest oil cluster was not affected after the second water flooding. However, there was no longer a large oil cluster after the third water flooding. Thus, when the capillary number reached 1 × 10⁵ the microscopic remaining oil was completely broken up into dispersion form.

Figure 12 shows the surface area of each oil cluster against its volume at each state. The results showed that the surface area and volume had an exponential relationship, which was consistent with the finding of Yu et al. [26]. In addition, as the flow rate increased, the index of the fitted formula decreased, which indicated that the surface area became larger with the same volume. During the water flooding process, the large oil clusters were broken up into multiple small oil clusters, and the shape became more irregular. For further determination, the shape factor distribution of the pores and the oil clusters under the four states was calculated (Figure 13). As shown, the shape factor distribution of the oil in Exp. 0 was similar to that of the pores, because the oil almost completely filled the pores when the oil was saturated. The shape factor of the oil clusters became large, and the morphology became irregular. When the capillary number reached 1 × 10⁶, the shape factor of the microscopic remaining oil no longer changed. We can conclude that the larger the shape factor of the oil clusters, the more difficult they are to recover.

Figure 14 shows the classification of microscopic remaining oil in the four states using the classification method in Section 2.2. It was found that clustered flow gradually decreased, and the discontinuous phase increased. There was basically no membranous flow in the core due to the water-wet system, and the membranous flow will not be considered in the following discussion. Further statistics on the volume ratio of the two kinds of microscopic remaining oil in different states can be found in Figure 15. As a result of the above discussion, the continuous phase was gradually broken up into discontinuous phase as the flow rate increased. The cluster flow was rarely recovered after Exp. 1, which was consistent with the result obtained from the two-dimensional image in Section 3.3.1. However, the cluster flow still accounted for 60% of the total oil volume after Exp. 2, which was a dominant position and did not match the result obtained from the two-dimensional image. This is because discontinuities in two dimensions may be continuous in three dimensions. After Exp. 3, the discontinuous phase dominated, and it was observed that cluster flows were no longer connected to form a large oil cluster. Therefore, the enhanced oil recovery should mainly study how to produce discontinuous phase in the later stage of high-speed water flooding.

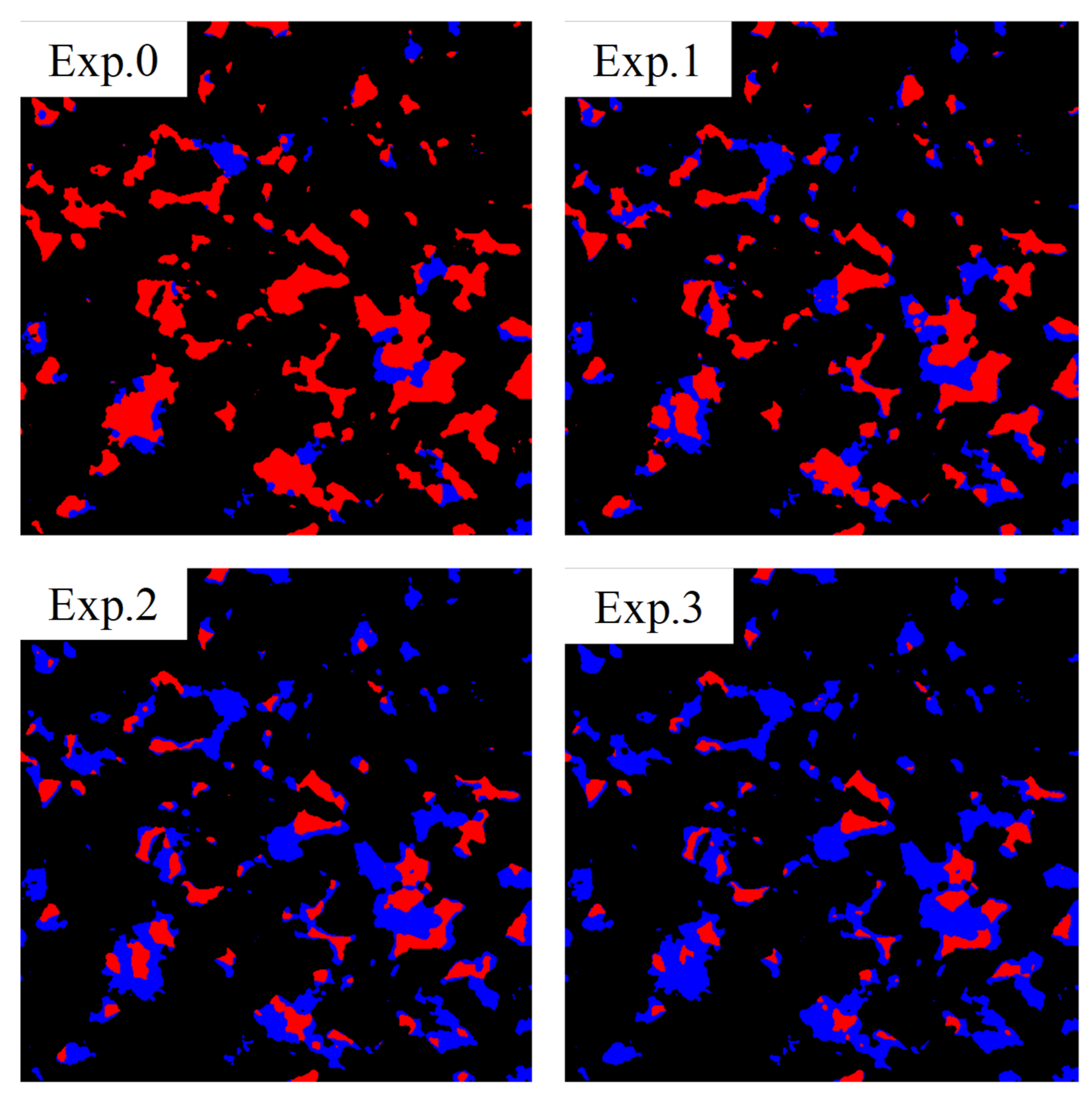
3.3.3. The Distribution Characteristics of Microscopic Remaining Oil

The oil saturation of each pore in each state was counted to calculate the average oil saturation of pores with equivalent radius (Figure 16). The formula for calculating the average oil saturation was as follows:

$$S_i^{average}=\frac{{\displaystyle \sum _k^n{S}_k{V}_k}}{{\displaystyle \sum _k^n{V}_k}},$$

(7)

where, $S_i^{average}$ is the average oil saturation of pores with equivalent radius $i$, $S_k$ is the oil saturation of the $k$-th pore with radius $i$ and $V_k$ is the volume of the $k$-th pore with radius $i$. We can observe from Figure 16 that the degree of saturated oil in the large pores is higher than that in the small pores after Exp. 0. This is because of the large capillary force in the small pores, which made it difficult for the entrance of the oil phase in the water-wet system. In addition, due to the presence of capillary force, the oil saturation in the large pores was still greater in the subsequent three water flooding processes.

In order to study the change characteristics of oil saturation in pores of different sizes as the flow rate increased, the average oil saturation in different sized pores against different flow rates is plotted in Figure 17. As expected, the curves show a downward trend. The smaller the pores, the lower the average oil saturation at each stage, which means that unlike the oil-wet system, the injected fluid invaded the small pores while the oil remained in the large ones. It is worth nothing that the average oil saturation in the micropores and the pores with a radius of 5 μm basically did not change from Exp. 2 to Exp. 3. As discussed above, the oil phase was recovered mainly based on capillary force. We can conclude that at the flow rate of 0.003 mL/min in Exp. 1, part of the micropores area was not affected. When the flow rate was increased from 0.03 mL/min to 0.3 mL/min, it did not continue to expand the spread range, but improved the recovery rate by increasing the viscous force.

In order to further explore the position of microscopic remaining oil in the pores, the deviation rate parameter was proposed to characterize the distance between the remaining oil and the pore center. As shown in Figure 18, the pores and the remaining oil inside were idealized into a spherical shape. Black represents pores, and red represents remaining oil. We calculated the volume of remaining oil and pores, V1 and V2, the equivalent radius and the coordinates of the center of gravity, respectively. The equivalent radius of the pore was R2. The distance between the radius and the center of gravity can be obtained through the two coordinates, and then combined with R2 to get R1. Therefore, the formula for the deviation rate is:

$$D=1-\frac{R_1}{R_2}\times \sqrt{\frac{V_2}{V_1}},$$

(8)

The range of deviation rate is 0~1. The smaller the deviation rate, the closer the oil phase was to the pore center. Based on the above formula, the distribution of the remaining oil deviation rate in the four experiments was calculated (Figure 19). In experiment 0, that is, when the oil was saturated, the deviation rate was concentrated in 0~0.1, indicating that the saturation effect was better and the oil phase could completely fill the pores. With the increase of the flow rate, the distribution of the deviation rate showed an interesting change: the deviation rate of 0~0.1 continuously decreased, the deviation rate of 0.2~0.8 showed a very small state, and the deviation rate of 0.9~1 was continuously decreasing. In the high water-cut stage, the microscopic remaining oil was mainly deposited in the pores in two forms: in the center of the pore, and attached to the edge of the pore. There are two main reasons for this result. One is that in the water-wet core, the oil phase tended to be in the center of the pores. The other is that due to hydrodynamic reasons, the corners of the pores were difficult to affect, causing part of the oil phase to adhere to the edges of the pores.

4. Conclusions

In this paper, the physical experiment of water flooding under different flow rate conditions based on the micro-CT was carried out. The pores were further divided into macro-pores and micro-pores by differential imaging method, and a comprehensive remaining oil classification method and remaining oil deviation rate calculation method are proposed to characterize the remaining oil occurrence state and distribution characteristics. The following conclusions have been concluded from this study:

(1)

From the perspective of oil saturation, the remaining oil saturations corresponding to the displacement rates from low to high were 61%, 35% and 23% respectively. At the same time, the standard deviation of the oil saturation along the core slice gradually decreased, which are 4.92, 4.87 and 4.35, respectively. As the displacement rate increased, the remaining oil saturation decreased, but the remaining oil was more evenly distributed along the slice.

(2)

From the perspective of remaining oil occurrence states, the lower two displacement speeds reduced the volume of huge oil clusters under oil-saturated conditions, and the highest displacement speed could completely break up large oil clusters into small oil droplets. At the same time, with the increase of the displacement rate, the shape factor of the oil clusters also gradually increased. The result of remaining oil classification is that the proportion of continuous remaining oil volume decreased, and the proportion of discontinuous remaining oil increased.

(3)

From the perspective of remaining oil distribution characteristics, after water flooding at different displacing speeds, the microscopic remaining oil was more inclined to the middle and corner parts of the larger pores.

Through the above conclusions, it can be concluded that microscopic remaining oil can be effectively used by increasing the displacement speed. After high-speed displacement, the microscopic remaining oil is mainly distributed in the middle and corners of the pores. Increasing the viscosity of the displacement phase and changing the microscopic flow path are the directions to take to further improve oil recovery.