Multi-Step Energy Demand and Generation Forecasting with Confidence Used for Specification-Free Aggregate Demand Optimization

Abstract

Energy demand and generation are common variables that need to be forecast in recent years, due to the necessity for energy self-consumption via storage and Demand Side Management. This work studies multi-step time series forecasting models for energy with confidence intervals for each time point, accompanied by a demand optimization algorithm, for energy management in partly or completely isolated islands. Particularly, the forecasting is performed via numerous traditional and contemporary machine learning regression models, which receive as input past energy data and weather forecasts. During pre-processing, the historical data are grouped into sets of months and days of week based on clustering models, and a separate regression model is automatically selected for each of them, as well as for each forecasting horizon. Furthermore, the multi-criteria optimization algorithm is implemented for demand scheduling with load shifting, assuming that, at each time point, demand is within its confidence interval resulting from the forecasting algorithm. Both clustering and multiple model training proved to be beneficial to forecasting compared to traditional training. The Normalized Root Mean Square Error of the forecasting models ranged approximately from 0.17 to 0.71, depending on the forecasting difficulty. It also appeared that the optimization algorithm can simultaneously increase renewable penetration and achieve load peak shaving, while also saving consumption cost in one of the tested islands. The global improvement estimation of the optimization algorithm ranged approximately from 5% to 38%, depending on the flexibility of the demand patterns.

1. Introduction

Time series forecasting is useful in many applications [1,2]. Before 1927, time series were forecast using extrapolation. Then, Yule introduced the autoregressive model in order to forecast future values of time series as weighted sums of previous ones, and linear modelling with noise was the common practice for forecasting within the next 50 years or so. Afterwards, the linear models proved to be inadequate to describe complex time series behaviour, and since 1980, along with the evolution of computers, time series forecasting has been addressed also using machine learning techniques and state-space reconstruction with time-delay embedding [3]. Examples of recent generic time series forecasting methods are random walk with drift, Autoregressive Fractionally Integrated Moving Average (ARFIMA), exponential smoothing state-space model with Box–Cox transformation, Autoregressive Moving Average (ARMA) errors, Trend and Seasonal components (BATS), simple exponential smoothing, Theta and Prophet methods [4], a hybrid approach linearly combining alternative neural network models based on a weighting automatically derived by the model errors [5], Bayesian models [6] and discretization with fuzzification [7].

One of the aforementioned applications is that of forecasting energy demand (consumption) and generation (production). The review in [8] explains why the variance of solar and wind generation leads to cost and how this cost is reduced thanks to generation forecasting.

Self-consumption of energy is achieved with an energy storage system and Demand Side Management. The most popular strategy for the latter is load shifting [9]. According to [10], with the increase of population, energy management through demand response (DR) programs has become an important need. Particularly, most of such programs are price-based, according to the following charging policies: (a) Time-of-Use (TOU), according to which the price depends on the time of the day and is determined by the historically average cost of energy delivery at each time, (b) Real-Time Pricing (RTP), where future prices are determined in real time on an hourly basis based on the current conditions, and (c) Critical-Peak Pricing (CPP), which is a dynamic pricing mechanism using elements of the above two to modify tariffs as a temporary response to events or conditions like high market prices or reserve being reduced. RTP is mentioned as the best DR technique [11].

The current paper presents first a generic forecasting algorithm, based on machine learning techniques, applied to predict aggregate demand and generation in three demonstrators (Orkney island, Ballen marina at Samsø and Madeira island). Past values of the variable to be forecast along with weather forecasts from [12] were considered as potential input to the forecasting regression models. However, only the variables that improved the performance of the models were finally selected. The historical dataset was grouped w.r.t. month and day of week by applying a clustering method to the data of the variable to be forecast. Along with each forecast, a confidence interval is automatically provided by the algorithm, according to the distribution of the forecasting error, considering the impact of the forecasting horizon, time of the day and month–day of week group resulting from the above clustering. The pre-processed input and output variables of the forecasting models were defined in such a way that they have near-linear dependencies. However, multiple regression architectures were tested with hyper-parameter tuning, including the contemporary Extreme Learning Machines (ELM), which is presented in [13] as better than the usual Artificial Intelligence techniques, due to its faster learning ability and its simpler architecture. Additionally, a demand optimization algorithm was developed, which assumes that the future demand can be shifted among the timestamps of the optimization interval (e.g., next 24 h). Regarding constraints, it was considered that the average demand across all timestamps of the interval should not be modified, and that the demand at each future timestamp always ranges within the respective confidence interval. This optimization algorithm is generic and was implemented for each demonstrator using relevant data. It considers three optimization criteria, namely minimum cost for the consumer, maximum usage of renewable energy and minimum power instability. The degree of deviation from the fulfilment of each of these criteria was evaluated based on a Key Performance Indicator (KPI), which was defined mathematically. In order that multiple criteria among the above three are considered for the optimization, a total KPI was defined as a weighted mean of the individual KPIs, which were scaled appropriately first. Not all three criteria were considered in all demonstrators, because some criteria were considered as non-applicable to some of them. The optimization algorithm is accompanied by a flexibility analysis for total demand, based on confidence intervals for demand, derived from the forecasting algorithm. Flexibility is the ability to increase or reduce the production of power plants or the consumption of demand processes [14]. A standard formula for quantifying flexibility does not exist, and flexibility depends on the settings of the problem in question.

Based on the above, the solution described in this paper may be considered as useful if at least one of the following hypotheses is valid:

• The end user is an energy consumer who views the recommendations about the time points in the near future when energy consumption should be preferred according to the desired weighting factors of the three optimization criteria and the unit prices of energy at every time point which are applicable to this user, and adjusts his/her consumption behavior accordingly.
• The end user is a Distribution Systems Operator that forwards the recommendations of these algorithms to its customers.
• The end user is someone authorized to determine the unit prices of energy consumption at every time point, so (s)he can examine to what extent the economic criterion contradicts the renewable energy penetration and power stability criteria and adjust unit prices accordingly, also dynamically.

The remainder of the paper is organized as follows: Section 2 presents the related work and the contribution of ours. In Section 3, the high-level architecture of the system of the forecasting and optimization algorithms is depicted, whereas in Section 4 and Section 5 the forecasting and optimization algorithms, respectively, are presented in detail, including their methodology and experimental results. The paper is concluded in Section 6. Finally, Appendix A provides more information about the raw data.

2. Related Work and Our Contribution

A literature review relevant to the specific problem of demand and generation forecasting follows: In [15] a multi-step forecasting algorithm similar to ours has been implemented in the field of heat load in district heating systems, evaluating also recursive apart from direct forecasting with similar results. However, in contrast with our paper, in order to quantify intrinsically categorical variables such as month and time of day, it applies one-hot encoding, thus highly increasing the number of input variables and enforcing the partial sharing of parameters among models for different months and times of day. The review in [16] deals with solar generation and electricity demand. The authors mention that demand response causes instability in the forecasts. In terms of algorithms, although they confirm that Artificial Neural Networks (ANNs) are still popular, other techniques are also used nowadays (random forests, support vector machines, gradient boosting). It is stated that there is no single forecasting model which is the best for all use cases, and this conforms with the findings of the present paper. This is argued also in the review of [17], which favors the trial and error strategy for this reason. The last review also mentions that clustering is a common approach to automatically group days, as done in our work, although generally this method was not found in the bibliography of the current research. However, that paper also argues that most of the researchers focus only on point forecasts and not so much on confidence intervals. (In some papers, including that one, the confidence intervals for predictions are mentioned as “prediction intervals”. In this paper, by “confidence interval” a prediction interval is implied). This is also a conclusion of [18], which summarizes the methods of the Global Energy Forecasting Competition 2014 winners. The authors of [19] take advantage of the method used by the winners of the above competition for load and price forecasting with the help of multiple weather stations, which was based on quantile regression using pinball loss minimization, and generalized additive models.However, in that work, a time of year variable was introduced, which seems to be inappropriate for two reasons. First, it does not take into account the dependencies among timestamps of same time of the day in different days of the year. Secondly, it increases linearly over time, so it has a non-linear dependence with the variable to be forecast, in contrast with the average time profile, which was used in our method. In that work, day of week clusters were defined manually based on experience. It seems that only during the last few years probabilistic forecasting has been studied more extensively. For example, in [16,20], quantile regression, quantile regression forests, Gaussian processes, bootstrapping, Lower Upper Bound Estimate, gradient boosting, kernel density estimation, k-nearest neighbor and analog ensemble are mentioned as the main statistical non-parametric methods for probabilistic energy forecasting, along with the statistical parametric, physical (parametric and non-parametric) and hybrid approaches. In the energy forecasting review of [21] it is confirmed, as observed also by the rest of this literature review, that regarding generation, mainly wind and solar forms have been studied. Nothing is mentioned about hydro and waste, which are studied in our paper for the Madeira demonstrator. In the case of wind generation there is no distinction between ANM (Active Network Management) and non-ANM, which was done in our work for Orkney, as discussed in more detail in Section 4.2. The work in [20] uses Gaussian processes for probabilistic forecasting of demand and solar generation in an isolated building, however it uses as input only past values of the variable to be forecast based on pre-defined time lags. Grey models are presented by [22,23] as appropriate for training of forecasting models in case of lack of sufficient historical data to train non-linear Artificial Intelligence models, which usually happens for high forecasting horizons (e.g., 1 year), as is the case in these two papers, where China’s yearly electricity and natural gas demand respectively are forecast using just some past values of the variable to be forecast as input. A similar horizon (2-year) is used in [24], where monthly electricity demand is predicted with bagging Autoregressive ntegrated Moving Average (ARIMA) and exponential smoothing techniques, again using only past values of the variable to be forecast as input. In [25], generation and demand in smart cities and factories are forecast using Markov chain, stride predictors, neural networks and combinations of them. In that study, the forecasting problem is discretized and only the recent values of the variable to be forecast are used as input. In the work of [26], yearly forecasts only for non-renewable generation are made for the next 14 years using linear regression, based only on the historical trend of generation. In [27], electricity consumption of a microgrid is forecast using the Nearest Neighbors algorithm for prediction after clustering in business days and weekends with Self-Organizing Maps. However, no comparison with other models is made, and weather data have not been used as input. In [28], demand, generation and battery state of charge of a microgrid are forecast with ARIMA, using only past data of the variable to be forecast among photovoltaic (PV) power production, load consumption and battery state of charge in a building, and a control algorithm is applied afterwards. However, in [29,30], which deals with microgrid demand, it is argued that ANNs are more appropriate for time series forecasting than ARIMA, especially in cases where the signals exhibit abrupt fluctuations and nonlinearity. In [30] especially, season (with arbitrary numbering) and time themselves instead of demand average over season/time have been inserted as input to the model, thus leading to non-linear instead of linear relations between input and output, in contrast to our approach. In [31], pp. 691–704, it is also mentioned that ANNs perform better, especially in cases where the signals exhibit abrupt fluctuations and nonlinearity. Therein, a Generalized Radial Basis Function Network (GRBFN) is used for forecasting solar generation, with modifications in the original algorithm such as the use of Evolutionary Particle Swarm Optimization (EPSO) for optimization during model training. However, overfitting is avoided with the weight decay method and the variables with unimportant weights are not mentioned, so the importance of all the considered input variables is questionable. No comparison is made with linear regression models. In [31], pp. 704–729, an ensemble technique with wavelet decomposition and reconstruction for forecasting demand and solar generation of an integrated smart building at the University of Queensland equipped with PVs is applied, again by introducing time-dependent variables instead of their average profile as model input. Finally, [32] is devoted exclusively to solar generation prediction, using only past solar irradiation as input instead of using also past solar generation and future solar irradiation forecasts; that paper uses a single, 10-min forecasting horizon, performing manual split of the data into seasons, and focuses on ANN without comparing multiple regression models.

The optimization algorithm of this paper regards a multi-criteria decision analysis (MCDA). Multi-attribute utility theory (MAUT), analytical hierarchy process (AHP) and multi-attribute value theory (MAVT) are particular MCDA techniques [33,34]. In the current work an alternative of MAVT, used in [34], is employed, as described later in detail.

The bibliographic research of this section continues with DR-related optimization algorithms. The work in [9] solves an optimization problem using the self-consumption percentage as criterion, and assesses the impact of weather forecast uncertainty. In [35], DR is applied to control the usage of home Air Conditioners by minimizing cost. Nevertheless, the only model applied is linear regression and the dataset used consists of only a single summer week with low weather variability. The approach in [36] performs specification-based cost optimization computing confidence intervals for uncertain variables with an introduced method, and uses reliability constraints. Similarly, in [37], cost optimization is performed in a single household with an energy storage system, based on confidence intervals for load and generation obtained using quantile regression and k-nearest neighbor methods, but without using weather data to improve forecasts. Cost is also optimized in [38,39] using a genetic algorithm. Those papers consider a PV and a battery to generate and store energy respectively, and the latter has additionally taken into account customer comfort constraints for which user input is needed. The work in [40] also performs specification-based cost optimization converting a non-linear optimization problem to a linear one, and employing a graph-theory-based energy hub model using coupling matrices. In [41], energy procurement cost for retailer from pool market is minimized, using a robust optimization method facing the uncertainty of the model input. The algorithm has been used by multiple DR programs (pool-order, forward, reward-based). The paper in [42] regards demand and electric vehicle (EV) usage forecasting for cost optimization and control, involving more than 300 active drivers in the experiment. In addition, in [43], a genetic algorithm performs demand response in an isolated microgrid of Terceira island based on the cost criterion, while considering the consumer and grid manager viewpoint. In [10,44], cost is optimized along with consumer satisfaction, which has also been formulated mathematically, either as a constraint [44] or as an additional term in the objective function [10], whereas additional constraints have been introduced. Once more, the non-linear programming optimization problem has been solved with a genetic algorithm. In those two papers, specifications of particular home appliances have been considered. Similarly, [11] executes specification-based cost and comfort optimization requiring user input, proposing separate DR schedules for multiple users. In [31], pp. 613–635, a mixed-integer nonlinear programming problem is solved using the Particle Swarm Optimization (PSO) and Simulated Annealing algorithms and their variants while performing also demand and generation forecasting so as to enhance the input of the cost optimization problem. From the literature review of [31], pp. 635–645, it is inferred that Tabu search (TS), PSO, multi-agent and fuzzy systems, as well as heuristics are commonly used in optimization, and TS is employed therein for cost minimization. An other alternative of PSO, named Quantum PSO (QPSO), is used in [31], pp. 680–691, to solve a specification-based cost optimization DR algorithm related to load shifting. The goal of [31], pp. 729–741, was to develop an algorithm to select the location of EV charging stations to be constructed by optimizing cost, mean usage rate of charging poles and user charging convenience under specification-based constraints, using an appropriate mathematical model. That work introduces an improved version of the strength Pareto evolutionary algorithm (SPEA), called SPEA2, for the computation of a set of optimal three-objective solutions. The work in [45] concerns a related paper that has performed specification-based optimization in one of the three demonstrators of the present work (Samsø), without including details about the forecasting approach. An other work for specification-based optimization has been published for the Madeira demonstrator [46]. It uses ARMA for forecasting and co-optimizes arbitrage, self-sufficiency, peak shaving and energy backup for Model Predictive Control, formulating all but one optimization criteria as constraints. In [47], a control algorithm for cost optimization is applied to an ice bank system for food refrigeration, considering temperature predictions, ice mass and energy consumption. However, renewable energy sources are not considered, and many data used in that work are simulated instead of real. The latter occurs also in [48], which deals with cost optimization in a microgrid based on weather forecasts, assuming demand as deterministic instead of introducing uncertainty or demand forecasting models. In [49], another specification-based problem is addressed about water consumption instead of electricity consumption, considering the economic viability and operational risks management criteria, but introducing only cost in the objective function and defining constraints for the other criterion. The work in [50] studies integrated instead of the typical demand response, which enables consumers also to change the type of the consumed energy. In [51], scenarios for uncertainty are used in a probabilistic model for a cost optimization problem, considering wind and PV production and using domain-specific constraints about energy conversion. However, also in that paper, power is simulated using random variables instead of actual data, and power forecasting is not studied. In [52], an optimization problem for production lines of heavy industries is solved, and flexibility is analysed, but without an obvious mathematical definition and numerical evaluation, as done in the current study. In [53], another industrial application to an electrolysis plant is discussed, using cost in the objective function and considering domain-specific operational constraints. In [54], multiple, potentially contradicting criteria are considered for optimization of distribution networks reconfiguration. The problem is solved using the epsilon-constrained method and the max-min fuzzy satisfying technique to balance the different criteria, but without weighting the contributions of the criteria to the total objective function after their normalization, which was done in our work to consider the subjective opinion of the end user about the relative importance of the criteria. Finally, [55], which deals with another optimization problem with PVs and wind turbines in a microgrid, introduces an arbitrary dynamic pricing model with respect to renewable and non-renewable energy, a basic price and constant parameters. Demand and price are optimized using the PSO method with respect to cost and comfort, but only for a 4-s interval and without using forecasting. It concludes that dynamic pricing results in higher customer profit than fixed pricing.

By studying the above bibliographic research, the main contribution of the present work follows. Instead of solving a specification-based optimization problem related to a (relatively) low number of energy consuming assets and requiring input from consumers to assess their comfort, this work deals with a specification-free, statistical-based approach, in order to optimize aggregate demand in larger areas, even whole islands, from which it is practically infeasible to acquire all specifications. Particularly, in the current study, demand flexibility is estimated thanks to the confidence interval for demand obtained based on test error distribution during training the demand forecasting models on historical data. Although a thorough evaluation of the confidence intervals and comparison among probabilistic forecasting methods are not a main focus of this study, the confidence interval reliability and sharpness are considered to be improved in this work by simultaneously taking into account the forecasting horizon, the time of the day and the month and day of week group to which the forecast corresponds, where grouping is based on automatic clustering. Thanks to clustering, any periodic and non-periodic seasonality is automatically identified. This is a step forward compared to the traditional seasonal ARIMA (SARIMA) models, which assume periodic seasonality exclusively. In this way, the closer the point forecasts are to the respective exact values, the narrower the confidence intervals are, while their reliability is based on the desired significance level. Apart from cost, this work considers also renewable energy penetration, based on energy generation forecasting models also trained on historical data, and power stability as optimization criteria. Finally, although weather data and time-related information are also involved in the input of the forecasting regression models apart from past values of the variable to be forecast, the paper defines the input variables in such a way that they have near-linear relation with the output, which not only enables the possibility for fast training, but also helps to select the best input variables and clustering algorithm during pre-processing using linear approximations of the forecasting models. Bibliographic references tend to focus on the selection of complex forecasting models rather than the appropriate definition of the input variables, which renders training of simpler models easier.

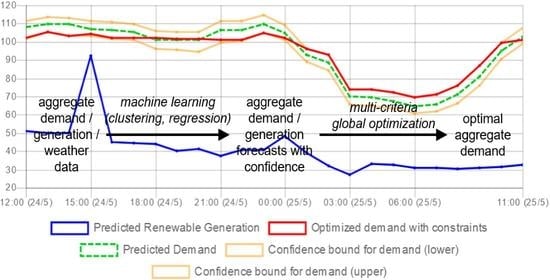
3. High-Level Architecture

The high-level architecture of the forecasting and optimization algorithms is depicted in Figure 1. The data sources refer to demand and generation data, for example, from application programming interfaces (APIs) in case of real-time data from Madeira, or files with previously downloaded historical data. Historical weather data and observed historical data from [12] are also considered. The forecasting module receives input data from these sources and is able to (re)train demand and generation forecasting models and use them for real-time predictions. Particularly, the models are saved for future reuse, and are also retrained if they are outdated, according to a configurable oldness threshold. The forecasts are stored in the output database and afterwards they are used by the optimization module, which delivers to the same database the optimal demand scheduling for the near future. Executing the forecasting module and posting the forecasting output before the optimization module is triggered was preferred as an option, because if the optimization module called the forecasting module instead, the forecasts could not be used as input by third party modules.

4. The Forecasting Algorithm

The forecasting algorithm has been implemented using data from all three demonstrators of Orkney, Samsø and Madeira. Forecasting models were trained for aggregate generation and demand (power).

4.1. Methodology of the Forecasting Algorithm

The goal of this algorithm is to forecast the values of a variable for multiple future time points, using data until present as input, from that and/or other variables. Each estimation is accompanied by a confidence interval. The forecasting problem is formulated based on both traditional and state-of-the art machine learning regression models.

The approach consists of the following steps:

• Scaling each raw variable so that it has mean equal to 0 and standard deviation equal to 1. This is required by some of the non-linear regression architectures.
• In particular cases, the target variable is transformed to one of its features, but typically all raw variables are directly used in the following steps, just after aggregation.
• Selection of input variables based on linear regression.
• Grouping the historical dataset w.r.t. month and day of week by applying a clustering algorithm to the data of the target variable (i.e., the variable to be forecast). The selection of the clustering algorithm and respective clusters is automatic, based on the behavior of the target variable, and particularly the selection of algorithm is also based on training of linear regression approximations of the forecasting models.
• Supervised training of all regression architectures on the selected input variables. A separate training is performed for each group and forecasting horizon. The best architecture, based on 3-fold cross-validation, is automatically selected in each case, and the respective model is retrained within the whole historical dataset. (Cross-validation is a common method to evaluate the ability of a model to generalize to unknown data. Since usually about 50–70% of a dataset is used for a single training, considering 3 folds is a reasonable choice).

Each forecasting model may be expressed mathematically as:

$${\widehat{y}}_s\left(t\right) = f_{G\left(t\right),s}\left(x_{G\left(t\right),s}\left(t\right),z_{G\left(t\right),s}\left(t\right),{\mathbf{p}}_{r,G\left(t\right),s}\left(t\right),h_{G\left(t\right)}\left(t\right),\mathbf{w}\left(t\right),{\overline{\mathbf{w}}}_{G\left(t\right),s}\left(t\right)\right),$$

(1)

according to the following notation:

• t: time point for which the forecast is made
• s: forecasting horizon
• ${\widehat{y}}_s\left(t\right)$: estimation of the value that the target variable will have at the time point t based on the forecasting horizon s
• $G\left(t\right)$: the group of months and days of week that t belongs to
• $x_{G\left(t\right),s}\left(t\right)$: latest known measurement of the target variable within $G\left(t\right)$ when forecasting for the time point t with horizon s (“present value”)
• r: duration such that all past values of the variable to be forecast, within $G\left(t\right)$, obtained after final aggregation (see Section 4.3.1), with a delay up to this duration, are used as input to the model
• $z_{G\left(t\right),s}\left(t\right)$: latest known measurement of the target variable at the same time of the day as t within $G\left(t\right)$ when forecasting for the time point t with horizon s (“last value at same time”)
• ${\mathbf{p}}_{r,G\left(t\right),s}\left(t\right)$: past values of the variable to be forecast, within $G\left(t\right)$, obtained after final aggregation, with a delay up to duration r, to be used as input to the model, when forecasting for the time point t with horizon s
• $h_{G\left(t\right)}\left(t\right)$: historical mean of the target variable at the same time of the day as t within $G\left(t\right)$ (“average time profile”)
• $\mathbf{w}\left(t\right)$: weather variables at the time point t (forecast weather in case of real-time forecast of the target variable, or exact weather in case of training on a historical interval)
• ${\overline{\mathbf{w}}}_{G\left(t\right),s}\left(t\right)$: mean of weather variables within the interval from the time point of $x_{G\left(t\right),s}\left(t\right)$ to t—in practice, no variable from this vector proved to be useful (and it would not make sense in most of the cases), so it will not be discussed later

It needs to be clarified that the time point of $x_{G\left(t\right),s}\left(t\right)$ is not necessarily $t - s$, and the time point of $z_{G\left(t\right),s}\left(t\right)$ is not necessarily $t - \left(1\mathrm{day}\right)$. It may also be earlier, because only the time points of the same group $G\left(t\right)$ are taken into account in the computation of the lag between the time point of $x_{G\left(t\right),s}\left(t\right)$ and t. For example, if $G\left(t\right)$ is a group of business days of summer months, then the earliest business day of June of some year is considered as the next day of the last business day of the August of the previous year. Similarly, the time interval of past values with previous output duration r is not necessarily $[t - r,t)$.

The confidence interval for ${\widehat{y}}_s\left(t\right)$ is computed based on the empirical distribution of the error of the test sets, which is considered as dependent on the group, the forecasting horizon and the time of the day. Thus, it can be written as $\left[{\widehat{y}}_s\left(t\right) + {\epsilon }_{G\left(t\right),s,t,\frac{a}{2}},{\widehat{y}}_s\left(t\right) + {\epsilon }_{G\left(t\right),s,t,1-\frac{a}{2}}\right]$, where a denotes the significance level and ${\epsilon }_{G\left(t\right),s,t,\frac{a}{2}}$, ${\epsilon }_{G\left(t\right),s,t,1-\frac{a}{2}}$ the $\frac{a}{2}$ and $1 - \frac{a}{2}$ percentiles of the error of a single prediction of the target variable respectively, within $G\left(t\right)$, for horizon s and time of the day equal to the time of the day of the time point t. In practice, the error distributions in this work are symmetric enough so that ${\epsilon }_{G\left(t\right),s,t,\frac{a}{2}} < 0$ and ${\epsilon }_{G\left(t\right),s,t,1-\frac{a}{2}} > 0$ in all cases for $a = 0.05$ (which is our choice), so the forecast belongs to its confidence interval. On the other hand, it was not assumed that the error distribution is necessarily Gaussian (or even fully symmetric), because this assumption could be wrong. So, it was preferred to estimate the confidence interval based on the historical data (non-parametric approach) rather than the critical values of some Gaussian or other known distribution (parametric approach).

4.1.1. Forecasting Regression Model Architectures and Tested Hyper-Parameters

The following regression architectures and respective hyper-parameters are tested using the scikit-learn Python library [56] (version 0.20.1):

• Multilayer Perceptron Regressor [MLP(hidden layer sizes)]—in case of absence of hidden layers [MLP()], this is reduced to linear regression

  -

  hidden layer sizes = (), (1), (2), (5), (1,1), (2,2), (5,5)

  -

  activation = “tanh”

  -

  solver = “lbfgs”

  -

  maximum number of iterations = ${10}^8$

  -

  alpha = 0

• Random Forest Regressor [RF(maximum depth)]

  -

  maximum depth = 1, 2, 5, 10

  -

  number of estimators = 100

• Nearest Neighbour Regressor [NN(number of neighbours, weights)]

  -

  number of neighbours = 5, 10, 20, 50, 100, 200

  -

  weights = “uniform”, “distance”

• Support Vector Regressor [SVR(penalty, kernel(degree), epsilon)]

  -

  penalty (C) = 0.1, 1, 10

  -

  kernel = “poly” (polynomial), “rbf” [Radial Basis Function (RBF)], “sigmoid”

  -

  degree = 1, 2 (applicable only to the “poly” kernel)

  -

  epsilon = 0.1, 0.01, ${10}^{-3}$, ${10}^{-4}$, ${10}^{-5}$

  -

  maximum number of iterations = ${10}^7$

• Gaussian Process Regressor [GPR(alpha)] (when the number of data points is less than ${10}^4$, so that training is memory-efficient)

  -

  alpha = ${10}^{-10}$, ${10}^{-9}$, ${10}^{-8}$, ${10}^{-7}$, ${10}^{-6}$, ${10}^{-5}$, ${10}^{-4}$, ${10}^{-3}$, 0.01, 0.1

In addition, some more recent algorithms from the scikit-learn extensions library [57] (version 0.0.2), which are not so widely-used in the bibliography compared to the previous ones, have been considered:

• Kernel Regression [KR(kernel, gamma)]

  -

  kernel = “poly”, “rbf”, “sigmoid”

  -

  gamma = 0.01, 0.1, 1, 10, 100, ${10}^3$

• Exteme Learning Machines [ELM(hidden layer units, alpha, RBF width, activation function)]

  -

  hidden layer units = 1, 2, 5, 10, 20, 50, 100

  -

  alpha = 0, 0.5, 1

  -

  RBF width = ${10}^{-3}$, 1

  -

  activation function = “gaussian”, “tanh”

The selected values of the aforementioned non-tuned hyper-parameters differ from the default values set by the respective library, because they seemed to generally perform better, based on preliminary experiments. For all other hyper-parameters of the above regressors the default values are considered. More information on the hyper-parameters may be found in the documentation of the above two libraries.

4.1.2. Clustering Methodology and Relevant Architectures Tested

As mentioned above, clustering aims at grouping the dataset by subsets of months and days of week combinations, so that different regression models are trained for each cluster. This is helpful when the behavior of the target variable depends on the month and/or day of week. Clustering addresses the problem of existence of qualitative variables (month and day of week), which, since their numbering is not meaningful, would traditionally need to be inserted as binary variables in the regression models (one-hot encoding), and this would lead to too many input variables in the models, as aforementioned, which would need to share their common parameters among different months, days of week and times of day.

Clustering is performed in two phases. In the first phase it is done w.r.t. months and in the second phase w.r.t. day of week for each cluster of months resulting from the first phase. The feature vector of each month used as input for months clustering consists of the mean values of the target variable at every pair of day of week and time of day during that month within all years with existing data. For example, when using a sampling step of 1h, the length of the feature vector is 7·24 = 168. In the second phase, the feature vector of each day of week which is used as input to cluster days of week consists of the mean values of the target variable at every time of the day during that day of week and within the set of months of the months group in question.

The following clustering architectures are tested using the first of the two above libraries [56]:

• Algorithms automatically selecting number of clusters:

  -

  Affinity Propagation (AP)

  -

  Mean Shift (MS)

• Algorithms requiring manual selection of number of clusters n (1, 2, 6 and 12 clusters are tested for month, whereas 1, 2 and 7 clusters are tested for day of week):

  -

  K-Means (KM(n))

  -

  Agglomerative Clustering (AC(n))

As above, it needs to be clarified that apart from the number of clusters (when applicable), for the rest of parameters of the clustering algorithms the default values have been considered, and may be found in the documentation of the library. In each of the two phases, among the candidate clustering architectures, the one minimizing the Normalized Root Mean Square Error (NRMSE) (see Section 4.1.3) after training the fast linear regression model separately for each cluster and for each forecasting horizon is automatically selected as the best. As will be demonstrated later by the forecasting results, although non-linear models contribute to the reduction of the errors, using linear regression as a much faster approximation is satisfactory, since the input variables in Equation (1) have been defined in a way that they are near-linearly associated with the output.

4.1.3. Evaluation

The performance of the forecasting algorithm is quantified based on the Normalized Root Mean Square Error (NRMSE), which is interpreted as the ratio of the standard error of the prediction error to the standard deviation of the target variable, and is a common evaluation metric for regression problems. In this work, the NRMSE for a particular forecasting horizon s is defined as

$$E\left(s\right) = \sqrt{\frac{{\sum }_F{\sum }_{t\in I_{s,F}}{[y\left(t\right) - {\widehat{y}}_s\left(t\right)]}^2}{{\sum }_F{\sum }_{t\in I_{s,F}}{[y\left(t\right) - \overline{y}]}^2}},$$

(2)

and the total NRMSE as

$$E = \sqrt{\frac{{\sum }_s{\sum }_F{\sum }_{t\in I_{s,F}}{[y\left(t\right) - {\widehat{y}}_s\left(t\right)]}^2}{{\sum }_s{\sum }_F{\sum }_{t\in I_{s,F}}{[y\left(t\right) - \overline{y}]}^2}},$$

(3)

according to the following notation:

• F: training-test set split of the cross-validation
• $I_{s,F}$: time interval for which forecasts are made based on horizon s, within all training/test sets obtained by split F when computing training/test NRMSE respectively and within all groups of months and days of week pairs resulting from clustering
• $y\left(t\right)$: exact value of the target variable at the time point t
• ${\widehat{y}}_s\left(t\right)$: forecast value of the target variable for the time point t
• $\overline{y}$: mean of the target variable within the whole historical dataset

The NRMSE is non-negative. Lower values are better, so the perfect value is 0. It is independent of the measurement unit of the target variable, because it is scaled by the denominator. When it equals 1, the model performance is the same as the performance of the naive model that always predicts the mean of the variable as the future value of the target variable. It is easy to prove that the latter is the best constant model, because the mean of a variable minimizes the sum of square differences between the variable’s observations and a constant number w.r.t. this constant.

The NRMSE is computed for the test sets (test NRMSE) and the persistence model, as defined in [31], pp. 704–729, the forecasts of which equal the latest available value (benchmark NRMSE), which is another naive approach to be compared with ours. The formula of this model is

$${\widehat{y}}_s\left(t\right) = x_{G\left(t\right),s}\left(t\right).$$

(4)

The performance measure for the models that has been used for model selection is the test NRMSE.

4.2. Raw Data Used from Each Demonstrator

Table 1. Power data used from each demonstrator for training of the forecasting models.

Demonstrator	Demand	Generation
Orkney	total (3 December 2018–6 April 2020)	wind ≃ total (ANM, non-ANM) (3 December 2018–6 April 2020)
Samsø	harbour (1 May 2016–19 June 2017)	PV estimation—harbour (2016)
Madeira	total (1 January 2018–30 November 2019)	hydro, wind, waste (“bio”), solar (1 January 2018–November 2019)

shows the demand and generation data from each demonstrator that were used for training. At Orkney, almost all generation is produced by wind, and it is separated into ANM and non-ANM. ANM stands for Active Network Management. This corresponds to the wind turbines to which curtailment is applied when generation is too high to be consumed or stored. Because some non-ANM turbines may become ANM in the future, forecasting models are trained also for the sum of ANM and non-ANM generation. In case of Samsø, only the harbour is studied. Harbour generation has not been measured yet directly, but it was estimated indirectly for a whole year by the partners of the demonstrator.

Before feeding the data to the Python code, some minor preliminary cleaning took place offline:

• Orkney generation was frozen within some intervals, which were discarded from the analysis. After that, about 5% and 6% of ANM and non-ANM generation timestamps respectively appeared to have missing values. Furthermore, a few negative values of generation were replaced by 0.
• In Madeira case, about 1% of the timestamps were discarded, because the sum of registered total demand was not within the range $\pm 1\%$ of the total generation, renewable and non-renewable (thermal), although total demand and total generation should be equal.

As mentioned above, weather data are also available for every location from [12], although some data are missing sometimes.

More details about the technical objective, the grid issues/constraints, the market, regulatory and legal context, as well as the suitable DR programs for each demonstrator are documented in [58]. More details about the raw power data may be found in Appendix A.

4.3. Experimental Results from the Forecasting Algorithm and Discussion

The results obtained by implementing the steps of the approach mentioned previously are presented and discussed in this subsection.

4.3.1. Algorithmic Specifications and Initial Pre-Processing

For all demonstrators, it is desired that forecasts are made for forecasting horizons of 1 h, 2 h,..., 24 h. So, the raw data, which have a sampling step of 15 min–1 h, are aggregated with a 1-h sampling step. (A constant sampling rate is needed for the models. It is worthless and time consuming to keep a finer resolution because all forecasting horizons are a multiple of 1 h and the algorithm is not required to be executed more frequently than once an hour, or even once a day). For each variable, missing values are addressed with linear interpolation only for data gaps up to 1 h.

Especially for the Samsø demonstrator, it is interesting and also easy to disaggregate the controllable from the non-controllable demand, because it is assumed that any control algorithm can affect only the former. Based on information from the demonstrator experts, the controllable demand corresponds to the harbour assets and usually to spikes in the demand plot, because controllable energy is consumed for short periods of time (usually up to 3 h) for particular purposes (e.g., sauna, wastewater pump, EV charger on harbour master’s office). On the other hand, demand for charging the numerous boats in the harbour, which is much smoother, is considered as non-controllable at this stage, although there is a plan to control it in the future. Therefore, in the analysis of this work, it has been assumed that the non-controllable demand may be expressed by the rolling median of demand with a window size of 9 h (9 time points). As for the controllable demand, because the exact time of the day when it is observed is partly vague, it has been expressed by the difference between the rolling mean and the rolling median of demand with a window size of 9 h, and the models for forecasting it use a sampling step of 12 h, obtained with a second aggregation, after the variable transformation.

4.3.2. Input Variables Selection and Timestamps Clustering

The input variables were selected using a forward-backward selection policy. Variables inclusion/exclusion was based on the test error obtained after training linear regression models on the dataset. Regarding the past values, maximum delays of 0, 1 h, 2 h, 6 h, 12 h and 23 h were examined, except for the controllable demand at Samsø, where the final sampling step is 12 h, as mentioned above, so only the delays 0, 12 h and 23 h were tested. The selections made are shown in

Table 2. Input variables selected and clustering details regarding the forecasting models.

Demonstrator	Output	Input	Clustering Algorithms for Month/Day of Week	Month Groups & Respective Day of Week Groups (Sets) on the Left & Right Respectively of Slashes and Colons [Days are Numbered from 0 (Monday) to 6 (Sunday)]
Orkney	generation—ANM	present value, average time profile, wind speed, wind gust	singletons/-	singletons/-
	generation—non-ANM	present value, wind speed, wind gust	KM(6)/-	{{10,1}, {11,12,2–4}, {5}, {6}, {7,8}, {9}}/-
	generation—total (wind)	present value, past values (≤23 h), wind speed, wind gust	MS/-	{{9–4}, {5}, {6–8}}/-
	demand	present value, past values (≤23 h), apparent temperature	KM(6)/-	{{11–2}, {3}, {4}, {5,10}, {6,9}, {7,8}}/-
Samsø	generation—solar	present value, last value at same time, past values (1 h), average time profile, sun, humidity	singletons/KM(2)	{{1}:{{6–1,3,4},{2,5}}, {2}:{{4–1},{2,3}}, {3}:{{0,4,6},{1–3,5}}, {4}:{{5–1,3},{2,4}}, {5}:{{2–0},{1}}, {6}:{{0–3},{4–6}}, {7}:{{3–1},{2}}, {8}:{{0–3},{4–6}}, {9}:{{0,1,4},{2,3,5,6}}, {10}:{{0,4,6},{1–3,5}}, {11}:{{4–2},{3}}, {12}:{{0,1,4,5},{2,3,6}}}
	demand—total	present value, past values (≤23 h)	singletons/-	singletons/-
	demand—non-controllable	present value, past values (≤23 h), average time profile	KM(6)/-	{{1–3,6}, {4,5}, {7}, {8}, {9–11}, {12}}/-
	demand—controllable	last value at same time, average time profile	KM(6)/AP	{{1,2}:{{0,2,6},{1,3},{4,5}}, {3,4}:{{0,2,6},{1,3},{4,5}}, {5,6,9}:{{0–4},{5,6}}, {7}:{{0–2,4,5},{3},{6}}, {8}:{{5–0},{1–4}}, {10–12}:{{0,2,4,6},{1,3},{5}}}}
Madeira	generation—hydro	present value, past values (≤23 h)	-/-	-/-
	generation—wind	present value, past values (≤23 h), average time profile, wind speed	AC(2)/-	{{10,11,1–4}, {5–9,12}}/-
	generation—waste	present value, last value at same time, average time profile	KM(2)/-	{{12,1,3–8}, {9–11,2}}/-
	generation—solar	present value, last value at same time, past values (1 h), average time profile, sun, humidity	KM(2)/-	{{10–2}, {3–9}}/-
	demand	present value, last value at same time, average time profile	singletons/MS	{{1}:{{0–4},{5},{6}}, {2}:{{0–4},{5},{6}}, {3}:{{0–4},{5},{6}}, {4}:{{0–4},{5},{6}}, {5}:{{0–4},{5},{6}}, {6}:{{0–4},{5},{6}}, {7}:{{0–4},{5},{6}}, {8}:{{0–4},{5},{6}}, {9}:{{0–4},{5},{6}}, {10}:{{0–4},{5},{6}}, {11}:{{0–4},{5},{6}}, {12}:{{0,3,4},{1,2},{5},{6}}

. It needs to be noted that the “sun” variable is not directly available by [12]. It is a variable defined in this work in order to quantify the sunlight and is computed as $1 - \left(\mathrm{cloudcover}\right)$ between the sunrise and sunset time (obtained also by [12]), and as 0 otherwise. It is also worth mentioning that the variable selection process is rendered more complex due to clustering, because some variables may be useful without clustering and useless when clustering is applied.

Overall, in Table 2 the input variables selected, the clustering algorithms that proved to be the most appropriate and the respective clusters obtained are presented.

Regarding the input variables, the present value is always selected, except for the case of controllable Samsø demand, where, as aforementioned, the data have been aggregated with a 12-h sampling step, and thus the forecasts are made only for 12-h and 24-h forecasting horizons. The average time profile and the last value at the same time point as the one for which the forecast is made, or also other past values of the target variable, are often helpful. As for the weather data, as expected, wind-related variables (especially wind speed) are always selected as input to models forecasting wind generation, whereas sunlight and humidity appear to affect solar generation.

Clustering in months improved the overall forecasting performance almost in any case, and particularly the clusters based on generation are separated more clearly into winter and summer months. Sometimes (especially for demand forecasting) clustering days of week also makes sense, because these are related to people’s consumption patterns. The most evident example is Madeira demand, where it seems that business days, Saturdays and Sundays have three different profiles almost every month. The clusters were also meaningful for Samsø controllable demand, which was relatively high during first or second halves of specific days of the week in winter, but other days of week in the summer. The benefit of clustering will be shown more clearly by the numerical evaluation in Section 4.3.3, as well as by the comparison of the average time profiles among the selected clusters in Appendix A.

4.3.3. Results from Training the Regression Models

In the pie charts of Figure 2, the number of cases (cluster and forecasting horizon pair) in which each regression model architecture was the best in terms of the selected evaluation measure mentioned above is shown for the three demonstrators. For example, the first pie depicts 24 × 12 = 288 groups, since there are 24 forecasting horizons and 12 clustering groups, as shown above. These architectures correspond to the results of

Table 3. Results (test NRMSE) from training the regression forecasting models.

Demonstrator	Output	Proposed Approach	No Clustering—All Candidate Regressors	Same Clusters—Linear Regression	Same Clusters—Benchmark Regressor
Orkney	generation—ANM	0.3419	0.4164	0.4283	0.9217
	generation—non-ANM	0.4282	0.4727	0.5725	0.9351
	generation—total (wind)	0.4022	0.4300	0.4877	0.8715
	demand	0.3879	0.4141	0.4087	0.6715
Samsø	generation—solar	0.3678	0.4360	0.4335	1.3081
	demand—total	0.4108	0.4379	0.4209	0.5649
	demand—non-controllable	0.3112	0.3263	0.3206	0.3959
	demand—controllable	0.7122	0.9668	0.8152	not computed
Madeira	generation—hydro	0.3846	0.3846	0.3855	0.6025
	generation—wind	0.6862	0.6994	0.6880	0.8171
	generation—waste	0.4524	0.4534	0.4567	0.4852
	generation—solar	0.3371	0.3440	0.3396	1.3826
	demand	0.1674	0.2781	0.1846	1.3447

. Furthermore, in Figure 3, Figure 4 and Figure 5, the training, test and benchmark errors of the selected architectures are plotted as a function of the forecasting horizon, but still aggregated for all clustering groups.

In the pies, each main colour corresponds to a particular model kind (e.g., blue to MLP), and every tone of that main colour corresponds to a different selection of hyper-parameters for that kind, although there is no standard correspondence between tone and values of hyper-parameters; instead, darker tones correspond to higher frequency.

It was observed that usually several architectures have comparable performance for the same learning task. However, sometimes the appropriateness of an architecture seemed to depend on the forecasting horizon. MLP and SVR tend to perform better for low horizons, whereas RF and NN for higher. GPR, KR and ELM were more rarely selected. GPR proved to be inefficient also in terms of memory cost, which was not even viable when a lot of training data (>10,000 time points) were used (mainly in some cases related to Madeira generation, where the clusters were not many).

In Table 3, higher error indicates that the variable is harder to forecast, especially when it does not regard an aggregate measurement (e.g., the controllable demand at Samsø, which constitutes a relatively small part of the total harbour -or island- demand). However, all errors (apart from the ones corresponding to the benchmark) are below 1, so all models offer an added value compared to any of the two naive approaches. A special outcome of this table is that the novel ANM wind generation at Orkney, which is gradually becoming more and more common, seems a bit easier to be forecast compared to the traditional non-ANM wind generation. The intermediate columns are of particular interest as well. Generally, in cases of many clusters, clustering considerably reduces the error, as shown by the first two numeric columns. The most important of these cases are the controllable demand at Samsø and the demand at Madeira, as aforementioned, where it is clear that demand patterns are affected by month and/or day of week. From the comparison of the first and third numeric columns it can be inferred that, in several cases, the selection of the numerous regression models, as shown previously in the pie charts, is beneficial compared to the usage of linear regression for all clustered groups and forecasting horizons; however, often, the improvement is not serious (at least as an average from all horizons), even in cases where linear regression is not the predominant model in the respective pie. On the one hand, this is advantageous because it shows that, thanks to the methodology based on which the input variables have been defined, the easy-to-train linear regression model is an acceptable estimation when used for selection of input variables and clustering algorithm before the final training. On average, the appropriate clustering proved to be approximately equally important as the testing of all considered regressors.

More information is provided by the error curves. As expected, the error is usually lower for low forecasting horizon, and this indicates that the more the error drops as the horizon decreases, the higher the impact of the present value to forecasting. When the benchmark error decreases as the horizon approaches 24 h, this implies that the value of the variable being forecast is relatively close to the value 1 day before within the same group. Therefore, the impact of variables apart from the present value and the last value at the same time as the time for the forecast is reflected by the difference of test and benchmark error for a horizon of 24 h. The cases with the most remarkable difference correspond to Orkney wind generation, which exhibits strong correlation with wind speed (Pearson 0.8048 and Spearman 0.8417 for total wind generation) and wind gust (Pearson 0.8082 and Spearman 0.8389 for total wind generation) in the dataset, in contrast with the Madeira case, where the correlation between wind generation and wind speed is much weaker (Pearson 0.3211 and Spearman 0.3689). Furthermore, a valley appears in the benchmark error curve of Samsø total demand and Madeira hydro generation, because these variables usually exhibit two increases and decreases of similar duration every day, so values with a time distance of 12 h are generally closer to each other compared to values with time distance of for example, 6 h or 18 h. Finally, the training error fluctuations are explained by the variety of architectures selected among forecasting horizons. The test error curves are smooth, and close to the training error ones, at least for some forecasting horizons, and this happens especially in the Madeira case, where the amount of data is higher. This provides evidence that no overfitting issue exists.

Figure 6 and Figure 7 demonstrate examples from the real-time execution of the forecasting algorithm in our dashboards, comparing actual and forecast values with 95% confidence intervals for the same timestamps in the Madeira case. These dashboards contain data from 2020 and 2021, that is, after the training and cross-validation time interval mentioned in Table 1, which covers 2018 and most of 2019. Especially, Figure 6 corresponds to demand, which obviously depends highly on the time of the day and generally it is lower during weekends, especially Sundays. The latter justifies the automatic clustering in business days, Saturdays and Sundays, as shown in Table 2. Due to the effect of the last value at same time within the same cluster as an input to the models, the algorithm can also identify the overall change of the pattern from week to week. There is comparable error both with 1-h and 24-h forecasting horizons, which conforms with the almost flat green curve for Madeira demand in Figure 5. Only the first day (Monday, 4th January) the forecasts are slightly lower than the exact values using an 24-h horizon, since the previous day of the same cluster (Friday, 1st January) was a public holiday, so demand was exceptionally lower than normal for business days. Finally, in Figure 7, apart from the effect of time of the day, the special impact of weather variables is depicted. In each column, intentionally, 2 consecutive days of the same cluster (based on Table 2) with clearly distinguishable weather and power profiles were selected, so that the alignment between forecasts and exact values using a 24-h horizon is not attributed just to the average time profile, or to the last values at same time, which would probably be almost equal to the values to be forecast otherwise. As anticipated, wind speed and sun have positive correlation with wind and solar generation respectively. Although an exhaustive evaluation of the confidence intervals was not a part of this work, these two figures convince that about 95% of the exact values are within the intervals.

5. The Optimization Algorithm

The optimization algorithm proposes the optimal demand for each time point of the next time interval (“optimization interval”), based on a pre-defined time granularity. Although the algorithm can be easily adapted, the following potential optimization criteria have been considered, based on the demonstrators’ needs known:

• minimum cost (minimum mean product of demand and price per energy unit of demand)
• maximum usage of renewable energy (minimum variance of difference between demand and forecast generation)
• minimum power instability (minimum demand variance)

under the following constraints:

• Within the optimization interval, the total demand equals the total forecast demand (w.r.t. time). This means that demand can only be shifted, but not reduced overall.
• At each time point of the optimization interval, demand is within a time-point-dependent interval.

A Key Performance Indicator (KPI) was defined to quantify each criterion.

The optimization approach followed regards a generic, specification-free optimization of the aggregate demand of the island (Orkney, Madeira) or the Ballen harbour (Samsø).

For Madeira, the future energy price is generally known and partially fixed. Particularly, every customer selects among programs with 1, 2, or 3 time zones with different prices in each (simple, bi-hour and tri-hour tariff respectively). The tariffs with more zones incentivize the customer to consume less during high-demand periods, by imposing higher price during them, while decreasing price during low-demand periods, compared to the tariffs with fewer zones. In Figure 8, the energy price zones for the tri-hour tariff are shown. In the bi-hour tariff case the peak and half-peak zones are merged, whereas, apparently, in the simple tariff case price is independent of time. In cases of multiple time zones, the customers can also select between the daily cycle, where the time periods of the zones depend only on the season, and the weekly cycle, where they depend also on the day of week, as also shown in the figure. The price in each zone depends not only on the tariff, but also on the contracted power of the customer. Prices change in the beginning of each year by the Energy Services National Regulator and not by the Distribution System Operator. In the remainder of the paper, the tri-hour daily cycle will be assumed with the following realistic prices for the current year:

• peak: €0.1773/kWh
• half-peak: €0.1272/kWh
• off-peak: €0.0624/kWh

5.1. The Mathematical Viewpoint of the Optimization Method

The optimization problem was formulated as a mathematical programming problem for constrained optimization of a non-linear scalar objective function. So, let $f\left(\mathbf{x}\right)$ the scalar objective function of a vector $\mathbf{x} = {[x_1,x_2,\dots ,x_n]}^{⊺}$ containing the variables the values of which that minimize $f\left(\mathbf{x}\right)$ under the multi-dimensional constraints $\mathbf{g}\left(\mathbf{x}\right) = \mathbf{0},$ $\mathbf{h}\left(\mathbf{x}\right) \ge \mathbf{0}$ [element-wise (in)equalities] have to be found. The constrained optimization problem

$$\underset{\mathbf{x}}{min}f\left(\mathbf{x}\right):\mathbf{g}\left(\mathbf{x}\right) = \mathbf{0}, \mathbf{h}\left(\mathbf{x}\right) \ge \mathbf{0}$$

(5)

is approximated by the following unconstrained problem:

$$\underset{\mathbf{x}}{min}\left(f\left(\mathbf{x}\right) + M\left({\left({\mathbf{g}}^2\left(\mathbf{x}\right)\right)}^{⊺}\mathbf{1} + {\left({\mathbf{h}}^2\left(\mathbf{x}\right)\circ \left(\mathbf{h}\left(\mathbf{x}\right) < \mathbf{0}\right)\right)}^{⊺}\mathbf{1}\right)\right),$$

(6)

where $M>>{min}_{\mathbf{x}:\mathbf{g}\left(\mathbf{x}\right)=\mathbf{0},\mathbf{h}\left(\mathbf{x}\right)\ge \mathbf{0}}f\left(\mathbf{x}\right),$ the quadratic functions are applied element-wise, $\mathbf{1}$ denotes a vector with all of its elements equal to 1, the expression $\mathbf{h}\left(\mathbf{x}\right) < \mathbf{0}$ is a vector of integers indicating if the condition holds (1) or not (0) element-wise, and finally ∘ denotes Hadamard (element-wise) product. Using this approximation, when the functions $f,$ $\mathbf{g}$ and $\mathbf{h}$ are differentiable, the same goes for the new objective function, so the derivative-based optimization methods can be applied. As follows from the following, in our cases $f\left(\mathbf{x}\right)$ ranges around 1, so it is concluded that setting $M = {10}^3$ is an appropriate choice.

For the implementation of optimization, the Basin-hopping global optimization algorithm has been used from the scipy Python library [59]. Apart from the objective function, its derivative has also been given as input in order that optimization is accelerated, although in this work optimization always lasts less than 1 s, and it has been confirmed that a single iteration of the Basin-hopping algorithm suffices to find the global optimum. Finally, it is worth mentioning that the Basin-hopping algorithm is faster than differential evolution, which is the other global optimization algorithm supported by the same library.

5.2. Methodology of the Optimization Algorithm

As shown in Figure 9, the optimization algorithm needs the following input data:

• optimization interval
• weighting coefficients of the optimization criteria
• aggregate demand forecast with confidence, based on a configurable significance level
• aggregate generation forecast (when the renewables-related criterion is considered)
• demand price at each time of the day, considering also day of week and month

The mathematical formulation of this approach is

$$\underset{\mathbf{d}}{min}\left(w_{c}KP{I}_c\left(\mathbf{d}\right) + w_{r}KP{I}_r\left(\mathbf{d}\right) + w_{p}KP{I}_p\left(\mathbf{d}\right)\right):\left\{\begin{array}{c}{\mathrm{mean}}_{t\in I_{opt}}d\left(t\right) = {\mathrm{mean}}_{t\in I_{opt}}\widehat{d}\left(t\right)\hfill \\ {\widehat{d}}_l\left(t\right) \le d\left(t\right) \le {\widehat{d}}_u\left(t\right)\forall t\in I_{opt}\hfill \end{array}\right.,$$

(7)

with the following notation:

• $I_{opt}$: interval for which the optimization takes place
• $d\left(t\right)$: aggregate demand (power) at time t
• $\mathbf{d}$: vector of all $d\left(t\right)$, $t\in I_{opt}$, in ascending order of time
• $\widehat{d}\left(t\right)$: forecast aggregate demand at time t
• $[{\widehat{d}}_l\left(t\right),{\widehat{d}}_u\left(t\right)]$: 95% confidence interval for demand at time t (as explained in Section 4.1, the bounds depend on the predicted demand, but their difference from predicted demand depends only on the forecasting horizon, time of the day and clustering group)
• $KP{I}_c\left(\mathbf{d}\right)$, $KP{I}_r\left(\mathbf{d}\right)$, $KP{I}_p\left(\mathbf{d}\right)$: KPIs for cost, renewables and power stability criteria respectively
• $w_c,w_r,w_p \ge 0,w_c + w_r + w_p = 1$: arbitrary weights of KPIs

The KPIs are defined as follows:

$$KP{I}_c\left(\mathbf{d}\right) = \frac{{\mathrm{mean}}_{t\in I_{opt}}\left(c\left(t\right)d\left(t\right)\right)}{{\mathrm{mean}}_{t\in I_h}\left(c\left(t\right)d\left(t\right)\right)}$$

(8)

$$KP{I}_r\left(\mathbf{d}\right) = \frac{{\mathrm{mean}}_{t\in I_{opt}}\left({\left(d\left(t\right) - g\left(t\right)\right)}^2\right)}{{\mathrm{mean}}_{t\in I_h}\left({\left(d\left(t\right) - g\left(t\right)\right)}^2\right)}$$

(9)

$$KP{I}_p\left(\mathbf{d}\right) = \frac{{\sigma }_{d\left(I_{opt}\right)}^2}{s_{d\left(I_h\right)}^2},$$

(10)

according to the following notation:

• $I_h$: interval of training data for the demand forecasting models
• $c\left(t\right)$: expected aggregate demand cost per energy unit at the time point t (historical prices are set according to the same pricing policy of the current year)
• $g\left(t\right)$: aggregate generation at the time point t
• ${\sigma }_{d\left(I_{opt}\right)}^2$: theoretical variance of $d\left(t\right)$ within $I_{opt}$ (assuming mean as constant equal to the historical mean demand)
• $s_{d\left(I_h\right)}^2$: sample variance of $d\left(t\right)$ within $I_h$

The denominators of the above formulas aim at scaling KPIs so that they are independent of the measurement units and in order that the contribution of each individual KPI to the entire objective function is independent of the way the KPI is defined. With this scaling, each KPI is non-negative, it is better when lower and the value 1 for the KPI may be interpreted as neutral.

5.3. Flexibility Analysis

In the specification-free optimization of this work, to express flexibility mathematically, the KPI reduction rate has been defined as

$$R{R}_{x,I_{opt}} = 1 - \frac{KP{I}_x\left({\widehat{\mathbf{d}}}_{opt}\right)}{KP{I}_x\left(\widehat{\mathbf{d}}\right)}$$

(11)

according to the following notation:

• x: type of KPI (cost, renewables or power criterion, or combination)
• $R{R}_{x,I_{opt}}$: reduction rate of $KP{I}_x$ within optimization interval $I_{opt}$
• $\widehat{\mathbf{d}}$: vector of forecast aggregate demand at all time points of $I_{opt}$ in ascending order of time
• ${\widehat{\mathbf{d}}}_{opt}$: vector of forecast optimal aggregate demand at all time points of $I_{opt}$ in ascending order of time

5.4. Implementation Examples of the Optimization Algorithm and Discussion

In Figure 10, Figure 11 and Figure 12, examples from the implementation of the optimization approach in the three demonstrators are shown. In each case, the algorithm has been executed for a particular 24-h time interval, with various considerations about the weights of the KPIs. Obviously, when considering multiple KPIs, the optimized value of each individual KPI is reduced no more than in case that optimization takes place based exclusively on that KPI. In the Orkney case, the cost KPI was never considered, because cost optimization is not a priority in this demonstrator, so real-time price forecasts are not available. It also does not make sense to consider the cost KPI for the Samsø demonstrator, because price is not predictable (based on our trials) and cannot be requested automatically in real time from Nord Pool due to policy constraint. Day-ahead price data are available from Nord Pool only manually through its website, so it would only make sense to consider the cost criterion if the end user provided manually the prices for every time point of the optimization interval. Furthermore, it is worth mentioning that, in the example for Samsø, the demand forecasts have relatively high uncertainty for the largest forecasting horizons, so it is assumed that there is greater margin for demand shifting, and thus the optimal global KPI is more reduced. An other factor that prevents especially the cost and renewables KPIs from being reduced in the Madeira case is the high distance between total renewable generation and demand.

In

Table 4. Unstandardized values of the optimization KPIs for standardized values equal to 1. Regarding Madeira cost, the unstandardized KPI is proportional to the standardized one. The unstandardized renewables and power stability KPIs are proportional to the square of the respective standardized ones.

Demonstrator	Cost	Renewables	Power
Orkney	not considered	12.9285 MW	3.9921 MW
Samsø	not considered	16.8783 KW	9.1264 KW
Madeira	266,180/day	73.5026 MW	17.7684 MW

, the unstandardized values of the KPIs in each pilot are shown, in cases where the standardized KPIs (i.e., those defined above) have the neutral value 1. Although in the standardized KPIs the measurement units are eliminated thanks to the denominators, this does not hold for the unstandardized ones, which translate the former in the usual measurement units. As anticipated, since the studied energy in the case of Samsø corresponds only to a harbour area instead of an entire island, the unstandardized values of the renewables and power instability KPIs are much lower than in the other two demonstrators. This explains the higher flexibility of demand in the Samsø case, which was observed above. The unstandardized Madeira cost has been computed with the assumption that all customers follow the tri-hour tariff policy with the prices shown previously. In fact, most customers still use the simple tariff, but the idea is to gradually persuade them to resort to the tri-hour tariff and follow a more appropriate consumption pattern as regards the environmental and power stability criteria.

6. Conclusions, Limitations and Future Work

This study demonstrated how energy consumption can be managed via load shifting recommendations in large areas, where the consideration of all specifications of the involved consumers is intractable. Instead, our generic methodology relied on the idea that the uncertainty in demand forecasts reflects the flexibility of the consumers’ consumption profiles. This uncertainty was evaluated thanks to confidence intervals for demand, which were produced by training demand forecasting models, considering the effect of forecasting horizon, time of the day, month and day of week on the forecasting error distribution. Unlike most works found in the literature, the current optimization algorithm took into account simultaneously multiple criteria (among cost, renewable resources penetration and demand stability) after appropriate scaling of the respective Key Performance Indicators so that they are comparable. To consider the renewable resources criterion, forecasting models for the generation of various forms were also trained. The grouping in pairs of months and days of week was based on automatically selected clustering algorithms, which took into account the behavior of the variable to be forecast (energy demand or generation). Since the best model was selected separately for each cluster and for each forecasting horizon, and secondly because several models, many of which had similar performance, were compared, it was not considered as necessary to select and fuse multiple (instead of one) models for a particular combination of cluster and horizon, which would cause unnecessary storage of too many selected models. Although there are similarities in the models forecasting similar variables in different islands (e.g., effect of sun and humidity on solar generation of Samsø and Madeira), there are also some differences without obvious reason (e.g., difference in performance between linear and non-linear regressors and effect of clustering on performance of regressors for wind generation in Orkney and Madeira), which demonstrates the need for performance comparison among candidate clustering and regression architectures. This conclusion conforms with the findings of our literature review. Despite the demonstrated positive effect of using multiple regressors for the different clusters and forecasting horizons, the input variables to the forecasting models (mainly the average time profile) were defined in a way that they have near-linear relation with the variable to be forecast (output), thus rendering the linear regression models satisfactory approximations considering their little training time. These linear approximations were also useful for preliminary training in order to select the most appropriate input variables and clustering architecture. Another benefit of the linear regression models is that they do not overfit the data, due to their low capacity. The forecasting models can be retrained manually or automatically (periodically), provided that the algorithm has access to more recent data. Retraining would be particularly useful in order to take into account previously unknown situations, for example, demand drop due to the coronavirus disease 2019, which was observed for example, within spring of 2020 in Madeira.

The limitations of the forecasting algorithm regard mainly the regression models, especially their training. Training with 3-fold cross validation took hours in case of the analyzed datasets, due to the comparison of numerous architectures, some of which have to learn numerous parameters with quadratic or cubic time complexity w.r.t. the number of observations. However, the training of the aforementioned linear approximations requires less than a minute for all groups and forecasting horizons together. Among all regressor kinds, only Gaussian Process Regressor has a memory limitation, since it is efficient for up to 10,000 training observations approximately. The storage of the high number of models shown in the pie charts required a few GB of space in our experiment. However, it appeared that for only few regressor kinds the size of the model file was tens or thousands of MB. The model file sizes of the most lightweight architectures (e.g., linear regression) was even below 10 KB.

The optimization methodology presented in this paper can easily be adapted to different KPIs and constraints. For example, an extension of the optimization algorithm could consider also Battery Energy Storage Systems (BESSs), which have been installed at Samsø and Madeira. With a BESS, different policies are often appropriate, for example, increasing demand when generation is currently low, but is going to increase in the near future, so that unexploited renewable energy because the battery gets full is avoided.

The forecasting and the optimization algorithms have been deployed for Madeira and are running in real time, using dashboards like the ones shown above. In the near future, the Distribution System Operator of Madeira will start to utilize them in order to make appropriate recommendations to its customers, so the impact of the algorithms will be verified.