1. Introduction
Time series forecasting is useful in many applications [
1,
2]. Before 1927, time series were forecast using extrapolation. Then, Yule introduced the autoregressive model in order to forecast future values of time series as weighted sums of previous ones, and linear modelling with noise was the common practice for forecasting within the next 50 years or so. Afterwards, the linear models proved to be inadequate to describe complex time series behaviour, and since 1980, along with the evolution of computers, time series forecasting has been addressed also using machine learning techniques and state-space reconstruction with time-delay embedding [
3]. Examples of recent generic time series forecasting methods are random walk with drift, Autoregressive Fractionally Integrated Moving Average (ARFIMA), exponential smoothing state-space model with Box–Cox transformation, Autoregressive Moving Average (ARMA) errors, Trend and Seasonal components (BATS), simple exponential smoothing, Theta and Prophet methods [
4], a hybrid approach linearly combining alternative neural network models based on a weighting automatically derived by the model errors [
5], Bayesian models [
6] and discretization with fuzzification [
7].
One of the aforementioned applications is that of forecasting energy demand (consumption) and generation (production). The review in [
8] explains why the variance of solar and wind generation leads to cost and how this cost is reduced thanks to generation forecasting.
Self-consumption of energy is achieved with an energy storage system and Demand Side Management. The most popular strategy for the latter is load shifting [
9]. According to [
10], with the increase of population, energy management through demand response (DR) programs has become an important need. Particularly, most of such programs are price-based, according to the following charging policies: (a) Time-of-Use (TOU), according to which the price depends on the time of the day and is determined by the historically average cost of energy delivery at each time, (b) Real-Time Pricing (RTP), where future prices are determined in real time on an hourly basis based on the current conditions, and (c) Critical-Peak Pricing (CPP), which is a dynamic pricing mechanism using elements of the above two to modify tariffs as a temporary response to events or conditions like high market prices or reserve being reduced. RTP is mentioned as the best DR technique [
11].
The current paper presents first a generic forecasting algorithm, based on machine learning techniques, applied to predict aggregate demand and generation in three demonstrators (Orkney island, Ballen marina at Samsø and Madeira island). Past values of the variable to be forecast along with weather forecasts from [
12] were considered as potential input to the forecasting regression models. However, only the variables that improved the performance of the models were finally selected. The historical dataset was grouped w.r.t. month and day of week by applying a clustering method to the data of the variable to be forecast. Along with each forecast, a confidence interval is automatically provided by the algorithm, according to the distribution of the forecasting error, considering the impact of the forecasting horizon, time of the day and month–day of week group resulting from the above clustering. The pre-processed input and output variables of the forecasting models were defined in such a way that they have near-linear dependencies. However, multiple regression architectures were tested with hyper-parameter tuning, including the contemporary Extreme Learning Machines (ELM), which is presented in [
13] as better than the usual Artificial Intelligence techniques, due to its faster learning ability and its simpler architecture. Additionally, a demand optimization algorithm was developed, which assumes that the future demand can be shifted among the timestamps of the optimization interval (e.g., next 24 h). Regarding constraints, it was considered that the average demand across all timestamps of the interval should not be modified, and that the demand at each future timestamp always ranges within the respective confidence interval. This optimization algorithm is generic and was implemented for each demonstrator using relevant data. It considers three optimization criteria, namely minimum cost for the consumer, maximum usage of renewable energy and minimum power instability. The degree of deviation from the fulfilment of each of these criteria was evaluated based on a Key Performance Indicator (KPI), which was defined mathematically. In order that multiple criteria among the above three are considered for the optimization, a total KPI was defined as a weighted mean of the individual KPIs, which were scaled appropriately first. Not all three criteria were considered in all demonstrators, because some criteria were considered as non-applicable to some of them. The optimization algorithm is accompanied by a flexibility analysis for total demand, based on confidence intervals for demand, derived from the forecasting algorithm. Flexibility is the ability to increase or reduce the production of power plants or the consumption of demand processes [
14]. A standard formula for quantifying flexibility does not exist, and flexibility depends on the settings of the problem in question.
Based on the above, the solution described in this paper may be considered as useful if at least one of the following hypotheses is valid:
The end user is an energy consumer who views the recommendations about the time points in the near future when energy consumption should be preferred according to the desired weighting factors of the three optimization criteria and the unit prices of energy at every time point which are applicable to this user, and adjusts his/her consumption behavior accordingly.
The end user is a Distribution Systems Operator that forwards the recommendations of these algorithms to its customers.
The end user is someone authorized to determine the unit prices of energy consumption at every time point, so (s)he can examine to what extent the economic criterion contradicts the renewable energy penetration and power stability criteria and adjust unit prices accordingly, also dynamically.
The remainder of the paper is organized as follows:
Section 2 presents the related work and the contribution of ours. In
Section 3, the high-level architecture of the system of the forecasting and optimization algorithms is depicted, whereas in
Section 4 and
Section 5 the forecasting and optimization algorithms, respectively, are presented in detail, including their methodology and experimental results. The paper is concluded in
Section 6. Finally,
Appendix A provides more information about the raw data.
2. Related Work and Our Contribution
A literature review relevant to the specific problem of demand and generation forecasting follows: In [
15] a multi-step forecasting algorithm similar to ours has been implemented in the field of heat load in district heating systems, evaluating also recursive apart from direct forecasting with similar results. However, in contrast with our paper, in order to quantify intrinsically categorical variables such as month and time of day, it applies one-hot encoding, thus highly increasing the number of input variables and enforcing the partial sharing of parameters among models for different months and times of day. The review in [
16] deals with solar generation and electricity demand. The authors mention that demand response causes instability in the forecasts. In terms of algorithms, although they confirm that Artificial Neural Networks (ANNs) are still popular, other techniques are also used nowadays (random forests, support vector machines, gradient boosting). It is stated that there is no single forecasting model which is the best for all use cases, and this conforms with the findings of the present paper. This is argued also in the review of [
17], which favors the trial and error strategy for this reason. The last review also mentions that clustering is a common approach to automatically group days, as done in our work, although generally this method was not found in the bibliography of the current research. However, that paper also argues that most of the researchers focus only on point forecasts and not so much on confidence intervals. (In some papers, including that one, the confidence intervals for predictions are mentioned as “prediction intervals”. In this paper, by “confidence interval” a prediction interval is implied). This is also a conclusion of [
18], which summarizes the methods of the Global Energy Forecasting Competition 2014 winners. The authors of [
19] take advantage of the method used by the winners of the above competition for load and price forecasting with the help of multiple weather stations, which was based on quantile regression using pinball loss minimization, and generalized additive models.However, in that work, a time of year variable was introduced, which seems to be inappropriate for two reasons. First, it does not take into account the dependencies among timestamps of same time of the day in different days of the year. Secondly, it increases linearly over time, so it has a non-linear dependence with the variable to be forecast, in contrast with the average time profile, which was used in our method. In that work, day of week clusters were defined manually based on experience. It seems that only during the last few years probabilistic forecasting has been studied more extensively. For example, in [
16,
20], quantile regression, quantile regression forests, Gaussian processes, bootstrapping, Lower Upper Bound Estimate, gradient boosting, kernel density estimation, k-nearest neighbor and analog ensemble are mentioned as the main statistical non-parametric methods for probabilistic energy forecasting, along with the statistical parametric, physical (parametric and non-parametric) and hybrid approaches. In the energy forecasting review of [
21] it is confirmed, as observed also by the rest of this literature review, that regarding generation, mainly wind and solar forms have been studied. Nothing is mentioned about hydro and waste, which are studied in our paper for the Madeira demonstrator. In the case of wind generation there is no distinction between ANM (Active Network Management) and non-ANM, which was done in our work for Orkney, as discussed in more detail in
Section 4.2. The work in [
20] uses Gaussian processes for probabilistic forecasting of demand and solar generation in an isolated building, however it uses as input only past values of the variable to be forecast based on pre-defined time lags. Grey models are presented by [
22,
23] as appropriate for training of forecasting models in case of lack of sufficient historical data to train non-linear Artificial Intelligence models, which usually happens for high forecasting horizons (e.g., 1 year), as is the case in these two papers, where China’s yearly electricity and natural gas demand respectively are forecast using just some past values of the variable to be forecast as input. A similar horizon (2-year) is used in [
24], where monthly electricity demand is predicted with bagging Autoregressive ntegrated Moving Average (ARIMA) and exponential smoothing techniques, again using only past values of the variable to be forecast as input. In [
25], generation and demand in smart cities and factories are forecast using Markov chain, stride predictors, neural networks and combinations of them. In that study, the forecasting problem is discretized and only the recent values of the variable to be forecast are used as input. In the work of [
26], yearly forecasts only for non-renewable generation are made for the next 14 years using linear regression, based only on the historical trend of generation. In [
27], electricity consumption of a microgrid is forecast using the Nearest Neighbors algorithm for prediction after clustering in business days and weekends with Self-Organizing Maps. However, no comparison with other models is made, and weather data have not been used as input. In [
28], demand, generation and battery state of charge of a microgrid are forecast with ARIMA, using only past data of the variable to be forecast among photovoltaic (PV) power production, load consumption and battery state of charge in a building, and a control algorithm is applied afterwards. However, in [
29,
30], which deals with microgrid demand, it is argued that ANNs are more appropriate for time series forecasting than ARIMA, especially in cases where the signals exhibit abrupt fluctuations and nonlinearity. In [
30] especially, season (with arbitrary numbering) and time themselves instead of demand average over season/time have been inserted as input to the model, thus leading to non-linear instead of linear relations between input and output, in contrast to our approach. In [
31], pp. 691–704, it is also mentioned that ANNs perform better, especially in cases where the signals exhibit abrupt fluctuations and nonlinearity. Therein, a Generalized Radial Basis Function Network (GRBFN) is used for forecasting solar generation, with modifications in the original algorithm such as the use of Evolutionary Particle Swarm Optimization (EPSO) for optimization during model training. However, overfitting is avoided with the weight decay method and the variables with unimportant weights are not mentioned, so the importance of all the considered input variables is questionable. No comparison is made with linear regression models. In [
31], pp. 704–729, an ensemble technique with wavelet decomposition and reconstruction for forecasting demand and solar generation of an integrated smart building at the University of Queensland equipped with PVs is applied, again by introducing time-dependent variables instead of their average profile as model input. Finally, [
32] is devoted exclusively to solar generation prediction, using only past solar irradiation as input instead of using also past solar generation and future solar irradiation forecasts; that paper uses a single, 10-min forecasting horizon, performing manual split of the data into seasons, and focuses on ANN without comparing multiple regression models.
The optimization algorithm of this paper regards a multi-criteria decision analysis (MCDA). Multi-attribute utility theory (MAUT), analytical hierarchy process (AHP) and multi-attribute value theory (MAVT) are particular MCDA techniques [
33,
34]. In the current work an alternative of MAVT, used in [
34], is employed, as described later in detail.
The bibliographic research of this section continues with DR-related optimization algorithms. The work in [
9] solves an optimization problem using the self-consumption percentage as criterion, and assesses the impact of weather forecast uncertainty. In [
35], DR is applied to control the usage of home Air Conditioners by minimizing cost. Nevertheless, the only model applied is linear regression and the dataset used consists of only a single summer week with low weather variability. The approach in [
36] performs specification-based cost optimization computing confidence intervals for uncertain variables with an introduced method, and uses reliability constraints. Similarly, in [
37], cost optimization is performed in a single household with an energy storage system, based on confidence intervals for load and generation obtained using quantile regression and k-nearest neighbor methods, but without using weather data to improve forecasts. Cost is also optimized in [
38,
39] using a genetic algorithm. Those papers consider a PV and a battery to generate and store energy respectively, and the latter has additionally taken into account customer comfort constraints for which user input is needed. The work in [
40] also performs specification-based cost optimization converting a non-linear optimization problem to a linear one, and employing a graph-theory-based energy hub model using coupling matrices. In [
41], energy procurement cost for retailer from pool market is minimized, using a robust optimization method facing the uncertainty of the model input. The algorithm has been used by multiple DR programs (pool-order, forward, reward-based). The paper in [
42] regards demand and electric vehicle (EV) usage forecasting for cost optimization and control, involving more than 300 active drivers in the experiment. In addition, in [
43], a genetic algorithm performs demand response in an isolated microgrid of Terceira island based on the cost criterion, while considering the consumer and grid manager viewpoint. In [
10,
44], cost is optimized along with consumer satisfaction, which has also been formulated mathematically, either as a constraint [
44] or as an additional term in the objective function [
10], whereas additional constraints have been introduced. Once more, the non-linear programming optimization problem has been solved with a genetic algorithm. In those two papers, specifications of particular home appliances have been considered. Similarly, [
11] executes specification-based cost and comfort optimization requiring user input, proposing separate DR schedules for multiple users. In [
31], pp. 613–635, a mixed-integer nonlinear programming problem is solved using the Particle Swarm Optimization (PSO) and Simulated Annealing algorithms and their variants while performing also demand and generation forecasting so as to enhance the input of the cost optimization problem. From the literature review of [
31], pp. 635–645, it is inferred that Tabu search (TS), PSO, multi-agent and fuzzy systems, as well as heuristics are commonly used in optimization, and TS is employed therein for cost minimization. An other alternative of PSO, named Quantum PSO (QPSO), is used in [
31], pp. 680–691, to solve a specification-based cost optimization DR algorithm related to load shifting. The goal of [
31], pp. 729–741, was to develop an algorithm to select the location of EV charging stations to be constructed by optimizing cost, mean usage rate of charging poles and user charging convenience under specification-based constraints, using an appropriate mathematical model. That work introduces an improved version of the strength Pareto evolutionary algorithm (SPEA), called SPEA2, for the computation of a set of optimal three-objective solutions. The work in [
45] concerns a related paper that has performed specification-based optimization in one of the three demonstrators of the present work (Samsø), without including details about the forecasting approach. An other work for specification-based optimization has been published for the Madeira demonstrator [
46]. It uses ARMA for forecasting and co-optimizes arbitrage, self-sufficiency, peak shaving and energy backup for Model Predictive Control, formulating all but one optimization criteria as constraints. In [
47], a control algorithm for cost optimization is applied to an ice bank system for food refrigeration, considering temperature predictions, ice mass and energy consumption. However, renewable energy sources are not considered, and many data used in that work are simulated instead of real. The latter occurs also in [
48], which deals with cost optimization in a microgrid based on weather forecasts, assuming demand as deterministic instead of introducing uncertainty or demand forecasting models. In [
49], another specification-based problem is addressed about water consumption instead of electricity consumption, considering the economic viability and operational risks management criteria, but introducing only cost in the objective function and defining constraints for the other criterion. The work in [
50] studies integrated instead of the typical demand response, which enables consumers also to change the type of the consumed energy. In [
51], scenarios for uncertainty are used in a probabilistic model for a cost optimization problem, considering wind and PV production and using domain-specific constraints about energy conversion. However, also in that paper, power is simulated using random variables instead of actual data, and power forecasting is not studied. In [
52], an optimization problem for production lines of heavy industries is solved, and flexibility is analysed, but without an obvious mathematical definition and numerical evaluation, as done in the current study. In [
53], another industrial application to an electrolysis plant is discussed, using cost in the objective function and considering domain-specific operational constraints. In [
54], multiple, potentially contradicting criteria are considered for optimization of distribution networks reconfiguration. The problem is solved using the epsilon-constrained method and the max-min fuzzy satisfying technique to balance the different criteria, but without weighting the contributions of the criteria to the total objective function after their normalization, which was done in our work to consider the subjective opinion of the end user about the relative importance of the criteria. Finally, [
55], which deals with another optimization problem with PVs and wind turbines in a microgrid, introduces an arbitrary dynamic pricing model with respect to renewable and non-renewable energy, a basic price and constant parameters. Demand and price are optimized using the PSO method with respect to cost and comfort, but only for a 4-s interval and without using forecasting. It concludes that dynamic pricing results in higher customer profit than fixed pricing.
By studying the above bibliographic research, the main contribution of the present work follows. Instead of solving a specification-based optimization problem related to a (relatively) low number of energy consuming assets and requiring input from consumers to assess their comfort, this work deals with a specification-free, statistical-based approach, in order to optimize aggregate demand in larger areas, even whole islands, from which it is practically infeasible to acquire all specifications. Particularly, in the current study, demand flexibility is estimated thanks to the confidence interval for demand obtained based on test error distribution during training the demand forecasting models on historical data. Although a thorough evaluation of the confidence intervals and comparison among probabilistic forecasting methods are not a main focus of this study, the confidence interval reliability and sharpness are considered to be improved in this work by simultaneously taking into account the forecasting horizon, the time of the day and the month and day of week group to which the forecast corresponds, where grouping is based on automatic clustering. Thanks to clustering, any periodic and non-periodic seasonality is automatically identified. This is a step forward compared to the traditional seasonal ARIMA (SARIMA) models, which assume periodic seasonality exclusively. In this way, the closer the point forecasts are to the respective exact values, the narrower the confidence intervals are, while their reliability is based on the desired significance level. Apart from cost, this work considers also renewable energy penetration, based on energy generation forecasting models also trained on historical data, and power stability as optimization criteria. Finally, although weather data and time-related information are also involved in the input of the forecasting regression models apart from past values of the variable to be forecast, the paper defines the input variables in such a way that they have near-linear relation with the output, which not only enables the possibility for fast training, but also helps to select the best input variables and clustering algorithm during pre-processing using linear approximations of the forecasting models. Bibliographic references tend to focus on the selection of complex forecasting models rather than the appropriate definition of the input variables, which renders training of simpler models easier.
6. Conclusions, Limitations and Future Work
This study demonstrated how energy consumption can be managed via load shifting recommendations in large areas, where the consideration of all specifications of the involved consumers is intractable. Instead, our generic methodology relied on the idea that the uncertainty in demand forecasts reflects the flexibility of the consumers’ consumption profiles. This uncertainty was evaluated thanks to confidence intervals for demand, which were produced by training demand forecasting models, considering the effect of forecasting horizon, time of the day, month and day of week on the forecasting error distribution. Unlike most works found in the literature, the current optimization algorithm took into account simultaneously multiple criteria (among cost, renewable resources penetration and demand stability) after appropriate scaling of the respective Key Performance Indicators so that they are comparable. To consider the renewable resources criterion, forecasting models for the generation of various forms were also trained. The grouping in pairs of months and days of week was based on automatically selected clustering algorithms, which took into account the behavior of the variable to be forecast (energy demand or generation). Since the best model was selected separately for each cluster and for each forecasting horizon, and secondly because several models, many of which had similar performance, were compared, it was not considered as necessary to select and fuse multiple (instead of one) models for a particular combination of cluster and horizon, which would cause unnecessary storage of too many selected models. Although there are similarities in the models forecasting similar variables in different islands (e.g., effect of sun and humidity on solar generation of Samsø and Madeira), there are also some differences without obvious reason (e.g., difference in performance between linear and non-linear regressors and effect of clustering on performance of regressors for wind generation in Orkney and Madeira), which demonstrates the need for performance comparison among candidate clustering and regression architectures. This conclusion conforms with the findings of our literature review. Despite the demonstrated positive effect of using multiple regressors for the different clusters and forecasting horizons, the input variables to the forecasting models (mainly the average time profile) were defined in a way that they have near-linear relation with the variable to be forecast (output), thus rendering the linear regression models satisfactory approximations considering their little training time. These linear approximations were also useful for preliminary training in order to select the most appropriate input variables and clustering architecture. Another benefit of the linear regression models is that they do not overfit the data, due to their low capacity. The forecasting models can be retrained manually or automatically (periodically), provided that the algorithm has access to more recent data. Retraining would be particularly useful in order to take into account previously unknown situations, for example, demand drop due to the coronavirus disease 2019, which was observed for example, within spring of 2020 in Madeira.
The limitations of the forecasting algorithm regard mainly the regression models, especially their training. Training with 3-fold cross validation took hours in case of the analyzed datasets, due to the comparison of numerous architectures, some of which have to learn numerous parameters with quadratic or cubic time complexity w.r.t. the number of observations. However, the training of the aforementioned linear approximations requires less than a minute for all groups and forecasting horizons together. Among all regressor kinds, only Gaussian Process Regressor has a memory limitation, since it is efficient for up to 10,000 training observations approximately. The storage of the high number of models shown in the pie charts required a few GB of space in our experiment. However, it appeared that for only few regressor kinds the size of the model file was tens or thousands of MB. The model file sizes of the most lightweight architectures (e.g., linear regression) was even below 10 KB.
The optimization methodology presented in this paper can easily be adapted to different KPIs and constraints. For example, an extension of the optimization algorithm could consider also Battery Energy Storage Systems (BESSs), which have been installed at Samsø and Madeira. With a BESS, different policies are often appropriate, for example, increasing demand when generation is currently low, but is going to increase in the near future, so that unexploited renewable energy because the battery gets full is avoided.
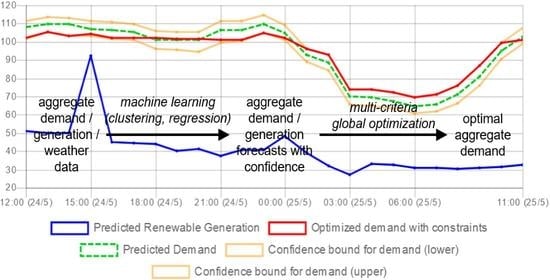
The forecasting and the optimization algorithms have been deployed for Madeira and are running in real time, using dashboards like the ones shown above. In the near future, the Distribution System Operator of Madeira will start to utilize them in order to make appropriate recommendations to its customers, so the impact of the algorithms will be verified.