Energy-Saving Strategies of Axial Flow Fans for Direct Dry Cooling System
Abstract
1. Introduction
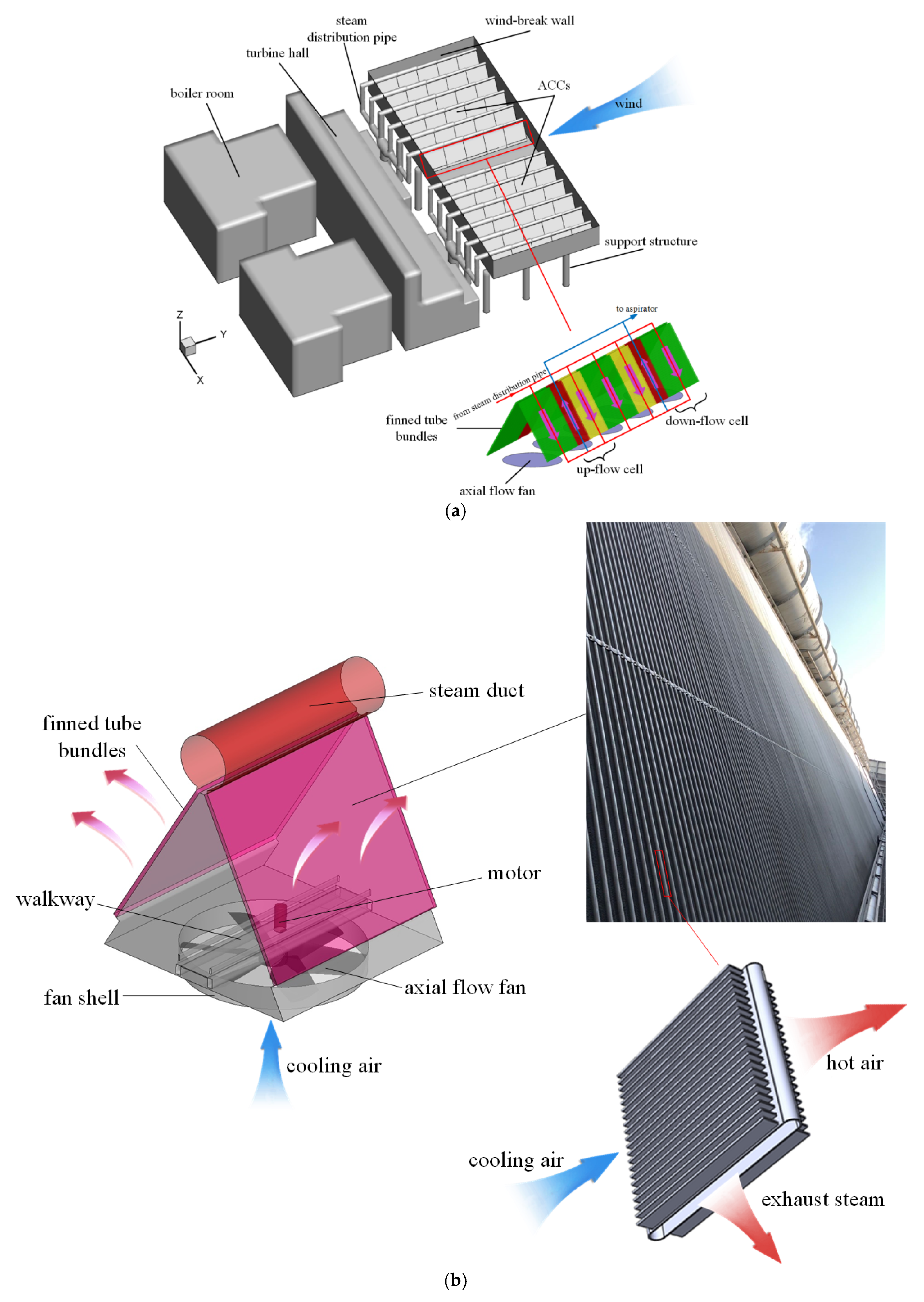
2. Physical Models
3. Numerical Models and Methods
3.1. Mathematical Models
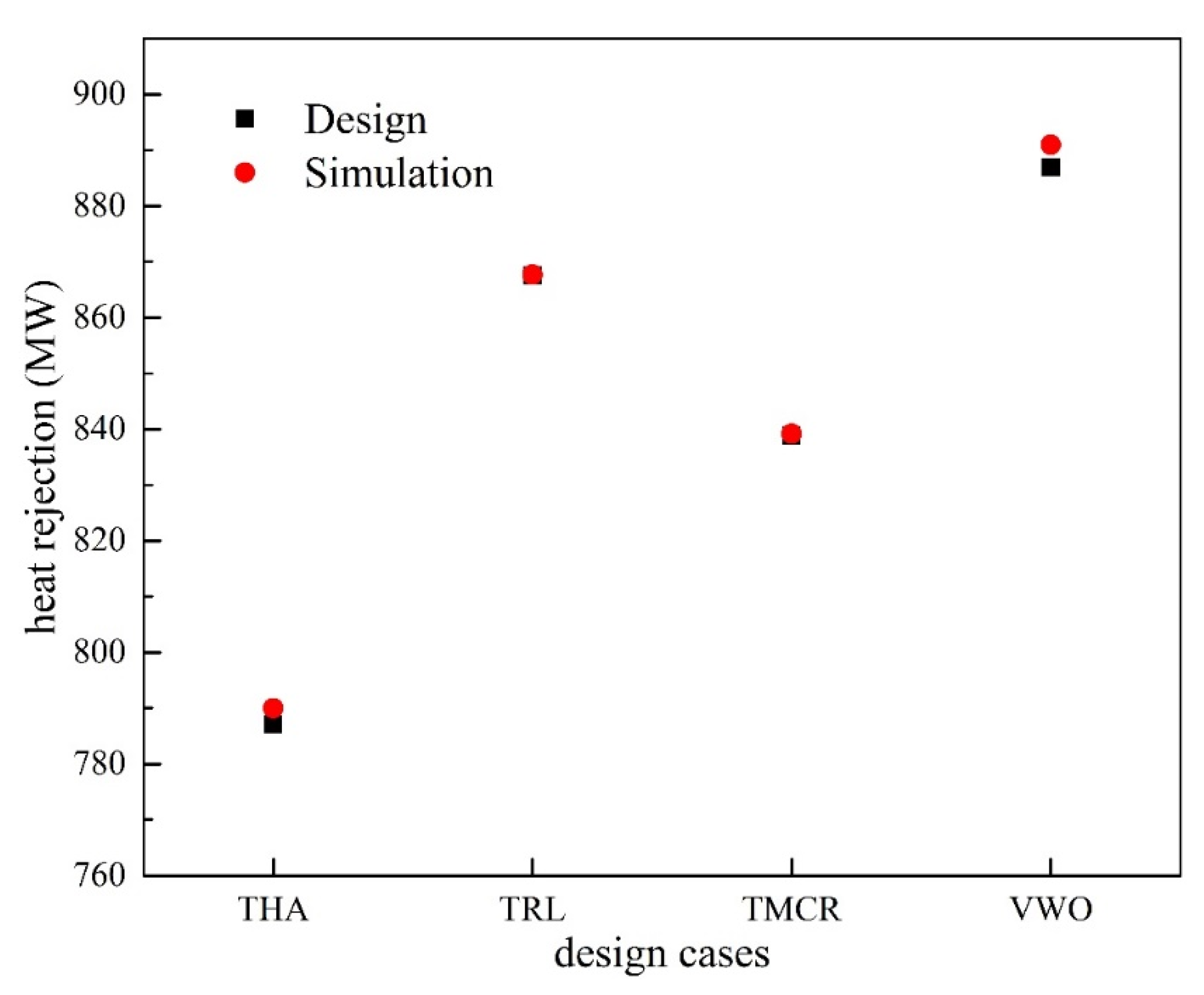
3.2. Grid Independence and Experimental Validation
4. Results and Discussion
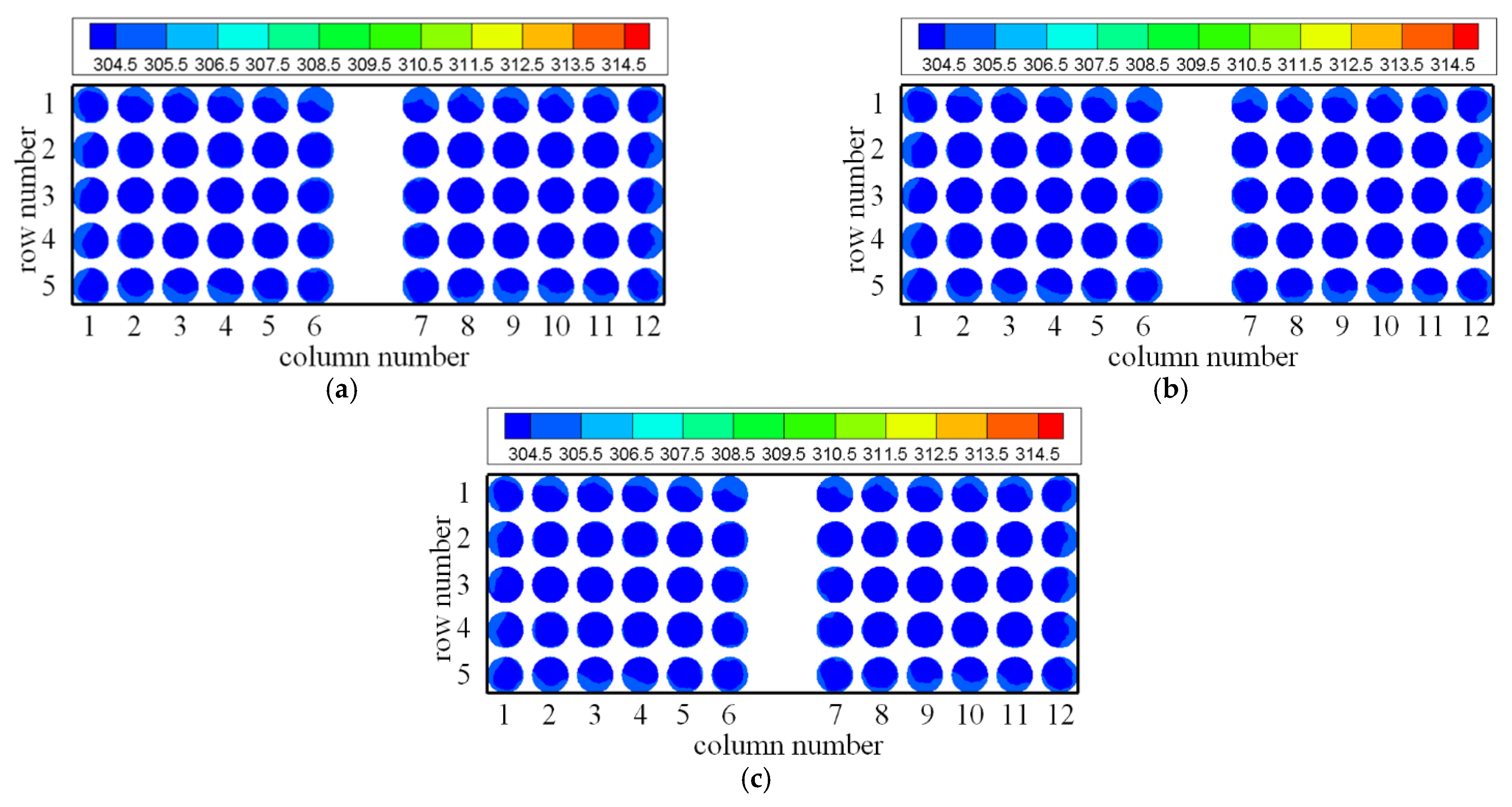
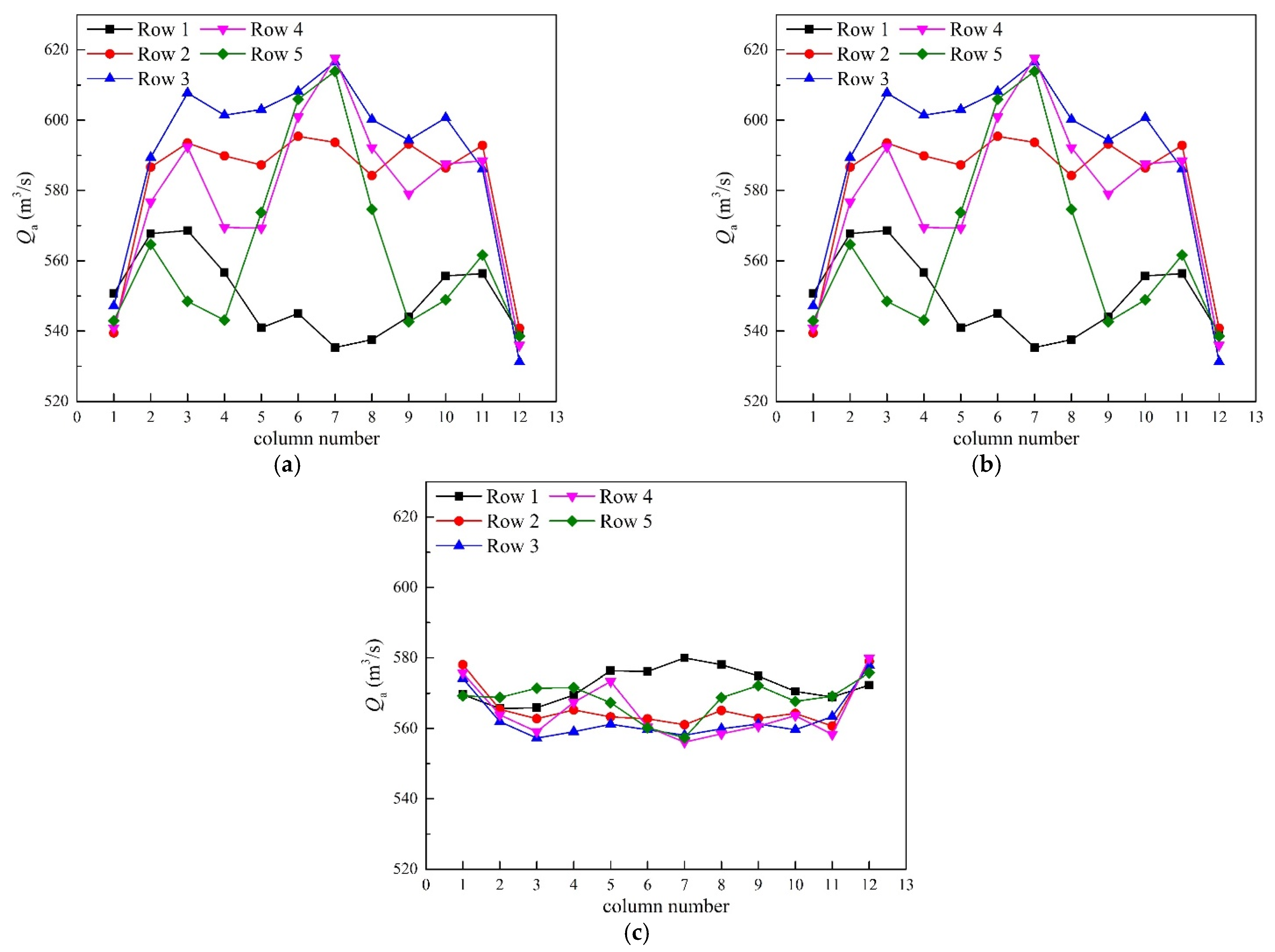
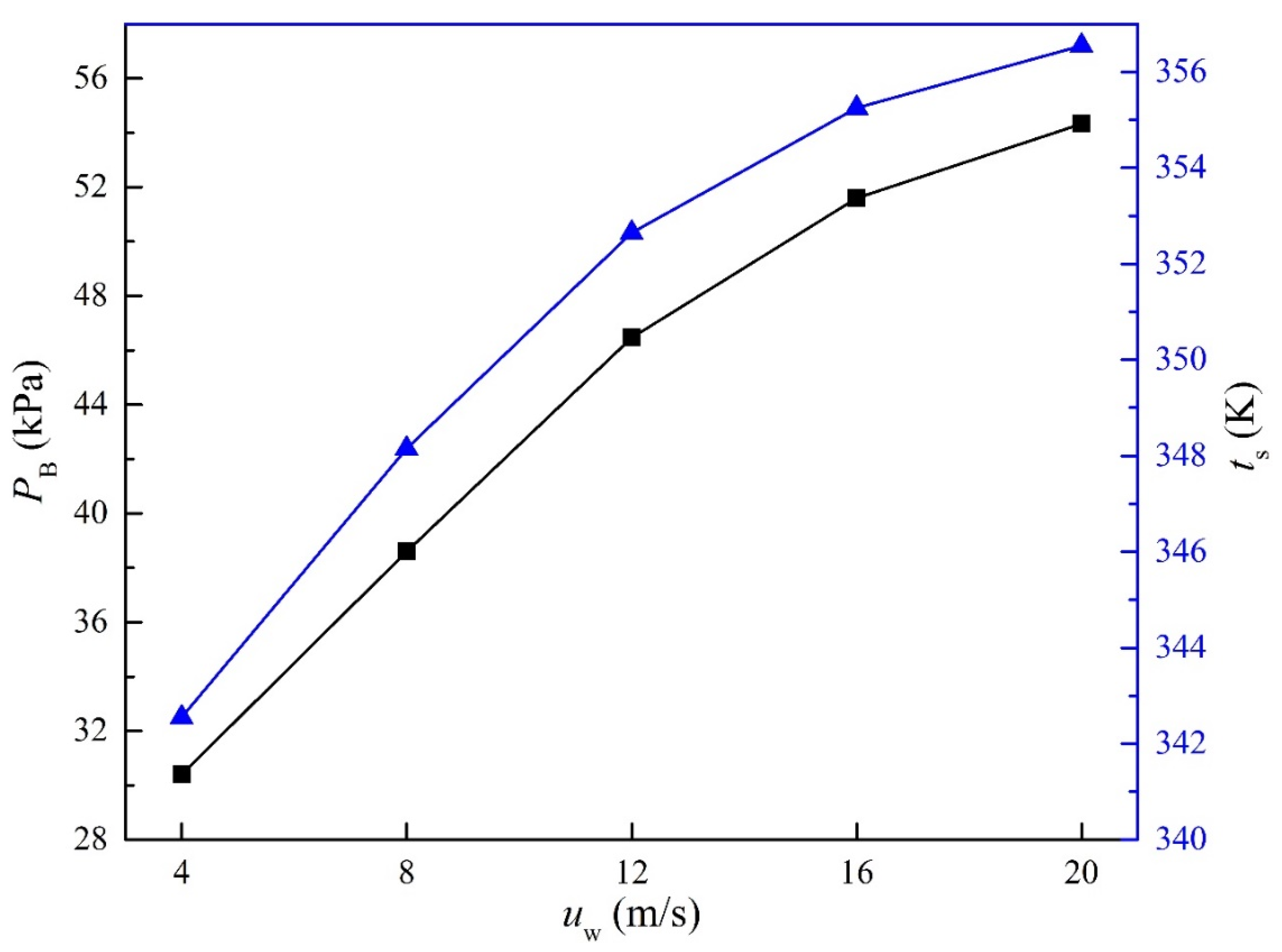
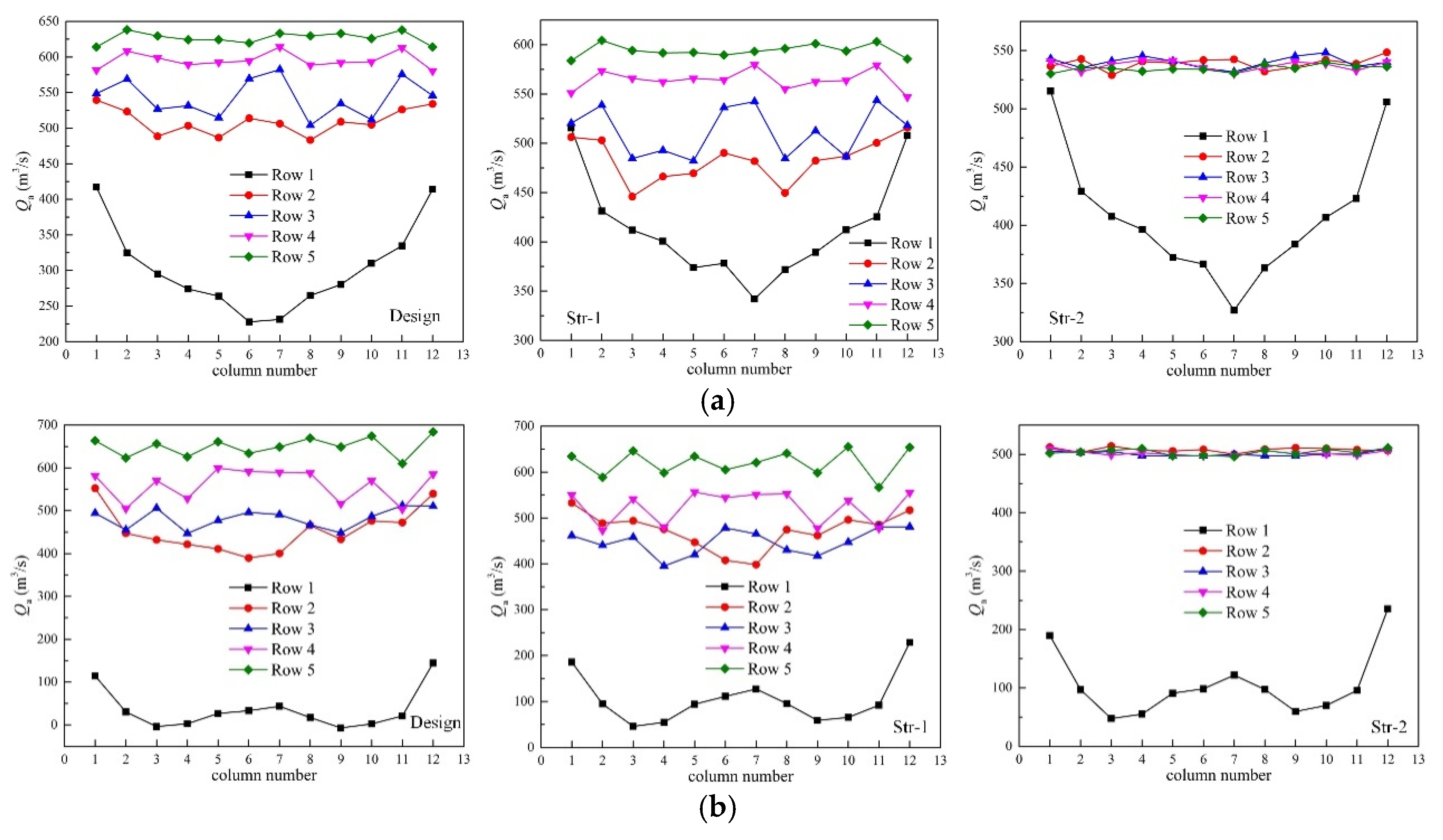
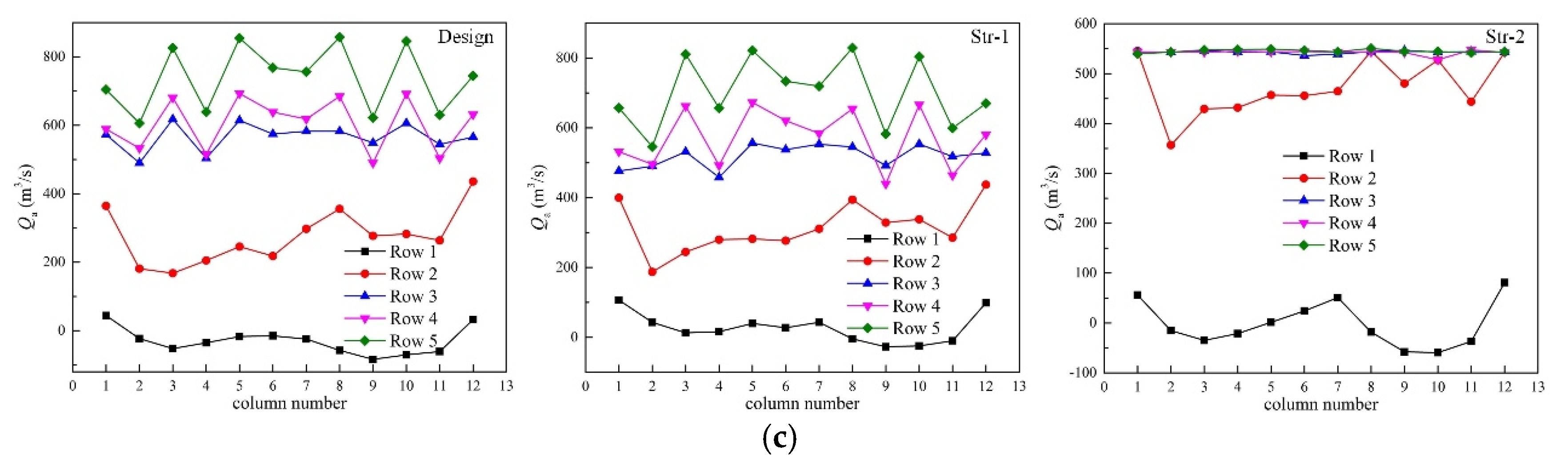
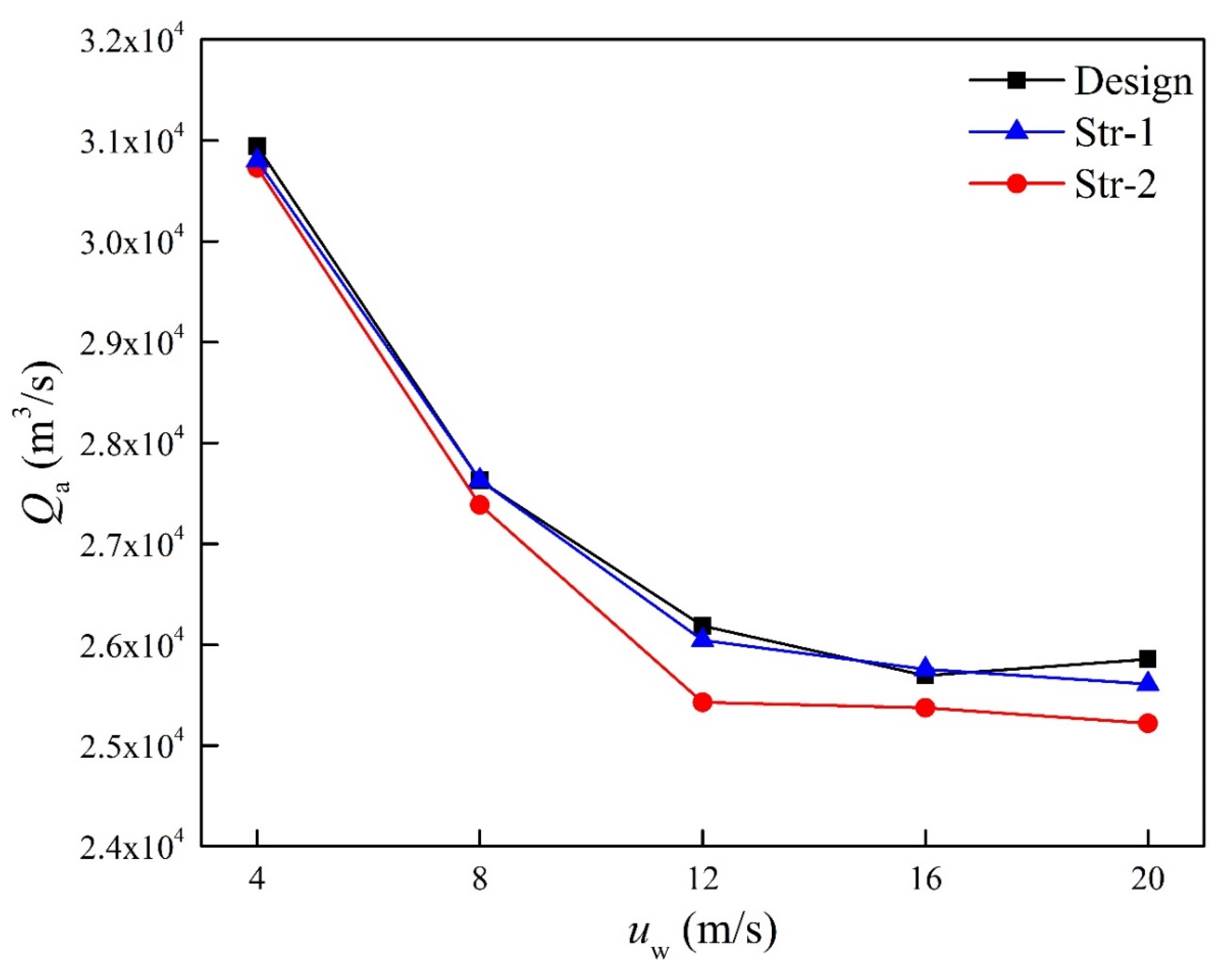
4.1. Temperature and Volumetric Flow Rate of Cooling Air
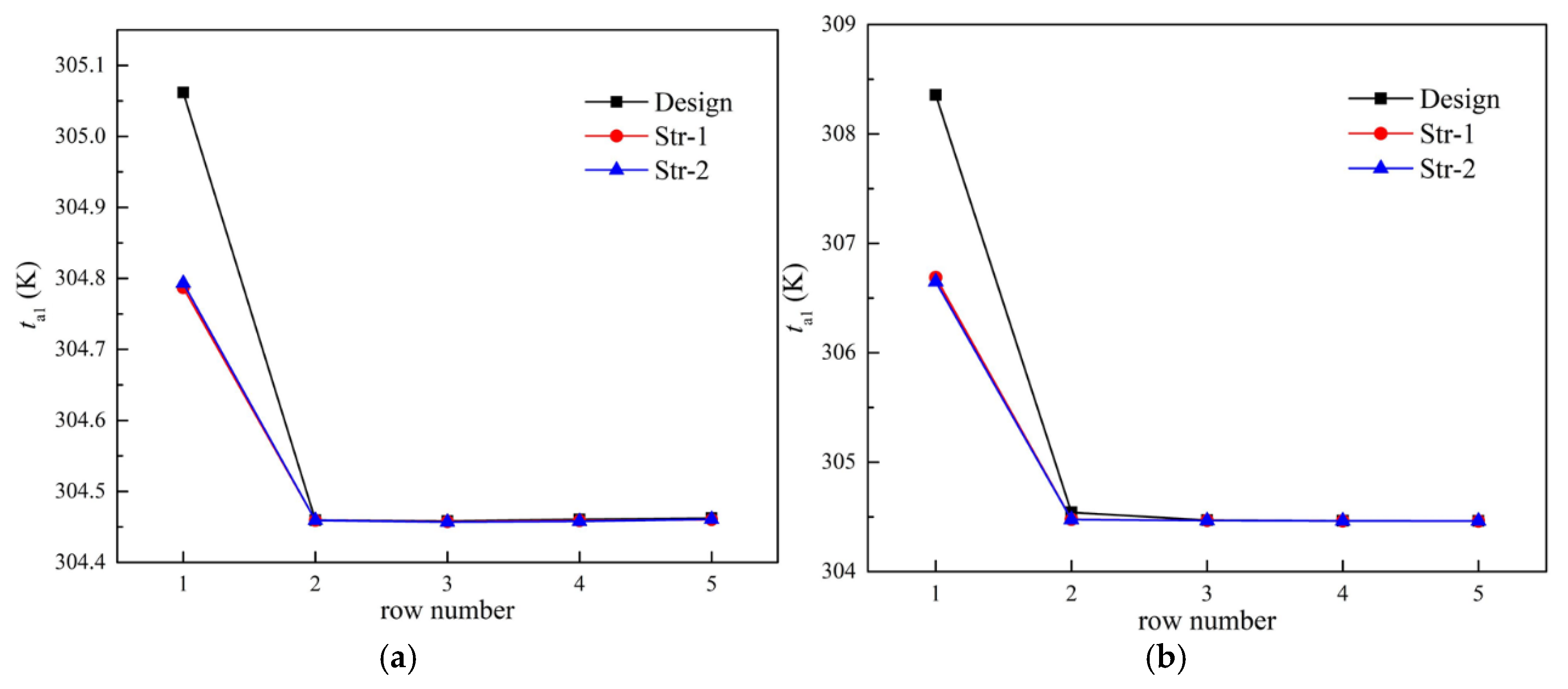
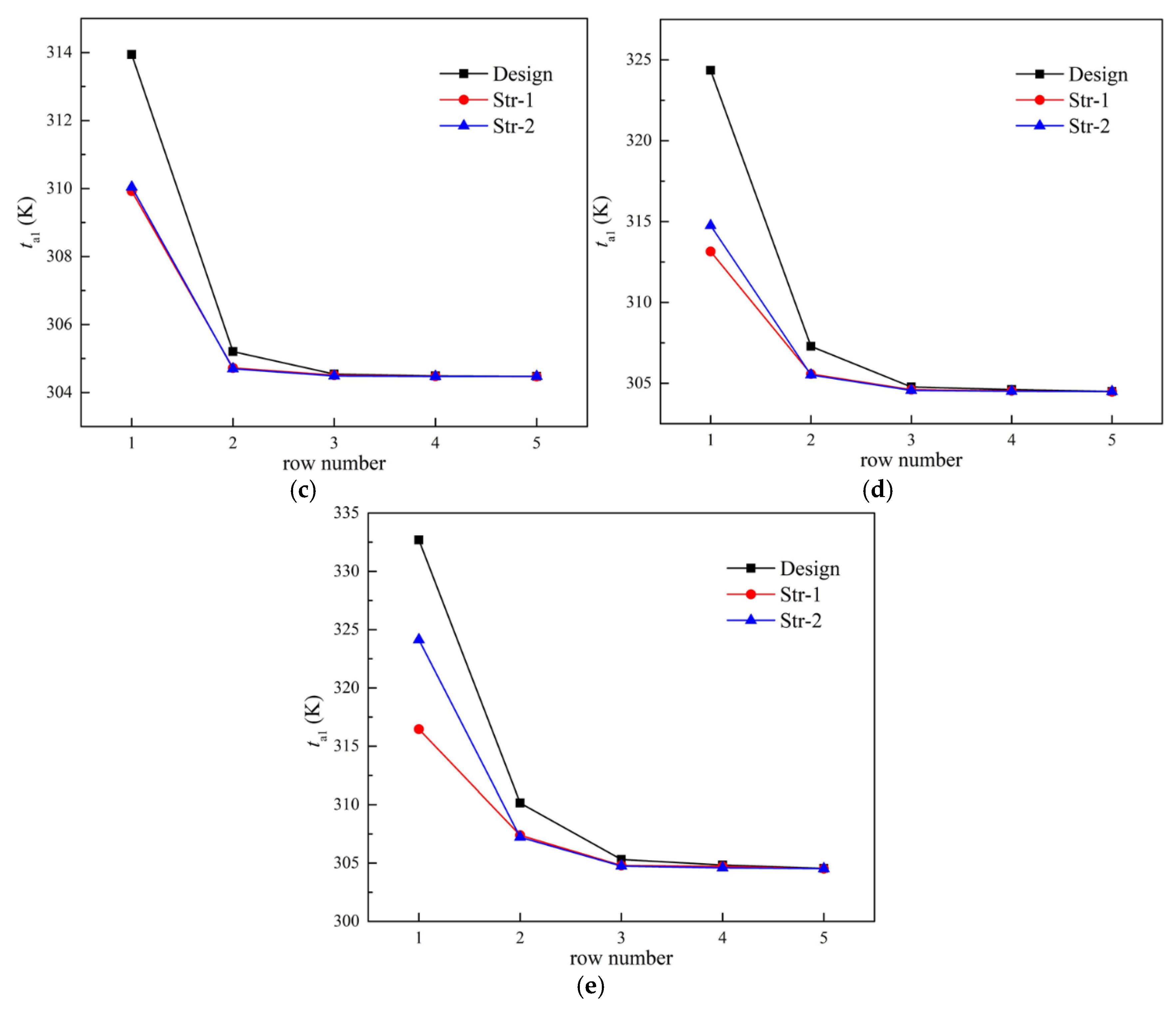
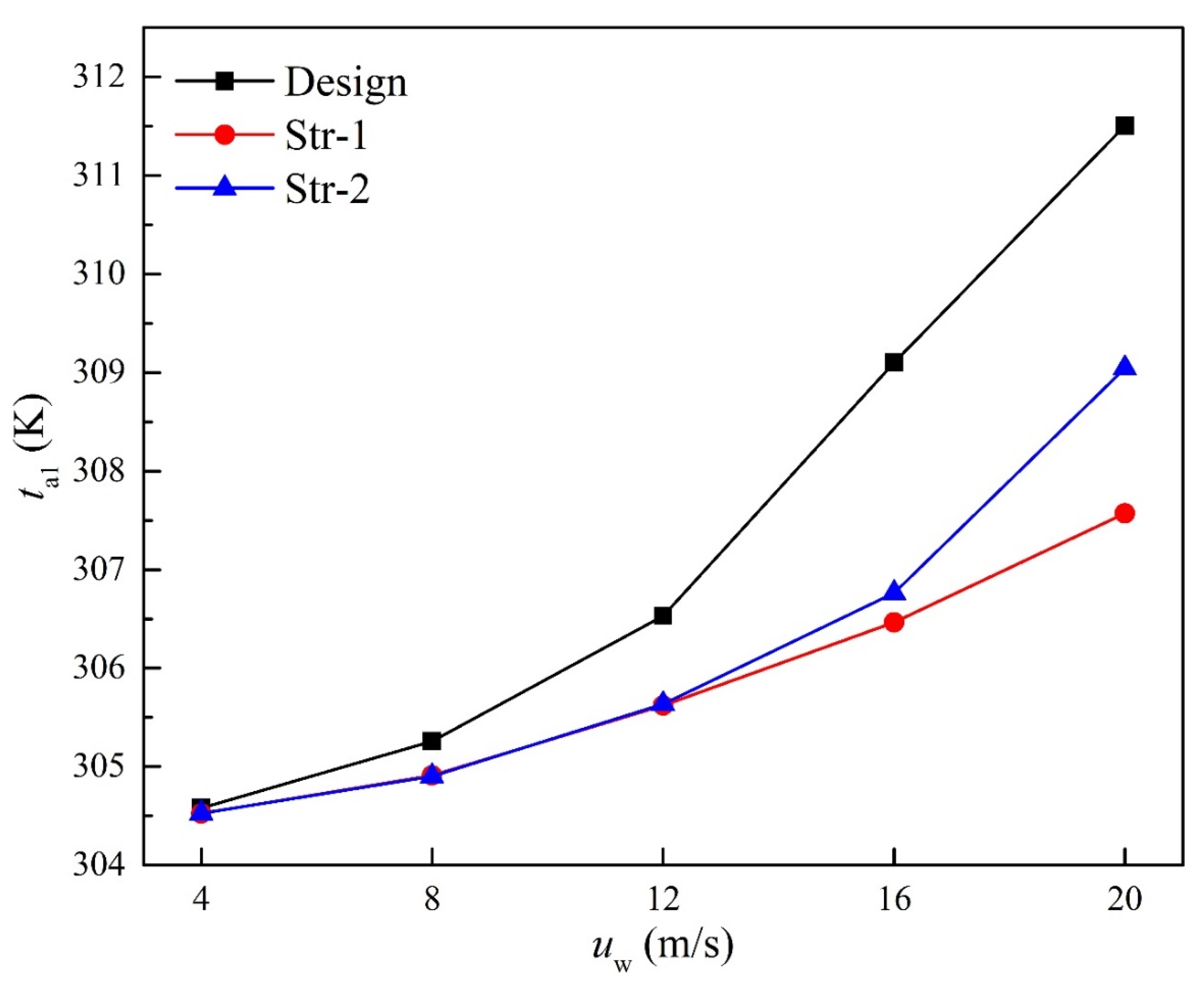
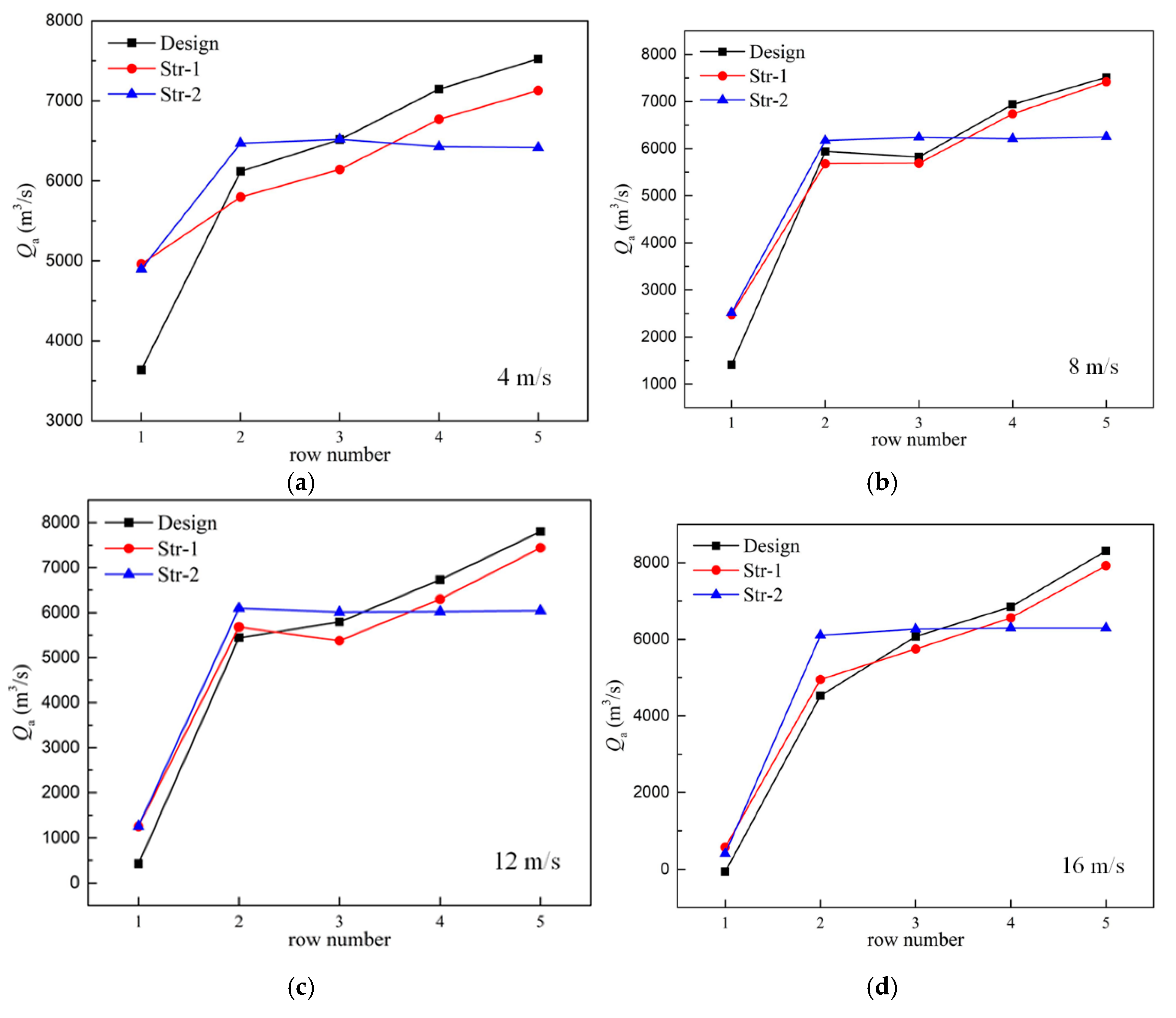
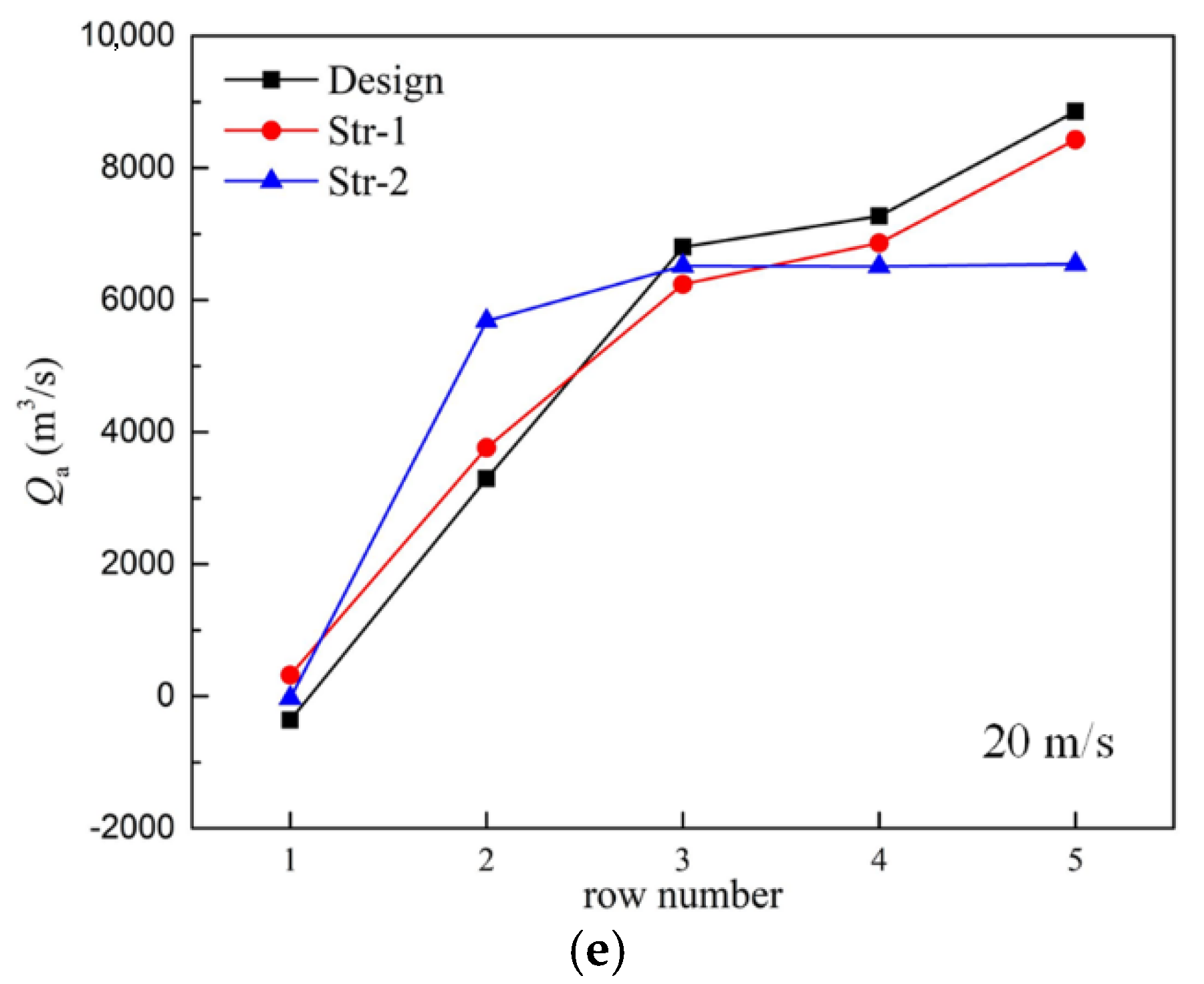
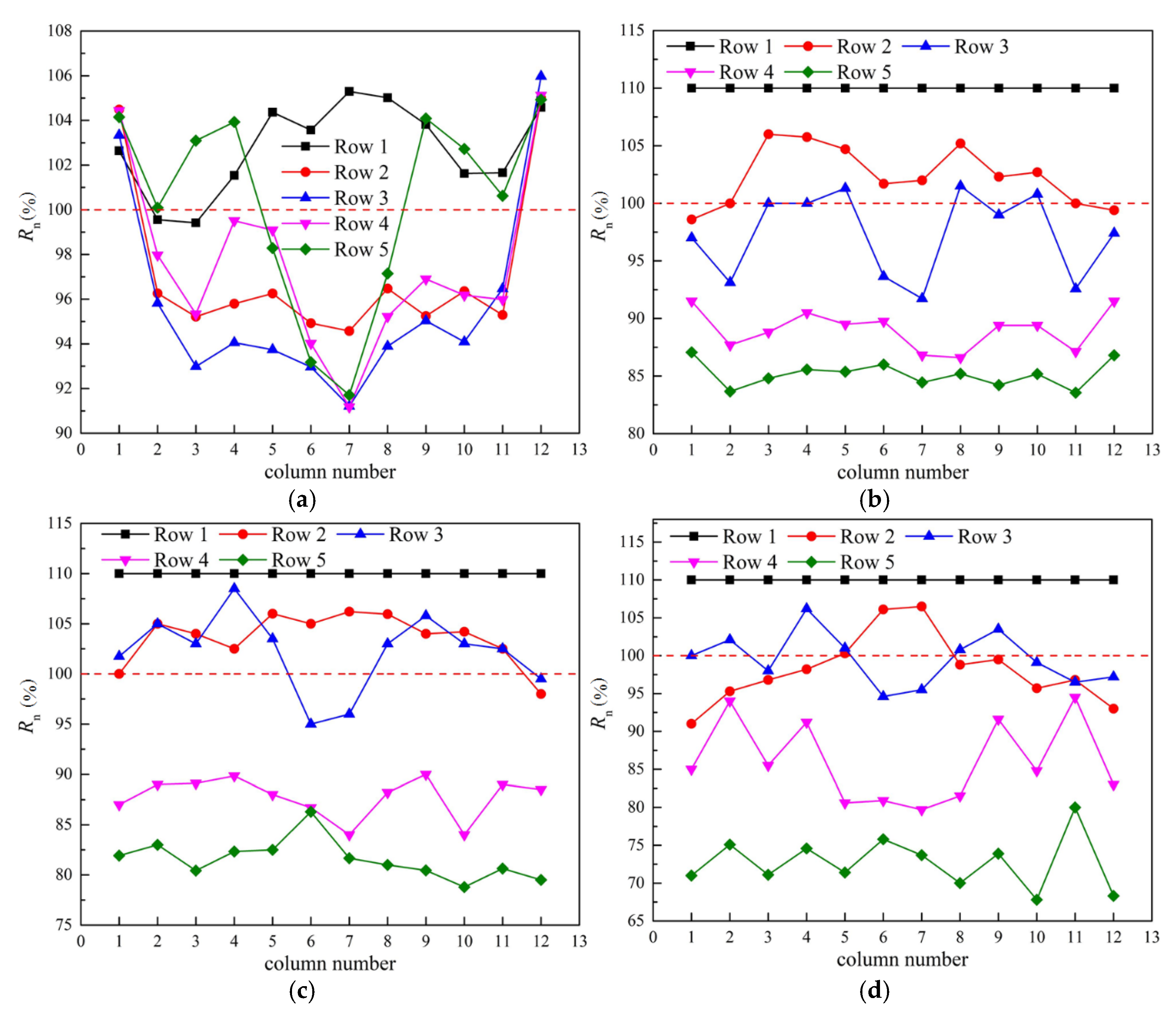
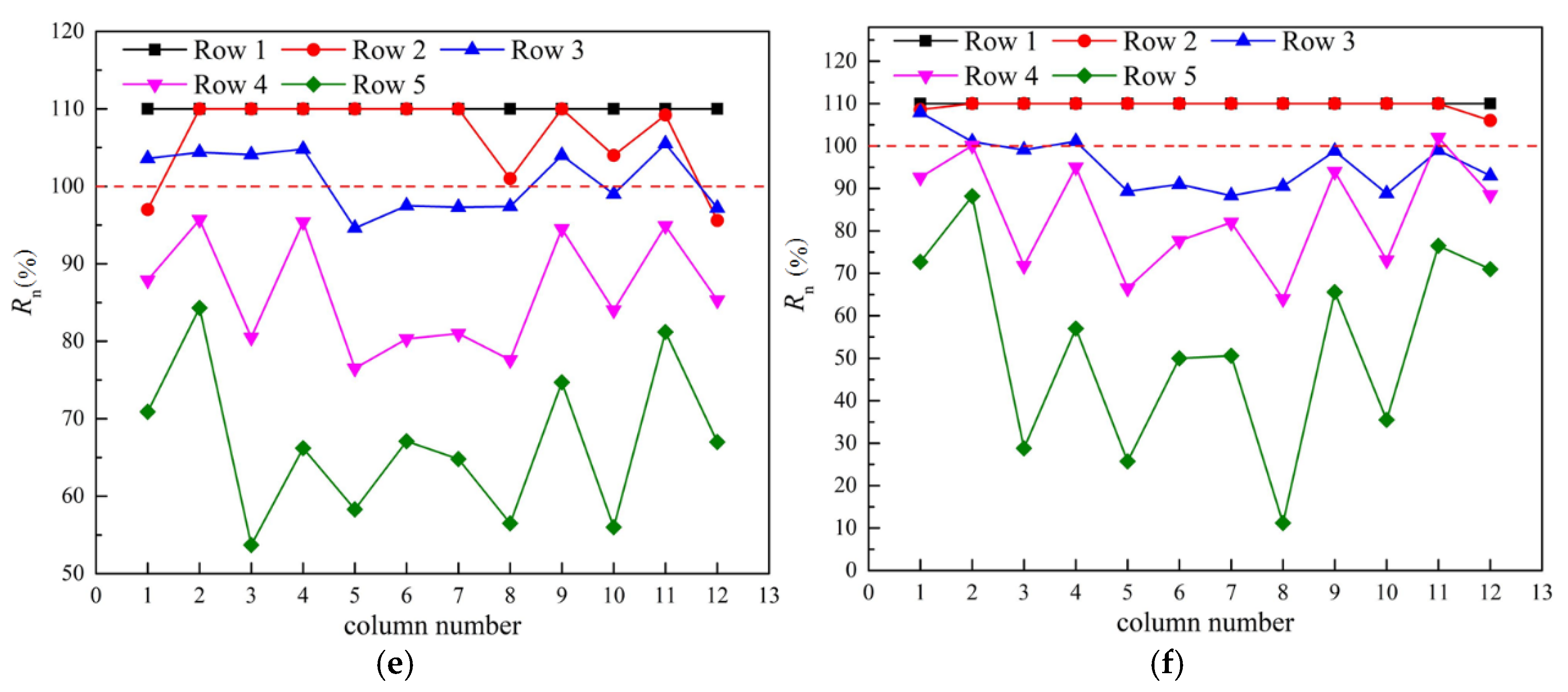
4.2. Rotational Speed
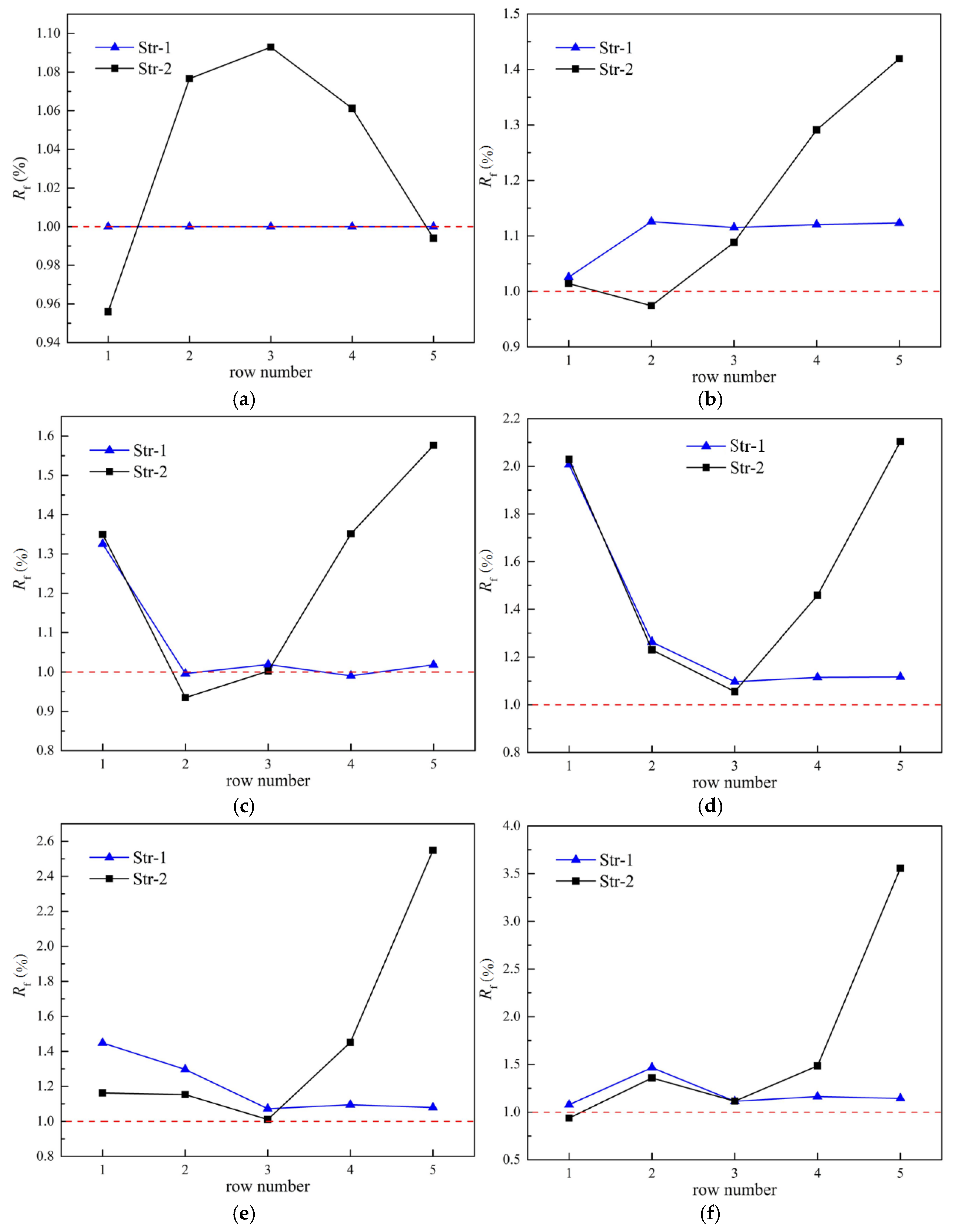
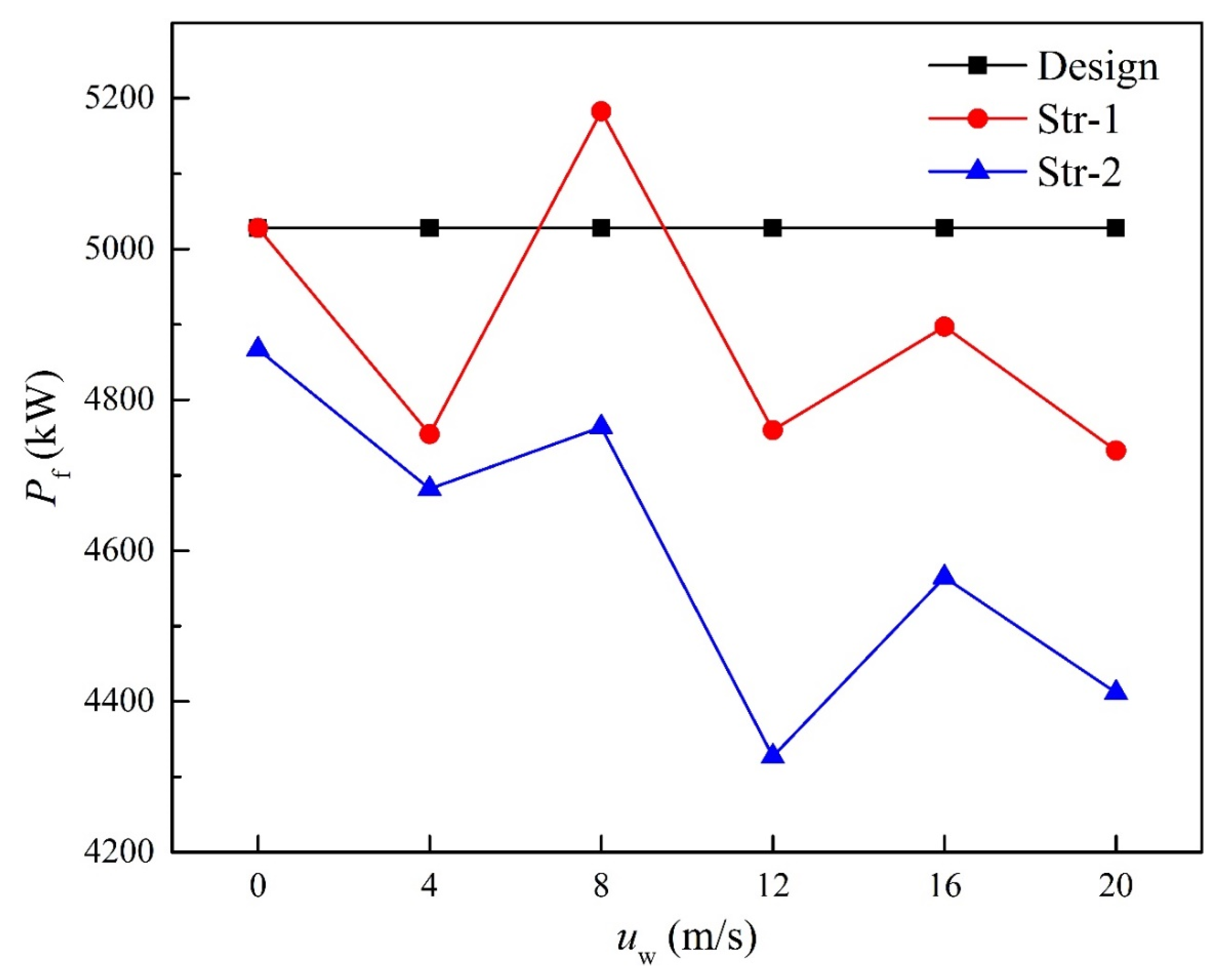
4.3. Power Consumption
5. Conclusions
- (1)
- In the absence of wind, the heat transfer efficiency of ACCs could be improved by Str-2, thereby reducing the demand of cooling air and power consumption of the fan array.
- (2)
- Under windy conditions, the inlet air temperatures of the strategies of Str-1 and Str-2 were reduced, especially at high wind speeds. Str-1 performed better and the average inlet air temperature of fans could be reduced by 3.93 K at the wind speed of 20 m/s.
- (3)
- The distribution of volumetric flow rates of Str-1 and Str-2 cases was more even, especially for Str-2 cases. The total volumetric flow rates of Str-2 cases were the smallest under various wind conditions, while the flow rates of Design and Str-1 cases were almost the same.
- (4)
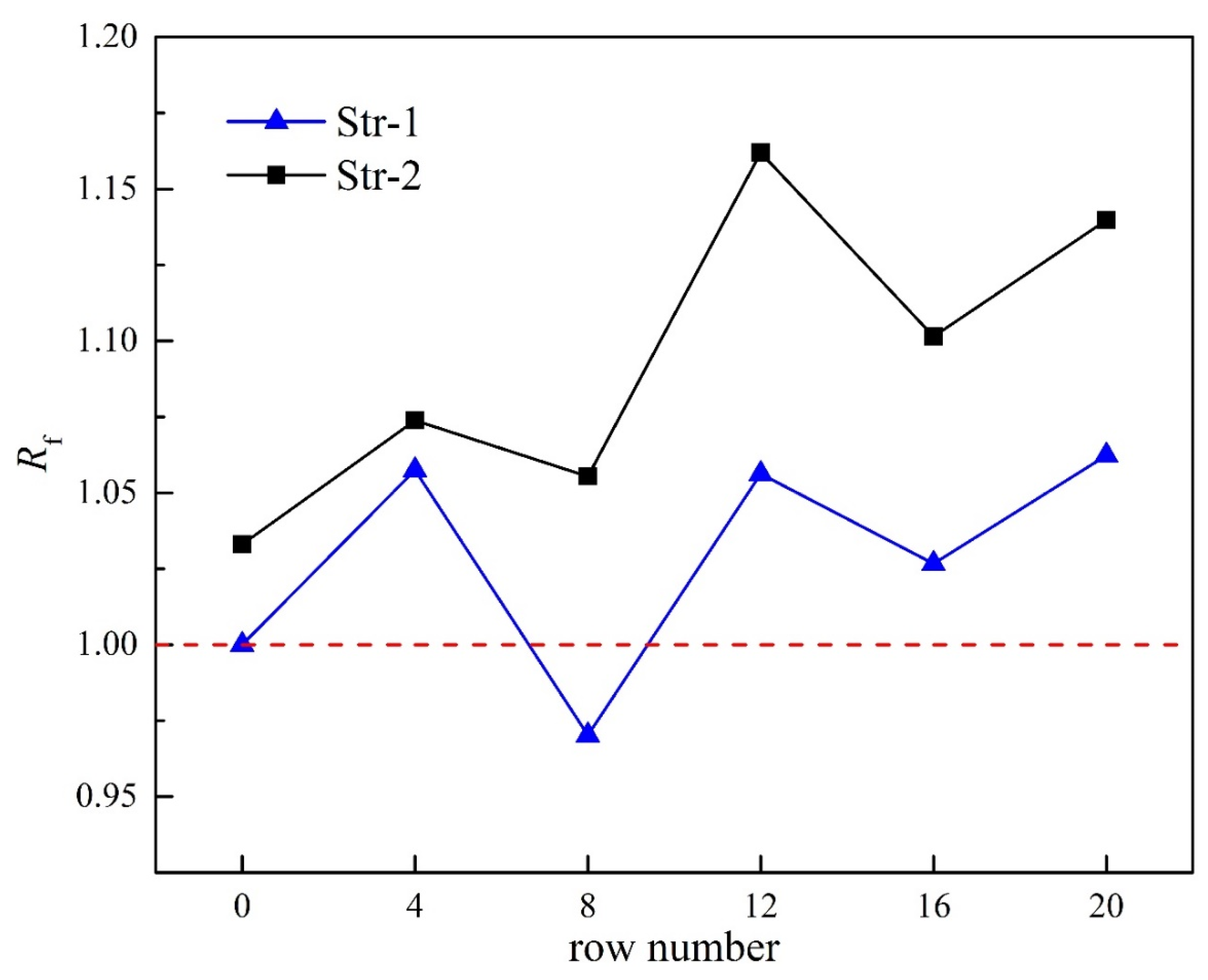
- The cost-effectiveness of the fans in Row 1 for Str-1 and Str-2 increased firstly and then decreased with the wind speed, and it was just the opposite in Row 2. The cost-effectiveness of the fans in Rows 4 and 5 for Str-2 cases was much higher than other cases. The cost-effectiveness of the fans in Row 3 did not change much.
- (5)
- The fan adjustment strategy Str-2 could greatly reduce the power consumption of the fan array, especially at high wind speeds. At the wind speed of 12 m/s, the energy-saving ratio of Str-2 reached 13.94%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | surface area of the finned tube bundles (m2) |
| C | specific heat capacity (kJ·kg−1·K−1) |
| fn | polynomial coefficient of the pressure drop for the fan |
| gn | polynomial coefficient for the tangential velocity |
| K | overall coefficient of heat transfer |
| L | thickness of the finned tube bundles (m) |
| n | rotational speed of axial flow fan (r·min−1) |
| p | pressure (Pa) |
| P | shaft power (kW) |
| q | heat flux (W·m−2) |
| qv | volumetric flow rate (m3·s−1) |
| Qa | volumetric flow rate of cooling air (m3·s−1) |
| r | the distance to the fan center (m) |
| S | source term |
| S’ | additional source term |
| t | temperature (°C) |
| u | velocity (m·s−1) |
| uf | face velocity (m·s−1) |
| Z | height above the ground (m) |
| Greek symbols | |
| Γ | diffusion coefficient (m2·s−1) |
| ρ | density (kg·m−3) |
| φ | dependent variable |
| ε | heat-exchanger effectiveness or diffusion rate of turbulence kinetic energy |
| δ | ratio |
| Φ | heat rejection (kJ) |
| Subscripts | |
| 0 | designed condition |
| 1 | inlet |
| a | air |
| B | back |
| f | axial flow fan |
| θ | peripheral direction |
| s | steam |
| v | volume |
References
- Duvenhage, K.; Kröger, D.G. The influence of wind on the performance of forced draught air-cooled heat exchangers. J. Wind Eng. Ind. Aerod. 1996, 62, 259–277. [Google Scholar] [CrossRef]
- Rooyen, J.A.V.; Kröger, D.G. Performance trends of an air-cooled steam condenser under windy conditions. J. Eng. Gas Turbines Power 2008, 130, 277–285. [Google Scholar] [CrossRef]
- Yang, L.J.; Du, X.Z.; Yang, Y.P. Space characteristics of the thermal performance for air-cooled condensers at ambient winds. Int. J. Heat Mass Transf. 2011, 54, 3109–3119. [Google Scholar] [CrossRef]
- Yang, L.J.; Du, X.Z.; Yang, Y.P. Wind effect on the thermo-flow performances and its decay characteristics for air-cooled condensers in a power plant. Int. J. Therm. Sci. 2012, 53, 175–187. [Google Scholar] [CrossRef]
- Owen, M.; Kröger, D.G. Contributors to increased fan inlet temperature at an air-cooled steam condenser. Appl. Therm. Eng. 2013, 50, 1149–1156. [Google Scholar] [CrossRef]
- Liu, P.; Duan, H.; Zhao, W. Numerical investigation of hot air recirculation of air-cooled condensers at a large power plant. Appl. Therm. Eng. 2009, 29, 1927–1934. [Google Scholar] [CrossRef]
- He, W.; Han, D.; Yue, C.; Pu, W.; Dai, Y. Mechanism of the air temperature rise at the forced draught fan inlets in an air-cooled steam condenser. Appl. Therm. Eng. 2014, 71, 355–363. [Google Scholar] [CrossRef]
- Yang, L.J.; Wang, M.H.; Du, X.Z.; Yang, Y.P. Trapezoidal array of air-cooled condensers to restrain the adverse impacts of ambient winds in a power plant. Appl. Energy 2012, 99, 402–413. [Google Scholar] [CrossRef]
- Jin, R.; Yang, X.; Yang, L.; Du, X.; Yang, Y. Square array of air-cooled condensers to improve thermo-flow performances under windy conditions. Int. J. Heat Mass Transf. 2018, 127, 717–729. [Google Scholar] [CrossRef]
- Chen, L.; Yang, L.; Du, X.; Yang, Y. A novel layout of air-cooled condensers to improve thermo-flow performances. Appl. Energy 2016, 165, 244–259. [Google Scholar] [CrossRef]
- Kong, Y.; Wang, W.; Huang, X.; Yang, L.; Du, X.; Yang, Y. Circularly arranged air-cooled condensers to restrain adverse wind effects. Appl. Therm. Eng. 2017, 124, 202–223. [Google Scholar] [CrossRef]
- Kong, Y.; Wang, W.; Huang, X.; Yang, L.; Du, X.; Yang, Y. Direct dry cooling system through hybrid ventilation for improving cooling efficiency in power plants. Appl. Therm. Eng. 2017, 119, 254–268. [Google Scholar] [CrossRef]
- Haffejee, R.A.; Laubscher, R. Development of a thermofluid network modeling methodology for double-row air-cooled condensers. Therm. Sci. Eng. Progress 2020, 19, 100646. [Google Scholar] [CrossRef]
- Zhou, Y.; Cheng, Y.; Zhang, N.; Shi, H. Numerical simulation study of novel air-cooled condenser with lateral air supply. Case Stud. Therm. Eng. 2019, 13, 100354. [Google Scholar] [CrossRef]
- Huang, X.; Chen, L.; Kong, Y.; Yang, L.; Du, X. Effects of geometric structures of air deflectors on thermo-flow performances of air-cooled condenser. Int. J. Heat Mass Transf. 2018, 118, 1022–1039. [Google Scholar] [CrossRef]
- Gu, H.; Zhe, Z.; Wang, H.; Qi, C. A numerical study on the effect of roof windbreak structures in an air-cooled system. Appl. Therm. Eng. 2015, 90, 684–693. [Google Scholar] [CrossRef]
- Owen, M.T.F.; Kröger, D.G. The effect of screens on air-cooled steam condenser performance under windy conditions. Appl. Therm. Eng. 2010, 30, 2610–2615. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, T. Effects of diffuser orifice plate on the performance of air-cooled steam condenser. Appl. Therm. Eng. 2016, 98, 179–188. [Google Scholar] [CrossRef]
- Yuan, W.; Sun, F.; Zhao, Y. Numerical study on the impact mechanism of windshield devices on frozen phenomena in a direct air-cooled system. Int. J. Heat Mass Transf. 2019, 142, 118206. [Google Scholar] [CrossRef]
- Chen, L.; Sun, Y.; Yang, L.; Du, X.; Yang, Y. Rotational speed adjustment of axial flow fans to maximize net power output for direct dry cooling power generating units. Heat Transf. Asian Res. 2019, 49, 356–382. [Google Scholar] [CrossRef]
- He, W.F.; Zhang, X.K.; Han, D.; Gao, L. Sensitivity analysis from the blade angle regulation of the forced draught fans in an air-cooled steam condenser. Appl. Therm. Eng. 2017, 123, 810–819. [Google Scholar] [CrossRef]
- He, W.; Dai, Y.; Han, D.; Yue, C.; Pu, W. Influence from the rotating speed of the windward axial fans on the performance of an air-cooled power plant. Appl. Therm. Eng. 2014, 65, 14–23. [Google Scholar] [CrossRef]
- He, W.F.; Chen, J.J.; Han, D.; Wen, T.; Luo, L.T.; Li, R.Y.; Zhong, W.C. Numerical analysis from the rotational speed regulation within the fan array on the performance of an air-cooled steam condenser. Appl. Therm. Eng. 2019, 153, 352–360. [Google Scholar] [CrossRef]
- Li, X.; Wang, N.; Wang, L.; Yang, Y.; Maréchal, F. Identification of optimal operating strategy of direct air-cooling condenser for Rankine cycle based power plants. Appl. Energy 2018, 209, 153–166. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Y.; Fu, P.; Feng, P.; Yang, Y. Heat transfer and thermal characteristics analysis of direct air-cooled combined heat and power plants under off-design conditions. Appl. Therm. Eng. 2018, 129, 260–268. [Google Scholar] [CrossRef]
- Li, J.; Bai, Y.; Li, B. Operation of air cooled condensers for optimised back pressure at ambient wind. Appl. Therm. Eng. 2018, 128, 1340–1350. [Google Scholar] [CrossRef]
- Huang, W.; Chen, L.; Wang, W.; Yang, L.; Du, X. Cooling Performance Optimization of Direct Dry Cooling System Based on Partition Adjustment of Axial Flow Fans. Energies 2020, 13, 3179. [Google Scholar] [CrossRef]
- Huang, W.; Chen, L.; Yang, L.; Du, X. Operation strategies of axial flow fans in a direct dry cooling system under various meteorological conditions. Heat Transf. Asian Res. 2021. [Google Scholar] [CrossRef]
- ANSYS Inc. Fluent User’s Guide; ANSYS Inc.: Lebanon, NH, USA, 2012. [Google Scholar]
- Chen, L.; Yang, L.; Du, X.; Yang, Y. Novel air-cooled condenser with V-frame cells and induced axial flow fans. Int. J. Heat Mass Transf. 2018, 117, 167–182. [Google Scholar] [CrossRef]
- Yang, L.J.; Wu, X.P.; Du, X.Z.; Yang, Y.P. Dimensional characteristics of wind effects on the performance of indirect dry cooling system with vertically arranged heat exchanger bundles. Int. J. Heat Mass Transf. 2013, 67, 853–866. [Google Scholar] [CrossRef]
- Yang, L.; Du, X.; Yang, Y. Measures against the adverse impact of natural wind on air-cooled condensers in power plant. Sci. China Technol. Sci. 2010, 53, 1320–1327. [Google Scholar] [CrossRef]
- Yang, L.J.; Du, X.Z.; Yang, Y.P. Influences of wind-break wall configurations upon flow and heat transfer characteristics of air-cooled condensers in a power plant. Int. J. Heat Mass Transf. 2011, 50, 2050–2061. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Number of condenser cells | 60 |
| Length of ACC cell (m) | 11.31 |
| Width of ACC cell (m) | 11.24 |
| Height of ACC platform (m) | 35 |
| Number of axial flow fans | 60 |
| Fan diameter (m) | 9.144 |
| Total power consumption of axial flow fans (kW) | 5028 |
| Rotational speed of fan (r/min) | 72 |
| Volumetric flow rate (m3/s) | 474.9 |
| Total pressure of fan (Pa) | 122.1 |
| Material of base tube/fin | Cs/Al |
| Density of fin (kg/m3) | 2719 |
| Specific heat of fin (J/kg/K) | 871 |
| Thermal conductivity of fin (W/m/K) | 202.4 |
| Major axis of base tube for finned tube bundles (mm) | 219 |
| Minor axis of base tube for finned tube bundles (mm) | 19 |
| Width of fin (mm) | 19 |
| Height of fin (mm) | 200 |
| Pitch of fins (mm) | 2.3 |
| Thickness of fin (mm) | 0.25 |
| Parameter | Value |
|---|---|
| Ambient temperature (K) | 304.45 |
| Atmospheric relative humidity (%) | 63 |
| Ambient pressure (Pa) | 101,325 |
| Pressure of main steam (MPa) | 16.67 |
| Temperature of main steam (°C) | 538 |
| Mass flow rate of main steam (t/h) | 1004.2 |
| Main steam enthalpy (kJ/kg) | 3397.2 |
| Pressure of reheat steam (MPa) | 3.427 |
| Temperature of reheat steam (°C) | 538 |
| Mass flow rate of reheat steam (t/h) | 821.988 |
| Reheat steam enthalpy (kJ/kg) | 3536.9 |
| Back pressure of turbine (MPa) | 0.031 |
| Temperature of exhaust steam (°C) | 69.9 |
| Mass flow rate of exhaust steam (t/h) | 689.378 |
| Exhaust steam enthalpy (kJ/kg) | 2557.71 |
| Case | pB (kPa) | ts (°C) | Qa (m3/s) | δv (%) | Pf (kW) |
|---|---|---|---|---|---|
| Design | 24.159 | 64.2 | 34,422 | 9.96 | 5028 |
| Str-1 | 24.159 | 64.2 | 34,422 | 9.96 | 5028 |
| Str-2 | 24.159 | 64.2 | 34,008 | 2.32 | 4867 |
| Case | Rn (%) | |||||
|---|---|---|---|---|---|---|
| uw = 0 m/s | uw = 4 m/s | uw = 8 m/s | uw = 12 m/s | uw = 16 m/s | uw = 20 m/s | |
| Str-1 | 100 | 94.7 | 98.5 | 94.75 | 96 | 94.5 |
| Case | δf (%) | |||||
|---|---|---|---|---|---|---|
| uw = 0 m/s | uw = 4 m/s | uw = 8 m/s | uw = 12 m/s | uw = 16 m/s | uw = 20 m/s | |
| Str-1 | 0 | 5.44 | −3.07 | 5.33 | 2.60 | 5.87 |
| Str-2 | 3.2 | 6.88 | 5.25 | 13.94 | 9.21 | 12.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Chen, L.; Yang, L.; Du, X. Energy-Saving Strategies of Axial Flow Fans for Direct Dry Cooling System. Energies 2021, 14, 3176. https://doi.org/10.3390/en14113176
Huang W, Chen L, Yang L, Du X. Energy-Saving Strategies of Axial Flow Fans for Direct Dry Cooling System. Energies. 2021; 14(11):3176. https://doi.org/10.3390/en14113176
Chicago/Turabian StyleHuang, Wenhui, Lei Chen, Lijun Yang, and Xiaoze Du. 2021. "Energy-Saving Strategies of Axial Flow Fans for Direct Dry Cooling System" Energies 14, no. 11: 3176. https://doi.org/10.3390/en14113176
APA StyleHuang, W., Chen, L., Yang, L., & Du, X. (2021). Energy-Saving Strategies of Axial Flow Fans for Direct Dry Cooling System. Energies, 14(11), 3176. https://doi.org/10.3390/en14113176







