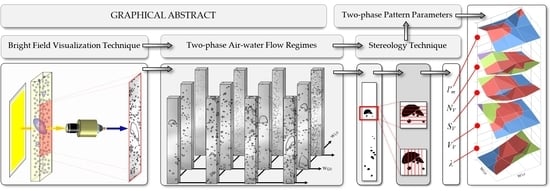
Precise Evaluation of Gas–Liquid Two-Phase Flow Pattern in a Narrow Rectangular Channel with Stereology Method
Abstract
:1. Introduction
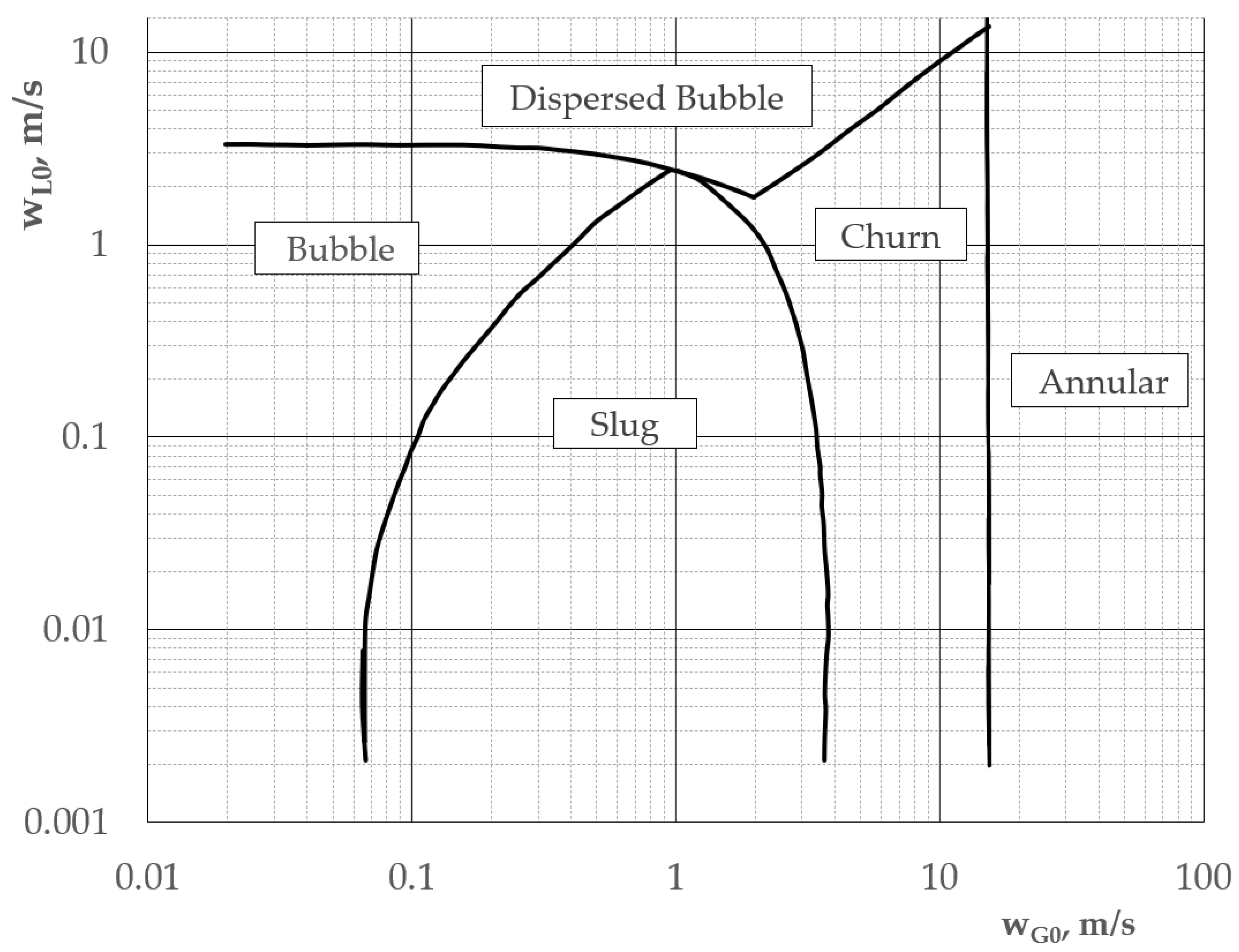
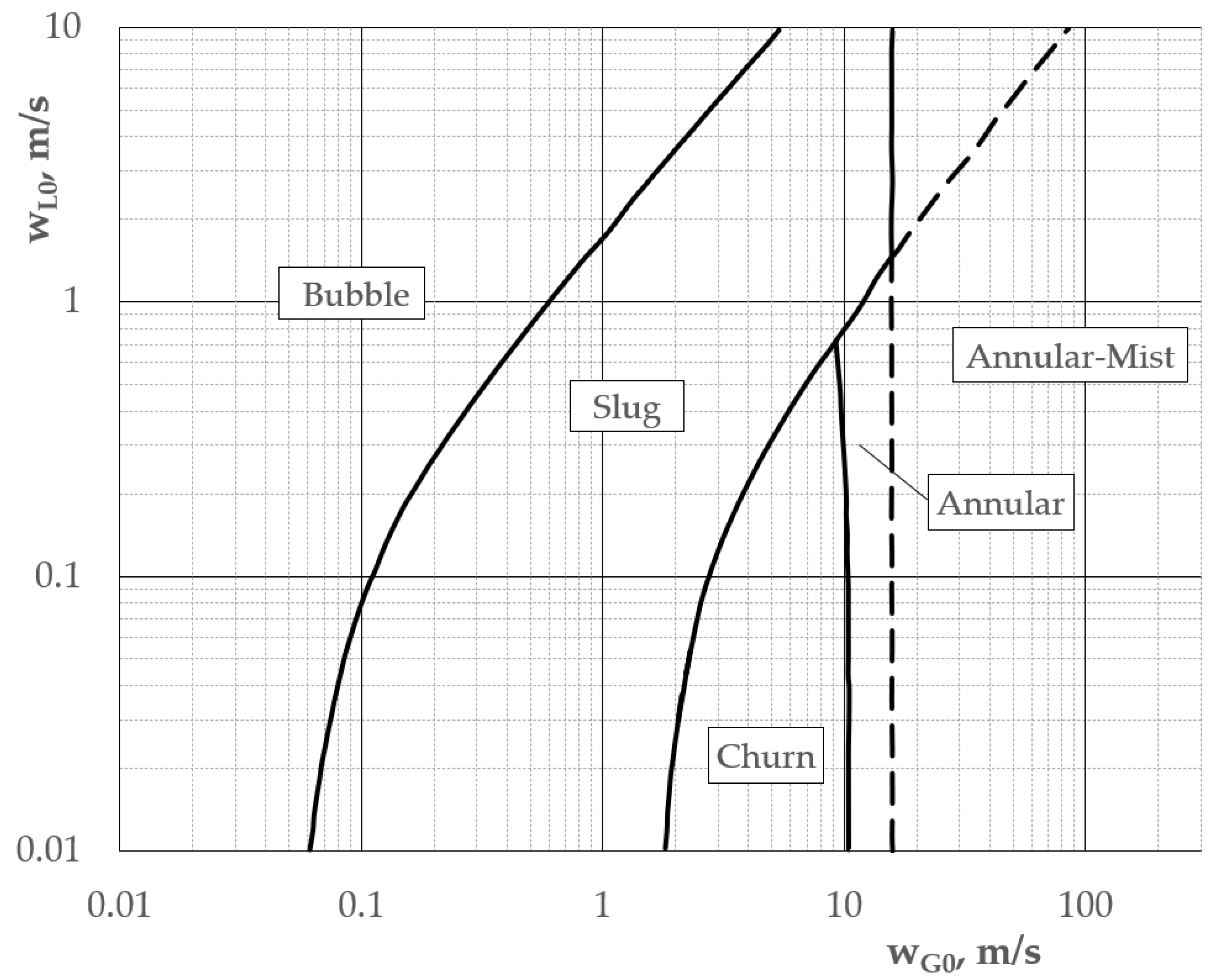
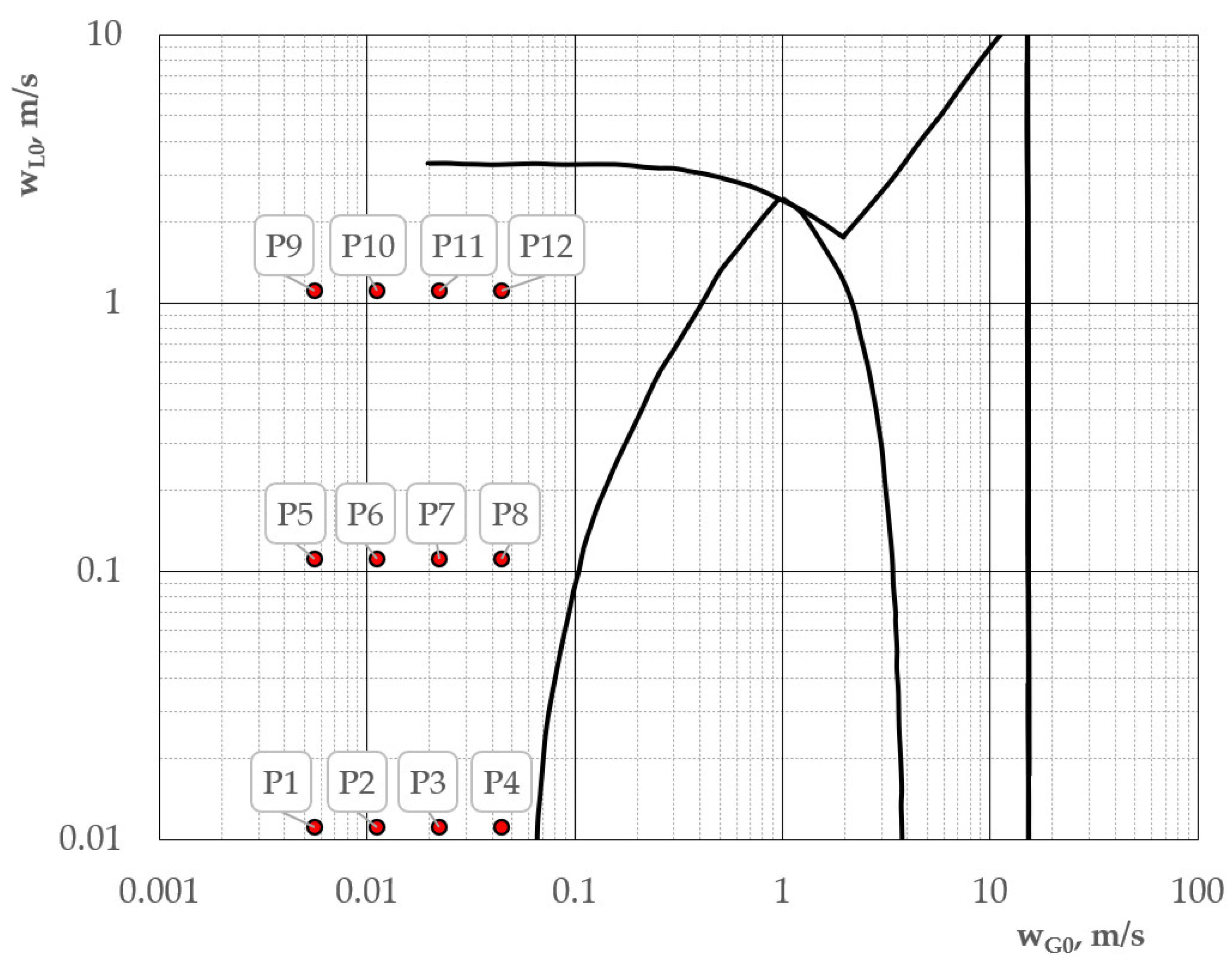
2. Flow Pattern Classification and Flow Maps
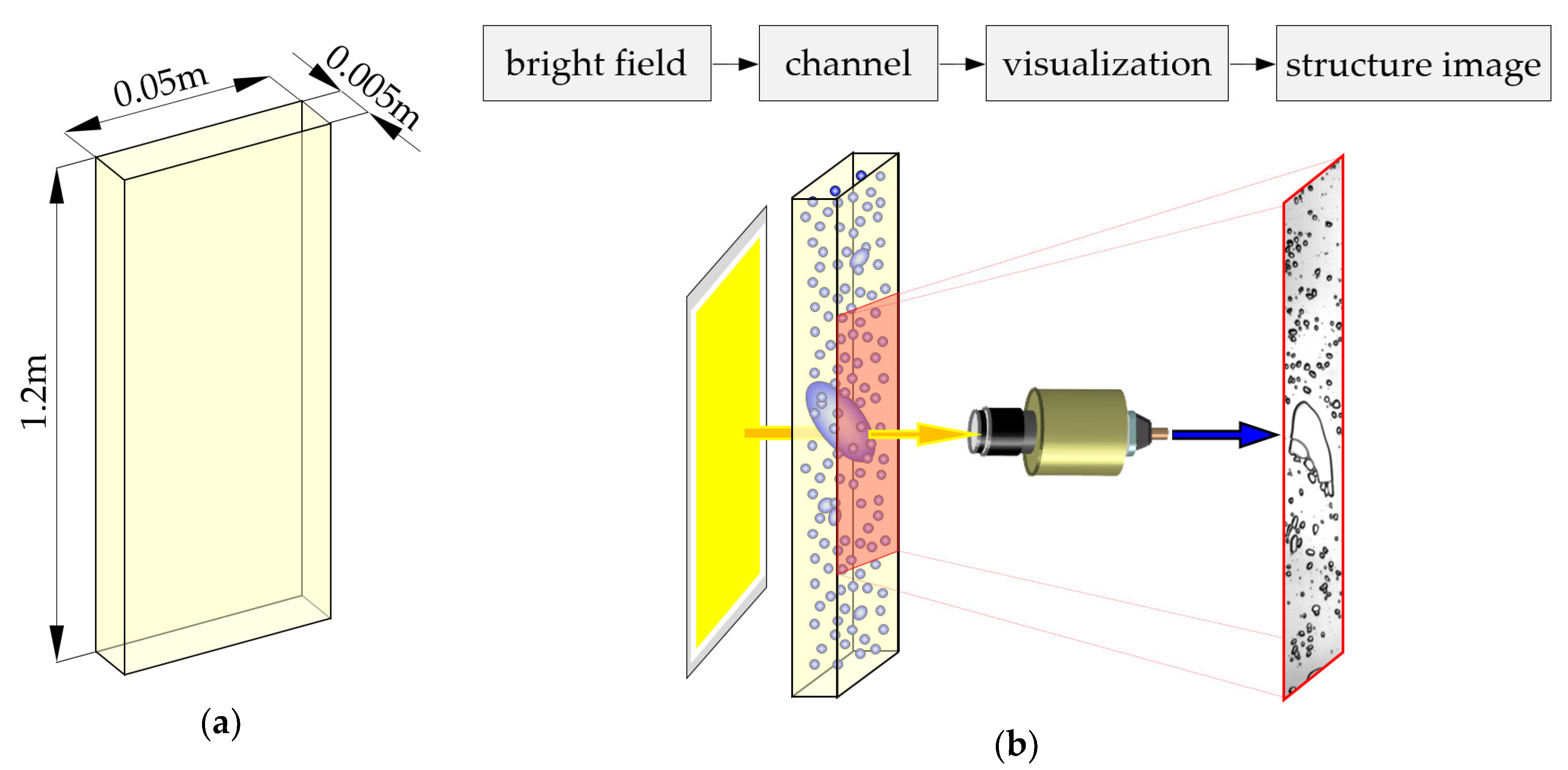
3. Problem Definition
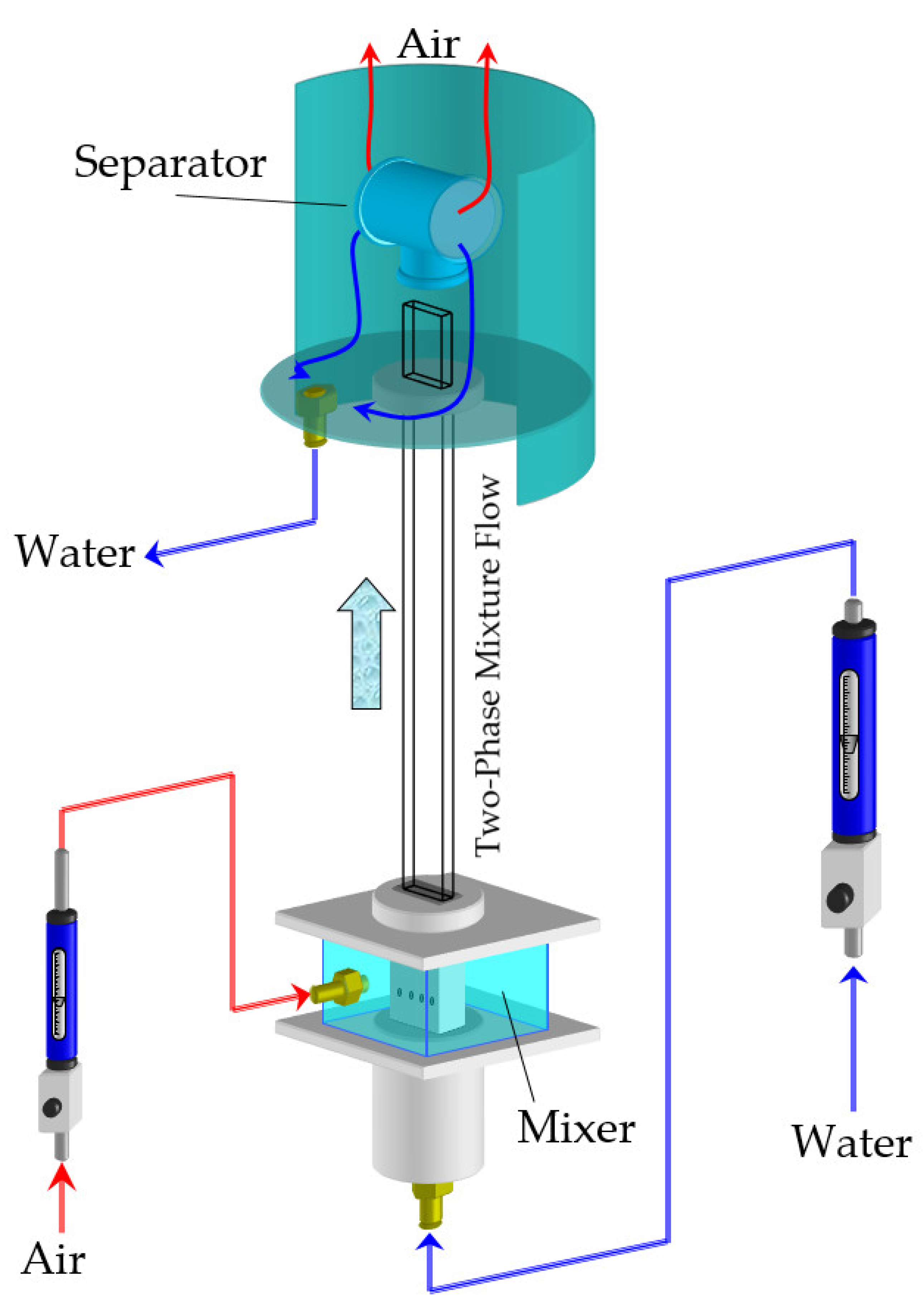
4. Materials and Methods
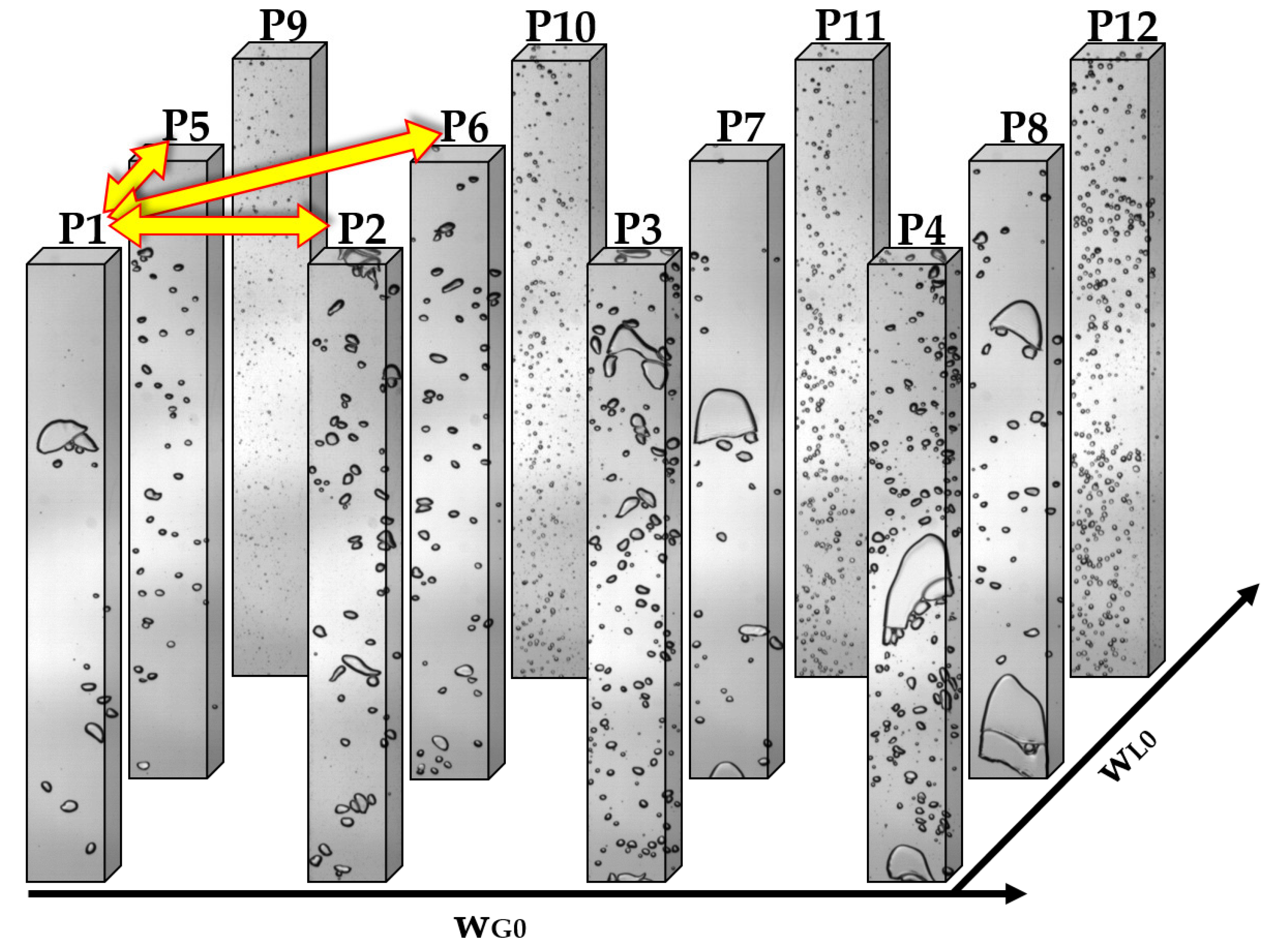
5. Results
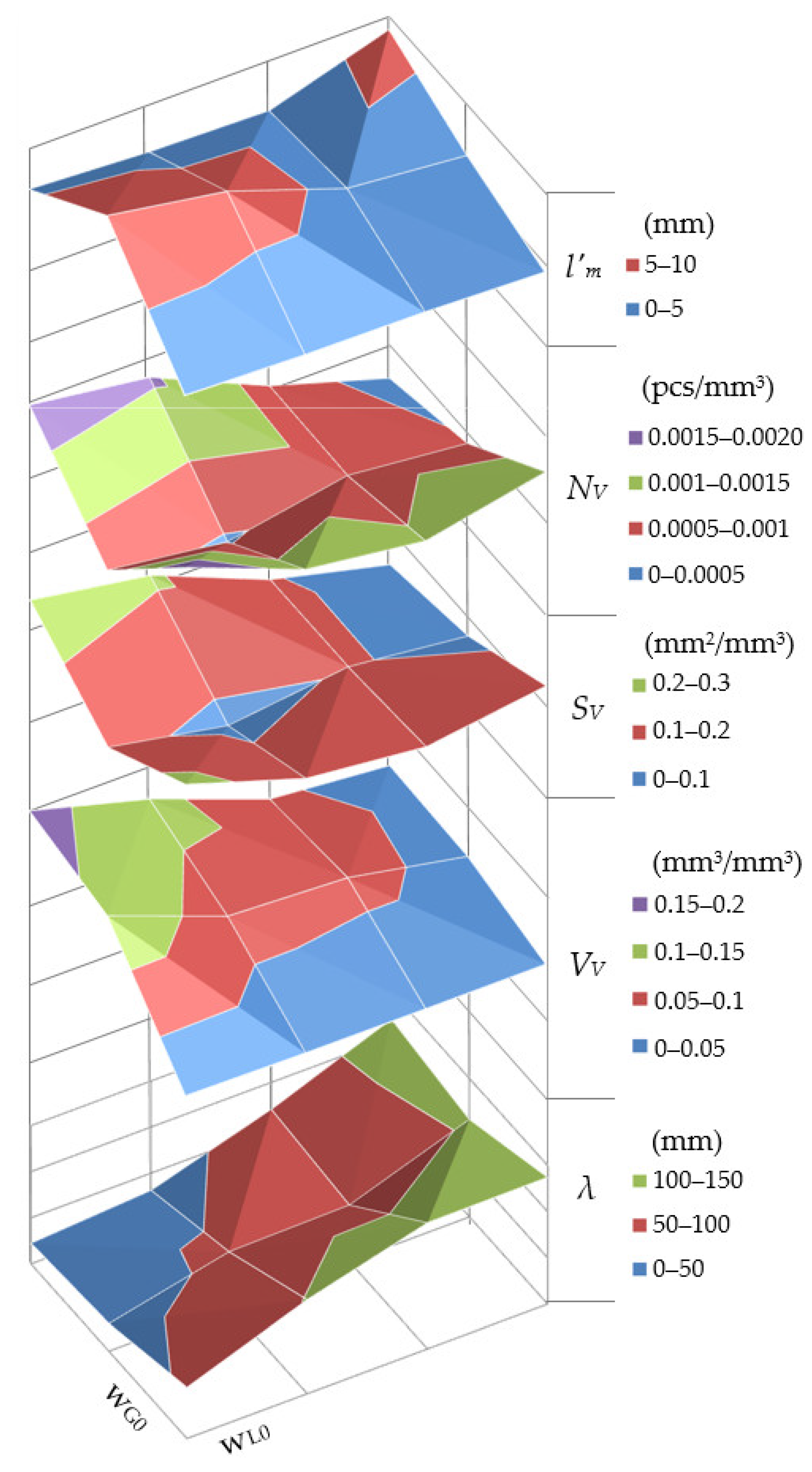
- the gas volume fraction VV increases by 42%,
- interfacial area SV increased by 150%,
- the number of bubbles NV increased by 200%,
- the mean bubble dimension l′m decreased by 45%
- the average distance between bubbles λ decreased by 41%.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pang, L.; Yi, S.; Duan, L.; Li, W.; Yang, Y. Thermal stress and cyclic stress analysis of a verticalwater-cooledwall at a utility boiler under flexible operation. Energies 2019, 12, 1170. [Google Scholar] [CrossRef] [Green Version]
- Oya, T. Upward Liquid Flow in a Small Tube into which Air Streams: 3rd Report, Pipe Friction I. Bull. JSME 1972, 15, 1522–1533. [Google Scholar] [CrossRef] [Green Version]
- Mikulčić, H.; Duić, N.; Dewil, R. Environmental management as a pillar for sustainable development. J. Environ. Manag. 2017, 203, 867–871. [Google Scholar] [CrossRef]
- Nicklin, D.J.; Wilkes, J.O.; Davidson, J.F. Two-phase flow in vertical tubes. Trans. Inst. Chem. Eng. 1962, 40, 61–68. [Google Scholar]
- Zaborowska, I.; Grzybowski, H.; Rafałko, G.; Mosdorf, R. Boiling dynamics in parallel minichannel system with different inlet solutions. Int. J. Heat Mass Transf. 2021, 165, 120655. [Google Scholar] [CrossRef]
- Tian, Z.; Gu, B.; Zhang, Y.; Gao, W. Flow boiling heat transfer under marine motions: A comprehensive review. Ann. Nucl. Energy 2020, 143, 107455. [Google Scholar] [CrossRef]
- Sikora, M.; Bohdal, T. Heat and flow investigation of NOVEC649 refrigerant condensation in pipe minichannels. Energy 2020, 209, 118447. [Google Scholar] [CrossRef]
- Bohdal, T.; Charun, H.; Sikora, M. Pressure drop during condensation of refrigerants in pipe minichannels. Arch. Thermodyn. 2012, 33, 87–106. [Google Scholar] [CrossRef]
- Barreto, E.X.; Oliveira, J.L.G.; Passos, J.C. Analysis of air-water flow pattern in parallel microchannels: A visualization study. Exp. Therm. Fluid Sci. 2015, 63, 1–8. [Google Scholar] [CrossRef]
- Kim, B.J.; Sohn, B.H.; Jeong, S. Two-phase flow regimes for counter-current air-water flows in narrow rectangular channels. KSME Int. J. 2001, 15, 941–950. [Google Scholar] [CrossRef]
- Gregorc, J.; Žun, I. Inlet conditions effect on bubble to slug flow transition in mini-channels. Chem. Eng. Sci. 2013, 102, 106–120. [Google Scholar] [CrossRef]
- Pecherkin, N.; Chekhovich, V. Mass Transfer in Two-Phase Gas-Liquid Flow in a Tube and in Channels of Complex Configuration. In Mass Transfer in Multiphase Systems and Its Applications; InTech Open: London, UK, 2011. [Google Scholar]
- Mohmmed, A.O.; Al-Kayiem, H.H.; Osman, A.B.; Sabir, O. One-way coupled fluid–structure interaction of gas–liquid slug flow in a horizontal pipe: Experiments and simulations. J. Fluids Struct. 2020, 97, 103083. [Google Scholar] [CrossRef]
- Ide, H.; Kariyasaki, A.; Fukano, T. Fundamental data on the gas–liquid two-phase flow in minichannels. Int. J. Therm. Sci. 2007, 46, 519–530. [Google Scholar] [CrossRef]
- Xu, J.; Liu, F.; Xiao, Q.; Huang, J.; Fei, Y.; Yang, Y.; Zhai, Y.; Pan, J.; Wang, H. Synergistic effect of flow pattern evolution of dispersed and continuous phases in direct-contact heat transfer process. Int. J. Refrig. 2020, 112, 201–214. [Google Scholar] [CrossRef]
- Almutairi, Z.; Al-Alweet, F.M.; Alghamdi, Y.A.; Almisned, O.A.; Alothman, O.Y. Investigating the characteristics of two-phase flow using electrical capacitance tomography (ECT) for three pipe orientations. Processes 2020, 8, 51. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Wu, F.; Yang, X.; Li, Y. Measurement of gas-oil two-phase flow patterns by using CNN algorithm based on dual ECT sensors with venturi tube. Sensors 2020, 20, 1200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roshani, M.; Phan, G.T.T.; Jammal Muhammad Ali, P.; Hossein Roshani, G.; Hanus, R.; Duong, T.; Corniani, E.; Nazemi, E.; Mostafa Kalmoun, E. Evaluation of flow pattern recognition and void fraction measurement in two phase flow independent of oil pipeline’s scale layer thickness. Alex. Eng. J. 2021, 60, 1955–1966. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.; Hossein Roshani, G.; Hanus, R.; Nazemi, B.; Corniani, E.; Nazemi, E. Combination of X-ray tube and GMDH neural network as a nondestructive and potential technique for measuring characteristics of gas-oil–water three phase flows. Meas. J. Int. Meas. Confed. 2021, 168, 108427. [Google Scholar] [CrossRef]
- Fang, L.; Zeng, Q.; Wang, F.; Faraj, Y.; Zhao, Y.; Lang, Y.; Wei, Z. Identification of two-phase flow regime using ultrasonic phased array. Flow Meas. Instrum. 2020, 72, 101726. [Google Scholar] [CrossRef]
- Troniewski, L.; Ulbrich, R. The analysis of flow regime maps of two-phase gas-liquid flow in pipes. Chem. Eng. Sci. 1984, 39, 1213–1224. [Google Scholar] [CrossRef]
- Mosdorf, R.; Górski, G. Identification of two-phase flow patterns in minichannel based on RQA and PCA analysis. Int. J. Heat Mass Transf. 2016, 96, 64–74. [Google Scholar] [CrossRef]
- Wajman, R. Computer methods for non-invasive measurement and control of two-phase flows: A review study. Inf. Technol. Control 2019, 48, 464–486. [Google Scholar] [CrossRef] [Green Version]
- Sikora, M.; Bohdal, T. Application of computer image analyzes in the investigation of refrigerants condensation in minichannels. Arch. Thermodyn. 2019, 40, 103–114. [Google Scholar]
- Ligus, G.; Zajac, D.; Masiukiewicz, M.; Anweiler, S. A new method of selecting the airlift pump optimum efficiency at low submergence ratios with the use of image analysis. Energies 2019, 12, 735. [Google Scholar] [CrossRef] [Green Version]
- Anweiler, S.; Szmolke, N. Analiza struktury przepŁywu mieszaniny gaz-ciaŁo staŁe z wykorzystaniem cyfrowej metody rozpoznawania obrazu. Inz. Chem. Proces. 2001, 22, 187–192. [Google Scholar]
- Wasilewski, M.; Anweiler, S.; Masiukiewicz, M. Characterization of multiphase gas–solid flow and accuracy of turbulence models for lower stage cyclones used in suspension preheaters. Chin. J. Chem. Eng. 2019, 27, 1618–1629. [Google Scholar] [CrossRef]
- Ligus, G.; Wasilewski, M.; Kołodziej, S.; Zając, D. CFD and PIV Investigation of a Liquid Flow Maldistribution across a Tube Bundle in the Shell-and-Tube Heat Exchanger with Segmental Baffles. Energies 2020, 13, 5150. [Google Scholar] [CrossRef]
- Gogolin, A.; Wasilewski, M.; Ligus, G.; Wojciechowski, S.; Gapinski, B.; Krolczyk, J.B.; Zajac, D.; Krolczyk, G.M. Influence of geometry and surface morphology of the U-tube on the fluid flow in the range of various velocities. Meas. J. Int. Meas. Confed. 2020, 164, 108094. [Google Scholar] [CrossRef]
- Sunde, C.; Avdic, S.; Pázsit, I. Classification of two-phase flow regimes via image analysis and a neuro-wavelet approach. Prog. Nucl. Energy 2005, 46, 348–358. [Google Scholar] [CrossRef]
- Ulbrich, R.; Krótkiewicz, M.; Szmolke, N.; Anweiler, S.; Masiukiewicz, M.; Zajac, D. Recognition of two-phase flow patterns with the use of dynamic image analysis. Proc. Inst. Mech. Eng. Part. E J. Process. Mech. Eng. 2002, 216, 227–234. [Google Scholar] [CrossRef]
- Fu, T.; Ma, Y.; Funfschilling, D.; Li, H.Z. Bubble formation and breakup mechanism in a microfluidic flow-focusing device. Chem. Eng. Sci. 2009, 64, 2392–2400. [Google Scholar] [CrossRef]
- Yue, J.; Chen, G.; Yuan, Q.; Luo, L.; Gonthier, Y. Hydrodynamics and mass transfer characteristics in gas-liquid flow through a rectangular microchannel. Chem. Eng. Sci. 2007, 62, 2096–2108. [Google Scholar] [CrossRef]
- Dang, M.; Hassan, I.; Muwanga, R. Adiabatic two phase flow distribution and visualization in scaled microchannel heat sinks. Exp. Fluids 2007, 43, 873–885. [Google Scholar] [CrossRef]
- Vázquez Blanco, M.; Grosso, O.; Bellido, C.A.; Iavícoli, O.R.; Berensztein, C.S.; Ruda Vega, H.; Lerman, J. Effect of flow on complex biological macromolecules in microfluidic devices. Biomed. Microdevices 2001, 3, 225–238. [Google Scholar]
- Liang, F.; Sun, Y.; Yang, G.Y.; Song, L. Gas-liquid two-phase flow rate measurement with a multi-nozzle sampling method. Exp. Therm. Fluid Sci. 2015, 68, 82–88. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, Y. Development of a robust image processing technique for bubbly flow measurement in a narrow rectangular channel. Int. J. Multiph. Flow 2016, 84, 217–228. [Google Scholar] [CrossRef]
- Amoresano, A.; Langella, G.; Di Santo, M.; Iodice, P. Advanced Imaging Techniques for Multiphase Flows Analysis. J. Phys. Conf. Ser. 2017, 882. [Google Scholar] [CrossRef]
- Masiukiewicz, M.; Anweiler, S. Two-phase flow structure assessment based on dynamic image analysis. Flow Meas. Instrum. 2019, 65, 195–202. [Google Scholar] [CrossRef]
- Anweiler, S.; Masiukiewicz, M. Application of stereology for two-phase flow structure validation in fluidized bed reactors. Therm. Sci. 2016, 20, 1199–1208. [Google Scholar] [CrossRef] [Green Version]
- Hughes, D.W. Two-Phase Flow and Heat Transfer; Butterworth, D., Hewitt, G.F., Eds.; Harwell Series; Oxford University Press: Oxford, UK, 1977; p. 514. [Google Scholar]
- Andruszkiewicz, A.; Hans-Dieter, S. Ultrasonic measurements of flow in two-phase liquid-gas systems. Part I, The method for measurements. Chem. Process. Eng. 2008, 29, 113–128. [Google Scholar]
- De Castro Teixeira Carvalho, F.; de Melo Freire Figueiredo, M.; Serpa, A.L. Flow pattern classification in liquid-gas flows using flow-induced vibration. Exp. Therm. Fluid Sci. 2020, 112, 109950. [Google Scholar] [CrossRef]
- Shanthi, C.; Pappa, N. An artificial intelligence based improved classification of two-phase flow patterns with feature extracted from acquired images. ISA Trans. 2017, 68, 425–432. [Google Scholar] [CrossRef] [PubMed]
- Taitel, Y.; Bornea, D.; Dukler, A.E. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J. 1980, 26, 345–354. [Google Scholar] [CrossRef]
- Kaichiro, M.; Ishii, M. Flow regime transition criteria for upward two-phase flow in vertical tubes. Int. J. Heat Mass Transf. 1984, 27, 723–737. [Google Scholar] [CrossRef]
- Pietrzak, M. Flow patterns and volume fractions of phases during liquid-liquid two-phase flow in pipe bends. Exp. Therm. Fluid Sci. 2014, 54, 247–258. [Google Scholar] [CrossRef]
- Ruspini, L.C.; Marcel, C.P.; Clausse, A. Two-phase flow instabilities: A review. Int. J. Heat Mass Transf. 2014, 71, 521–548. [Google Scholar] [CrossRef]
- Bhutani, G.; Brito-Parada, P.R.; Cilliers, J.J. Polydispersed flow modelling using population balances in an adaptive mesh finite element framework. Comput. Chem. Eng. 2016, 87, 208–225. [Google Scholar] [CrossRef] [Green Version]
- Aarsnes, U.J.F.; Ambrus, A.; Di Meglio, F.; Karimi Vajargah, A.; Morten Aamo, O.; Van Oort, E. A simplified two-phase flow model using a quasi-equilibrium momentum balance. Int. J. Multiph. Flow 2016, 83, 77–85. [Google Scholar] [CrossRef]
- Masiukiewicz, M.; Anweiler, S. Two-phase flow phenomena assessment in minichannels for compact heat exchangers using image analysis methods. Energy Convers. Manag. 2015, 104, 44–54. [Google Scholar] [CrossRef]
- Underwood, E.E. Quantitative Stereology for Microstructural Analysis. In Microstructural Analysis; Springer: Boston, MA, USA, 1973; pp. 35–66. [Google Scholar]
- Ondracek, G. Key position of stereology in quantitative microstructure-correlations of multiphase materials. Acta Stereol. 1982, 1, 5–21. [Google Scholar]
- Wojnar, L. Image Analysis: Applications in Materials Engineering, 1st ed.; CRC Press: Boca Raton, FL, USA, 1998; ISBN 9780849382260. [Google Scholar]
- Gupta, S.; Sarkar, J.; Kundu, M.; Bandyopadhyay, N.R.; Ganguly, S. Automatic recognition of SEM microstructure and phases of steel using LBP and random decision forest operator. Meas. J. Int. Meas. Confed. 2020, 151, 107224. [Google Scholar] [CrossRef]
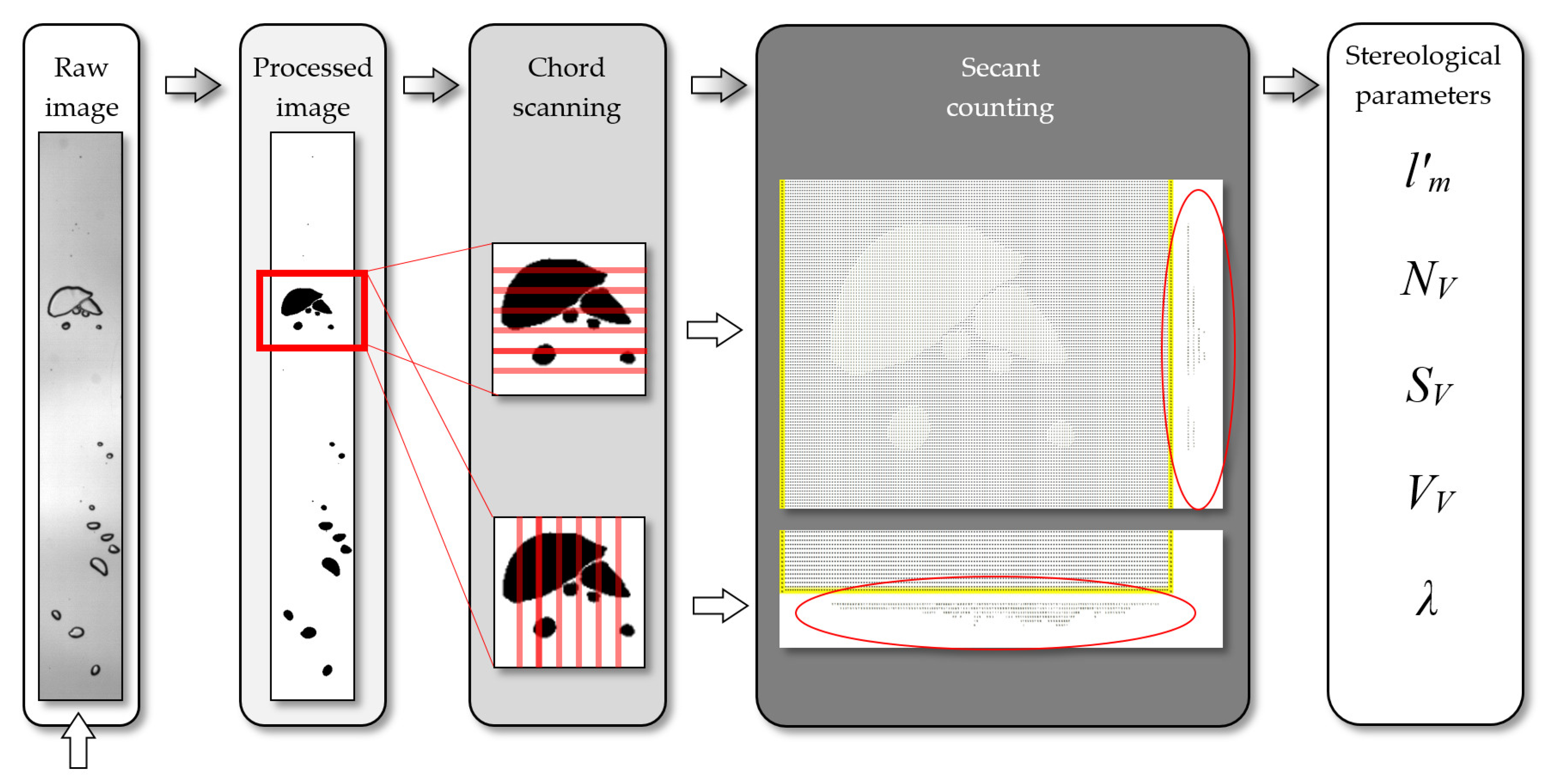

| Class Interval of Chord Lengths (Vertical) | 1–3 | 4–6 | 7–9 | 10–12 | 13–15 | 16–18 | 19–21 | 22–24 | 25–27 | 28–30 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Class No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Midpoint of the class li′ | 2 | 5 | 8 | 11 | 14 | 17 | 20 | 23 | 26 | 29 | |
| Count ni′ | 55 | 121 | 152 | 209 | 250 | 127 | 43 | 25 | 4 | 5 | 991 |
| Calculated chord length ni′ li′ | 110 | 605 | 1216 | 2299 | 3500 | 2159 | 860 | 575 | 104 | 145 | 11,573 |
| Actual chord length | 108 | 621 | 1233 | 2318 | 3521 | 2114 | 854 | 568 | 105 | 142 | 11,584 |
| Image Scanning Parameter | Symbol | Value | Unit |
|---|---|---|---|
| total length of secants in the projection | L′ | 303,104 | pixels |
| total length of the secants on the cross-section | L | 354,291 | pixels |
| total number of chords obtained from the projection | n′c | 1880 | pcs. |
| total number of chords obtained from the section | nc | 7609 | pcs. |
| total length of the chords obtained from the projection | Σ′nili | 23,161 | pixels |
| total length of the chords obtained from the section | Σnili | 119,540 | pixels |
| Stereological Parameter | wL0 (m/s) | wG0 (m/s) | |||
|---|---|---|---|---|---|
| 0.0056 | 0.0111 | 0.0222 | 0.0444 | ||
| volume fraction VV (%) | 0.0111 | 3.8 | 5.4 | 11.9 | 16.7 |
| 0.1111 | 3.3 | 6.6 | 7.5 | 14.1 | |
| 1.1111 | 0.2 | 0.2 | 0.3 | 0.6 | |
| interfacial surface SV (m2/m3) | 0.0111 | 42.7 | 107.0 | 213.7 | 256.9 |
| 0.1111 | 76.2 | 106.6 | 75.8 | 125.6 | |
| 1.1111 | 157.3 | 121.8 | 150.0 | 233.9 | |
| number of objects NV (pcs/dm3) | 0.0111 | 267.4 | 802.7 | 1574.6 | 1822.5 |
| 0.1111 | 579.5 | 761.3 | 445.0 | 678.4 | |
| 1.1111 | 1427.6 | 1071.4 | 1304.0 | 1979.3 | |
| mean chord l′m (m) | 0.0111 | 0.0060 | 0.0033 | 0.0036 | 0.0041 |
| 0.1111 | 0.0032 | 0.0040 | 0.0070 | 0.0085 | |
| 1.1111 | 0.0010 | 0.0014 | 0.0015 | 0.0018 | |
| free distance λ (m) | 0.0111 | 0.1205 | 0.0708 | 0.0313 | 0.0223 |
| 0.1111 | 0.1058 | 0.0612 | 0.0591 | 0.0298 | |
| 1.1111 | 0.1373 | 0.1365 | 0.1017 | 0.0553 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masiukiewicz, M.; Anweiler, S. Precise Evaluation of Gas–Liquid Two-Phase Flow Pattern in a Narrow Rectangular Channel with Stereology Method. Energies 2021, 14, 3180. https://doi.org/10.3390/en14113180
Masiukiewicz M, Anweiler S. Precise Evaluation of Gas–Liquid Two-Phase Flow Pattern in a Narrow Rectangular Channel with Stereology Method. Energies. 2021; 14(11):3180. https://doi.org/10.3390/en14113180
Chicago/Turabian StyleMasiukiewicz, Maciej, and Stanisław Anweiler. 2021. "Precise Evaluation of Gas–Liquid Two-Phase Flow Pattern in a Narrow Rectangular Channel with Stereology Method" Energies 14, no. 11: 3180. https://doi.org/10.3390/en14113180
APA StyleMasiukiewicz, M., & Anweiler, S. (2021). Precise Evaluation of Gas–Liquid Two-Phase Flow Pattern in a Narrow Rectangular Channel with Stereology Method. Energies, 14(11), 3180. https://doi.org/10.3390/en14113180