Comprehensive Model for Real Battery Simulation Responsive to Variable Load

Abstract

This paper proposes a battery voltage model that is suitable for variable operation. The model combines the features of the Kinetic Battery Model (KiBaM) and voltage model (VM), and it improves the accuracy and quality of the solution, addressing four characteristics of operation: charging, discharging, rest after charge, and rest after discharge. This model will be known as 4-KiVM and shows low impact on computational burden. The proposed model can keep track of the voltage even when the load is inverted or turned off. To calibrate and validate the model, a NASA-provided dataset was used composed of a battery with variable charges and discharges, simulating real applications. A metaheuristic method based on tabu search is used to extract constants from this dataset and validate this hybrid model. In addition, a comparison of performance of the 4-KiVM against KiBaM, VM, and the electric circuit model (ECM) was made, showing its advantages. The results of the simulations showed a good prediction of the battery voltage response and SOC prediction in random (variable) use.

1. Introduction

Through the years, battery applications have gained attention toward power system application and mobility solutions. For instance, it is known that batteries implementation in Electric Vehicles (EVs) around the world had significant growth over the last few years [1]. It is estimated that there will be over 250 million EVs by 2030 [2]. In addition, batteries have been requested for the support of renewable sources of energy [3] such as solar photovoltaic and wind, with the possibility for improvement of energy quality considering loss reduction, voltage regulation, load following, and peak shaving [4,5]. For type of technology, lithium-ion batteries are the most used, as they are lightweight, with high energy density, small size, and with high duration [1,6,7,8].

As battery applications grow, so does the requirement for more detailed models to accurately represent the behavior regarding voltage, current, degradation, state of health (SOH), and state of charge (SOC), SOC prediction being one of the most widespread applications of battery models. Nevertheless, battery evaluation based only on the SOC provided by the energy injection is quite imprecise [9]; the review made in [10] shows some of the approaches seeking a more accurate representation of batteries behavior. These approaches are related to empirical models [11,12], abstract models [8,13,14], physics-based models [15,16], and hybrid models [17]. Hybrids models seek to use two or more approaches to improve results [17], each one with tradeoffs.

Physical models describe the structure of the battery materials and the chemical reactions that happen inside their cells. These are models with high accuracy but require a high number of parameters to run properly. In addition, they have a high complexity and may require extensive computational time for simulation. Examples can be found in [15,16].

Empirical models are based on empirical parameters. They are also called black boxes, and they try to mathematically define a transfer function from the outputs and inputs of the system. Their accuracy varies but is usually lower than other methods. Examples can be found in [11,12].

Abstract models are very simple and practical. These models offer an alternative way to visualize the problem while maintaining the dynamics of the battery. Their accuracy and complexity are variable. Through the studied models, the KiBaM based on [10] has been normally used due to its speed and application in commercial software for simulation as Homer [11]. In 1993, researchers explained the phenomena that went far beyond estimating SOC with just two constants and simple equations. The original KiBaM has limitations (such as lack of voltage response), but it has been proven and studied in multiple articles [12,13,14,15].

Electric Circuit models (ECMs) are also part of abstract models. They are the most studied and complete model used in the literature. Their accuracy varies according to the mathematical order in the formulation of the circuit model. Many papers use ECM models for their simplicity, even in lower orders given the good accuracy presented [7,8,16,17,18,19,20]. As temperature and aging are included, the accuracy is increased [1,8,9,17]. However, as commented by [21], ECMs take extended time to compute when compared to KiBaM, but they have greater precision.

The search for a comprehensive model that allows fast simulation and accurate representation of batteries’ electrical behavior is a challenging task. It is seen that the KiBaM model had good characteristics in speed and simplicity but requires some improvements in accuracy to be comparable to the ECM model. In addition, it is seen that the calibration process for batteries tends to evaluate fixed behaviors. This brings the necessity to present a model that is able to respond for alternating current, being suitable to real-world performance.

To achieve these objectives, this paper proposes a more detailed model for battery simulation, adding to KiBaM a voltage model (VM) that can be used in several applications. The model considers an iterative process for selection of the battery parameters and reduction of errors, and it combines four characteristics of operation: charging, discharging, rest after charge, and rest after discharge. For further reference, the proposed model will be called the 4-Ki-VM model. It should be noted that although some works focus on SOC prediction for the determination of batteries’ performance (even ECM), this work considers the modeling of voltage behavior more important. Voltage behavior has an important impact on the SOC prediction capabilities of the system. Nevertheless, as SOC can be calculated by voltage variables, the model could be further extended applying state estimators.

The proposed work has the following features:

• Fast and accurate representation of battery behavior for simulation purposes considering electrical impact, and variability in the cycling process.
• An improvement of the KiBaM model currently applied in commercial software as Homer, by considering voltage impact in battery degradation and cycling process.
• An algorithm for error reduction of the parametrization of battery variables related to cycling behavior, based on an iterative process.
• A novel combination of KiBaM and VM is proposed and called 4-Ki-VM. It uses four KiBaM cores and allows describing battery behavior more accurately than KiBaM with low computational cost compared to ECM models.

The model is validated and calibrated with a series of open-source data provided by NASA, being easy for reproduction and able for comparison against other studies using the same data.

This paper is presented as follows: Section 2 discusses the key factors related to battery behavior required for simulation purposes, Section 3 presents the Kinetic Battery Model, Section 4 adds to the proposed contribution by explaining ECM models, Section 5 presents the optimization process for the selection of parameters, Section 6 presents the proposed model, Section 7 validates the results, and Section 8 discusses the model features.

2. Battery Behavior

Batteries’ lifetimes are limited due to degradation and working conditions. For instance, a battery works only within a defined voltage range. In the case of lithium-ion batteries, the interval from 3 to 4.2 V is very common. Using the battery outside this voltage limit strongly affects the lifetime.

When the cell is not in use, the Open Circuit Voltage (OCV) reflects the amount of stored energy. For example, when the measured OCV is 4.2 V, the battery is full, and if it is 3 V, the battery is empty. Therefore, it is possible to measure the charging state by reading the voltage, but for that, the battery must not be in use, so this method is not practical. In addition, the battery must be resting for some time, because the voltage fluctuates after use.

During intense use, the voltage fluctuates beyond the joule effect, indicating a wrong charging state. During a discharge, for example, the voltage reflects an SOC smaller than the real one, it being common for a battery with 3 V to have 10–20% of charge left on it. To keep using the battery and access this remaining energy, the load must be disconnected to provide a slow voltage rising. Batteries’ behavior are related to two main phenomena:

Apparent Capacity: The battery capacity varies according to the intensity of use. If the load is increased, the capacity is decreased both in charge and in discharge.

Recovery effect: After use, the unavailable capacity slowly returns to the battery.

When the battery is being charged and reaches its maximum voltage, due to the apparent capacity, it will be not fully charged and cannot keep charging. This can happen at 60–80% capacity at fast charging.

To keep the battery charging after 4.2 V, the constant current–constant voltage (CC-CV) method is used (Figure 1). The battery is charged with CC until it reaches maximum voltage. At this point, the current slows down exponentially to keep maximum voltage.

During CC charge, the voltage and power rise 40% until peaking at 4.2 V, when the power starts to decrease exponentially. This power limitation also happens during discharge because the current is limited by the manufacturer of the battery.

Those limitations in power and capacity change with battery degradation. As the battery is cycling, not only the capacity changes but also the internal resistance and the response to transient (recovery effect) is different. When aged, the battery takes more time to do a complete charge and holds less energy compared to a new one. Furthermore, the required features of the battery model are to determine the following:

• Time of charging and power.
• Availability of energy during discharge.
• Battery charge process during CV.
• Maximum allowed power output.
• Impact of degradation in power injection.

These criteria can be found in some datasheets and papers [18]. An issue found for validation is the common use of simple reference curves with constant charging and discharging tests. These curves do not reflect reality, as in daily use, the battery does not experience complete and uninterrupted cycles with constant current. It is common in real operation to stop in the middle of the charge and start discharging. However, to use the model in these real switching loads, a validation for these cases is required. If there is no validation, there is no guarantee that the model response is correct. In this paper, the 4-Ki-VM model will be developed based on the previous literature, proposing new ideas, and it will be validated through real use.

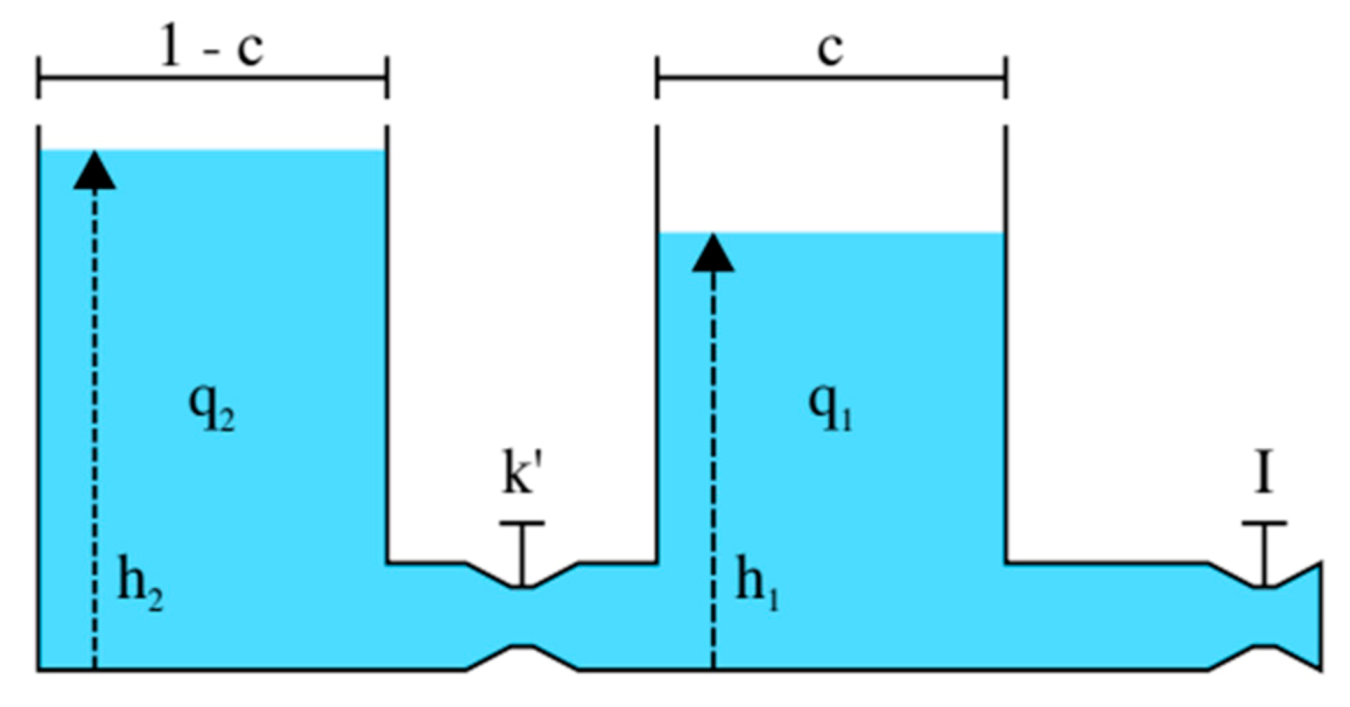
3. Kinetic Battery Model (KiBaM)

The KiBaM was developed by Manwell and McGowan in 1993 to emulate lead-acid batteries [10]. It is a simple and effective model that works well to simulate lithium-ion and other chemistries [22,23,24]. Only two constants rule the model, and it can emulate state of charge (SOC) fluctuations. The KiBaM model is presented in Figure 2.

According to Figure 2, the KiBaM transforms the battery into two reservoirs of size c and (1-c), and the energy is represented as water. One of the water tanks represents the charge available to use ($q_1$), and the other one represents the unavailable charge $q_2$. Constant ${\mathrm{k}}^{\prime }$ is a restriction to the fluid flow.

Considering that $q_1$ is emptied fast, water will remain in the system, but there will be no energy to use, representing apparent capacity phenomena. If the discharge stops, the water will start rising, modeling the recovery of charge.

In this model, the SOC, total, available, and unavailable capacity can be expressed as follows:

$$\left\{\begin{array}{l}{\mathrm{C}}_{\mathrm{Avaliable}}={\mathrm{C}}_{\mathrm{Total}}-{\mathrm{C}}_{\mathrm{Unvaliable}}\\ {\mathrm{C}}_{\mathrm{Total}} \left(\mathrm{t}\right)={\mathrm{q}}_1\left(\mathrm{t}\right)+{\mathrm{q}}_2\left(\mathrm{t}\right)\\ {\mathrm{C}}_{\mathrm{Unavaliable}}=\left(1- \mathrm{c}\right)\left({\mathrm{q}}_2\left(\mathrm{t}\right)-{ \mathrm{q}}_1\left(\mathrm{t}\right)\right)\\ \mathrm{SOC} \left(\%\right)={\mathrm{C}}_{\mathrm{Avaliable}}/{\mathrm{C}}_{\mathrm{Total}}\end{array}\right.$$

(1)

where ${\mathrm{q}}_1$ is the charge in the available water tank, ${\mathrm{q}}_2$ is the charge in the unavailable water tank, and c is the distribution of capacity of the battery. This two-reservoirs system can be described by a set of Bernoulli’s Equation (2), which are the core of the model:

$$\{\begin{array}{r}{\mathrm{q}}_1{\left(\mathrm{t}\right)=\mathrm{q}}_{1,0}{\mathrm{e}}^{-{\mathrm{k}}^{\prime }\mathrm{t}}+\frac{({\mathrm{q}}_0{\mathrm{k}}^{\prime }\mathrm{c}-\mathrm{I})(1-{\mathrm{e}}^{-{\mathrm{k}}^{\prime }\mathrm{t}})}{{\mathrm{k}}^{\prime }}\\ -\frac{\mathrm{Ic}({\mathrm{k}}^{\prime }\mathrm{t}-1+\mathrm{e}-{\mathrm{k}}^{\prime }\mathrm{t})}{{\mathrm{k}}^{\prime }}\\ {\mathrm{q}}_2{\left(\mathrm{t}\right)=\mathrm{q}}_{2,0}{\mathrm{e}}^{-{\mathrm{k}}^{\prime }\mathrm{t}}{+\mathrm{q}}_0(1-\mathrm{c})(1-{\mathrm{e}}^{-{\mathrm{k}}^{\prime }\mathrm{t}})\\ -\frac{\mathrm{I}(1-\mathrm{c})({\mathrm{k}}^{\prime }\mathrm{t}-1+{\mathrm{e}}^{-{\mathrm{k}}^{\prime }\mathrm{t}})}{{\mathrm{k}}^{\prime }}\end{array}$$

(2)

where ${\mathrm{q}}_{1,0}$ and ${\mathrm{q}}_{2,0}$ are the amount of charge at $\mathrm{t}=0$, and ${\mathrm{q}}_0={\mathrm{q}}_{1,0}+{\mathrm{q}}_{2,0}$.

The representation of Figure 2 also explains CC-CV charging, but the model output is in SOC (%) metrics, so it needs to be paired with some voltage model to consider voltage impact, as proposed in this paper.

3.1. Voltage Model (VM)

For most systems, the battery terminal voltage is the predilect and most useful information for battery control, as it rules battery charge and discharge limits. It is common to use the KiBaM with an $n^{th}$-order equation to interpolate the voltage response; however, this approach is hard to manipulate and change the curve characteristics. The method used is composed by a set of equations that are fast to compute and offer four constants to control the curve characteristics.

Using a generic lithium-ion battery as an example, the voltage behavior during discharge can be simplified by a curve as shown in Figure 3, where initially the voltage suffers an exponential drop, followed by a nominal zone [25].

The modeling of voltage impact presented in Figure 3 is defined in Equation (3). It should be noted that this model only operates inside the nominal voltage range, and disregard temperature impact.

$${\mathrm{V}}_{\mathrm{batt}}={\mathrm{E}}_0- \mathrm{K}\frac{\mathrm{Q}}{\mathrm{Q} - \mathrm{it}}\times \mathrm{t}+\mathrm{Aexp}\left(- \mathrm{B} \mathrm{it}\right)-\mathrm{R}\times \mathrm{i}$$

(3)

where

${\mathrm{V}}_{\mathrm{batt}}=$ battery terminal voltage ($\mathrm{V})$

${\mathrm{E}}_0=$ battery constant voltage ($\mathrm{V})$

$\mathrm{K} =$ polarization voltage ($\mathrm{V}$)

$\mathrm{A} =$ exponential zone amplitude ($\mathrm{V})$

$\mathrm{B} =$ exponential zone time constant inverse ($\mathrm{Ah}{)}^{-1}$

$\mathrm{R} =$ internal resistance (Ω)

$\mathrm{i} =$ battery current

$\mathrm{Q} =$ battery capacity $\left(\mathrm{Ah}\right)$

$\mathrm{it} =\left(1- \mathrm{SOC}\right)\times \mu$, the energy taken from battery (Ah)

$\mu =$ SOC equalizer.

This model is a variation of [25,26] and follows the same principle. By changing ${\mathrm{E}}_0, \mathrm{A},\mathrm{B}$, and $K$, the voltage curve can be easily manipulated. The accuracy of the output curve depends on the resistance model considered. Thus, a variable resistance is normally used.

The SOC calculated on Equation (1) relies on the KiBaM’s capacity and c constants, which describe the apparent capacity and recovery effect. With different constants for charge and discharge, not all values of c allow smooth voltage transition from charge to discharge constants. Therefore, it is necessary to have a parameter to balance model transition; otherwise, voltage spikes will appear. In this scenario, $\mu$ was proposed to make the model swap more uniformly and create an SOC free from the KiBaM’s constant c. Without the need for constant c from KiBaM, the model becomes more precise.

3.2. SOC Forecast

To estimate the energy stored in the battery, its necessary to sum the water volumes in the KiBaM tanks, according to Equation (4).

$$Total stored energy \left(t\right)=q_1\left(t\right)+q_2\left(t\right)-C_{extra}$$

(4)

$q_1\left(t\right)$ and $q_2\left(t\right)$ are obtained with Equation (2). Meanwhile, $C_{extra}$ expresses the extra capacity in the KiBaM tanks, since the model is more stable when the battery is simulated with this parameter.

Equation (1) calculates the apparent SOC and defines when there is no more available energy for use. Nevertheless, the model is not directly calibrated for this equation, as it does not consider the effects of internal battery resistance. To estimate the remaining usable time, the voltage must be projected until it intercepts a limit, as shown in Figure 4. Therefore, it is possible to identify the remaining usable energy according to the predicted load profile. This SOC estimation method requires that the battery and the model selected are in synchrony. This process is difficult to implement and sensible to noise.

SOC estimation is a common battery concern. The research in [27] presents a novel approach for calculating the remaining discharge energy of lithium-ion batteries. A load prediction algorithm is prepared using a Markov model and data clustering. It used a second-order ECM model associated with a thermal model to avoid high complexity problems.

In [28], a KiBaM–ECM hybrid model is presented for a lead-acid home storage systems. For this approach, the KiBaM is used for SoC determination, and not for counting ampere-hours (Ah) as usual. Then, an ECM model simulates the current–voltage behavior of the system.

To avoid noise in SOC estimation of lithium-ion batteries, references [29,30] develops novel methods for noise immunity. Regarding accuracy and complexity, they used first-order RC models in both battery models.

Reference [18] proposes a novel method for online SOC estimation for lithium-ion batteries. The model features high accuracy and low complexity. To achieve high accuracy, a particle swarm optimization (PSO) is used to optimize model parameters. A Kalman Filter extended model is used for SOC estimation due to being one of the most used models for LIBs. In addition, the cited method is compared with 1RC, 2RC, 3RC, and PNGV, which are the most common EMCs models.

The use of EKF (Extended Kalman Filters) is the most adequate method to solve this SOC prediction problem. It provides an optimal state estimator using the minimum square error with the information obtained from the model and considers the assumptions of noise [31,32]. The use of state estimators to monitor SOC is almost mandatory, but it is not the objective of this paper, as accuracy in description relies on voltage determination. Thus, this SOC determination could be further extended for future work considering EKF or similar tools.

4. Electric Battery Model (ECM)

ECMs are known for their simplicity and performance, in addition to being very flexible in their implementation. Different circuits can be used to describe batteries [8,29,31,33,34]. Based on the work done by [28,35], a second-order RC circuit was implemented, using Coulomb counting to estimate SOC. The advantage of using this circuit is the balance between performance and precision. Adding more order to the RC circuits increases the accuracy but also the computational cost. Thus, second-order implementation presents a balance between computational burden and precision, and the 4-Ki-VM would try to compare the performance against this approach. Figure 5 presents the ECM model.

Applying Kirchhoff equations to this circuit, Equation (5) can be obtained from [28]:

$$\left\{\begin{array}{c}{V}_{C_s}\left(t+1\right)=V_{C_s}\left(t\right)\times e^{\left(\raisebox{1ex}{$-T$}\!\left/ \!\raisebox{-1ex}{$C_s\times R_s$}\right.\right)}+R_S\times I_{Batt}\left(t\right)\times (1-e^{\left(\raisebox{1ex}{$-T$}\!\left/ \!\raisebox{-1ex}{$C_s\times R_s$}\right.\right)})\\ V_{C_L}\left(t+1\right)=V_{C_L}\left(t\right)\times e^{\left(\raisebox{1ex}{$-T$}\!\left/ \!\raisebox{-1ex}{$C_L\times R_L$}\right.\right)}+R_L\times I_{Batt}\left(t\right)\times (1-e^{\left(\raisebox{1ex}{$-T$}\!\left/ \!\raisebox{-1ex}{$C_L\times R_L$}\right.\right)})\\ V_{\begin{array}{c}Batt\\ \end{array}}=V_{OC}\left(SOC\right)-V_{C_L}\left(t\right)-V_{C_s}\left(t\right)-R_{series}\times I_{Batt}\end{array}\right.$$

(5)

where T represents the timestep and $t$ represents the simulation time. $V_{C_L}$ and $V_{C_s}$ are the transient response with long- and short-time duration (voltage across $C_L$ and $C_s$). $I_{Batt}$ is defined as positive for charging and negative for discharging.

For this application, the capacitors and resistors are variable and change their value according to the battery SOC. This approach increases the model’s accuracy with little computational cost [21].

SOC predictions are very important and require good battery models; ECMs have a diverse range of add-ons that assist in the task of estimating SOC. On this front, many techniques have already been developed as explained in Section 3.2. Synchronizing the model with the battery and evaluating the SOC in real time are not simple tasks, especially when uncertainties are considered in the measurements. The objective of this paper is to compare the performance of the voltage prediction in different models. This directly impacts the SOC estimation error; therefore, there is no need to use more complex ECM models.

5. Proposed Model

One of the most complete and simple models used in the literature is the ECM. The ECM incorporates and simulates the most important characteristics of batteries, making it possible to increase the accuracy by compromising performance. However, as commented by [21], even the simple 2° order ECM has a longer runtime than KiBaM but with greater precision. To increase the accuracy of the KiBaM approach, achieving a performance comparable to ECM, the 4-Ki-VM was developed.

As [4] explains in depth, a lot of papers in the battery model literature seek to create complete models to simulate battery response for charge and discharge [18,28,36,37,38,39,40,41,42]. However, batteries have very different characteristics if they are being charged or discharged, so it is difficult to find a solution that works both ways. The solution proposed is to use four different models to gain precision, one representation for each kind of use; they are charge, discharge, rest after charge, and rest after discharge.

For each type of use, a different KiBaM core rules the behavior of the battery, and the 4-Ki-VM has an optimized core for each use scenario. The only constant maintained through the cores is the capacity and the KiBaM’s ${\mathrm{q}}_1$ and ${\mathrm{q}}_2$. This four-way model can be seen in Figure 6.

The hybrid 4-Ki-VM is robust and fast to compute. It uses KiBaM simple multiplications to express battery behavior [15]. A great advantage of splitting this hybrid model in four representations is that just one core works per iteration. Thus, there is almost no increase in the computational effort for this solution, even though it is apparently more complex. The only additional task for the CPU is to select the core to run the simulation based on the current value. This method does not require an interpolation.

6. Parameter Estimation

There are a lot of efficient numerical approaches for finding parameters of big and complex systems. Most of them are based on metaheuristics and mimic nature behavior by improving in each iteration based on a fitness function [43,44]. In this paper, a metaheuristic process is used, which was inspired by a tabu search [45]. First, for the 4-Ki-VM, all cores were considered equal and the parameters are taken from [13,15]. The ECM initial parameters are taken from [35]. This initial approximation presented a high error but it helped to speed the iterative process, since the models are similar and the parameters have the same order of magnitude. To improve these initial models, a python code changed every constant by a random value with probabilistic Gaussian distribution and calculated the error with Equation (6). If the model improved after randomization, the random parameters would compose the new base for iteration.

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum }_0^n{\left(Reference Voltage-Model prediction\right)}^2}$$

(6)

As [46] explains, RMSE is usually better at revealing model performance differences. The metaheuristic loop can be seen in Figure 7.

The parameters are randomized following a normal distribution, which improves efficiency by reducing the risk of large variations. This loop has as a stopping criterion a number of 8000 iterations without improvement; then, the base constants are randomized. This parameter searching using randomization is very well known [30] and gave good results for being simple and flexible to implement. Future work can enhance the process to make it faster. It should be noted that this metaheuristic method does not affect model performance.

Model Extraction

To use as a reference and evaluate the simulation error, a set of data available at the NASA Data Repository was applied [47]. These open-source data are high quality and avoid the need for practical testes, helping in cases of low resources [24]. An 18650 Li-ion battery (Identified as RW9) was continuously operated using a sequence of charging and discharging currents between −4.5 and 4.5 A. As described in [48], each variable use (random use) lasts up to 5 min. After 1500 periods (about 5 days), a series of reference charging and discharging cycles were performed to provide reference benchmarks. The battery was used for over 5 months, and the data logged each second contain the voltage, current, temperature, and time. More experiments with this dataset are found in [47].

To calibrate the model, a virtual battery was created, and the 4-Ki-VM, the ECM, and the KiBaM-VM were submitted to the loads in the NASA dataset. The predicted voltage and the real voltage were compared each second, and the error was calculated as shown in Equation (6). There are 11 h of reference data extracted from the NASA dataset, divided in five tests, completing the benchmark:

Charge test: The battery was charged from 3.2 V with CC of 1 A and CV of 4.2 V.

Discharge test: The battery was discharged from 4.2 V with CC of 1 A until 3.2 V.

Pulse Charge test: The battery was charged from 3.2 V with CC of 1 A for 10 min and rest for 20 min multiple times, until 4.2 V.

Pulse Discharge test: The battery was discharged from 4.2 V with CC of 1 A for 10 min and rest for 20 min multiple times, until 3.2 V.

Alternating test: The battery was used with CC from −4.5 A to 4.5 A for 5 min or until a voltage limit.

With the reference curves provided in [47], a few virtual batteries were created, the metaheuristic process was initiated, and the KiBaM, ECM, and 4-Ki-VM were iterated for 3 h. This time was overstated to guarantee the best possible results for each model, but 2 h should be enough if a good first approximation is provided. The parameters found can be seen in

Table 1. Model parameters.

		4-Ki-VM				KiBaM-VM
	Parameter	Charge	Discharge	Rest Charge	Rest Discharge	All Scenarios
KiBaM	c	0.5394	0.3494	0.4350	0.3987	0.0155
	k’	0.0078	0.0062	0.0075	0.0071	0.0064
	C	7200 As				7200 As
Voltage Model	A	0.3648	0.4671	0.3609	0.6761	0.6683
	B	0.3732	1.9196	1.5027	1.6687	1.5118
	K	0.0384	0.0479	0.0128	0.0172	0.0338
	$E_0$	3.7434	3.7990	3.7893	3.7127	3.7428
	µ	0.9752	0.9008	1.2344	0.8815	0.0762

and Equation (7).

The constants are very different from the charge to discharge cores; for example, the VM parameter B grows more than four times from one 4-Ki-VM core to another. This big change happened with a lot of parameters and made the software take a long time to search and to estimate the constants for this new 4-Ki-VM. Future batteries can be modeled using Table 1 and be faster to iterate. Thus, this method not only allows the simulation but also the parametrization of new batteries. The battery capacity was improved along the parameters to increase accuracy. The ECM was simulated with a capacity of 550As and the model is ruled by the following equations:

$$\{\begin{array}{c}{\mathrm{R}}_0(\mathrm{SOC})=0.157\times e^{-13.893\times SOC}+0.101\\ {\mathrm{R}}_{\mathrm{S}}(\mathrm{SOC})=0.518\times e^{-13.349\times \mathrm{SOC}}+0.393\\ {\mathrm{R}}_{\mathrm{L}}(\mathrm{SOC})=4.701\times e^{-123.055\times \mathrm{SOC}}+0.065\\ {\mathrm{C}}_{\mathrm{S}}(\mathrm{SOC})=-578.902\times e^{-3.363\times \mathrm{SOC}}+1538.1\\ {\mathrm{C}}_{\mathrm{L}}(\mathrm{SOC})=-5894.827\times e^{-36.19\times \mathrm{SOC}}+6801.7\\ {\mathrm{V}}_{\mathrm{OCV}}(\mathrm{SOC})=0.32\times {\mathrm{SOC}}^3-0.1178\times {\mathrm{SOC}}^2\\ +0.2156\times \mathrm{SOC}+3.685-1.031\times e^{-35\times \mathrm{SOC}}\end{array}$$

(7)

Capacity is different from the KiBaM and the ECM simulation due to different combination in this model’s parameter. This capacity increase in the KiBaM should be accounted when calculating the remaining energy; as commented in Section 5, the $C_{extra}=1700 As$.

Resistance was approximated and taken from the pulse tests. Once the current is zero in multiple moments, the voltage drop gives the resistance value for various SOC. This resistance approximation was improved in the Figure 7 process, which raised or lowered all values together to avoid a ripple. This approach is based on a reduction of the simulation error in the Figure 4 loop rather than representing real resistance estimation. The CV charging was done by numerically searching a current value that did not surpass the voltage limit in the next iteration.

7. Results

The comparison of performance for the ECM, the KiBaM (with voltage adjust as [15]), and the proposed 4-KiVM models are presented in Figure 8. From Figure 8, the line in black shows the model response to the load, and the blue line shows the reference voltage. The initial SOC for each model and test was acquired prior to simulation.

The single core KiBaM results showed high distortion in the voltage simulation. This lack of precision is more pronounced in the Discharge tests (Figure 8g–i), since the model only has one set of constants to choose from, and thus, it cannot perform equally in all tests. It is remarkable that the KiBaM-based models have an advantage in predicting current behavior while CV is charging, as seen in Figure 8a–c, due the selection of constant k’ for this test.

For these simulation results, there is a major source of error. During parameter estimation, was found that if the models from Figure 8 were calibrated without the (m)–(o) tests, the (a)–(l) result curves were fitted with improved accuracy as seen in

Table 2. Error analysis.

Model	RMSE (mV)
	Discharge	Charge	Pulse Charge	Pulse Discharge	Alternating
KiBaM	1.06	1.05	0.62	0.93	0.9
ECM	0.93	0.54	0.83	0.65	0.62
4-Ki-VM	0.73	0.36	0.47	0.55	0.62
KiBaM *	0.91	0.56	0.55	0.68	2.54
ECM *	0.81	0.52	0.7	0.46	1.26
4-Ki-VM *	0.47	0.39	0.41	0.56	1.05

* Model calibrated without alternating use.

. When the (m)–(o) loads were tested in these conditions, the results present high error, as seen in Figure 8p–r. This behavior proves the proposed argument that a simple calibration curve can create biases when determining simulation accuracy, making the model underperform in real applications. An extended error comparison for the models is presented in Table 2.

As seen in Table 2, the quality of the prediction when the models were calibrated without variable use (alternating) was much better in isolated applications. Nevertheless, the ability to predict voltage in alternating use was not great. The error was calculated according to Equation (6). In addition, from Table 2, the precision of the proposed 4-Ki-VM model was greater than the ECM and KiBaM competitors. Regarding simulation time, the 4-Ki-VM took less simulation time compared to the second-order ECM. This comparison is presented in

Table 3. Models’ comparison.

Mode Used	Time per Iteration	Characteristics
ECM	6.0 µs	-Fast to compute and simplicity in implementation -Can describe VxI characteristics and apparent capacity -Great accuracy, which can be improved with more RC circuits
4-Ki-VM	5.5 µs	-With four models can precisely describe charging characteristics -Best accuracy -Fast to compute -Can describe VxI characteristics and SOC fluctuations
KiBaM	5.28 µs	-Simplicity in implementation -Requires few constants -Explains SOC fluctuation and apparent capacity -Lacks accuracy

.

It should be noted that a first-order ECM and second-order ECM with constant RC were also implemented, but they were unable to maintain the accuracy in the pulse and random tests and thus, they were discarded.

8. Discussion

This paper proposed a detailed model for simulating the operation of batteries, considering the impact of different loads in the voltage response and how this affects power injection. The model performed similarly in all scenarios, giving great results even when the load was randomly changed.

Model performance under random discharge/charge is very important. Batteries in real use do not experience complete and uninterrupted cycles with constant current since they are used as needed. A model that explains battery behavior in this scenario is necessary, and this only happens if the model is calibrated correctly; Figure 8p–r showed the performance of the model calibrated without alternating use.

The performance of 4-Ki-VM compared to ECM was superior. The original KiBaM is a simpler and faster model to compute, but it lacks precision. ECM can increase the accuracy by increasing the number and RC circuits, and similarly, the 4-Ki-VM can be implemented with four cores and increase the accuracy without significant performance impact.

The disadvantage of modeling the 4-Ki-VM is the number of constants required. The original KiBaM with two parameters created a model with more than 30. Obtaining these parameters with an evolutionary process is an intensive computational task, but it is fast to implement. The solution proposed does not need the iteration process to simulate a battery. Virtual use is done using the KiBaM cores with a smart constant selection. The 4-Ki-VM demands similar processing power as the original two constants KiBaM, making the simulation possible on weak CPUs.

SOC monitoring is an important work made by the BMS, which helps operate the battery efficiently. Nevertheless, the quality of the SOC prediction is proportional to the voltage following the capabilities of the model. The objective of this paper was to evaluate voltage response, SOC prediction being a task for future work. This adaptation can be made applying state estimators such as EKT in the SOC prediction. Moreover, KiBaM can project the voltage as shown in Figure 4 and estimate the remaining usable energy, making a SOC prediction algorithm.

The original KiBaM already proved to work with different chemistries (NiMn and lead-acid [22]). The 4-Ki-VM can also work in different chemistries. In [22], the KiBaM is extended for temperature dependency; this is useful in more extreme temperature variation environments. For the 4-Ki-VM to work with temperature dependency, the voltage model and the model selection will require further adjustment.

Even ignoring temperature, in vigorous random use, the model can predict the battery voltage with good accuracy, as seen in Figure 8. If the load is uniform, the precision in voltage prediction is higher.

These outcomes for the proposed model make it suitable for implementation in battery simulations with some extended features when compared against ECM. EV simulation is a great application for the model, since the core switching of the 4-Ki-VM is robust and suitable for fast load switching. For validation in this specific application, it will require testing with high frequency load switching. Future works can verify this implementation.