2. Considered Irrigation System and Proposed Methodology
The paper considers an irrigation system, powered by an autonomous hybrid system with photovoltaic and wind generators. The structure of the studied system is presented in
Figure 3. During the sizing procedure, the rated power of the hybrid system varies to find the most appropriate installation. The share of both generators in this rated power also varies. The hybrid system powers a submersible pump via a pump converter. During the operation of the generators, the pumped water is stored in an elevated water tank, which supplies a drip irrigation system. When battery storage is considered, it is part of the hybrid system.
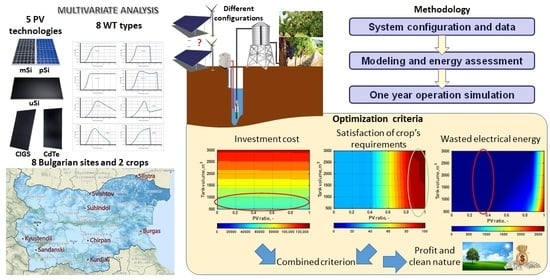
The proposed sizing methodology has three elements: (1) the information for the system configuration and meteorological data; (2) the modelling and energy and water assessment; and (3) the simulation of the system’s operation during the year.
2.1. System Configuration and Meteorological Data
The necessary input information is the meteorological data for the installation site, and the parameters for the hydraulic configuration and for the hybrid system. In this first step, one of the optimization criteria is calculated: the investment cost, as discussed below.
2.1.1. Meteorological Data
The meteorological data are provided by Meteonorm [
71] with a one-hour step for one-year period. These hourly data are used as an input for the generators’ models, and the operation of the system is simulated for one year in view in order to take into account the seasonal variability of wind and solar radiation. The needed data are:
Global solar irradiation on horizontal surface: G, Wh/m2;
Wind speed at 10 m height: V10, m/s;
Ambient temperature: Ta, °C;
Precipitation: P, mm.
2.1.2. Hydraulic Configuration
The methodology uses information for:
The pump parameters: the head and flow rate, which depend on the height of the level of the groundwaters, the elevation of the water tank, the height losses in the pipes, the maximal debit (which is limited by the authorities in the country and the crop’s needs), and the depth of the well and of the pump.
The pump converter starting threshold, which depends on the selected pump.
The tank size, which is variable during the optimization.
2.1.3. Hybrid System Configuration
As mentioned above, the HRES rated power varies during the optimization (respectively the PV peak power and WT rated power). For PV generators, information on the PV cells’ technology and tilt angle is required, while for the WT, the hub height and the power curve are necessary. The five most popular PV cells’ technologies [
72] are used: monocrystalline (mSi), polycrystalline (pSi) and microcrystalline silicone (uSi), Copper indium gallium selenide (CIGS), and Cadmium telluride (CdTe). The PV panels are south-oriented (because the sites are located in the Northern Hemisphere) and tilted according to the site latitude. The WT hub height depends on its rated power (18 m for powers up to 10 kW, 23 m for powers up to 20 kW, and otherwise 28 m). The WT is characterized by its power curves, which vary greatly according to the manufacturer and have a strong effect on its productivity; eight typical power curves are used, which originate from the manufacturers’ database for small WT of NREL’s SAM software [
73]. They are presented in a per-unit power scale in
Figure 4 in order to be applied for various peak powers.
2.1.4. Investment Cost
The first optimization parameter considered is the investment cost (IC), which includes the HRES equipment (generators, power converters, wiring and water tank) and its installation. The IC utilization facilitates the study because the operation and maintenance costs require precise information for the inflation rate, which is not always available. The investment cost depends on the water tank’s volume and the rated powers of the generators in the HRES. The costs can vary for the different countries. In the proposed sizing methodology, the costs are sourced from [
74,
75] for the PV generators, [
76] for the WT and [
77] for the water tank.
2.2. Modeling and Energy Assessment
The measured meteorological data are first converted into appropriate data, and the WT and PV generators and the pump are then modelled.
2.2.1. Meteorological Data Conversion
As the PV modules are tilted, the solar irradiation on the horizontal plane (as measured in most meteorological stations) must be converted into the solar irradiation on a tilted panels’ surface. For this purpose, different approaches are used in the literature. The approach in [
33] is very simple but has low precision. Artificial Neural Networks can be used [
78], but this requires a significant amount of data and is very specific for each site. A good compromise between simplicity and precision is proposed in [
79], in which a combination of the CLIMED2 and Klutcher’s methods and geometric relationships is used. The CLIMED 2 method determines the diffuse radiation
Gd on horizontal surface by the following equations:
where
Gext is the solar irradiation outside Earth’s atmosphere. The numbers in the right side conditions, given by the authors of the CLIMED 2 method [
80], represent clear sky conditions (up to 0.21 for high cloud density, from 0.21 to 0.76 for average cloud density, and clear sky for values greater of 0.76).
The diffuse solar irradiation is used to calculate the diffuse solar radiation on the tilted surface
Gdβ by Klutcher’s method:
where
β is the inclination angle of the tilted surface,
θs is the incidence angle (the angle between the Sun’s rays and the normal of the tilted surface), and
θz is the zenith angle (the angle between the Sun’s rays and the normal vector of the horizontal surface).
The incidence and zenith angles are used to determine the beam component of the solar radiation on the tilted surface
Gbβ:
Finally, the reflected solar radiation on the inclined surface
Grβ is calculated by:
where
ρg is the albedo coefficient used for the estimation of the reflection of the Sun’s rays by the ground.
The wind speed is generally measured at a 10 m height in meteorological stations, but the WT hub height is rarely 10 m; as such, it is then necessary to convert it. The wind speed
Vh at the hub height
h is calculated from the 10 m measured wind speed using the Justus’s Equation [
81] and the Hellmann exponent
αJ.
The electrical efficiency of a PV module depends on the solar irradiation and also the cell temperature
Tcell, which is calculated from the ambient temperature
Ta, the inclined solar radiation
Gβ and the coefficient
hR using Ross’ Equation [
82]:
2.2.2. Renewable Energy Generator Models
The PV generator can be presented by an electrical model [
83], a polynomial model [
84] or an efficiency model [
34,
85]. The proposed methodology uses the last possibility, applying the reduced Durisch’s model [
86], which allows the modelling of different PV cell technologies without astronomical calculations for the air mass. The reduced and the original Durisch’s model were verified experimentally by the authors, and showed the best accuracy compared with other models with a relative root mean square error of around 3–4% [
86,
87]. The PV module efficiency is given by:
where
ηPV is the PV efficiency,
Gref = 1000 Wh/m
2 and
Tref = 25 °C, which are the reference values, respectively, for the solar radiation and the cell temperature and
p,
q,
m and
r: empirical coefficients with specific values for each PV technology.
The values of the empirical coefficients, including the coefficient
hR from Ross’ formula (Equation (6)) are determined in [
86] and are presented in
Table 1. The five PV technologies are affected differently by the solar radiation and the cell temperature. Thus, the application of a given technology with lower efficiency can be justified by its better performances during the summer: a period with high temperatures and solar radiations. The variation of the PV technology in the sizing methodology seeks the verification of this hypothesis.
The wind turbine’s output can be estimated from the wind speed, the swept area and the power coefficient [
88]. Another possibility is the use of the modelled power curve or the interpolation of real power curves. Due to the complex form of the eight WT power curves, in
Figure 4, a modelling with a monotone piecewise cubic interpolation (MPCI) is used. The wind turbine output power is determined for a given wind speed by the interpolation of the power curve’s points, as provided by the manufacturer. The MPCI takes into account the form of the curve, and thus its precision is better than the linear one. The interpolation uses the following interpolant [
89]:
where
x is the argument that is between the two points
xi and
xi+1. The coefficients are determined by:
where
fi is the function value in the point
xi,
is its derivative,
is the derivative of the function for
xi+1, and
is the slope of the linear interpolant.
The applied necessary and sufficient condition for monotone interpolation is that the interpolant in (8) is monotone in the interval [
xi,
xi+1] if, for each
I, the derivative
respects the following interval:
where
si is determined by:
where
sign = 1 for a positive argument and
sign = −1 for a negative one.
The interpolation’s limiter function is defined by:
The Monotone piecewise cubic interpolation is integrated in Matlab®, which is used for the methodology implementation.
The last element in the hybrid system is the battery storage. The aim of the sizing methodology is only to estimate the profit from the introduction of the battery into the power supply. This is why the battery model is not sophisticated: a constant value (80% [
90]) for the charging and the discharging efficiency is chosen, while the other parameters of the battery are neglected.
2.2.3. Pump Model
Usually, the pump manufacturer provides information that links the head, the flow rate and the consumed power. On the basis of this information, the variation of the flow rate per hour
Qout is determined, depending on the input power
PHS, which is considered to be constant during the hour. This dependence is used for the pump modeling. Using [
91], the modelling Equation (13) for the pump is obtained. In the case of battery storage in the hybrid system, the inverse Equation (14) is used to determine the power requested from the battery to fulfill the irrigation needs.
2.3. One Year Operation Simulation
Two processes are simulated during the year: the pumping and the irrigation. They are illustrated in
Figure 5.
2.3.1. Pumping
The pumping starts several days before the required irrigation period in order to guarantee a full water tank during the first irrigations. In this study, this preliminary period is 15 days. The pumping period ends with the irrigation period. During the pumping period, for each hour, the hybrid system’s output power is compared with the pump converter’s starting threshold. In the case of insufficient power, no water is pumped. In the opposite case, the pumped water volume is determined by (13) and added to the stored water. If, during this hour, the tank is filled, the rest of the produced energy is considered wasted. This wasted electrical energy (WEE) is the second optimization criterion. For the simulations with batteries, this wasted energy increases the state of charge of the battery.
2.3.2. Irrigation
The irrigation in this study is simplified by considering only the reduction of water volume in the tank, because only this process is related to the HRES sizing.
During the irrigation period, the needed water depends on the crops’ needs, the irrigated area and the precipitation. If this water is available in the water tank, the irrigation is realized and the water volume in the tank is reduced. If the stored water is not sufficient, the tank is emptied and the satisfaction of crop’s requirements (SCR) is reduced. SCR is the third optimization criterion used in this study.
For the systems with batteries, in the case of insufficient water in the tank, an additional verification is performed, i.e., the sufficient state of charge of the battery to pump additional water to meet the irrigation needs. In the case of there being enough energy in the battery, the tank is filled to the needed level. After that, the irrigation is performed and the tank is emptied. At the same time, the battery’s state of charge is reduced.
If the energy in the battery is not sufficient, the energy remaining in the battery is used for pumping, and then the irrigation is done and the tank is emptied. The satisfaction of the crop’s requirements is decreased according to the shortfall of water.
2.4. Multivariate Analysis
Several configurations are studied iteratively conducing to a multivariable analysis. Firstly, the site and the irrigated crop are chosen. The HRES rated power takes different values, seeking the optimum. It is the sum of the PV and WT’ rated powers, which also vary. The term ‘PV ratio’ is defined as the percentage of the PV peak power in the total HRES power. It varies between 0 and 1 (1 for a PV system alone and 0 for a WT system alone). For each PV ratio, the water tank volume is changed and a variety of combinations are obtained.
The number of configurations is then very high, keeping in mind that the PV cells’ technology and the WT power curve change too. For each combination (site, crop, HRES rated power, PV technology, PV ratio, WT power curve, water tank volume), the system operation is simulated during one year. The generators’ output varies according to the meteorological data. The investment cost is calculated for each configuration and the other optimization criteria are calculated during the simulation. Finally, the configurations’ results are compared and analyzed in order to guide the sizing of the irrigation system.
The proposed methodology is implemented in Matlab® program code.
4. Conclusions and Final Discussions
The realized literature overview shows a high variety of approaches for the study of HRES for different applications, including irrigation. This overview guided the authors to define their aim to propose a multivariate sizing methodology for an irrigation system, using a stand-alone hybrid system with a PV generator and a wind turbine for power supply, and a water tank as an energy storage device. The proposed methodology takes into account the energy conversion phenomena in the generators. The sizing is based on the simulation of one year’s operation of the HRES with a one hour time step without limitations for smaller steps. The meteorological conditions and the HRES configuration are used as the input data after appropriate conversion and treatment. Five PV cell technologies and eight WT types are considered. Each subsystem is modelled with an appropriate and accurate model (previously verified and adopted): a reduced Durisch’s model (for the PV generator) and a monotone piecewise cubic interpolation (for the WT). A pump model is proposed, using a logarithmic function, which links the pumped water with the input electrical power. During the system’s simulation, two operation modes were considered: pumping and irrigation. Three initial optimization criteria—the investment cost, the SCR and the wasted electrical energy—were proposed and used, and a fourth one, a combined criterion, was then added. The smaller time step for the simulations increases its precision, but sometimes it is difficult to obtain such meteorological data.
Numerous sizing parameters were taken into account: the HRES rated power, PV ratio and water tank volume. The results were given for different PV cell technologies and WT types. Those multivariate combinations allow the selection of the optimal HRES rated power with the respective PV and WT power, and tank volume. The methodology requires specific input data and was applied on eight Bulgarian sites, which allowed us to choose the best PV technology and WT type for each site and two agricultural crops (five sites for each crop): wine grapes and cherries. The share of PV and WT generators varied according to the site, but as the solar potential is relatively the same for all Bulgarian sites it is mainly the wind potential of the site which influences the ratio PV/WT. Generally, for the Bulgarian sites considered in this study, the PV generator has a much greater peak power than the associated wind turbine.
It has been shown that it is impossible to satisfy the three optimization criteria together: to obtain at the same time a cheaper HRES system, which satisfies totally the irrigation needs and for which no wind or solar energy is lost. Thus, a new (fourth) combined criterion was introduced, as the ratio between the investment cost and the SCR, two criteria which are both important for the HRES owner. This new criterion allowed a better comparison of the different HRES configurations.
The three initial optimization criteria increase with the HRES power, especially for a higher PV generator share due to the better solar potential of the considered sites. The PV domination confirms some results in the literature. The combined criterion determines an optimal solution with relatively small oversizing of the generators and a low water tank volume. Unfortunately, the optimum does not guarantee full SCR. If this condition is essential, then an additional weight of the SCR criterion should be given. For greater HRES powers, the combined criterion is not optimal but the SCR is 100%.
The consideration of various PV technologies and wind turbine types gives a specific originality and attractiveness to this work because it has never been considered in the read literature, and it appears that the influence of these two aspects is not negligible. The pSi shows an increase of the SCR with a medium water tank volume, while the investment cost and the combined criterion for the uSi are lower. However, it should be noted that the technology’s influence is significant only for PV-dominated hybrid systems, and is due to differences in the influence of the solar radiation and ambient temperature on the PV panels’ efficiency. The relatively low wind potential of the sites favors wind turbines with better efficiencies for low wind speeds.
The complementarity of the two primary resources (wind and solar) is particularly visible for a site like Kurdjali, for which good performance (in terms of SCR) is reached for a medium PV ratio. For sites with low wind potential, a full SCR is obtained for HRES with a high PV ratio and, unfortunately, high wasted solar energy. Similar results are reported by other authors in the literature. The solar and wind generators’ coupling improves the performances when wind energy is present, taking into account that the solar energy is often more available everywhere.
Another distinctiveness of this study is the modelling of the irrigation requirements for two crops—cherries and wine grapes—which influences the HRES sizing. The longer irrigation period of the cherries improves SCR for low PV ratios due to higher wind speeds and precipitations in the spring, when their irrigation period starts. Along with that, the wasted electrical energy increases because of the greater electrical energy production, which cannot be transformed in pumped water due to the water tank constraints.
The introduction of an additional energy storage device (battery) both improves the HRES performance and reduces the water tank volume. Because the optimal HRES sizing according to the combined criterion Cr is obtained with a minimal water tank, the introduction of batteries increases the SCR. The observed decrease in the Cr value is not indicative because the battery’s cost is not taken into account. For PV-dominated hybrid systems, the state of charge of the battery at the end of the irrigation period is relatively high.
The presence of wasted electrical energy during the irrigation period, the high state of charge of the battery (when it is present in the HRES) and the possibility of the HRES to produce energy outside the irrigation period can be driving factors to use the hybrid system’s overage production for other purposes. This utilization will increase the profit which was already realized with the HRES application for irrigation. Different applications are possible, but they depend on the HRES’s surroundings (farming facilities, grid connection, etc.) and are not considered in this paper.
The experimental validation of the proposed methodology with all of the combinations for a given site (purchased or rented) is a very expensive (different PV installations, WT with various types and power, and tanks with different volumes, along with the measurement and monitoring of the system are required) and long (at least one year per configuration) procedure. This deters the authors from such a type of validation. However, the precision of the methodology is considered to be good enough because the accuracy of the used physical models was verified experimentally by the authors for the PV technologies, and by the manufacturers for the WT and the pump, providing the respective datasheet. Thus, the results’ precision depends only on the input meteorological data. The use of accurate data with a small time step (one hour in this study) improves the results’ precision.
Numerous highlights can be summarized as having been introduced in this work: the utilization of accurate models for PV and WT generators; the utilization of hourly meteorological data, allowing us to observe more precisely the dephasing between productions, and between production and consumption; the introduction of various PV and WT technologies; and the introduction of the particularities of two crop irrigations. The used multivariate analysis is more intuitive and simple for application in comparison to other complex mathematical optimization approaches. It can be successfully used for feasibility studies or during the design process of HRES for irrigation.