An Overview of Fully Integrated Switching Power Converters Based on Switched-Capacitor versus Inductive Approach and Their Advanced Control Aspects
Abstract
1. Introduction
2. Integrated SC Converters
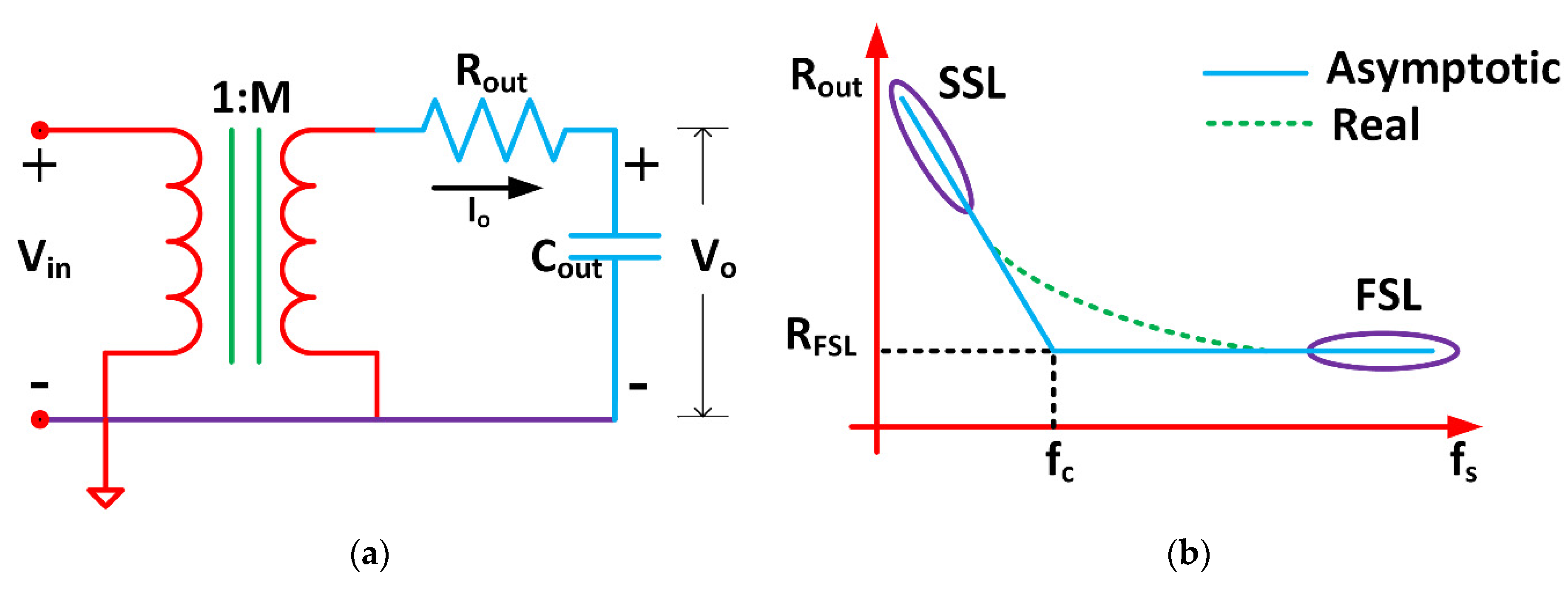
2.1. SC Converter Average Modelling
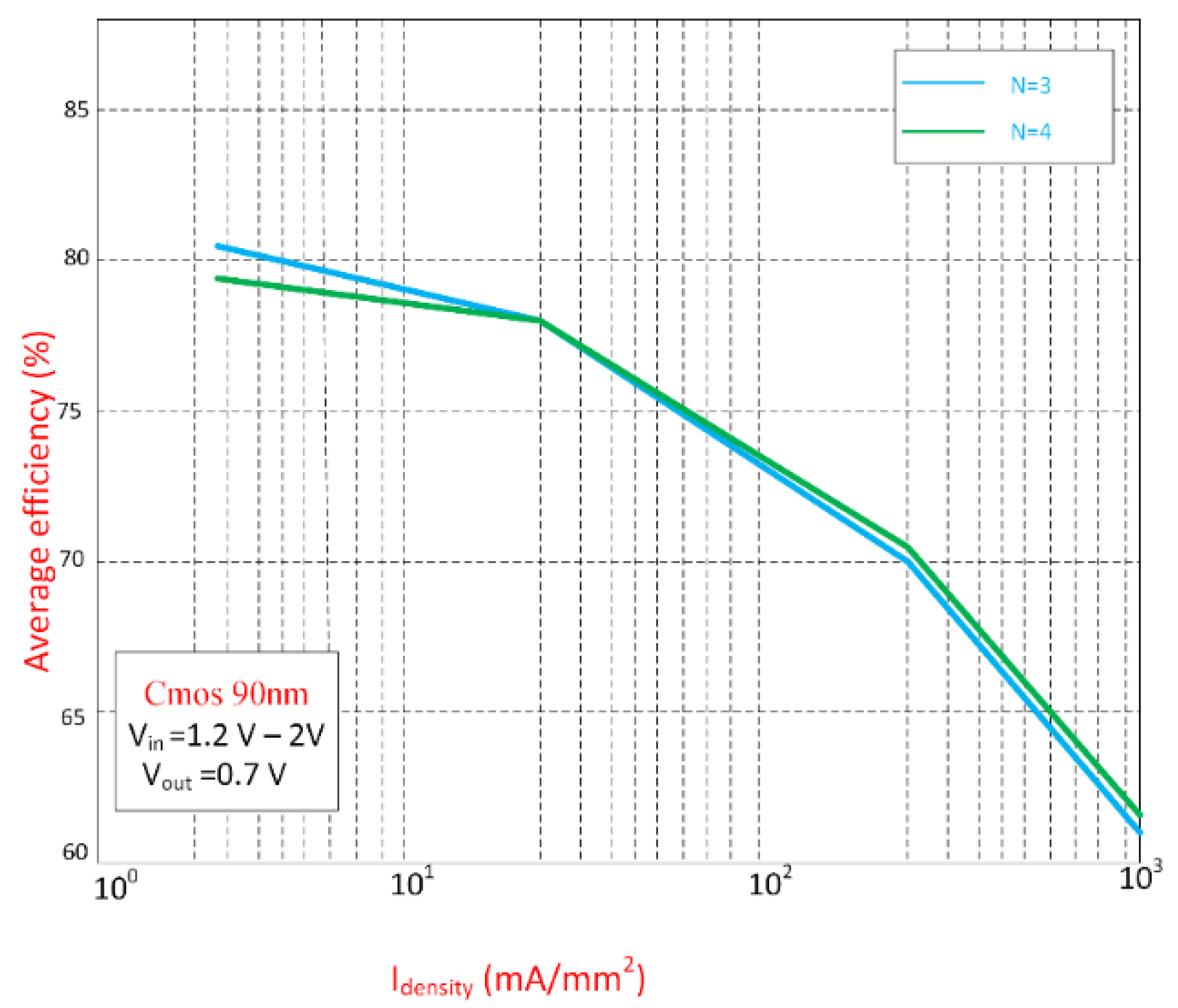
2.2. Efficiency and Power-Loss Distribution
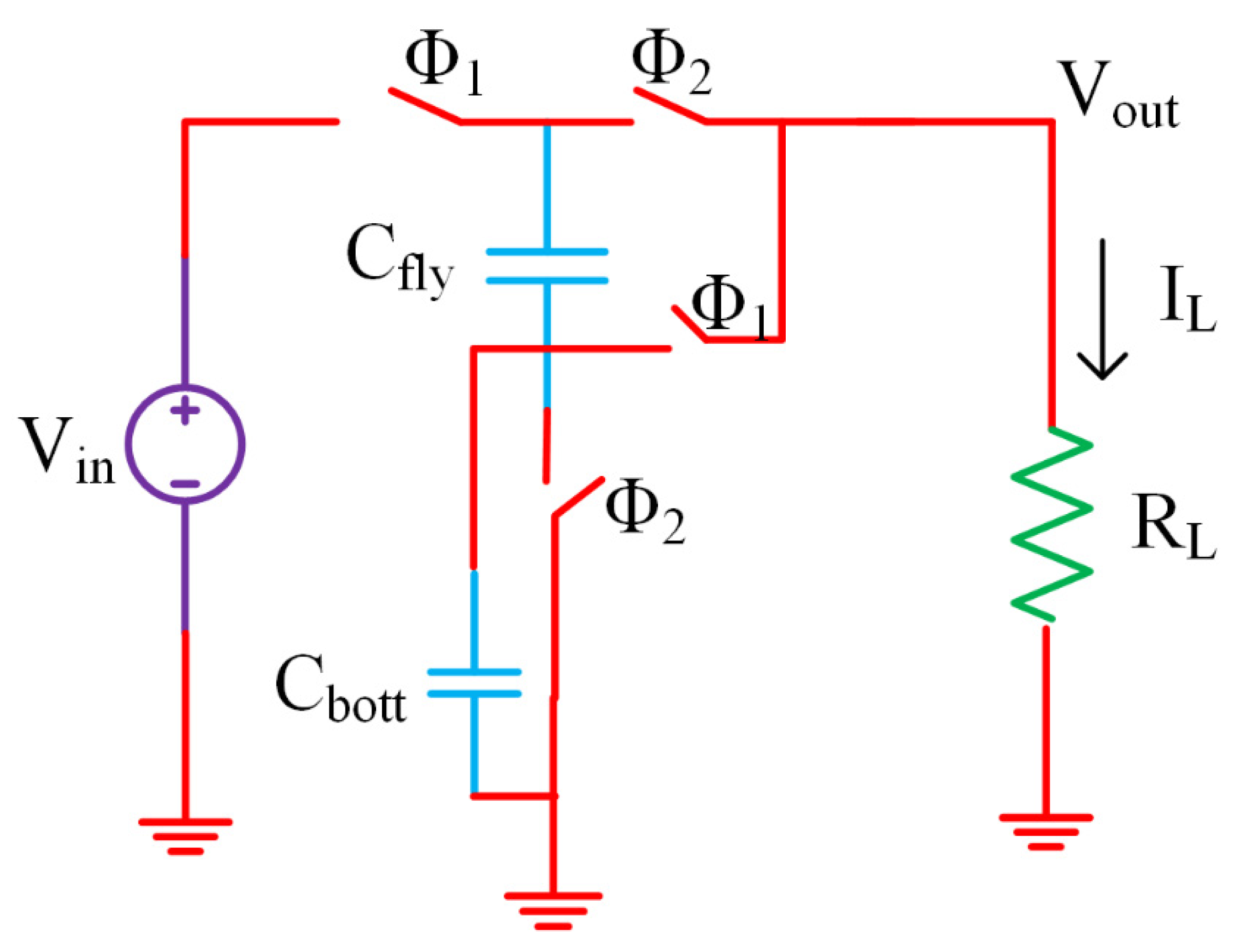
2.2.1. Bottom-Plate Losses
2.2.2. Driver Losses
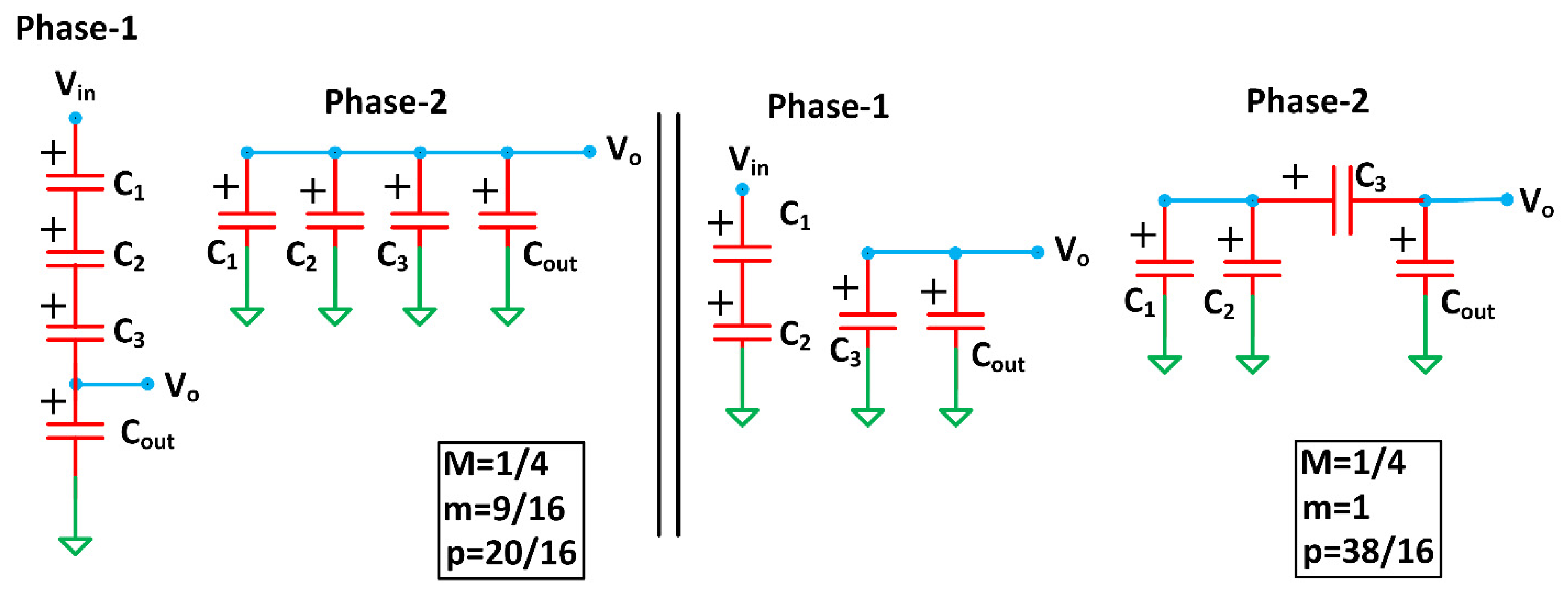
2.3. Multiratio SC Power Converters (MR-SCPC)
2.4. Integrated SC Converter Control Schemes
2.4.1. Conversion Ratio Control
2.4.2. Duty-Cycle Control
2.4.3. Switching Frequency Modulation
2.4.4. Ron Modulation
- (1)
- The width of MOS transistor is varied using segmented switches [26]. This mechanism has a limitation in that it only works with the discrete Ron values and produces a complex control signals for routing.
- (2)
- The second mechanism uses the Ron for modulating the Vgs voltage of a MOS (METAL OXIDE SEMICONDUCTOR) transistor. It generates the uninterrupted values for the complete ON duration of the switch. However, the strong nonlinearity between the Ids and Vgs makes the control loop unstable, whenever Vgs approaches the threshold voltage. For example, Ref. [31] used the transistor as a switch in an SCPC.
2.4.5. Series LDO
2.4.6. Floating-Capacitor Size Modulation
2.5. Multiphase SC Power Converters (MP-SCPC)
2.6. SC Converters Technology Options
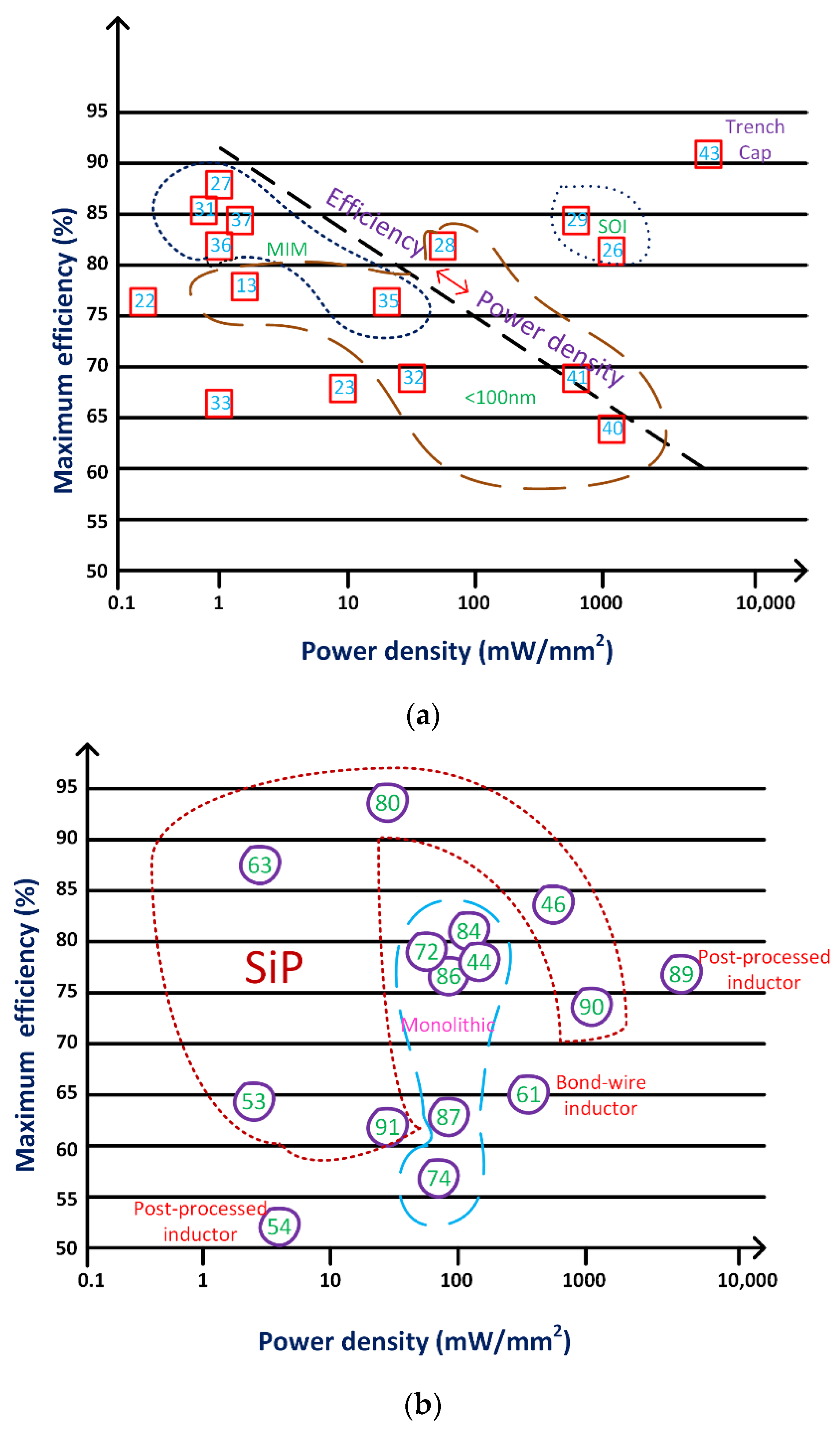
- The present trend is to use the gate capacitance of MOS transistors (MOSCAPs) in bulk CMOS technologies to offer a capacitance density that varies from 4 nF/mm2 to 12 nF/mm2. Its main benefit is to integrate SCPCs with the remaining portion of the system, especially in large ICs. The thin-gate oxide transistors provide a low breakdown voltage, and this allows providing higher gate capacitance values. Due to the usage of floating capacitors, a separate well is required for the gate capacitance of MOS transistors. Moreover, N-type MOSCAPs exhibit a lower ESR than their counter, the P-type, and essentially require a triple-well process. The fringe metal capacitors offer low capacity density (<1 nF/mm2) even with lower parasitic, and are neglected [13,22,23,28,32,33,40,41].
- An alternative is to use metal–insulator–metal (MIM) capacitors in bulk technologies; this requires additional masks in the fabrication stage, which increases the cost. However, this reduces the bottom-plate parasitic capacitance to approximately 1%, but increases the desired area due to low capacitive density (up to 2 nF/mm2) and the cost [27,35,36,37,39].
- Silicon-on insulator (SOI) technology is another alternative to bulk CMOS technology. In this technology, the components are positioned on a high-impedance substrate for reducing the bottom-plate parasitic capacitance of a gate capacitance of the MOS transistor. As a result, high capacitive density of about 0.1% is achievable with MOSCAP parasitic capacitances. Due to its higher cost, this technology is used only if an application demands it. This is the major limitation of SOI technology [26,29].
- Another important technology is the use of trench capacitors that can offer as high as 400 nF/mm2 of capacitive density [42]. It can be seen that this technology is far ahead of the others in terms of its higher capacitive density, breakdown voltage, and the parasitic (<1%). Despite their benefits, trench capacitors are unsuited for use with active components, and therefore need to be on a separate die. The complexity becomes more pronounced between the interconnection of two separate dies in the case of MR-SCPCs or MP-SCPCs. The complete assembling of this technology is associated with cost [43].
3. Integrated Switched Inductive Converters
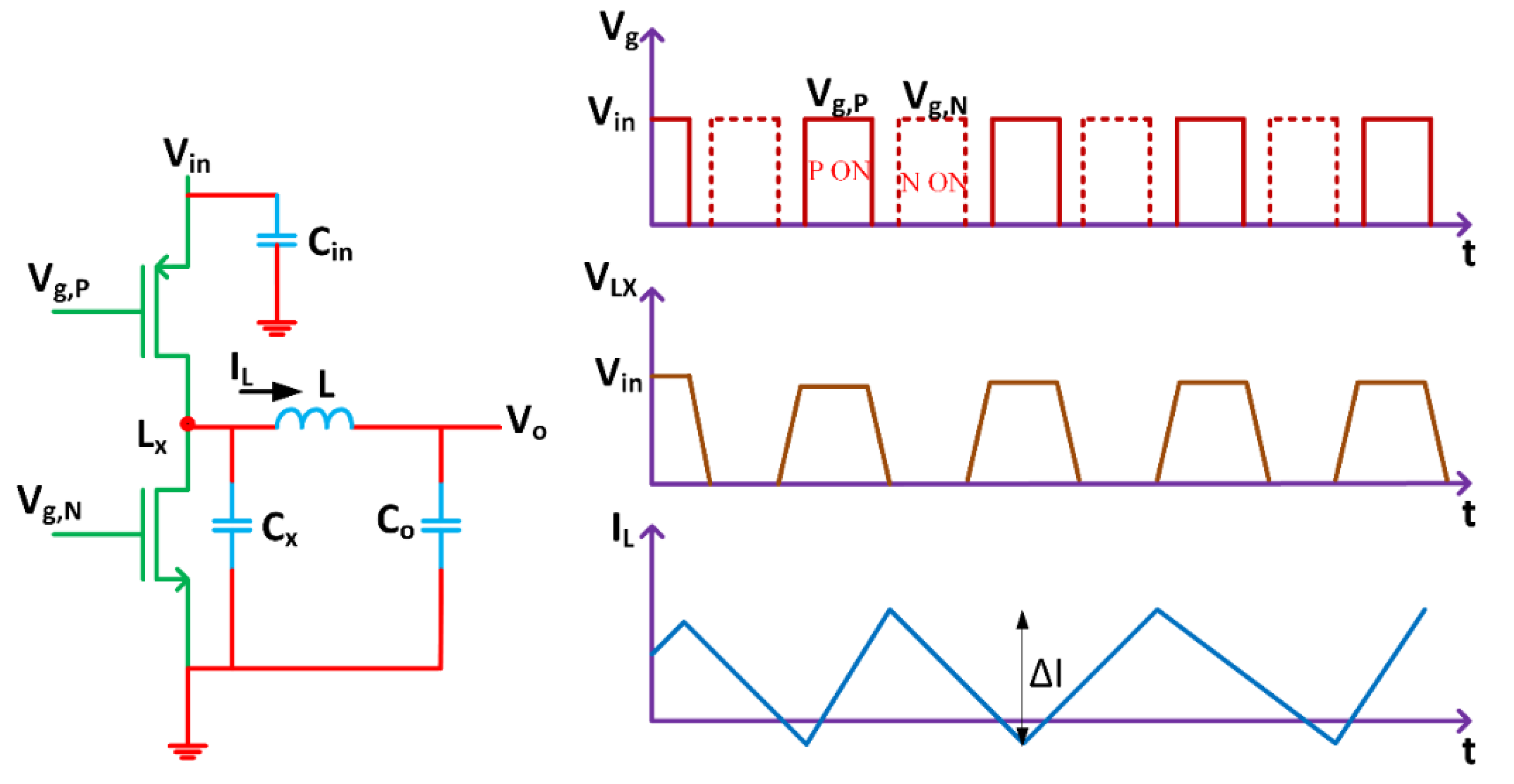
3.1. Power-Loss and Efficiency Calculations
3.1.1. Conduction Losses
3.1.2. Switching Losses
3.1.3. Dead-Time Losses
3.1.4. Inductor Core Losses
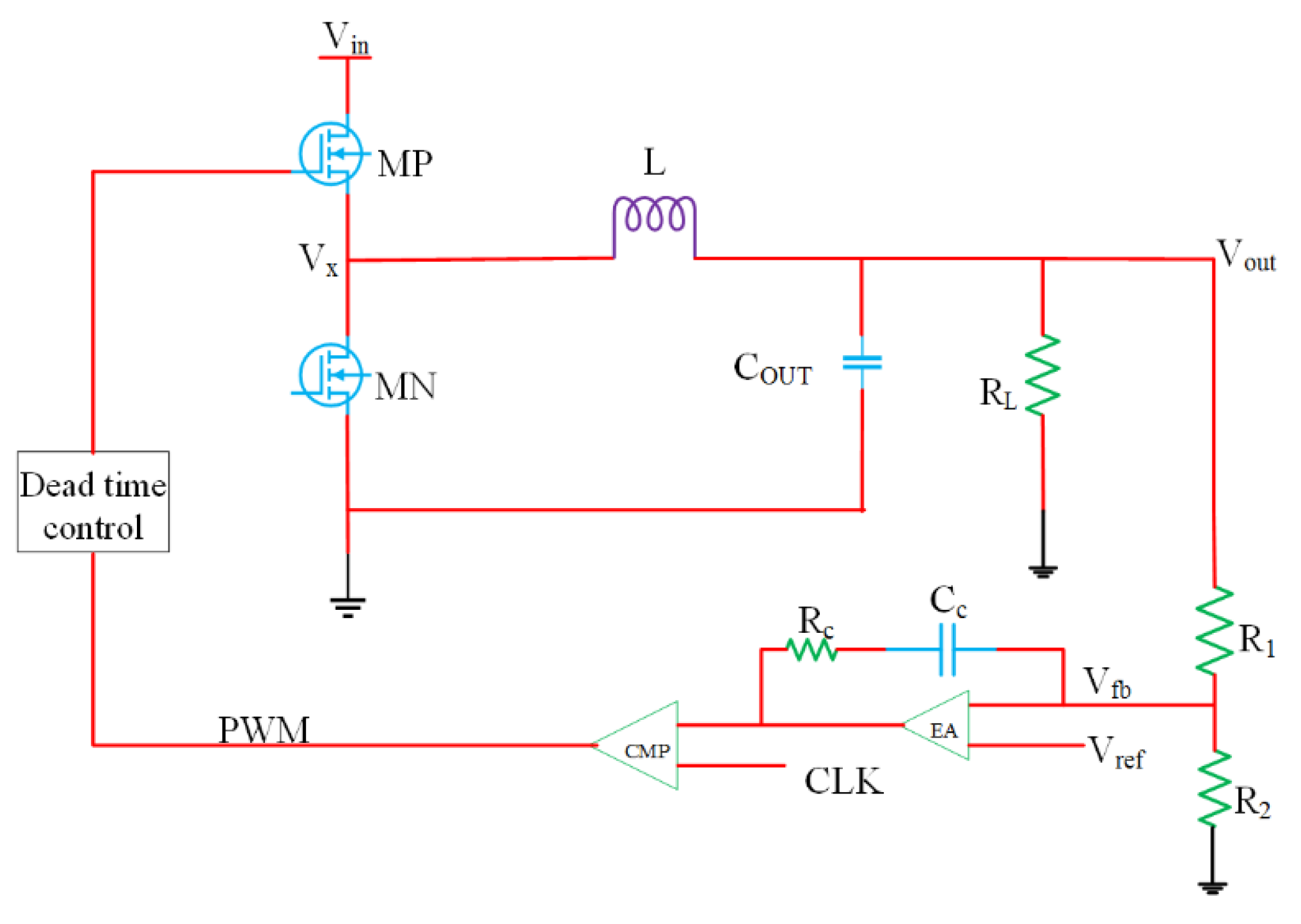
3.2. Control and Modulation Strategies
3.3. Implementation Issues
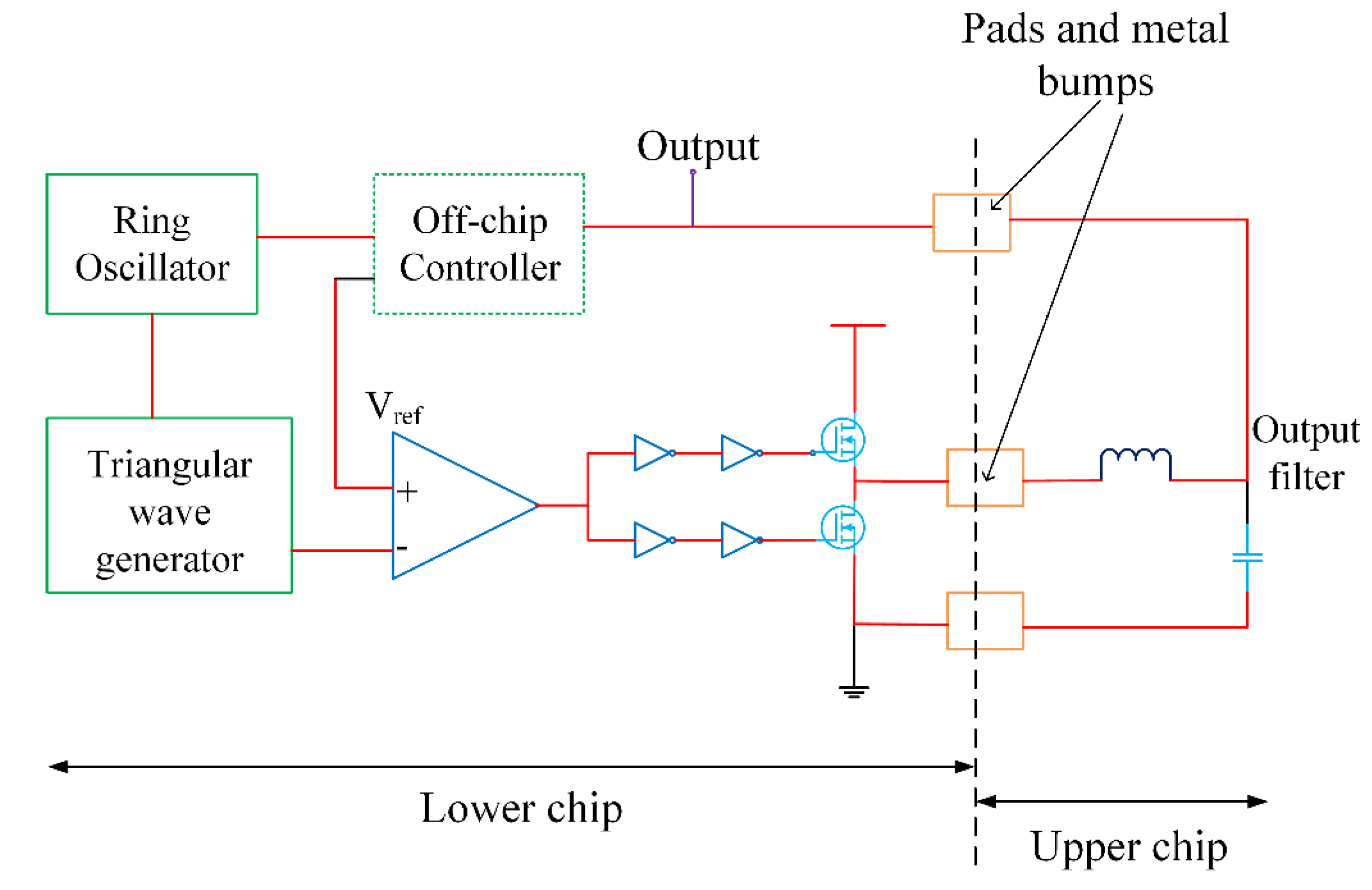
3.4. Integration Technology Options
4. Comparison between Integrated SC and Inductive Converters
- (1)
- There is a comprehensible tradeoff between the maximum efficiency and the power density in bulk CMOS applications that include MIM capacitors. Using MIM capacitors allows higher peak efficiency designs, whereas lower capacitive density leads to lower power densities.
- (2)
- Operating the SCPC at higher switching frequencies results in a small size design, around 100 nm. This will give high power density at acceptable efficiencies for gate capacitance of MOS transistors.
- (3)
- (4)
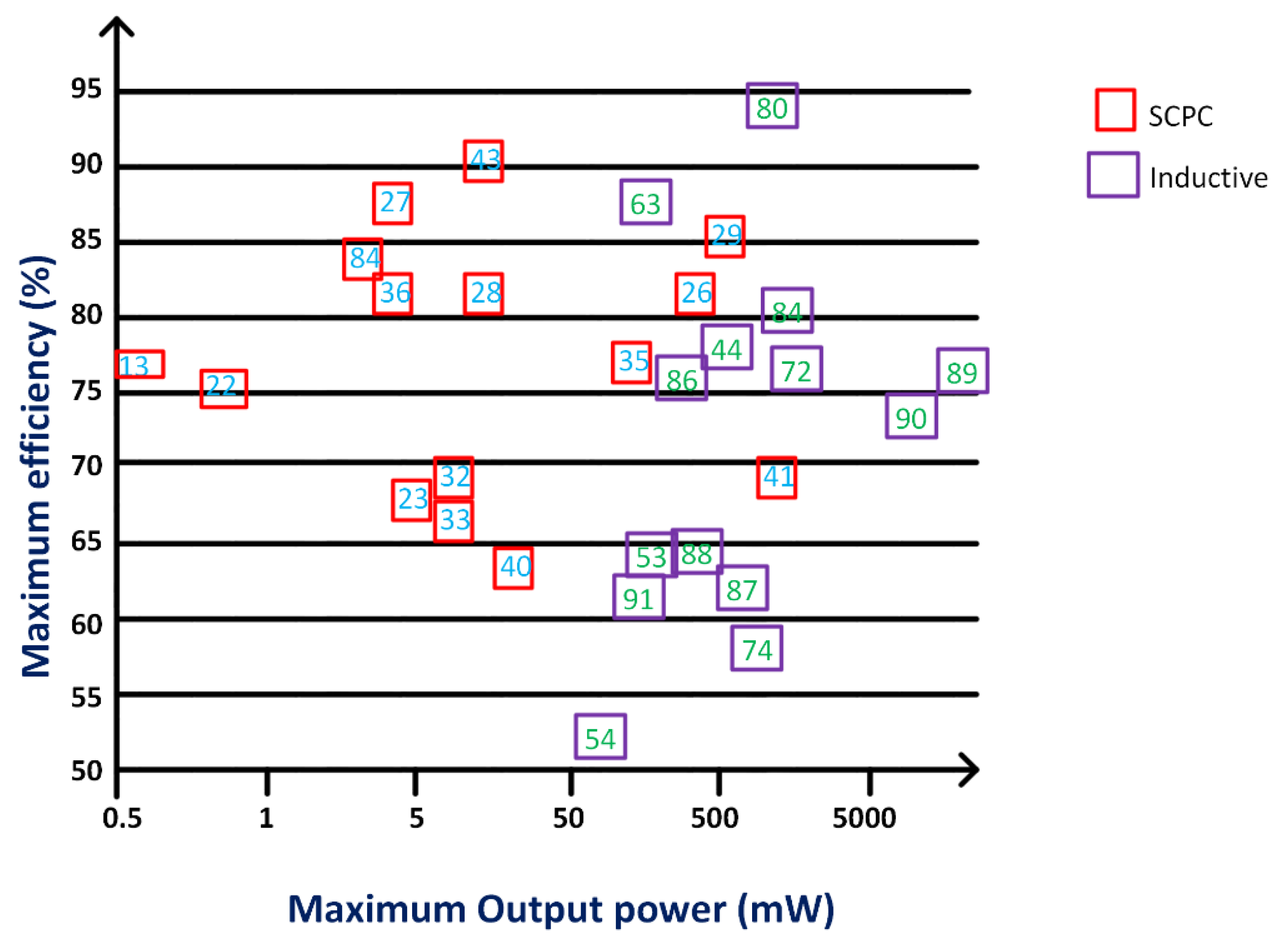
- It is challenging to determine the type of converter circuit (i.e., either SCPC or inductive converter) that can provide the satisfactory overall performance between the power density and the efficiency as depicted in Figure 6. The SCPC is the best possible design [43], but it engages at corresponding low voltage and affords low absolute output power. Therefore, it should be noted that the defined results strongly depend on application in relation to Po, Vo, Vin and other limitations.
- (1)
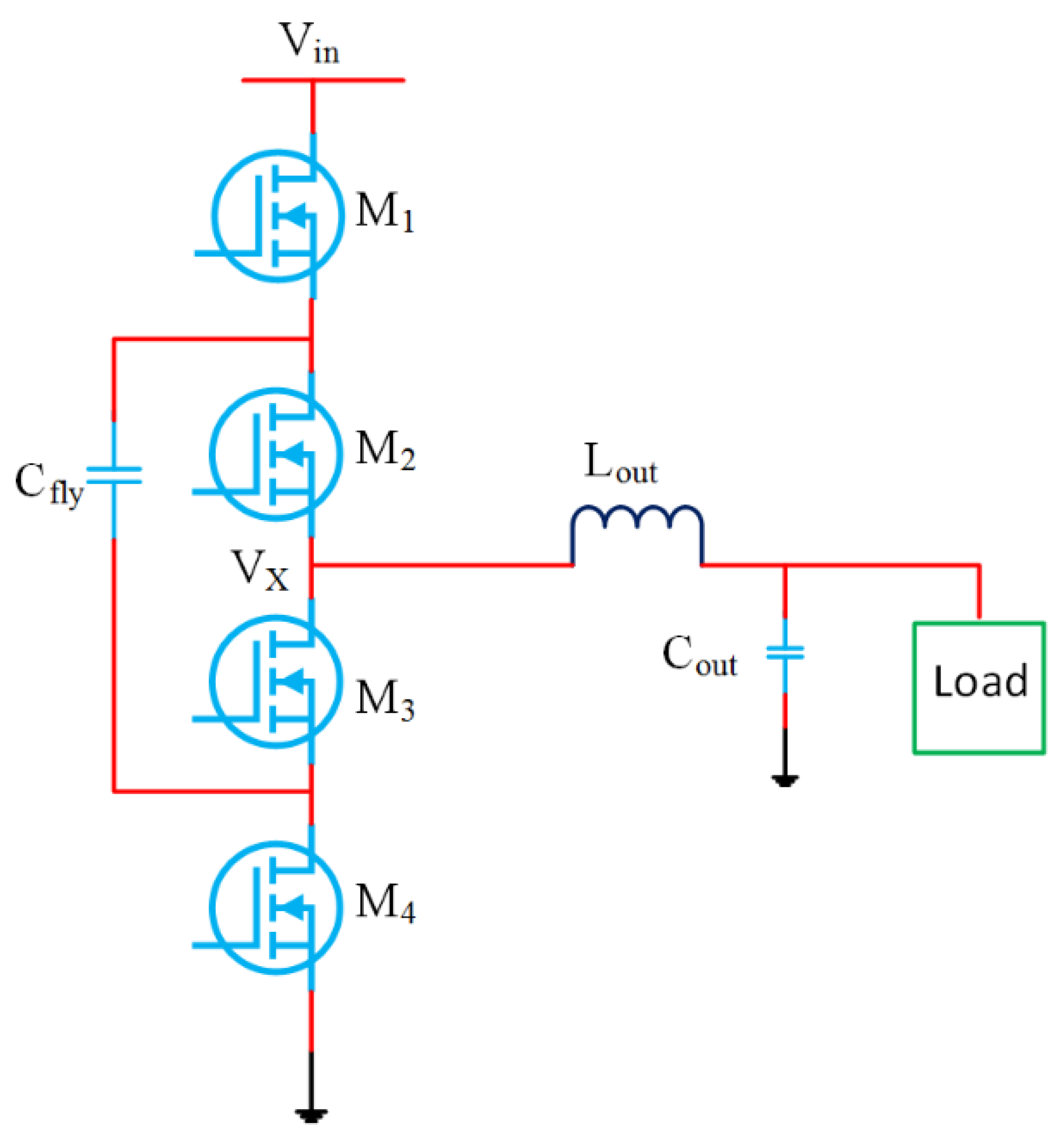
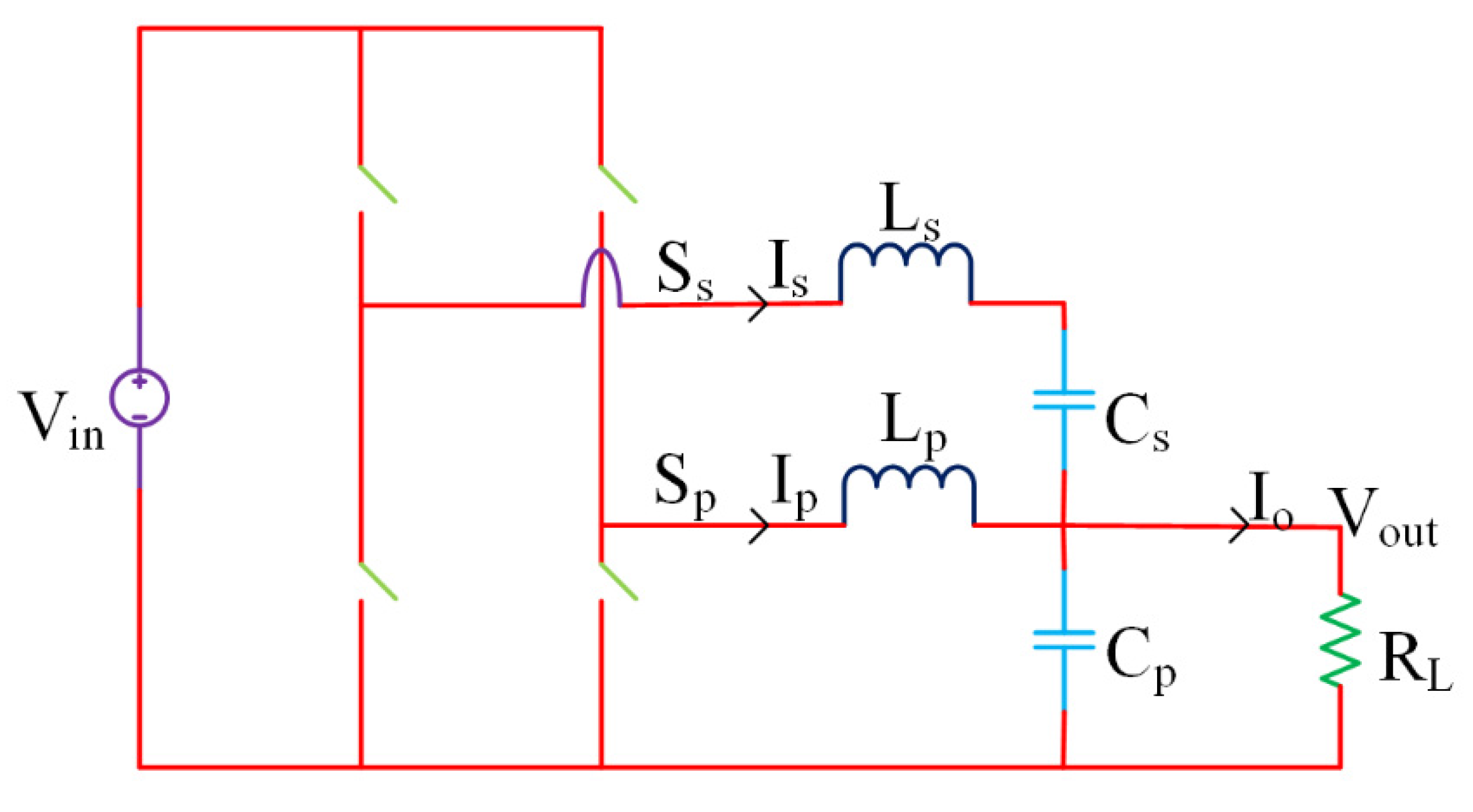
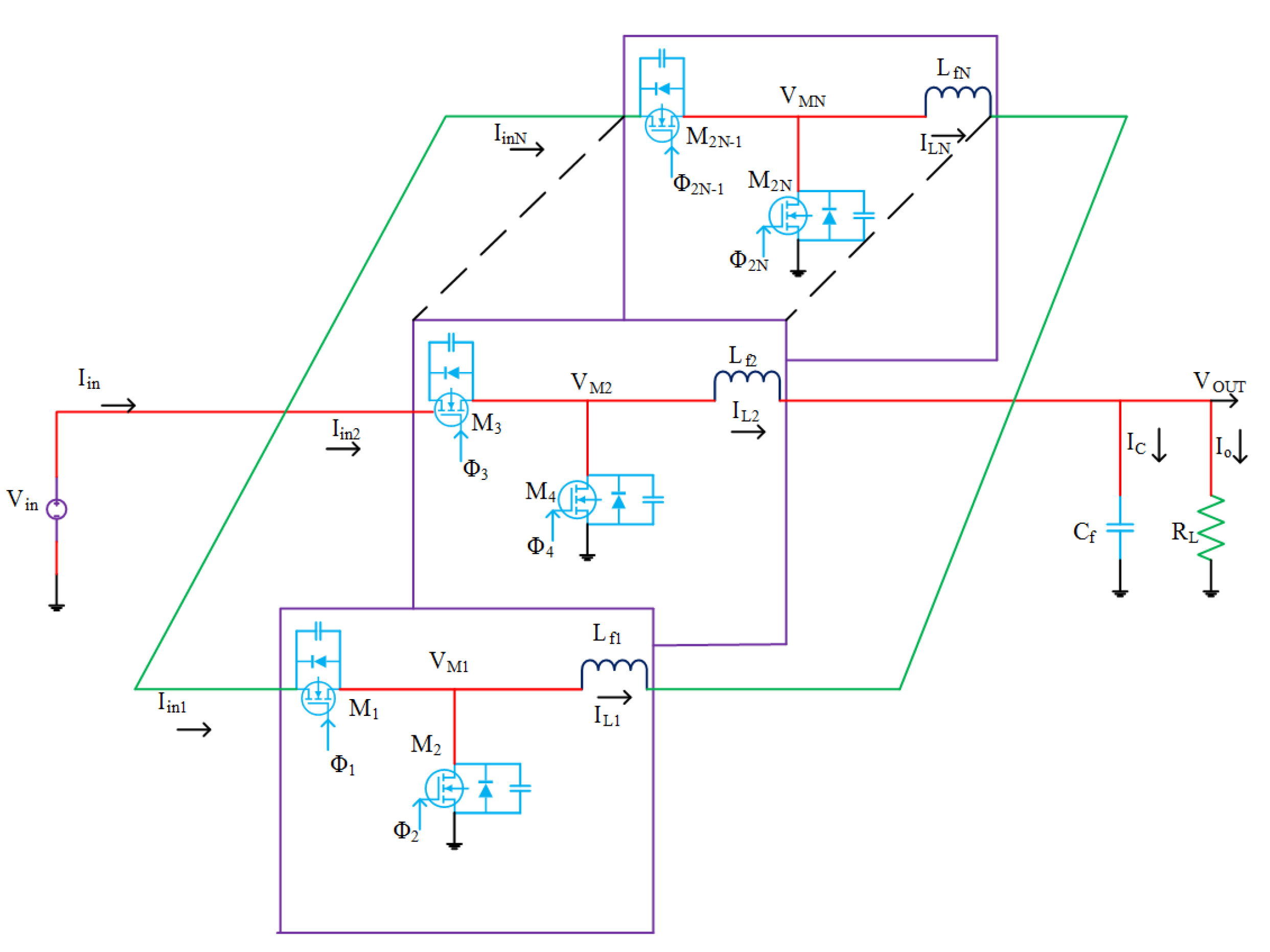
- Without demanding special alterations, all the true monolithic converters realize comparable power densities [72] (fully integrated 3-level buck converter), as shown in Figure 8; Ref. [44] (fully integrated stacked interleaved buck converter), as shown in Figure 9; Ref. [74] (fully integrated four-phase step-down converter), as shown in Figure 10; Ref. [84] (fully integrated synchronous buck converter), as shown in Figure 11; Ref. [86] (fully integrated 3-level buck converter); and [87] (fully integrated multistage interleaved synchronous buck converter), as shown in Figure 12 (Ref. [87] is synthesized with SiGe rather than CMOS). Synthesizing the inductor using bond wires did not cause a large variation in the power density [88].
- (2)
- Compared to monolithic converters, SiP-based converters provide both higher [47] (integrated eight-phase synchronous buck converter), Ref. [90] (eight-phase integrated buck converter) and lower power densities [54] (integrated inductive step-down converter), Ref. [63] (integrated inductive step-down converter), Ref. [80] (integrated step-down converter), Ref. [91] (on-chip buck converter with stacked-chip implementation), as shown in Figure 13. The use of committed and advanced small SMD inductors and capacitors results in a higher power density [47]. So, the main motive for selecting SiP over the monolithic approach is the lower cost, but not the power density.
- (3)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bergveld, H.J.; Kruijt, W.S.; Notten, P.H.L. Battery Management Systems: Design by Modelling. In Philips Research Book Series; Kluwer: Norwell, MA, USA, 2002; Volume 1. [Google Scholar]
- Lei, Y.; Liu, W.C.; Podgurski, R.C.N.P. An analytical method to evaluate and design hybrid switched-capacitor and multilevel converters. IEEE Trans. Power Electron. 2018, 33, 2227–2240. [Google Scholar] [CrossRef]
- Uno, M.; Sugiyama, K. Switched capacitor converter based multiport converter integrating bidirectional PWM and series-resonant converters for standalone photovoltaic systems. IEEE Trans. Power Electron. 2019, 34, 1394–1406. [Google Scholar] [CrossRef]
- Jiale, X.; Gu, L.; Rivas-Davila, J. Effect of Class 2 Ceramic Capacitor Variations on Switched-Capacitor and Resonant Switched-Capacitor Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2268–2275. [Google Scholar]
- Steyaert, M.; Tavernier, F.; Meyvaert, H.; Sarafianos, A.; Butzen, N. When Hardware Is Free, Power Is Expensive! Is Integrated Power Management the Solution? In Proceedings of the 41st European Solid-State Circuits Conference, Graz, Austria, 14–18 September 2015; pp. 26–34. [Google Scholar]
- Lu, Y.; Jiang, J.; Ki, W.-H.; Yue, C.P. A 123-Phase DC-DC Converter-Ring with Fast-DVS for Microprocessors. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 22–26 February 2015; pp. 1–3. [Google Scholar]
- Karadi, R.; Piqué, G.V.; Bergveld, H.J. Switched-capacitor power converter topology overview and performance comparison. In Wideband Continuous-Time ∑ ∆ ADCs, Automotive Electronics, and Power Management; Springer: Cham, Switzerland, 2017; pp. 239–261. [Google Scholar]
- Lu, Y.; Jiang, J.; Ki, W.-H. Design considerations of distributed and centralized switched-capacitor converters for power supply on-chip. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 515–525. [Google Scholar] [CrossRef]
- Sanders, S.R.; Alon, E.; Le, H.P.; Seeman, M.D.; John, M.; Ng, V.W. The road to fully integrated DC–DC conversion via the switched-capacitor approach. IEEE Trans. Power Electron. 2012, 28, 4146–4155. [Google Scholar] [CrossRef]
- Meijer, M.; Liu, B.; van Veen, R.; de Gyvez, J.P. Post-Silicon Tuning Capabilities of 45nm Low-Power CMOS Digital Circuits. In Proceedings of the IEEE Symposium VLSI Circuits, Kyoto, Japan, 16–18 June 2009; pp. 110–111. [Google Scholar]
- Meijer, M.; de Gyvez, J.P.; Kapoor, A. Ultra-low-power digital design with body biasing for low area and performance-efficient operation. J. Low Power Electron. 2010, 6, 521–532. [Google Scholar] [CrossRef]
- Piqué, G.V.; Meijer, M. A 350nA Voltage Regulator for 90nm CMOS Digital Circuits with Reverse-Body-Bias. In Proceedings of the IEEE 37th Solid-State Circuits Conference, Helsinki, Finland, 12–16 September 2011; pp. 379–382. [Google Scholar]
- Kwong, J.; Ramadass, Y.K.; Verma, N.; Chandrakasan, A.P. A 65nm sub-Vt microcontroller with integrated SRAM and switched-capacitor DC-DC converter. IEEE J. Solid State Circuits 2009, 44, 115–126. [Google Scholar] [CrossRef]
- Van Breussegem, T.; Wens, M.; Redouté, J.-M.; Geukens, E.; Geys, D.; Steyaert, M. A DMOS Integrated 320mW Capacitive 12V to 70V DC/DC Converter for LIDAR Applications. In Proceedings of the 2009 Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3865–3869. [Google Scholar]
- Ebrahim, M.A.; Abdel Fattah, R.M.; Saied, E.M.; Abdel Maksoud, S.M.; El Khash, H. Droop Control of an Islanded Microgrid Using Harris Hawks Optimization Algorithm. Int J. Appl. Math. Comput. Sci. Syst. Eng. 2021, 3, 48–53. [Google Scholar]
- El-Bayeh, C.Z. A Review on Charging Strategies of Plug-in Electric Vehicles. Eng. World 2019, 1, 9–33. [Google Scholar]
- Wittmann, J.; Neidhardt, J.; Wicht, B. EMC optimized design of linear regulators including a charge pump. IEEE Trans. Power Electron. 2013, 28, 4594–4602. [Google Scholar] [CrossRef]
- Khan, M.N.H.; Forouzesh, M.; Siwakoti, Y.P.; Li, L.; Blaabjerg, F. Switched capacitor integrated (2n + 1)-level step-up single-phase inverter. IEEE Trans. Power Electron. 2019, 35, 8248–8260. [Google Scholar] [CrossRef]
- Arntzen, B.; Maksimovic, D. Switched-capacitor DC/DC converters with resonant gate drive. IEEE Trans. Power Electron. 1998, 13, 892–902. [Google Scholar] [CrossRef][Green Version]
- Seeman, M.D.; Sanders, S.R. Analysis and optimization of switched capacitor DC–DC converters. IEEE Trans. Power Electron. 2008, 23, 841–851. [Google Scholar] [CrossRef]
- Makowski, M.; Maksimovic, D. Performance Limits of Switched Capacitor DC–DC Converters. In Proceedings of the IEEE Power Electronics Specialists Conference, Atlanta, GA, USA, 18–22 June 1995; pp. 1215–1221. [Google Scholar]
- Ramadass, Y.K.; Chandrakasan, A.P. Voltage Scalable Switched Capacitor DC–DC Converter for Ultra-Low Power On-Chip Applications. In Proceedings of the IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2353–2359. [Google Scholar]
- Maksimovic, D.; Dhar, S. Switched-Capacitor DC-DC Converters for Low-Power On-Chip Applications. In Proceedings of the IEEE Power Electronics Specialists Conference, Charleston, SC, USA, 1 July 1999; pp. 54–59. [Google Scholar]
- Villar, G.; Alarcon, E.; Madrenas, J.; Guinjoan, F.; Poveda, A. Energy Optimization of Tapered Buffers for CMOS On-Chip Switching Power Converters. In Proceedings of the IEEE International Symposium Circuits System, Piscataway, NJ, USA, 23–26 May 2005; pp. 4453–4456. [Google Scholar]
- Villar-Pique, G.; Bergveld, H.J.; Alarcon, E. Survey and benchmark of fully integrated switching power converters: Switched-capacitor versus inductive approach. IEEE Trans. Power Electron. 2013, 28, 4156–4167. [Google Scholar] [CrossRef]
- Le, H.P.; Seeman, M.; Sanders, S.R.; Sathe, V.; Naffziger, S.; Alon, E. A 32nm Fully Integrated Reconfigurable Switched-Capacitor DC-DC Converter Delivering 0.55w/mm2 at 81% Efficiency. In Proceedings of the IEEE International Solid-State Circuit Conference, San Francisco, CA, USA, 7–11 February 2010; pp. 210–211. [Google Scholar]
- Van Breussegem, T.; Steyaert, M. A Fully Integrated Gearbox Capacitive DC/DC-Converter in 90nm CMOS: Optimization, Control and Measurements. In Proceedings of the IEEE Workshop Control Modeling Power Electronics, Boulder, CO, USA, 28–30 June 2010; pp. 1–5. [Google Scholar]
- Villar Piqué, G. A 41-Phase Switched-Capacitor Power Converter with 3.8 mv Output Ripple and 81% Efficiency in Baseline 90 nm CMOS. In Proceedings of the IEEE International Solid-State Circuit Conference, San Francisco, CA, USA, 19–23 February 2012; pp. 98–100. [Google Scholar]
- Le, H.P.; Sanders, S.R.; Alon, E. Design techniques for fully integrated switched-capacitor DC-DC converters. IEEE J. Solid State Circuits 2011, 46, 2120–2131. [Google Scholar] [CrossRef]
- Bin, S.; Yujia, Y.; Ying, W.; Zhiliang, H. High Efficiency, Inductor Less Step-Down DC/DC Converter. In Proceedings of the IEEE International Conference ASIC, Shanghai, China, 24–27 October 2005; pp. 364–367. [Google Scholar]
- Rao, A.; McIntyre, W.; Moon, U.K.; Temes, G.C. Noise-shaping techniques applied to switched-capacitor voltage regulators. IEEE J. Solid State Circuits 2005, 40, 422–429. [Google Scholar] [CrossRef]
- Ramadass, Y.K.; Fayed, A.A.; Chandrakasan, A.P. A fully-integrated switched-capacitor step-down DC-DC converter with digital capacitance modulation in 45 nm CMOS. J. Solid State Circuits 2010, 45, 2557–2565. [Google Scholar] [CrossRef]
- Ling, S.; Dongsheng, M.; Brokaw, A.P. A Monolithic Step-down SC Power Converter with Frequency-Programmable Sub-threshold Z-Domain Dpwm Control for UL-Tra-Low Power Microsystems. In Proceedings of the IEEE European Solid-State Circuit Conference, Edinburgh, UK, 15–19 September 2008; pp. 56–61. [Google Scholar]
- Ling, S.; Dongsheng, M.; Brokaw, A.P. Design and analysis of monolithic step-down SC power converter with sub-threshold DPWM control for self-powered wireless sensors. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 280–290. [Google Scholar] [CrossRef]
- Van Breussegem, T.; Steyaert, M. A Fully Integrated 74% Efficiency 3.6v to 1.5v 150mw Capacitive Point of Load DC/DC Converter. In Proceedings of the IEEE European Solid-State Circuit Conference, Seville, Spain, 13–17 September 2010; pp. 434–437. [Google Scholar]
- Van Breussegem, T.; Steyaert, M. A 82% Efficiency 0.5% Ripple 16-Phase Fully Integrated Capacitive Voltage Doubler. In Proceedings of the IEEE Symposium VLSI Circuits, Kyoto, Japan, 16–18 June 2009; pp. 198–199. [Google Scholar]
- Seeman, M.D.; Sanders, S.R.; Rabaey, J.M. An Ultra-Low-Power Power Management IC for Energy-Scavenged Wireless Sensor Nodes. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 925–931. [Google Scholar]
- Bhattacharyya, K.; Kumar, P.V.R.; Mandal, P. Embedded Hybrid DC-DC Converter with Improved Power Efficiency. In Proceedings of the IEEE International Midwest Symposium Circuits System, Cancun, Mexico, 2–5 August 2009; pp. 945–948. [Google Scholar]
- Wieckowski, M.; Chen, G.K.; Seok, M.; Blaauw, D.; Sylvester, D. A Hybrid DC-DC Converter for Sub-Microwatt Sub-1V Implantable Applications. In Proceedings of the IEEE Symposium VLSI Circuits, Kyoto, Japan, 16–18 June 2009; pp. 166–167. [Google Scholar]
- Somasekhar, D.; Srinivasan, B.; Pandya, G.; Hamzaoglu, F.; Khellah, M.; Karnik, T.; Zhang, K. Multi-phase 1GHz voltage doubler charge pump in 32nm logic process. IEEE J. Solid State Circuits 2010, 45, 751–758. [Google Scholar] [CrossRef]
- Meyvaert, H.; van Breussegem, T.; Steyaert, M. A Monolithic 0.77w/mm2 Power Dense Capacitive DC-DC Step-Down Converter in 90nm Bulk CMO. In Proceedings of the IEEE 37th Solid-State Circuits Conference, Helsinki, Finland, 12–16 September 2011; pp. 483–486. [Google Scholar]
- Klootwijk, J.H.; Jinesh, K.B.; Dekkers, W.; Verhoeven, J.F.; van den Heuvel, F.C.; Kim, H.D.; Blin, D.; Verheijen, M.A.; Weemaes, R.; Kaiser, M. Ultrahigh capacitance density for multiple ALD-grown MIM capacitor stacks in 3-D silicon. IEEE Electron Device Lett. 2008, 29, 740–742. [Google Scholar] [CrossRef]
- Leland, C.; Montoye, R.K.; Ji, B.L.; Weger, A.J.; Stawiasz, K.G.; Dennard, R.H. A Fully-Integrated Switched-Capacitor 2:1 Voltage Converter with Regulation Capability and 90% Efficiency at 2.3a/mm2. In Proceedings of the IEEE Symposium VLSI Circuits, Honolulu, HI, USA, 15–17 June 2010; pp. 55–56. [Google Scholar]
- Wibben, J.; Harjani, R. A high-efficiency DC-DC converter using 2 nH integrated inductors. J. Solid State Circuits 2008, 43, 844–854. [Google Scholar] [CrossRef]
- Wibben, J.; Harjani, R. A High Efficiency DC-DC Converter Using 2 nH On-Chip Inductors. In Proceedings of the 2007 IEEE Symposium VLSI Circuits, Kyoto, Japan, 14–16 June 2007; pp. 22–23. [Google Scholar]
- Musunuri, S.; Chapman, P. Design of Low Power Monolithic DC-DC Buck Converter with Integrated Inductor. In Proceedings of the IEEE Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 1773–1779. [Google Scholar]
- Schrom, G.; Hazucha, P.; Paillet, F.; Rennie, D.J.; Moon, S.T.; Gardner, D.S.; Kamik, T.; Sun, P.; Nguyen, T.T.; Hill, M.J. A 100 mhz Eight-Phase Buck Converter Delivering 12 a in 25 mm2 Using Air-Core Inductors. In Proceedings of the IEEE Applied Power Electronics Conference, Anaheim, CA, USA, 25 February–1 March 2007; pp. 727–730. [Google Scholar]
- Schrom, G.; Hazucha, P.; Hahn, J.; Gardner, D.; Bloechel, B.; Dermer, G.; Narendra, S.; Karnik, T.; De, V. A 480-MHz, Multi-Phase Interleaved Buck DC-DC Converter with Hysteretic Control. In Proceedings of the IEEE Power Electronics Specialists Conference, PESC’04, Piscataway, NJ, USA, 20–25 June 2004; Volume 6, pp. 4702–4707. [Google Scholar]
- Hazucha, P.; Schrom, G.; Hahn, J.; Bloechel, B.A.; Hack, P.; Dermer, G.E.; Narendra, S.; Gardner, D.; Karnik, T.; De, V. A 233 MHz 80%–87% efficient four-phase DC-DC converter utilizing air-core inductors on package. J. Solid State Circuits 2005, 40, 838–845. [Google Scholar] [CrossRef]
- Gardner, D.S.; Schrom, G.; Paillet, F.; Jamieson, B.; Karnik, T.; Borkar, S. Review of on-chip inductor structures with magnetic films. IEEE Trans. Magn. 2009, 45, 4760–4766. [Google Scholar] [CrossRef]
- Morrow, P.R.; Park, C.M.; Koertzen, H.W.; Dibene, J.T. Design and fabrication of on-chip coupled inductors integrated with magnetic material for voltage regulators. IEEE Trans. Magn. 2011, 47, 1678–1686. [Google Scholar] [CrossRef]
- Sturcken, N.; Davies, R.; Cheng, C.; Baileys, W.E.; Shepard, K.L. Design of Coupled Power Inductors with Crossed Anisotropy Magnetic Core for Integrated Power Conversion. In Proceedings of the 27th Annual IEEE Applied Power Electronics Conference Exposition, APEC 2012, Orlando, FL, USA, 5–9 February 2012; pp. 417–423. [Google Scholar]
- Sturcken, N.; Petracca, M.; Warren, S.; Mantovani, P.; Carloni, L.P.; Peterchev, A.V.; Shepard, K.L. A switched-inductor integrated voltage regulator with nonlinear feedback and network-on-chip load in 45 nm SOI. J. Solid State Circuits 2012, 47, 1935–1945. [Google Scholar] [CrossRef]
- Bergveld, H.J.; Karadi, R.; Nowak, K. An Inductive Down Converter System-in-Package for Integrated Power Management in Battery-Powered Applications. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 3335–3341. [Google Scholar]
- Meere, R.; O’Donnell, T.; Bergveld, H.J.; Ningning, W.; O’Mathuna, S.C. Analysis of micro inductor performance in a 20-100 MHz DC/DC converter. IEEE Trans. Power Electron. 2009, 24, 2212–2218. [Google Scholar] [CrossRef]
- Schrom, G.; Faillet, F.; Hahn, J. A 60 Mhz 50wfine-Grain Package Integrated vr Powering a CPU from 3.3 V. In Proceedings of the Applied Power Electronics Conference, Palm Springs, CA, USA, 21–25 February 2010. [Google Scholar]
- Wens, M. Monolithic Inductive CMOS DC-DC Converters—Theory Study and Implementation. Ph.D. Thesis, Dep. Elektrotechniek, Katholieke Universiteit Leuven, Leuven, Belgium, October 2010. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Akroum, H.; Kidouche, M.; Aibeche, A. Scalar Control of Induction Motor Drives Using dSPACE DS1104. In Proceedings of the International Conference on Systems, Control and Informatics, 28 September 2013; pp. 322–327. [Google Scholar]
- Deleage, O.; Crebier, J.C.; Brunet, M.; Lembeye, Y.; Manh, H.T. Design and realization of highly integrated isolated DC/DC microconverter. IEEE Trans. Ind. Appl. 2011, 47, 930–938. [Google Scholar] [CrossRef]
- Haizoune, F.; Bergveld, H.J.; Popovic-Gerber, J.; Ferreira, J.A. Topology Comparison and Design Optimisation of the Buck Converter and the Single-Inductor Dual-Output Converter for Sys-Tem-in-Package in 65 nm CMOS. In Proceedings of the IEEE International Power Electronic Motion Control Conference, Piscataway, NJ, USA, 17–20 May 2009; pp. 295–301. [Google Scholar]
- Piqué, G.V.; Alarcón, E. CMOS Integrated Switching Power Converters: A Structured Design Approach, 1st ed.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Bergveld, H.J.; Nowak, K.; Karadi, R.; Iochem, S.; Ferreira, J.; Ledain, S.; Pieraerts, E.; Pommier, M. A 65-NM CMOS 100-Mhz 87%-Efficient DC-DC Down Converter Based on Dual-Die System-in-Package Integration. In Proceedings of the IEEE Energy Conversion Congress Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3698–3705. [Google Scholar]
- Bathily, M.; Allard, B.; Hasbani, F. A 200-MHz integrated buck converter with resonant gate drivers for an RF power amplifier. IEEE Trans. Power Electron. 2012, 27, 610–613. [Google Scholar] [CrossRef]
- Maksimovic, D. Design of the Zero-Voltage-Switching Quasi-Square-Wave Resonant Switch. In Proceedings of the IEEE Power Electronics Specialists Conference, Seattle, WA, USA, 20–24 June 1993; pp. 323–329. [Google Scholar]
- Trescases, O.; Ng, W.T. Variable Output, Soft-Switching DC/DC Converter for Vlsi Dynamic Voltage Scaling Power Supply Applications. In Proceedings of the IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4149–4155. [Google Scholar]
- Lau, W.; Sanders, S. An Integrated Controller for a High-Frequency Buck Converter. In Proceedings of the IEEE Power Electronics Specialists Conference, Saint Louis, MO, USA, 27 June 1997; pp. 246–254. [Google Scholar]
- Chen, S.; Trescases, O.; Ng, W.T. Fast Dead-Time Locked Loops for a High-Efficiency Microprocessor-Load Zvs-Qsw DC/DC Converter. In Proceedings of the IEEE Conference on Electron Devices and Solid-State Circuits, Hong Kong, China, 16–18 December 2003; pp. 391–394. [Google Scholar]
- Trescases, O.; Ng, W.T.; Chen, S. Precision Gate Drive Timing in a Zero-Voltage-Switching DC-DC Converter. In Proceedings of the IEEE Symposium Power Semiconductor Devices ICs, Kitakyushu, Japan, 17–24 May 2004; pp. 55–58. [Google Scholar]
- Maderbacher, G.; Jackum, T.; Pribyl, W.; Wassermann, M.; Petschar, A.; Sandner, C. Automatic Dead Time Optimization in a High Frequency Dcdc Buck Converter in 65 NM CMOS. In Proceedings of the European Solid-State Circuits Conference, Helsinki, Finland, 12–16 September 2011; pp. 487–490. [Google Scholar]
- Piqué, G.V.; Alarcon, E. Monolithic Integration of a 3-Level Dcmoperated Low-Floating-Capacitor Buck Converter Fordc-DC Step-down Conversion in Standard CMOS. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 4229–4235. [Google Scholar]
- Kim, W.; Brooks, D.; Wei, G.-Y. A fully-integrated 3-level DC-DC converter for nanosecond-scale DVFS. IEEE J. Solid State Circuits 2012, 47, 206–219. [Google Scholar] [CrossRef]
- Wens, M.; Steyaert, M. An 800 MW Fully Integrated 130nm CMOS DC-DC Step-down Multi-Phase Converter with on-Chip Spiral Inductors and CA-Pacitors. In Proceedings of the IEEE Energy Conversion Congress Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3706–3709. [Google Scholar]
- Schrom, G.; Hazucha, P.; Hahn, J.H.; Kursun, V.; Gardner, D.; Narendra, S.; Karnik, T.; De, V. Feasibility of Monolithic and 3d-Stacked DC-DC Converters for Microprocessors in 90nm Technology Generation. In Proceedings of the IEEE International Symposium of Low-Power Electronics and Design, Newport Beach, CA, USA, 5 August 2004; pp. 263–268. [Google Scholar]
- Kursun, V.; Narendra, S.G.; De, V.K.; Friedman, E.G. High Input Voltage Step-down DC-DC Converters for Integration in a Low Voltage CMOS Process. In Proceedings of the IEEE International Symposium Quality Electronic Design, San Jose, CA, USA, 22–24 March 2004; pp. 517–521. [Google Scholar]
- Heringa, A.; Sonsky, J. Novel Power Transistor Design for a Process Independent High Voltage Option in Standard CMOS. In Proceedings of the IEEE Symposium Power Semiconductor Devices IC’s, Naples, Italy, 4–8 June 2006; pp. 1–4. [Google Scholar]
- Calvillo-Cortes, D.A.; Acar, M.; van der Heijden, M.P.; Apostolidou, M.; de Vreede, L.C.N.; Leenaerts, D.; Sonsky, J. A 65 nm Pulse-Widthcontrolled Driver with 8Vpp Output Voltage for Switched-Mode RF Pas up to 3.6ghz. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 20–24 February 2011; pp. 12–14. [Google Scholar]
- Peng, H.; Wright, P.; Hella, M.M.; Chow, T.P. Integrated high frequency power converters based on GaAs pHEMT: Technology characterization and design examples. IEEE Trans. Power Electron. 2012, 27, 2644–2656. [Google Scholar]
- Li, P.; Bhatia, D.; Xue, L.; Bashirullah, R. A 90–240 MHz hysteretic controlled DC-DC buck converter with digital phase locked loop synchronization. J. Solid State Circuits 2011, 46, 2108–2119. [Google Scholar] [CrossRef]
- Hayashi, Z.; Katayama, Y.; Edo, M.; Nishio, H. High-efficiency DCDC converter chip size module with integrated soft ferrite. IEEE Trans. Magn. 2003, 39, 3068–3072. [Google Scholar] [CrossRef]
- Su, F.; Ki, W.; Tsui, C. Regulated switched-capacitor doubler with interleaving control for continuous output regulation. J. Solid State Circuits 2009, 44, 1112–1120. [Google Scholar] [CrossRef]
- Xiaojian, Y.; Moez, K.; Wey, I.-C.; Sawan, M.; Chen, J. A fully integrated multistage cross-coupled voltage multiplier with no reversion power loss in a standard CMOS process. IEEE Trans. Circuits Syst. II Express Briefs 2016, 64, 737–741. [Google Scholar]
- Lee, H.; Mok, P. Switching noise and shoot-through current reduction techniques for switched-capacitor voltage doubler. J. Solid State Circuits 2005, 40, 1136–1146. [Google Scholar] [CrossRef]
- Jinhua, N.; Hong, Z.; Liu, B.Y. Improved On-Chip Components for Integrated DC-DC Converters in 0.13 μm CMOS. In Proceedings of the IEEE European Solid-State Circuits Conference, Athens, Greece, 14–18 September 2009; pp. 448–451. [Google Scholar]
- Alimadadi, M.; Sheikhaei, S.; Lemieux, G.; Mirabbasi, S.; Dunford, W.G.; Palmer, P.R. A fully integrated 660 MHz low-swing energy-recycling DC-DC converter. IEEE Trans. Power Electron. 2009, 24, 1475–1485. [Google Scholar] [CrossRef]
- Kudva, S.S.; Harjani, R. Fully-integrated on-chip DC-DC converter with a 450× output range. J. Solid State Circuits 2011, 46, 1940–1951. [Google Scholar] [CrossRef]
- Abedinpour, S.; Bakkaloglu, B.; Kiaei, S. A multistage interleaved synchronous buck converter with integrated output filter in 0.18μm SiGe process. IEEE Trans. Power Electron. 2007, 22, 2164–2175. [Google Scholar] [CrossRef]
- Wens, M.; Steyaert, M. A Fully Integrated 0.18 μM CMOS DC-DC Step-down Converter, Using a Bondwire Spiral Inductor. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 21–14 September 2008; pp. 17–20. [Google Scholar]
- DibeneII, J.T. Power on Silicon with on-Die Magnetics—the Start of a Revolution in Power Delivery and Power Management for Soc’s and High-Performance Applications. In Proceedings of the 2nd International Workshop Power Supply Chip, Cork, Ireland, 13 October 2010. [Google Scholar]
- Sturcken, N.; O’Sullivan, E.J.; Wang, N.; Herget, P.; Webb, B.; Romankiw, L.T.; Petracca, M.; Davies, R.; Fontana, R.; Decad, G.M.; et al. A 2.5d Integrated Voltage Regulator Using Coupled Magnetic-Core Inductors on Silicon Interposer Delivering 10.8a/mm2. In Proceedings of the IEEE International Solid-State Circuit Conference, San Francisco, CA, USA, 19–23 February 2012. Session 23. [Google Scholar]
- Onizuka, K.; Inagaki, K.; Kawaguchi, H.; Takamiya, M.; Sakurai, T. Stacked-chip implementation of on-chip buck converter for distributed power supply system in SiPs. J. Solid State Circuits 2007, 42, 2404–2410. [Google Scholar] [CrossRef]
- Hernandez, H.; Kofuji, S.T.; van Noije, W. Fully Integrated Boost Converter for Thermoelectric Energy Harvesting. In Proceedings of the 2013 IEEE 4th Latin American Symposium on Circuits and Systems (LASCAS), Cusco, Peru, 27 February–1 March 2013. [Google Scholar]
- Wens, M.; Steyaert, M. A Fully-Integrated 0.18 μm CMOS DC-DC Step-Up Converter, Using a Bondwire Spiral Inductor. In Proceedings of the 33rd European Solid State Circuits Conference, Muenchen, Germany, 11–13 September 2007; pp. 268–271. [Google Scholar]
- Dam, S.; Mandal, P. An integrated DC–DC boost converter having low-output ripple suitable for analog applications. IEEE Trans. Power Electron. 2017, 33, 5108–5117. [Google Scholar] [CrossRef]
- Kennedy, S.; Yuce, M.R.; Redouté, J.-M. A Low-EMI Fully Integrated Switched-Capacitor DC/DC Converter. IEEE Trans. Electromagn. Compat. 2017, 60, 225–233. [Google Scholar] [CrossRef]

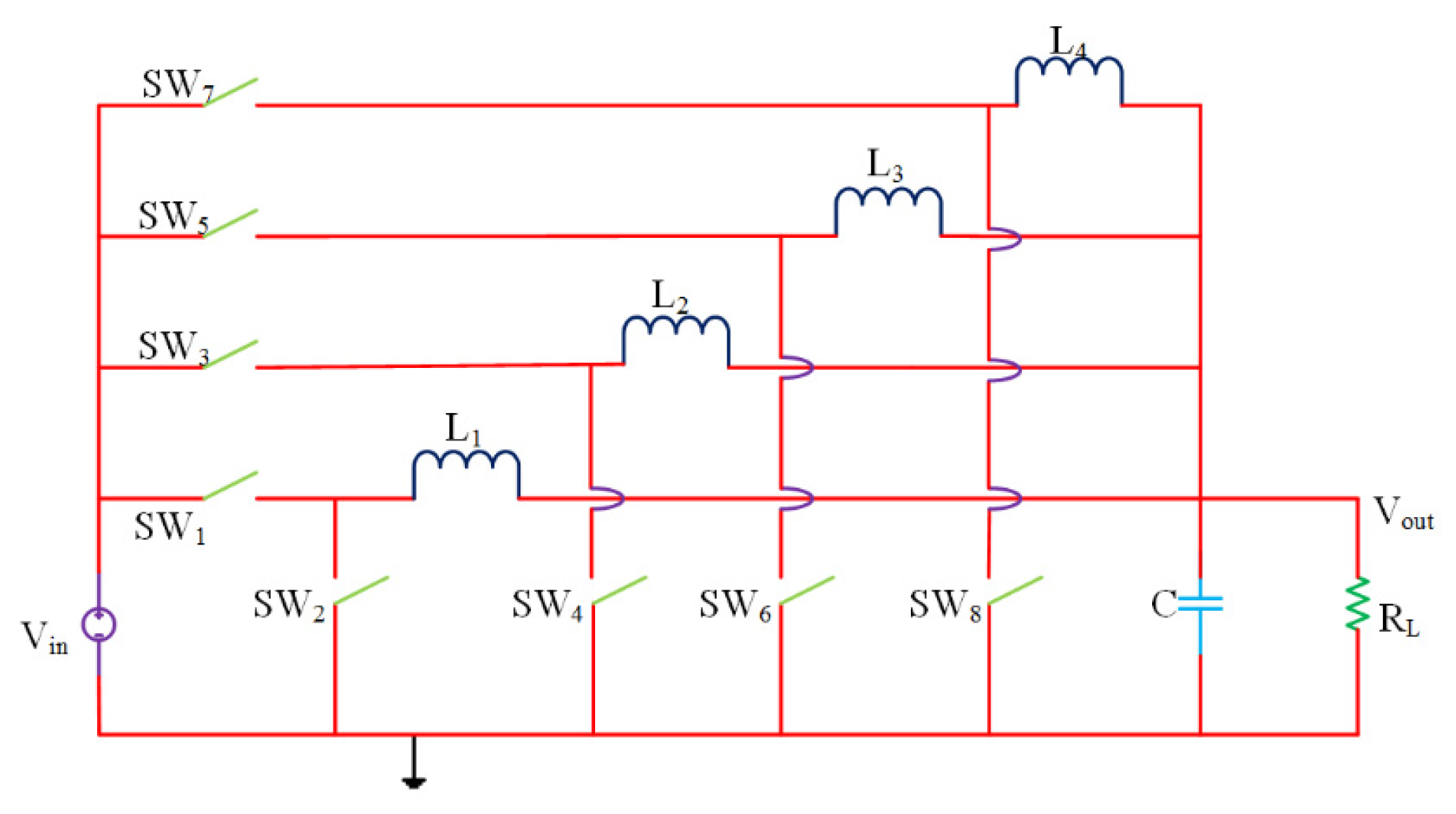
| Floating Capacitors | Feasible Conversion Ratios |
|---|---|
| 1 | ½; 1; 2 |
| 2 | 1/3; ½; 2/3; 1; 3/2; 2; 3 |
| 3 | 1/5; 1/4; 1/3; 2/5; ½; 3/5; 2/3; ¾; 4/5; 1; 5/4; 4/3; 3/2; 5/3; 2;5/2;3; 4; 5 |
| 4 | 1/8; 1/7; 1/6; 1/5; ¼; 2/7; 1/3; 3/8; 2/5; 3/7; ½; 4/7; 3/5; 5/8; 2/3; 5/7; ¾; 4/5; 5/6; 6/7; 7/8; 1; 8/7; 7/6; 6/5; 5/4; 4/3; 7/5; 3/2; 8/5; 5/3; 7/4; 2; 7/3; 5/2; 8/3; 3; 7/2; 4; 5; 6; 7; 8 |
| Control Strategy | Switching Losses | Conduction Losses | Noise | Continuous/Discrete |
|---|---|---|---|---|
| Conversion ratio [13,22,26,27,28] | -- | Reduces | Reduces | Discrete |
| Duty-cycle control [32,33,34] | Increases | -- | Reduces | Continuous |
| Switching frequency modulation [32,35,36,37] | Highly reduces | -- | Highly increases | Continuous |
| Ron modulation (Wch) [26,32] | Reduces | -- | Reduces | Discrete |
| Ron modulation (Vgs) [31] | Reduces | -- | Reduces | Continuous |
| Series LDO [38,39] | Highly increases | -- | Reduces | Continuous |
| Capacitor size modulation [32] | Highly reduces | -- | Reduces | Discrete |
| Parameters | [26] | [32] | [43] | [44] | [49] | [56] | [71] | [72] | [73] |
|---|---|---|---|---|---|---|---|---|---|
| Process technology | 32 nm SOI | 45 nm CMOS | 45 nm SOI | 130 nm CMOS | 90 nm CMOS | 130 nm CMOS | 250 nm CMOS | 130 nm CMOS | 130 nm CMOS |
| Topology | Fully integrated step-down SC converter | Fully integrated step-down SC converter | Fully integrated SC 2:1 voltage converter | Stacked interleaved buck converter | Four-phase buck converter | Buck | Step-down 3-level 2-phase converter | 3-level DC–DC converter (hybrid of buck and switched-capacitor) | Step-down four-phase converter |
| Inductor/Capacitor technology | Standard CMOS technology | Standard CMOS technology | Integrated on-chip trench capacitors | On-chip spiral inductors | Off-chip air-core inductors soldered to the package | Fe-core on-pkg | Bond-wire inductor | On-chip spiral inductors | On-chip spiral inductor |
| Vin (V) | 2 | 1.8 | 2 | 1.2 | 1.2–1.4 | 3.3 | 3.6 | 2.4 | 2–2.6 |
| VOUT (V) | 0.5–1.1 | 0.8–1 | 0.95 | 0.9 | 0.9 | 0–1.6 | 1 | 0.4–1.4 | 1.1–1.5 |
| Frequency (MHz) | 70 | 30 | 100 | 170 | 233 | 60 | 37.3 | 50–250 | 225 |
| No. of phases | 32 | - | - | 1 | 4 | 16 | 2 | 4 | 4 |
| L per phase (nH) | N/A | N/A | N/A | 2 | 6.8 | - | 26.7 | 1 | 3.9 |
| Total flying Capacitance (nF) | - | 0.534 | 0.2 | N/A | N/A | N/A | 5.07 | 18 | N/A |
| Output capacitance(nF) | 0 | 0.7 | - | 5.2 | 2.5 | - | 25.9 | 10 | 12.2 |
| Maximum power (W) | 0.3 | 0.008 | 0.0026 | 0.32 | 0.27 | 120 | 0.1 | 1 | 0.8 |
| Area (mm2) | 0.378 | 0.16 | 0.0012 | 1.5 | 1.26 | 37.6 | 5.01 | 5 | 3.8 |
| Power density (W/mm2) | 0.55 | 0.05 | 2.19 | 0.21 | 0.213 | 3.19 | 0.02 | 0.2 | 0.213 |
| Efficiency at peak (%) | 81 | 68.5 | 90 | 77.9 | 84.5 | 87.9 | 69.68 | 77 | 58 |
| Parameters | [92] | [93] | [94] |
|---|---|---|---|
| Process technology | 0.18 μm | 0.18 μm | 0.18 μm |
| Topology | Step-Up DC–DC converter | Step-Up DC–DC converter | Step-Up DC–DC converter |
| Capacitor (F) | 1.2 n (MOS) | 1.3 n (MIM) | 1.08 n (MOS) |
| Inductor (H) | 22 n (on-chip) | 18 n (bond wire) | 30 n (bond wire) |
| Vin (V) | 0.3 | 1.6–2 | 1.0–2.7 |
| VOUT (V) | 1.1 | 2.5–4 | 3.2 |
| Frequency (MHz) | - | 100 | 118 |
| Area (mm2) | 0.63 | 1 | 0.52 |
| Power density (W/mm2) | 0.032 | 0.149 | 0.387 |
| Efficiency at peak (%) | 45% | 63% | 75.9% |
| Ripple | - | 6.1% | 0.62% |
| Parameters | [14] | [17] | [36] | [81] | [82] | [83] | [95] |
|---|---|---|---|---|---|---|---|
| Process technology | 0.35 μm CMOS | 0.35 μm CMOS | 0.13 μm CMOS | 0.35 μm CMOS | 0.13 μm CMOS | 0.6 μm CMOS | 0.18 μm CMOS |
| Topology | Dickson | Dickson | SC Voltage Doubler | SC Interleaved Voltage Doubler | SC Voltage Doubler | SC Voltage Doubler | SC Voltage Doubler |
| Fully integrated | Yes | Yes | Yes | No | Yes | No | Yes |
| Capacitor technology | Finger | Integrated | MIM | External | On-chip | External | MIM |
| Total flying capacitance | 740 pF | 20 pF | 400 pF | 2 μF | 210 pF | 1 μF | 20 pF |
| Control mechanism | Frequency | Open loop | Frequency | Phase delay | Open loop | Open loop | Current |
| Clock frequency | 0–35.4 MHz | 6 MHz | 20 MHz | 200–500 kHz | 60 MHz | 500 kHz | 5–60 MHz |
| Ripple voltage | 2.7 V | - | 10 mV | 20 mV | - | - | 40 mV |
| Input capacitance | - | 10 pF | - | - | - | 220 nF | Parasitic Capacitance Only 3–5 pF |
| Output capacitance | - | 10 pF | 400 pF | 2 μF | 200 pF | 2.2 μF | 20 pF |
| Vin | 12 V | - | 1–1.2 V | 1.8–2.0 V | 1.2 V | 1.5–2.5 V | 1–1.8 V |
| IOUT | 4.57 mA | 50 μA | - | 10–180 mA | 1 mA | 50 mA | 1 mA |
| VOUT | 70 V | 3 × Vin | 1.8–2.1 V | 3.3 V | 1.99 × Vin | 2 × Vin | Vin–2 × Vin |
| ηmax | 21% | - | 82% | 91.5% | 88% | 95.7% | IEC 61,967 Class L (<24 dBμV) |
| Measured emissions | - | CISPR-25 Class 5 (<34 dBμV) | - | - | - | >69 dBμV | IEC 61,967 Class L (<24 dBμV) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiran Kumar, G.; Kobaku, T.; Sahoo, S.; Subudhi, B.; Elangovan, D.; Blaabjerg, F. An Overview of Fully Integrated Switching Power Converters Based on Switched-Capacitor versus Inductive Approach and Their Advanced Control Aspects. Energies 2021, 14, 3250. https://doi.org/10.3390/en14113250
Kiran Kumar G, Kobaku T, Sahoo S, Subudhi B, Elangovan D, Blaabjerg F. An Overview of Fully Integrated Switching Power Converters Based on Switched-Capacitor versus Inductive Approach and Their Advanced Control Aspects. Energies. 2021; 14(11):3250. https://doi.org/10.3390/en14113250
Chicago/Turabian StyleKiran Kumar, G, Tarakanath Kobaku, Subham Sahoo, Bidyadhar Subudhi, Devaraj Elangovan, and Frede Blaabjerg. 2021. "An Overview of Fully Integrated Switching Power Converters Based on Switched-Capacitor versus Inductive Approach and Their Advanced Control Aspects" Energies 14, no. 11: 3250. https://doi.org/10.3390/en14113250
APA StyleKiran Kumar, G., Kobaku, T., Sahoo, S., Subudhi, B., Elangovan, D., & Blaabjerg, F. (2021). An Overview of Fully Integrated Switching Power Converters Based on Switched-Capacitor versus Inductive Approach and Their Advanced Control Aspects. Energies, 14(11), 3250. https://doi.org/10.3390/en14113250









