Advancing Wind Resource Assessment in Complex Terrain with Scanning Lidar Measurements
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methodology
2.1.1. On-Site Measurements
2.1.2. Wind Flow Simulation and Projection of Numerical Data
2.1.3. Calibration of Numerical Flow Data
2.2. Demonstration Study
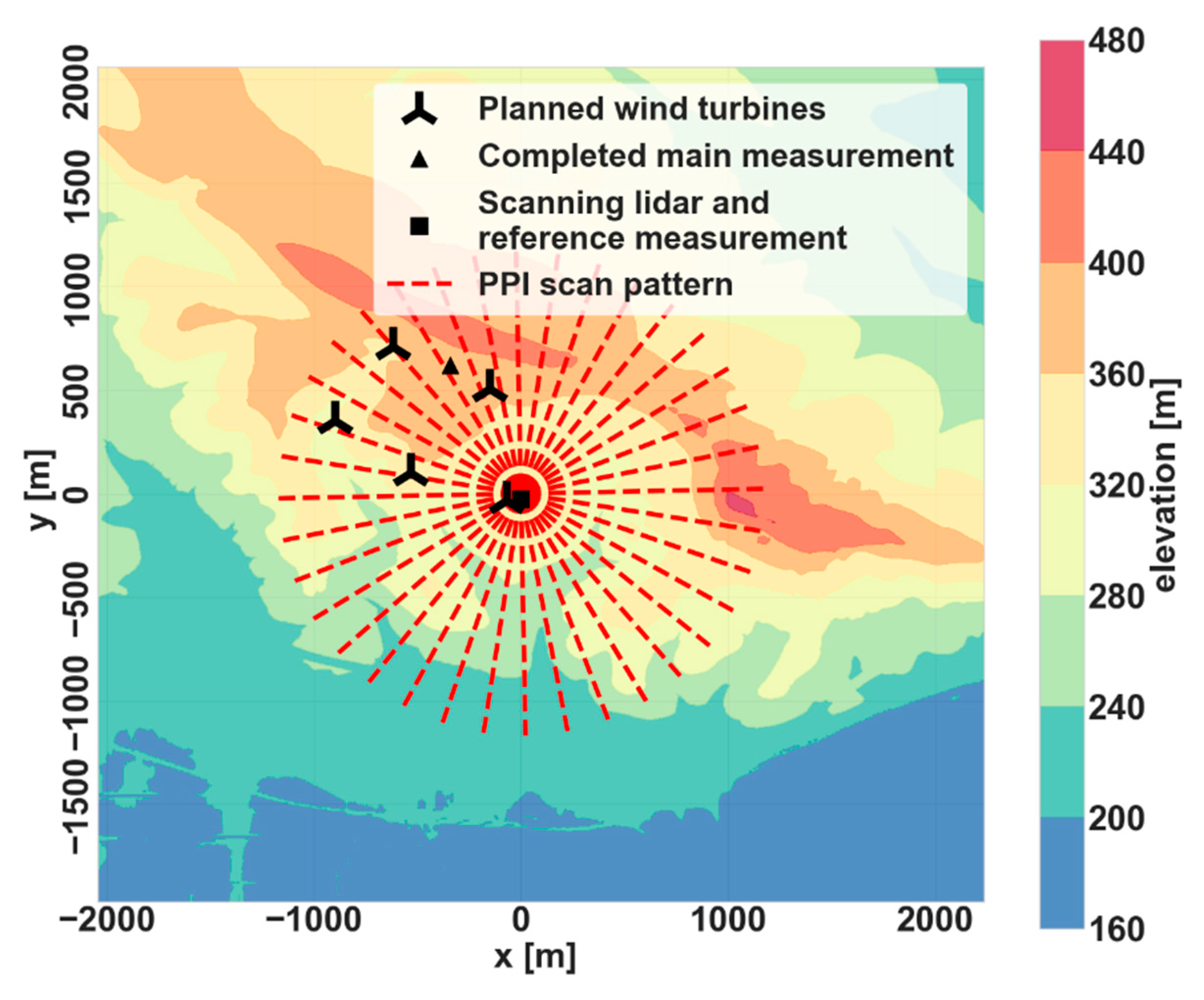
2.2.1. Description of Site
2.2.2. Used Measurements
2.2.3. Applied Flow Modelling
3. Results
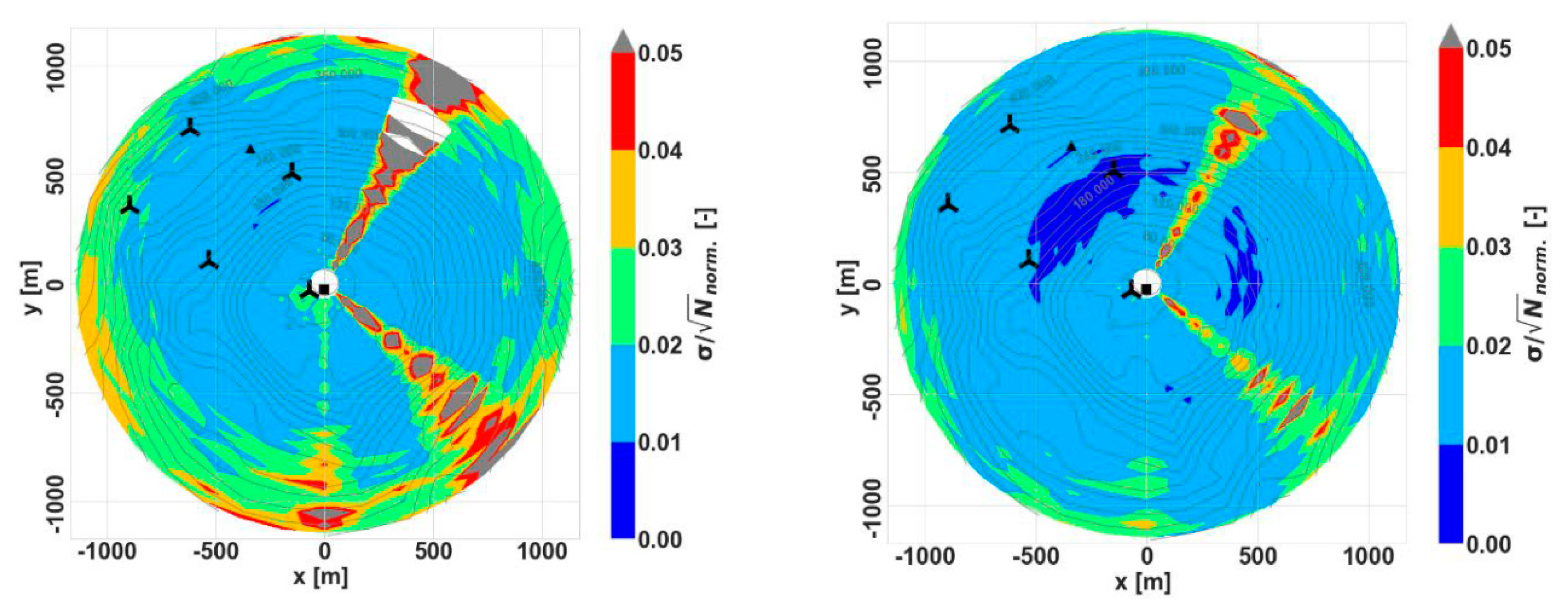
3.1. Data Coverage
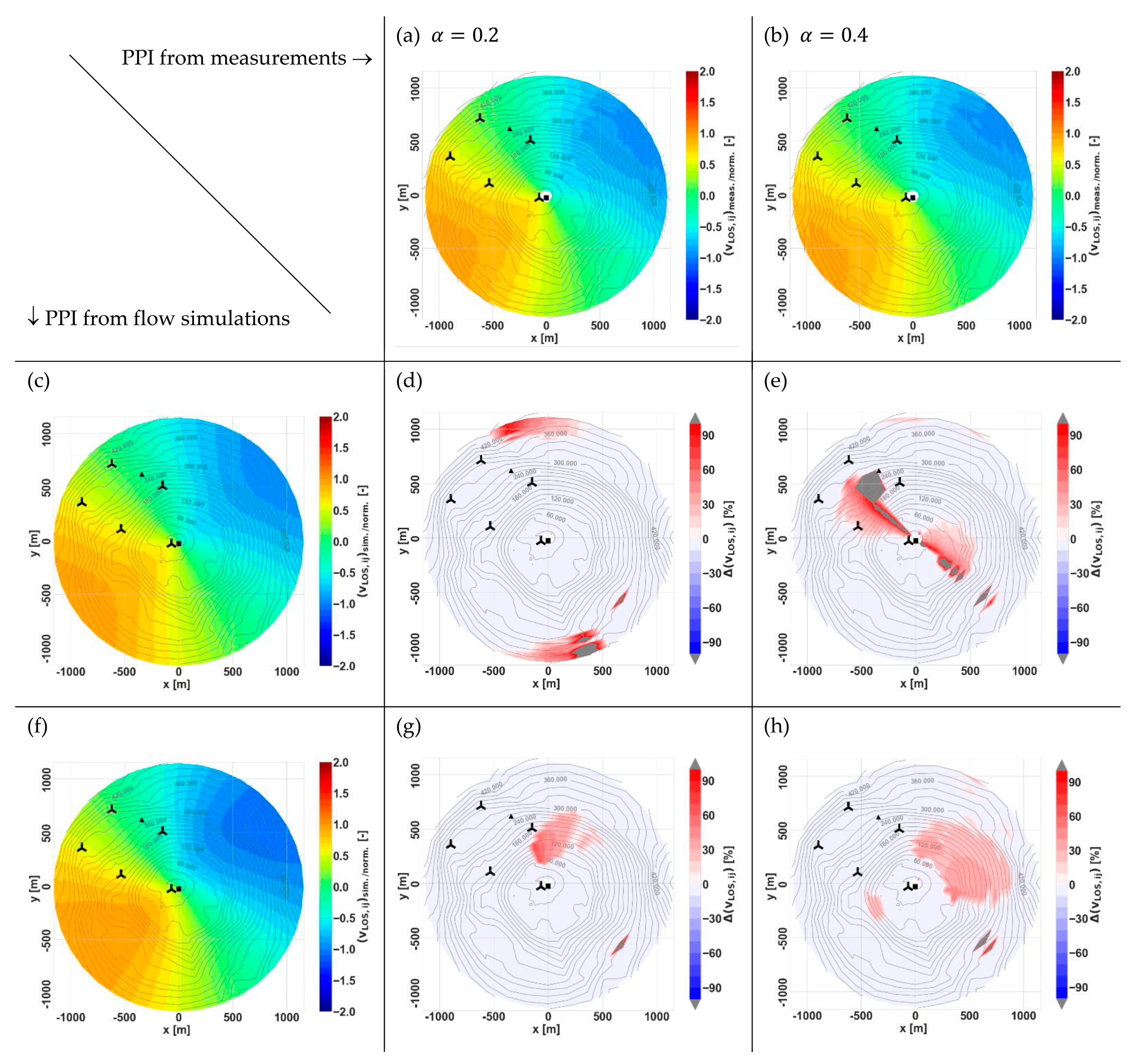
3.2. Single Flow Situation
3.3. Selected Flow Cases
- -
- When comparing the contour plots for the individual flow situation in Figure 5 and the averaged flow cases in Figure 7, with the same wind direction sector (240°) studied here, it is obvious that any local inhomogeneities, which are seen in the single flow situation comparison and can be connected with the non-stationarity of the wind conditions, are now averaged out.
- -
- The conical gray patterns again indicate a misalignment of the measurements with the simulations—for the averaged flow cases, this misalignment is however in a similar order for the two models.
- -
- For both wind directions shown in Figure 6 and Figure 7, the absence of the veer, i.e., wind direction shear (or rotation of wind with increasing height), in FIWind is indicated in terms of the pronounced deviations of the simulation results to the measurements at the outer parts of the PPI contour plots, which correspond due to the conical shape of the scan to higher altitudes. The results for FITNAH do not show these deviations to this extent, which may be explained by the fact that the veer is covered by the model as pointed out in Section 2.2.3.
- -
- Furthermore, we observe an over-speeding around the hill on which the scanning lidar was placed for the FITNAH results. This effect is reduced for the case with the lower shear exponent . Since the same terrain data is used as input to FITNAH and FIWind, we assume this over-speeding to be due to the other boundary conditions, i.e., the considered wind profile and again the reference wind direction.
4. Discussion
4.1. Potential of the Found Results
4.2. Limitations and Challenges to the Introduced Methodology
4.3. Application within WRA Study
- -
- no significant errors are found for the device under test,
- -
- a significant error is found but no adjustment is considered, or
- -
- an adjustment is undertaken to correct the error to some acceptable level.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
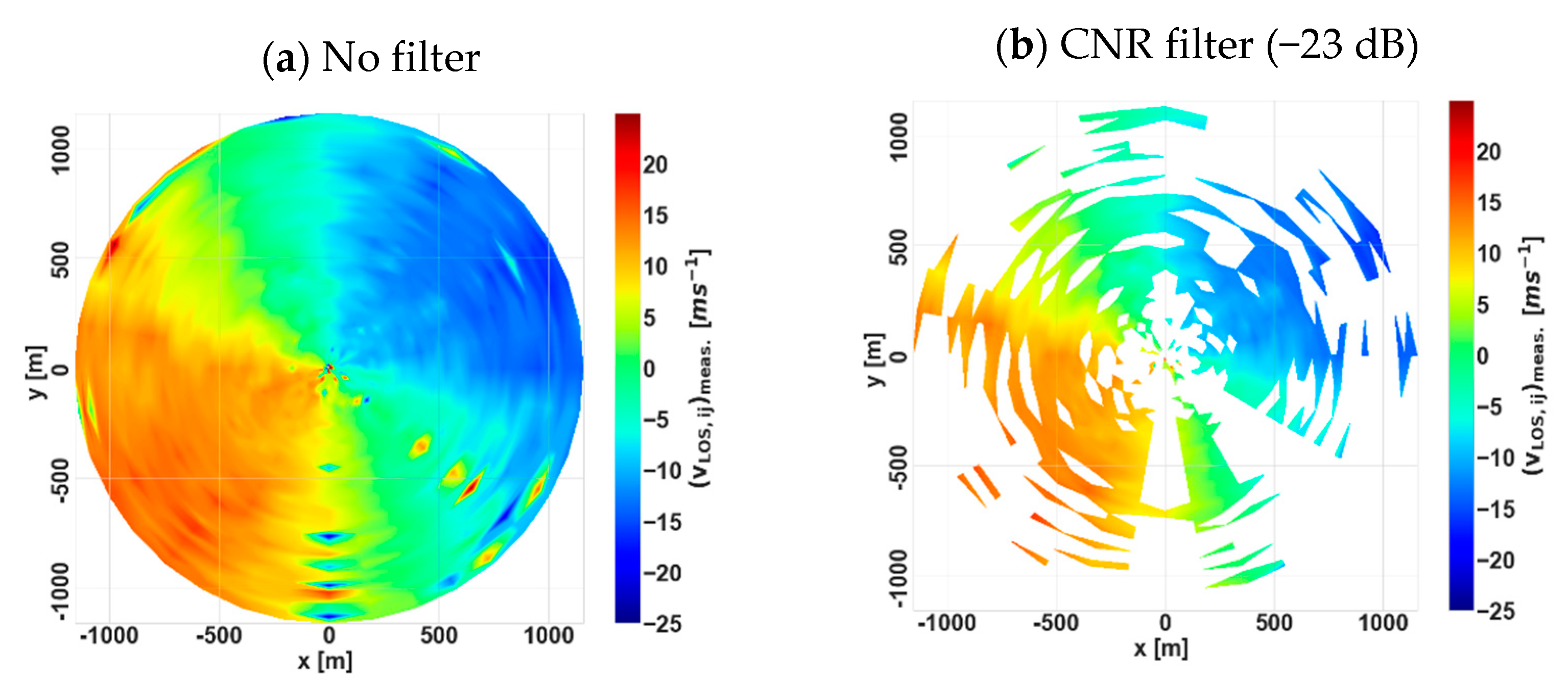
Appendix A. Filter Applied to Scanning Lidar Data

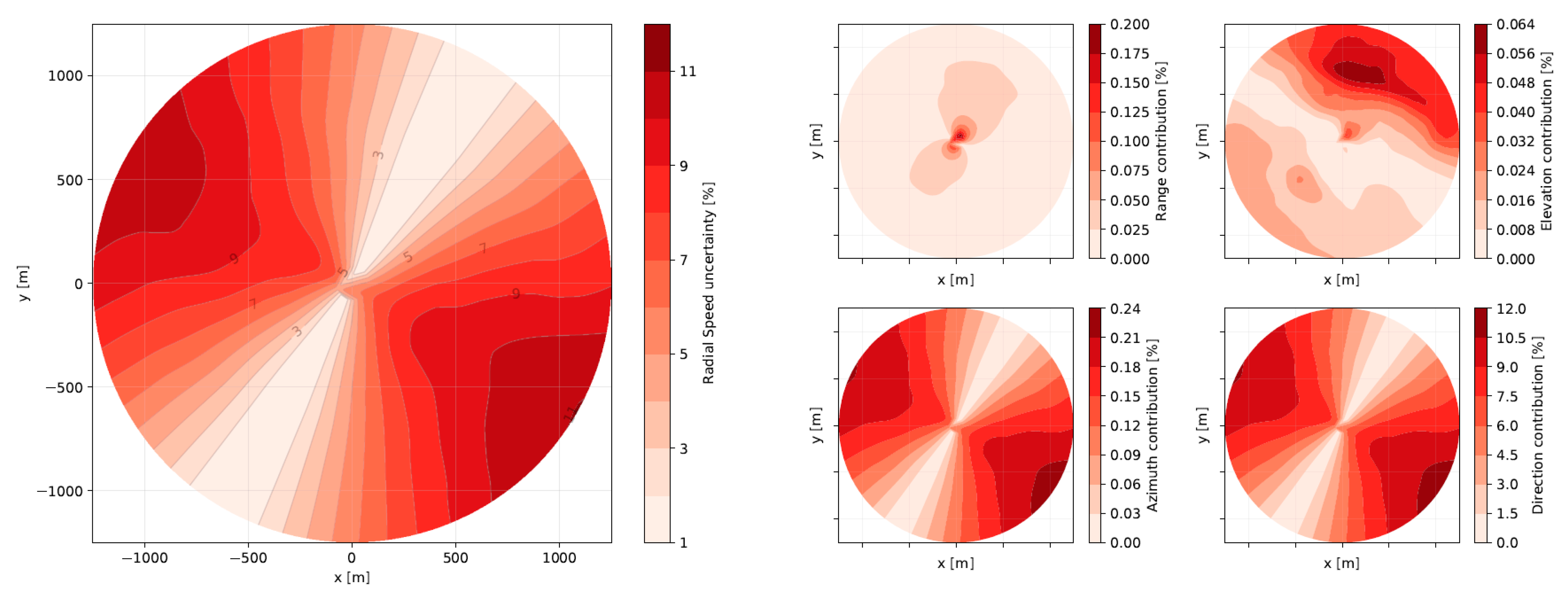
Appendix B. Scanning Lidar Uncertainty Modelling
References
- BMWi (German Federal Ministry of Economic Affair and Energy) Renewable Energy Sources Act (EEG 2017). Available online: https://www.bmwi.de/Redaktion/DE/Downloads/E/eeg-2017-gesetz-en.pdf?__blob=publicationFile&v=8 (accessed on 31 January 2021).
- Lee, J.C.Y.; Fields, J.M. An Overview of Wind Energy Production Prediction Bias, Losses, and Uncertainties. Wind Energy Sci. 2021. [Google Scholar] [CrossRef]
- Clifton, A.; Smith, A.; Fields, J.M. Wind Plant Preconstruction Energy Estimates: Current Practice and Opportunities; NREL/TP-5000-64735; National Renewable Energy Laboratory: Golden, CO, USA, 2016.
- Brower, M.C. Wind Resource Assessment: A Practical Guide to Developing a Wind Project; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- MEASNET: Evaluation of Site-Specific Wind Conditions. Version 2. April 2016. Available online: https://www.measnet.com/wp-content/uploads/2016/05/Measnet_SiteAssessment_V2.0.pdf (accessed on 31 January 2021).
- FGW. TR 6—Bestimmung von Windpotenzial und Energieertrag; Revision 11; Fördergesellschaft Windenergie und andere Dezentrale Energien: Berlin, Germany, 2020. [Google Scholar]
- IEC. IEC CD 61400-15: Wind Energy Generation Systems—Part 15-1: Site Suitability Input Conditions for Wind Power Plants; Committee Draft (CD); IEC: Geneva, Switzerland, 2020. [Google Scholar]
- Tang, X.; Stoevesandt, B.; Fan, B.; Li, S.; Yang, Q.; Tayjasanant, T.; Sun, Y. An on-site measurement coupled CFD based approach for wind resource assessment over complex terrains. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Saarnak, E.; Bergström, H.; Söderberg, S. Uncertainties Connected to Long-Term Correction of Wind Observations. Wind Eng. 2014, 38. [Google Scholar] [CrossRef]
- IEA Wind Expert Group Study on Recommended Practices 15. Ground-Based Vertically Profiling Remote Sensing for Wind Resource Assessment, First Edition. January 2013. Available online: https://community.ieawind.org/publications/rp (accessed on 31 January 2021).
- Vasiljevic, N.; Vignaroli, A.; Bechmann, A.; Wagner, R. Digitizing scanning lidar measurement campaign planning. Wind Energy Sci. 2020, 5, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Vasiljevic, N.; Lea, G.; Courtney, M.; Cariou, J.-P.; Mann, J.; Mikkelsen, T. Long-Range WindScanner System. Remote Sens. 2016, 8, 896. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Barthelmie, R.J.; Clifton, A.; Pryor, S.C. Wind measurements from arc scans with Doppler wind lidar. J. Atmos. Ocean. Technol. 2015, 32, 2024–2040. [Google Scholar] [CrossRef]
- Barkwith, A.; Collier, C.G. Lidar observations of flow variability over complex terrain. Meteorol. Appl. 2011, 18, 372–382. [Google Scholar] [CrossRef]
- Puccioni, M.; Iungo, G.V. Spectral correction of turbulent energy damping on wind lidar measurements due to spatial averaging. Atmos. Meas. Tech. 2021, 14, 1457–1474. [Google Scholar] [CrossRef]
- Drobinski, P.; Carlotti, P.; Redelsperger, J.-L.; Masson, V.; Banta, R.M.; Newsom, R.K. Numerical and Experimental Investigation of the Neutral Atmospheric Surface Layer. J. Atmos. Sci. 2007, 64, 137–156. [Google Scholar] [CrossRef]
- Pichugina, Y.L.; Tucker, S.C.; Banta, R.M.; Brewer, W.A.; Kelley, N.D.; Jonkman, B.J.; Newsom, R.K. Horizontal-Velocity and Variance Measurements in the Stable Boundary Layer Using Doppler Lidar: Sensitivity to Averaging Procedures. J. Atmos. Ocean. Technol. 2008, 25, 1307–1327. [Google Scholar] [CrossRef]
- van der Laan, M.P.; Andersen, S.J.; Réthoré, P.-E. Brief Communication: Wind-Speed-Independent Actuator Disk Control for Faster Annual Energy Production Calculations of Wind Farms Using Computational Fluid Dynamics. Wind Energy Sci. 2019, 4, 645–651. [Google Scholar] [CrossRef] [Green Version]
- van der Laan, M.P.; Andersen, S.J.; Kelly, M.; Baungaard, M.C. Fluid Scaling Laws of Idealized Wind Farm Simulations. J. Phys. Conf. Ser. 2020, 1618, 062018. [Google Scholar] [CrossRef]
- Buhr, R.; Kassem, H.; Steinfeld, G.; Alletto, M.; Witha, B.; Dörenkämper, M. A Multi-Point Meso–Micro Downscaling Method Including Atmospheric Stratification. Energies 2021, 14, 1191. [Google Scholar] [CrossRef]
- Svenningsen, L.; Slot, R.M.M.; Thøgersen, M.L. A novel method to quantify atmospheric stability. J. Phys. Conf. Ser. 2018, 1102, 012009. [Google Scholar] [CrossRef]
- Wood Galion Lidar Unit. Available online: https://www.woodplc.com/capabilities/digital-and-technology/software,-applications-and-analytics/galion-lidar-unit (accessed on 31 January 2021).
- Gross, G. The exploration of boundary layer phenomena using a nonhydrostatic mesoscale model. Meteorol. Z. 2002, 11, 295–302. [Google Scholar] [CrossRef]
- Gross, G.; Frey, T.; Trute, P. Die Anwendung numerischer Simulationsmodelle zur Berechnung der lokalen Windverhältnisse in komplexem Gelände. DEWI-Magazin 2002, 20, 28–36. [Google Scholar]
- Chang, C.-Y.; Schmidt, J.; Dörenkämper, M.; Stoevesandt, B. A Consistent Steady State CFD Simulation Method for Stratified Atmospheric Boundary Layer Flows. J. Wind Eng. Ind. Aerodyn. 2018, 172, 55–67. [Google Scholar] [CrossRef]
- Bonan, G.B.; Patton, E.G.; Harman, I.N.; Oleson, K.W.; Finnigan, J.J.; Lu, Y.; Burakowski, E.A. Modeling Canopy-Induced Turbulence in the Earth System: A Unified Parameterization of Turbulent Exchange within Plant Canopies and the Roughness Sublayer (CLM-Ml V0)’. Geosci. Model Dev. 2018, 11, 1467–1496. [Google Scholar] [CrossRef] [Green Version]
- Akbarzadeh, S.; Kassem, H.; Buhr, R.; Steinfeld, G.; Stoevesandt, B. Adjoint-Based Calibration of Inlet Boundary Condition for Atmospheric Computational Fluid Dynamics Solvers’. Wind Energy Sci. 2019, 4, 619–632. [Google Scholar] [CrossRef] [Green Version]
- Irwin, J.S. A Theoretical Variation of the Wind Profile Power-Law Exponent as a Function of Surface Roughness and Stability. Atmos. Environ. 1979, 13, 191–194. [Google Scholar] [CrossRef]
- Xu, C.; Hao, C.; Li, L.; Han, X.; Xue, F.; Sun, M.; Shen, W. Evaluation of the Power-Law Wind-Speed Extrapolation Method with Atmospheric Stability Classification Methods for Flows over Different Terrain Types. Appl. Sci. 2018, 8, 1429. [Google Scholar] [CrossRef] [Green Version]
- Lenschow, D.H.; Wulfmeyer, V.; Senff, C. Measuring second-through fourth-order moments in noisy data. J. Atmos. Ocean. Technol. 2000, 17, 1330–1347. [Google Scholar] [CrossRef]
- Foken, T.; Göockede, M.; Mauder, M.; Mahrt, L.; Amiro, B.; Munger, W. Post-field data quality control. In Handbook of Micrometeorology; Springer: Dordrecht, The Netherlands, 2014; pp. 181–208. [Google Scholar]
- JCGM 200:2012 International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM) 3rd Edition. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf (accessed on 31 January 2021).
- Beck, H.; Kühn, M. Dynamic Data Filtering of Long-Range Doppler LiDAR Wind Speed Measurements. Remote Sens. 2017, 9, 561. [Google Scholar] [CrossRef] [Green Version]
- Manninen, A.J.; O’Connor, E.J.; Vakkari, V.; Petäjä, T. A generalised background correction algorithm for a Halo Doppler lidar and its application to data from Finland. Atmos. Meas. Tech. 2016, 9, 817–827. [Google Scholar] [CrossRef] [Green Version]
- Bailey, D.G.; Hodgson, R.M. Range filters: Local intensity subrange filters and their properties. Image Vision Comput. 1985, 3, 99–110. [Google Scholar] [CrossRef]
- Würth, I.; Ellinghaus, S.; Wigger, M.; Niemeier, M.J.; Clifton, A.; Cheng, P.W. Forecasting wind ramps: Can long-range lidar increase accuracy? J. Phys. Conf. Ser. 2018, 1102, 012013. [Google Scholar] [CrossRef] [Green Version]
- Vasiljevic, N.; Courtney, M.; Tegtmeier Pedersen, A. Uncertainty model for dual-Doppler retrievals of wind speed and wind direction. Atmos. Meas. Tech. Discuss. 2020. [Google Scholar] [CrossRef]
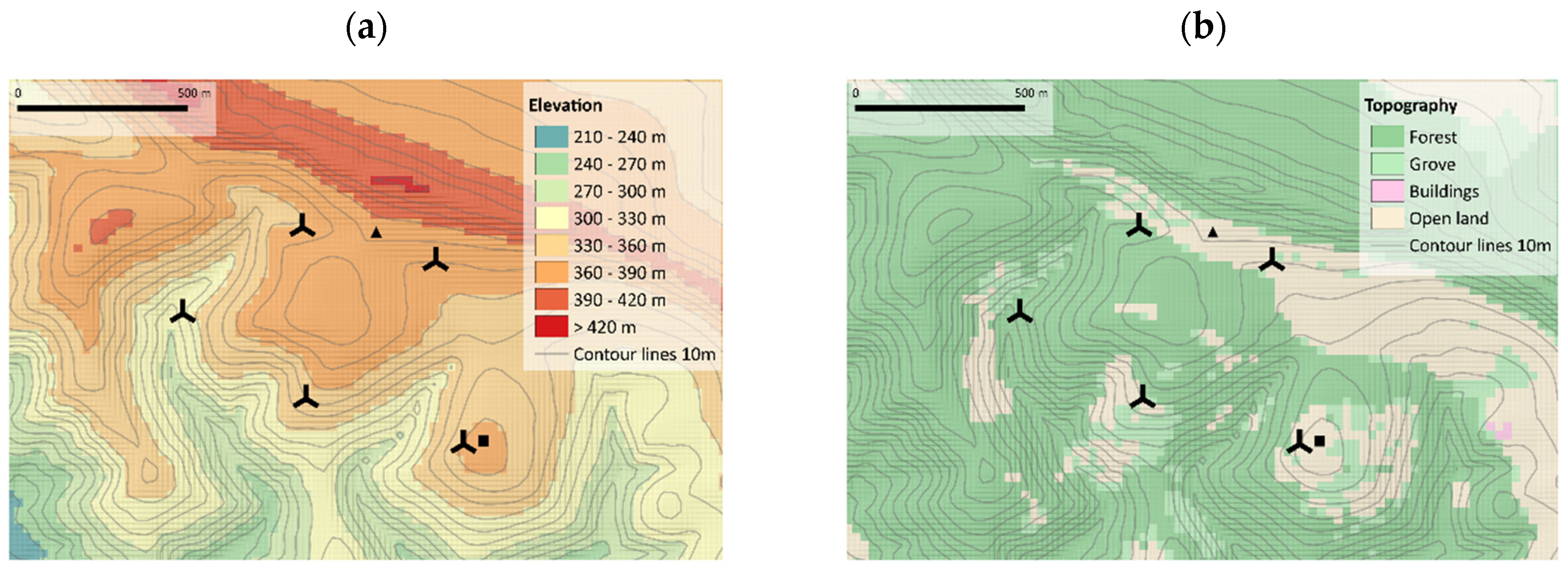




| Roughness Length | Height | Plant Area Index | |
| Forest | 0.6 m | 20 m | 4.2 |
| Grove | 0.5 m | 16 m | 0.9 |
| Buildings | 0.5 m | 7 m | - |
| Open land | 0.1 m | - | - |
| Period of (Concurrent) Measurement | 31 October to 11 November 2019, 7 to 26 February 2020 (Corresponds to 912 30-min Datasets) |
| Scanning lidar measurement specifications: | |
| Range of azimuth angles | 0–360° in steps of 10° (36 beams in scan) |
| Fixed elevation angle | 20° (with system 364 m ASL and 3 m above ground) |
| Range gates | 42 range gates with 30 m resolution starting at 80 m |
| Completion time of scan | 95 s |
| Reference sodar measurement specifications: | |
| Range of measurement heights | 30–180 m in steps of 10 m |
| Measurement configuration | 3 beams: 1 vertical, and x-/y-direction along 16°-cone |
| Transmitter frequency | 4.5 kHz |
| Sampling frequency | 0.25 Hz |
| FIWind | FITNAH | |
|---|---|---|
| Direction sectors | 36 (first centered at 5°) | 12 (first centered at 0°) |
| Input wind speed | 10 ms−1 | 5 ms−1 |
| Height of input wind speed | 100 m | 9000 m |
| Atmospheric stability | neutral | neutral |
| Grid spacing | 25 m | 25 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gottschall, J.; Papetta, A.; Kassem, H.; Meyer, P.J.; Schrempf, L.; Wetzel, C.; Becker, J. Advancing Wind Resource Assessment in Complex Terrain with Scanning Lidar Measurements. Energies 2021, 14, 3280. https://doi.org/10.3390/en14113280
Gottschall J, Papetta A, Kassem H, Meyer PJ, Schrempf L, Wetzel C, Becker J. Advancing Wind Resource Assessment in Complex Terrain with Scanning Lidar Measurements. Energies. 2021; 14(11):3280. https://doi.org/10.3390/en14113280
Chicago/Turabian StyleGottschall, Julia, Alkistis Papetta, Hassan Kassem, Paul Julian Meyer, Linda Schrempf, Christian Wetzel, and Johannes Becker. 2021. "Advancing Wind Resource Assessment in Complex Terrain with Scanning Lidar Measurements" Energies 14, no. 11: 3280. https://doi.org/10.3390/en14113280
APA StyleGottschall, J., Papetta, A., Kassem, H., Meyer, P. J., Schrempf, L., Wetzel, C., & Becker, J. (2021). Advancing Wind Resource Assessment in Complex Terrain with Scanning Lidar Measurements. Energies, 14(11), 3280. https://doi.org/10.3390/en14113280






