Rotor Current Feedback Based Direct Power Control of a Doubly Fed Induction Generator Operating with Unbalanced Grid

Abstract

The paper presents a decoupled direct power-controlled (DPC) of a doubly fed induction generator (DFIG) connected to an unbalanced power grid, executed in an orthogonal stationary reference frame related to the stator side. The control allows to maintain constant electromagnetic torque despite stator connection to the unbalanced power grid and to achieve controllable low-voltage ride through (LVRT) capability. The control does not require any signal decomposition into positive and negative sequence order, which allows to reduce its complexity and computational requirements. Then, the paper presents positive influence of rotor current feedback in the stator-controlled reference frame on control performance. It facilitates significant transient reduction and minor steady state control improvement. All the mentioned functionalities were validated both in simulation and in laboratory conditions and the obtained results are described in the paper.

1. Introduction

Rapid growth of electric power generation connected with renewable energy sources (RES) has forced power grid operators to impose some new operation regulations on these units. These regulations are now called Grid Codes [1,2]. They focus mainly on maintaining constant voltage amplitude, its frequency and reduction of total harmonics distortion factor in voltage and current generated to the grid (THD_U, THD_I). In wind-based power generation units a commonly used power generator is the doubly fed induction generator (DFIG) [1,3]. It is a three-phase induction type generator with access to three-phase stator windings and three-phase rotor windings. In case of DFIG used in wind power plants the rotor is supplied by a back-to-back voltage converter and the stator is directly connected to the grid as it is presented in Figure 1. Due to this direct stator connection to the grid, DFIG is sensitive to voltage disturbances, which leads to distortions of stator and rotor currents as well as electromagnetic torque pulsation [4]. Control of generated power by the stator side is executed through the rotor circuit by a reduced power three-phase back-to-back (B2B) voltage power converter. The converter consists of two three-phase voltage converters, the one connected to the rotor is called the rotor side converter (RSC), whereas the other connected to the grid—the grid side converter (GSC). The main purpose of the former is to control the power generated by the stator, while the purpose of the latter is to maintain the DC-link voltage at the required reference level and sometimes also power conditioning. In the paper the main focus is on RSC, whereas in analysis and laboratory verification GSC is treated and controlled as a DC voltage source. The nominal power of the B2B converter for which it is usually designed varies from 1/4 up to 1/3 of the whole total nominal set-up power.

The technology based on DFIG allows to control the voltage shape, amplitude, phase and its frequency on the stator side, which in grid connection operation is equivalent to control of generated power. DFIG can operate with variable rotational speed. It means that it can produce constant voltage amplitude and maintain its frequency on the stator side despite shaft variable rotational speed. Usually, the speed is allowed to change from 2/3 up to 4/3 of DFIG synchronous speed.

The main drawback of the presented DFIG based power plant technology is its sensitivity to voltage disturbances occurring in the power grid [3]. Any voltage imbalance or higher harmonics are directly transferred to the rotor side as well as to electromagnetic torque. Especially voltage imbalance has significant harmful influence on stator and rotor currents shape and in consequence leads to electromagnetic torque pulsation [5]. Depending on the applied control strategy and voltage imbalance level torque pulsation can have an amplitude close to its nominal value. The pulsation in the torque signal in case of voltage imbalance condition has a double frequency of stator voltage and if not compensated, could lead to mechanical and/or electrical damage of DFIG [1,6].

Currently, there are a few control approaches to DFIG operation with an asymmetrical power grid. One is connected with current control (stator or rotor) [7,8,9] the second with torque control [10,11] and the last with instantaneous power control [5,12]. Each approach has some advantages and disadvantages connected directly with the controlled variables and control targets. In the case of current control, physically measured variables are being controlled, it is easy to implement control path decoupling but in order to reduce the torque oscillation or generate specific power to the grid some additional calculation of instantaneous power and signal decomposition into positive and negative sequence is necessary. It leads to an increase in the number of parallel control paths. In the case of torque based control, its advantage is direct control of torque, which, when the target is torque pulsation reduction, provides a simple way to maintain torque amplitude constant but it also requires advanced calculation of flux magnitude (rotor or stator depending on the type of control) and in case of operation with power grid torque and flux should depend on instantaneous power requirements. The last of the mentioned group is power control. Since the controlled variables are the same as the requirements from power gride operators, in this aspect control is favorable, but when additional goals are set for control like torque pulsation reduction or higher harmonics compensation, additional signal calculation and their implementation in the main control are necessary.

The paper focuses on direct power control (DPC) of DFIG connected to the power grid where grid voltage is not symmetrical. The first studies connected with DPC for a symmetrical power grid were based on hysteresis controllers [13,14]. The control was executed in rotor flux coordinates [13], which yields decoupled control of instantaneous q and p component. It is based on a look up table (LUT) and hysteresis controllers. For symmetrical grid operation of DFIG it allows to obtain fast control response but like as all hysteresis methods it requires, high DC-link voltage level. Because it is implemented in rotor coordinates, it is sensitive in case of synchronous speed when rotor flux is the DC signal. The approach presented in [14] is also based on LUT and hysteresis controllers but it is connected with stator flux in rotor coordinates, which eliminates problems occurring at synchronous speed operation. The paper focuses on symmetrical grid operation and approach presented in it allows to obtain decoupled instantaneous power control. Research which was presents in [14] was expanded into linear control of instantaneous power in [15], while the presented method was tested and designed for a symmetrical power grid and yields very good performance. Control was executed in a stator reference frame and strongly depends on the exact flux calculation, both stator and rotor. Additional research was done in the area of DFIG and hysteresis control focused on elimination of B2B converter and its replacement with a matrix converter [16]. The presented method gives many more number of active states of voltage vectors, which allows to reduce the amount of harmonics in currents and level of DC-link voltage. The presented control also allows to obtain good performance for the controlled power signals. Another method connected with DFIG DPC with good performance and decoupled power control was given in [17], the paper focuses on senseless control (no position sensor) and deals only with a symmetrical power grid. Superior regulation controls instantaneous power components, while the inferior one controls rotor flux vector components. Currently, there is an approach where in order to deal with the stator current distortion and electromagnetic torque oscillation, stator voltage and current signal decomposition is widely proposed [5,18,19]. The control allows to mitigate the negative consequence of DFIG imbalance voltage operation but it requires many control loops and decomposition of signals into their positive and negative sequences. Each distortion, which can be present as negative sequence voltage component or higher harmonics, is controlled separately. The distortion signal has to be extracted and an additional control path for it must be implemented. It implies that an additional controllers which must be then tuned, which is sometimes not a trivial task. A similar approach was presented in [20], where a DPC-SVM method is adopted to unbalance DFIG operation. It uses signal decomposition and allows to obtain good steady state performance and operates with constant p component of instantaneous power. Unfortunately, no transient were given, which is crucial in case of DFIG wind power plants [3]. Research concentrating on nonlinear and/or predictive control are also developed [21,22]. Methods need much more advance mathematical approach and are sensitive to parameter identification; also all of compensated signals need to be extracted and separately controlled what significantly increase computation complexity. The presents results have very good performance but all of them are given for steady state control; in case of symmetrical and asymmetrical DFIG grid operation, but no transient was given. Recently published research papers connected with the DPC algorithm as a means to reduce torque and/or instantaneous power pulsation propose compensation of extracted negative order sequence signals [23]. The presented method is based on delayed-signal calculation extraction method of stator voltage negative sequence component and elimination of obtained and calculated, based on it, pulsating elements of instantaneous power components. The case with symmetrical and asymmetrical power grid is presented but no transient was given. Some aspects of DFIG DPC decoupling were recently presented in [24]. The control was executed with PI controllers and its main target is to maintain constant the instantaneous power signals, even with identification parameter variation. No laboratory set-up results with unbalance grid or transient were given, but simulation with imbalanced voltage transient time reduction were presented.

This paper proposes an approach where no signal decomposition for implementing DFIG DPC while connected to imbalance power grid is needed. The control is explained and its performance is described. The control is executed in a stationary reference frame; furthermore, control path decoupling is presented and its modification which significantly improves performance and imbalance voltage transient is outlined.

2. Materials and Methods

In order to efficiently explain the control approach and its assumption, some mathematical description of the DFIG model will be given. Then, the control signal calculation which allows to meet the control requirements will be presented. After the reference signal calculation part the control method will be explained and the control scheme will be provided. At the end of the chapter a control paths decoupling, feedforward mechanism and an additional DPC extension will be presented.

2.1. DFIG Mathematical Model

In the context of a control plant, DFIG can be analyzed in different reference frames. In the paper two possible reference frame models will be presented; one in the stationary orthogonal frame—αβ and the other in the rotating orthogonal frame—dq.

The stationary reference frame is based on a natural three-phase frame. If for transformation from the stationary three-phase to the stationary two-phase a Clarke transform is used, the version where vector length is preserved, the equation for the equivalent circuit given in Figure 2 takes the form presented in Equations (1) and (2). The first equation presents the relation for the stator’s circuit, the second for the rotor’s circuit. All equations given in the paper will be referenced to the stator side of DFIG.

$$u_s=R_s{i}_s+\frac{d{\psi }_s}{dt}$$

(1)

$$u_r=R_r{i}_r+\frac{d{\psi }_r}{dt}-j{\omega }_m{\psi }_r$$

(2)

where: u_s, u_r—instantaneous space voltage vector of stator and rotor respectively, i_s, i_r, i_m—instantaneous space current vector of stator, rotor and magnetizing circuit respectively, ψ_s, ψ_r—instantaneous space flux vector of stator and rotor respectively, R_s, R_r—stator and rotor resistance respectively, L_σs, L_σr—stator and rotor leakage inductance respectively, L_m—mutual inductance, ω_m—rotor mechanical speed scaled by the number of pole pairs.

In case of DFIG, due to direct access to the rotor circuit, DFIG flux can be calculated in many different ways. A possible manner of calculation is presented in Equations (3) and (4). The other, often used for calculation of squirrel cage motor stator flux, is given by Equation (5).

$${\psi }_s=L_s{i}_s+L_m{i}_r$$

(3)

$${\psi }_r=L_r{i}_r+L_m{i}_s$$

(4)

$${\psi }_s\left(t\right)={{\displaystyle \int }}_t^{t+T}\left(u_s\left(t\right)-R_s{i}_s\left(t\right)\right)dt$$

(5)

where: L_s, L_r—stator and rotor inductance, respectively.

Stator and rotor inductances are calculated according to Equations (6) and (7).

$$L_s=L_{\sigma s}+L_m$$

(6)

$$L_r=L_{\sigma r}+L_m$$

(7)

When the circuit given in Figure 2 and related Equations (1) and (2) are presented in the dq orthogonal rotating frame with the Park transform, they take the form given in Figure 3. Two additional voltage sources are present-one connected with stator flux and its rotational speed in the αβ frame, the other connected with rotor flux and its rotational speed. Equations describing the model from Figure 3 are given as (8) and (9).

$$u_s=R_s{i}_s+\frac{d{\psi }_s}{dt}-j{\omega }_s{\psi }_s$$

(8)

$$u_r=R_r{i}_r+\frac{d{\psi }_r}{dt}+j{\omega }_{ir}{\psi }_r$$

(9)

where: ω_ir—rotor flux rotational speed (slip pulsation).

$${\omega }_{ir}={\omega }_s-{\omega }_m$$

(10)

Taking into consideration flux Equations (3) and (4) and Kirchhoff’s current law for DFIG circuit (11) stator and rotor fluxes can be expressed as the relation where only the other side measured signals are used, as given in Equations (12) and (13).

$$i_m=i_s+i_r$$

(11)

$${\psi }_s=-\frac{\sigma L_s{L}_r}{L_m}{i}_r+\frac{L_s}{L_m}{\psi }_r$$

(12)

$${\psi }_r=-\frac{\sigma L_s{L}_r}{L_m}{i}_s+\frac{L_r}{L_m}{\psi }_s$$

(13)

where: σ—leakage factor.

$$\sigma =1-\frac{L_m^2}{L_s{L}_r}$$

(14)

Electromagnetic torque generated by DFIG due to quite easy access to stator and rotor variables measurements can be calculated in many different ways, one of which is presented in Equation (15).

$$T_{em}=\frac{3}{2}{p}_{b}Im\left\{{\psi }_s^{*}{i}_s\right\}$$

(15)

where: T_em—electromagnetic torque, p_b—number of pole pairs, ψ_s*—coupled stator flux space vector.

Equation (15) after solving, when the stationary αβ space vector is taken into consideration, takes the form given by (16).

$$T_{em}=\frac{3}{2}{p}_b\left({\psi }_{s\alpha }{i}_{s\beta }-{\psi }_{s\beta }{i}_{s\alpha }\right)$$

(16)

Instantaneous power generated by the stator, according with the concept presented by Akagi [25], can be calculated with Equation (17) for the p component and (18) for the q component, respectively.

$$p_s=\frac{3}{2}\left(u_{s\alpha }{i}_{s\alpha }+u_{s\beta }{i}_{s\beta }\right)$$

(17)

$$q_s=\frac{3}{2}\left(u_{s\beta }{i}_{s\alpha }-u_{s\alpha }{i}_{s\beta }\right)$$

(18)

where: p_s, q_s—p and q component of instantaneous stator power, respectively.

All the presented equations are valid for balanced and unbalanced voltage operation. Due to the fact that stator voltage is given by the power network, only the stator current can be manipulated in a wide range in order to change the generated instantaneous power in the DPC algorithm. The paper includes an approach where no signal decomposition for control purposes or reference signal calculation is used, which allows its significant simplification. The only case when signal decomposition was used is for depicting the voltage imbalance level, for which relation is given in (19). This is one of the possible ways of expressing the level of voltage imbalance in a three-phase system.

$$V_{ASM}=\frac{U_{RMS}^n}{U_{RMS}^P}\times 100\%$$

(19)

where: $V_{ASM}$—voltage asymmetry factor, $U_{RMS}^n$—rms value of the negative voltage component, $U_{RMS}^p$—rms value of the positive voltage component.

DFIG can operate with different control targets [5,6] like constant torque operation, constant power components, symmetrical sinusoidal stator current and others. The paper focuses on a case when DFIG operates with constant electromagnetic torque and sinusoidal stator current, which limits the stress on mechanical parts of DFIG and does not increase the level of generated higher current harmonics to the power grid. Conditions required for this control target have been given in [8]. It can be stated that the reference stator currents have to be calculated according to Equations (20) and (21).

$$i_{s\alpha }^{ref}=\frac{2}{3}\frac{q_s^{ref}{\psi }_{s\beta }+\frac{T_{em}^{ref}{u}_{s\beta }}{p_b}}{u_{s\beta }{\psi }_{s\alpha }-u_{s\alpha }{\psi }_{s\beta }}$$

(20)

$$i_{s\beta }^{ref}=\frac{2}{3}\frac{q_s^{ref}{\psi }_{s\beta }+\frac{T_{em}^{ref}{u}_{s\beta }}{p_b}}{u_{s\beta }{\psi }_{s\alpha }-u_{s\alpha }{\psi }_{s\beta }}$$

(21)

where: $i_{s\alpha }^{ref}$, $i_{s\beta }^{ref}$—reference stator space vector current component in the α and β frame respectively, $q_s^{ref}$—reference q component of instantaneous DFIG stator power, $T_{em}^{ref}$—reference DFIG electromagnetic torgue.

The reference q component of instantenious power and electromagnetic torque T_em^ref have to be non-oscilating when torque oscillations can be calculated on the basis of external control algorithm requirements (22), (23), for example from grid operators.

$$T_{em}{}^{ref}=p_b\frac{P_{total}^{ref}}{{\omega }_m}$$

(22)

$$q_s^{ref}=Q_s^{ref}$$

(23)

where: $P_{total}^{ref}$—total reference generated DFIG power, $Q_s^{ref}$—reference value of the stator’s reactive power.

2.2. Direct Power Control Description

The concept of direct power control (DPC) in the case of DFIG can be derived from rotor voltage equation. Inserting (13) for ψ_r into (9) allows to build a relation which expresses rotor voltage as a function of stator side signals (24), all represented in the stationary orthogonal dq frame.

$$u_r=R_r{i}_r+\frac{d}{dt}\left(\frac{L_r}{L_m}{\psi }_s-\frac{\sigma L_s{L}_r}{L_m}{i}_s\right)+j{\omega }_{ir}\left(\frac{L_r}{L_m}{\psi }_s-\frac{\sigma L_s{L}_r}{L_m}{i}_s\right)$$

(24)

In order to eliminate the stator flux derivative, in Equation (24) the expression given in (5) can be inserted, which is given in Equation (25).

$$u_r=R_r{i}_r+\frac{d}{dt}\frac{L_r}{L_m}\left({\displaystyle \int }\left(u_s-R_s{i}_s\right)dt\right)-\frac{\sigma L_s{L}_r}{L_m}\frac{d{i}_s}{dt}+j{\omega }_{ir}\left(\frac{L_r}{L_m}{\psi }_s-\frac{\sigma L_s{L}_r}{L_m}{i}_s\right)$$

(25)

The relation for rotor voltage in the d and q axis takes the form given in Equations (26) and (27). Now the rotor voltage is the function of the stator measured and calculated variables.

$$u_{rd}=R_r{i}_{rd}+\frac{L_r}{L_m}\left(u_{sd}-R_s{i}_{sd}\right)-\frac{\sigma L_s{L}_r}{L_m}\frac{d{i}_{sd}}{dt}+{\omega }_{ir}\left(-\frac{L_r}{L_m}{\psi }_{sq}+\frac{\sigma L_s{L}_r}{L_m}{i}_{sq}\right)$$

(26)

$$u_{rq}=R_r{i}_{rq}+\frac{L_r}{L_m}\left(u_{sq}-R_s{i}_{sq}\right)-\frac{\sigma L_s{L}_r}{L_m}\frac{d{i}_{sq}}{dt}+{\omega }_{ir}\left(\frac{L_r}{L_m}{\psi }_{sd}-\frac{\sigma L_s{L}_r}{L_m}{i}_{sd}\right)$$

(27)

When the transformation from the stationary orthogonal frame to the synchronously rotating frame is conducted with the stator voltage vector angle θ_us, the u_sq component is equal to zero so it does not appear in relation to instantaneous power (28), (29), which can be simplified to the form given in Equations (30) and (31).

$$p_s=\frac{3}{2}\left(u_{sd}{i}_{sd}+u_{sq}{i}_{sq}\right)$$

(28)

$$q_s=\frac{3}{2}\left(u_{sq}{i}_{sd}-u_{sd}{i}_{sq}\right)$$

(29)

$$p_s=\frac{3}{2}{u}_{sd}{i}_{sd}$$

(30)

$$q_s=-\frac{3}{2}{u}_{sd}{i}_{sq}$$

(31)

The obtained relation (30) and (31) when solved for stator current vector i_s can be inserted into (26) and (27), which after factorization gives the rotor voltage control vector, which depends on the stator instantaneous power (32), (33), its d and q component respectively.

$$u_{rd}=\stackrel{control plant}{\overbrace{-\frac{2}{3}\frac{R_s{L}_r}{L_m}\frac{p_s}{u_{sd}}-\frac{2}{3}\frac{\sigma L_s{L}_r}{L_m}\frac{d}{dt}\left(\frac{p_s}{u_{sd}}\right)}} +\stackrel{cross coupling}{\overbrace{{\omega }_{ir}\left(-\frac{L_r}{L_m}{\psi }_{sq}-\frac{2}{3}\frac{\sigma L_s{L}_r}{L_m}\frac{q_s}{u_{sd}}\right)}} +\stackrel{voltage drop}{\overbrace{R_r{i}_{rd}}} +\stackrel{feedforward}{\overbrace{\frac{L_r}{L_m}{u}_{sd}}}$$

(32)

$$u_{rq}=\stackrel{control plant}{\overbrace{\frac{2}{3}\frac{R_s{L}_r}{L_m}\frac{q_s}{u_{sd}}+\frac{2}{3}\frac{\sigma L_s{L}_r}{L_m}\frac{d}{dt}\left(\frac{q_s}{u_{sd}}\right)}} +\stackrel{cross coupling}{\overbrace{{\omega }_{ir}\left(\frac{L_r}{L_m}{\psi }_{sd}-\frac{2}{3}\frac{\sigma L_s{L}_r}{L_m}\frac{p_s}{u_{sd}}\right)}} +\stackrel{voltage drop}{\overbrace{R_r{i}_{rq}}} +\stackrel{feedforward}{\overbrace{\frac{L_r}{L_m}{u}_{sq}}}$$

(33)

The first part of (32), (33) represents the control plant model, the second the cross coupling factor and the last is resistive voltage drop and feedforward component.

The control vector presented in (32), (33) allows to implement the direct stator power control method in the synchronously rotating dq frame. The control along with calculation of necessary signals for its execution takes the form given in Figure 4. Implementation of control does not require any signal decomposition into positive and negative sequence for balanced or unbalanced grid voltage operation, which is commonly used in the case of current [7], torque [10] or power control [6]. Due to the fact that control is executed in the synchronously rotating reference frame for symmetrical grid voltage operation, two term controllers are needed–proportional integral (PI), but for unbalanced voltage operation an additional oscillating component with the double grid frequency component is present in power and torque signals as well as in the requested rotor voltage. Therefore, for general operation a resonant term, tuned for double grid frequency is implemented, which finally gives the proportional-integral-resonant controller (PIR_100Hz) given in Figure 4. Principles of resonant controllers are given in [26,27].

It is also possible to reduce the number of necessary control terms and implement the whole control in the orthogonal stationary frame as it is given in Figure 5. In the stationary reference frame the controlled signals are sinusoidal and oscillate with grid frequency. In order to minimize the control error, for those types of signals it is enough to use a proportional-resonant controller. Due to the fact that the control given in Figure 5 is equivalent to the one presented in Figure 4 and has fewer control terms and lower computation complexity, it was chosen and will be presented in the paper as the main DPC of DFIG.

Figure 5 presents the basic control scheme for the DPC algorithm executed in the stationary reference frame connected to the stator used for DFIG. The first stator current and voltage are measured and transformed to the stationary orthogonal αβ frame. Then, the stator flux ψ_sαβ is calculated based on (5) and its components are filtered with a band pass filter (BPF), the resonant frequency of which is set to the grid frequency (50 Hz). Its passband width, in order to obtain fast performance, was set to 10 Hz and the gain factor was calculated in such a manner that the signal amplitude for grid frequency would be maintained, in the logarithmic scale equal to zero. In the same manner the stator voltage components are being filtered with BPF. Output signals of voltage BPF are used for calculation of stator space voltage vector angle θ_s, which is next used in the control for frame transformation. Next, based on stator flux ψ_sαβ, stator voltage u_sαβ, reference torque T_em^ref and reference q component of instantaneous power q_s^ref, the reference stator current is calculated (20), (21). The obtained reference currents values allow to calculate the reference p component of instantaneous power p_s^ref according to (34). Next, the instantaneous power components flowing from the DFIG stator p_s (17), q_s (18) are calculated.

$$p_s{}^{ref}=\frac{3}{2}\left(u_{s\alpha }{i}_{s\alpha }{}^{ref}+u_{s\beta }{i}_{s\beta }{}^{ref}\right)$$

(34)

The difference between reference signals (34), (24) and calculated instantaneous power components values: p_s (17), q_s (18) gives error signals, which are transformed with the stator instantaneous voltage vector to the stationary orthogonal frame connected with the stator. The control error signals oscillating with grid frequency are inputs of proportional-resonant controllers, the outputs of which are transformed with the rotor angle to the stationary orthogonal frame connected with the rotor. The obtained reference rotor voltage signals oscillate with the rotor electrical frequency but contain also a negative sequence component of frequency equal to double grid frequency reduced by slip frequency. Next, with the pulse width modulation (PWM) algorithm gate control signals are generated and sent to the rotor side converter (RSC), which controls the rotor circuit of DFIG.

The presented control algorithm allows to operate a DFIG with balanced and unbalanced grid voltage and to generate unbalanced sinusoidal stator current with simultaneous constant torque waveform. The results will be presented in further parts of the paper. The form of the used PR controllers is given in (35). In case of discrete control Tustin approximation of s operator with a pre-warping mechanism was used [26] to obtain the form used in digital control in the simulation as well as in the microcontroller.

$$G_{PR}\left(s\right)=\frac{k_I}{s^2+{\omega }_0^2}+k_P$$

(35)

where: G_PR(s)—controller transfer function, k_I—generalized integral (resonant part) gain, s—Laplace operator, 0—resonant pulsation, k_P—proportional gain.

2.3. Decoupling and Feedforward Implementation

It is common in control that cross coupling terms between control axes are compensated for by decoupling terms. Similarly, the feedforward mechanism in the algorithms is implemented to improve the control loops properties; in this particular DFIG system for the rotor current control loop [7,28]. For the control executed in the synchronously rotating frame those feedforward and decoupling terms are given in (36), (37) for the d and q control axis of rotor voltage, respectively.

$$\Delta u_{rd}=\frac{L_r}{L_m}{u}_{sd}+{\omega }_{ir}\left(-\frac{L_r}{L_m}{\psi }_{sq}-\frac{2}{3}\frac{\sigma L_s{L}_r}{L_m}\frac{q_s}{u_{sd}}\right)$$

(36)

$$\Delta u_{rq}=\frac{L_r}{L_m}{u}_{sq}+{\omega }_{ir}\left(\frac{L_r}{L_m}{\psi }_{sd}-\frac{2}{3}\frac{\sigma L_s{L}_r}{L_m}\frac{p_s}{u_{sd}}\right)$$

(37)

Equivalent relations for the stationary orthogonal αβ frame are given in (38) and (39).

$$\Delta u_{r\alpha }=\frac{L_r}{L_m}{u}_{s\alpha }+{\omega }_m\left(L_r{i}_{r\beta }+L_m{i}_{s\beta }\right)$$

(38)

$$\Delta u_{r\beta }=\frac{L_r}{L_m}{u}_{s\beta }-{\omega }_m\left(L_r{i}_{r\alpha }+L_m{i}_{s\alpha }\right)$$

(39)

Implementation of decoupling and feedforward structures in the control scheme is given in Figure 6. It is implemented behind the current controllers and before the transformation of the reference frame in which vectors rotate with stator pulsation to the one in which vectors rotate with rotor pulsation.

The decoupling mechanism helps in separation of the control paths and reduction of undesirable influences between them. In the case of DPC controlled DFIG when control is executed in the stator side mechanism presented in Figure 6 uncontrollable operation may take place. The reason is that the control does not involve rotor side measurements and part of the plant is not observed. The results of such a case will be presented in the next chapter.

2.4. Rotor Current Signal Implementation in DPC of DFIG

Due to the DFIG electrical construction and operation principles given in equivalent electrical circuit in Figure 2, stator current depends not only on rotor current but also on the magnetizing current (11). To elaborate stator power control based on the information on rotor current, the magnetizing current should be determined. A possible DPC modification is given in (40), (41) for control in the rotating reference frame and (42), (43) for the stationary reference frame. The relations are derived from (3), (4) and (11). Similar principles were published in [8] for stator voltage oriented rotor current vector control.

$$i_{sd}^{\prime }=\frac{{\psi }_{sd}-\left(L_s-L_m\right)i_{sd}}{L_m}-i_{rd}$$

(40)

$$i_{sq}^{\prime }=\frac{{\psi }_{sq}-\left(L_s-L_m\right)i_{sq}}{L_m}-i_{rq}$$

(41)

$$i_{s\beta }^{\prime }=\frac{{\psi }_{s\beta }-\left(L_s-L_m\right)i_{s\beta }}{L_m}-i_{r\beta }$$

(42)

$$i_{s\alpha }^{\prime }=\frac{{\psi }_{s\alpha }-\left(L_s-L_m\right)i_{s\alpha }}{L_m}-i_{r\alpha }$$

(43)

where: $i_{sd}^{\prime }, i_{sq}^{\prime }$—calculated stator current value, which includes rotor current information in the synchronously rotating frame in the d and q axis respectively, $i_{s\alpha }^{\prime }, i_{s\beta }^{\prime }$—calculated stator current value in the stationary orthogonal frame in the α and β axis respectively.

In case of basic control executed in the stator frame of DFIG, there is no direct information about rotor current, which deteriorates the ability of control even more when full decoupling between control paths is implemented. In order to regain control, the mechanism given in (40)–(43) is strongly recommended. For steady state of DFIG each relation (40)–(43) is reduced to its basic form given by (44).

$$i_{sx}^{\prime }=i_{sx}$$

(44)

where: x—axis name d, q, α, β respectively.

For stator control executed in the rotor circuit it is beneficial to contain information about the rotor current. What is more, it will be shown that it allows to significantly reduce transient in both stator and rotor circuit.

3. Simulation and Experimental Results of the Proposed Control

The concepts described in Section 2 Materials and Methods were validated, tested and implemented in simulation as well as in a laboratory set-up. In this section, the set-up as well as waveforms obtained during the tests will be presented and commented on.

3.1. Simulation Results

In order to validate the proposed control of DFIG power generation set-up simulations were conducted in PSIM software. As a control plant a 2 MW DFIG model was used; it is a machine used in wind power plants [1]. The whole control was implemented in a dll block written in the C language. The control is executed in the stationary αβ frame according to the scheme given in Figure 5 with simulation frequency equal to 4 kHz. RSC was simulated as ideal controlled voltage sources. Voltage asymmetry level, calculated according to (19), during the imbalance grid voltage operation tests was set to 20%. The DFIG shaft was rotating with constant speed given by a constant mechanical speed source with n_m = 2000 rpm, which is the worst condition for control due to the highest amplitude of induced in the rotor circuit negative sequence voltage connected with the asymmetrical grid voltage. The obtained results were elaborated using the MATLAB^® software. The nominal parameters of the simulated DFIG are given in

Table 1. 2 MW DFIG nominal parameters.

Parameter	Description	Value
Pn	Rated power	2 MW
Usn	Stator nominal voltage	690 V
Isn	Stator nominal current	1760 A
Ur	Rotor voltage (0 rpm)	2600 V
nz	Stator/rotor turns ratio	0.34
Rs	Stator resistance	2.6 mΩ
Rr	Rotor resistance	2.6 mΩ
Lσs	Stator leakage inductance	0.087 mH
Lσr	Rotor leakage inductance	0.087 mH
Lm	Magnetizing inductance	2.5 mH
pb	Number of poles pairs	2

.

Changes of reference signals for all simulation cases with the 2 MW DFIG are not done in a step manner but the reference signals used in the control are obtained from a prefilter–second order low pass filter (LPF) with the gain factor set to 1 and the damping factor set also to 1. The basic reference signals are reactive power Q_s^ref (23) and electromagnetic torque T_em^ref (22), based on which the reference stator current component is calculated (20), (21) and finally reference power signals used in DPC control p_s—(34) indirectly and directly q_s—(23).

Changes of reference signals levels for steady state operation in case of symmetrical and asymmetrical voltage are given in

Table 2. Reference signal values set in simulation.

Parameter	Value
time	4.44–4.5 s	4.5–4.6 s	4.6–4.7 s	4.6–4.7 s
Temref	0	0	0	12.7 kNm
qsref	0	−2 MVAR	0

.

PR controller gains at first were calculated according to the Naslin polynomial approach for a linear decoupled standardized model of DFIG according to [29]. In case of different models they were chosen by the trial and error method with the starting point obtained from the Naslin polynomial approach.

The simulation results of DFIG connected to symmetrical grid are presented in Figure 7. The order of signals is as follows: stator phase voltages, stator phase currents, rotor phase currents, instantaneous stator power and finally electromagnetic torque. Control performance is presented for the change of reference instantaneous power calculated on the basis of the signal given in Table 2. The control presented in Figure 5 allows stable operation in the whole power range of DFIG.

The extended DPC of DFIG is presented in Figure 8. The main part of control is extended at t = 3.5 s by the decoupling and feedforward mechanism as given in Figure 6.

Control of the stator side variables in the rotor circuit without taking into consideration rotor side current does not allow DFIG stable operation when the decoupling terms are applied. The case of DPC control when in the stator instantaneous power signals rotor current information is included (42), (43), is given in Figure 9 for the case of balanced voltage operation. The control is stable and its performance is better than the basic structure given in Figure 7. Figure 10 presents, the basic control case given in Figure 5 without any amendment, in case of voltage asymmetry condition.

The control is stable but some signal oscillation and control axis coupling is visible. For the amended DPC by feedforward, decoupling and information about rotor current simulation results are given in Figure 11. Coupling between the control axis is eliminated and better performance is obtained, in comparison to Figure 10.

The most significant control improvement is obtained when transients are being considered. In case of simple DPC transients are long lasting, they are visible in stator and rotor current, instantaneous power as well as on electromagnetic torque signal. The simulation results of this case are given in Figure 12.

Implementation of the feedforward and decoupling mechanism with incorporation of information about rotor current, presented in Figure 13, in reference instantaneous power signals allows to significantly reduce transients time and improve the quality of generated currents with almost no transient in case of stator and electromagnetic torque.

Finally, the total amended control performance in case of DFIG variable speed operation is presented in Figure 14.

The control allows to maintain constant torque operation for a vast range of speed variance.

3.2. Laboratory Set-Up

The laboratory set-up scheme and photos of its corresponding elements are given in Figure 15. It consists of two mechanically coupled electrical motors. The prime motor is an induction squirrel cage machine with two pole pairs and nominal power 11 kW. The generator is a doubly-fed induction motor with two pole pairs and nominal power 7.5 kW. Detailed generator parameters are given in

Table 3. Laboratory set-up 7.5 kW DFIG nominal parameters.

Parameter	Description	Value
Pn	Rated power	7.5 kW
Usn	Rated stator voltage (Δ/Y)	220/380 V
Isn	Rated stator current (Δ/Y)	27.4/15.7 A
Irn	Rated rotor current	15 A
Ur	Rated rotor voltage (0 rpm)	182 V
nz	Stator/rotor turns ratio	2.08
Rs	Stator resistance	0.43 Ω
Rr	Rotor resistance	0.71 Ω
Lσs	Stator leakage inductance	10 mH
Lσr	Rotor leakage inductance	10 mH
Lm	Magnetizing inductance	120 mH
n	Rated speed	1445 rpm
pb	Number of poles pairs	2

.

The driving induction motor is supplied by an industrial power converter with speed control and external speed reference. In the case of laboratory tests, the speed reference was set manually. The machine set is equipped with an incremental encoder on the shaft. The DFIG stator is connected to the grid via a multi-tap transformer (G_Transf., yY connection). On the rotor side there is a back to back three phase power converter controlled from a microcontroller interface with a DSP TMS320F28335 microprocessor. The power converter consists of two three phase AC/DC converters with a common DC-link. The converter connected to the rotor side-RSC manages DFIG rotor current flow and controls indirectly stator electrical power components, whereas the second converter–GSC has the main purpose of maintaining the DC-link voltage at the reference level. From the grid side of GSC a three phase induction current filter and a step-down transformer (R_Transf., yY connection) are connected, the sole purpose of which is to match the voltage level to the rotor side nominal parameters. For GSC the implemented control algorithm was voltage oriented control (VSC) and its only purpose was to maintain the level of DC-link voltage. The control of GSC has been widely known for many years and will not be discussed in the paper.

The laboratory tests were done with 230 V rms line-to-line voltage for symmetrical case operation, whereas in case of asymmetrical voltage, one-phase voltage was reduced-in steady states tests by arbitrarily set lower voltage terminal of the multi-tap transformer, whereas in transient states by significant line-to-line overloading of the grid transformer. The switching frequency of the two level back to back power converter is set to 4 kHz. The waveforms were acquired by a YOKOGAWA 16-channel DL750 scope as digital samples and processed in the MATLAB^® software. The currents and voltages were measured directly by measurement equipment, whereas instantaneous power component p_s and q_s and electromagnetic torque T_em were calculated in the microcontroller, for control purposes and in MATLAB^® for unification of graphics in the paper. The DC-link voltage level for all tests was set to 150 V. Experimental tests were conducted in a laboratory placed in the city centre where most electrical loads are nonlinear. In consequence, small distortions connected with 5th and 7th harmonic are observed in the grid voltage.

3.3. Experiment Results

The experiments were conducted for both symmetrical and asymmetrical grid voltage condition. The main aim of the paper is DPC of DFIG connected to asymmetrical grid. Therefore, the major part of the recorded waveforms will present operation with unbalanced voltage. In case of DFIG steady state operation with an asymmetrical grid, voltage imbalance level—V_ASM, measured according to (19) was about 17%. In the case of transient–asymmetric voltage drop, the measured V_ASM was about 22%. The value of V_ASM was calculated as the ratio of signals after decomposition to positive and negative sequence components from the space vector voltage using the delayed signal cancelation method [30].

The balanced grid voltage operation of the presented DPC control executed in the stationary reference frame (concept given in Figure 5) without any additional control extension is given in Figure 16. Stator current is sinusoidal, while electromagnetic torque T_em and instantaneous power components p_s and q_s are maintained constant. The DPC performance of DFIG connected to an unbalanced grid is presented in Figure 17. The control like in the case of asymmetrical grid allows to generate sinusoidal current and maintain constant electromagnetic torque operation despite grid voltage imbalance conditions.

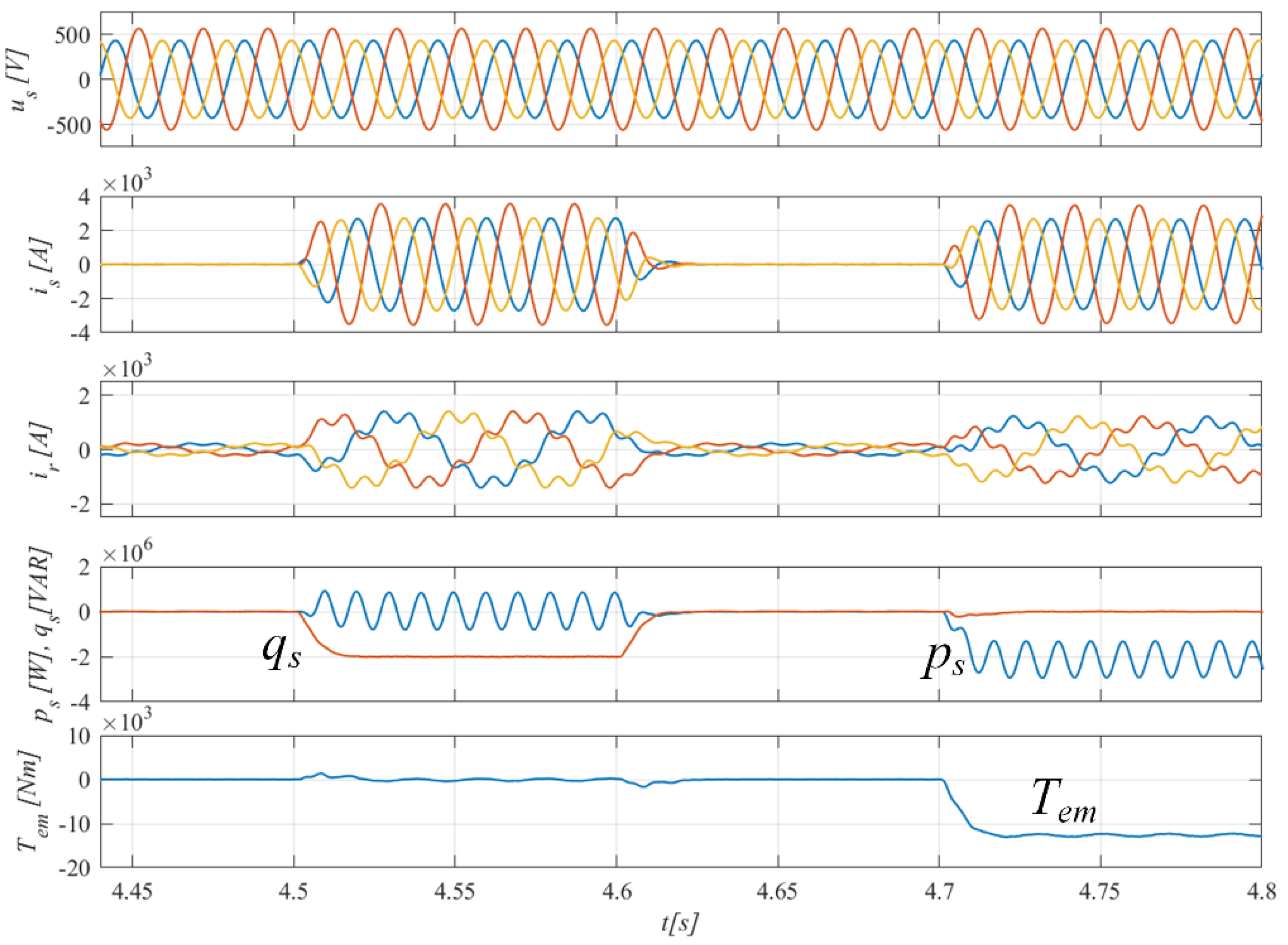
Variable speed operation of the proposed DPC is presented in Figure 18. Electromagnetic torque T_em is kept constant in a wide range of speed from sub-synchronous to super-synchronous. Figure 19 presents a transient of asymmetric voltage drop applied to basic DPC. The control is stable but significant oscillation occurs in rotor current, instantaneous stator power signals and electromagnetic torque. The pulsation is slowly decaying with time due to the natural damping introduced by coupling terms.

Figure 20 presents experimental results of a case when feedforward and decoupling is applied in control. At t = 0.12 s, an asymmetric voltage drop occurs and it leads to unstable operation even after the voltage asymmetry disappears. Significant undamped oscillations are visible at rotor phase current, instantaneous power signals and electromagnetic torque. The case of DPC with feedback, decoupling and with stator power calculated with rotor current information is given in Figure 21.

At t = 0.48 s an asymmetric voltage drop occurs and it disappears at t = 0.68 s. During the experiment the control is stable, transient state of control signals is significantly reduced, which allows to maintain constant torque operation as fast as 0.1 s after the transient occurs.

4. Conclusions

The paper presents decoupled direct power control with rotor current feedback of DFIG connected to unbalanced grid. The whole methodology of control design and implementation is given. The control is executed with linear PR controllers. The control method was tested in simulation with a 2 MW DFIG and in a laboratory set-up with a 7.5 kW machine. The obtained waveforms are presented and described in the paper followed by presentation of the results of tests of steady state load change and variable speed operation for symmetrical and asymmetrical grid. Moreover, asymmetrical voltage dip transient tests were executed and the obtained results are presented. While the basic DPC allows to operate with symmetrical and asymmetrical grid, coupling between the control path is visible and consequences of asymmetrical voltage drop transients in instantaneous power and torque are significant. Implementing the full control path decoupling and feedforward mechanism in stator current based power calculation of the DPC leads to unstable operation even with symmetrical grid. Modifying the DPC by inserting to the control stator power signals calculated with the rotor current information allows to regain total control and fully utilize the decoupling and feedforward mechanism. Coupling between the control path is significantly reduced as well as duration of transient in the controlled signals. The presented control does not require any signal decomposition into positive and negative component. Since the control is executed in a stationary orthogonal αβ frame with proportional-resonant controllers, only two control paths with one PR controller each are needed to maintain control for DFIG imbalance voltage operation.

The proposed DPC structure and implemented amendments in particular inclusion of rotor current, allows to significantly improve basic control structure performance especially when asymmetrical grid transients are considered.