Influence of Errors in Known Constants and Boundary Conditions on Solutions of Inverse Heat Conduction Problem
Abstract
:1. Introduction
2. Inverse Methods
2.1. Inverse Problem and Equations
2.2. Discretization
2.3. Implementations
- ①
- Update with current by solving Equation (4a).
- ②
- Calculate the gradient in Equation (5) by solving Equation (6a).
- ③
- Calculate the update direction by Equation (8) with the conjugate coefficient from Equation (9).
- ④
- Solve Equation (11a) with setting in Equation (11c) as the update direction.
- ⑤
- Determine the step length by Equation (10).
- ⑥
- Update by Equation (7).
3. Results and Discussions
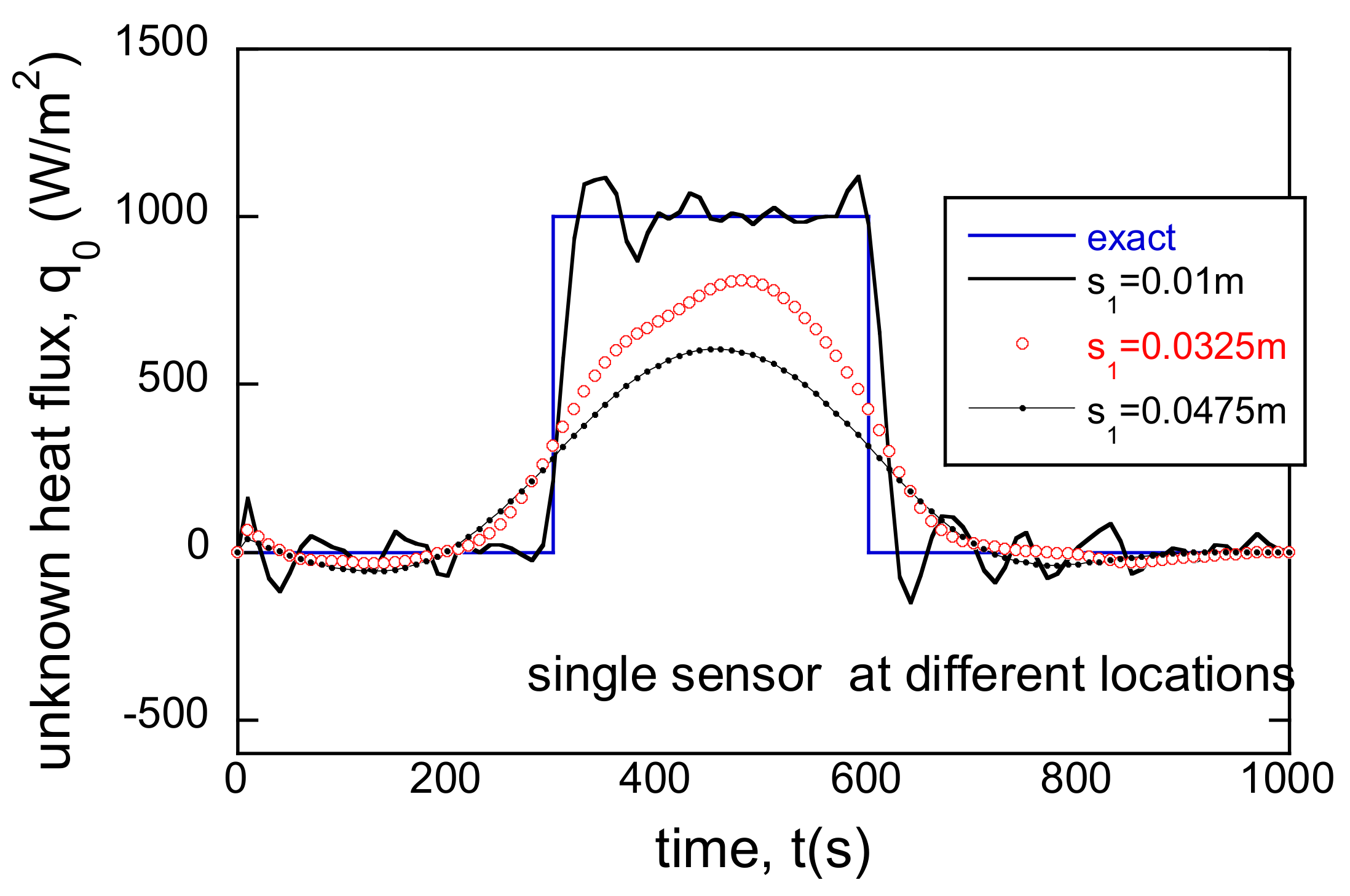
3.1. Basic Results and Sensor Locations
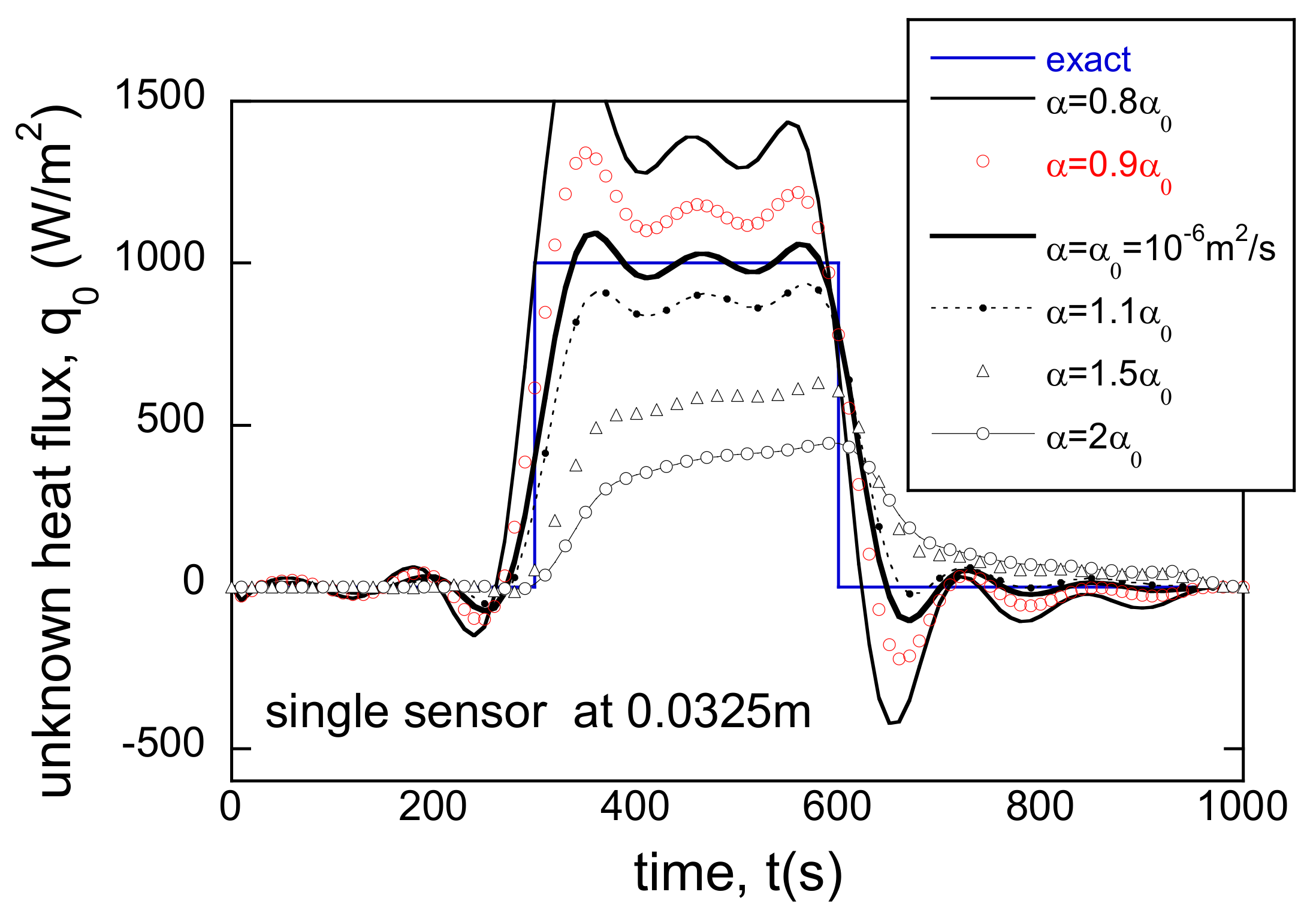
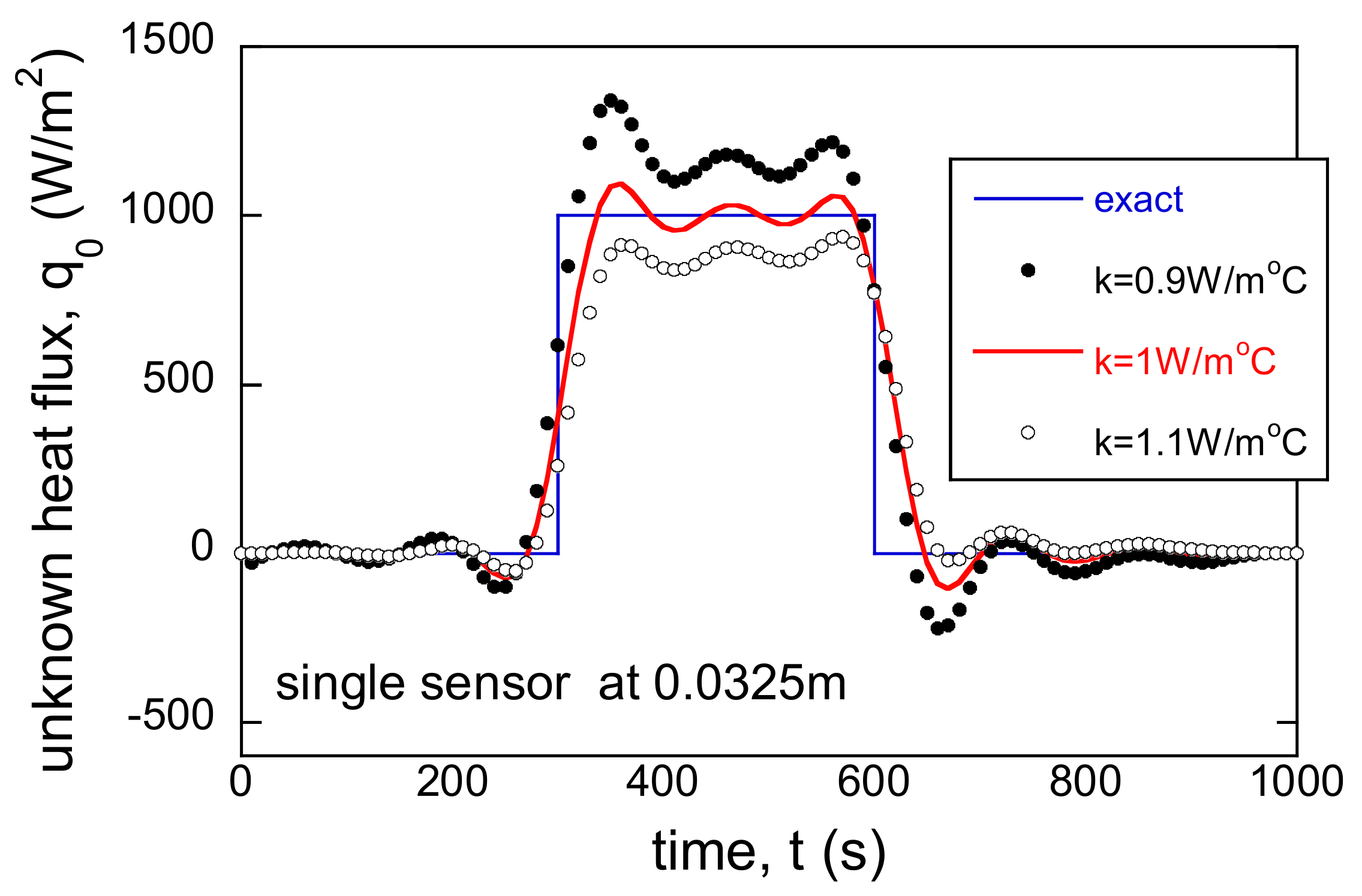
3.2. Material Properties
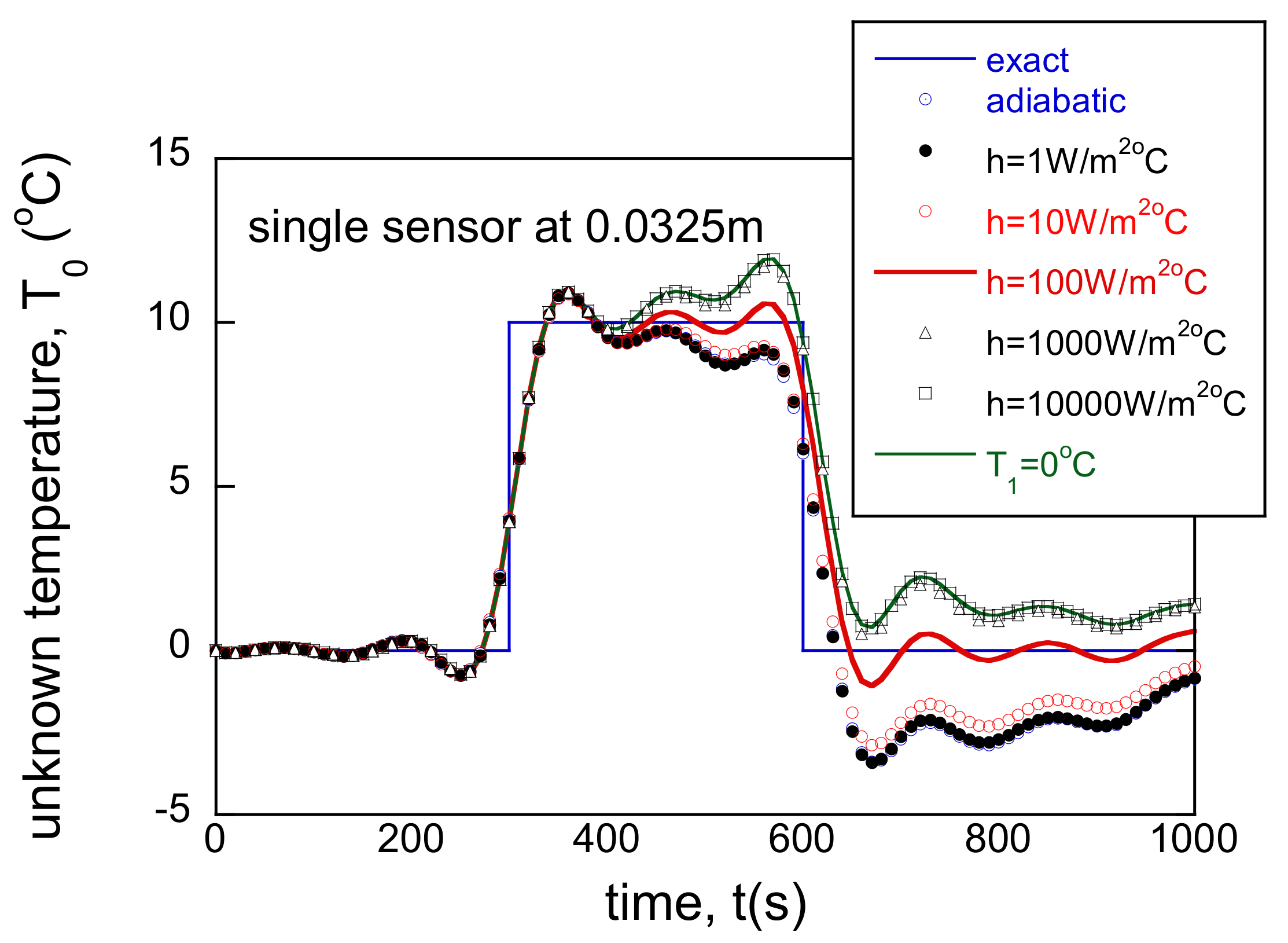
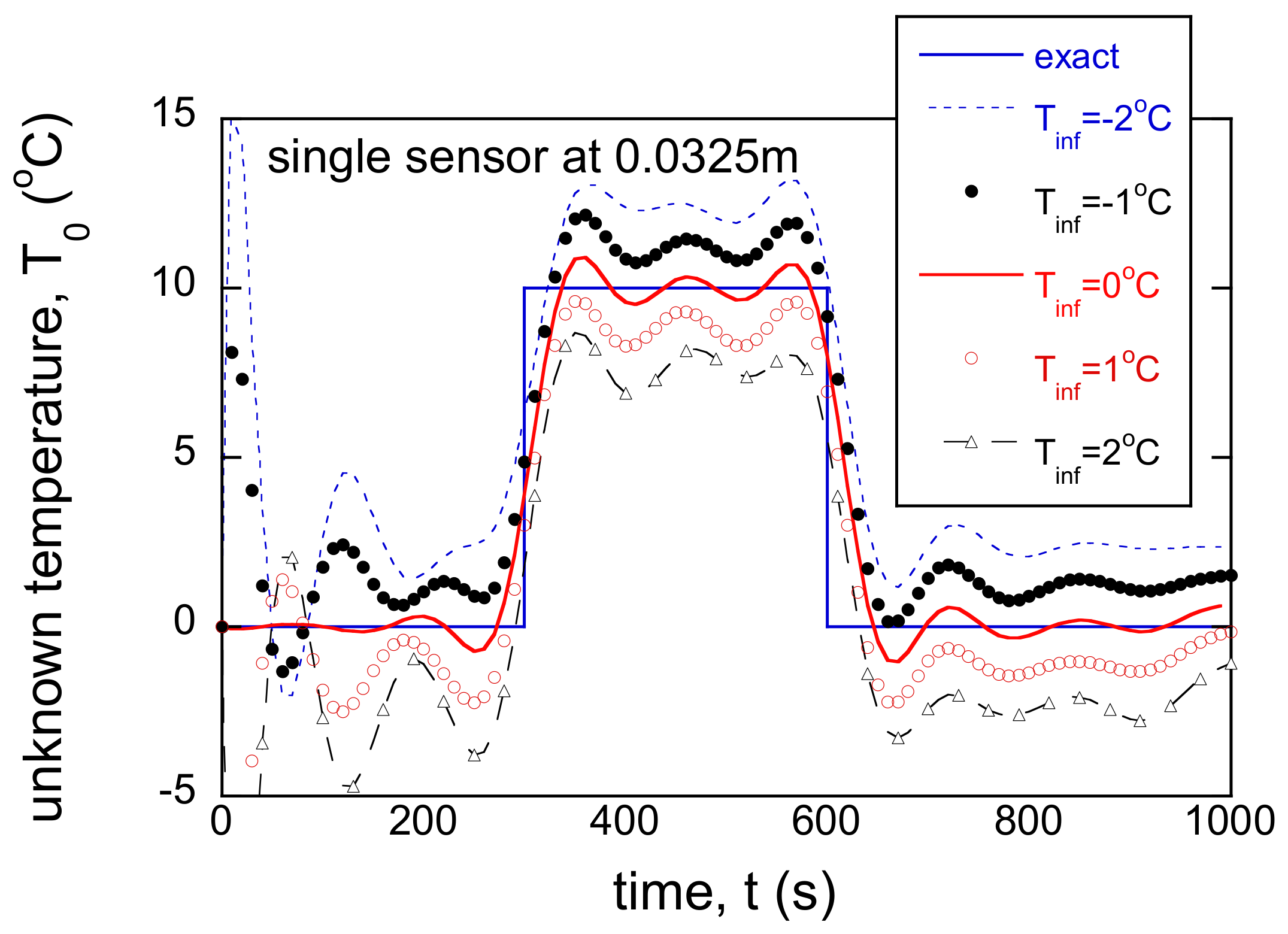
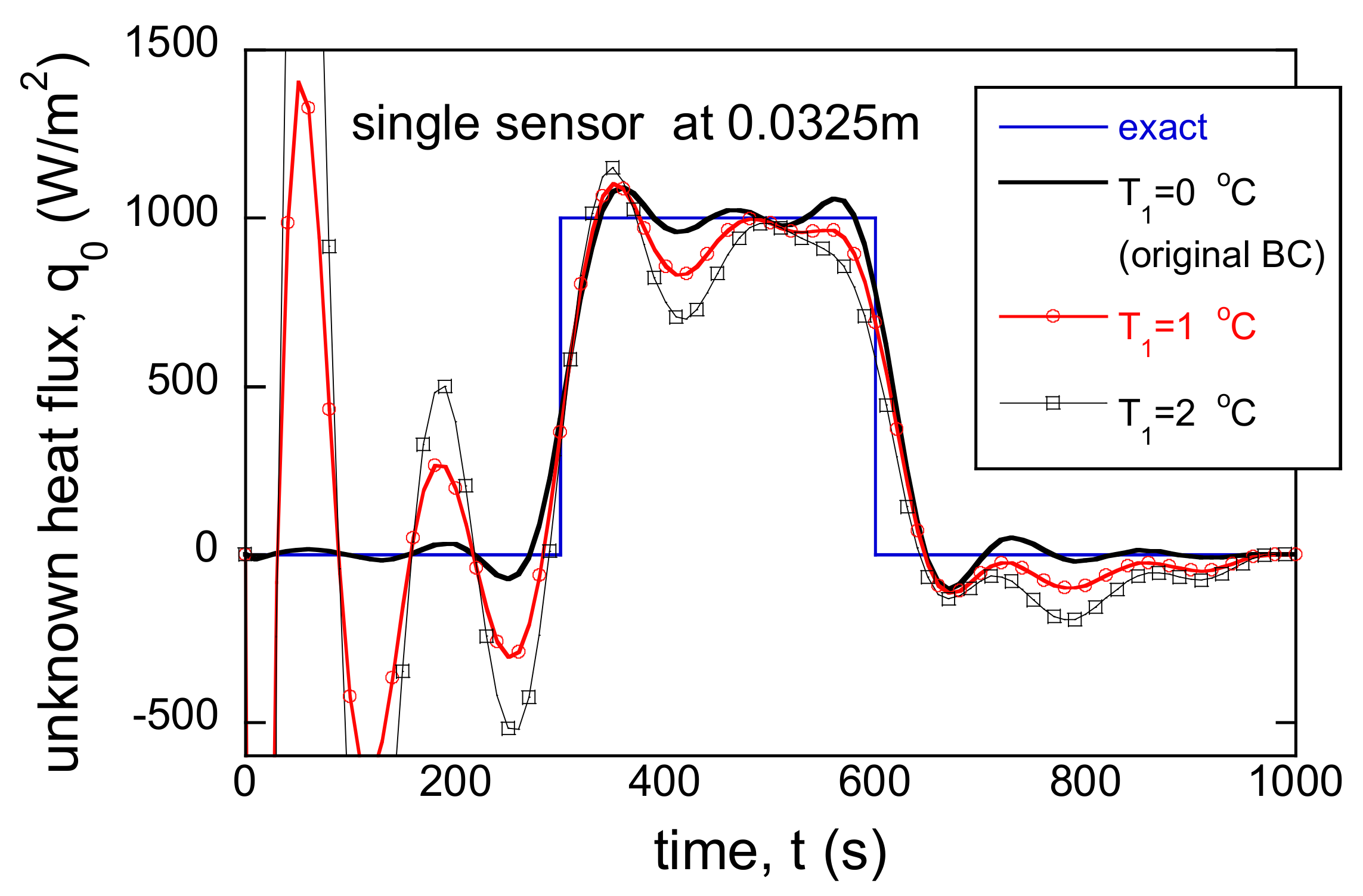
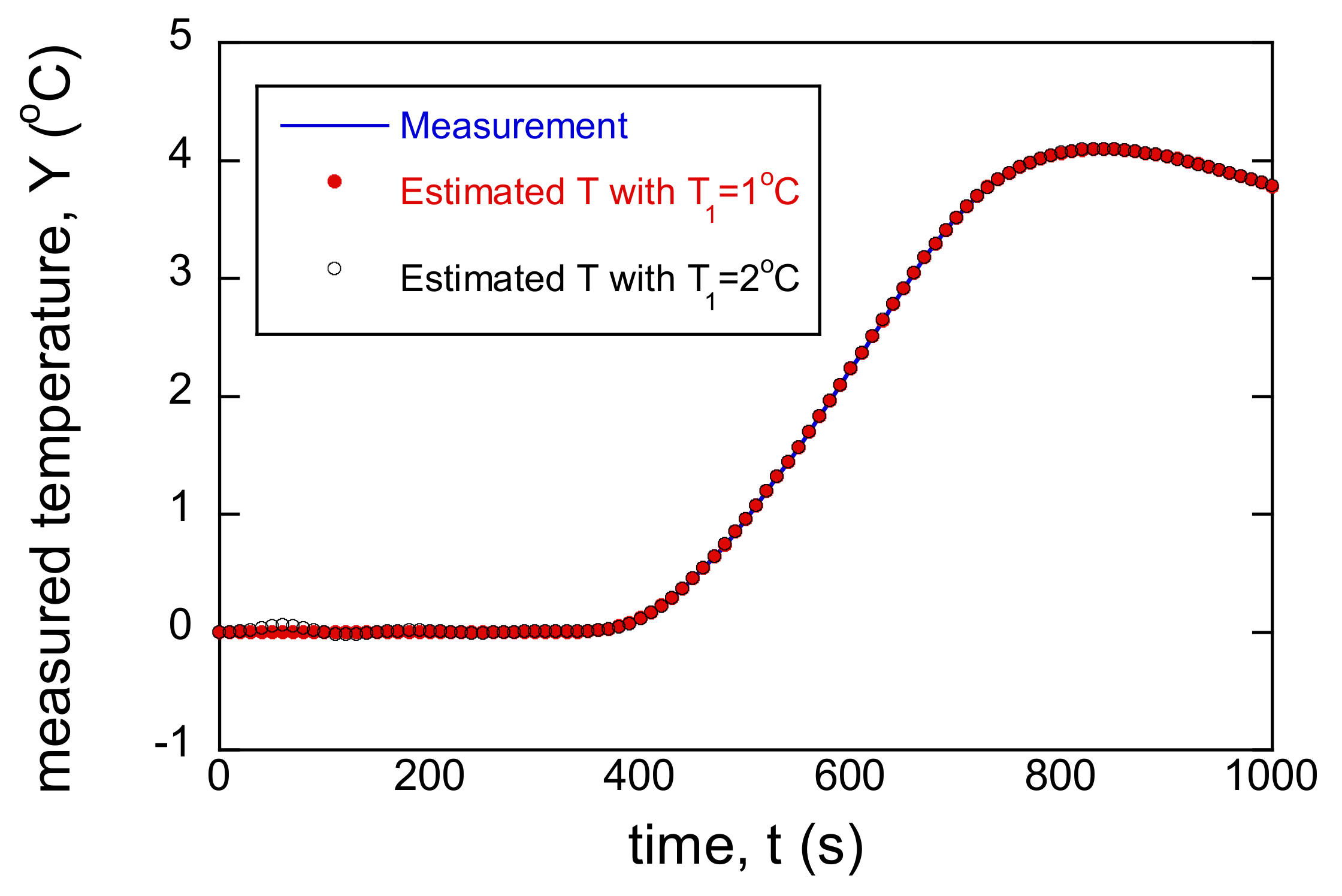
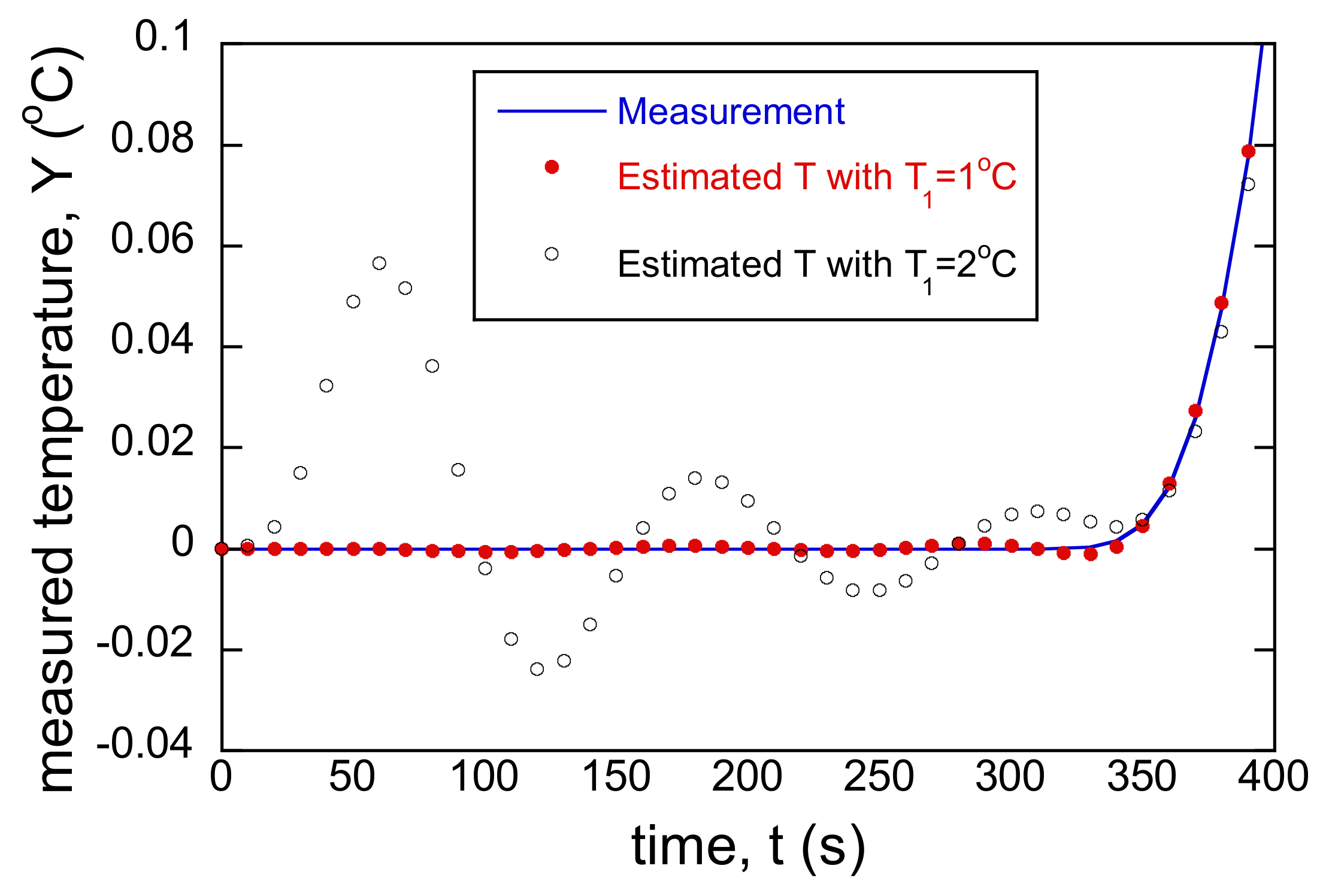
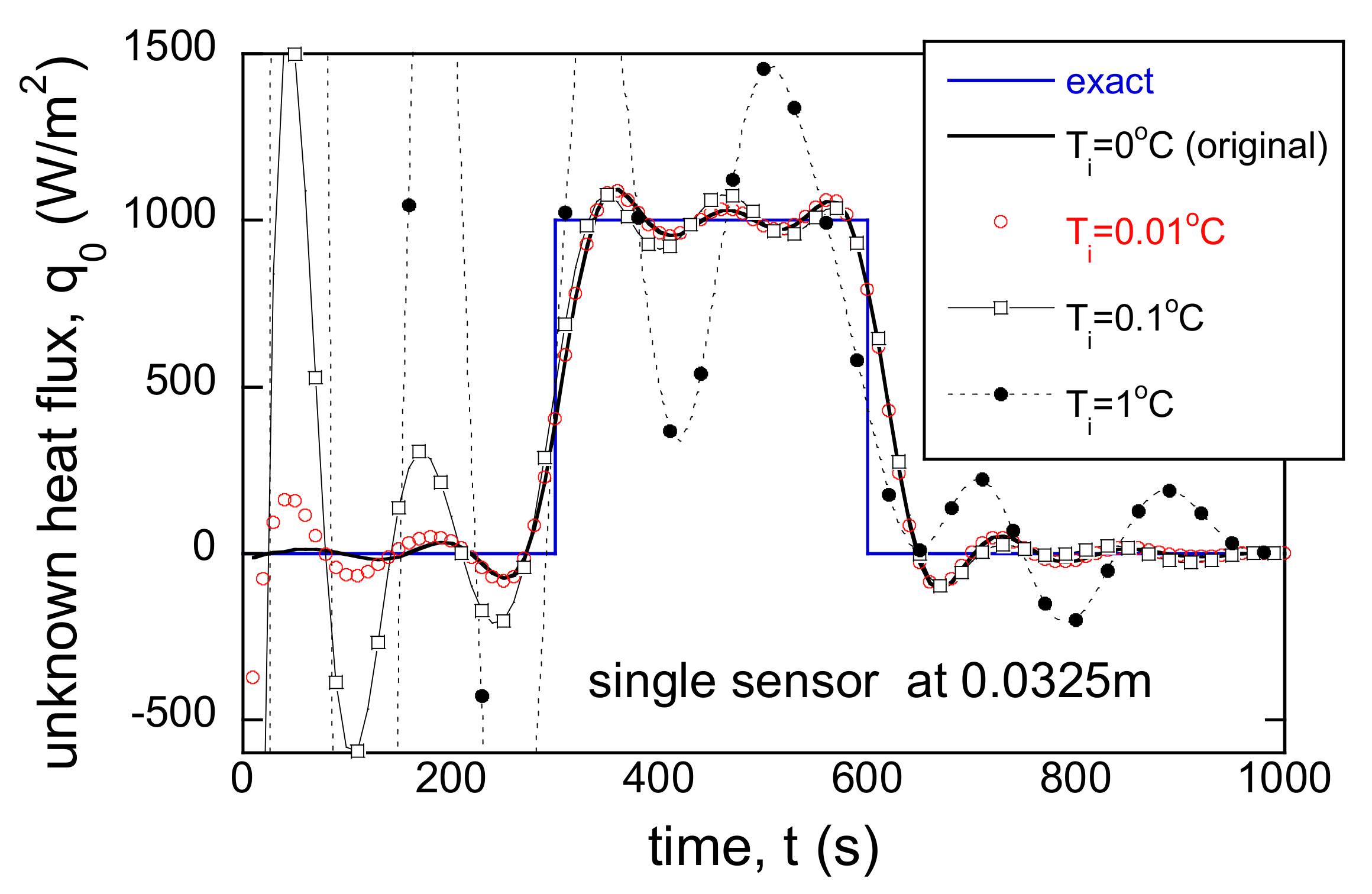
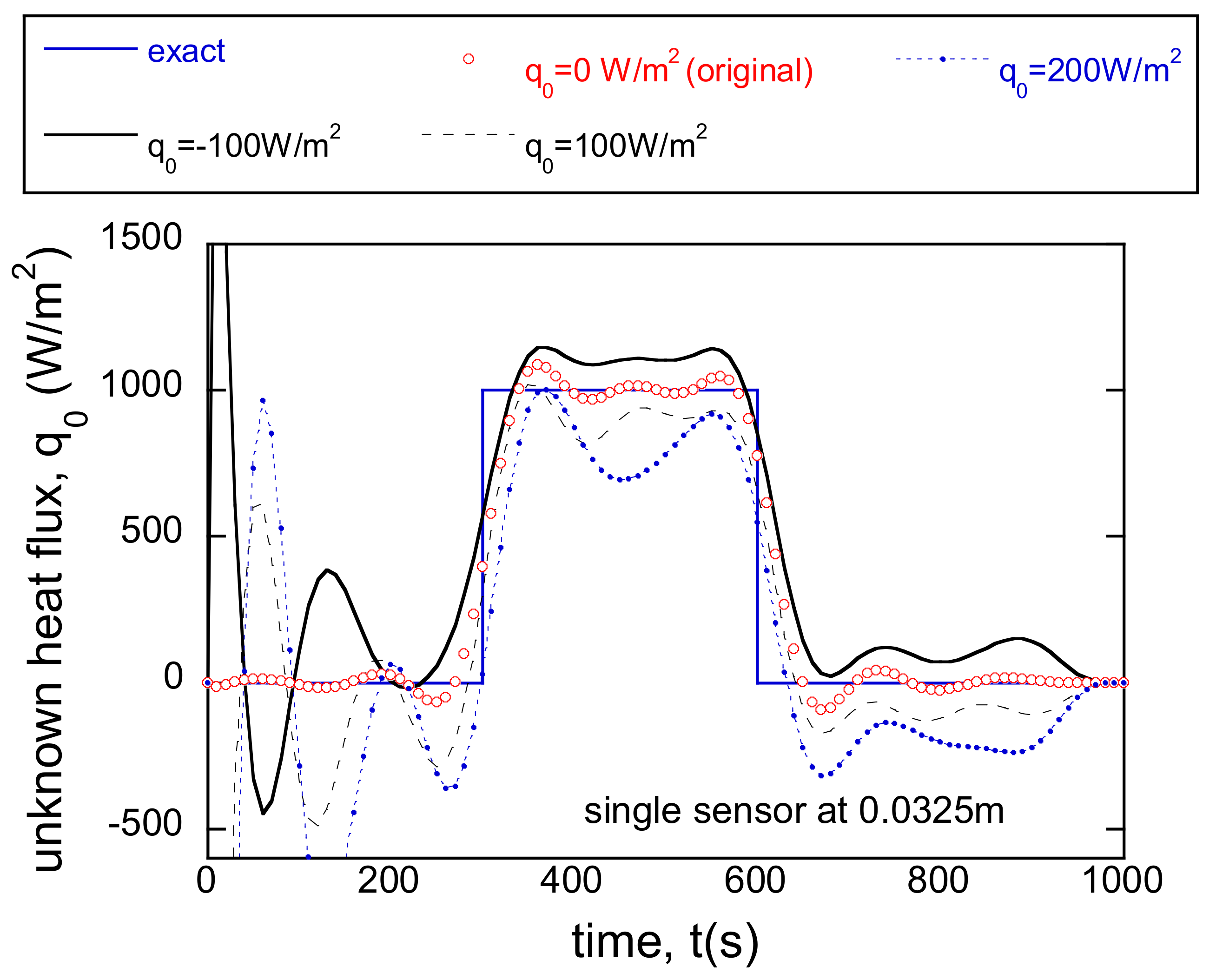
3.3. Incorrect BC and Single Sensor
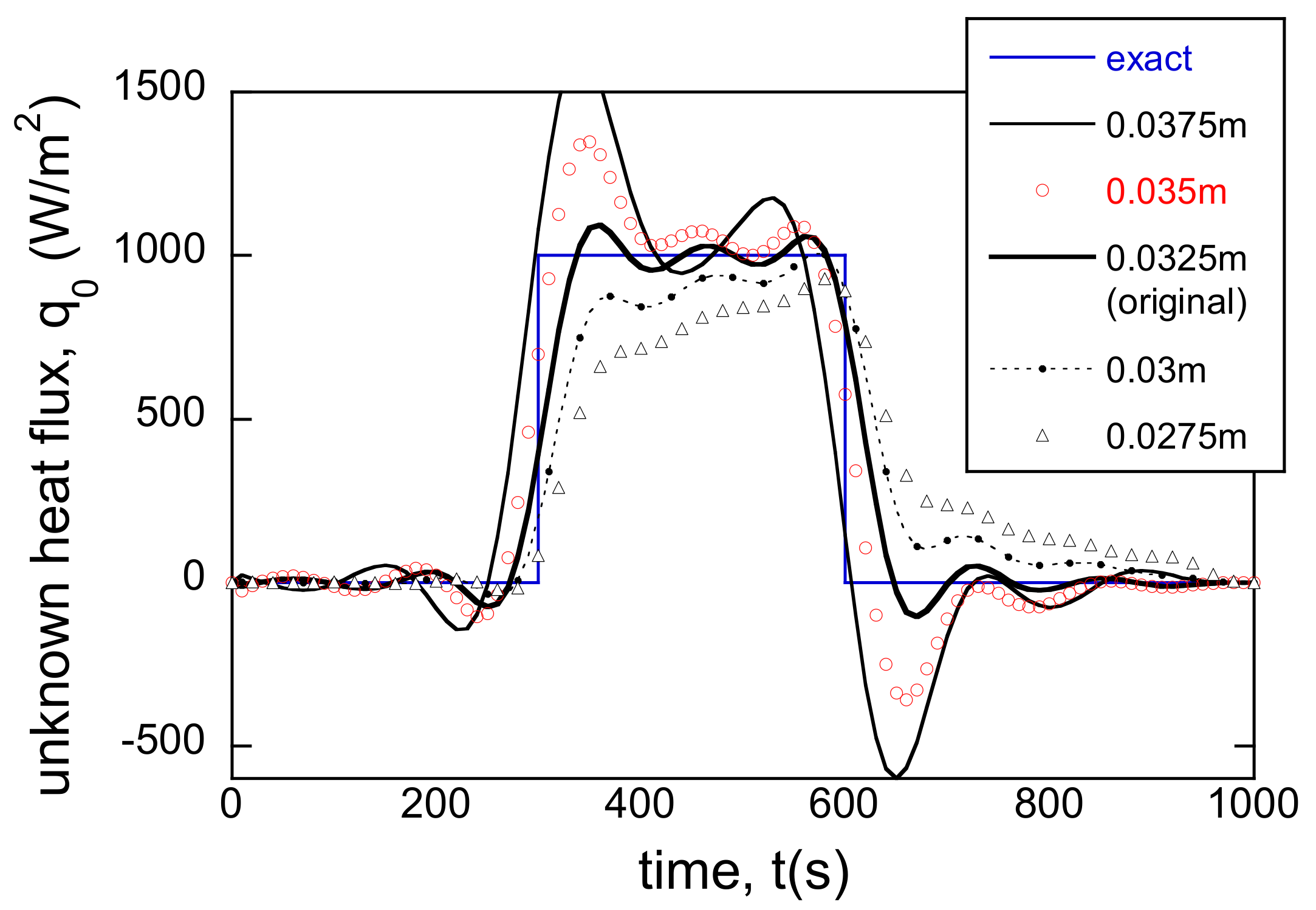
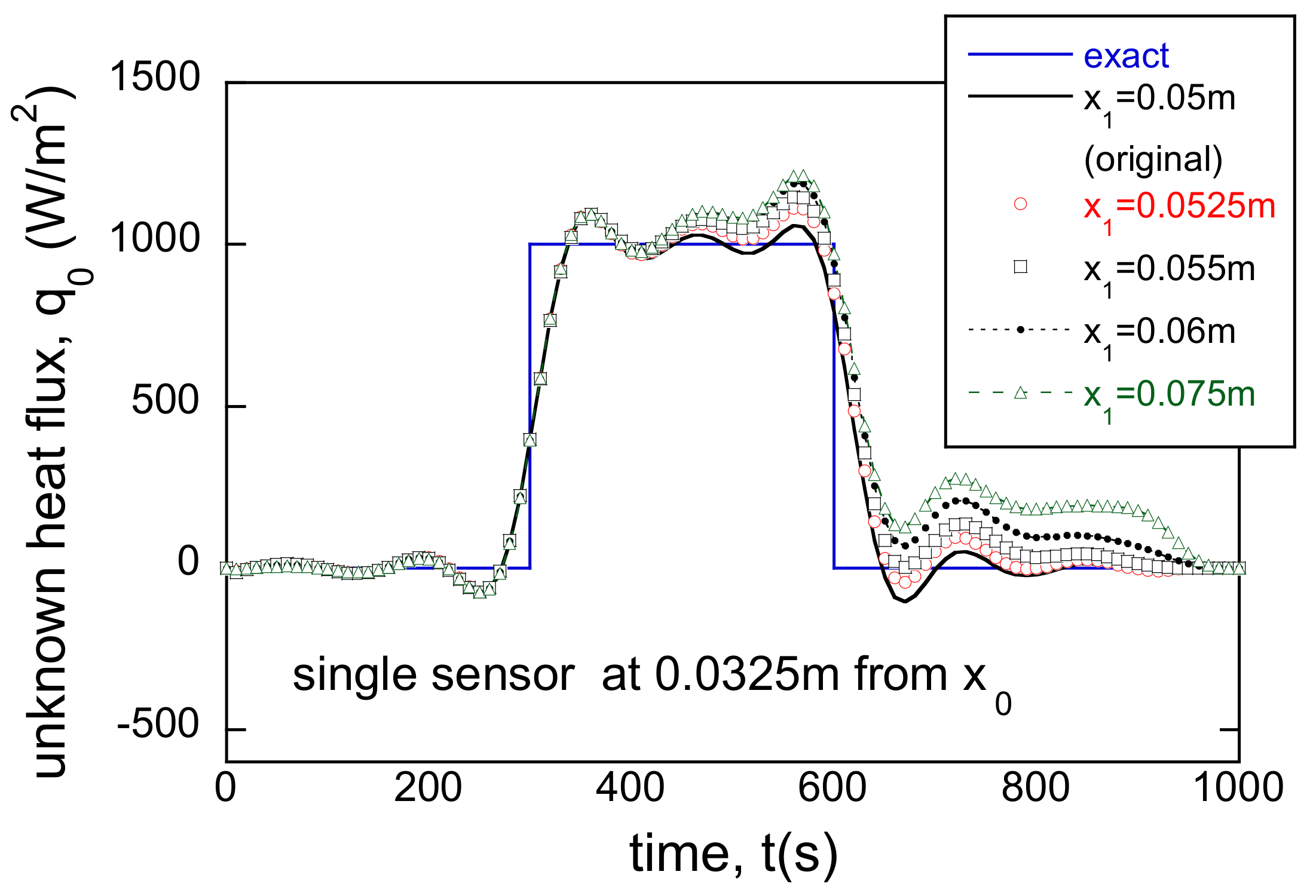
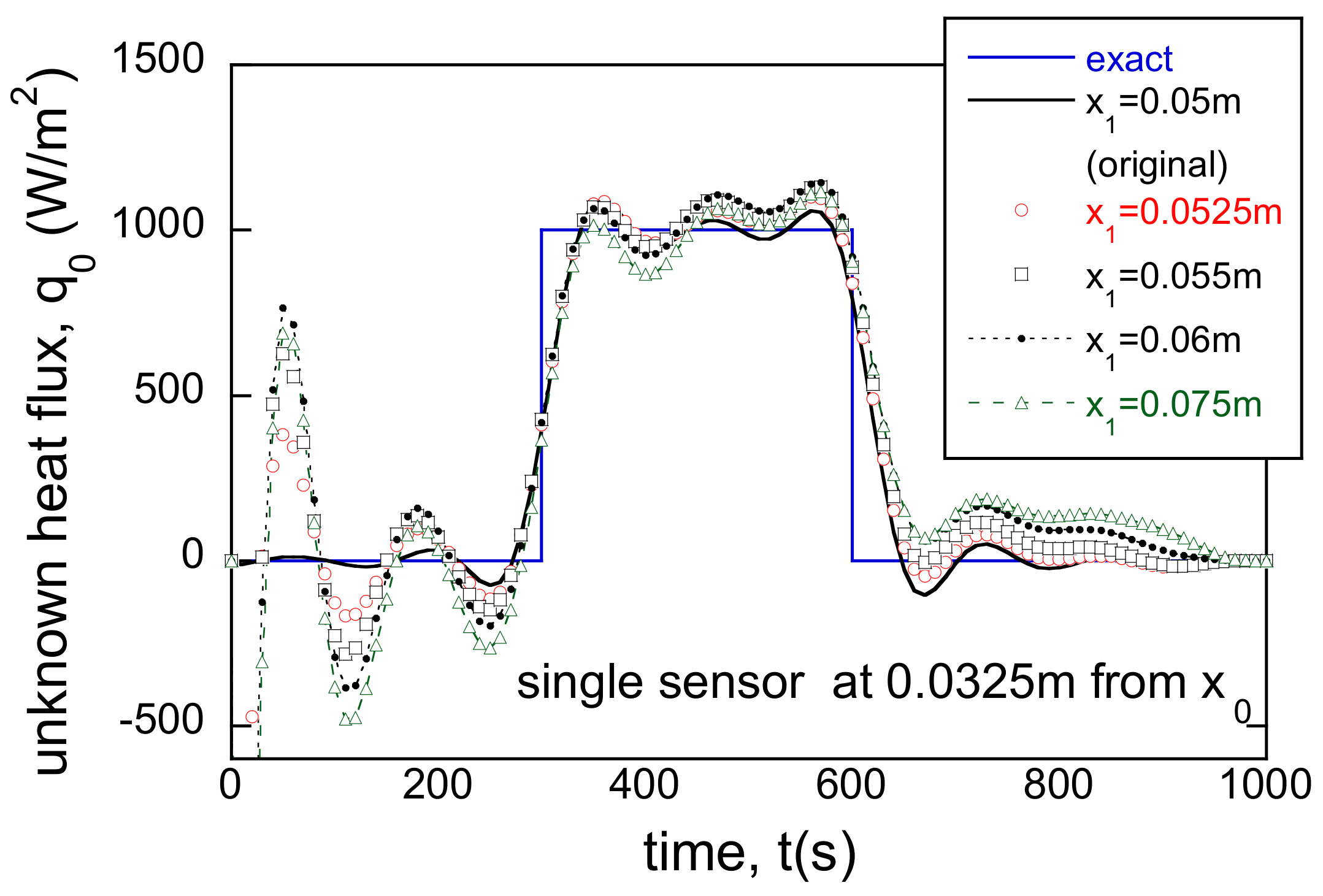
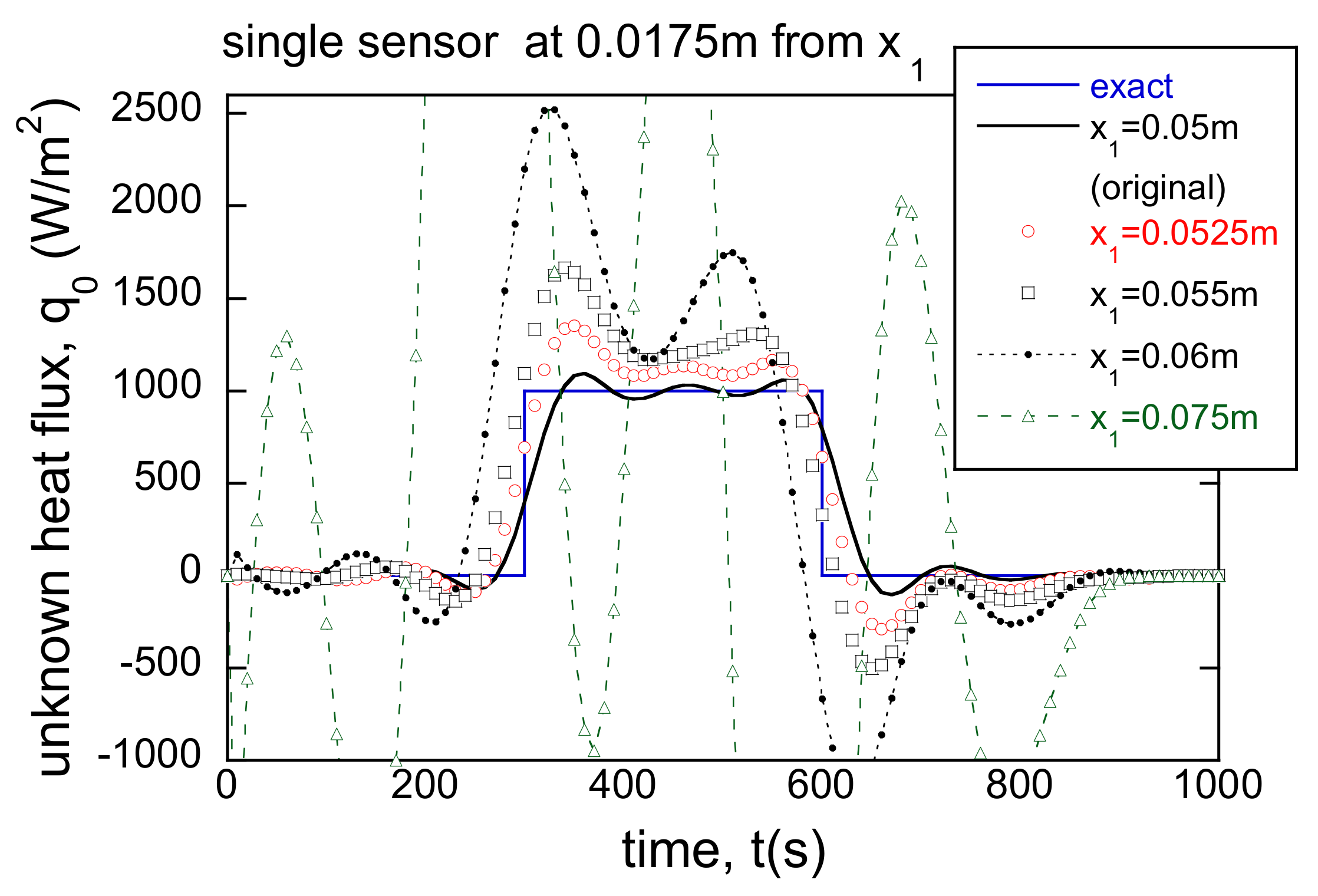
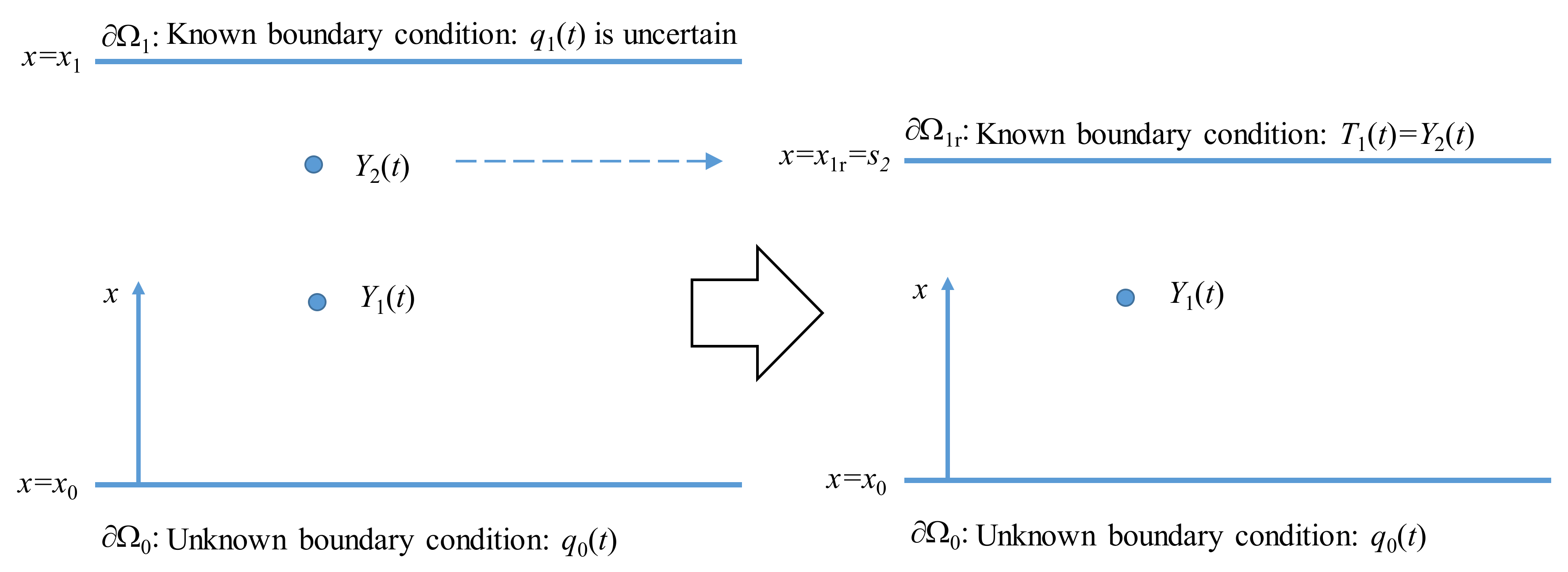
3.4. Incorrect Boundary Locations
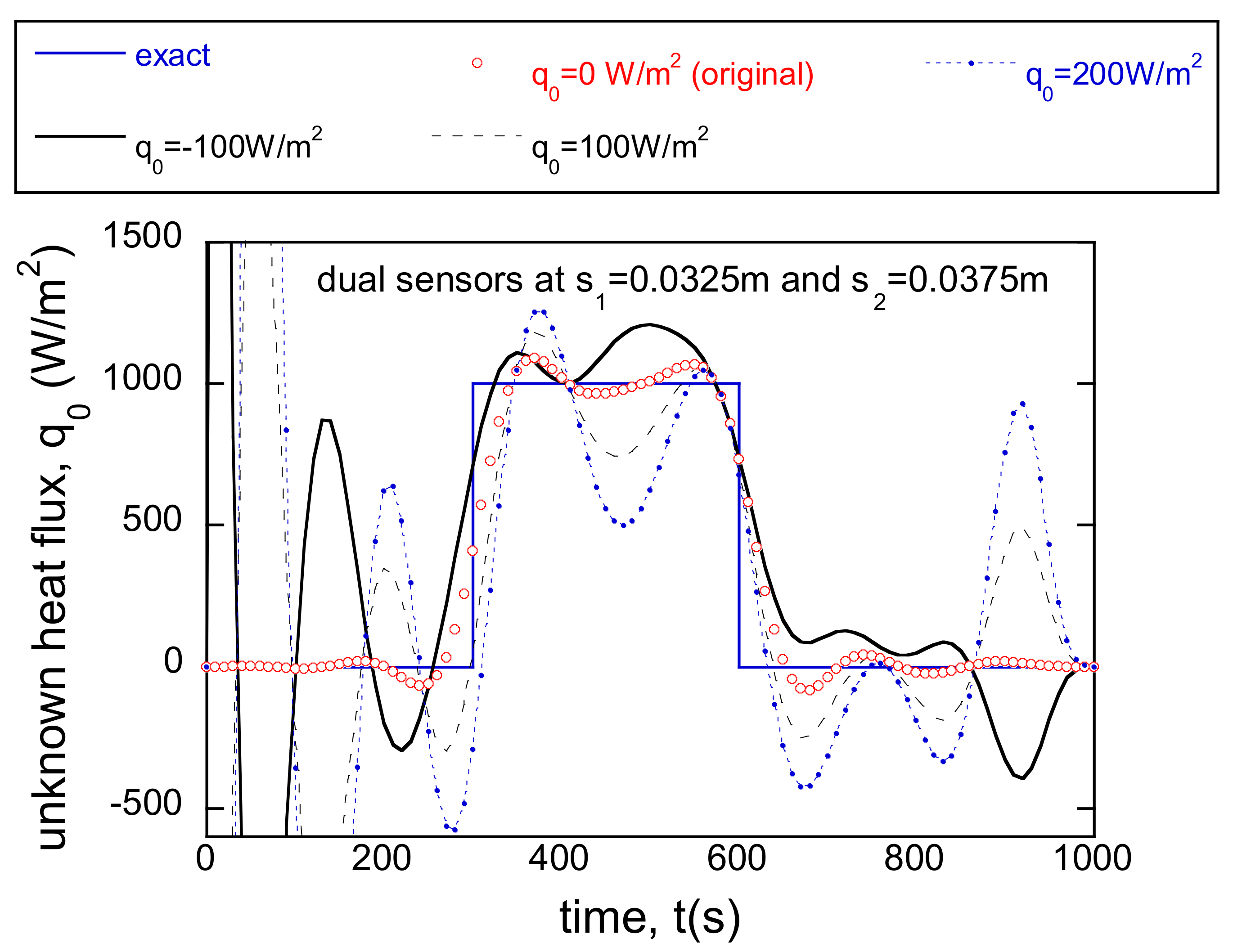
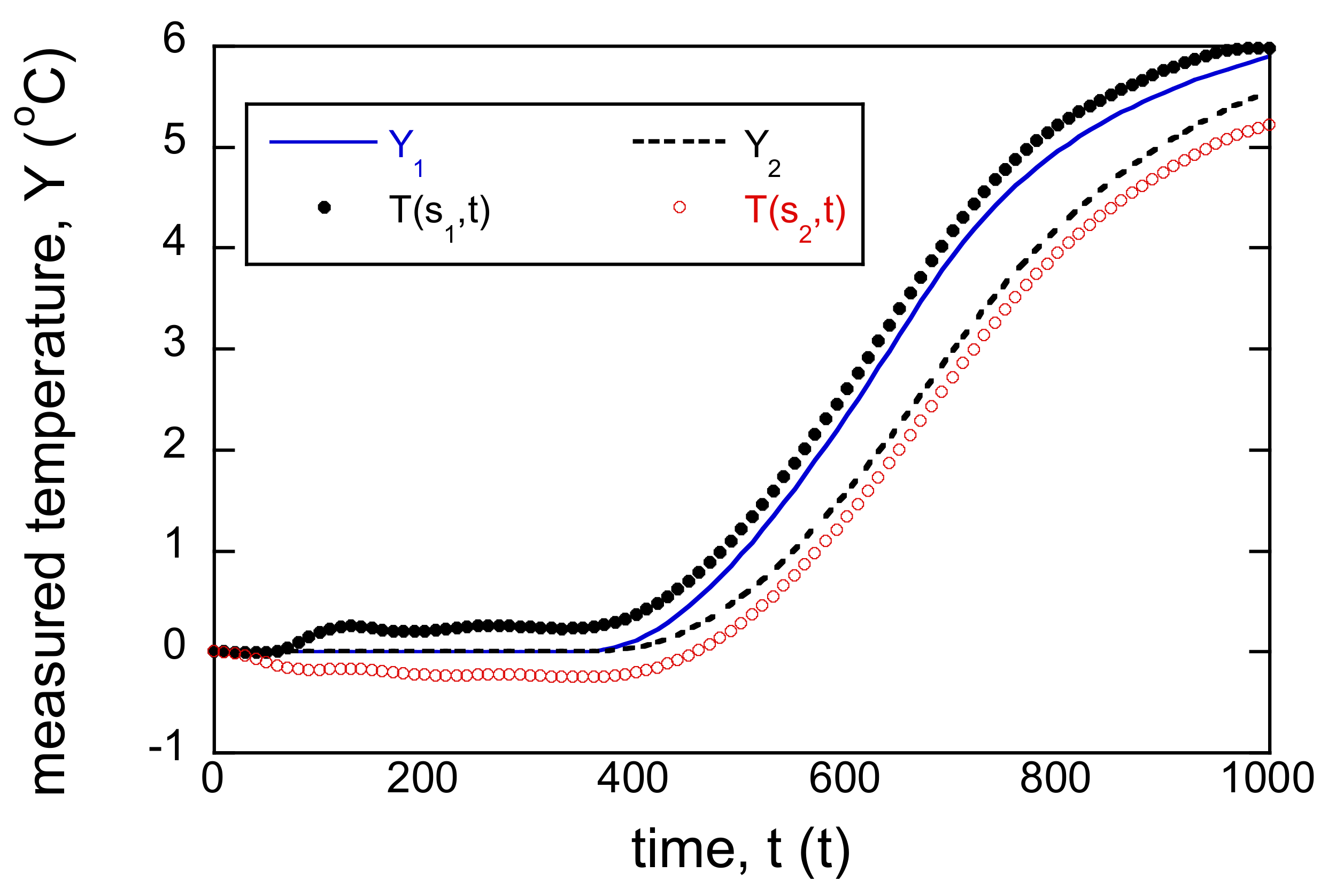
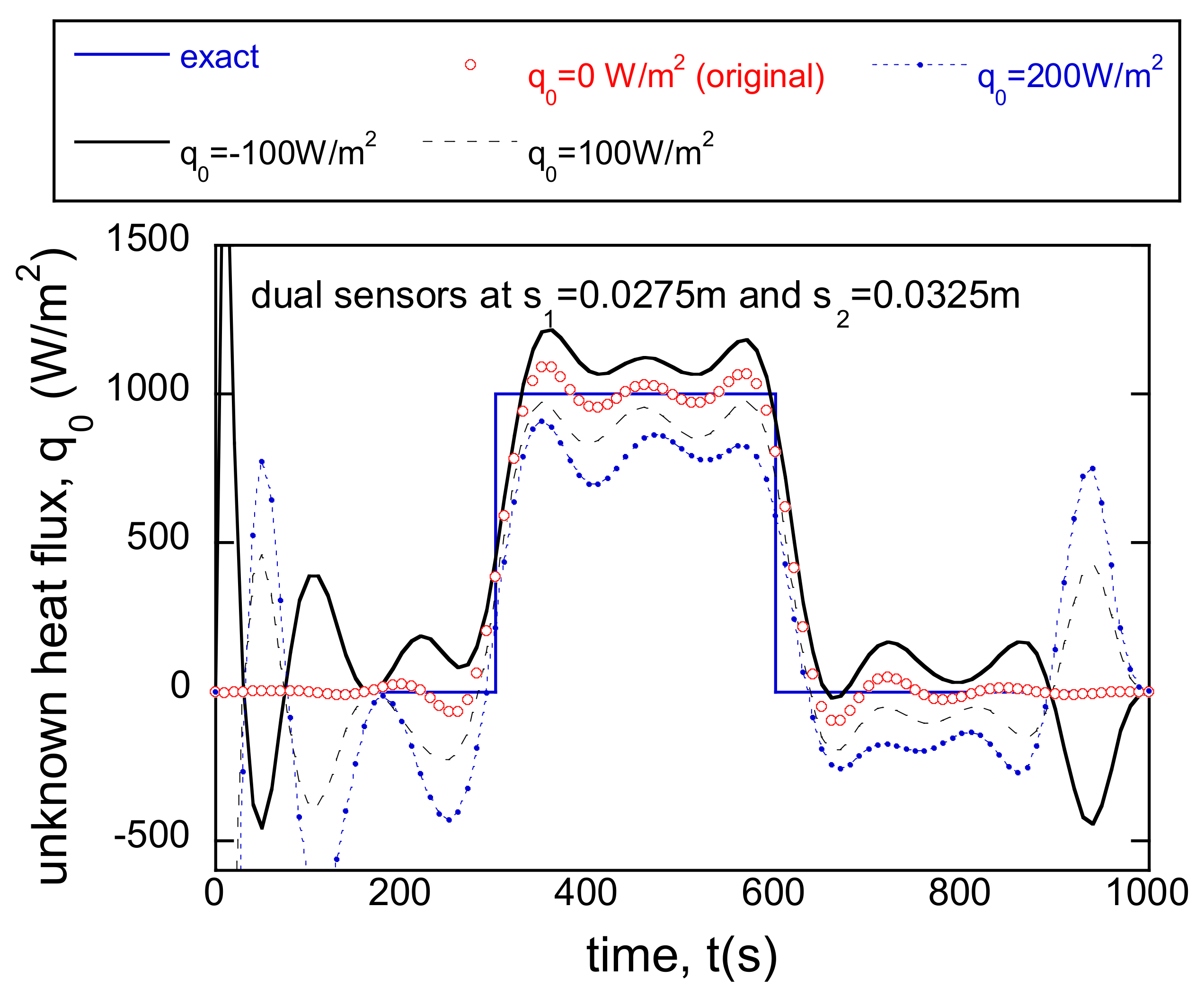
3.5. Dual Sensors
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a0 | coefficient for discretization (, m/s) |
| ap | coefficient for discretization (, m/s) |
| h | heat transfer coefficient at x1 (W/m2 °C) |
| J | residual (°C2s) |
| k | thermal conductivity (W/m°C) |
| Ns | number of total sensors |
| Nt | number of total time steps |
| the search direction in the r-th iteration (°C2s m2/W) | |
| q0 | unknown heat flux at the bottom boundary (x = x0) (W/m2) |
| q1 | known heat flux at the top boundary (x = x1) (W/m2) |
| R0 | the regularization parameter (0th order) (°C2m4/W2) |
| sj | j-th sensor location (m) |
| T | temperature (°C) |
| T1 | the known temperature at x1 (°C) |
| T0 | unknown temperature at x0 (°C) |
| Ti | initial temperature (°C) |
| Tik | temperature at discrete point xi and discrete time tk (°C) |
| estimated temperature at the j-th sensor location and at the discrete time tk (°C) | |
| reference temperature for convective boundary condition at x1 (°C) | |
| t | time (s) |
| t0 | initial time (s) |
| tk | k-th discrete time (s) |
| tf | final time (s) |
| x0 | the position of the bottom boundary (m) |
| x1 | the position of the top boundary (m) |
| Yj | measurement data at the j-th location (°C) |
| Yjk | measured temperature at the j-th sensor location and at the discrete time tk (°C) |
| α | thermal diffusivity (m2/s) |
| β | step size (dimensionless) |
| conjugate coefficient (dimensionless) | |
| ΔT | increment of temperature (°C) |
| Δτ | time step (s) |
| Δξ | spatial step (s) |
| δ | Dirac delta function |
| ε | convergence control parameter (°C) |
| φ | relaxation parameter (W2/m4°C2 s) |
| λ | adjoint variable (°C2s m2/W) |
| θ | relaxation parameter for temporal discretization (dimensionless) |
| σ | standard deviation of the measurement data (°C) |
| the internal domain | |
| the bottom boundary | |
| the top boundary |
References
- Ozisik, M.N.; Orlande, H.R.B. Inverse Heat Transfer: Fundamentals and Applications; Taylor & Francis: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Beck, J.V.; Blackwell, B.; St. Clair, C.R., Jr. Inverse Heat Conduction; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Alifanov, M. Inverse Heat Transfer Problem; Springer: Berlin, Germany, 1994. [Google Scholar] [CrossRef]
- Singh, D.P.K.; Mallinson, G.D.; Panton, S.M. Applications of optimization and inverse modeling to alloy wheel casting. Numer. Heat Transf. A 2002, 41, 741–756. [Google Scholar] [CrossRef]
- Marois, M.A.; Desilets, M.; Lacroix, M. Prediction of a 2-D solidification front in high temperature furnaces by an inverse analysis. Numer. Heat Transf. A 2011, 59, 151–166. [Google Scholar] [CrossRef]
- Kim, S.K.; Kim, H.J.; Lee, W.I. Characterization of boundary conditions during thermoplastic composite tape lay-up process using an inverse method. Model. Simul. Mater. Sci. Eng. 2003, 11, 417–426. [Google Scholar] [CrossRef]
- Zhao, C.F.; Luo, Z.; Li, Y.; Feng, M.; Xuan, W.B. Inverse heat conduction model for the resistance spot welding of aluminum alloy. Numer. Heat Transf. A 2016, 70, 1330–1344. [Google Scholar] [CrossRef]
- Yang, Y.-C.; Chen, W.-L.; Lee, H.-L. A nonlinear inverse problem in estimating the heat generation in rotary friction welding. Numer. Heat Transf. A 2011, 59, 130–149. [Google Scholar] [CrossRef]
- Hożejowska, S.; Piasecka, M. Numerical Solution of Axisymmetric Inverse Heat Conduction Problem by the Trefftz Method. Energies 2020, 13, 705. [Google Scholar] [CrossRef] [Green Version]
- McAliley, W.A.; Li, Y. Methods to Invert Temperature Data and Heat Flow Data for Thermal Conductivity in Steady-State Conductive Regimes. Geosciences 2019, 9, 293. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.K.; Lee, W.I. Inverse estimation of steady-state surface temperature on a three-dimensional body. Int. J. Numer. Methods Heat Fluid Flow 2002, 12, 1032–1050. [Google Scholar] [CrossRef]
- Kim, S.K.; Lee, J.S.; Lee, W.I. A solution method for a nonlinear three-dimensional inverse heat conduction problem using the sequential gradient method combined with cubic-spline function specification. Numer. Heat Transf. B 2003, 43, 43–61. [Google Scholar] [CrossRef]
- Yang, D.; Yue, X.; Yang, Q. Virtual boundary element method in conjunction with conjugate gradient algorithm for three-dimensional inverse heat conduction problems. Numer. Heat Transf. B 2017, 72, 421–430. [Google Scholar] [CrossRef]
- Bergagio, M.; Li, H.; Anglart, H. An iterative finite-element algorithm for solving two-dimensional nonlinear inverse heat conduction problems. Int. J. Heat Mass Transf. 2018, 126, 281–292. [Google Scholar] [CrossRef]
- Chen, H.; Frankel, J.I.; Keyhani, M. Nonlinear inverse heat conduction problem of surface temperature estimation by calibration integral equation method. Numer. Heat Transf. B 2018, 73, 263–291. [Google Scholar] [CrossRef]
- Karimi, M.; Moradlou, F.; Hajipour, M. Regularization Technique for an Inverse Space-Fractional Backward Heat Conduction Problem. J. Sci. Comput. 2020, 83, 37. [Google Scholar] [CrossRef]
- Samadia, F.; Woodbury, K.; Kowsary, F. Optimal combinations of Tikhonov regularization orders for IHCPs. Int. J. Therm. Sci. 2021, 161, 106697. [Google Scholar] [CrossRef]
- Kim, S.K. Resolving the Final Time Singularity in Gradient Methods for Inverse Heat Conduction Problems. Numer. Heat Transf. B 2010, 57, 74–88. [Google Scholar] [CrossRef]
- Kim, S.K. Parameterized Gradient Integration Method for Inverse Heat Conduction Problems. Numer. Heat Transf. B. 2012, 61, 116–128. [Google Scholar] [CrossRef]
- Alifanov, O.M.; Nenarokomov, A.V. Boundary inverse heat conduction problem: Algorithm and error analysis of space systems. Engineering 2001, 9, 619–644. [Google Scholar] [CrossRef]
- Mohebbi, F. Function Estimation in Inverse Heat Transfer Problems Based on Parameter Estimation Approach. Energies 2020, 13, 4410. [Google Scholar] [CrossRef]
- Kim, S.K. Gradient Method Code for Inverse Heat Conduction Problem—Excel VBA. 2019. Available online: http://dx.doi.org/10.13140/RG.2.2.35985.38249/1 (accessed on 24 July 2020).







| k (thermal conductivity) | 1 W/m °C |
| α (thermal diffusivity) | 10−6 m2/s |
| x0 (position of Ω) | 0 m |
| x1 (thickness or position of Ω) | 0.05 m |
| q0 (when unknown heat flux is specified) | 1000 W/m2 for 300 s ≤ t ≤ 600 s 0 for other time |
| T0 (when unknown temperature is specified) | 10 °C for 300 s ≤ t ≤ 600 s 0 for other time |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.K. Influence of Errors in Known Constants and Boundary Conditions on Solutions of Inverse Heat Conduction Problem. Energies 2021, 14, 3313. https://doi.org/10.3390/en14113313
Kim SK. Influence of Errors in Known Constants and Boundary Conditions on Solutions of Inverse Heat Conduction Problem. Energies. 2021; 14(11):3313. https://doi.org/10.3390/en14113313
Chicago/Turabian StyleKim, Sun Kyoung. 2021. "Influence of Errors in Known Constants and Boundary Conditions on Solutions of Inverse Heat Conduction Problem" Energies 14, no. 11: 3313. https://doi.org/10.3390/en14113313
APA StyleKim, S. K. (2021). Influence of Errors in Known Constants and Boundary Conditions on Solutions of Inverse Heat Conduction Problem. Energies, 14(11), 3313. https://doi.org/10.3390/en14113313






