Optimization of IEDs Position in MV Smart Grids through Integer Linear Programming
Abstract
1. Introduction
2. Automated Fault Location in Smart Grids
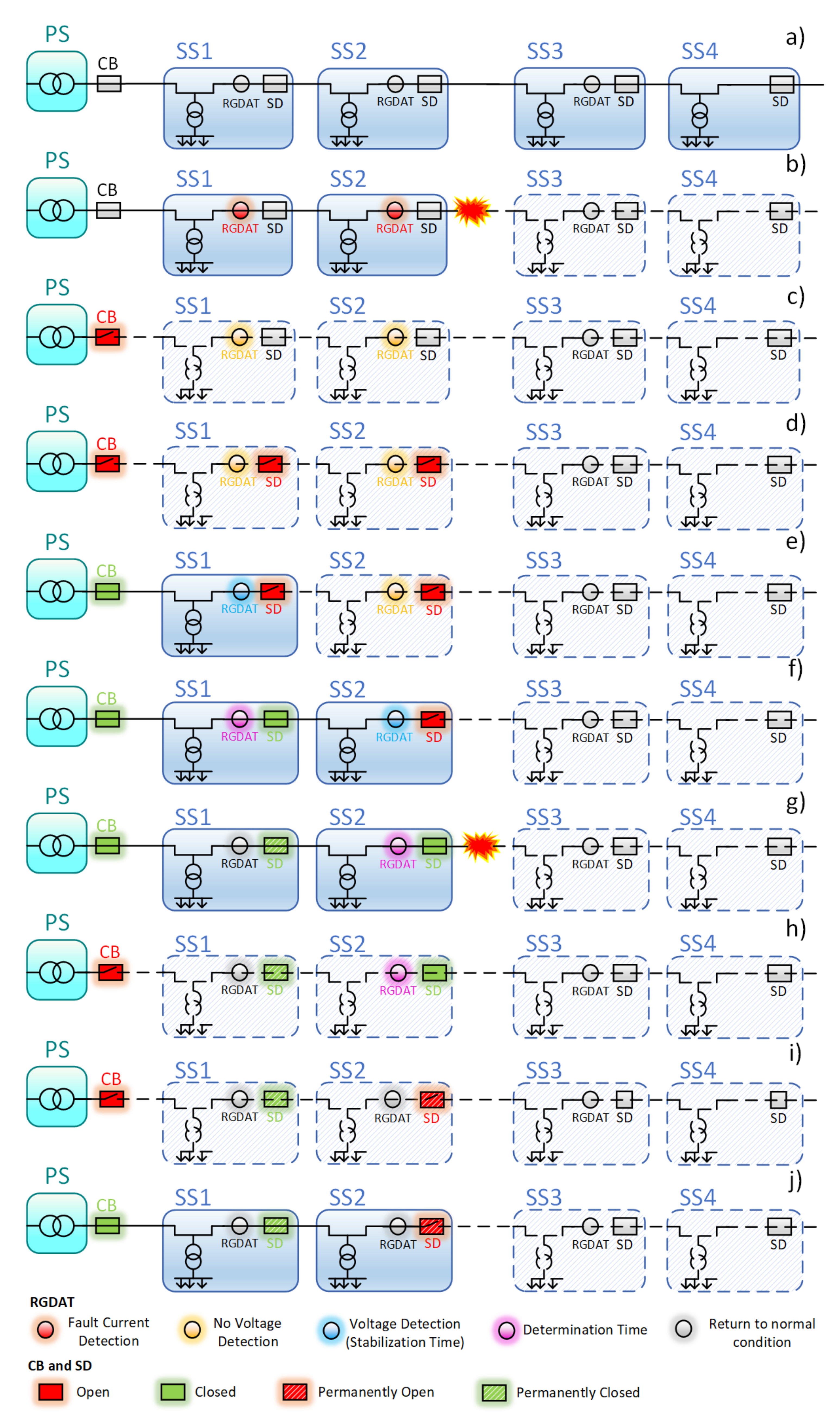
2.1. Traditional Automation
- If the RGDAT does not detect any voltage (upstream of the MV line with respect to the point where it is installed) for a certain period of time and has previously detected the presence of a fault current, the RTU automatically commands the opening of the SD;
- When the SD is opened and a voltage is detected (the line upstream is powered again), the RTU waits for a programmed stabilization time and then sends a closing command to the SD; at this time, a timer for measuring a programmed determination time starts;
- If the voltage is present for the duration of the determination time, the RTU leaves the SD closed and inhibits its opening in the successive steps. Otherwise, if no voltage is detected during the determination time, the RTU opens the SD permanently. This information is sent to the Operations Center.
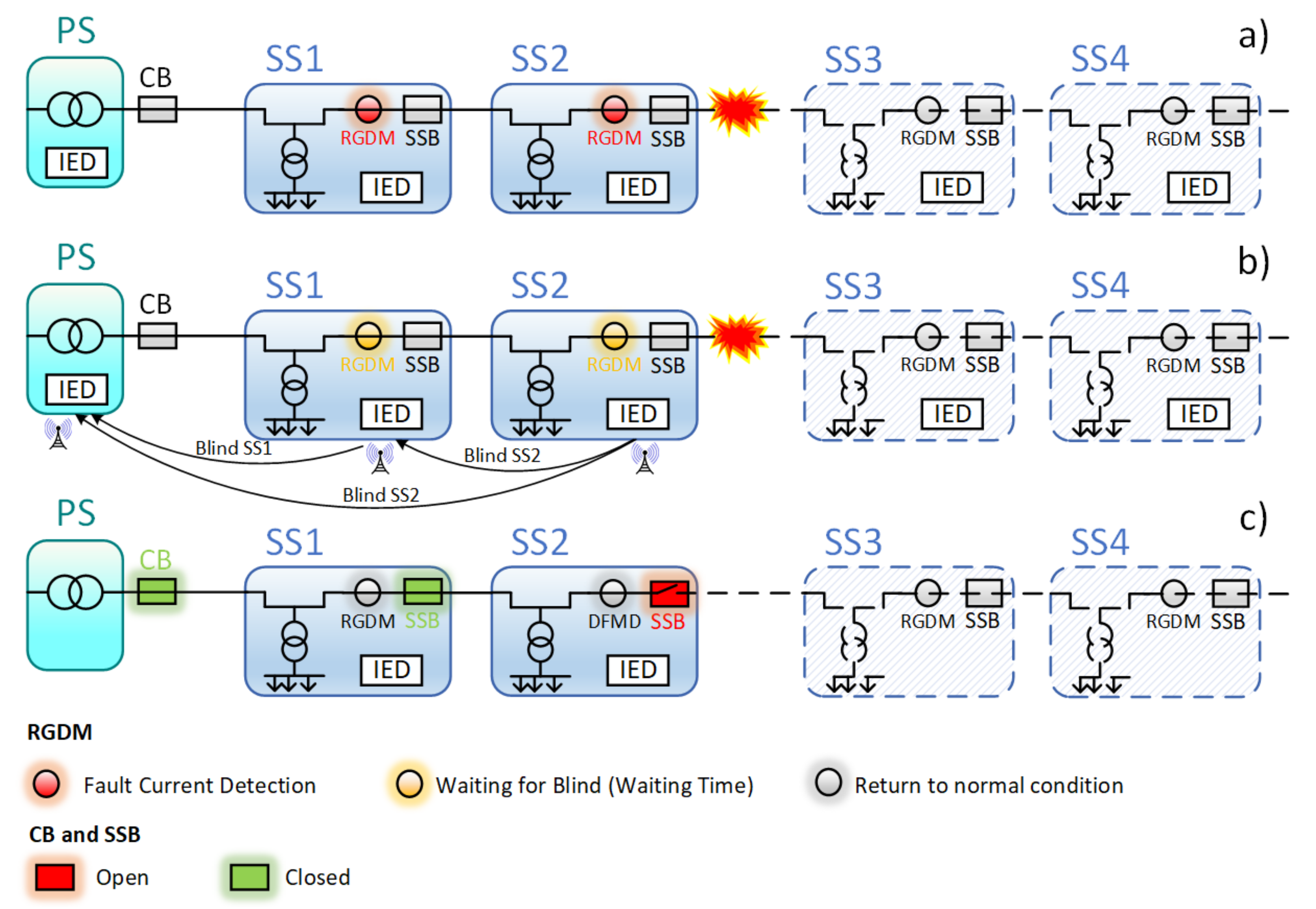
2.2. Logic Selectivity and Smart Fault Selection
- It transmits a block signal, called Blind, to the other IEDs installed on the grid; then it starts a timer to measure a programmed waiting time;
- If it receive a Blind message from a downstream node during the waiting time, it leaves the breaker SSB closed; otherwise, it commands opening of the SSB.
3. Optimal Location of Automated IEDs on a Grid Network
3.1. Problem Description
- i.
- We considered smart grids with radial topologies, composed of one primary line and one or more secondary lines. The primary line is composed of a single PS and several SSs. The primary line is powered by the PS and it can be re-powered through a boundary switch by a back-up PS in case of a fault.
- ii.
- Only LV customers were considered, since MV customers can be converted into equivalent LV customers;
- iii.
- Only the penalties determined by the number of LV customers interrupted for a long duration were considered. Indeed, in SFS automation, short duration interruptions (greater than 1 s and lower than 3 min) do not occur;
- iv.
- The case of double fault is not considered, and thus the faults are nonconcurrent. Moreover, the faults occurring in two sections are considered as disjoint and independent events.
- Upstream customers: they are located between the PS and the faulty section and they do not suffer any service interruption in case of a fault;
- Faulty customers: they are located in the faulty section and they suffer a service interruption for the time needed to identify and isolate the faulty section and re-power the customers. The duration of the interruption is proportional to the number of SSs present in the faulty section;
- Downstream customers: they are located after the faulty section and they are re-powered by the boundary switch within 1 s. Therefore, they do not experience any interruption.
3.2. Problem Setting and Formulation
| P | set of primary substations; |
| S | set of secondary substations/disconnectors, which are the potential locations for the IEDs deployment; |
| C | set of customers, each of them supplied by one secondary substation; |
| set of all the nodes composing the network; | |
| A | set of arcs , composing the network; |
| F | set of potential faults occurring on the network, or, in other words, set of the failure scenarios. Being each fault associated with an arc, these two sets coincide. In the following we keep the distinction in order to make the formulation more general; |
| p | number of IEDs to be installed on the network; |
| a penalty matrix reporting the AV20 value deriving from a fault f isolated by the couple of IEDs installed in nodes i and j. This value coincides with the AV20 value achievable when only a couple of IEDs is installed on the network. |
| IED location variable, | equal to 1 if an IED is installed in secondary |
| substation , 0 otherwise; | |
| Assignment variable, | equal to 1 if the couple of substations , |
| intervenes to isolate the fault , | |
| 0 otherwise. |
4. Assessment on a Real Mv Grid
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- 568/2019/R/EEL: Update of the Tariff Regulation of Electricity Transmission, Distribution and Metering Services for the Period 2020–2023; Standard, Regulatory Authority for Energy; Networks and Environment (ARERA): Milan, Italy, 2019. (In Italian)
- Bonavolontà, F.; Caputi, C.; Liccardo, A.; Teotino, A. Protection of MV smart grid based on IoT technology. In Proceedings of the 2019 II Workshop on Metrology for Industry 4.0 and IoT (MetroInd4. 0&IoT), Naples, Italy, 4–6 June 2019; pp. 112–116. [Google Scholar]
- Cepeda, C.; Orozco-Henao, C.; Percybrooks, W.; Pulgarín-Rivera, J.D.; Montoya, O.D.; Gil-González, W.; Vélez, J.C. Intelligent fault detection system for microgrids. Energies 2020, 13, 1223. [Google Scholar] [CrossRef]
- Nam, S.R.; Ko, W.H.; Key, S.; Kang, S.H.; Lee, N.H. IEC 61850-Based Centralized Protection against Single Line-To-Ground Faults in Ungrounded Distribution Systems. Energies 2021, 14, 722. [Google Scholar] [CrossRef]
- IEC 61850: Communication Networks and Systems in Substations; Standard, International Electrotechnical Commission: Geneva, Switzerland, 2013.
- Blair, S.M.; Booth, C.D. A practical and open source implementation of IEC 61850-7-2 for IED monitoring applications. IEEE Trans. Smart Grid 2015, 6, 1992–1993. [Google Scholar] [CrossRef]
- Angrisani, L.; Bonavolontà, F.; Liccardo, A.; Schiano Lo Moriello, R. On the use of LORA technology for logic selectivity in MV distribution networks. Energies 2018, 11, 3079. [Google Scholar] [CrossRef]
- Della Giustina, D.; Alvarez de Sotomayor, A.; Dedè, A.; Ramos, F. A Model-Based Design of Distributed Automation Systems for the Smart Grid: Implementation and Validation. Energies 2020, 13, 3560. [Google Scholar] [CrossRef]
- Dede, A.; Della Giustina, D.; Franzoni, F.; Pegoiani, A. IEC 61850-based logic selectivity scheme for the MV distribution network. In Proceedings of the 2014 IEEE International Workshop on Applied Measurements for Power Systems Proceedings (AMPS), Aachen, Germany, 24–26 September 2014; pp. 1–5. [Google Scholar]
- Pala, D.; Proserpio, G.; Bionda, E.; Pugliese, S.; Della Giustina, D. IEC CIM-61850 harmonization—The logic selectivity case. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–5. [Google Scholar]
- Bezerra, J.R.; Barroso, G.C.; Leão, R.P.S.; Sampaio, R.F. Multiobjective optimization algorithm for switch placement in radial power distribution networks. IEEE Trans. Power Deliv. 2014, 30, 545–552. [Google Scholar] [CrossRef]
- Das, S.; Santoso, S.; Gaikwad, A.; Patel, M. Impedance-based fault location in transmission networks: Theory and application. IEEE Access 2014, 2, 537–557. [Google Scholar] [CrossRef]
- Dutta, P.; Guan, Y.; Kezunovic, M. Use of substation IED data for improved alarm processing and fault location. In Proceedings of the 2008 40th North American Power Symposium, Calgary, AB, Canada, 28–30 September 2008; pp. 1–8. [Google Scholar]
- Gong, Y.; Guzmán, A. Distribution feeder fault location using IED and FCI information. In Proceedings of the 2011 64th Annual Conference for Protective Relay Engineers, College Station, TX, USA, 11–14 April 2011; pp. 168–177. [Google Scholar]
- Heidari, S.; Fotuhi-Firuzabad, M.; Lehtonen, M. Planning to equip the power distribution networks with automation system. IEEE Trans. Power Syst. 2017, 32, 3451–3460. [Google Scholar] [CrossRef]
- Prévé, C. Protection of Electrical Networks; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Sallam, A.A.; Malik, O.P. Electric Distribution Systems; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Masone, A.; Sforza, A.; Sterle, C.; Vasilyev, I.; Masone, A.; Sterle, C.; Vasilyev, I.; Ushakov, A.; Sforza, A.; Sidorov, D.; et al. A graph clustering based decomposition approach for large scale p-median problems. Int. J. 2018, 13, 229–242. [Google Scholar]
- Masone, A.; Sterle, C.; Vasilyev, I.; Ushakov, A. A three-stage p-median based exact method for the optimal diversity management problem. Networks 2019, 74, 174–189. [Google Scholar] [CrossRef]
- Tansel, B.C.; Francis, R.L.; Lowe, T.J. State of the Art—Location on Networks: A Survey. Part I: The p-Center and p-Median Problems. Manag. Sci. 1983, 29, 482–497. [Google Scholar] [CrossRef]
- Mladenović, N.; Brimberg, J.; Hansen, P.; Moreno-Pérez, J.A. The p-median problem: A survey of metaheuristic approaches. Eur. J. Oper. Res. 2007, 179, 927–939. [Google Scholar] [CrossRef]
- Masone, A.; Nenni, M.E.; Sforza, A.; Sterle, C. The Minimum Routing Cost Tree Problem. Soft Comput. 2019, 179, 2947–2957. [Google Scholar] [CrossRef]





| CD | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 30% | 4532 | 3279 | 2433 | 1742 | 1467 | 1295 | 1194 |
| 50% | 5122 | 3076 | 1992 | 1229 | 859 | 650 | 595 |
| 70% | 6114 | 4420 | 3114 | 2312 | 2082 | 1904 | 1765 |
| 90% | 6086 | 4366 | 3120 | 2435 | 1996 | 1787 | 1647 |
| 100% | 6334 | 4479 | 3252 | 2437 | 2000 | 1811 | 1651 |
| CD | SM | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Average |
|---|---|---|---|---|---|---|---|---|---|
| 30% | ILP | 5.4 | 3.2 | 4.9 | 1.5 | 2 | 2 | 1.6 | 2.9 |
| BF | 0.2 | 0.7 | 3.3 | 11.9 | 40 | 156.4 | 432.1 | 92.1 | |
| 50% | ILP | 7.5 | 7.2 | 2.7 | 5.4 | 2.8 | 3.4 | 2.9 | 4.6 |
| BF | 0.3 | 1.2 | 3.3 | 126.2 | 379.6 | 134.9 | 381.2 | 146.7 | |
| 70% | ILP | 6.7 | 4.8 | 4.4 | 2.6 | 1.7 | 1.2 | 1.1 | 3.2 |
| BF | 0.7 | 1.4 | 4.5 | 19.8 | 50.7 | 157.7 | 370.7 | 86.5 | |
| 90% | ILP | 7.7 | 5.5 | 7.9 | 4.1 | 3.4 | 2.3 | 4.3 | 5.0 |
| BF | 0.3 | 1.2 | 5.4 | 19.8 | 53 | 174.2 | 503.7 | 108.2 | |
| 100% | ILP | 8.4 | 6.6 | 4.3 | 5.6 | 3.1 | 3.7 | 4.8 | 5.2 |
| BF | 0.4 | 1.5 | 5.6 | 21.2 | 68.8 | 222.1 | 482.4 | 114.6 |
| CD | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 30% | 237 | 181 | 105 | 92 | 68 | 57 | 57 |
| 50% | 228 | 145 | 121 | 70 | 64 | 60 | 60 |
| 70% | 260 | 209 | 122 | 122 | 122 | 122 | 122 |
| 90% | 361 | 190 | 163 | 113 | 101 | 98 | 87 |
| 100% | 271 | 210 | 141 | 105 | 92 | 71 | 70 |
| CD | OF | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 30% | z | 9, 24 | 9, 30, 32 | 4, 9, 30, 32 | 4, 9, 29, 30, 32 | 4, 9, 12, 29, 30, 32 | 4, 9, 12, 15, 24, 29, 32 | 4, 9, 12, 15, 24, 29, 31, 32 |
| w | 9, 24 | 9, 29, 30 | 4, 9, 24, 29 | 4, 9, 12, 29, 30 | 4, 9, 15, 24, 29, 32 | 4, 9, 13, 29, 30, 31, 32 | 4, 8, 9, 12, 13, 24, 29, 31 | |
| 50% | z | 20, 24 | 9, 24, 32 | 9, 20, 24, 32 | 4, 9, 20, 24, 32 | 4, 9, 16, 20, 24, 32 | 4, 9, 15, 16, 20, 24, 32 | 4, 9, 15, 16, 20, 24, 32, 34 |
| w | 24, 25 | 9, 30, 32 | 4, 9, 24, 32 | 4, 16, 20, 24, 32 | 4, 15, 20, 24, 29, 32 | 4, 15, 16, 20, 24, 31, 32 | 4, 9, 13, 16, 17, 20, 24, 32 | |
| 70% | z | 20, 24 | 24, 31, 32 | 13, 24, 31, 32 | 13, 20, 24, 31, 32 | 13, 15, 20, 24, 31, 32 | 13, 15, 20, 24, 27, 31, 32 | 4, 13, 15, 20, 24, 27, 31, 32 |
| w | 20, 30 | 20, 24, 26 | 13, 24, 31, 32 | 4, 9, 13, 24, 32 | 4, 9, 13, 16, 24, 32 | 4, 8, 9, 11, 13, 24, 32 | 4, 8, 9, 12, 13, 23, 24, 32 | |
| 90% | z | 12, 24 | 8, 12, 24 | 8, 12, 24, 32 | 8, 9, 12, 24, 32 | 8, 9, 12, 15, 24, 32 | 4, 8, 9, 12, 15, 24, 32 | 4, 8, 9, 12, 15, 24, 30, 32 |
| w | 12, 30 | 8, 20, 30 | 8, 15, 20, 24 | 4, 15, 25, 30, 32 | 4, 8, 13, 25, 30, 32 | 15, 20, 23, 24, 26, 31, 32 | 4, 15, 20, 23, 24, 25, 30, 32 | |
| 100% | z | 12, 30 | 25, 30, 32 | 15, 25, 30, 32 | 9, 12, 15, 30, 32 | 12, 15, 25, 29, 30, 32 | 4, 12, 15, 24, 25, 29, 32 | 4, 12, 15, 24, 25, 29, 30, 32, |
| w | 30, 31 | 15, 24, 25 | 9, 12, 15, 30 | 8, 13, 20, 24, 31 | 4, 12, 15, 30, 31, 32 | 4, 9, 12, 15, 29, 30, 32 | 9, 15, 20, 24, 26, 29, 30, 32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonavolontà, F.; Caragallo, V.; Fatica, A.; Liccardo, A.; Masone, A.; Sterle, C. Optimization of IEDs Position in MV Smart Grids through Integer Linear Programming. Energies 2021, 14, 3346. https://doi.org/10.3390/en14113346
Bonavolontà F, Caragallo V, Fatica A, Liccardo A, Masone A, Sterle C. Optimization of IEDs Position in MV Smart Grids through Integer Linear Programming. Energies. 2021; 14(11):3346. https://doi.org/10.3390/en14113346
Chicago/Turabian StyleBonavolontà, Francesco, Vincenzo Caragallo, Alessandro Fatica, Annalisa Liccardo, Adriano Masone, and Claudio Sterle. 2021. "Optimization of IEDs Position in MV Smart Grids through Integer Linear Programming" Energies 14, no. 11: 3346. https://doi.org/10.3390/en14113346
APA StyleBonavolontà, F., Caragallo, V., Fatica, A., Liccardo, A., Masone, A., & Sterle, C. (2021). Optimization of IEDs Position in MV Smart Grids through Integer Linear Programming. Energies, 14(11), 3346. https://doi.org/10.3390/en14113346








