Optimising Energy Flexibility of Boats in PV-BESS Based Marina Energy Systems
Abstract
:1. Introduction
2. Ballen Marina on Samsø
3. Marina’s Demand Analysis
- Night valley: 21.00–6.00.
- Morning peak: 6.00–10.00.
- Noon valley: 10.00–15.00.
- Afternoon peak: 15.00–21.00.
- Pearson correlation coefficient r: statistical measure of the linear correlation between two data sets, in the range of . A value of indicates perfect negative correlation, whereas signifies perfect positive correlation.
- p-value: probability of obtaining test results equal to or more extreme than the observed results. Very small p-values indicate that null hypothesis can be rejected. Typically, the null hypothesis is tested under the significance level of , leading to 95% confidence interval.
4. Electricity Pricing
4.1. Hourly-Varying Tariff for Marina
4.2. Time of Use Tariff for Sailors
- Green zone: 0.22 EUR/kWh, 21.00–6.00.
- Yellow zone: 0.34 EUR/kWh, 10.00–15.00.
- Red zone: 0.40 EUR/kWh, 6.00–10.00 and 15.00–21.00.
5. Modelling of Demand Response
6. Proposed Optimal Operation of Marina’s Energy System
- Base Scenario,
- Cost-Efficient Operation of BESS,
- Boat Flexibility and BESS,
- Late Summer and Late Autumns Seasons.
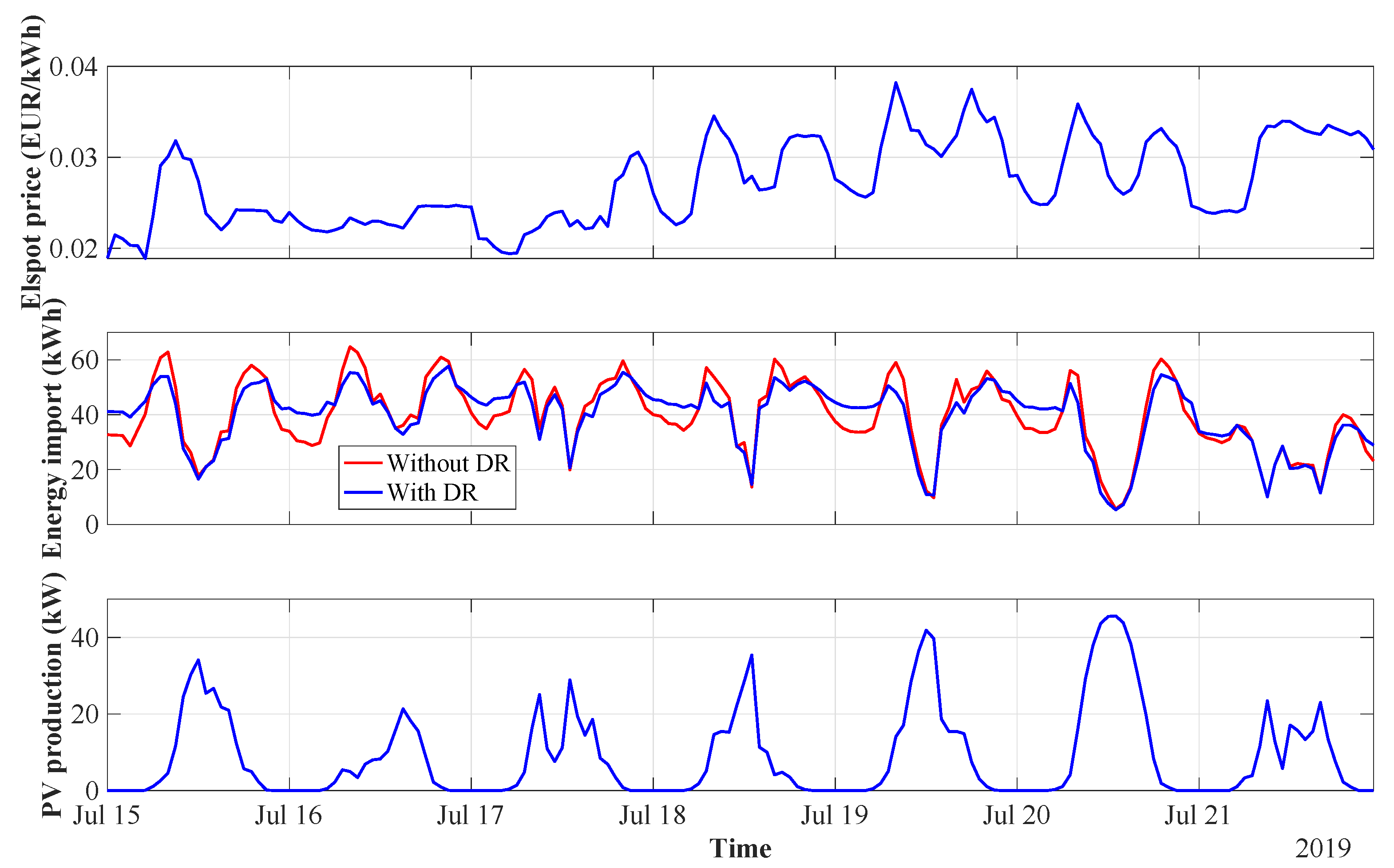
7. Results and Discussion
7.1. Base Scenario
7.2. Cost-Efficient Operation of BESS
7.3. Boat Flexibility and BESS
7.4. Late Summer and Late Autumn Seasons
- Late summer: 9–15 September 2019, low load (341 kWh) and high PV generation (1759 kWh).
- Late autumn: 21–27 October 2019, low load (324 kWh) and low PV generation (355 kWh).
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BESS | Battery energy storage system |
| CPP | Critical peak pricing |
| DLC | Direct load control |
| DR | Demand response |
| DSM | Demand-side management |
| EDR | Emergency demand response |
| EMS | Energy management system |
| ESS | Energy storage system |
| EV | Electric vehicle |
| ICES | Integrated community energy system |
| PSO | Public Service Obligations |
| PV | Photovoltaic |
| RTP | Real-time pricing |
| SOC | State of charge |
| TOU | Time-of-use |
| V2G | Vehicle-to-grid |
References
- Smart Grid Strategy: The Intelligent Energy System of the Future; Technical Report; Danish Ministry of Climate, Energy and Building: Copenhagen, Denmark, 2013.
- Albadi, M.H.; El-Saadany, E.F. Demand Response in Electricity Markets: An Overview. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar]
- Carli, R.; Dotoli, M.; Jantzen, J.; Kristensen, M.; Ben Othman, S. Energy scheduling of a smart microgrid with shared photovoltaic panels and storage: The case of the Ballen marina in Samsø. Energy 2020, 198, 1–16. [Google Scholar] [CrossRef]
- Ma, R.; Chen, H.; Huang, Y.; Meng, W. Smart Grid Communication: Its Challenges and Opportunities. IEEE Trans. Smart Grid 2013, 4, 36–46. [Google Scholar] [CrossRef]
- Deng, R.; Yang, Z.; Chow, M.; Chen, J. A Survey on Demand Response in Smart Grids: Mathematical Models and Approaches. IEEE Trans. Ind. Inform. 2015, 11, 570–582. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Mancarella, P.; Monti, A. Unlocking Flexibility: Integrated Optimization and Control of Multienergy Systems. IEEE Power Energy Mag. 2017, 15, 43–52. [Google Scholar] [CrossRef]
- Ipakchi, A.; Albuyeh, F. Grid of the future. IEEE Power Energy Mag. 2009, 7, 52–62. [Google Scholar] [CrossRef]
- Strbac, G. Demand side management: Benefits and challenges. Energy Policy 2008, 36, 4419–4426. [Google Scholar] [CrossRef]
- Chiu, W.; Sun, H.; Poor, H.V. Demand-side energy storage system management in smart grid. In Proceedings of the 2012 IEEE Third International Conference on Smart Grid Communications (SmartGridComm), Tainan, Taiwan, 5–8 November 2012; pp. 73–78. [Google Scholar]
- Arteconi, A.; Hewitt, N.J.; Polonara, F. State of the art of thermal storage for demand-side management. Appl. Energy 2012, 93, 371–389. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Jordehi, A.R. Optimisation of demand response in electric power systems, a review. Renew. Sustain. Energy Rev. 2019, 103, 308–319. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A Survey on Demand Response Programs in Smart Grids: Pricing Methods and Optimization Algorithms. IEEE Commun. Surv. Tutorials 2015, 17, 152–178. [Google Scholar] [CrossRef]
- Datchanamoorthy, S.; Kumar, S.; Ozturk, Y.; Lee, G. Optimal time-of-use pricing for residential load control. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications, Brussels, Belgium, 17–20 October 2011; pp. 375–380. [Google Scholar] [CrossRef]
- DR. Regeringen Klar Med Udspil til Transportaftale: Målet er 500.000 Elbiler i 2030. Available online: https://www.dr.dk/nyheder/politik/regeringen-klar-med-udspil-til-transportaftale-maalet-er-500000-elbiler-i-2030 (accessed on 29 September 2020).
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Grid Integration of Electric Vehicles and Demand Response With Customer Choice. IEEE Trans. Smart Grid 2012, 3, 543–550. [Google Scholar] [CrossRef]
- Rizvi, S.A.A.; Xin, A.; Masood, A.; Iqbal, S.; Jan, M.U.; Rehman, H. Electric Vehicles and their Impacts on Integration into Power Grid: A Review. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Saele, H.; Petersen, I. Electric vehicles in Norway and the potential for demand response. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Mohammad, A.; Zamora, R.; Lie, T.T. Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling. Energies 2020, 13, 4541. [Google Scholar] [CrossRef]
- Yang, H.; Shen, W.; Yu, Q.; Liu, J.; Jiang, Y.; Ackom, E.; Dong, Z.Y. Coordinated demand response of rail transit load and energy storage system considering driving comfort. Csee J. Power Energy Syst. 2020, 6, 749–759. [Google Scholar] [CrossRef]
- Calvillo, C.F.; Sánchez-Miralles, A.; Villar, J. Synergies of Electric Urban Transport Systems and Distributed Energy Resources in Smart Cities. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2445–2453. [Google Scholar] [CrossRef]
- Hein, K.; Yan, X.; Wilson, G. Multi-Objective Optimal Scheduling of a Hybrid Ferry with Shore-to-Ship Power Supply Considering Energy Storage Degradation. Electronics 2020, 9, 849. [Google Scholar] [CrossRef]
- Kanellos, F.D.; Tsekouras, G.J.; Hatziargyriou, N.D. Optimal Demand-Side Management and Power Generation Scheduling in an All-Electric Ship. IEEE Trans. Sustain. Energy 2014, 5, 1166–1175. [Google Scholar] [CrossRef]
- Shang, C.; Srinivasan, D.; Reindl, T. Economic and Environmental Generation and Voyage Scheduling of All-Electric Ships. IEEE Trans. Power Syst. 2016, 31, 4087–4096. [Google Scholar] [CrossRef]
- Shang, C.; Srinivasan, D.; Reindl, T. NSGA-II for joint generation and voyage scheduling of an all-electric ship. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 5113–5119. [Google Scholar] [CrossRef]
- Huang, Y.; Lan, H.; Hong, Y.Y.; Wen, S.; Fang, S. Joint voyage scheduling and economic dispatch for all-electric ships with virtual energy storage systems. Energy 2020, 190, 116268. [Google Scholar] [CrossRef]
- Ponnaganti, P.; Bak-Jensen, B.; Pillai, J. Maximizing the self-consumption of Solar-PV using Battery Energy Storage System in Samsø-Marina. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe, ISGT-Europe 2019. IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Bucharest, Romania, 29 September–2 October 2019. [Google Scholar] [CrossRef]
- Jozwiak, D.; Pillai, J.R.; Ponnaganti, P.; Bak-Jensen, B.; Jantzen, J. Integrated Community Energy Systems: Case Study of Ballen Marina on Samsø. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021. [Google Scholar]
- Rusu, E.; Onea, F. Estimation of the wave energy conversion efficiency in the Atlantic Ocean close to the European islands. Renew. Energy 2016, 85, 687–703. [Google Scholar] [CrossRef]
- Rusu, E. Wave energy assessments in the Black Sea. J. Mar. Sci. Technol. 2009, 14, 359–372. [Google Scholar] [CrossRef]
- Bonanno, A.; Franzitta, V.; Muzio, F.P.; Trapanese, M. A multiphysics approach to the design of a seawave energy conversion system. In Proceedings of the 2008 IEEE International Conference on Sustainable Energy Technologies, Singapore, 24–27 November 2008; pp. 665–668. [Google Scholar] [CrossRef]
- Franzitta, V.; Viola, A.; Trapanese, M. Description of Hysteresis in Lithium Battery by Classical Preisach Model. Adv. Mater. Res. 2012, 622–623, 1099–1103. [Google Scholar] [CrossRef]
- Tran, Q.T.T.; Riva Sanseverino, E.; Zizzo, G.; Di Silvestre, M.L.; Nguyen, T.L.; Tran, Q.-T. Driven Primary Regulation for Minimum Power Losses Operation in Islanded Microgrids. Energies 2018, 11, 2890. [Google Scholar] [CrossRef] [Green Version]
- Gangale, F.; Vasiljevska, J.; Covrig, C.F.; Mengolini, A.; Fulli, G. Smart Grid Projects Outlook 2017: Facts, Figures and Trends in Europe; Technical Report; Joint Research Centre: Luxembourg, Luxembourg, 2017. [Google Scholar]
- Marczinkowski, H.M.; Østergaard, P.A. Evaluation of electricity storage versus thermal storage as part of two different energy planning approaches for the islands Samsø and Orkney. Energy 2019, 175, 505–514. [Google Scholar] [CrossRef] [Green Version]
- Jantzen, J.; Bak-Jensen, B. Deliverable D3.1: Specifications and Data Report for the Samsø Demonstrator; Technical Report; Smart Island Energy Systems: Brussels, Belgium, 2017. [Google Scholar]
- Marczinkowski, H.M. Deliverable D8.2: Short and Medium-Term Scenarios for the Three Pilot Islands; Technical Report; Smart Island Energy Systems: Brussels, Belgium, 2018. [Google Scholar]
- Jantzen, J.; Kristensen, M. The Ballen2016 Data Set. Available online: http://arkiv.energiinstituttet.dk/643/ (accessed on 29 October 2020).
- Agresti, A. Statistical Methods for the Social Sciences, 5th ed.; Pearson: New York, NY, USA, 2018. [Google Scholar]
- Energinet.dk. Flexafregning af Kunders Elforbrug. Available online: https://energinet.dk/El/Private-elkunder/Flexafregning (accessed on 3 February 2021).
- Elpris. SPOT PLUS Prisen. Available online: https://elpris.dk/ (accessed on 25 February 2021).
- Albertsen, L.H.; Andersen, M.; Boscán, L.R.; Santos, A.Q. Implementing dynamic electricity taxation in Denmark. Energy Policy 2020, 143, 111543. [Google Scholar] [CrossRef]
- Samsø Kommune. Takster 2021. Available online: https://www.samsoe.dk/kommunen/oekonomi/takster-2021 (accessed on 16 April 2021).
- Wikner, E.; Thiringer, T. Extending Battery Lifetime by Avoiding High SOC. Appl. Sci. 2018, 8, 1825. [Google Scholar] [CrossRef] [Green Version]














| Parameter | Value |
|---|---|
| Nominal PV plant power | 60 kWp |
| Battery maximum power | 49 kW |
| Battery capacity | 237 kWh |
| Number of sockets for boats | 340 |
| Maximum allowed import from grid | 86 kW 1 |
| Maximum allowed export to grid | 49 kW |
| Parameter | Case | |
|---|---|---|
| Without DR | With DR | |
| Shifted energy (kWh) | 0 | 347 |
| Load factor (%) | 66.5 | 78.1 |
| Marina’s energy cost (EUR) | 1260 | 1258 |
| Sailors’ energy cost (EUR) | 2726 | 2668 |
| Parameter | Flexibility Factor (%) | ||||
|---|---|---|---|---|---|
| 0 | 25 | 50 | 75 | 100 | |
| Shifted energy (kWh) | 0 | 173 | 347 | 520 | 694 |
| Load factor (%) | 66.5 | 71.8 | 78.1 | 82.3 | 83.9 |
| Marina’s energy cost (EUR) | 1260 | 1259 | 1258 | 1257 | 1256 |
| Sailors’ energy cost (EUR) | 2726 | 2697 | 2668 | 2639 | 2610 |
| Parameter | Case | |||
|---|---|---|---|---|
| Baseline | DR | BESS | DR and BESS | |
| Shifted energy (kWh) | 0 | 347 | 0 | 368 |
| Energy import (kWh) | 6657 | 6657 | 6678 | 6671 |
| Load factor (%) | 66.5 | 78.1 | 66.5 | 78.3 |
| Marina’s energy cost (EUR) | 1260 | 1258 | 1259 | 1256 |
| Sailors’ energy cost (EUR) | 2726 | 2668 | 2726 | 2663 |
| Parameter | Late Summer | Late Autumn | ||
|---|---|---|---|---|
| Baseline | DR and BESS | Baseline | DR and BESS | |
| Shifted energy (kWh) | 0 | 18 | 0 | 15 |
| Energy import (kWh) | 203 | 0 | 225 | 0 |
| Energy export (kWh) | 1621 | 1439 | 256 | 0 |
| Load factor (%) | 19.8 | 28.7 | 31.8 | 36.9 |
| Marina’s energy cost (EUR) | 34 | 0 | ||
| Sailors’ energy cost (EUR) | 111 | 108 | 107 | 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jozwiak, D.; Pillai, J.R.; Ponnaganti, P.; Bak-Jensen, B.; Jantzen, J. Optimising Energy Flexibility of Boats in PV-BESS Based Marina Energy Systems. Energies 2021, 14, 3397. https://doi.org/10.3390/en14123397
Jozwiak D, Pillai JR, Ponnaganti P, Bak-Jensen B, Jantzen J. Optimising Energy Flexibility of Boats in PV-BESS Based Marina Energy Systems. Energies. 2021; 14(12):3397. https://doi.org/10.3390/en14123397
Chicago/Turabian StyleJozwiak, Dawid, Jayakrishnan Radhakrishna Pillai, Pavani Ponnaganti, Birgitte Bak-Jensen, and Jan Jantzen. 2021. "Optimising Energy Flexibility of Boats in PV-BESS Based Marina Energy Systems" Energies 14, no. 12: 3397. https://doi.org/10.3390/en14123397
APA StyleJozwiak, D., Pillai, J. R., Ponnaganti, P., Bak-Jensen, B., & Jantzen, J. (2021). Optimising Energy Flexibility of Boats in PV-BESS Based Marina Energy Systems. Energies, 14(12), 3397. https://doi.org/10.3390/en14123397






