Boost Voltage Single Phase Full Bridge Inverter with No Voltage Drop Based on Switched Capacitor
Abstract
:1. Introduction
2. Circuit Structure and Working Principle
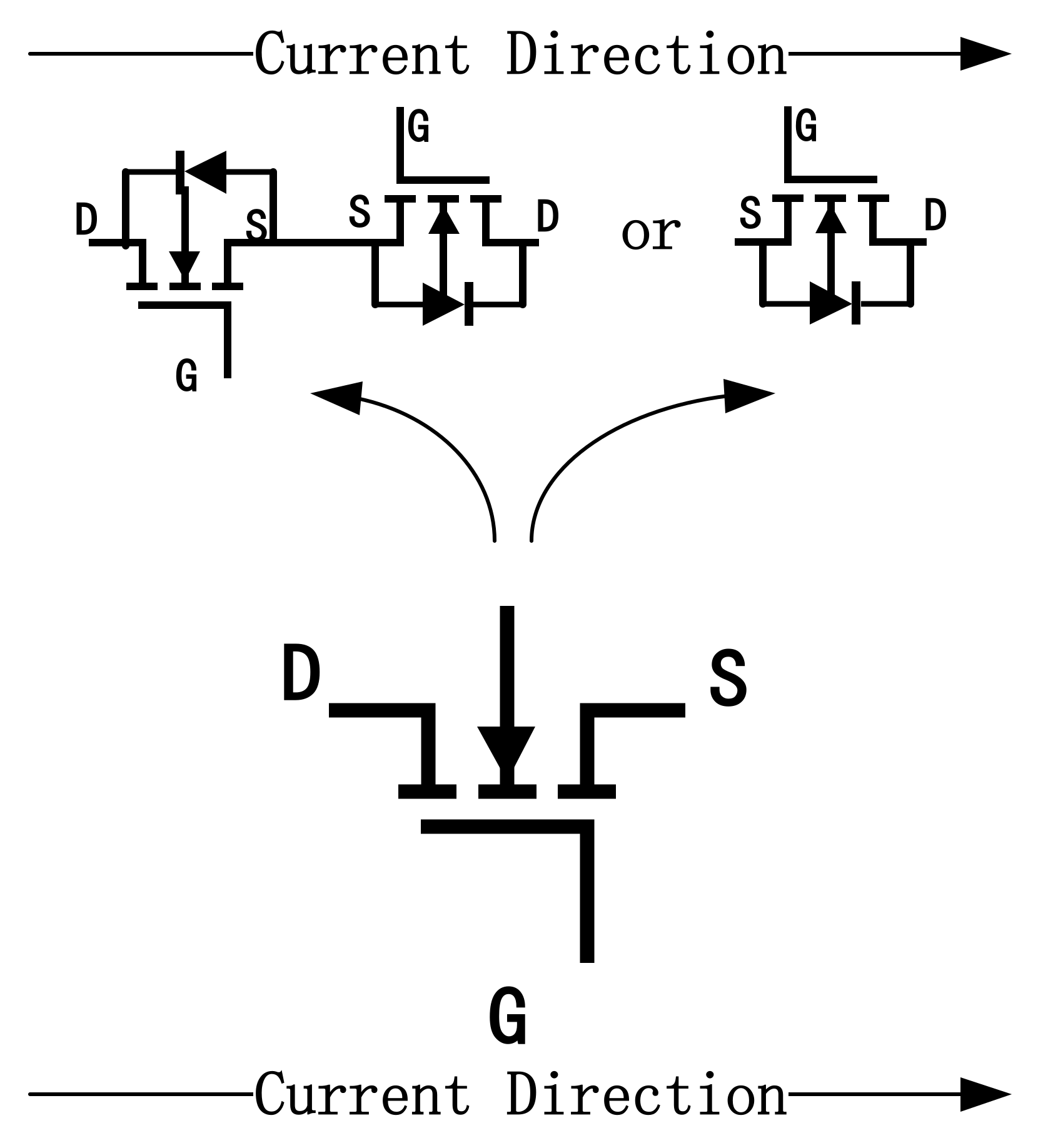
2.1. Circuit Structure
2.2. Working Principle
3. Modulation Strategy and Capacitance Analysis
3.1. Modulation Strategy Analysis
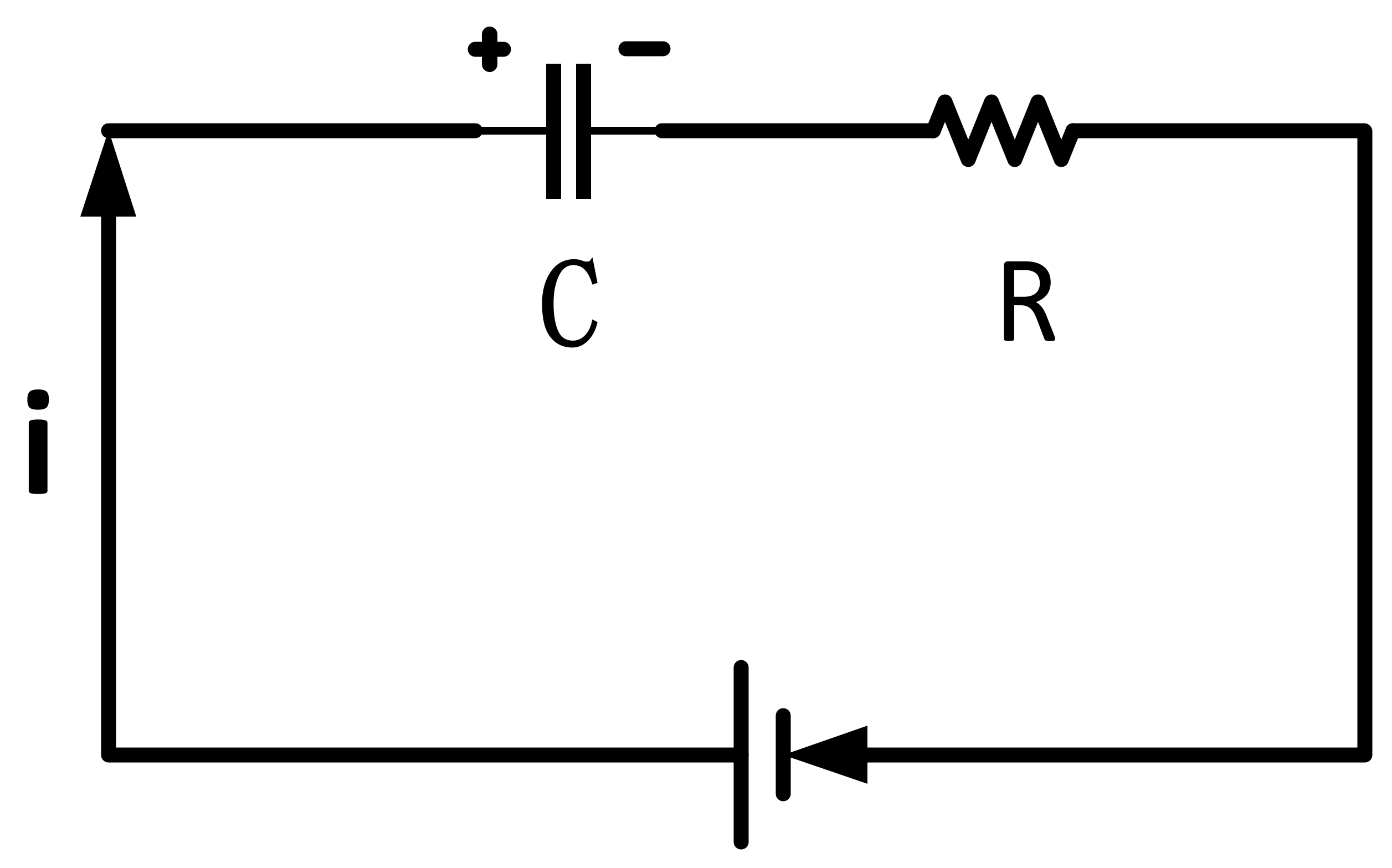
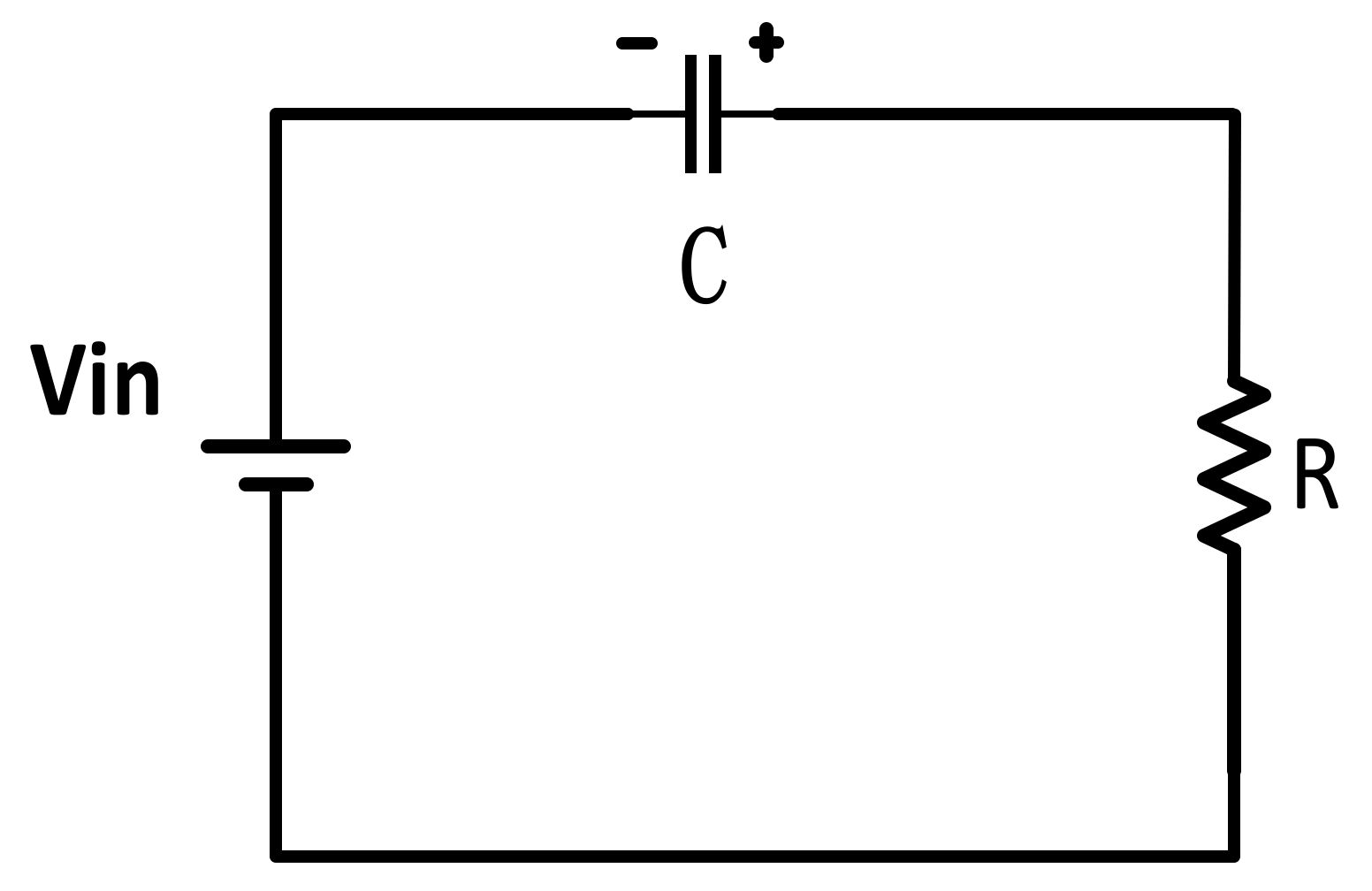
3.2. Capacitance Parameter Analysis
4. Loss Analysis
4.1. Switch Tube Loss
4.2. Capacitance Loss Analysis
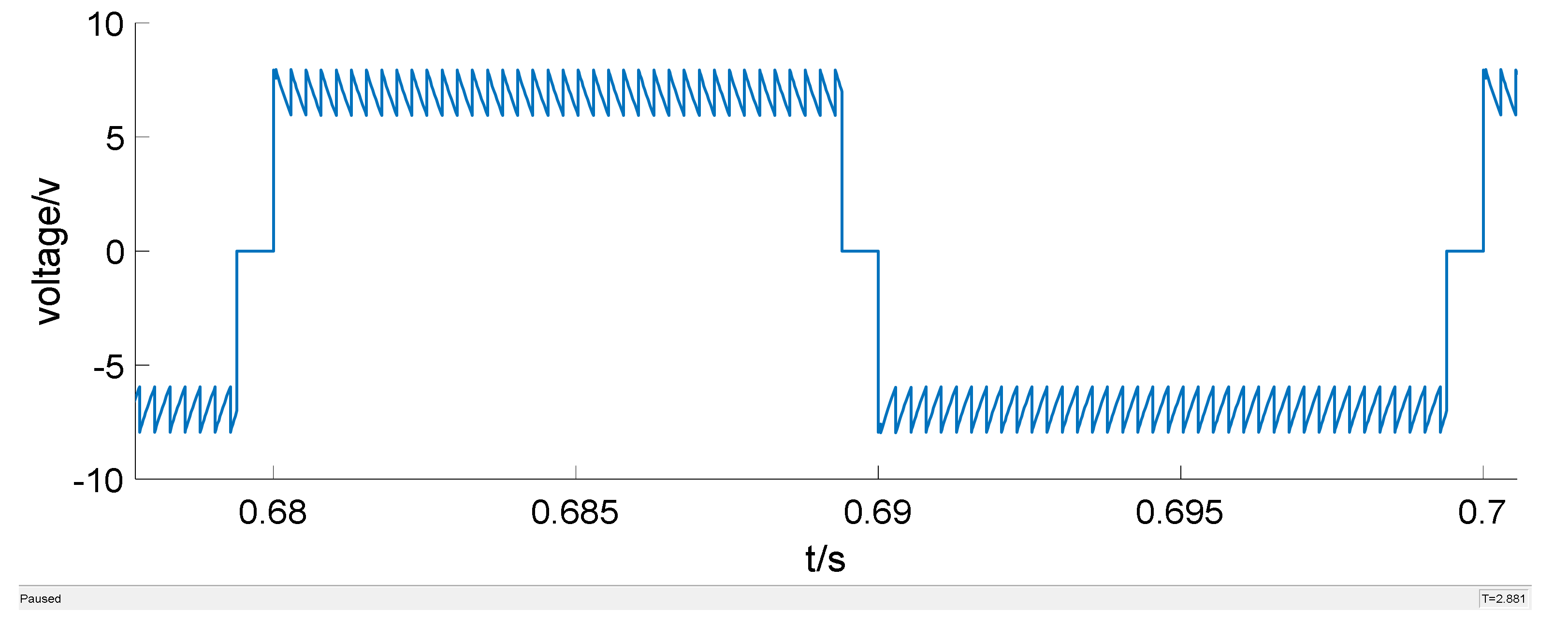
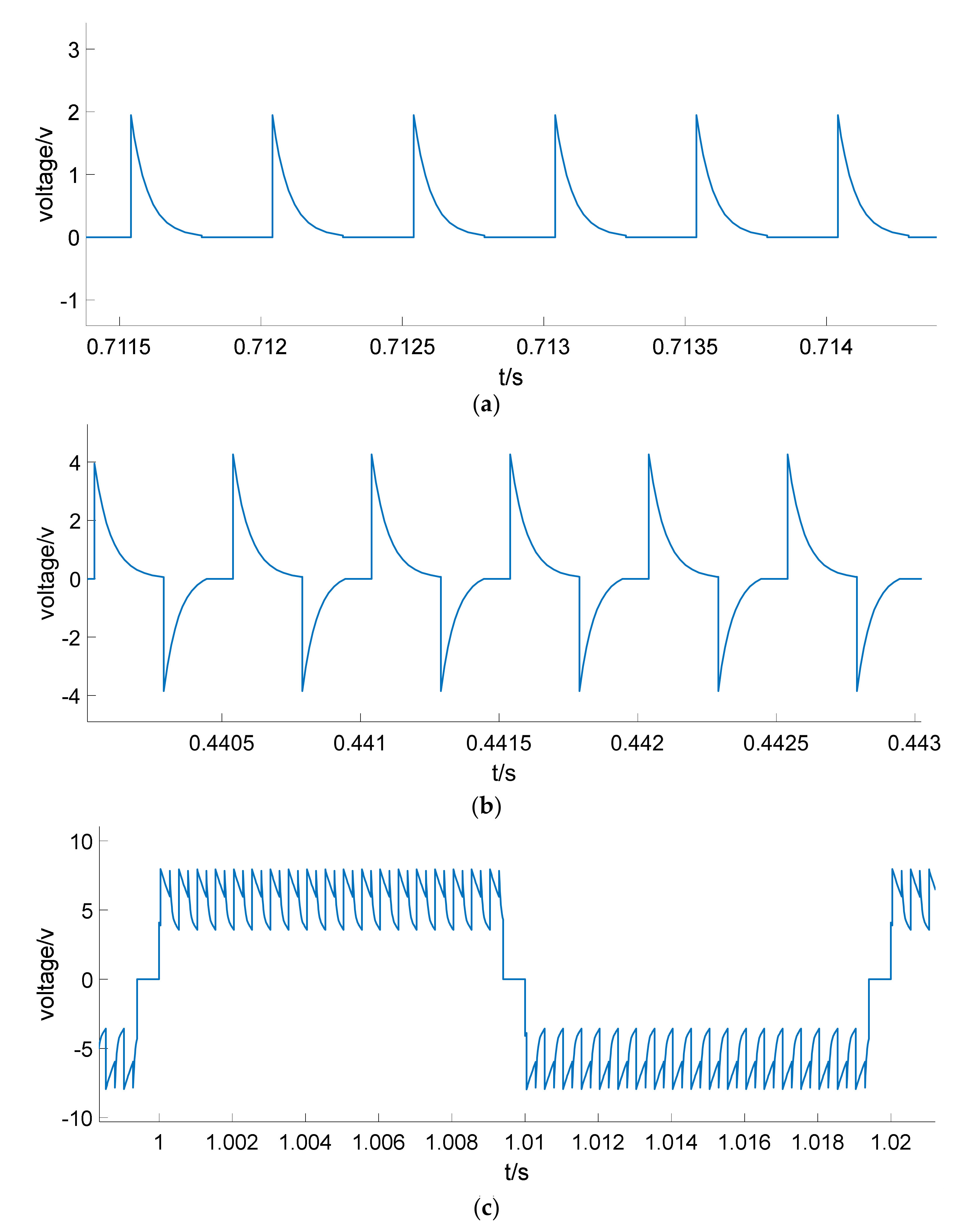
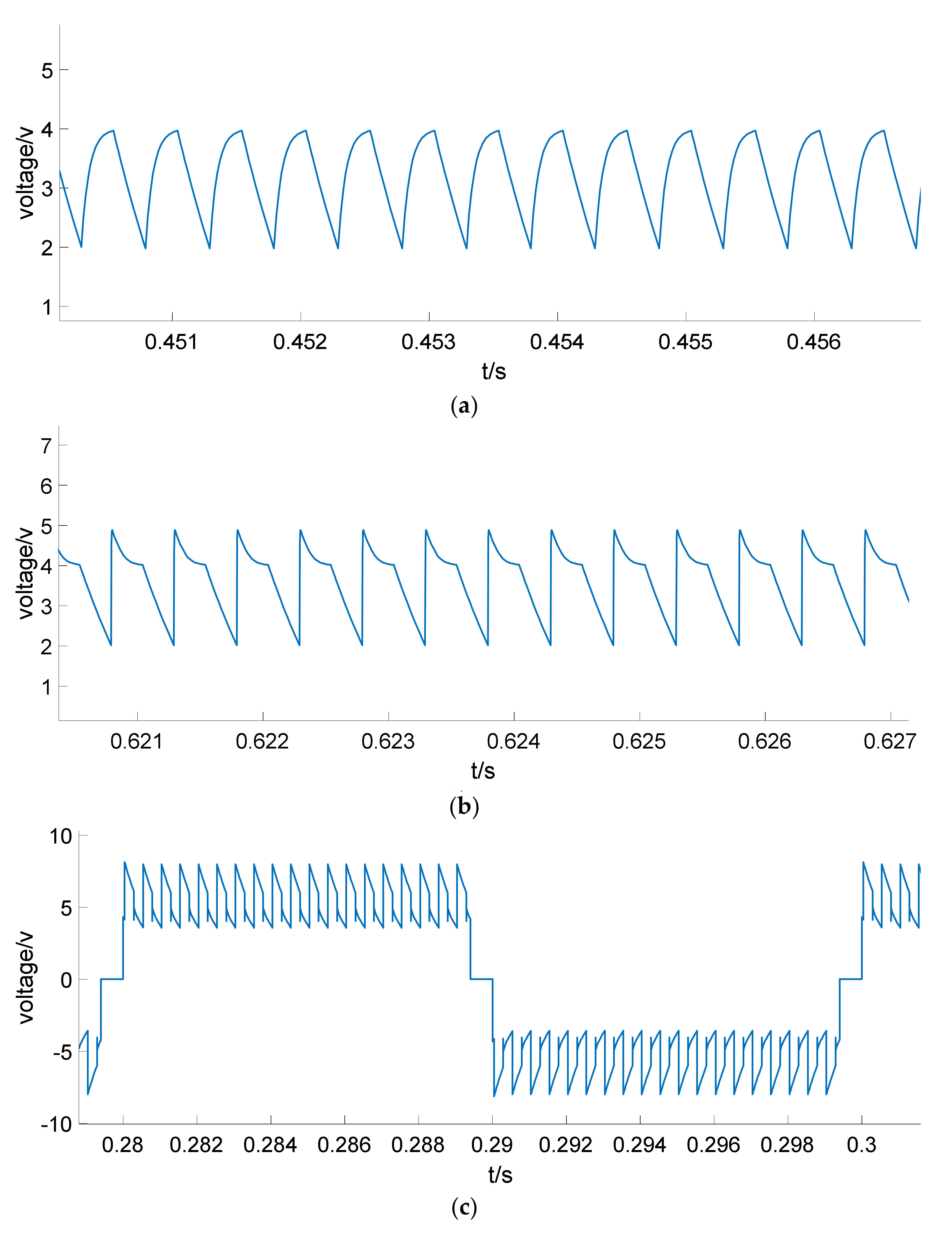
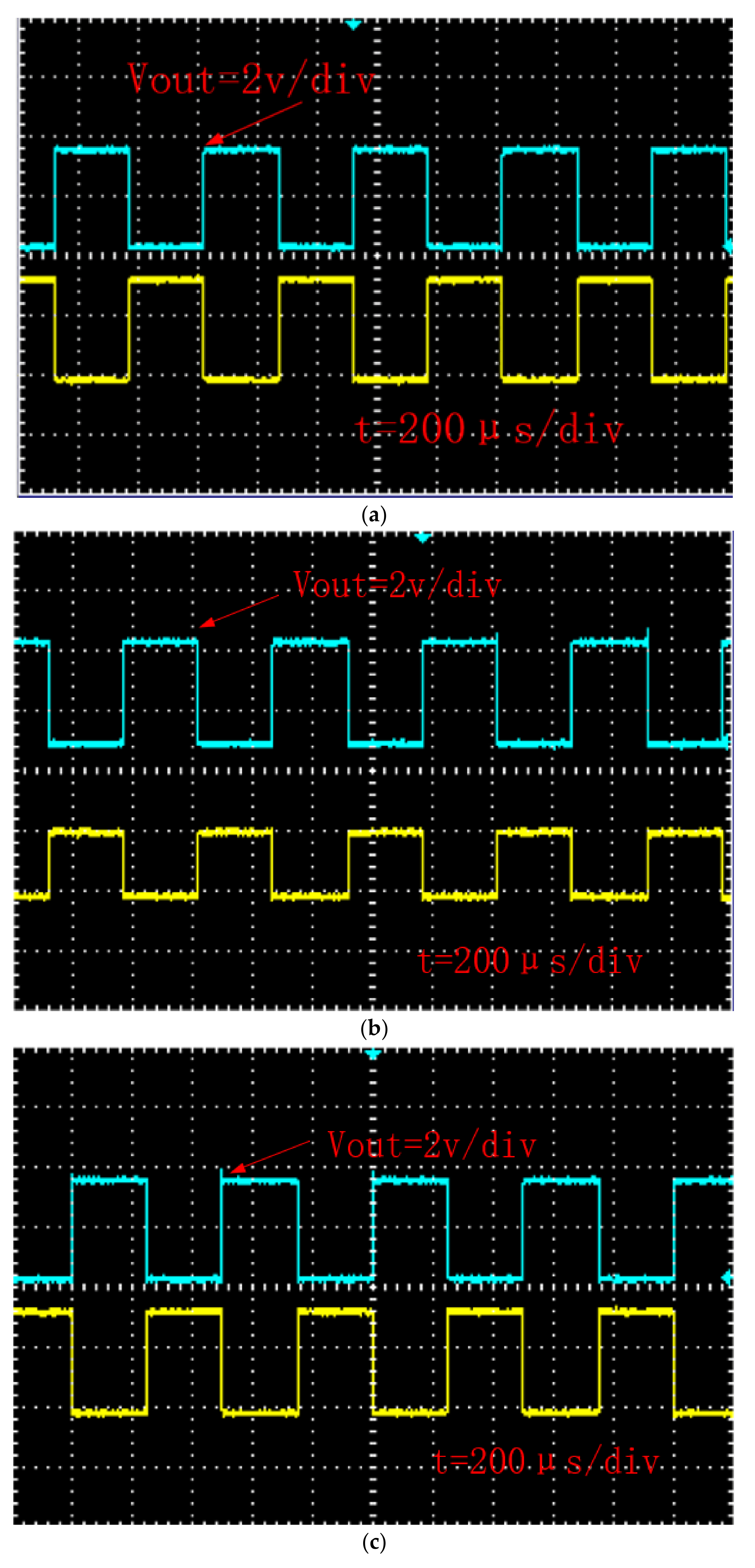
5. Simulation and Experiment
5.1. Simulation Result Analysis
5.2. Experimental Results
6. Conclusions
7. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gang, W.U.; Xinbo, R.U.A.N.; Zhihong, Y.E. Non-isolated High Step-up DC-DC Converters Adopting Switched-capacitor Cell. Proc. CSEE 2015, 35, 442–450. [Google Scholar]
- Shan, L.I.; Wenxu, S.I.; Yan, C.H.E.N.; Sen, C.U.I. Modeling and Analysis of High-frequency Isolated Quasi-Z Source Inverter. J. Power Supply 2018, 16, 52–60. [Google Scholar]
- Qingfa, G.U.; Jie, W. Parameter selection and stability analysis of inverter type microgrid droop controller. Adv. Technol. Electr. Eng. Energy 2017, 36, 34–40. [Google Scholar]
- Wenhua, L.I.; Qi, H.U.; Shannian, L.U.; He, Z.; Hang, Z. Research on the Working Characteristics of the Secondary Boost Inverter. Adv. Technol. Electr. Eng. Energy 2018, 37, 39–44. [Google Scholar]
- Hussan, M.R.; Sarwar, A.; Siddique, M.D.; Mekhilef, S.; Ahmad, S.; Sharaf, M.; Zaindin, M.; Firdausi, M. A Novel Switched-Capacitor Multilevel Inverter Topology for Energy Storage and Smart Grid Applications. Electronics 2020, 9, 1703. [Google Scholar] [CrossRef]
- Guanqian, J.; Zhiyong, L.; Huixia, Y.; Jing, Y. Research review on topological structure of flexible HVDC system. Power Syst. Prot. Control 2015, 43, 145–153. [Google Scholar]
- Zhaohui, D.; Junxi, O.; Bin, B.; Wenguang, C. Design of a frequency adjustable and single-phase output boost type inverter. Electron. Des. Eng. 2017, 25, 110–113. [Google Scholar]
- Yonggao, Z.; Lingtao, K.; Yingying, X. Novel Micro-inverter Power Decoupling Circuit Based on Buck/Boost Circuit. Proc. CSU-EPSA 2020, 32, 29–34. [Google Scholar]
- Shou, L.; Shengyun, J.; Liyong, Y. Research on the Topology of Three-phase Continuous Switching Boost Inverter. Electr. Drive 2018, 48, 31–36. [Google Scholar]
- Lei, C.; Tinglong, P. High gain step-up converter based on switched-capacitor network. Electron. Des. Eng. 2016, 24, 173–177. [Google Scholar]
- Anas, M.; Sarwar, A.; Ahmad, A.; Alam, A.; Ahmad, S.; Sharaf, M.; Zaindin, M.; Firdausi, M. Generalized Structures for Switched-Capacitor Multilevel Inverter Topology for Energy Storage System Application. Appl. Sci. 2021, 11, 1319. [Google Scholar] [CrossRef]
- Nan, L.; Ping, W.; Taizhou, B.; Likun, X.; Cai, Q. Novel high-gain switched capacitor DC boost converter. J. Electr. Power Syst. Autom. 2017, 29, 83–89. [Google Scholar]
- Shiying, H.; Jianfei, C.; Tao, S.; Buyun, M.; Ming, L.; Jia, D. A Single-Switch Step-Up Converter Based on Switched-Capacitor Networks in Parallel. Transact. Chin. Electrotech. Soc. 2015, 30, 242–248. [Google Scholar]
- Luo, F.L.; Ye, H. Positive output cascade boost converters. Proc. Inst. Elect. Eng. Elect. Power Appl. 2004, 151, 590–606. [Google Scholar] [CrossRef]
- Ma Guadalupe Ortiz Lopez, J.; Leyva Ramos, L.H. Multiloop controller for n-stage cascade boost converter. In Proceedings of the 16th IEEE International Conference on Control Applications, Hokkaido, Japan, 6–9 July 2020; pp. 587–592. [Google Scholar]
- Hong, P.; Lejie, T. Boost and Neutral-point Balance Control of Z-source Three-level Inverter Based on SPWM. J. Power Supply 2019, 17, 63–69. [Google Scholar]
- Yikun, J.; Shaoru, Z.; Lingling, L.; Shuai, W. Improved Switching Boost Inverter. Electr. Drive 2016, 46, 33–36. [Google Scholar]
- Li, J.; Jianyong, Z. Z-source photovoltaic grid-connected direct current single-cycle control system. Autom. Electr. Power Syst. 2008, 32, 87–90. [Google Scholar]
- Xuhui, Z.; Xuhui, W.; Feng, Z. A Direct Power Control Scheme for Bi-directional BUCK/Boost Converters in Motor Drive Systems. Proc. CSEE 2012, 32, 15–22. [Google Scholar]
- Cungang, H.; Pei, Y.; Yunlei, Z.; Qunjing, W.; Changbao, Z. Topology and Control Strategy for High-Efficient Non-Isolated Single-Phase Grid-Connected MOSFET Inverter. Transact. Chin. Electrotech. Soc. 2016, 31, 82–91. [Google Scholar]
- Zhao, Q.; Lee, F. High-efficiency, high step-up dc-dc converter. IEEE Trans. Power Electron. 2003, 18, 65–73. [Google Scholar] [CrossRef] [Green Version]
- Wai, R.; Lin, C.; Chu, C. High step-up dc-dc converter for fuel cell generation system. In Proceedings of the 30th Annual Conference of IEEE Industrial Electronics Society, Busan, Korea, 2–6 November 2004; pp. 57–62. [Google Scholar]
- Wu, T.-F.; Lai, Y.-S.; Hung, J.-C.; Chen, Y.-M. Boost convener with coupled inductors and buck-boost type of active clamp. IEEE Trans. Ind. Electron. 2008, 55, 154–162. [Google Scholar] [CrossRef]
- Zhengguo, P.; Yongjie, H.; Yuqi, G. High-Frequency Isolated Grid-Connected Inverter Based on Parallel Resonance. Trans. Chin. Electrotech. Soc. 2018, 33, 322–330. [Google Scholar]
- Covic, G.A.; Boys, J.T.; Kissin, M.L.G.; Lu, H.G. A three-phase inductive power transfer system for roadway-powered vehicles. IEEE Trans. Ind. Electron. 2007, 54, 3370–3378. [Google Scholar] [CrossRef]
- Matsumoto, H.; Neba, Y.; Ishizaka, K.; Itoh, R. Model for a three-phase contactless power transfer system. IEEE Trans. Power Electron. 2011, 26, 2676–2687. [Google Scholar] [CrossRef]
- Dongyuan, Q.; Bo, Z. Composition Principles and Development Trends of Switched Capacitor Converters. Electr. Appl. 2007, 26, 6–12. [Google Scholar]
- Singer, Z.; Emanuel, A.; Erlicki, M.S. Power regulation by means of a switched capacitor. Proc. Inst. Electr. Eng. 1972, 119, 149–153. [Google Scholar] [CrossRef]
- Midgley, D.; Sigger, M. Switched capacitors in power control. Proc. Inst. Electr. Eng. 1974, 121, 703–704. [Google Scholar] [CrossRef]
- Xun, Z.; Ding, H.; He, Z. A Novel Switched-Capacitor Inverter with Reduced Capacitance and Balanced Neutral-Point Voltage. Electronics 2021, 10, 947. [Google Scholar] [CrossRef]
- Umeno, T.; Takahashi, K.; Ueno, F.; Inoue, T. A new approach to low ripple-noise switching converters on the basis of switched-capacitor converters. In Proceedings of the IEEE International Sympoisum on Circuits and Systems, Singapore, 11–14 June 1991; pp. 1077–1080. [Google Scholar]
- Ueno, F.; Inoue, T.; Oota, I.; Harada, I. Power supply for electroluminescence aiming integrated circuit. In Proceedings of the IEEE International Symposium on Circuits & Systems, San Diego, CA, USA, 10–13 May 1992; pp. 1903–1906. [Google Scholar]
- Yang, L.S.; Liang, T.J.; Lee, H.C.; Chen, J.F. Novel high step-up DC-DC converter with coupled-in-ductor and voltage-doubler circuits. In Proceedings of the IEEE Trans on Industrial Electronics, Tainan, Taiwan, 3–6 November 2013; Volume 58, pp. 4196–4206. [Google Scholar]
- Hsieh, Y.P.; Chen, J.F.; Liang, T.J.; Yang, L.S. Novel high step-up DC-DC converter with coupled-inductor and switched capacitor techniques. IEEE Trans Ind. Electron. 2012, 59, 998–1007. [Google Scholar] [CrossRef]
- Fuzhuan, W.; Yongping, D.; Haiquan, W.; Sheng, P.; Geng, W.; Qiangsong, Z.; Tao, H.; Hongli, L. Principle of TMS320F28335 and Its Application in Electrical Engineering; Electronic Industry Press: BeiJing, China, 2020. [Google Scholar]

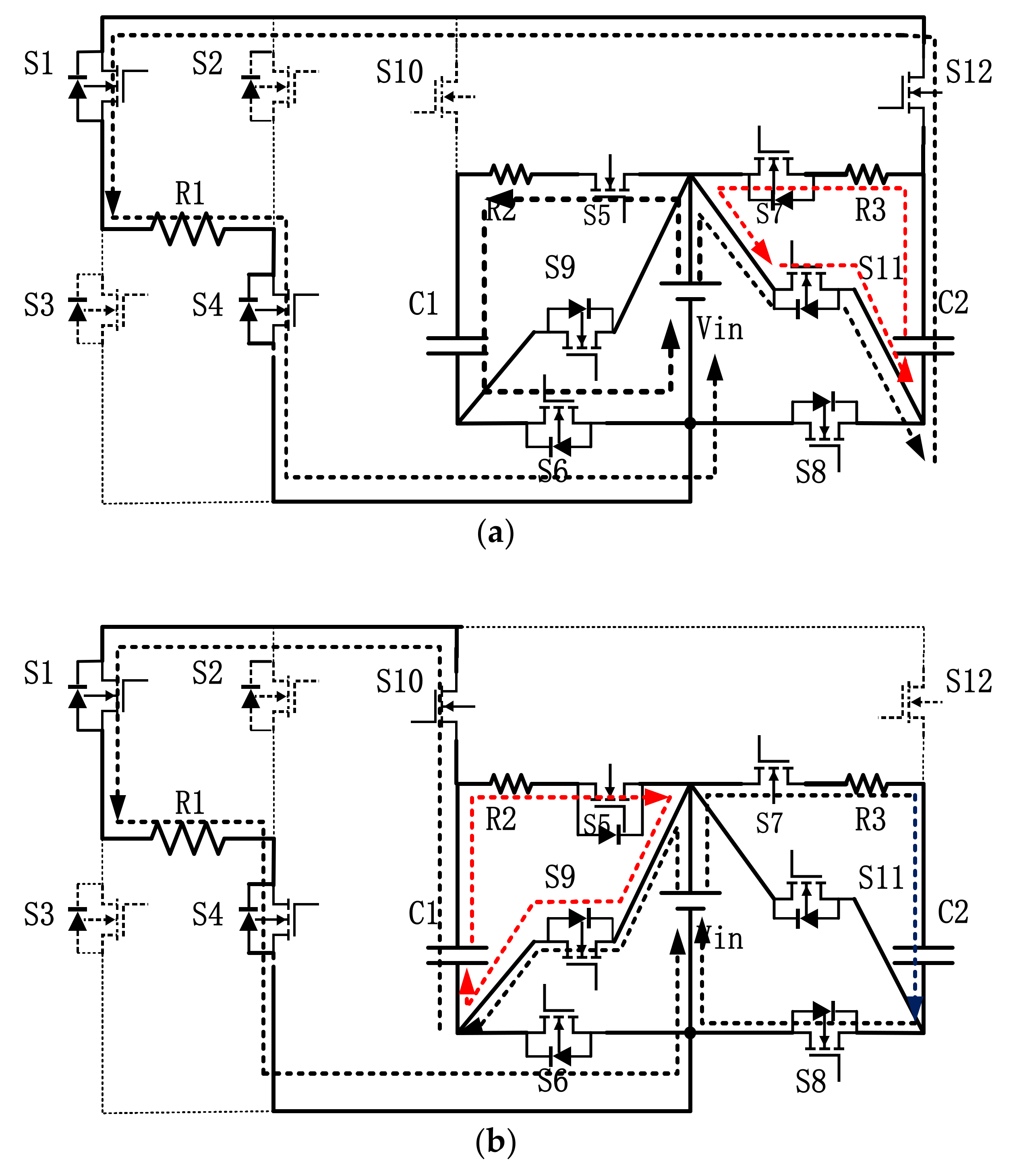
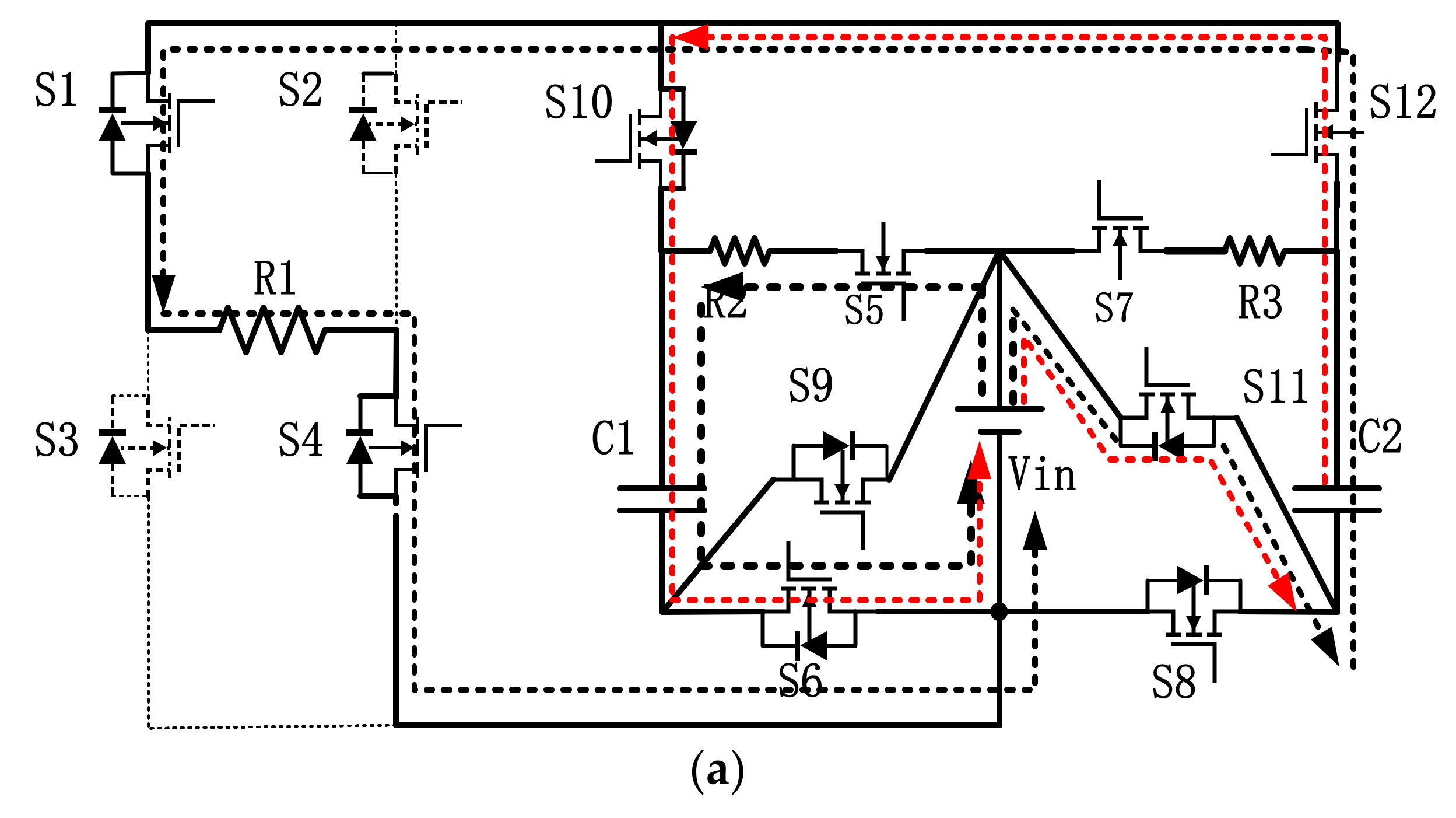


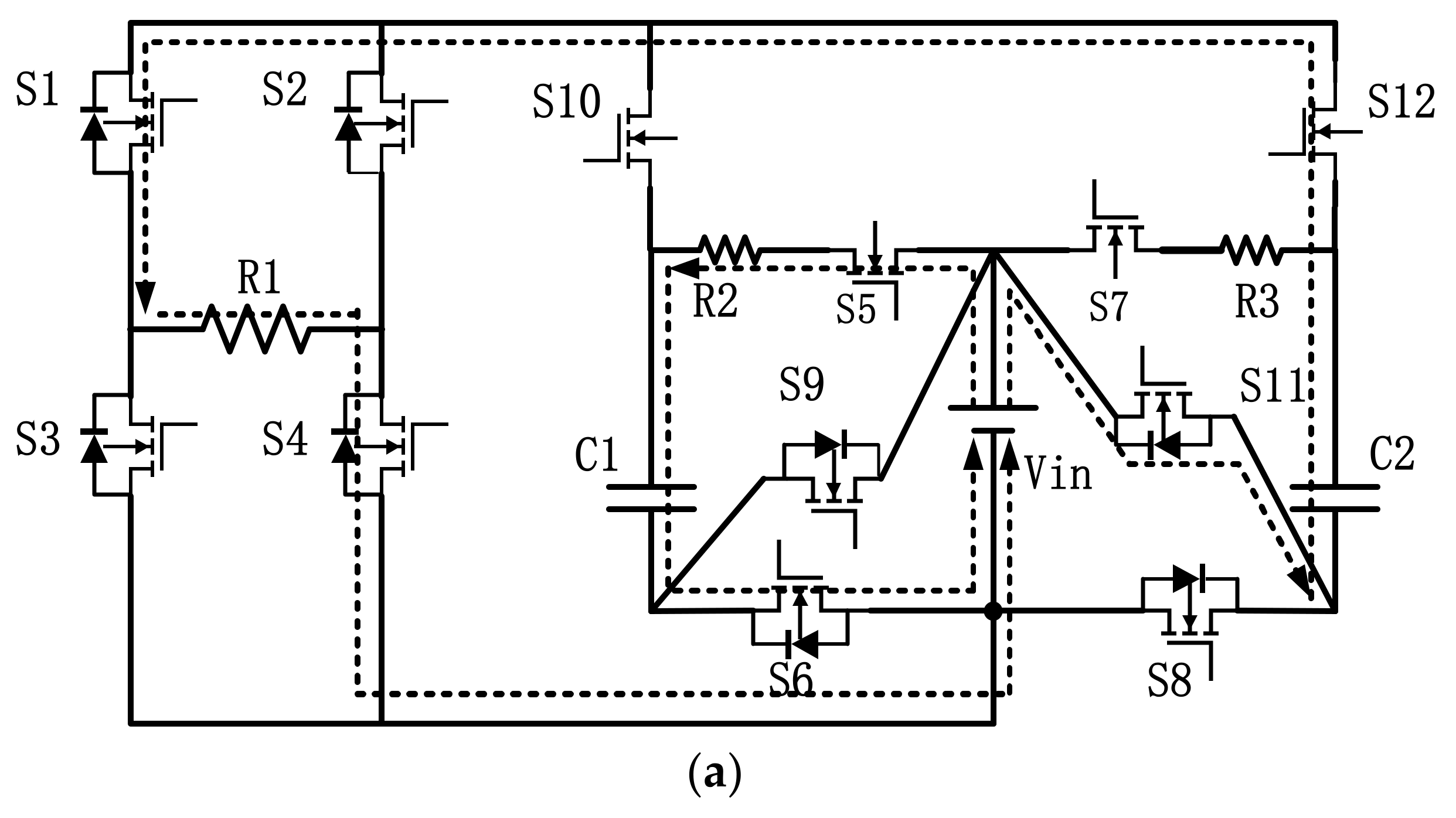

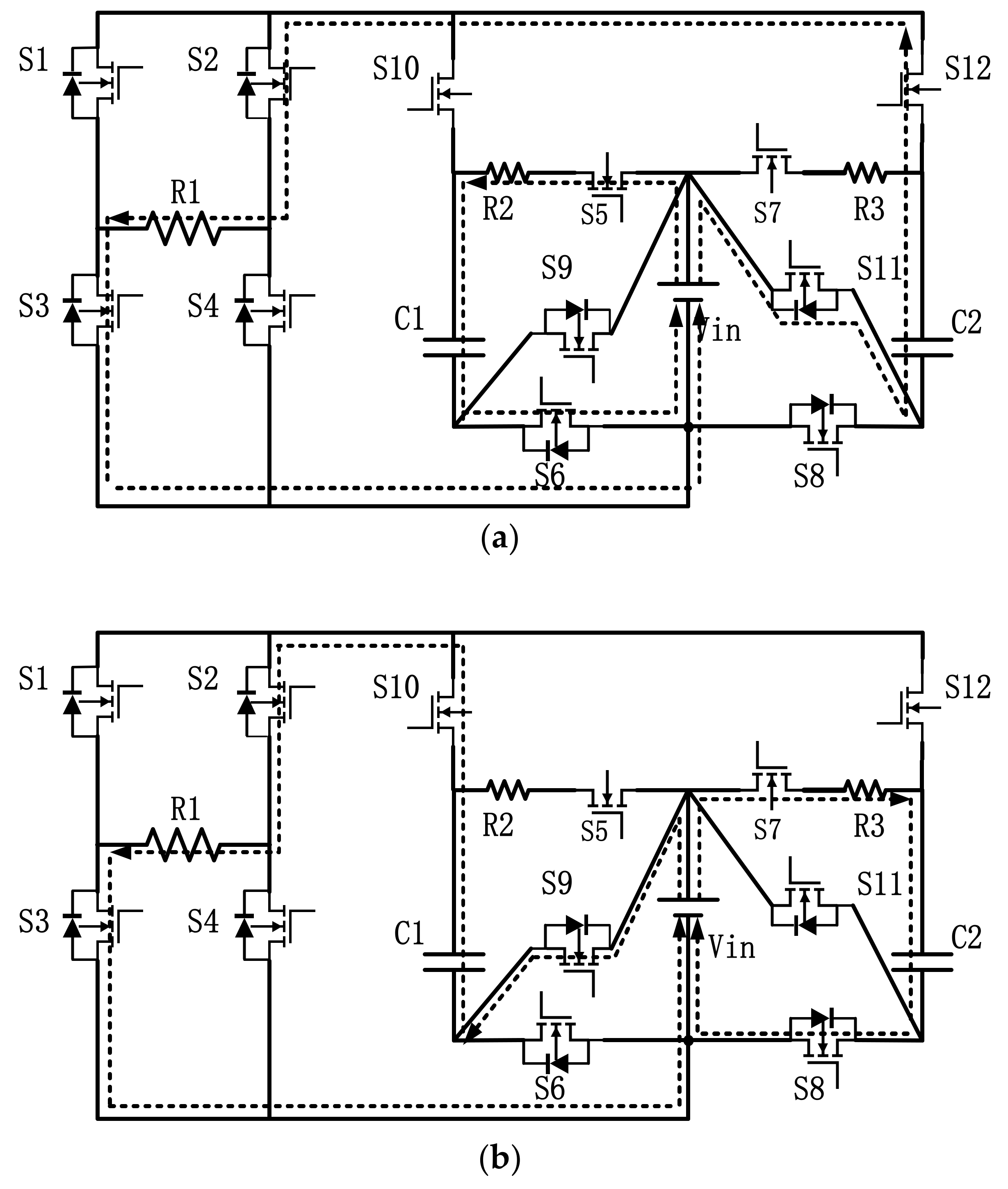
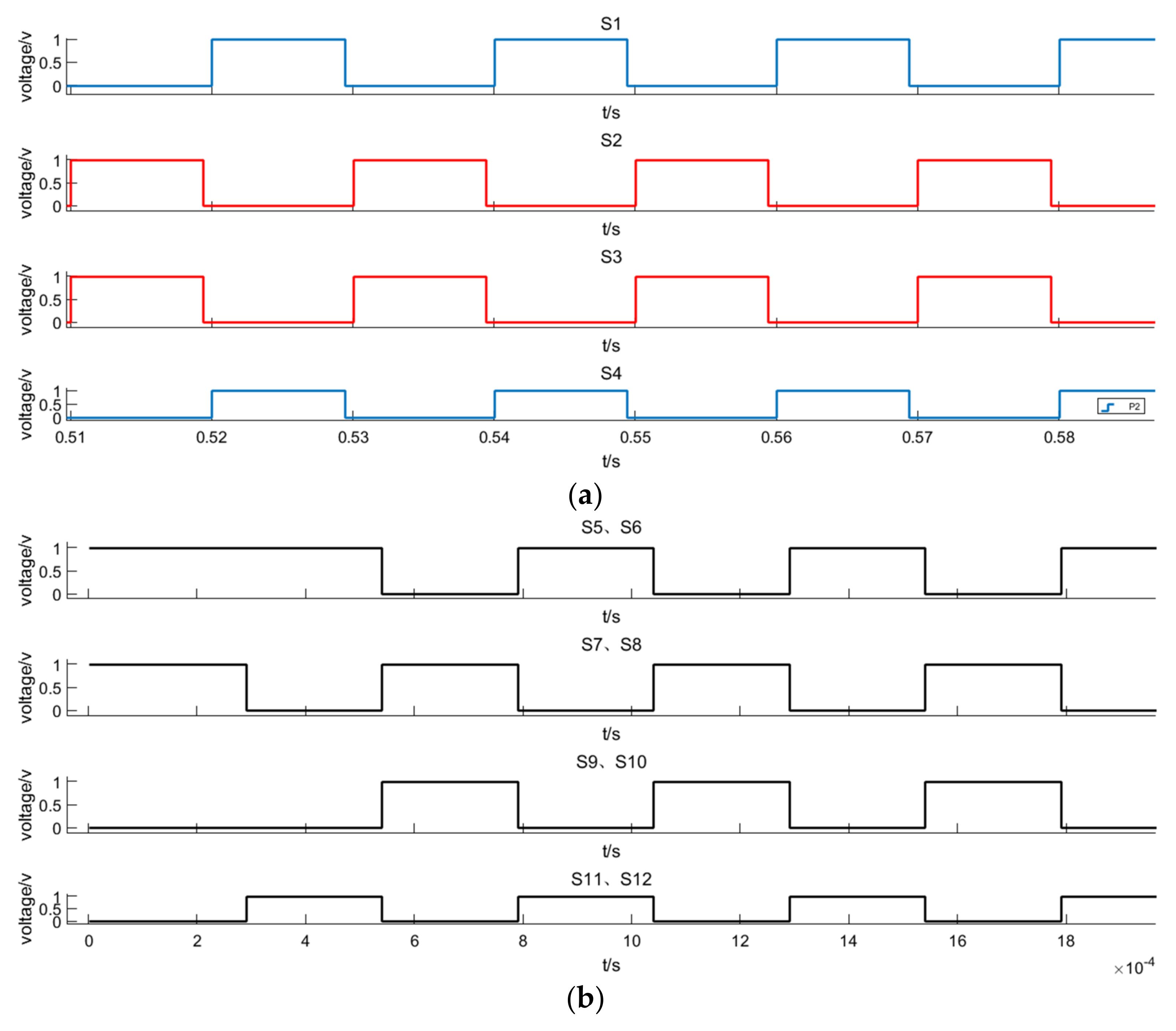





| Working Status | Modal | S1, S4 | S2, S3 | S5, S6 | S7, S8 | S9, S10 | S11, S12 | C1 | C2 |
|---|---|---|---|---|---|---|---|---|---|
| Charging | I | 0 | 0 | 1 | 1 | 0 | 0 | C | C |
| 1. 4-bridge arm work | II | 1 | 0 | 1 | 0 | 0 | 1 | C | F |
| III | 1 | 0 | 0 | 1 | 1 | 0 | F | C | |
| 2. 3-bridge arm work | IV | 0 | 1 | 1 | 0 | 0 | 1 | C | F |
| V | 0 | 1 | 0 | 1 | 1 | 0 | F | C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiang, H.; Wu, Z.; Xu, T.; Kong, P.; Mao, S.; Zheng, J. Boost Voltage Single Phase Full Bridge Inverter with No Voltage Drop Based on Switched Capacitor. Energies 2021, 14, 3466. https://doi.org/10.3390/en14123466
Qiang H, Wu Z, Xu T, Kong P, Mao S, Zheng J. Boost Voltage Single Phase Full Bridge Inverter with No Voltage Drop Based on Switched Capacitor. Energies. 2021; 14(12):3466. https://doi.org/10.3390/en14123466
Chicago/Turabian StyleQiang, Hao, Zhenyu Wu, Tian Xu, Pengcheng Kong, Shuren Mao, and Jianfeng Zheng. 2021. "Boost Voltage Single Phase Full Bridge Inverter with No Voltage Drop Based on Switched Capacitor" Energies 14, no. 12: 3466. https://doi.org/10.3390/en14123466
APA StyleQiang, H., Wu, Z., Xu, T., Kong, P., Mao, S., & Zheng, J. (2021). Boost Voltage Single Phase Full Bridge Inverter with No Voltage Drop Based on Switched Capacitor. Energies, 14(12), 3466. https://doi.org/10.3390/en14123466








