Modeling Sea Ice Effects for Wave Energy Resource Assessments
Abstract
:1. Introduction
2. Materials and Methods
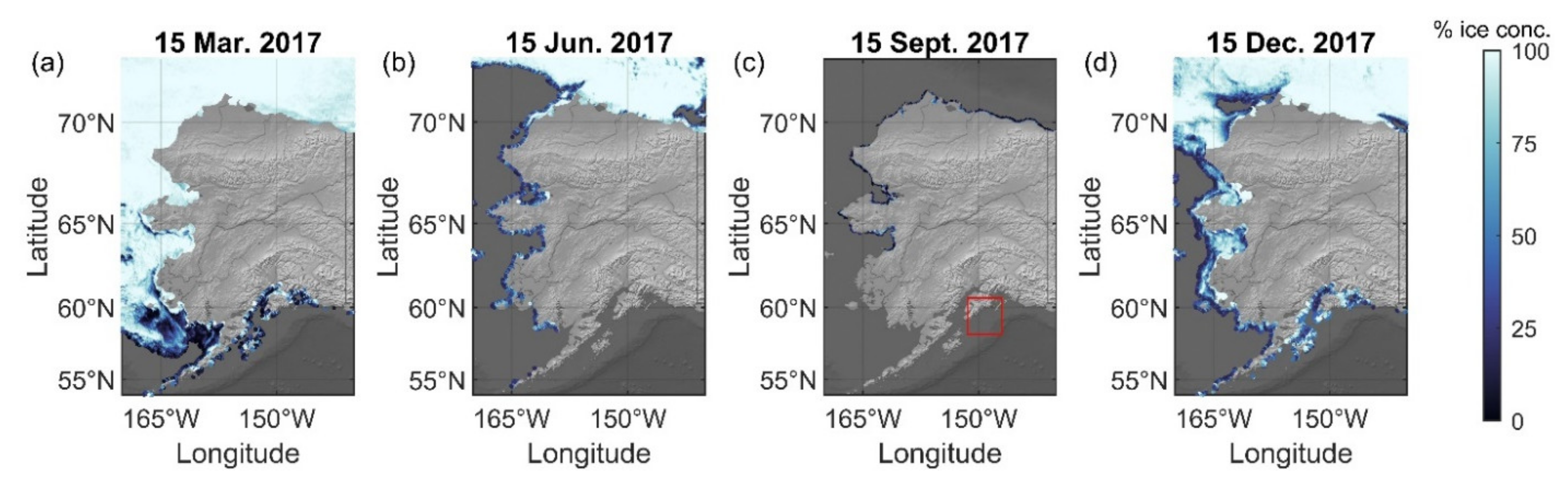
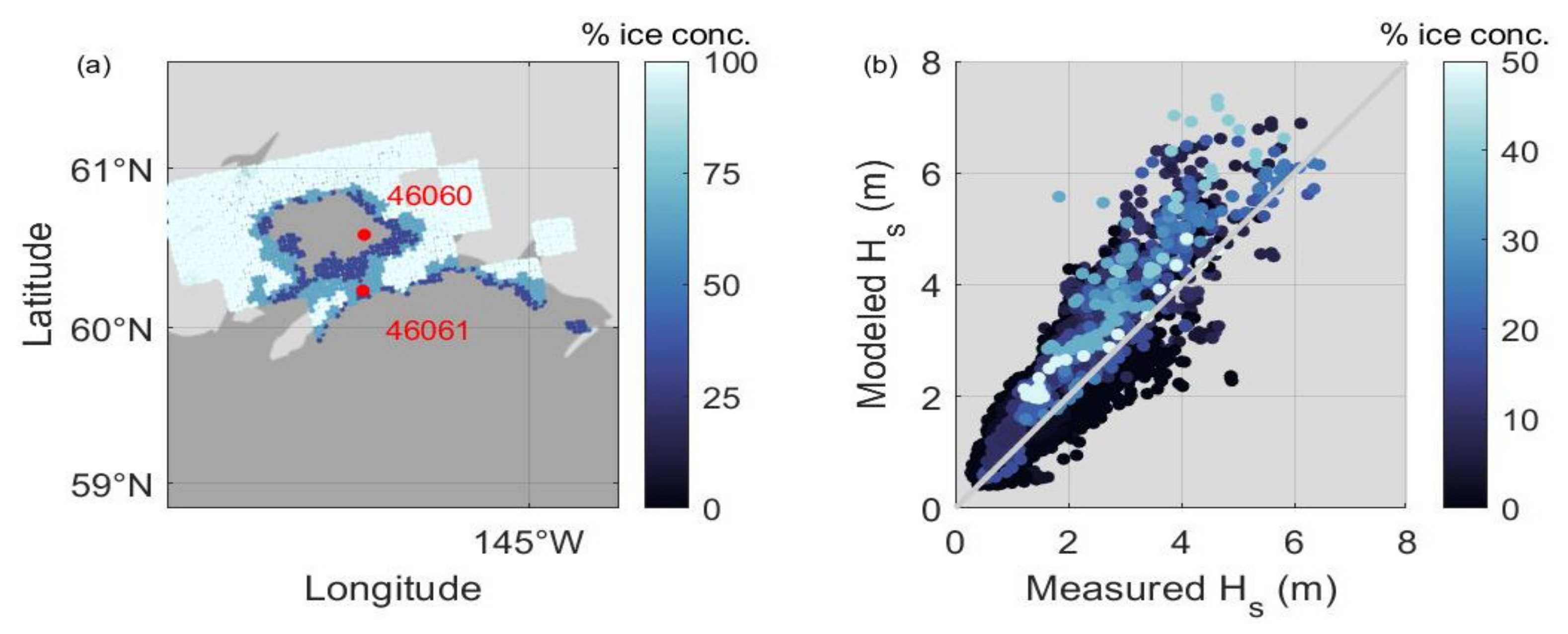
2.1. Study Area
2.2. Wave Model
2.3. Boundary Conditions and Sea Ice Input
3. Results
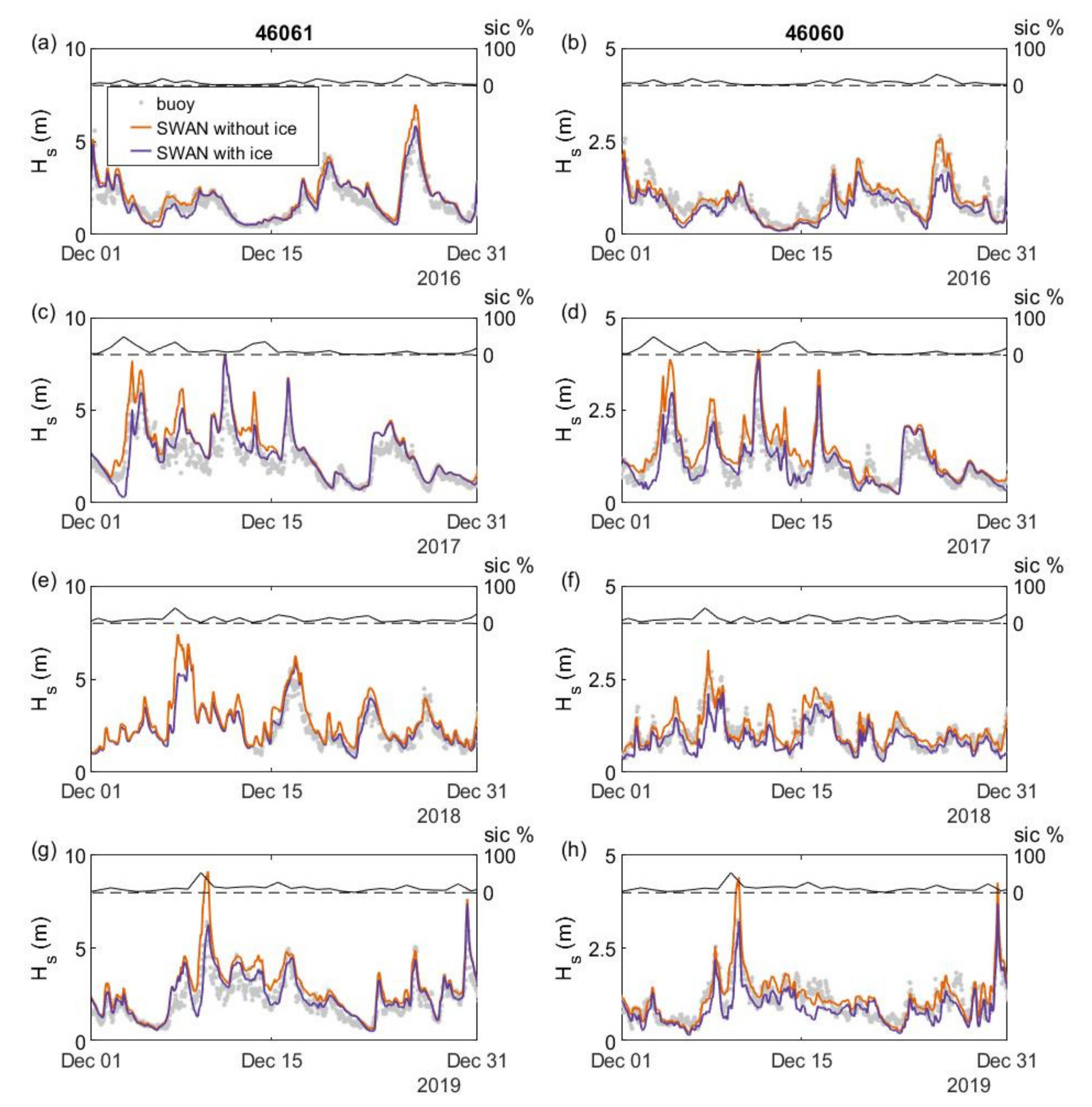
3.1. Model Validation
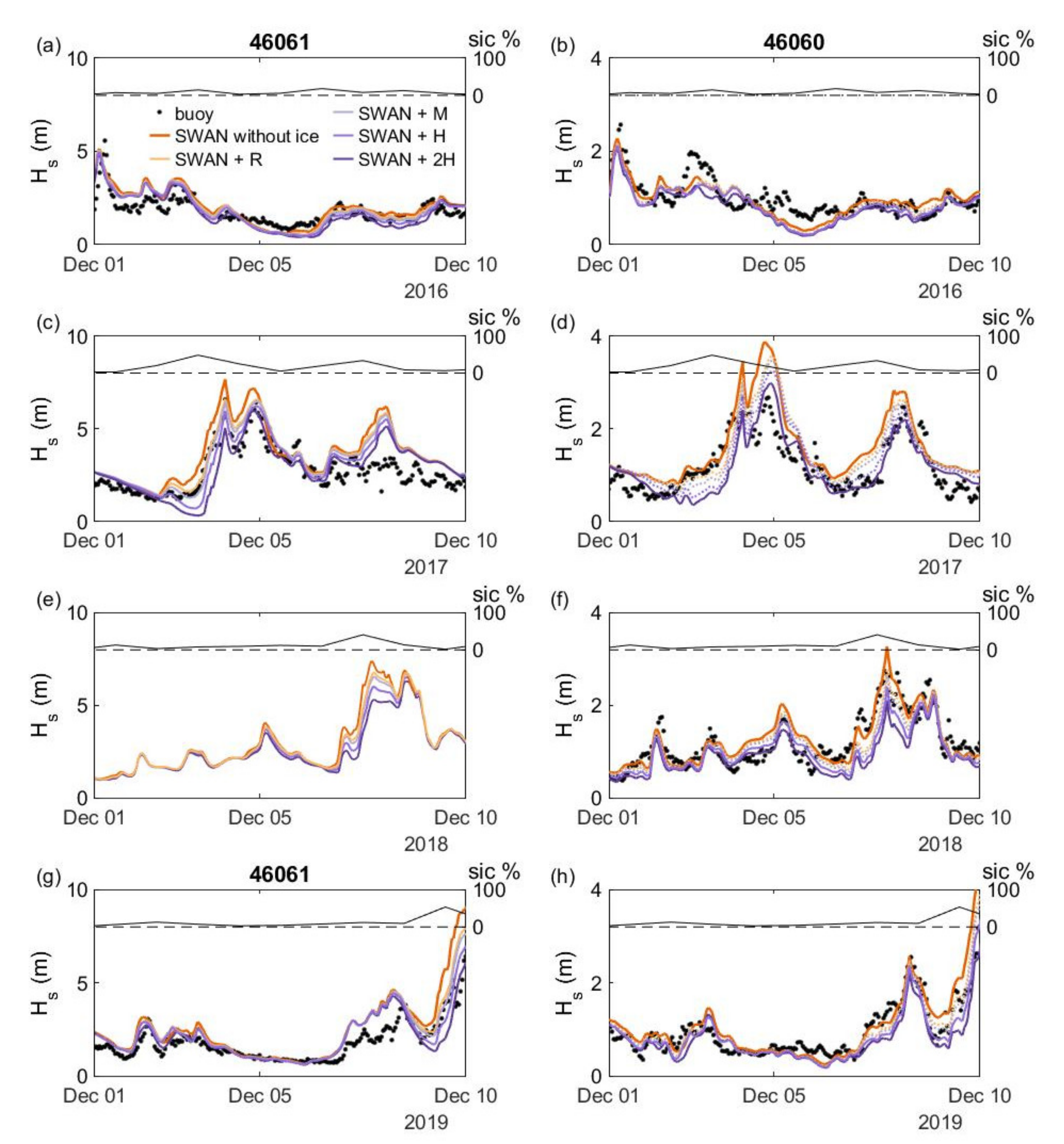
3.2. Parameterization of Sea Ice/Wave Interaction in SWAN
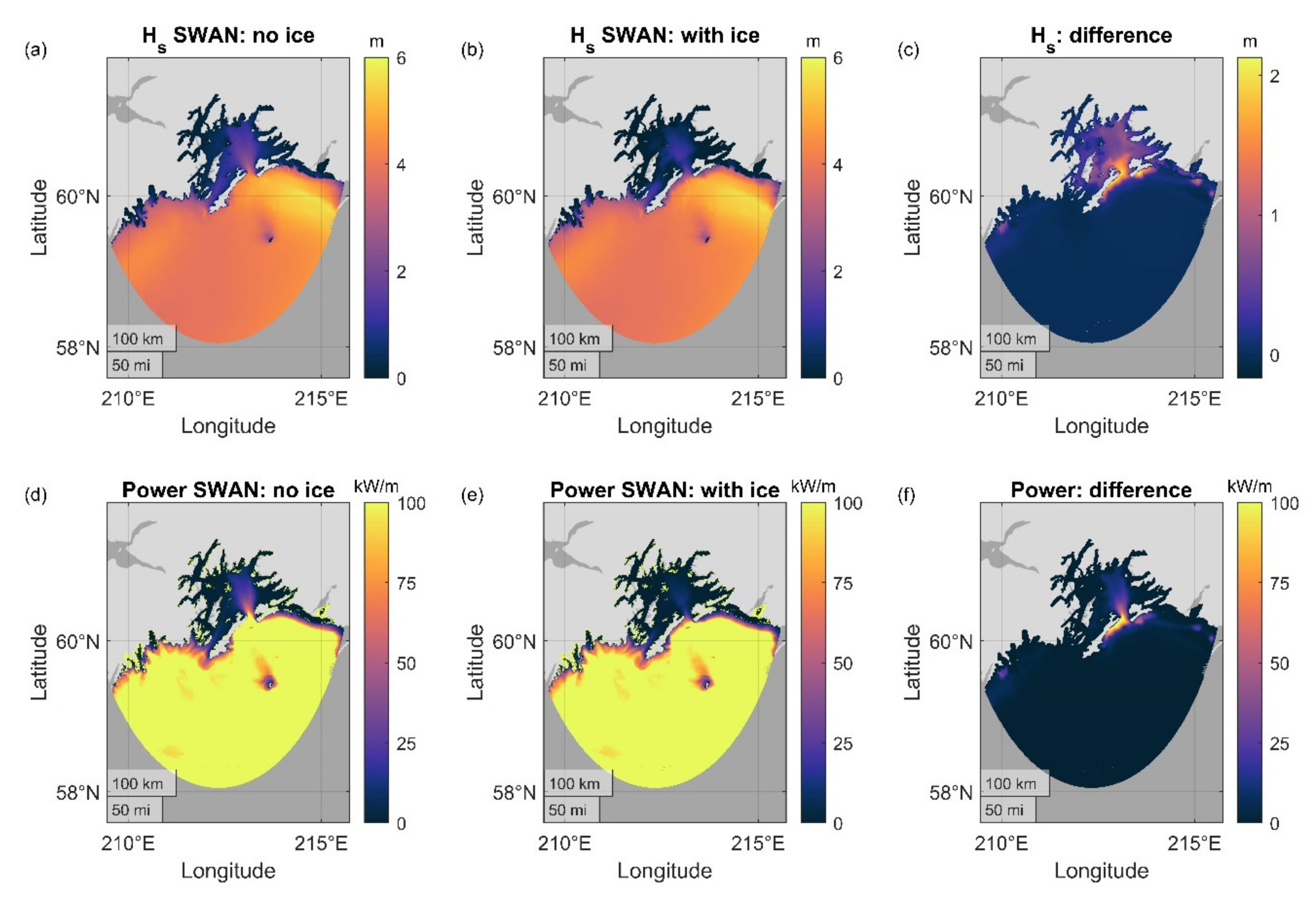
3.3. Effect of Sea Ice on the Wave Resource
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Error Statistics
References
- Chang, G.; Jones, C.A.; Roberts, J.D.; Neary, V.S. A comprehensive evaluation of factors affecting the levelized cost of wave energy conversion projects. Renew. Energy 2018, 127, 344–354. [Google Scholar] [CrossRef]
- Fairley, I.; Lewis, M.; Robertson, R.; Hemer, M.; Masters, I.; Horrillo-Caraballo, J.; Karunarathna, H.; Reeve, D.E. A classification system for global wave energy resources based on multivariate clustering. Appl. Energy 2020, 262, 114515. [Google Scholar] [CrossRef]
- Garcia-Medina, G.; Yang, Z.; Wu, W.; Wang, T. Wave resource characterization at regional and nearshore scales for the U.S. Alaska coast based on a 32-year high-resolution hindcast. Renew. Energy 2021, 170, 595–612. [Google Scholar] [CrossRef]
- Wadhams, P.; Squire, V.A.; Goodman, D.J.; Cowan, A.M.; Moore, S.C. The attenuation rates of ocean waves in the marginal ice zone. J. Geophys. Res. Ocean. 2018, 93, 6799–6818. [Google Scholar] [CrossRef]
- Doble, M.J.; Bidlot, J.-R. Wave buoy measurements at the Antarctic sea ice edge compared with an enhanced ECMWF WAM: Progress towards global waves-in-ice-modeling. Ocean. Model. 2013, 70, 166–173. [Google Scholar] [CrossRef]
- Meylan, M.H.; Bennetts, L.G.; Kohout, A.L. In situ measurements and analysis of ocean waves in the Antarctic marginal ice zone. Geophys. Res. Lett. 2014, 41, 5046–5051. [Google Scholar] [CrossRef]
- Doble, M.J.; De Carolis, G.; Meylan, M.H.; Bidlot, J.-R.; Wadhams, P. Relating wave attenuation to pancake ice thickness, using field measurements and model results. Geophys. Res. Lett. 2015, 42, 4473–4481. [Google Scholar] [CrossRef] [Green Version]
- Thomson, J.; Rogers, W.E. Swell and sea in the emerging Arctic ocean. Geophys. Res. Lett. 2014, 41, 3136–3140. [Google Scholar] [CrossRef]
- Gemmrich, J.; Rogers, W.E.; Thomson, T.; Lehner, S. Wave evolution in off-ice wind conditions. J. Geophys. Res. Ocean. 2018, 123, 5543–5556. [Google Scholar] [CrossRef]
- Thomson, J.; Ackley, S.; Girard-Ardhuin, F.; Ardhuin, F.; Babanin, A.; Boutin, G.; Brozena, J.; Cheng, S.; Collins, C.; Doble, M.; et al. Overview of the Arctic sea state and boundary layer physics program. J. Geophys. Res. Ocean. 2018, 23, 8674–8687. [Google Scholar] [CrossRef]
- Hosekova, L.; Malila, M.P.; Rogers, W.E.; Roach, L.A.; Eidam, E.; Rainville, L.; Kumar, N.; Thomson, J. Attenuation of ocean surface waves in pancake and pancake sea ice along the coast of the Chukchi Sea. J. Geophys. Res. 2020, 125, 1–15. [Google Scholar] [CrossRef]
- Zhang, N.; Li, S.; Wu, Y.; Wang, K.-H.; Zhang, Q.; You, Z.-J.; Wang, J. Effects of sea ice on wave energy flux distributions in the Bohai Sea. Renew. Energy 2020, 162, 2330–2343. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Beardsley, R.C.; Perrie, W.; Gao, G.; Zhang, Y.; Qi, J.; Lin, H. Applications of an unstructured grid surface wave model (FVCOM-SWAVE) to the Arctic Ocean: The interaction between ocean waves and sea ice. Ocean. Model. 2020, 145, 101532. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, W.-C.; Wang, T.; Garcia-Medina, G.; Castrucci, L. High-Resolution Regional Wave Hindcast for the U.S. Alaska Coast. PNNL Rep. 2019. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F.; Chen, Y.-L. Assessment of wave energy resources in Hawaii. Renew. Energy 2011, 36, 554–567. [Google Scholar] [CrossRef]
- Li, N.; Cheung, K.F.; Stopa, J.E.; Hsiao, F.; Chen, Y.-L.; Vega, L.; Cross, P. Thirty-four years of Hawaii wave hindcast from downscaling of climate forecast system reanalysis. Ocean. Model. 2016, 100, 78–95. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.-C.; Yang, Z.; Wang, T. Wave resource characterization using an unstructured grid modeling approach. Energies 2018, 11, 605. [Google Scholar]
- Wu, W.-C.; Wang, T.; Yang, Z.; Garcia-Medina, G. Development and validation of a high-resolution regional wave hindcast model for US West Coast wave resource characterization. Renew. Energy 2020, 152, 736–753. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions 2. Model description and validation. J. Geophys. Res. 1999, 104, 7646–7666. [Google Scholar] [CrossRef] [Green Version]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions 2. Verification. J. Geophys. Res. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Rogers, W.E. Implementation of Sea Ice in the Wave Model SWAN; Technical Report; Naval Research Lab.: Washington, DC, USA, 2019. [Google Scholar]
- Rogers, W.E.; Thomson, J.; Shen, H.H.; Doble, M.J.; Wadhams, P.; Cheng, S. Dissipation of wind waves by pancake and frazil ice in the autumn Beaufort Sea. J. Geophys. Res. 2016, 121, 7991–8007. [Google Scholar] [CrossRef] [Green Version]
- Canals Silander, M.F.; Garcio Moreno, C.G. On the spatial distribution of the wave energy resource in Puerto Rico and the United States Virgin Islands. Renew. Energy 2019, 136, 442–451. [Google Scholar] [CrossRef]
- Li, N.; Garcia-Medina, G.; Cheung, K.F.; Yang, Z. Wave energy resources assessment for the multi-modal sea state of Hawaii. Renew. Energy 2021, 174, 1036–1055. [Google Scholar] [CrossRef]
- Ahn, S.; Neary, V.S.; Allahdadi, M.N.; He, R. Nearshore Wave Energy Resource Characterization along the East Coast of the United States. Renew. Energy 2021, 172, 1212–1224. [Google Scholar] [CrossRef]
- Yang, Z.; Garcia-Medina, G.; Wu, W.-C.; Wang, T. Characteristics and variability of the nearshore wave resource on the US West Coast. Energy 2020, 203, 117818. [Google Scholar] [CrossRef]
- Zijlema, M. Computation of wind-wave spectra in coastal waters with SWAN on unstructured grids. Coast. Eng. 2010, 57, 267–277. [Google Scholar] [CrossRef]
- Lim, E.; Eakins, B.W.; Wigley, R. Coastal Relief Model of Southern Alaska: Procedures Data Sources and Analysis; NOAA Technical Memorandum NESDIS NGDC-43; National Geophysical Data Center: Boulder, CO, USA, 2011. [Google Scholar]
- Zimmermann, M.; Prescott, M.M. Smooth Sheet Bathymetry of the Aleutian Islands; NOAA Technical Memorandum NMFS-AFSC-250; National Geophysical Data Center: Boulder, CO, USA, 2013. [Google Scholar]
- Zimmermann, M.; Prescott, M.M. Smooth Sheet Bathymetry of Cook Inlet Alaska; NOAA Technical Memorandum NMFS-AFSC-275; National Geophysical Data Center: Boulder, CO, USA, 2014. [Google Scholar]
- Zimmermann, M.; Prescott, M.M. Smooth Sheet Bathymetry of the Central Gulf of Alaska; NOAA Technical Memorandum NMFS-AFSC-287; National Geophysical Data Center: Boulder, CO, USA, 2015. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Krusemann, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); Deutches Hydrographisches Institut: Hamburg, Germany, 1973; pp. 1–95. [Google Scholar]
- Battjes, J.A.; Janssen, J.P.F.M. Energy loss and set-up due to breaking of random waves. In Proceedings of the 16th International Conference on Coastal Engineering, ASCE, Hamburg, Germany, 27 August–3 September 1978; pp. 569–587. [Google Scholar]
- Eldeberky, Y.; Battjes, J.A. Spectral modeling of wave breaking: Application to Boussinesq equations. J. Geophys. Res. 1996, 101, 1253–1264. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M.; et al. The NCEP climate forecast system Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Chawla, A.; Spindler, D.M.; Tolman, H.L. Validation of a thirty year wave hindcast using the Climate Forecast System Reanalysis winds. Ocean. Model. 2013, 70, 189–206. [Google Scholar] [CrossRef]
- Kaleschke, L.; Lupkes, C.; Vihma, T.; Haarpainter, J.; Bochert, A.; Hartmann, J.; Heygster, G. SSM/I sea ice remote sensing for mesoscale ocean-atmosphere interaction analysis. Can. J. Remote Sens. 2001, 27, 526–537. [Google Scholar] [CrossRef]
- Beitsch, A.; Kaleschke, L.; Kern, S. Investigating high-resolution AMSR2 sea ice concentrations during the February 2013 fracture event in the Beaufort Sea. Remote Sens. 2014, 6, 3841–3856. [Google Scholar] [CrossRef] [Green Version]






| Coefficient | Rogers et al., 2018 | Meylan et al., 2014 | Hosekova et al., 2020 | 2H 1 |
|---|---|---|---|---|
| C2 (s2 m−1) | 0.284 × 10−3 | 1.06 × 10−3 | 3.8 × 10−3 | 7.6 × 10−3 |
| C4 (s4 m−1) | 1.53 × 10−2 | 2.3 × 10−2 | 1.8 × 10−2 | 3.6 × 10−2 |
| Model | RMSE (m) | Bias (m) | R | PE (%) | SI | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | |
| SWAN no ice | 0.64 | 0.28 | 0.44 | 0.12 | 0.94 | 0.87 | 31.52 | 22.83 | 0.33 | 0.33 |
| SWAN + ice | 0.57 | 0.28 | 0.35 | 0.02 | 0.92 | 0.81 | 26.94 | 10.56 | 0.31 | 0.37 |
| Model | RMSE (m) | Bias (m) | R | PE (%) | SI | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | |
| SWAN no ice | 1.00 | 0.47 | 0.73 | 0.31 | 0.92 | 0.90 | 30.73 | 31.46 | 0.44 | 0.44 |
| SWAN + R | 0.90 | 0.45 | 0.65 | 0.25 | 0.93 | 0.87 | 27.83 | 26.77 | 0.39 | 0.42 |
| SWAN + M | 0.87 | 0.42 | 0.60 | 0.21 | 0.92 | 0.86 | 22.64 | 22.64 | 0.38 | 0.39 |
| SWAN + H | 0.82 | 0.39 | 0.50 | 0.12 | 0.90 | 0.84 | 21.86 | 14.14 | 0.36 | 0.37 |
| SWAN + 2H | 0.81 | 0.37 | 0.35 | 0.00 | 0.86 | 0.82 | 15.96 | 2.50 | 0.35 | 0.34 |
| Model | RMSE (m) | Bias (m) | R | PE (%) | SI | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | 46061 | 46060 | |
| SWAN no ice | 0.82 | 0.36 | 0.56 | 0.13 | 0.93 | 0.86 | 28.83 | 14.32 | 0.39 | 0.35 |
| SWAN + R | 0.73 | 0.33 | 0.48 | 0.07 | 0.93 | 0.84 | 22.26 | 7.93 | 0.34 | 0.33 |
| SWAN + M | 0.69 | 0.33 | 0.43 | 0.03 | 0.92 | 0.83 | 20.35 | 4.48 | 0.33 | 0.32 |
| SWAN + H | 0.64 | 0.33 | 0.35 | −0.04 | 0.91 | 0.91 | 16.61 | −1.98 | 0.31 | 0.32 |
| SWAN + 2H | 0.62 | 0.35 | 0.23 | −0.13 | 0.89 | 0.89 | 11.42 | −10.54 | 0.29 | 0.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Branch, R.; García-Medina, G.; Yang, Z.; Wang, T.; Ticona Rollano, F.; Hosekova, L. Modeling Sea Ice Effects for Wave Energy Resource Assessments. Energies 2021, 14, 3482. https://doi.org/10.3390/en14123482
Branch R, García-Medina G, Yang Z, Wang T, Ticona Rollano F, Hosekova L. Modeling Sea Ice Effects for Wave Energy Resource Assessments. Energies. 2021; 14(12):3482. https://doi.org/10.3390/en14123482
Chicago/Turabian StyleBranch, Ruth, Gabriel García-Medina, Zhaoqing Yang, Taiping Wang, Fadia Ticona Rollano, and Lucia Hosekova. 2021. "Modeling Sea Ice Effects for Wave Energy Resource Assessments" Energies 14, no. 12: 3482. https://doi.org/10.3390/en14123482
APA StyleBranch, R., García-Medina, G., Yang, Z., Wang, T., Ticona Rollano, F., & Hosekova, L. (2021). Modeling Sea Ice Effects for Wave Energy Resource Assessments. Energies, 14(12), 3482. https://doi.org/10.3390/en14123482








